Geographische Koordinaten auf der Kugel

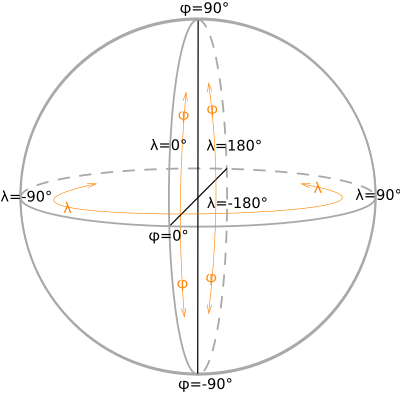
Geographische Koordinaten beziehen sich auf eine Referenzkugel. Ihre größte Bedeutung hatten sie in früheren Zeiten in der Seefahrt, also einer Anwendung mit niedrigen Anforderungen an die Genauigkeit. Da sich die tatsächliche Gestalt der Erde besser durch ein Rotationsellipsoid beschreiben lässt, sind geographische Koordinaten heute kaum noch von Bedeutung.

Orientierung der Winkel

Das Gradnetz der Erde ist ein gedachtes Koordinatensystem auf einer die Erdoberfläche approximierende Kugel mit sich rechtwinklig schneidenden Kreisen. Die Breitengrade werden dabei vom Äquator aus gezählt, die Pole liegen bei 90° für den Nordpol bzw. -90° für den Südpol, alternativ werden die Vorzeichen weggelassen und stattdesen "90° Nord" bzw. "90° Süd" angegeben. Die Längengrade werden von einem willkürlichen Nullmeridian nach Osten positiv und nach Westen negativ gezählt bis 180°. Auch hier können statt der Vorzeichen die Winkelbeträge zusammen mit den Himmelsrichtungen genannt werden.

Wo der Nullmeridian liegt und wie er wieder aufgefunden werden kann, geht über die Festlegung eines Koordinatensystems hinaus. Diese Angaben sind Teil der Festlegung eines Bezugsystems.

Geographische Koordinaten

Jedem Punkt auf der Oberfläche bzw. dessen Projektion entlang geradlinig gedachter Lotlinien lässt sich ein Koordinatenpaar $\lambda$ und $\phi$ zuordnen.

Der Begriff geographische Koordinaten (Referenzkörper: Kugel) ist zu unterscheiden von geodätische Koordinaten (Referenzkörper: Rotationsellipsoid). Das gilt auch für die Symbole $\lambda$ und $\phi$ für geographische Koordinaten bzw. B, L für geodätische Koordinaten.

Meridiankonvergenz

Die Meridiankonvergenz $\chi$ ist Winkel zwischen der Nordrichtung in einem beliebigen Oberflächenpunkt C und der Nordrichtung in einem beliebigen Oberflächenpunkt D. Siehe dazu auch die in der Zeichnung eingetragenen Tangenten. Ursächlich für den Winkelunterschied ist die Krümmung der Oberfläche, weswegen die in Nord-Süd Richtung verlaufenden Gitterlinien (Meridiane) an den Polen zusammenlaufen, also konvergieren.

$\chi$ lässt sich folgendermaßen berechnen:

$\chi =\Delta \lambda -\epsilon '$

$\chi =\epsilon _{0}+\epsilon$

Das in der Zeichnung eingetragene $\epsilon$ ist der sphärische Exzess der jeweiligen Dreiecke bzw. des Vierecks.