Ing Mathematik: Approximation und Interpolation

|

Vor zu Numerische Berechnung bestimmter Integrale

Interpolation

Gegeben seien z.B. Messwerte (Stützpunkte). Diese sollen durch eine Funktion (Interpolante, Interpolierende, inter = zwischen, polire = glätten, schleifen) abgebildet werden.

Zu diesem Zweck gibt es eine Reihe von Methoden. Einige davon sollen nun besprochen werden.

Siehe auch Interpolation (Mathematik), Knorrenschild: Seite78ff, Burg, Haf, Wille, Meister: 393ff

Interpolation durch Polynome

Existenz und Eindeutigkeit: Seinen $n+1$ paarweise verschiedene Stützpunkte gegeben. Dann gibt es genau ein Polynom vom Grad maximal $n$ , das die Gleichungen erfüllt. Dieses Polynom existiert und ist eindeutig bestimmt.

n=1: linare Interpolation
n=2: quadratische Interpolation
n=3: kubische Interpolation
etc.

$\sum _{i=0}^{n}a_{i}x_{k}^{i}=f_{k};\quad k=0,\dots ,n$

$a_{i}$ seien die unbekannten Koeffizienten des Interpolationspolynoms, $x_{i}$ die Stützstellen und $f_{k}$ die Stützwerte.

${\begin{pmatrix}1&x_{0}&\cdots &x_{0}^{n}\\\vdots &\vdots &\ddots &\vdots \\1&x_{n}&\cdots &x_{n}^{n}\end{pmatrix}}{\begin{pmatrix}a_{0}\\\vdots \\a_{n}\end{pmatrix}}={\begin{pmatrix}f_{0}\\\vdots \\f_{n}\end{pmatrix}}$

Die Matrix in obiger Formel wird auch Vandermonde-Matrix genannt.

Das Problem mittels linearem Gleichungssystem lösen zu wollen. wäre aber unnötig aufwendig (das Problem ist auch schlecht konditioniert). Es gibt effizientere Verfahren, denen wir uns nun widmen wollen.

Siehe auch Polynominterpolation, Vandermonde-Matrix

Lineare Interpolation zwischen zwei Punkten

Vorerst wollen wir aber noch ein einfaches Beispiel durchexerzieren. Gegeben seien zwei Stützpunkte. Damit ist das Interpolationspolynom vom Grad 1 (linear, eine Gerade).

Die Gleichungssystem mit der Vandermonde-Matrix ist ${\begin{pmatrix}1&x_{0}\\1&x_{1}\end{pmatrix}}{\begin{pmatrix}a_{0}\\a_{1}\end{pmatrix}}={\begin{pmatrix}f_{0}\\f_{1}\end{pmatrix}}$

Dieses lineare Gleichungssystem lässt sich einfach lösen (z.B. mit dem Gauß-Algorithmus, der cramerschen Regel). Es ergibt sich

$a_{0}=f_{0}-x_{0}{\frac {f_{1}-f_{0}}{x_{1}-x_{0}}}$ und $a_{1}={\frac {f_{1}-f_{0}}{x_{1}-x_{0}}}$ .

$p(x)=y=a_{0}+a_{1}x=f_{0}+{\frac {x-x_{0}}{x_{1}-x_{0}}}(f_{1}-f_{0})=y_{0}+{\frac {x-x_{0}}{x_{1}-x_{0}}}(y_{1}-y_{0})$ .

Das Problem lässt sich aber auch einfach geometrisch lösen.

Aus der Ähnlichkeit der Dreiecke ergibt sich:

${\frac {y-y_{0}}{x-x_{0}}}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}$ .

Und damit wieder die mit der Vandermonde-Matrix hergeleitete Formel: $y=y_{0}+{\frac {x-x_{0}}{x_{1}-x_{0}}}(y_{1}-y_{0})$ .

Interpolationsformel von Lagrange

Joseph-Louis de Lagrange (italienisch-französischer Mathematiker, 1736-1813)

$\ell _{i}(x)=\prod _{\begin{smallmatrix}j=0\\j\neq i\end{smallmatrix}}^{n}{\frac {x-x_{j}}{x_{i}-x_{j}}}={\frac {x-x_{0}}{x_{i}-x_{0}}}\cdots {\frac {x-x_{i-1}}{x_{i}-x_{i-1}}}\cdot {\frac {x-x_{i+1}}{x_{i}-x_{i+1}}}\cdots {\frac {x-x_{n}}{x_{i}-x_{n}}}\,,$

mit $\ell _{i}(x_{k})=\prod _{\begin{smallmatrix}j=0\\j\neq i\end{smallmatrix}}^{n}{\frac {x_{k}-x_{j}}{x_{i}-x_{j}}}=\delta _{ik}$ . Dabei ist $\delta _{ik}$ das Kronecker-Delta . Damit entspricht die Matrix $\left(\ell _{i}\left(x_{j}\right)\right)_{i,j=0,1,\dotsc ,n}$ der Einheitsmatrix.

Lösung des Interpolationsproblems:

$P(x)=\sum _{i=0}^{n}f_{i}\ell _{i}\left(x\right)$ .

Beispiel:

Gegeben sind die Stützpunkte gemäß folgendem Bild:

Gesucht ist das Interpolationspolynom.

$\ell _{0}={\frac {x-x_{1}}{x_{0}-x_{1}}}{\frac {x-x_{2}}{x_{0}-x_{2}}}={\frac {x-2}{1-2}}{\frac {x-3}{1-3}}={\frac {x^{2}-5x+6}{2}}$

$\ell _{1}={\frac {x-x_{0}}{x_{1}-x_{0}}}{\frac {x-x_{2}}{x_{1}-x_{2}}}={\frac {x-1}{2-1}}{\frac {x-3}{2-3}}=-x^{2}+4x-3$

$\ell _{2}={\frac {x-x_{0}}{x_{2}-x_{0}}}{\frac {x-x_{1}}{x_{2}-x_{1}}}={\frac {x-1}{3-1}}{\frac {x-2}{3-2}}={\frac {x^{2}-3x+2}{2}}$

$P(x)=f_{0}\ell _{0}+f_{1}\ell _{2}+f_{2}\ell _{2}=1\cdot {\frac {x^{2}-5x+6}{2}}+1\cdot (-x^{2}+4x-3)+2\cdot {\frac {x^{2}-3x+2}{2}}={\frac {x^{2}}{2}}-{\frac {3x}{2}}+2$

Wie zu erwarten, ist das Interpolationspolynom vom Grad 2 (quadratisch), da drei Stützpunkte vorgegeben sind.

Auch dieses Verfahren ist für den praktischen Einsatz zu aufwändig.

Baryzentrische Interpolationsformel

$P(x)={\frac {\sum _{j=1}^{n}{\frac {\lambda _{j}f_{j}}{x-x_{j}}}}{\sum _{j=1}^{n}{\frac {\lambda _{j}}{x-x_{j}}}}}\,$ für $x\neq x_{1},\ldots ,x_{n}$ ,

Baryzentrische Gewichte: $\lambda _{j}:=\prod _{\begin{smallmatrix}i=1\\i\neq j\end{smallmatrix}}^{n}{\frac {1}{x_{j}-x_{i}}}\,.$

Siehe auch Polynominterpolation#Baryzentrische_Interpolationsformel

Diese Methode ist deutlich effizienter als die Verwendung der lagrangeschen Interpolationsformel. Auch die SciPy-Bibliothek stellt eine entsprechende Funktion barycentric_interpolate zur Verfügung. Mit dieser ist folgender Python-Code erstellt:

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import barycentric_interpolate

x_mess = (1., 2., 3., 4., 5.)
y_mess = (1., 1., 1., 1., 2.)

x = np.linspace(min(x_mess), max(x_mess), num=100)
y = barycentric_interpolate(x_mess, y_mess, x)

plt.plot(x, y, label="baryzentrische Interpolation")
plt.plot(x_mess, y_mess, "x", label="Messwerte")
plt.legend()
plt.show()

Ausgabe:

Newtonsche Interpolationsformel

Gegeben sind wieder Stützpunkte $(x_{i},f_{i});\quad i=0,\dots ,n$ .

Newton-Interpolationsformel:

$P(x)=\sum _{i=0}^{n}c_{i}\cdot N_{i}(x)=c_{0}+c_{1}\left(x-x_{0}\right)+c_{2}\left(x-x_{0}\right)\left(x-x_{1}\right)+\dotsb +c_{n}\left(x-x_{0}\right)\dotsm \left(x-x_{n-1}\right)$

Gleichungssystem:

${\begin{pmatrix}1&&&&0\\1&(x_{1}-x_{0})&&&\\1&(x_{2}-x_{0})&(x_{2}-x_{0})(x_{2}-x_{1})&&\\\vdots &\vdots &&\ddots &\\1&(x_{n}-x_{0})&\cdots &&\prod _{i=0}^{n-1}(x_{n}-x_{i})\\\end{pmatrix}}\cdot {\begin{pmatrix}c_{0}\\\vdots \\c_{n}\end{pmatrix}}={\begin{pmatrix}f_{0}\\\vdots \\f_{n}\end{pmatrix}}$

Es werden nun die dividierten Differenzen berechnet. Diese lassen sich mit einem Dreiecksschema (Neville-Schema) übersichtlich darstellen:

${\begin{array}{crcrccrcrc}f[x_{0}]\\&\searrow \\{}f[x_{1}]&\rightarrow &f[x_{0},x_{1}]\\&\searrow &&\searrow \\{}f[x_{2}]&\rightarrow &f[x_{1},x_{2}]&\rightarrow &f[x_{0},x_{1},x_{2}]\\{}\vdots &\vdots &\vdots &\vdots &\vdots &\ddots \\{}&\searrow &&\searrow &&&\searrow \\{}f[x_{n-1}]&\rightarrow &f[x_{n-2},x_{n-1}]&\rightarrow &f[x_{n-3},x_{n-2},x_{n-1}]&\cdots &\rightarrow &[x_{0},\ldots ,x_{n-1}]f\\&\searrow &&\searrow &&&\searrow &&\searrow \\{}f[x_{n}]&\rightarrow &f[x_{n-1},x_{n}]&\rightarrow &f[x_{n-2},x_{n-1},x_{n}]&\cdots &\rightarrow &f[x_{1},\ldots ,x_{n}]&\rightarrow &f[x_{0},\ldots ,x_{n}]\end{array}}$

Mit $c_{i}=f[x_{0},\dots ,x_{i}]$ .

Beispiel: Es soll wieder das Interpolationspolynom durch die 3 Stützpunkte $P_{0}=(1,1),P_{1}=(2,1),P_{2}=(3,2)$ gelegt werden.

${\begin{array}{crcrccrcrc}f[x_{0}]=1\\&\searrow \\{}f[x_{1}]=1&\rightarrow &f[x_{0},x_{1}]={\frac {f[x_{1}]-f[x_{0}]}{x_{1}-x_{0}}}={\frac {1-1}{2-1}}=0\\&\searrow &&\searrow \\{}f[x_{2}]=2&\rightarrow &f[x_{1},x_{2}]={\frac {f[x_{2}]-f[x_{1}]}{x_{2}-x_{1}}}={\frac {2-1}{3-2}}=1&\rightarrow &f[x_{0},x_{1},x_{2}]={\frac {f[x_{1},x_{2}]-f[x_{0},x_{1}]}{x_{2}-x_{0}}}={\frac {1-0}{3-1}}={\frac {1}{2}}\\\end{array}}$

Mit der Newton-Interpolationsformel ergibt sich wiederum

$P(x)=1+0\cdot (x-1)+{\frac {1}{2}}(x-1)(x-2)={\frac {x^{2}-3x+4}{2}}$

Mit dem Horner-Schema lässt sich das Interpolationspolynom auswerten (siehe Horner-Schema).

Siehe auch Polynominterpolation#Newtonscher_Algorithmus, Knorrenschild: Seite 81ff, Burg, Haf, Wille, Meister: Seite: 401ff

Neville-Aitken-Schema

Oft interessiert das Interpolationspolynom selbst nicht. Man will nur den Interpolationswert an einer bestimmten Stelle bestimmen. Das kann mit dem Neville-Aitken-Schema effizient gemacht werden.

Hier soll das Verfahren von Neville-Aitken an Hand eines rudimentären Python-Programms dargestellt werden:

import numpy as np

x = (1., 2., 3.) # Stützstellen
y = (1., 1., 2.) # Stützwerte
xinter = 2.5     # Auswertung an der Stelle xinter

n = 3
p = np.zeros((n,n))

for i in np.arange(0, n):
    p[i,0] = y[i]

for k in np.arange(1, n):
    for i in np.arange(0, n-k):
        p[i,k] = p[i+1,k-1] + (x[i+k]-xinter) / (x[i+k]-x[i]) * (p[i,k-1] - p[i+1,k-1])

print("f(", xinter, ") = ", p[0,n-1])

Ausgabe:

f( 2.5 ) =  1.375

Siehe auch Polynominterpolation#Algorithmus_von_Neville-Aitken, Burg, Haf, Wille, Meister: Seite 401ff, Knorrenschild: Seite 84f

Sonstiges

Interpolationspolynome höherer Ordnung können deutliche Überschwinger aufweisen. Knorrenschild zeigt auf Seite: 88f seines Buches diese Problematik anhand eines Beispiel auf. Aus diesem Grunde ist auch die Extrapolation außerhalb des Stützstellenintervalls kaum möglich. Genaueres siehe auch Polynominterpolation#Runges_Phänomen.

Splines

Isaac Jacob Schoenberg (rumänisch-amerikanischer Mathematiker, 1903-1990)]]
Carl-Wilhelm Reinhold de Boor (deutsch-amerikanischer Mathematiker, geb. 1937)
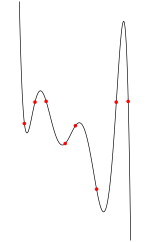
Spline mit 8 Knoten

Der Name Spline leitet sich vom englischen Begriff "Spline" für Straklatte ab und kommt aus dem Schiffbau.

Nunmehr wird nicht mehr nur ein Interpolationspolynom durch die Stützpunkte gelegt, sondern es wird das Stützintervall in mehrere Teilintervalle aufgeteilt. In jeweils einem Teilintervall lassen sich dann Interpolationspolynome niedrigeren Grades verwenden (typischerweise kubische Polynome).

Lineare Splines

$y=y_{n-1}+{\frac {x-x_{n-1}}{x_{n}-x_{n-1}}}(y_{n}-y_{n-1})$

Diese Formel folgt direkt aus derjenigen für die lineare Interpolation zwischen 2 Punkten.

Python-Code (rudimentär):

import numpy as np
import matplotlib.pyplot as plt

x = (1., 2., 3., 4.) # Stützstellen
y = (1., 2., 1., 4.) # Stützwerte
xinter = 3.5     # Auswertertung an der Stelle xinter
 
n = 3
yinter = y[n-1] + (xinter - x[n-1]) / (x[n]-x[n-1]) * (y[n]-y[n-1])

print("f(", xinter, ") = ", yinter)

plt.plot(x,y)
plt.plot(xinter, yinter, "o")
plt.grid()
plt.show()

Grafikausgabe:

Konsolenausgabe:

f( 3.5 ) =  2.5

Kubische Splines

Python-Code:

from scipy.interpolate import CubicSpline
import matplotlib.pyplot as plt
import numpy as np

x = (1., 2., 3., 4.) # Stützstellen
y = (1., 2., 1., 4.) # Stützwerte
xinter = 2.5

spl = CubicSpline(x, y)
s = spl(xinter)

print(s)

xspline = np.arange(1., 4.1, 0.1)
yspline = spl(xspline)

plt.plot(x, y, "x", label="Stützpunkte")
plt.plot(xspline, yspline, label="kubischer Spline")
plt.plot(xinter, s, "o", label="Interpolationspunkt")
plt.legend()
plt.grid()
plt.show()

Grafikausgabe:

Konsolenausgabe:

1.375

Siehe auch [1]

Für weitere Details siehe auch Spline, Spline-Interpolation, Hanke-Bourgeois: Seite 355ff, Burg, Haf, Wille, Meister: Seite 410ff, Knorrenschild: Seite 89ff.

Bernstein-Polynome

Siehe Bernsteinpolynom, Burg, Haf, Wille, Meister: Seite 387ff

Gedruckte Werke (auszugsweise)

Burg, Haf, Wille, Meister: Höhere Mathematik für Ingenieure, Band I: Analysis. 9. Auflage, Vieweg+Teubner, 2011, ISBN 978-3-8348-1218-6
Hanke-Bourgeois: Grundlagen der Numerischen Mathematik und des Wissenschaftlichen Rechnens. 3. Aufl., Vieweg+Teubner, 2009, ISBN 978-3-8348-0708-3
Knorrenschild: Numerische Mathematik, Eine beispielorientierte Einführung. 6. Aufl., Hanser, 2017, ISBN 978-3-446-45161-2

|

Hoch zu Gesamtinhaltsverzeichnis |

Vor zu Numerische Berechnung bestimmter Integrale