Karnaugh-Veitch-Diagramm: Beispiele (Teil 1)

Beispiel: Lampe

A	B	C	Lampe
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

Eine Lampe soll durch bestimmte Muster dreier Schalter ein- oder ausgeschaltet werden. Die drei Schalter A, B und C sind entweder geschlossen (1) oder offen (0). Wir fertigen eine Wahrheitstabelle an: Zuerst schreiben wir alle möglichen Kombinationen von Schaltzuständen von A, B und C auf. Dann bestimmen wir, bei welchen Schalterstellungskombinationen die Lampe leuchten (1), oder dunkel bleiben soll (0).

Aus der Wahrheitstabelle kann man die disjunktive Normalform (DNF) aufstellen. Diese zeichnet sich durch die Disjunktion aller Minterme, wo Lampe=1 ist, aus. Dazu betrachten wir alle Fälle, in denen die Lampe an sein soll (Lampe = 1). In der ersten Zeile, wo $A=0,B=0,C=0$ , ist folglich der Minterm ${\bar {A}}{\bar {B}}{\bar {C}}$ . Wir stellen für alle Lampe=1 den entsprechenden Minterm auf, und erhalten

$l={\bar {A}}{\bar {B}}{\bar {C}}\vee {\bar {A}}{\bar {B}}C\vee {\bar {A}}B{\bar {C}}\vee {\bar {A}}BC\vee AB{\bar {C}}\vee ABC$ ,

Diesen Ausdruck jedoch direkt in eine Schaltung zu gießen, würde unnötig Gatter kosten (nämlich in der straight-forward-Implementation ein 6-fach-Oder, sechs 3-fach-Unds, und drei Negationen). Also wollen wir $l$ vereinfachen. Dies geht - wie wir schon mitbekommen haben - auf ziemlich komfortable Weise mit KV-Diagrammen.

Wir fertigen das dazugehörige KV-Diagramm an, indem wir den schon im Kapitel 1 benannten Umstand beachten, dass sich entweder horizontal oder vertikal eine Variable ändern muss, und füllen die Felder entsprechend der bereits gebildeten DNF aus.

Nach der Minterm-Methode kann man im Diagramm nun zwei rechteckige Viererblöcke bilden. Um nun den minimalen disjunktiven Ausdruck zu ermitteln, betrachten wir zuerst die blaue Gruppe. An der Wertebildung in der blauen Gruppe sind $A,{\bar {A}},B,C,{\bar {C}}$ beteiligt. Daraus kann man die sowohl in einfacher, als auch negierter Form auftauchenden Variablen, einfach rausstreichen, sodass $B$ überbleibt. An der Wertebildung der grünen Gruppe sind die Variablen ${\bar {A}},B,{\bar {B}},C,{\bar {C}}$ beteiligt. Auch hier streichen wir die sowohl positiv, als auch negativ auftauchenden Variable heraus, wodurch ${\bar {A}}$ verbleibt. Diese beiden Terme verbinden wir letztendlich durch Disjunktion, sodass die optimierte Funktion demnach $l={\bar {A}}\vee B$ lautet.

Nach der Maxterm-Methode bildet man aus den beiden 0-Felder einen Zweierblock. An den Rändern sind zusammengefasst die Variablen $A,{\bar {A}},B,{\bar {B}},C,{\bar {C}}$ aufgelistet. An der Wertebildung der roten Gruppe sind ${\bar {A}}$ und $B$ nicht beteiligt. Wir erhalten ohne weiteres $l={\bar {A}}\vee B$ .

Um zu überprüfen, ob nun unsere ermittelte Vereinfachung der Wahrheit entspricht, kann man, ggf. anhand der bereits angefertigten Wahrheitstabelle, Stück für Stück den neuen Ausdruck überprüfen.

Aus der Interpretation der Vereinfachung, stellen wir fest, dass die Lampe l leuchtet, wenn der Schalter A offen oder der Schalter B geschlossen ist. Der Schalter C hat keine Wirkung.

Der durch die Schaltnetzsynthese resultierende Ausdruck lässt sich eins-zu-eins in einen Schaltplan übertragen (siehe Abbildung rechts) und kommt mit zwei Gattern aus (anstatt mit wie oben aufgeführt neun).

Beispiel: Wechselschalter

Vorbetrachtung: Zuerst wird das zu lösende logische Problem mit Worten beschrieben: Es gibt die Schalter A und B, die als Wechselschaltung die Lampe L betätigen. Wenn beide Schalter in der Position 0 sind, dann ist die Lampe aus (Position 0) – Zeile 1 der Tabelle. Sind beide Schalter in der Position 1, dann ist die Lampe ebenfalls aus – Zeile 4. Ansonsten ist die Lampe an – Zeile 2 und 3. Alle weiteren Arbeitsschritte, einschließlich des erst weiter unten folgenden KV-Diagramms, können dann fast mechanisch erfolgen.

Aus der logischen Problembeschreibung wird eine Wahrheitstabelle erstellt.

Schalter A	Schalter B	Lampe L
0	0	0
0	1	1
1	0	1
1	1	0

Aus den Zeilen der Wahrheitstabelle kann man direkt die Disjunktive Normalform (DNF) ablesen.

Zeile 1: da das Ergebnis 0 ist (L = 0) wird keine Bedingung aus dieser Zeile geschrieben. Eine Bedingung wird nur geschrieben, wenn das Ergebnis 1 ist (L = 1).
Zeile 2: ¬AB (Erklärung: wegen A=0 wurde ¬A geschrieben; für B=1 wurde B geschrieben)
Zeile 3: A¬B (Erklärung: wegen A=1 wurde A geschrieben; für B=0 wurde ¬B geschrieben)
Zeile 4: siehe Bemerkungen in Zeile 1

Bemerkung zu Zeile 2: Die Schreibweise ¬A ist gleichbedeutend mit ${\bar {A}}$ (gesprochen "A-quer") oder NICHT-A oder NOT-A oder A' (gesprochen "A-Strich"). Außerdem wurde bei dieser Schreibweise das UND zwischen ¬A und B weggelassen. ¬AB ist also gleichbedeutend mit:

¬A AND B
¬A UND B
$\neg A\land B$
${\bar {A}}\land B$

Die Ausdrücke aus Zeile 2 und 3 werden noch mit einem ODER verbunden. So erhält man die Disjunktive Normalform (DNF) der in der Wahrheitstabelle dargestellten logischen Verknüpfung:

¬AB ∨ A¬B (Disjunktive Normalform)

Erst diese DNF ist der Ausgangspunkt für die Anwendung des Karnaugh-Veitch-Diagramms, das bisher noch nicht im Spiel war. Das Karnaugh-Veitch-Diagramm stellt lediglich einen Versuch dar, die Disjunktive Normalform weiter zu vereinfachen und zu kürzen. Selbst lange und große Ausdrücke lassen sich jedoch nicht immer weiter vereinfachen. Das lässt sich nicht abschätzen und stellt sich erst nach Anwendung des Karnaugh-Veitch-Diagramms heraus.

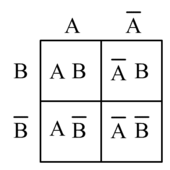
Bild 1: Für 2 logische Variablen (A, B) wird ein leeres 2x2 KV-Diagramm benötigt. Jedes Feld im KV-Diagramm repräsentiert eine Zeile der Wahrheitstabelle.
Bild 2: Es gibt 4 Felder, in die Eintragungen vorgenommen werden können (a, b, c, d)
Bild 3: Den 4 leeren Feldern sind die hier (nur vorübergehend zur Veranschaulichung) eingetragenen logischen Werte zugeordnet (das UND Zeichen wurde wieder weggelassen: AB bedeutet A∧B usw.)
Bild 4: In unserem konkreten Beispiel (siehe oben) wird für ¬AB eine 1 eingetragen (Feld b – oben rechts) und für A¬B eine 1 eingetragen (Feld c – unten links).

Aus Bild 4 ergibt sich, dass sich die eingesetzten Einsen nicht zu Gruppen zusammenfassen lassen. Folglich ist keine weitere Vereinfachung der DNF möglich. Im vorliegenden Fall ist die DNF der kürzeste logische Ausdruck (formale Bezeichnung: Minimalform = Minterm = Minimalterm) des Problems. Es sei nochmals daran erinnert, dass mit „1“ ausgefüllte Felder, die sich nur an ihren Ecken berühren nicht als Gruppe zusammengefasst werden. Bild 5 zeigt eine solche Gruppierung, die nicht zulässig ist.

Bild 6 ist eine alternative Darstellung des 2x2 KV-Diagramms. Zu beachten ist, dass im vorliegenden Fall die Positionen von A und ¬A vertauscht sind, ebenfalls von B und ¬B. Üblicherweise lässt man das Eintragen der Nullen weg. Leere Felder werden also als 0 gelesen (Bild 7 und 8).

Beispiel: Identität von B

A	B	X
1	1	1
1	0	0
0	1	1
0	0	0

Die Wahrheitstabelle (rechts) stellt die Identität von B dar, das heißt die Ausgabe X ist identisch mit der Eingabe B. Aus der Tabelle leitet sich direkt die DNF ab: AB ∨ ¬AB. Dieser Term ist in Bild 9 in das KV-Diagramm eingetragen. Die linke „1“ steht für AB (aus der ersten Zeile der Wahrheitstabelle entnommen) und die rechte „1“ steht für ¬AB (aus der dritten Zeile der Wahrheitstabelle abgelesen). In Bild 10 ist dieser Term zu einer Gruppe zusammengefasst. Die Bedingungen sind erfüllt: 1.) benachbarte Felder und 2.) eine Gruppe aus 2 oder 4 Feldern. Das Wesentliche am KV-Diagramm, den man besser als KV-Algorithmus bezeichnen sollte, ist das Ableiten der Formel aus dieser Gruppe. Aus der Kenntnis, dass A ∨ ¬A = 1 ist, kann man A weglassen und es bleibt nur noch B übrig. Aus dem KV-Diagramm liest man die Lösung direkt ab: B. Das KV-Diagramm hat also gezeigt, dass AB ∨ ¬AB = B.

Bei diesem einfachen Beispiel könnte man das gleiche Ergebnis auch durch algebraische Umformung erreichen:

Gleichung	Erklärung
AB ∨ ¬AB = (A ∧ B) ∨ (¬A ∧ B)	UND-Symbol zur Veranschaulichung mitgeschrieben;
AB ∨ ¬AB = (A ∨ ¬A) ∧ B	B ausgeklammert (Distributivgesetz der Booleschen Algebra angewendet)
AB ∨ ¬AB = 1 ∧ B	(A ∨ ¬A) durch 1 ersetzt, denn bekanntlich ist A ∨ ¬A = 1
AB ∨ ¬AB = B	denn 1 ∧ X = X (wie auch eine Überprüfung mittels Wahrheitstabelle beweist: 1∧W=W; 1∧F=F), – also kann man die 1 auch wegfallen lassen

Mit dem KV-Diagramm wurde faktisch das gleiche erreicht, jedoch auf graphische Art. Der Vorteil eines Diagramms ist, dass der Mensch Regelmäßigkeiten, also Muster bei einer bildlichen Darstellung viel einfacher erfassen kann (Mustererkennung), als bei abstrakten logischen Ausdrücken. Noch deutlicher wird der Unterschied zwischen bildlicher und abstrakter Mustererkennung bei 3, 4 oder 5 Variablen, wo das KV-Diagramm erst seine wirklichen Stärken ausspielen kann. Bei 6 Variablen versagt dann allerdings auch die Mustererkennung am KV-Diagramm, da es dafür keine geeigneten, einfachen KV-Diagramme gibt.

Beispiel: Negation von A

A	B	X
1	1	0
1	0	0
0	1	1
0	0	1

Die Wahrheitstabelle (rechts) stellt die Negation von A dar, das heißt die Ausgabe X ist identisch mit dem umgekehrten Signal der Eingabe A. Aus der Tabelle (Zeile 3 und 4) leitet sich direkt die DNF ab: ¬AB ∨ ¬A¬B. Dieser Term ist in Bild 11 in das KV-Diagramm eingetragen. Die rechte obere „1“ steht für ¬AB und die rechte untere „1“ steht für ¬A¬B. In Bild 12 ist dieser Term zu einer Gruppe zusammengefasst. Die Bedingungen sind erfüllt: 1.) benachbarte Felder und 2.) eine Gruppe aus 2 oder 4 Feldern. Jetzt kann aus dem KV-Diagramm und der umzeichneten Gruppe der Minterm abgeleitet werden.

Aus der Kenntnis, dass B ∨ ¬B = 1 ist, kann man B weglassen und es bleibt nur noch ¬A übrig – die Schreibweise ${\bar {A}}$ ist identisch. Aus dem KV-Diagramm liest man die Lösung ¬A also direkt ab. Das KV-Diagramm hat also gezeigt, dass ¬AB ∨ ¬A¬B = ¬A.

Beispiel: Implikation von A auf B

A	B	X
1	1	1
1	0	0
0	1	1
0	0	1

Die Wahrheitstabelle (rechts) stellt die Implikation von A auf B. Aus der Tabelle (Zeile 1, 3 und 4) leitet sich direkt die DNF ab:
AB ∨ ¬AB ∨ ¬A¬B.
Dieser Term ist in Bild 1-1 in das KV-Diagramm eingetragen. Die linke obere „1“ steht für AB, die rechte obere „1“ steht für ¬AB und die rechte untere „1“ steht für ¬A¬B. In Bild 1-2 ist dieser Term zu zwei Gruppen zusammengefasst. Die Bedingungen sind erfüllt: 1.) benachbarte Felder und 2.) eine Gruppe aus 2 oder 4 Feldern. Jetzt kann aus dem KV-Diagramm und der umzeichneten Gruppe der Minterm abgeleitet werden.

Die rote (waagerechte) Gruppe wird zu B zusammengefasst, da A ∨ ¬A = 1. Die blaue (senkrechte) Gruppe wird zu ¬A vereinfacht, da B ∨ ¬B = 1.

Aus dem KV-Diagramm liest man die Lösung ¬A ∨ B also direkt ab. Das KV-Diagramm hat also gezeigt, dass
AB ∨ ¬AB ∨ ¬A¬B = ¬A ∨ B.
Damit wurde der Term durch Bearbeitung im KV-Diagramm wesentlich vereinfacht. Der Term ¬A ∨ B ist nicht weiter zu vereinfachen. Bei manchen Lösungen lässt sich nach dem KV-Diagramm noch eine Variable ausklammern. Das Zusammenfassen der drei Einsen zu einer einzigen Gruppe ist nicht erlaubt, da Gruppen nicht „um die Ecke“ gehen dürfen. Außerdem darf eine Gruppe nur 2 oder 4 Einsen enthalten.

Nach einer anderen, v.a. bei Elektrotechnikern verbreiteten Schreibweise schreibt man für UND (∧) einen Punkt, wie bei der Multiplikation (·), da sich der UND-Operator, beispielsweise beim Ausklammern wie eine Multiplikation verhält. Für ODER (∨) schreibt man ein Pluszeichen (+), da sich der ODER-Operator beispielsweise beim Ausklammern wie eine Addition verhält. Statt AB ∨ ¬AB ∨ ¬A¬B = ¬A ∨ B kann man also auch A·B + ¬A·B + ¬A·¬B = ¬A + B schreiben.

Beispiel: Tautologie

A	B	X
1	1	1
1	0	1
0	1	1
0	0	1

Diese Wahrheitstabelle (rechts) stellt eine Tautologie dar, die als Ausgabewert immer „1“ ergibt. Aus der Tabelle (Zeile 1, 2, 3 und 4) leitet sich direkt die DNF ab:
AB ∨ ¬AB ∨ A¬B ∨ ¬A¬B.
Dieser Term ist in Bild 2-1 in das KV-Diagramm eingetragen. Die linke obere „1“ steht für AB, die rechte obere „1“ steht für ¬AB, die linke untere „1“ steht für A¬B und die rechte untere „1“ steht für ¬A¬B. In Bild 2-2 ist dieser Term zu zwei Gruppen zusammengefasst. Die Bedingungen sind erfüllt: 1.) benachbarte Felder und 2.) eine Gruppe aus 2 oder 4 Feldern. Jetzt kann aus dem KV-Diagramm und der umzeichneten Gruppe der Minterm abgeleitet werden.

Die obere (grüne) Gruppe wird zu B zusammengefasst. Die untere (blaue) Gruppe wird zu ¬B zusammengefasst. Aus dem KV-Diagramm liest man die Lösung B ∨ ¬B ab. Allerdings kann man mittels algebraischer Umformung weiter vereinfachen: B ∨ ¬B = 1.

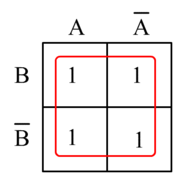Korrekterweise hätte man gleich eine große Gruppe aus 4 Einsen bilden können (Bild 2-3). Und direkt die Lösung 1 ablesen können, denn A ∨ ¬A = 1 und B ∨ ¬B = 1

Zur Titelseite: Karnaugh-Veitch-Diagramm - zum vorherigen Kapitel: Theorie des KV-Diagramms - zum nächsten Kapitel: Beispiele (Teil 2)