Hier gibt es eine aktualisierte PDF-Version.
In der Kinematik geht es um grundlegende Vorgänge und Begriffe im Zusammenhang mit der Bewegung von Körpern: um Verschiebung, Geschwindigkeit, Beschleunigung, gleichförmige Bewegung, gleichmäßig beschleunigte Bewegung, um Bewegungen auf gekrümmten Bahnen – und natürlich um die mathematische Behandlung der entsprechenden physikalischen Vorgänge und Größen. Da es sich dabei meist um »gerichtete Größen«, also um Vektoren handelt, ist die Vektoranalysis [1] das angemessene mathematische Handwerkszeug dafür.
Die einfachste vektorielle Größe der Kinematik ist die »Verschiebung« Δs, die ein Körper während einer Zeitspanne Δt erfährt. Dass die Verschiebung ein Vektor ist, folgt daraus, dass sie den Gesetzen der Vektoraddition folgt. Erfährt nämlich ein Körper nacheinander oder gleichzeitig zwei Verschiebungen a und b, so ist die daraus resultierende Verschiebung gleich der Vektorsumme a + b der beiden einzelnen Verschiebungen.
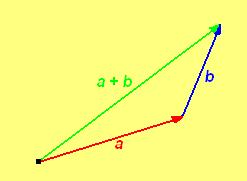
Zwei gleichzeitige Bewegungen treten vor allem dann auf, wenn sich ein Körper relativ zu einem Bezugssystem bewegt und dieses Bezugssystem selbst sich relativ zu einem anderen Bezugssystem bewegt. Beispiel: Die Bewegung eines Reisenden in einem fahrenden Zug, der vom Bahndamm aus beobachtet wird.
Anmerkung zur Schreibweise:
Im Text und in den Abbildungen werden Vektoren mit fett und kursiv gedruckten Buchstaben benannt. In den Formeln und Gleichungen, die mit TeX geschrieben wurden, sind Vektoren durch einen Pfeil über dem Formelzeichen gekennzeichnet.
Bahngeschwindigkeit und Bahnbeschleunigung
[Bearbeiten]Bahngeschwindigkeit und Bahnbeschleunigung werden im Alltag (zum Beispiel bei Fahrzeugen) schlicht Geschwindigkeit bzw. Beschleunigung genannt. In der Physik jedoch sind Geschwindigkeit und Beschleunigung Vektoren, und so sind klare Begriffe und Unterscheidungen notwendig.
Legt ein Massenpunkt von einem Punkt P aus in der Zeit Δt die Strecke Δs zurück, so heißt der Quotient Δs / Δt seine mittlere Bahngeschwindigkeit vm im Zeitintervall Δt oder auf der Strecke Δs.


Man beachte, dass Δs hier nicht die Verschiebung, sondern die Bogenlänge, also die zurückgelegte Wegstrecke ist.
Von mittlerer Bahngeschwindigkeit sprechen wir darum, weil sich der Massenpunkt auf der betrachteten Strecke möglicherweise nicht gleichmäßig schnell bewegt hat.
Machen wir die Strecke Δs immer kleiner, so wird auch das Zeitintervall Δt immer kleiner. Für Δs gegen null (oder Δt gegen null, was auf dasselbe hinausläuft) nähert sich der Quotient Δs/Δt unbeschränkt einem Grenzwert, den wir die Bahngeschwindigkeit v des Massenpunktes im Punkt P nennen:

In der Analysis wird dieser Grenzwert auch mit ds/dt bezeichnet, also:

Nehmen wir weiter an, der Massenpunkt habe im Punkt P und zur Zeit t die Bahngeschwindigkeit v und zur Zeit t + Δt die Bahngeschwindigkeit v + Δv. Dann bezeichnen wir den Quotienten Δv/Δt als die mittlere Bahnbeschleunigung am des Massenpunktes im Zeitintervall Δt:

Für Δt gegen null strebt dieser Quotient einem Grenzwert zu, der Bahnbeschleunigung a des Massenpunktes zur Zeit t heißt.

Für diesen Grenzwert wird auch folgende Abkürzung benutzt:

Ist der Weg s als analytische Funktion der Zeit t beschrieben, also s = s (t), so ist die Bahngeschwindigkeitsfunktion v (t) die erste Ableitung der Funktion s (t) nach der Zeit, die Bahnbeschleunigungsfunktion a (t) ihre zweite Ableitung. Ableitungen nach der Zeit können auch durch einen Punkt über dem Formelzeichen bezeichnet werden.

Umgekehrt können die Bahngeschwindigkeitsfunktion und die Wegfunktion durch Integration gefunden werden:

Die zu den unbestimmten Integralen gehörigen additiven Konstanten müssen aus den Anfangsbedingungen oder Randbedingungen bestimmt werden.
Beispiel: Beim freien Fall erfährt der Massenpunkt die konstante Beschleunigung g. Dann ist, wenn er zur Zeit t = 0 die senkrecht nach oben oder unten gerichtete Bahngeschwindigkeit v0 und die Ortskoordinate s0 hat,

Wir betrachten nun einen Massenpunkt, der im Raum eine beliebige Kurve durchläuft. Zur Zeit t befinde er sich in P, zur Zeit t + Δt in Q. Der Ort des Punktes wird durch seinen Ortsvektor r beschrieben. Dieser ist eine Funktion von t und wird durch eine Vektorfunktion r(t) beschrieben.

Es sei

und

wobei i, j und k die Einheitsvektoren auf den Koordinatenachsen sind.
Die Verschiebung des Massenpunktes im betrachteten Zeitintervall ist dann

Der Quotient Δr/Δt ist die mittlere (vektorielle) Geschwindigkeit vm des Massenpunkts im Zeitintervall Δt. Es ist

Dabei ist (siehe oben: Bahngeschwindigkeit und Bahnbeschleunigung) Δx/Δt die mittlere Bahngeschwindigkeit des Massenpunktes parallel zur X-Achse, Δy/Δt seine mittlere Bahngeschwindigkeit parallel zur Y-Achse und Δz/Δt seine mittlere Bahngeschwindigkeit parallel zur Z-Achse im Intervall Δt.
Der »Grenzvektor«, dem der Bruch Δr/Δt für Δt gegen 0 zustrebt, heißt Geschwindigkeit vP = v(t) des Massenpunktes in P oder zur Zeit t.

Die Vektorfunktion v(t) ist also die erste Ableitung der Ortsfunktion r(t) nach der Zeit.

Wie man sieht, sind die skalaren Komponenten des Vektors v(t) identisch mit den Bahngeschwindigkeiten parallel zu den Achsen:

Die Gerade durch P mit der Richtung des Vektors vP heißt Tangente der Bahnkurve in P.
Analog definieren wir nun die Vektorfunktion der Beschleunigung:

Die Vektorfunktion der Beschleunigung ergibt sich aus den skalaren Komponenten der Geschwindigkeitsfunktion und der Ortsfunktion wie folgt:


Wie zu erkennen, sind die skalaren Komponenten des Beschleunigungsvektors gleich der Bahnbeschleunigung in Richtung der jeweiligen Koordinatenachse.
Umgekehrt können durch Integration die entsprechenden Stammfunktionen gefunden werden.
Beispiel: Freier Fall mit Anfangsgeschwindigkeit v0 von einem Punkt mit dem Ortsvektor r0 aus (senkrechter oder schräger Wurf).
Wenn die +Z-Achse (Einheitsvektor k) senkrecht nach oben gerichtet ist, gilt


Während der Geschwindigkeitsvektor immer die Richtung der Bahntangente hat, kann der Beschleunigungsvektor beliebig gerichtet sein. Zu einer näheren Untersuchung ist es sinnvoll, die Beschleunigung in zwei Komponenten zu zerlegen, von denen die eine die Richtung der Bahntangente hat (»Tangentialbeschleunigung«) und die andere darauf senkrecht steht (»Normalbeschleunigung«).
Die Tangentialbeschleunigung verändert nur den Betrag der Geschwindigkeit (das ist die Bahngeschwindigkeit), die Normalbeschleunigung verändert nur die Richtung des Geschwindigkeitsvektors.
Für diese Zerlegung des Vektors der Beschleunigung führen wir die »Bogenlänge s« ein, das ist die Länge des Weges, den der betrachtete Massenpunkt auf der Bahnkurve zurückgelegt hat. Die Bogenlänge zählt von einem beliebig gewählten Nullpunkt aus, der hier ohnehin keine Rolle spielt, da wir nur das Differential ds der Bogenlänge brauchen. Außerdem führen wir den Tangenteneinheitsvektor t ein und machen einige Anleihen bei der Differentialgeometrie (Siehe dazu: Vektoranalysis: 3. Anwendungen auf die Differentialgeometrie)
Der Tangenteneinheitsvektor t ist der Vektor

das heißt, er ist gleich dem Vektor v dividiert durch dessen Betrag v. Dieser Betrag aber ist gleich der Bahngeschwindigkeit und diese wiederum ist die Ableitung der Bogenlänge nach der Zeit. Also ist

Durch Differenzieren nach der Zeit ergibt sich daraus

Da die Länge des Tangenteneinheitsvektors t konstant (nämlich gleich 1) ist, steht der Ableitungsvektor dt/ds – wenn er nicht gleich null ist - auf t senkrecht.
Der Differentialgeometrie entnehmen wir, dass der Ableitungsvektor dt'/ds
- die Richtung des Normaleneinheitsvektors n und
- den Betrag k = 1/ρ hat.
Dabei ist k die Krümmung der Kurve im betrachteten Punkt und ρ ihr Krümmungsradius. Der Normaleneinheitsvektor n ist auf den (momentanen) Krümmungsmittelpunkt (also »nach innen«) hin gerichtet.
Folglich ist

Damit ergibt sich

Der Vektor a liegt also in der durch t und n aufgespannten Ebene, der so genannten Schmiegungsebene der Kurve im betrachteten Punkt.
Der Betrag der Tangentialbeschleunigung ist – wie zu erwarten war:

der Betrag der Normalbeschleunigung ist

Diese beiden Gleichungen sind so zu interpretieren: Die Beschleunigung des Massenpunktes erfolgt durch das Wirken einer Kraft. Die Richtung dieser Kraft bestimmt die Richtung der Beschleunigung. Die Tangentialkomponente der Beschleunigung verursacht eine Veränderung der Bahngeschwindigkeit, die Normalkomponente der Beschleunigung verursacht eine Krümmung der Bahnkurve. Der Krümmungsradius der Kurve im betrachteten Punkt ergibt sich aus der Normalbeschleunigung und der Geschwindigkeit zu:

Ein Massenpunkt P bewege sich auf einer Kreisbahn. Wir legen die XY-Ebene in die Bahnebene und den Ursprung O des Koordinatensystems in den Mittelpunkt des Kreises.

Dann ist

Analog zur »Bahngeschwindigkeit« und zur »Bahnbeschleunigung« definieren wir die »Winkelgeschwindigkeit» ω

und die »Winkelbeschleunigung« α

Wenn für t = 0 auch φ = 0 und ω = 0 ist, dann ist
![{\displaystyle \varphi \left(t\right)=\int _{0}^{t}{\omega \,\operatorname {d} t}=\int _{0}^{t}{\left[{\int _{0}^{t}{\alpha \,\operatorname {d} t}}\right]}\operatorname {d} t\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f88051e114316d650fb4fd419d2f83eac12c73e1)
Eine Kreisbewegung mit konstanter Winkelgeschwindigkeit heißt gleichförmig. Dann ist

Die Gleichung des Ortsvektors ist dann

Daraus ergibt sich für die Geschwindigkeit

und

Außerdem ist das Skalarprodukt

Für die Beschleunigung ergibt sich

und daraus

Die Beschleunigung ist also auf O hin gerichtet (Zentripetalbeschleunigung), ihr Betrag ist konstant.
Gleichmäßig beschleunigte Kreisbewegung
[Bearbeiten]Hier ist die Winkelbeschleunigung α konstant und folglich für ω(0) = 0

Wenn auch φ(0) = 0 ist, folgt daraus für den Drehwinkel

Dann folgt aus

![{\displaystyle {\overrightarrow {v}}={\frac {\operatorname {d} {\overrightarrow {r}}}{\operatorname {d} t}}=r\alpha \,t\left[{-\left({\sin \,{\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}+\left({\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right]=r\omega \left[{-\left({\sin \,{\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}+\left({\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/610a2564823b8defefeeecbe611e585aca6af86a)
und
![{\displaystyle {\overrightarrow {a}}={\frac {\operatorname {d} {\overrightarrow {v}}}{\operatorname {d} t}}=r\alpha \left[{-\left({\sin {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}+\left({\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right]+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f27d7325d8770cf13ee8446c138f086d328e25d8)
![{\displaystyle +\,r\alpha ^{2}t^{2}\left[{\left({-\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}-\left({\sin {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b85262543608f244520a74930287c29b567f7430)
oder
![{\displaystyle {\overrightarrow {a}}=\left[{-r\alpha \left({\sin \varphi }\right)-r\omega ^{2}\left({\cos \varphi }\right)}\right]{\overrightarrow {i}}+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5796d2f39e4a3a173a01ac6885e4fd4703696c98)
![{\displaystyle +\left[{r\alpha \left({\cos \varphi }\right)-r\omega ^{2}\left({\sin \varphi }\right)}\right]{\overrightarrow {j}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f61d1f3b5ba7920a08d07a4d4628620cad7e77e3)
Daraus ersieht man, dass die (nach innen gerichtete) Radialkomponente der Beschleunigung

und ihre Tangentialkomponente

ist.
Die Winkelgeschwindigkeit als gerichtete Größe
[Bearbeiten]Manchmal ist es nützlich, die Winkelgeschwindigkeit als gerichtete Größe aufzufassen und durch einen Vektor darzustellen, der in der Drehachse liegt und dessen Betrag gleich der Winkelgeschwindigkeit ω ist. Dazu führt man z. B. einen Einheitsvektor e von der Richtung der Drehachse ein und bezeichnet dann die Größe ω e als den »Vektor ω der Winkelgeschwindigkeit«. Dies ist – wie gesagt – manchmal recht nützlich; aber das darf uns nicht darüber hinwegtäuschen, dass die Winkelgeschwindigkeit kein Vektor ist. Ihr fehlt nämlich die wesentliche und unabdingbare Eigenschaft eines Vektors: sie kann nicht vektoriell addiert werden. Das heißt: Wenn ein Körper (z. B. die Erde) gleichzeitig zwei Rotationen mit der Winkelgeschwindigkeit ω1 bzw. ω2 um zwei verschiedene Drehachsen ausführt (im Beispiel: um die eigene Achse und um eine Achse, die durch die Sonne geht und auf der Ekliptik senkrecht steht), dann kann die resultierende Bewegung nicht durch die Vektorsumme der beiden Winkelgeschwindigkeiten beschrieben werden.
Nur wenn es um Berechnungen im Zusammenhang mit einer einzigen Drehbewegung oder um die Ermittlung der Geschwindigkeit eines Körpers geht, der gleichzeitig zwei Drehbewegungen ausführt (wobei dann die beiden Teilgeschwindigkeiten einzeln ermittelt werden müssen), ist die Einführung eines »Drehvektors« sinnvoll und nützlich.
Bewegungsgleichungen in einem Polarkoordinatensystem
[Bearbeiten]Die Geschwindigkeit v eines Massenpunktes kann auf beliebig viele Arten in Komponenten zerlegt werden. Geläufig und wichtig ist vor allem die bisher benutzte Zerlegung in Komponenten in Richtung der Achsen eines kartesischen Koordinatensystems, also die Darstellung in der Form:

Alternativ werden wir nun die Darstellung einer in der XY-Ebene verlaufenden ebenen Bewegung in Polarkoordinaten betrachten.

Die Lage eines Punktes P kann nun beschrieben werden
- durch seine kartesischen Koordinaten x, y und
- durch seine Polarkoordinaten r, φ
Dabei gelten folgende Transformationsgleichungen:

und

Ein Massenpunkt bewege sich in der Zeit Δt von P1 nach P2. Wir zerlegen nun die Verschiebung P1 P2 in eine radiale und eine dazu senkrechte »transversale« Komponente


Analog zur Definition der mittleren Bahngeschwindigkeit definieren wir nun
die mittlere Radialgeschwindigkeit im Zeitintervall Δt

und die mittlere Transversalgeschwindigkeit im Zeitintervall Δt

Daraus ergeben sich die Definitionen für die (momentane) Radial- und Transversalgeschwindigkeit im Punkt P1:


Die Berechnung der Geschwindigkeiten aus diesen Gleichungen ist natürlich nur möglich, wenn die Funktion r = r (φ) - das ist die Gleichung der Bahnkurve – und φ = φ (t) oder r = r (t) – das ist die Beschreibung des zeitlichen Ablaufs der Bewegung – gegeben sind.
Den Zusammenhang zwischen den Geschwindigkeiten in kartesischen Koordinaten einerseits und in Polarkoordinaten andererseits findet man entweder graphisch oder durch Rechnung wie folgt durch Differenzieren der Gleichungen (B):


Mit

folgt daraus

und andererseits

Dieselben Ergebnisse gewinnt man auch aus der folgenden Graphik

Mit Hilfe der grau eingezeichneten Hilfslinien findet man

und

Die Verwendung eines Polarkoordinatensystems und die Zerlegung der betrachteten Größen (Geschwindigkeit, Beschleunigung) in radiale und transversale Komponenten hat zur Folge, dass diese Komponenten keine feste Richtung bezüglich des Koordinatensystems (hier speziell bezüglich der Polarachse) haben, sondern sich bei Bewegung des Punktes P in der Ebene drehen. Man kann dies auch so ausdrücken: das der Komponentenzerlegung zugrunde liegende Koordinatensystem rotiert für einen im kartesischen Koordinatensystem ruhenden Beobachter. Damit hängt es zusammen, dass man die radiale und transversale Beschleunigung nicht einfach durch die Ableitung der radialen bzw. transversalen Geschwindigkeit nach der Zeit finden kann. Wir müssen vielmehr so vorgehen:
Ersetzt man in obiger Abbildung den Vektor v durch den Vektor a der Beschleunigung, so braucht man nur alle Buchstaben v durch a zu ersetzen und findet dann

Differenziert man ferner die Gleichungen

und

nochmals nach der Zeit, so erhält man


oder nach Ausklammern von cos φ und sin φ
![{\displaystyle {\frac {\operatorname {d} ^{2}x}{\operatorname {d} t^{2}}}=\left[{{\frac {\operatorname {d} ^{2}r}{\operatorname {d} t^{2}}}-r\left({\frac {\operatorname {d} \varphi }{\operatorname {d} t}}\right)^{2}}\right]\cos \varphi -\left[{2{\frac {\operatorname {d} r}{\operatorname {d} t}}{\frac {\operatorname {d} \varphi }{\operatorname {d} t}}+r{\frac {\operatorname {d} ^{2}\varphi }{\operatorname {d} t^{2}}}}\right]\sin \varphi \,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daa0a594102c7e37e587dc09942d0666651cb7c6)
![{\displaystyle {\frac {\operatorname {d} ^{2}y}{\operatorname {d} t^{2}}}=\left[{{\frac {\operatorname {d} ^{2}r}{\operatorname {d} t^{2}}}-r\left({\frac {\operatorname {d} \varphi }{\operatorname {d} t}}\right)^{2}}\right]\sin \varphi +\left[{2{\frac {\operatorname {d} r}{\operatorname {d} t}}{\frac {\operatorname {d} \varphi }{\operatorname {d} t}}+r{\frac {\operatorname {d} ^{2}\varphi }{\operatorname {d} t^{2}}}}\right]\cos \varphi \,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d84132fc9a80a9022248fca1d0f5c2d36a0616e6)
Ein Vergleich dieser beiden Gleichungen mit den Gleichungen (A) - ein so genannter Koeffizientenvergleich – ergibt

1. Die gleichförmige Kreisbewegung (Mittelpunkt M, Radius R, Winkelgeschwindigkeit ω.)
Hier gilt mit (rM = Ortsvektor von M):



Für rM = 0 ist einfach a = -ω2 r
2. Die Planetenbewegung
Johannes Kepler (1571-1630) hatte aus den langjährigen sorgfältigen Planetenbeobachtungen Tycho Brahes (1546-1601) die drei nach ihm benannten Gesetze der Planetenbewegung abgeleitet. Diese lauten:
- 1. Die Planeten bewegen sich auf Ellipsen, in deren einem Brennpunkt die Sonne steht.
- 2. Der von diesem Brennpunkt aus auf einen Planeten gerichtete Ortsvektor (»Radiusvektor«) überstreicht in gleichen Zeiten gleiche Flächen (»Flächensatz«).
- 3. Die Quadrate der Umlaufszeiten der Planeten verhalten sich wie die 3. Potenzen der großen Halbachsen ihrer Bahnen.
Isaac Newton (1643-1727) benutzte bei der Aufstellung seines Gravitationsgesetzes (1666) die Keplerschen Gesetze und zeigte 1687, wie diese umgekehrt mit Hilfe der Differentialrechnung (damals »Fluxionsrechnung«) aus seinem Gravitationsgesetz abgeleitet werden können.
Hier soll als Anwendungsbeispiel gezeigt werden, wie sich das quadratische Abstandsgesetz der Gravitation aus dem ersten und zweiten Keplerschen Gesetz herleiten lässt.
Dazu machen wir zunächst eine Anleihe bei der Analytischen Geometrie: Legt man den Pol eines Polarkoordinatensystems in den linken Brennpunkt der Ellipse und richtet die Polarachse zum rechten Brennpunkt hin, dann lautet die Polargleichung der Ellipse:

wobei p und e zwei hier uninteressante Ellipsenparameter sind.
So anschaulich und einleuchtend das 2. Keplersche Gesetz formuliert ist, so ist es doch in dieser Form mathematisch nicht auszudrücken. Eine »moderne« und umsetzbare, dabei gleichwertige Form lautet: Die vom Ortsvektor des Planeten überstrichene Fläche ΔA ist der Zeit Δt proportional: ΔA = C Δt.
Für hinreichend kleine Werte Δφ ist:

Nach dem 2. Keplerschen Gesetz ist

Für Δt gegen null folgt daraus:

Dies ist die mathematische Form des 2. Keplerschen Gesetzes.
Durch Differenzieren folgt daraus:

Der Term auf der linken Seite der zweiten Gleichung ist aber (siehe oben bei »In ebenen Polarkoordinaten«) nichts anderes als der Betrag aφ der transversalen Komponente der Beschleunigung.
Also: Bei der Planetenbewegung ist die Transversalbeschleunigung null; es gibt offenbar nur eine Radialbeschleunigung. Für die (skalare) Radialkomponente der Beschleunigung gilt (siehe wiederum a. a. O.):

Die Radialbeschleunigung der Planetenbewegung muss nun aus den Gleichungen berechnet werden, die wir aus dem ersten und dem zweiten Keplerschen Gesetz gewonnen haben. Da in der ersten Gleichung r als Funktion von φ und nicht von t auftritt, werden wir mit Hilfe der zweiten Gleichung die Ableitung nach t durch eine solche nach φ ersetzen:
Aus

und daraus

Nochmaliges Differenzieren der Gleichung (A) ergibt:

und zusammen mit den Gleichungen (A) und (B):

Dem Flächensatz entnehmen wir, dass

Damit ergibt sich schließlich:
![{\displaystyle a_{r}={\frac {\operatorname {d} ^{2}r}{\operatorname {d} t^{2}}}-r\left({\frac {\operatorname {d} \varphi }{\operatorname {d} t}}\right)^{2}={\frac {C^{2}}{r^{3}}}\left[{{\frac {1}{r}}{\frac {\operatorname {d} ^{2}r}{\operatorname {d} \varphi ^{2}}}-{\frac {2}{r^{2}}}\left({\frac {\operatorname {d} r}{\operatorname {d} \varphi }}\right)^{2}-1}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ccadbf68dc8c0aab93ea714d73112f27e5f2ce8)
Durch Differenzieren der Ellipsengleichung nach φ findet man dr/dφ und d2r/dφ2 und nach einer etwas mühsamen Rechnung schließlich:

wobei der Term in der Klammer gemäß der Ellipsengleichung den Wert – r hat.
Damit ergibt sich schließlich für die skalare Radialkomponente der Beschleunigung:

Die Radialbeschleunigung ist also dem Ortsvektor entgegengesetzt gerichtet, also auf die Sonne hin und ist dem Quadrat der Entfernung umgekehrt proportional.
Der Faktor C²/p hängt von den Parametern der Bahn des jeweiligen Planeten ab. Es ist zu erwarten, dass er bei jedem Planeten einen anderen Wert hat. Hier greifen wir nun auf das 3. Keplersche Gesetz zurück, das wir bisher noch nicht benutzt haben. Seine ursprüngliche Formulierung ("Die Quadrate der Umlaufszeiten T verhalten sich wie die 3. Potenzen der großen Halbachsen a.") lässt sich mathematisch als fortlaufende Proportion ausdrücken:

Stattdessen kann man auch schreiben:

oder

wobei K für alle Planeten des Systems denselben Wert hat, also eine für das ganze Sonnensystem gültige Konstante ist.
Wir beeinträchtigen die Allgemeingültigkeit des Ergebnisses nicht, vereinfachen aber die Rechnung erheblich, wenn wir nun einen Planeten betrachten, der sich auf einer Kreisbahn bewegt (selbst wenn dieser hypothetisch ist). Dann würde auch für ihn das obige Gesetz gelten und die große Halbachse a seiner Bahn wäre durch den Bahnradius R zu ersetzen. Dann lautet das 3. Keplersche Gesetz für diesen Planeten:

Mit T = (2πR)/v erhalten wir daraus R v2 = K. Bei einer Kreisbewegung ist ferner v2 = a R, womit sich schließlich ergibt

Das bedeutet verallgemeinert, dass die Radialbeschleunigung umgekehrt proportional zum Quadrat der Entfernung von der Sonne ist. Später wird sich zeigen, dass die Konstante K nur von der Gravitationskonstanten und der Sonnenmasse abhängt.



































![{\displaystyle \varphi \left(t\right)=\int _{0}^{t}{\omega \,\operatorname {d} t}=\int _{0}^{t}{\left[{\int _{0}^{t}{\alpha \,\operatorname {d} t}}\right]}\operatorname {d} t\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f88051e114316d650fb4fd419d2f83eac12c73e1)










![{\displaystyle {\overrightarrow {v}}={\frac {\operatorname {d} {\overrightarrow {r}}}{\operatorname {d} t}}=r\alpha \,t\left[{-\left({\sin \,{\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}+\left({\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right]=r\omega \left[{-\left({\sin \,{\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}+\left({\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/610a2564823b8defefeeecbe611e585aca6af86a)
![{\displaystyle {\overrightarrow {a}}={\frac {\operatorname {d} {\overrightarrow {v}}}{\operatorname {d} t}}=r\alpha \left[{-\left({\sin {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}+\left({\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right]+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f27d7325d8770cf13ee8446c138f086d328e25d8)
![{\displaystyle +\,r\alpha ^{2}t^{2}\left[{\left({-\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}-\left({\sin {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b85262543608f244520a74930287c29b567f7430)
![{\displaystyle {\overrightarrow {a}}=\left[{-r\alpha \left({\sin \varphi }\right)-r\omega ^{2}\left({\cos \varphi }\right)}\right]{\overrightarrow {i}}+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5796d2f39e4a3a173a01ac6885e4fd4703696c98)
![{\displaystyle +\left[{r\alpha \left({\cos \varphi }\right)-r\omega ^{2}\left({\sin \varphi }\right)}\right]{\overrightarrow {j}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f61d1f3b5ba7920a08d07a4d4628620cad7e77e3)






















![{\displaystyle {\frac {\operatorname {d} ^{2}x}{\operatorname {d} t^{2}}}=\left[{{\frac {\operatorname {d} ^{2}r}{\operatorname {d} t^{2}}}-r\left({\frac {\operatorname {d} \varphi }{\operatorname {d} t}}\right)^{2}}\right]\cos \varphi -\left[{2{\frac {\operatorname {d} r}{\operatorname {d} t}}{\frac {\operatorname {d} \varphi }{\operatorname {d} t}}+r{\frac {\operatorname {d} ^{2}\varphi }{\operatorname {d} t^{2}}}}\right]\sin \varphi \,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daa0a594102c7e37e587dc09942d0666651cb7c6)
![{\displaystyle {\frac {\operatorname {d} ^{2}y}{\operatorname {d} t^{2}}}=\left[{{\frac {\operatorname {d} ^{2}r}{\operatorname {d} t^{2}}}-r\left({\frac {\operatorname {d} \varphi }{\operatorname {d} t}}\right)^{2}}\right]\sin \varphi +\left[{2{\frac {\operatorname {d} r}{\operatorname {d} t}}{\frac {\operatorname {d} \varphi }{\operatorname {d} t}}+r{\frac {\operatorname {d} ^{2}\varphi }{\operatorname {d} t^{2}}}}\right]\cos \varphi \,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d84132fc9a80a9022248fca1d0f5c2d36a0616e6)















![{\displaystyle a_{r}={\frac {\operatorname {d} ^{2}r}{\operatorname {d} t^{2}}}-r\left({\frac {\operatorname {d} \varphi }{\operatorname {d} t}}\right)^{2}={\frac {C^{2}}{r^{3}}}\left[{{\frac {1}{r}}{\frac {\operatorname {d} ^{2}r}{\operatorname {d} \varphi ^{2}}}-{\frac {2}{r^{2}}}\left({\frac {\operatorname {d} r}{\operatorname {d} \varphi }}\right)^{2}-1}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ccadbf68dc8c0aab93ea714d73112f27e5f2ce8)






