Komplexe Zahlen/ Anwendung in der Mathematik

Dieses Kapitel enthält – mit nur kurzen Erläuterungen – Hinweise zu mathematischen Anwendungen, bei denen die komplexen Zahlen relevant sind. Über Verweise auf Wikipedia-Artikel sind ausführliche Erklärungen und in der Regel auch Literaturhinweise zu finden.

Die Beispiele beziehen sich auf verschiedene Gebiete der Mathematik und zeigen die universelle Bedeutung der komplexen Zahlen:

• Analysis
• Topologie
• Zahlentheorie
• Chaosforschung

Exponentialdarstellung

Euler’sche Formeln

In der reellen Analysis definiert man die sogenannte e-Funktion (= natürliche Exponentialfunktion exp) $e^{x}$ mit $\;-\infty <x<+\infty \;$ durch die unendliche (Taylor-) Reihe (mit Nutzung der Fakultät $n!$):

$e^{x}\;=\;1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{3!}}+\dotsb +{\frac {x^{n}}{n!}}+\dotsb \;=\;\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}$

Ersetzen wir in der Reihe für $e^{x}$ formal $x$ durch $\mathrm {i} x\!$, so erhalten wir:

$e^{\mathrm {i} x}\;=\;1+{\frac {\mathrm {i} x}{1!}}+{\frac {\mathrm {i} ^{2}x^{2}}{2!}}+{\frac {\mathrm {i} ^{3}x^{3}}{3!}}+\dotsb \;=\;1+{\frac {\mathrm {i} x}{1!}}-{\frac {x^{2}}{2!}}-{\frac {\mathrm {i} x^{3}}{3!}}+\dotsb$

Die Zusammenfassung der Realteile und der Imaginärteile liefert dann:

$e^{\mathrm {i} x}\;=\;1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\dotsb +\mathrm {i} \cdot \left({\frac {x}{1!}}-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\dotsb \right)$

Der Vergleich dieser Formel mit Taylor-Reihen zeigt: Der Realteil ist die Taylor-Reihe für Cosinus, der Imaginärteil diejenige für Sinus. Wir erhalten damit die 1. Euler’sche Formel:

$e^{\mathrm {i} x}\;=\;\cos x+\mathrm {i} \,\sin x$

In gleicher Weise erhält man die 2. Euler’sche Formel mit $\mathrm {i} x$ statt $x\!$:

$e^{-\mathrm {i} x}\;=\;\cos x-\mathrm {i} \,\sin x$

Durch Addition bzw. Subtraktion der Euler’schen Formeln erhält man zwei nützliche Beziehungen;

${\begin{aligned}\cos x\;&=\;{\frac {e^{\mathrm {i} x}+e^{-\mathrm {i} x}}{2}}\\\sin x\;&=\;{\frac {e^{\mathrm {i} x}-e^{-\mathrm {i} x}}{2\,\mathrm {i} }}\end{aligned}}$

Für $e^{z}$ mit $\;z=x+\mathrm {i} y\;$ ergibt sich die folgende Darstellung:

$e^{z}\;=\;e^{x+\mathrm {i} y}\;=\;e^{x}e^{\mathrm {i} y}\;=\;e^{x}(\cos y+\mathrm {i} \,\sin y)$

Polarform und Exponentialform

Die Exponentialform einer komplexen Zahl $\;z=a+\mathrm {i} \,b\;$ ergibt sich unmittelbar aus dem Vergleich der 1. Euler’schen Formel mit der Polarform:

$z\;=\;r\cdot e^{\mathrm {i} \varphi }\;=\;r\cdot (\cos \varphi +\mathrm {i} \,\sin \varphi )$

Die Exponentialform kann also auch als Verkürzung der Polarform angesehen werden. Es gelten die gleichen Beziehungen wie bei der Definition der Polarform:

$r\;=\;{\sqrt {a^{2}+b^{2}}}\qquad \varphi \;=\;\arctan {\frac {b}{a}}+k\,\pi$

Rechenregeln

Einige Rechenregeln für komplexe Zahlen vereinfachen sich bei Verwendung der Exponentialform. Dies ergibt sich aus den Rechenregeln für Potenzen mit e als Basis:

${\begin{array}{lrcl}{\text{Multiplikation:}}\quad &z_{1}\cdot z_{2}&=&r_{1}\cdot e^{\mathrm {i} \varphi _{1}}\cdot r_{2}\cdot e^{\mathrm {i} \varphi _{2}}\\&&=&r_{1}\cdot r_{2}\cdot e^{\mathrm {i} \,(\varphi _{1}+\varphi _{2})}\\{\text{Division:}}\quad &{\frac {z_{1}}{z_{2}}}&=&{\frac {r_{1}\cdot e^{\mathrm {i} \varphi _{1}}}{r_{2}\cdot e^{\mathrm {i} \varphi _{2}}}}\\&&=&{\frac {r_{1}}{r_{2}}}\cdot e^{\mathrm {i} \,(\varphi _{1}-\varphi _{2})}\\{\text{Potenzen:}}\quad &z^{n}&=&\left(r\cdot e^{\mathrm {i} \varphi }\right)^{n}\\&&=&r^{n}\cdot e^{\mathrm {i} (n\varphi )}\\{\text{Wurzeln:}}\quad &{\sqrt[{n}]{z}}&=&z^{\frac {1}{n}}\;=\;\left(r\cdot e^{\mathrm {i} \varphi }\right)^{\tfrac {1}{n}}\;=\;{\sqrt[{n}]{r}}\cdot e^{\mathrm {i} {\tfrac {\varphi }{n}}}\\\end{array}}$

Siehe auch  Eulersche Formel sowie  Taylorreihe

Die Riemann’sche Zahlenkugel

Die komplexen Zahlen lassen sich durch die Punkte einer Ebene (mit einem rechtwinkligen Koordinatensystem) darstellen, der Gauß-Ebene oder komplexen Zahlenebene. Jeder komplexen Zahl z entspricht genau ein Punkt der Ebene und umgekehrt. Der Abstand eines Punktes z vom Nullpunkt ist die reelle Zahl $|z|$.

Das Innere des Kreises um einen Punkt $z_{0}$ mit dem Radius $r$ wird durch $\;|z-z_{0}|<r\;$ bezeichnet. Demgegenüber meint $\;|z-z_{0}|>r\;$ denjenigen Teil der Gauß’schen Ebene, der außerhalb des Kreises liegt. Das Äußere eines Kreises bezeichnet man auch als eine Umgebung des uneigentlichen Punktes $\;z=\infty \!$. (Dabei wird „Umgebung“ als Verallgemeinerung des üblichen Begriffs verstanden; das ist ein Thema der Topologie.)

Auf der riemannschen Zahlenkugel sind die komplexen Zahlen einschließlich ∞ darstellbar.

Stereographische Rückprojektionen der komplexen Zahlen $A$ und $B$ auf die Punkte $\alpha$ und $\beta$ der riemannschen Zahlenkugel.

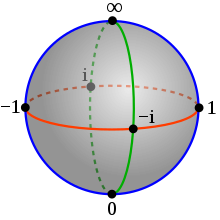
Wenn man einen solchen Punkt in der Unendlichkeit zur komplexen Ebene hinzunimmt, erhält man die riemannsche Zahlenkugel $\;{\hat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}\!$.

Anschaulich handelt es sich um eine Kugel vom Radius 1, deren Nordpol auf (0,0,1) liegt (man darf die Kugel beliebig wählen, solange ihr Nordpol (0,0,1) ist). Dem unendlich fernen Punkt $\infty$ wird dieser Nordpol $U$ der Kugel zugeordnet und jedem Punkt $P$ der komplexen Zahlenebene der von $U$ verschiedene Schnittpunkt der Kugeloberfläche mit der Geraden durch $PU$ (stereografische Projektion).

Siehe auch  Riemannsche Zahlenkugel

Gauß’sche Zahlen

Einführung

Gauß’sche Zahlen als Gitterpunkte in der komplexen Zahlenebene

Die gaußschen Zahlen sind eine Verallgemeinerung der ganzen Zahlen in den komplexen Zahlen. Eine gaußsche Zahl g ist definiert durch:

$g=a+b\,\mathrm {i} \quad {\text{mit}}\quad a,b\in \mathbb {Z}$

In der gaußschen Zahlenebene entsprechen die gaußschen Zahlen den Punkten mit ganzzahligen Koordinaten. Sie bilden ein zweidimensionales Gitter.

Primelemente in der komplexen Ebene.

Die gaußschen Zahlen werden mit $\mathbb {Z} [\mathrm {i} ]$ bezeichnet. Sie bilden einen Ring (im Sinne der Algebra) bezüglich Addition und Multiplikation, und zwar mit den Zahlen $\pm 1,\pm \mathrm {i}$ als Einheiten.

Primelemente

Auf dieser Grundlage lassen sich Primelemente als Verallgemeinerung des Begriffs Primzahl definieren (wir befassen uns bei der Verallgemeinerung nur mit $\mathbb {Z} [\mathrm {i} ]\!$):

Definition (Primelement der gaußschen Zahlen)

Ein Element $c\in \mathbb {Z} [\mathrm {i} ]$ heißt Primelement, falls $c$ weder 0 noch eine Einheit ist und für alle Elemente $a,\;b\in \mathbb {Z} [\mathrm {i} ]$ gilt: Ist $c$ ein Teiler des Produkts $ab\!$, so ist $c$ stets ein Teiler von $a$ oder von $b\!$.

Für Primelemente gelten u. a. folgende Sätze:

• Ist $c$ ein Primelement und $e$ eine Einheit, so ist $ce$ ebenfalls ein Primelement. – Dies lässt sich in der Darstellung rechts ablesen: Durch Multiplikation mit den Einheiten entsteht die Rotationssymmetrie um 90°. Weil mit $\;a+b\,\mathrm {i} \;$ auch $\;b+a\,\mathrm {i} \;$ Primelement ist, liegen die Primelemente zusätzlich symmetrisch zu den Diagonalen.
• Die Eindeutigkeit der Primfaktordarstellung gilt (abgesehen von der Multiplikation mit Einheiten) auch für die gaußschen Zahlen.

Ein „kleinstes“ Primelement kann nicht angegeben werden, weil die komplexen Zahlen nicht angeordnet werden können. Wir können aber den Betrag prüfen: Abgesehen von den Einheiten hat jede gaußsche Zahl einen Betrag von mindestens ${\sqrt {2}}\!$, nämlich für $\;1+\mathrm {i} \!$. Also hat (nach den Multiplikationsregeln) jedes Produkt zweier gaußschen Zahlen, die keine Einheiten sind, einen Betrag von mindestens 2. Die einzige gaußsche Zahl im ersten Quadranten mit einem Betrag kleiner als 2 ist gerade $\;1+\mathrm {i} \;$ und ist also ein Primelement. Durch Multiplikation mit den Einheiten erhält man als weitere Primelemente $\;\pm 1\pm \mathrm {i} \!$. Siehe dazu beispielsweise die folgenden Beziehungen:

$1+\mathrm {i} \;=\;\mathrm {i} \cdot (1-\mathrm {i} )\;=\;-\mathrm {i} \cdot (\mathrm {i} -1)\;=\;-(-\mathrm {i} -1)$

Primzahlen und Primelemente

Die Primelemente im Ring der gaußschen Zahlen haben einen engen Bezug zu den gewöhnlichen Primzahlen. Die Primzahlen $\mathbb {P} \subset \mathbb {Z}$ (betrachtet als gaußsche Zahlen, also als komplexe Zahlen) zerfallen in drei Klassen:

Der doppelte Primfaktor von 2

Die Zahl 2 kann als Produkt der Primelemente $\;1+\mathrm {i} \;$ und $\;1-\mathrm {i} \;$ geschrieben werden, die sich aber eben nur um eine Einheit unterscheiden (das wird als „verzweigt“ bezeichnet):

$2\;=\;-\mathrm {i} \cdot (1+\mathrm {i} )^{2}\;=\;(1+\mathrm {i} )(1-\mathrm {i} )$

Diese Primfaktorzerlegung der Zahl 2 im Ring der gaußschen Zahlen ist im Wesentlichen eindeutig, aber es kann keiner Darstellung der Vorzug gegeben werden, da die komplexen Zahlen und damit auch die gaußschen Zahlen und deren Einheiten nicht angeordnet werden können.

Faktoren von Primzahlen der Form 4k + 1

Ist $p$ eine Primzahl, die die Form $\;p=4k+1\;$ mit $\;k\in \mathbb {Z} \;$ hat, so kann man zeigen, dass sich $p$ auf im Wesentlichen eindeutige Weise als Summe zweier Quadratzahlen schreiben lässt:

$p\;=\;a^{2}+b^{2}\qquad {\mbox{mit gewissen}}\quad a,\;b\in \mathbb {Z}$

Dann ist dies die Primfaktorzerlegung von p:

$p\;=\;(a+b\,\mathrm {i} )(a-b\,\mathrm {i} )$

p selbst ist also kein Primelement im Ring der gaußschen Zahlen, sondern Produkt von zwei zueinander konjugierten Primelementen (p wird als „zerlegt“ bezeichnet). Beispielsweise ist $\;5=(2+\mathrm {i} )(2-\mathrm {i} )\;$ kein Primelement, aber $\;2+\mathrm {i} \;$ und $\;2-\mathrm {i} \;$ sind zwei Primelemente.

Primzahlen der Form 4k + 3

Ist p eine Primzahl der Form $\;4k+3\;$ mit $\;k\in \mathbb {Z} \!$, so ist p auch im Ring der gaußschen Zahlen ein Primelement (p bleibt prim, es wird als „träge“ bezeichnet).

Folgerungen

In der Zahlentheorie wird gezeigt, dass jedes Primelement von $\mathbb {Z} [\mathrm {i} ]$ genau eine Primzahl $\;p\in \mathbb {P}$ teilt. Dadurch erhält man auch eine Zerlegung der Primelemente von $\mathbb {Z} [\mathrm {i} ]\!$:

• den Teiler $\;1+\mathrm {i} \;$ der verzweigten Primzahl $\;2\in \mathbb {Z} \;$ sowie dessen Produkte mit den Einheiten
• die Teiler $\;a\pm \mathrm {i} b\;$ der zerlegten Primzahlen $\;a^{2}+b^{2}\in \mathbb {P} \;$ sowie deren Produkte mit den Einheiten
• die trägen Primzahlen selbst sowie ihre Produkte mit den Einheiten (diese Primzahlen haben außer sich selbst ja nur Einheiten als Teiler)

Siehe auch  Gaußsche Zahl –  Primelement –  Ring

Mandelbrot-Menge

Mandelbrot-Menge (schwarz) mit farbig dargestellter Umgebung. Jedem Pixel ist eine komplexe Zahl $c$ zugeordnet. Farbig kodiert ist die Anzahl der Iterationen $\;x=x^{2}+c\!$, die notwendig ist, einen Betrag von 10³ zu überschreiten. Sie wächst von Farbstreifen zu Farbstreifen um 1.

Animierte Zoomfahrt in die Mandelbrot-Menge.

Die Mandelbrot-Menge ist eine fraktal erscheinende Menge, die eine bedeutende Rolle in der Chaosforschung spielt. Die Visualisierung der Menge wird im allgemeinen Sprachgebrauch oft Apfelmännchen genannt.

Die Mandelbrot-Menge $\mathbb {M}$ ist die Menge aller komplexen Zahlen c, für welche die rekursiv definierte Folge komplexer Zahlen $\;z_{0},\;z_{1},\;z_{2}\;\dotsc \;$ mit dem Bildungsgesetz

$z_{n+1}\;=\;z_{n}^{2}+c$

und dem Anfangsglied

$z_{0}\;=\;0$

beschränkt bleibt, das heißt, der Betrag der Folgenglieder wächst nicht über alle Grenzen. Die grafische Darstellung dieser Menge erfolgt in der komplexen Ebene. Die Punkte der Menge werden dabei in der Regel schwarz dargestellt und der Rest farbig, wobei die Farbe eines Punktes den Grad der Divergenz der zugehörigen Folge widerspiegelt.

Das Bildungsgesetz, das der Folge zugrundeliegt, ist die einfachste nichtlineare Gleichung, anhand der sich der Übergang von Ordnung zu Chaos durch Variation eines Parameters provozieren lässt.

Die grafische Darstellung der Mandelbrot-Menge und ihrer Strukturen im Randbereich ist nur mittels Computer durch sogenannte Fraktalgeneratoren möglich. Der Computer ermittelt für jeden Bildpunkt, ob die zugehörige Folge divergiert oder nicht. Sobald der Betrag $|z_{n}|$ eines Folgengliedes den Wert $\;R=2\;$ überschreitet, divergiert die Folge. Die Zahl der Iterationsschritte N gemäß obiger Rekursionsformel, nach denen das erfolgt, kann als Maß für den Divergenzgrad herangezogen werden. Über eine zuvor festgelegte Farbtabelle, die jedem Wert N eine Farbe zuordnet, wird in diesem Fall dem Bildpunkt eine Farbe zugewiesen.

Im Wikipedia-Artikel Mandelbrot-Menge finden sich grafische Darstellungen über die Iteration. Eine animierte Darstellung der Entwicklung bietet Wolfgang Beyer.

Siehe auch  Fraktal –  Chaosforschung