Linearisierung von resistiven Sensoren/ Kaltleiter

Einleitung

Widerstand des Si-Kaltleiters als Funktion der Temperatur T

Schaltung für linearisierten Betrieb des KTY11

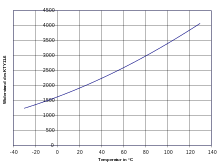
Zur elektrischen Messung der Temperatur werden häufig Kaltleiter eingesetzt. Für den Kaltleiter KTY11-6 gilt im Temperaturbereich von –50 °C bis +150 °C folgender Zusammenhang zwischen Widerstand R_KTY und der Temperatur T:

$R_{KTY}=2000\Omega \cdot (1+\alpha \cdot (T-25^{0}C)+\beta \cdot (T-25^{0}C)^{2})$

mit den Konstanten

$\alpha =7,88\cdot 10^{-3}\cdot 1/K$ ; $\beta =1,937\cdot 10^{-5}\cdot 1/K^{2}$

Dieser reproduzierbare Zusammenhang zwischen Temperatur und Widerstand ist Teil einer Parabel (Bild rechts). Wenn durch den Kaltleiter ein konstanter Strom von z. B. 1 mA läuft, ist die Spannungsänderung nicht proportional zur Temperaturänderung, weil die Kurve immer steiler wird. So gehört zu einer Temperaturerhöhung von -30 °C auf -20 °C eine Spannungsänderung von 119 mV. Bei einer Temperaturerhöhung von 120 °C auf 130 °C steigt die Spannung aber um 235 mV - das ist fast doppelt so viel! Dieser Messfehler ist nicht tragbar und lässt sich in einem weiten Bereich eliminieren:

Eine einfache Schaltungsänderung sorgt dafür, dass der Strom durch den Kaltleiter abnimmt, wenn sein Widerstand steigt. Dann kann die Spannung am Kaltleiter nicht immer weiter wie eine Parabel ansteigen, sie muss sich asymptotisch der Maximalspannung nähern. Die Kurve wird S-förmig mit einem Wendepunkt, in dessen Umgebung ein fast linearer Verlauf vorliegt. Die nebenstehende Schaltung hat zusätzlich den Vorteil, dass die aufwendige Konstantstromquelle durch die üblicherlicherweise sowieso vorhandene Konstantspannungsquelle (hier +5 V) ersetzt wird. Kritisch ist der Wert des Vorwiderstandes (in diesem Fall 5000 Ohm), der sich auf zwei Arten bestimmen lässt:

• Man stellt den Funktionsterm der Schaltung auf und ermittelt den Wendepunkt durch zweimaliges Differenzieren. Dann wird der Vorwiderstand so festgelegt, dass der Wendepunkt in der Mitte des gewünschten Temperaturintervalls liegt.
• Man startet eine Tabellenkalkulation, programmiert die Gleichung für die im Bild rechts gezeigte Spannungsteilerschaltung. Der Wert des Vorwiderstandes wird so lange variiert, bis gute Linearität erreicht ist. Das lässt sich einfach mit der "1. Differenz" überprüfen. Aus dieser Tabelle wird zuletzt die gesuchte Geradengleichung ermittelt. Dieses Vorgehen führt rasch zum Ziel und wird nachfolgend schrittweise erläutert.

Tabelle erzeugen

Kalkulationsblatt für Linearisierung

In den Spalten A und B wird der Widerstand des KTY11 mit der oben angegebenen Formel für den gewünschten Temperaturbereich von -30 °C bis 130 °C berechnet. In der Spalte C wird für die Spannung am Kaltleiter für die im Bild gezeigte Schaltung mit der Spannungsteiler-Formel

$U_{KTY}={\frac {U_{0}\cdot R_{KTY}}{R_{KTY}+R_{Serie}}}$

berechnet. Über der Spalte C kann man sehen, wie diese Formel in der Syntax der Tabellenkalkulation für das Feld C9 aussieht.

Linearität optimieren

Der einzige änderbare Wert dieser Schaltung - der Serienwiderstand R_Serie - muss nun bestimmt werden. Dazu werden in der Spalte D die "1. Differenzen" berechnet, das ist die Differenz der Nachbarn. Beispielsweise gilt: D12 = 100000*(C12-C11); (Der Faktor 100000 wurde eingefügt, um die Werte im Kalkulationsblatt lesbarer darzustellen; jeder andere Faktor ist genauso gut). Zweckmäßigerweise stellt man die Werte der D-Spalte graphisch dar und variiert den Wert von R_Serie (im gelb unterlegten Feld D2) nach folgenden Kriterien:

• Die absoluten Werte der D-Spalte sind nicht ausschlaggebend, sie sollen nur möglichst gleich groß sein.
• Das Gesamtbild der Funktion darf nicht nur monoton steigen oder fallen; es sollte etwa achsensymmetrisch sein.
• Wenn alle Werte gleich sind, ist die Linearität perfekt.

Geradengleichung ermitteln

Abweichung der berechneten Temperatur nach 1.Linearisierung der Kennlinie

Abweichung der berechneten Temperatur nach der Koordinatenverschiebung

Kalkulationsblatt für Linearisierung 3. Grades

Ziel der Linearisierung ist, die Werte der Spalte A durch eine simple Geradengleichung der Form

$\!\,T=m\cdot U_{KTY}-t$

aus den Werten der Spalte C zu errechnen. Die beiden Parameter m und t kann man entweder durch lineare Regression bestimmen oder auch durch "Versuch und Irrtum":

• m bestimmt man aus der ersten und letzten Zeile mit der Formel m = (A21-A5)/(C21-C5)
• Für t wählt man einen Schätzwert (hier zunächst 160)

Damit wird für jeden "Messwert" der Spalte C die Temperatur berechnet und in Spalte F eingetragen. Für das Feld F5 lautet die entsprechende Formel so: =C5*$F$2-$F$3. Die Parameter m und t werden so variiert, dass die Spalte A etwa reproduziert wird.

Die Differenz zum Sollresultat aus Spalte A wird zeilenweise in Spalte G berechnet - hier sollten idealerweise nur Nullen stehen. Diesem Ziel kann man durch Feinabgleich der Parameter m und t mit der Funktion "Zielwertsuche" näher kommen. Die Lösung lautet in diesem Beispiel

$T=128,3\cdot U_{KTY}-158,8$

Im Bild rechts erkennt man, dass der absolute Fehler von maximal ±1 °C bei Temperaturen um -5 °C und +85 °C erreicht wird und an den Bereichsenden wieder abnimmt. Wenn diese Genauigkeit ausreicht, ist die Aufgabe abgeschlossen.

Weitere Verbesserung der Linearität

Ein Mathematiker erkennt am S-förmigen Kurvenverlauf im Bild, dass die geringen Restfehler nach der 1.Linearisierung durch ein Polynom 3. Grades verursacht werden, das zur Geradengleichung addiert werden muss. Dieses Polynom lautet in der allgemeinsten Form

$T=a\cdot (U_{KTY})^{3}+b\cdot (U_{KTY})^{2}+c\cdot U_{KTY}+d$

Der Faktor b kann durch eine Koordinatenverschiebung (dU) eliminiert werden, c und d entsprechen geringen Änderungen von m und t. Ziel ist, den diagonal verlaufenden mittleren Teil der S-Kurve horizontal zu "biegen". Der Wendepunkt muss auf der horizontalen Achse liegen. Dazu werden die "alten" Werte von m und t zu Vergleichszwecken in die Felder G2 und G3 kopiert und dann die "neuen" Werte in den Feldern F2 und F3 experimentell ermittelt. Das Ergebnis mit m =124 und t =152,13 ist im Bild darunter zu sehen und wird durch die Funktion

$diff=a\cdot (U_{KTY}-dU)^{3}$

mit a = -10,89 und dU = 1,56 modelliert. Diese Faktoren werden wieder durch Versuch-und-Irrtum gefunden, indem man die "Korrektur 3. Grades" in der Spalte H des Kalkulationsblattes für jeden Wert von U_KTY berechnet und a und dU so lange variiert, bis die Restfehler der Nachbarspalte G nachvollzogen sind. Werden am Schluss die errechneten Daten der Spalten F und H in der Spalte G zusammengefasst und mit den Sollwerten der Spalte A verglichen, weicht kein Ergebnis um mehr als 0,1 °C vom Sollwert ab. Das übertrifft die Fertigungstoleranz von ±1 % bei weitem, auf weitere Verbesserungen kann verzichtet werden.

Zusammenfassung

Die Gesamtformel als Zahlenwertgleichung lautet:

$T=124\cdot U_{KTY}-152,13+10,89\cdot (U_{KTY}-1,56)^{3}$

Einzelnachweise

Zurück zum Inhaltsverzeichnis