Materialwirtschaft: Beschaffung: Arten der Bedarfsdeckung: Vorratsbeschaffung: Optimale Bestellmenge
Definition der optimalen Bestellmenge
[Bearbeiten]Die optimale Bestellmenge bezeichnet den Punkt, an dem die fixen und variablen Lager- und Bezugskosten ihr Minimum annehmen. Die optimale Bestellmenge ist daher sowohl für das Bestellpunktverfahren als auch für das Bestellrhythmusverfahren von großer Bedeutung zur Festsetzung von Bestellmenge und Höchstbestand.
Was zunächst einfach klingt wird kompliziert, wenn man sich vor Augen führt, dass Lager- und Bezugskosten konträre Elemente sind:

- Je höher die georderte Bestellmenge, desto höher fallen die Lagerkosten aus, während sich die Bezugskosten durch Rabatte mindern. Das im Lager gebundene Kapital kann nicht anderweitig im Unternehmen verwendet werden.
- Je geringer die Bestellmenge, desto niedriger sind Lagerkosten und Kapitalbindung bei gleichzeitig hoher Lagerumschlagshäufigkeit. Jedoch bedeutet eine geringe Bestellmenge auch mehr Bestellungen bei gleichem Bedarf und damit höhere Kosten für Transport und Verpackung bei gleichzeitig geringeren Rabatten. Dem Unternehmen steht allerdings aktuell Kapital zur Verfügung, welches sonst im Lager gebunden wäre.
Dieser Zielkonflikt macht das Bestimmen der optimalen Bestellmenge nötig.
Tabellarische Lösung
[Bearbeiten]In der tabellarischen Lösung werden die Kosten tabellarisch für verschiedenen mögliche Bestellmengen aufgeschlüsselt und schließlich die Bestellmenge ausgesucht, welche die niedrigsten Gesamtkosten hat. Die Lagerkosten und Kapitalbindung werden dabei meist prozentual vom durchschnittlichen Lagerbestand berechnet:
|
Beispiel
|
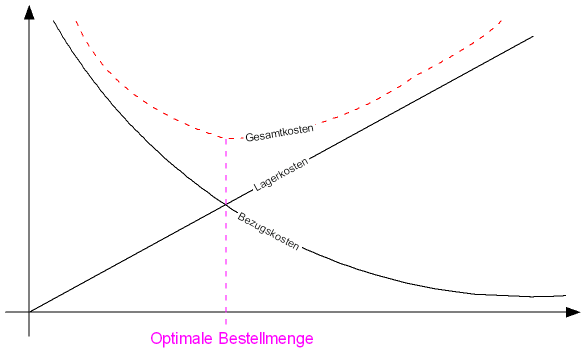
Grafische Lösung
[Bearbeiten]Mittels eines Kostengraphen lässt sich bei konstantem Verbrauch ebenso die optimale Bestellmenge ermitteln:
- Am Minimum der Gesamtkostenkurve
- Am Schnittpunkt zwischen Lagerkostengerade und Bezugskostenkurve
Rechnerische Lösung nach Kurt Andler
[Bearbeiten]Noch leichter lässt sich die optimale Bestellmenge mit der sogenannten Andlerschen Formel (allgemein: Klassische Losformel) berechnen, welche obige graphische Lösung rechnerisch umsetzt:
- : Optimale Bestellmenge
- : Jahresbedarfsmenge
- : Bestellkosten
- : Kaufpreis je Mengeneinheit (auch: Einstandspreis)
- : Lagerhaltungskostensatz (Zinssatz + Lagerkostensatz in %)
Aber funktioniert das auch? Nehmen wir die Angaben aus der tabellarischen Lösung und setzen sie in die Andlersche Formel ein. Das Ergebnis müsste ja ähnlich aussehen.
|
Beispiel
|
Übungsaufgaben
[Bearbeiten]
|
Übung 1
|
|
Übung 2 (Transfer)
|