Mathe für Nicht-Freaks: Buchanfang Maßtheorie by Richard4321/ Jordan-Inhalt
Formale Herleitung und wichtige Eigenschaften des w:Jordan-Maß
Innerer und äußerer Peano-Jordan-Inhalt[Bearbeiten]
Definition
Sei .
-
Der innere Peano-Jordan-Inhalt ist definiert als
Wir nehmen also das "Maximum" der Flächeninhalte von Quaderfiguren innerhalb von . Da das Maximum eventuell durch Quaderfiguren nicht angenommen wird, wählen wir das Supremum, das immer existiert.
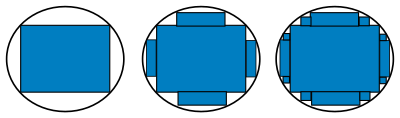
Ausschöpfung eines Kreises mit Rechtecken -
Der äußere Peano-Jordan-Inhalt ist definiert als
Wir nehmen also das "Minimum" der Flächeninhalte von Quaderfiguren, die überdecken. Da das Minimum eventuell durch Quaderfiguren nicht angenommen wird, wählen wir das Infimum, das immer existiert.

Überdeckung eines Kreises mit Rechtecken -
Die Menge heißt Peano-Jordan-messbar genau dann wenn innerer und äußerer Peano-Jordan-Inhalt gleich sind
Der innere Inhalt ist kleiner als der äußere[Bearbeiten]
Da der innere Inhalt berechnet wird über Quaderfiguren, die innerhalb liegen, und der äußere berechnet wird über Quaderfiguren, die überdecken, sollte der äußere Peano-Jordan-Inhalt immer größer sein als der innere. Und das ist auch der Fall:
Satz
Es gilt für jedes
Beweis
Es gilt
Wir haben im letzten Kapitel gezeigt, dass der Inhalt auf den Quaderfiguren monoton ist Mathe_für_Nicht-Freaks: Buchanfang_Maßtheorie_by_Richard4321/ Quader-_und_Rechtecksfiguren#Eigenschaft_eines_Inhalts:_Monotonie, daher folgt
Geht man links zum Supremum und rechts zum Infimum über, bleibt das Kleiner-Gleich-Zeichen erhalten.
Das ist aber genau die Definition von innerem und äußerem Peano-Jordan-Inhalt
Quaderfiguren sind messbar mit bekanntem Inhalt[Bearbeiten]
Für Quaderfiguren erwarten wir, dass sie messbar sind der Inhalt aus dem letzten Kapitel denselben Wert annimmt wie der Peano-Jordan-Inhalt. Das müssen wir dennoch kurz beweisen.
Satz
Quaderfiguren sind Peano-Jordan-messbar und ihr Peano-Jordan-Inhalt ist genau der Inhalt, den wir in letztem Kapitel festgelegt haben
Beweis
Verwende selbst als echtes Maximum der Ausschöpfungen von mit Quaderfiguren und als echtes Minimum der Überdeckungen mit Quaderfiguren, das ergibt
Damit liegt der Wert fest und insbesondere sind Quaderfiguren Peano-Jordan-messbar.
Sub-/Superadditivität von äußerem/innerem Inhalt[Bearbeiten]
Wir wollen im übernächsten Satz die Additivität des Peano-Jordan-Inhaltes zeigen und benötigen dazu folgende zwei Ungleichungen .
Satz
Seien beliebig. Dann gilt
-
Der äußere Peano-Jordan-Inhalt ist subadditiv
Wenn sich die Mengen überschneiden, ist anschaulich ihre Fläche kleiner als die Summe der Einzelflächen. Das sagt die Gleichung aus.
-
Seien die zudem disjunkt. Dann ist der innere Peano-Jordan-Inhalt superadditiv
Beweis
Sei . Da das äußere Maß als Infimum definiert ist, gibt es für jedes ein sodass
Weil die Vereinigung der wieder eine Quaderfigur ist Mathe_für_Nicht-Freaks: Buchanfang_Maßtheorie_by_Richard4321/_Quader-_und Rechtecksfiguren#Vereinigung_zweier_Quaderfiguren, die zudem enthält, gilt mit der Definition des äußeren Maßes als Infimum
Mit der Subadditivität des Inhaltes auf Quaderfiguren Mathe_für_Nicht-Freaks:_Buchanfang_Maßtheorie_by_Richard4321/ Quader-_und_Rechtecksfiguren#Eigenschaft_von_Inhalten: Subadditivität folgen dann
Da beliebig war, folgt die Behauptung.
Ganz analog folgt Superadditivität: Sei . Da das innere Maß als Supremum definiert ist, gibt es für jedes ein sodass
Weil die disjunkte Vereinigung der (da die schon disjunkt waren) wieder eine Quaderfigur ist, die zudem enthält, gilt mit der Definition des inneren Maßes als Supremum
Mit der Additivität des Inhaltes auf Quaderfiguren Mathe_für_Nicht-Freaks: Buchanfang_Maßtheorie_by_Richard4321/ Quader-_und_Rechtecksfiguren#Inhaltsfunktion folgen dann
Da beliebig war, folgt die Behauptung.
Der Peano-Jordan-Inhalt ist additiv[Bearbeiten]
Nun kommen wir zur entscheidenden Eigenschaft des Peano-Jordan-Imhaltes.
Satz
Seien Peano-Jordan-messbar und disjunkt. Dann ist Peano-Jordan-messbar und es gilt
Beweis
Mit dem letzten Satz folgt die Behauptung.
Eigenschaften des Jordanmaßes[Bearbeiten]
Inhalt statt Maß
Ergänzung: Der Jordan-Inhalt ist Subadditiv (wurde im vorherigen Abschnitt für Quaderfiguren gezeigt)
Zeige: Positivität und Monotonie von innerem und äußerem Jordan- Inhalt
Zeige: Nullmengen des äußeren Maßes sind Jordan-messbar.
Zeige: für beschränkte Jordan-messbare und beliebige (!) Zeige : Sind beschränkt und Jordan messbar, so auch und
Zeige: Sei beschränkt und Jordan messbar. Dann ist die Klasse der Jordan-messbaren Teilmengen von eine Algebra
Topologie: und etc...
Zeige ist nicht Jordan-messbar.
Zeige die Menge ist nicht Jordan-messbar, obwohl anschaulich der Flächeninhalt sein müsste.
warum können diese Mengen disjunkt vereinigt werden? Konstruiere die zu vereinigenden Mengen, sodass sie disjunkt sind:
Daher erweitern wir unsere Definition auf abzählbare Überdeckungen zum Lebesguemaß
Literatur[Bearbeiten]
- Eigenschaften: http://www.jkrieger.de/mathe/analysis/node66.html
- Zusammenfassung: https://www.encyclopediaofmath.org/index.php/Jordan_measure
- Skript, welches mit Jordan-Maß beginnt: https://www.alt.mathematik.uni-mainz.de/Members/froehli/skripte/ws2011/kapitel04.pdf











































![{\displaystyle \mathbb {Q} \cap [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/822d49c61001a9fd0fee4578855b367df40dc4ca)
![{\displaystyle (0,1]\times (0,1]\uplus (0,1]\times (0,1/2]\uplus (0,1]\times (0,1/4]\uplus ...}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84d8a97ac675f8a9c66ff8881fe7c7d85224cd36)

![{\displaystyle A_{n}=(0,1]\times (0,1/2^{n}],\quad \bigcup _{n\in \mathbb {N} }A_{n}=\bigsqcup _{n\in \mathbb {N} }A_{n}\setminus A_{n+1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d86077034f79d9016baabd5b5d58b0ee811cbbf6)