Näherung 1

(Planimetrie/ Die drei antiken Probleme/ Näherung 1)

(Planimetrie/ Die drei antiken Probleme/ Näherung 1)

Transformation Quadrat in Kreis

Tranformation Quadrat in Kreis

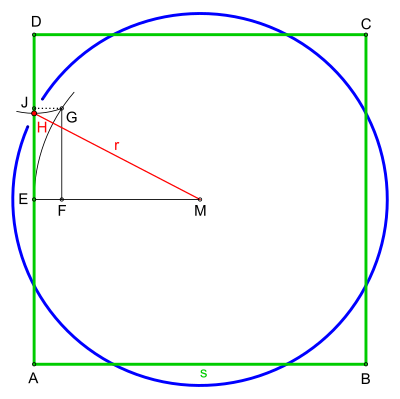
Näherungskonstruktion: Aus einem gegebenen Quadrat wird ein Kreis mit nahezu gleichem Flächeninhalt konstruiert, auch mit Zirkel und Lineal ohne Maßeinteilung darstellbar.

Die gepunktete Linie ab Punkt G sowie der Punkt J, dienen als Hilfe für die Berechnung des Radius r.

Konstruktion

1. Konstruiere ein Quadrat ABCD, dessen halbe Seitenlänge gleich EM ist.
2. Bestimme die Strecke EF, sie ist ein Sechstel der Strecke EM.
3. Zeichne einen Kreisbogen um den Mittelpunkt M mit dem Radius EM ab E.
4. Errichte eine Senkrechte auf EM in F bis sie den Kreisbogen um M in G schneidet.
5. Zeichne einen Kreisbogen um D mit dem Radius |DG| ab G bis er die Strecke AD in H schneidet.
6. Verbinde den Punkt H mit M; die Strecke HM ist der gesuchte Radius r.
7. Zeichne abschließend einen Kreis um den Mittelpunkt M mit dem Radius r.

Fehler

Bei einem Quadrat mit der Seite s = 1 [LE]:

• Konstruierter Radius r = 0,564189924824387...[LE]
• Soll-Radius r_s = ${\sqrt {\frac {1}{\pi }}}$ = 0,564189583547756...[LE]
• Absoluter Fehler = r - r_s = 0,000000341276631... = 3,412...E-7 [LE]
• Mit konstruiertem Radius r erzeugte Kreisfläche A = r² ⋅ ${\pi }$ = 1,000001209794523... [FE]
• Soll-Kreisfläche A_s = 1,0 [FE]
• Absoluter Fehler = A - A_s = 0,000001209794523... = 1,209...E-6 [FE]
  • Bei einem Quadrat mit der Seite s = 10 km wäre der Fehler des Radius r ≈ 3,4 mm
  • Bei einem Quadrat mit der Seite s = 1 m wäre der Fehler der Kreisfläche A ≈ 1,2 mm²

Berechnung

Die gepunktete Linie ab Punkt G sowie der Punkt J, dienen als Hilfe für die Berechnung des Radius r.

Rechtwinkeliges Dreieck FMG

(nicht eingezeichnet)

1.0  $\triangle {FMG}$

 Gegeben:

 ${\overline {GM}}={\overline {EM}}={\frac {1}{2}}\cdot s$

 ${\overline {EF}}={\frac {1}{12}}\cdot s$

1.1  ${\overline {FM}}={\overline {EM}}-{\overline {EF}}={\frac {1}{2}}\cdot s-{\frac {1}{12}}\cdot s={\frac {5}{12}}\cdot s$

1.2  ${\overline {FG}}={\overline {EJ}}={\sqrt {{\overline {GM}}^{2}-{\overline {FM}}^{2}}}=s\cdot {\sqrt {{\frac {1}{4}}-{\frac {25}{144}}}}=s\cdot {\sqrt {\frac {11}{144}}}$

 ${\overline {FG}}\approx 0,276385399196283\cdot s$

Rechtwinkeliges Dreieck JGD

(nicht eingezeichnet)

2.0  $\triangle {JGD}$

 Gegeben:

 ${\overline {DE}}={\overline {EM}}={\frac {1}{2}}\cdot s$

 ${\overline {GJ}}={\overline {EF}}={\frac {1}{12}}\cdot s\;\;\mathrm {(aus\;1.0)}$

 ${\overline {EJ}}={\overline {FG}}=s\cdot {\sqrt {\frac {11}{144}}}\;\;\mathrm {(aus\;1.2)}$

2.1  ${\overline {DJ}}={\overline {DE}}-{\overline {EJ}}={\frac {1}{2}}\cdot s-s\cdot {\sqrt {\frac {11}{144}}}=s\cdot {\frac {6-{\sqrt {11}}}{12}}$

 ${\overline {DJ}}\approx 0,223614600803716\cdot s$

2.2  ${\overline {DG}}={\sqrt {{\overline {DJ}}^{2}+{\overline {GJ}}^{2}}}=s\cdot {\sqrt {\left({\frac {6-{\sqrt {11}}}{12}}\right)^{2}+\left({\frac {1}{12}}\right)^{2}}}\;\;\Rightarrow s\cdot {\frac {1}{2}}\cdot {\sqrt {{\frac {1}{3}}\left(4-{\sqrt {11}}\right)}}$

 ${\overline {DG}}\approx 0,238637662863702\cdot s$

Rechtwinkeliges Dreieck EMH

(nicht eingezeichnet)

3.0  $\triangle {EMH}$

 Gegeben:

 ${\overline {EM}}={\frac {1}{2}}\cdot s$

 ${\overline {DH}}={\overline {DG}}=s\cdot {\frac {1}{2}}\cdot {\sqrt {{\frac {1}{3}}\left(4-{\sqrt {11}}\right)}}\;\;\mathrm {(aus\;2.2)}$

3.1  ${\overline {EH}}={\overline {DE}}-{\overline {DH}}=s\cdot {\frac {1}{2}}-s\cdot {\frac {1}{2}}\cdot {\sqrt {{\frac {1}{3}}\left(4-{\sqrt {11}}\right)}}\;\;\Rightarrow s\cdot \left({\frac {1}{2}}-{\frac {1}{2}}\cdot {\sqrt {{\frac {1}{3}}\left(4-{\sqrt {11}}\right)}}\right)$

 ${\overline {EH}}\approx 0,261362337136297\cdot s$

3.2 ${\overline {HM}}=r={\sqrt {{\overline {EH}}^{2}+{\overline {EM}}^{2}}}=s\cdot {\sqrt {\left({\frac {1}{2}}-{\frac {1}{2}}\cdot {\sqrt {{\frac {1}{3}}\left(4-{\sqrt {11}}\right)}}\right)^{2}+\left({\frac {1}{2}}\right)^{2}}}\;\;\Rightarrow s\cdot {\frac {1}{6}}\cdot {\sqrt {\left(3-{\sqrt {3\left(4-{\sqrt {11}}\right)}}\right)^{2}+9}}$

Konstruierter Radius des Kreises

$\mathbf {r=s\cdot {\frac {1}{6}}\cdot {\sqrt {\left(3-{\sqrt {3\left(4-{\sqrt {11}}\right)}}\right)^{2}+9}}\;\approx 0,564189924824387\cdot s} .$

Schema für die Näherungskonstruktion regelmäßiger Vielecke

01- Schema-Vielecke-wiki

Verwendungszweck: Als Hilfsmittel für regelmäßige Vielecke mit gegebenem Umkreis, die keine exakte Lösung haben.

Konstruktionsprinzip

• Eine Anwendung des dritten Strahlensatzes in Kombination mit Zahlenstrahlen.
• Die Hauptelemente sind zwei zueinander parallele Teilerstrahlen s₁ und s₄, ein auf s₁ senkrecht stehender Zahlenstrahl s₂ und ein zu s₂ paralleler Scheitelstrahl s₃.
• Es sind echte und unechte Brüche sowie Dezimalbrüche, die im Schema Platz finden, einsetzbar.
• Tipp: Auf einem Ausdruck der Basiskonstruktion die entsprechende Konstruktion manuell mit Schreibstift, Zirkel und Lineal fortsetzen.

Konstruktion

1. Zeichne durch den Punkt M einen Kreis - den späteren Umkreis des Vielecks - mit Radius r.
2. Zeichne zwei zueinander senkrechte Mittelachsen des Kreises. Der unten liegende Schnittpunkt (Mittelachse mit dem Umkreis) ist die erste Ecke A des Vielecks.
3. Zeichne eine Parallele s₁ zur Strecke MA durch den Punkt K.
4. Zeichne eine Parallele s₂ zur Strecke MK durch den Punkt A, es ergibt sich der Schnittpunkt L.
   
5. Teile die Strecke MA in drei Teile, es ergibt sich der Schnittpunkt r/3.
6. Trage die Länge r/3, vom Punkt K wegführend, ab Punkt L zweimal auf die Parallele s₁ ab, es ergeben sich die Schnittpunkte N und O.
7. Zeichne eine Parallele s₃ zur Parallele s₂ durch den Punkt O.
8. Setze den Punkt P, mit dem Abstand Strecke KO + Strecke MK (oder mit einem ähnlich großen Abstand) zum Punkt O auf die Parallele s₃.
9. Zeichne eine Parallele s₄ zur Parallele s₁ durch den Punkt P ca. gleich lang wie die Parallele s₁.
10. Trage die Strecke L r/3, einmal ab Punkt r/3 und fünfmal ab Punkt K auf der Parallele s₁ ab, es ergibt sich als zehnter Teilungspunkt der Schnittpunkt Q. Die Parallele s₁ wird im Folgenden als Teilerstrahl s₁ bezeichnet.
11. Trage die Strecke L r/3, ab Punkt P, zehnmal auf der Parallele s₄ ab, es ergibt sich als zehnter Teilungspunkt der Schnittpunkt S. Die Parallele s₄ wird im Folgenden als Teilerstrahl s₄ bezeichnet.
12. Verbinde den Punkt N mit dem Punkt R, es ergibt sich der Schnittpunkt V.
13. Zeichne eine Gerade ab dem Punkt S durch den Punkt N bis auf die Parallele s₃, es ergibt sich der Schnittpunkt T. Der Punkt T ist der Scheitelpunkt für die Strahlen, die vom Teilerstrahl s₄ ausgehen.
14. Zeichne eine Gerade ab dem Punkt Q durch den Punkt R bis auf die Parallele s₃, es ergibt sich der Schnittpunkt U. Der Punkt U ist der Scheitelpunkt für die Strahlen, die vom Teilerstrahl s₁ ausgehen.
15. Verbinde den Punkt L mit dem Punkt V, somit ist das Schema konstruiert.

Regelmäßige Vielecke mit gegebener Seite

Ohne Umkreis und ohne die beiden Mittelachsen ist das Schema auch für regelmäßige Vielecke mit gegebener Seite, die keine exakte Lösung haben, anwendbar.

Siehe hierzu die Beschreibung im Abschnitt "Das regelmäßige Neuneck" unter "Regelmäßiges Neuneck mit gegebener Seite".

Weblinks

  Dritter Strahlensatz
  Zahlenstrahl

Neuneck (Nonagon)

Näherungskonstruktion mit gegebenem Umkreis

Konstruktionsprinzip

• Die Hauptelemente sind zwei zueinander parallele Teilerstrahlen s₁ und s₄, ein auf s₁ senkrecht stehender Zahlenstrahl s₂ und ein zu s₂ paralleler Scheitelstrahl s₃.
• Von dem vorgegebenen Zähler werden die Dezimalstellen in der Reihenfolge Einer, Zehner, Hunderter u. s. w. jeweils mittels Projektion mit dem Faktor ${\frac {1}{10}}$ bzw. falls die nächste Dezimalstelle eine "0" ist, mit dem Faktor ${\frac {1}{100}}$ verkleinert und auf einem Teilerstrahl s₁ oder s₄ geometrisch addiert oder subtrahiert.
• Ansatz: Ein Bruch der die gewünschte Näherung an 2 ⋅ sin(180°/9) hat, sowie die Anwendung des dritten Strahlensatzes in kompakter Form.

Konstruktion

01-Neuneck-wiki-2

• Als Basiskonstruktion ist das Schema für die Näherungskonstruktion regelmäßiger Vielecke eingearbeitet.
• Alternative: Die Konstruktion manuell mit Zirkel und Lineal auf einem Ausdruck der Basiskonstruktion erstellen.

1. Wähle einen Dezimalbruch der die gewünschte Näherung an 2 ⋅ sin(180°/9) hat.
   • Die Qualität der Näherung ist einfach voraussehbar, wenn ein Dezimalbruch (Anzahl der Nullen im Nenner) eingesetzt wird.
   • Im dargestellten Beispiel ist der Dezimalbruch 68404/1E+5 = 684040/1E+6 = gewählt.
   • Sechs Nachkommastellen sind gleich dem Wert 2 ⋅ sin(180°/9) = 0,684040286651337...
2. Verbinde den vierten Punkt des Zahlenstrahls s₄ (Zahl 4, Einerstelle des Zählers vom Dezimalbruch) mit dem Scheitelpunkt T, es ergibt sich der Punkt 4 auf dem Zahlenstrahl s₁. Der Wert der Zahl 4 vom Zahlenstrahl s₄ ist dadurch verkleinert (Faktor 1/10).
   • Beachte: Die nächste Stelle (Zehner) des Zählers ist eine Null (0), deshalb muss der Wert der Zahl 4 vom Zahlenstrahl s₄, vor der geometrischen Addition mit der nächsten Dezimalstelle 4, mit dem Faktor 1/100 verkleinert sein!
3. Verbinde den Punkt 4 des Zahlenstrahls s₁ mit dem Scheitelpunkt U, es ergibt sich der Punkt 04. Der Wert der Zahl 4 vom Zahlenstrahl s₄ ist nun mit Faktor 1/100 verkleinert.
4. Greife die Strecke R04 ab und subtrahiere sie vom fünften Teilungspunkt des Zahlenstrahls s₁, es ergibt sich der Punkt 404. Da der Wert 404 sehr nahe am vierten Teilungspunkt liegt, wird dieser vor der geometrischen Subtraktion entfernt.
5. Verbinde den Punkt 404 des Zahlenstrahls s₁ mit dem Scheitelpunkt U, es ergibt sich der Punkt 404 auf dem Zahlenstrahl s₄.
6. Greife die Strecke P404 ab und addiere sie zum achten Teilungspunkt des Zahlestrahls s₄, es ergibt sich der Punkt 8404.
7. Verbinde den Punkt 8404 des Zahlenstrahls s₄ mit dem Scheitelpunkt T, es ergibt sich der Punkt 8404 auf dem Zahlenstrahl s₁.
8. Greife die Strecke O8404 ab und addiere sie zum sechsten Teilungspunkt des Zahlestrahls s₄, es ergibt sich der Punkt 68404.
9. Verbinde den Punkt 68404 des Zahlenstrahls s₄ mit dem Scheitelpunkt T, es ergibt sich der Punkt 68404 auf dem Zahlenstrahl s₁.
10. Greife die Strecke O68404 ab und addiere sie zum ersten Teilungspunkt N des Zahlestrahls s₁, es ergibt sich der Punkt W.
11. Zeichne eine Parallele zur Strecke LV durch den Punkt W bis zur Strecke NR, es ergibt sich der Schnittpunkt X. Die rote Strecke NX ist die Seite des Neunecks.
12. Trage die Strecke NX, ab Punkt A, achtmal mit dem Zirkel auf dem Umkreis ab.
13. Verbinde die benachbarten Eckpunkte miteinander, somit ergibt sich das Neuneck ABCDEFGHJ.

Fehler

Bei einem Umkreisradius r = 1 [LE]:

• Konstruierte Neuneckseite s = 0,68404 [LE]
• Soll-Neuneckseite s_s = 2 ⋅ sin(180°/9) ⋅ 1 [LE] = 0,684040286651337... [LE]
• Absoluter Fehler = s − s_s = -0,000000286651337... = -2.866...E-7 [LE]
  • Bei einem Umkreisradius r = 10 km wäre die Abweichung ≈ -2,9 mm

Berechnung

a) Für das dargestellte Beispiel: Konstruierte Neuneckseite $s=0{,}68404\cdot r$

b) Allgemein: Konstruierte Neuneckseite $s=Dezimalbruch\cdot r;$   Neuneckseite $s_{s}=0,684040286651337...\cdot r$   ($r$ = Umkreisradius)

• Die Berechnung der konstruierten Neuneckseite $s$ geschieht, aufgrund des Konstruktionsprinzips, schrittweise durch die geometrischen Additionen / Subtraktionen der einzelnen Zwischenergebnissen auf den Zahlenstrahlen $s_{1}$ bzw. $s_{4}$.
• Der vorgegebene Dezimalbruch ${\frac {68404}{1E+5}}\cdot r$ und somit die konstruierte Seite des Neunecks $s=0{,}68404\cdot r$ werden auf der Strecke ${\overline {NR}}$ prinzipiell exakt dargestellt.

Die Quadratur des Kreises

Näherungskonstruktion: Aus einem gegebenen Kreis wird ein Quadrat mit nahezu gleichem Flächeninhalt sowie der halbe Kreisumfang konstruiert, auch mit Zirkel und Lineal ohne Maßeinteilung darstellbar.

Version 1, halber Kreisumfang (π) als Strecke

Die Quadratur des Kreises und daraus den halben Kreisumfang (π) als Strecke

1. Zeichne zwei zueinander senkrechte Mittelachsen des Kreises.
2. Zeichne einen Kreis um den Mittelpunkt M, es ergeben sich die Schnittpunkte F und G auf den Mittelachsen.
3. Errichte eine Senkrechte zur Strecke MG durch den Punkt G und eine Senkrechte zur Strecke MF durch den Punkt F, die Senkrechten schneiden sich im Punkt H.
4. Konstruiere die Strecke GJ, sie ist ein Drittel der Strecke GH.
5. Halbiere die Strecke GJ, es ergibt sich der Punkt K.
6. Übertrage die Strecke GK auf die Strecke MG, es ergibt sich der Punkt L.
7. Zeichne eine Parallele zur Strecke GH ab dem Punkt L etwas länger als die Strecke GJ.
8. Übertrage die Strecke GK auf die Parallele aus 7., es ergibt sich der Punkt N.
9. Übertrage die Strecke GJ auf die Parallele aus 7., es ergibt sich der Punkt O.
10. Verbinde den Punkt K mit dem Punkt O.
11. Verbinde den Punkt N mit dem Punkt H, es ergibt sich der Schnittpunkt P.
12. Zeichne einen Kreisbogen mit dem Radius GK um den Punkt F, er schneidet die Strecke FH im Punkt Q, den Kreis im Punkt R und die Strecke FM im Punkt S.
13. Errichte eine Senkrechte zur Strecke FM durch den Punkt S und eine Parallele zur Strecke FM durch den Punkt R, es ergibt sich der Schnittpunkt T.
14. Verbinde den Punkt H mit dem Punkt T.
15. Zeichne eine Parallele zur Strecke HT durch den Punkt P bis zur Strecke Strecke NO, es ergibt sich der Schnittpunkt U auf dem Kreis und der Schnittpunkt V auf der Strecke NO.
16. Verbinde den Punkt V mit dem Punkt M. Die Strecke MV ist die halbe Seitenlänge bzw. der Inkreisradius des gesuchten Quadrates.
17. Zeichne einen Kreisbogen ab dem Punkt V bis auf die Strecke MG, es ergibt sich der Schnittpunkt W.
18. Übertrage die Strecke MW zweimal auf die Mittelachse MF und einmal auf die Mittelachse MG, es ergeben sich die Schnittpunkte X, Z, u. Y.
19. Konstruiere das Quadrat ABCD. Die Punkte W, X, Y u. Z sind Mittelpunkte der betreffenden Seiten des Quadrates.

Halber Kreisumfang (π) als Strecke

20. Errichte eine Senkrechte auf die Strecke FM im Punkt F.
21. Zeichne einen Kreisbogen um den Punkt M mit dem Radius AB (s), es ergibt sich der Schnittpunkt F₁.
22. Verbinde den Punkt F₁ mit dem Punkt M.
23. Verlängere die Strecke FM mit einer Geraden ab dem Punkt F.
24. Errichte eine Senkrechte auf die Strecke MF₁ im Punkt F₁, es ergibt sich der Schnittpunkt B₁ mit der Geraden aus 23..

Die Strecke $\mathbf {\overline {MF_{1}}}$ entspricht $\mathbf {\approx {\frac {1}{2}}U\;sowie\approx r\cdot \pi }$.

Fehler

Bei einem Kreis mit Radius r = 1 [LE]:

• Konstruierte Seite des Quadrates s = 1,77245384141934376... [LE]
• Soll-Seite des Quadrates s_s = ${\sqrt {\pi }}\cdot 1$ = 1,772453850905516... [LE]
• Absoluter Fehler = s - s_s = -0,000000009486172... = -9,486...E-9 [LE]
• Fläche des konstruierten Quadrates A = s² = 3,141592619962188... [FE]
• Soll-Fläche des Quadrates A_s = ${\pi }\cdot 1$ = 3,141592653589793... [FE]
• Absoluter Fehler = A - A_s = -0,000000033627605... = -3,3627...E-8 [FE]
• Fazit: Sieben Nachkommastellen sind gleich denen von ${\sqrt {\pi }}$ bzw. sind gleich denen von $\pi$.
  • Bei einem Kreis mit dem Radius r = 1000 km wäre der Fehler der Seite s ≈ -9,5 mm
  • Bei einem Kreis mit dem Radius r = 10 m wäre der Fehler der Fläche A ≈ -3,4 mm²
  • Bei einem Kreis mit dem Radius r = 100 km wäre der Fehler des halben Kreisumfanges U/2 ≈ -3,4 mm

Berechnung

Die gepunkteten schwarzen Linien sowie die Punkte A₁, B₁, C₁, D₁ und E₁ dienen als Hilfe für die Berechnung der Seite des Quadrates s.

Rechtwinkeliges Dreieck A₁HN

01-Quadratur-des Kreises-9-0-Berechnung-wiki

1.0   $\triangle {A_{1}HN}$

  Gegeben aus Zeichnung:

${\overline {A_{1}L}}={\overline {GH}}=r$

${\overline {A_{1}H}}={\overline {LN}}={\overline {NO}}={\overline {JK}}={\frac {1}{6}}r$

$\angle {OKJ}=\alpha =45^{\circ }$

1.1   $\sin \alpha =\cos \alpha ={\frac {1}{2}}{\sqrt {2}}={\frac {1}{\sqrt {2}}}$

1.2   ${\overline {A_{1}N}}={\overline {A_{1}L}}-{\overline {LN}}=r-{\frac {1}{6}}r={\frac {5}{6}}r$

1.3   Hypotenuse ${\overline {HN}}={\sqrt {{\overline {A_{1}N}}^{2}+{\overline {A_{1}H}}^{2}}}=r\cdot {\sqrt {\left({\frac {5}{6}}\right)^{2}+\left({\frac {1}{6}}\right)^{2}}}$   $\Rightarrow {\overline {HN}}=r\cdot {\sqrt {\frac {13}{18}}}$

01-Quadratur-des Kreises-9-0-Berechnung-wiki

  ${\overline {HN}}\approx 0{,}849836585598797\cdot r$

1.4   $\angle {A_{1}NH}=\beta =\arctan \left({\frac {\overline {A_{1}H}}{\overline {A_{1}N}}}\right)=\arctan \left({\frac {{\frac {1}{6}}r}{{\frac {5}{6}}r}}\right)\Rightarrow \beta =\arctan \left({\frac {1}{5}}\right)$

  $\beta \approx 11{,}30993247402021308^{\circ }$

1.5   $\tan \beta ={\frac {1}{5}}=0,2$

1.6   $\sin \beta ={\frac {\tan \beta }{\sqrt {1+\tan ^{2}\beta }}}={\frac {\frac {1}{5}}{\sqrt {1+\left({\frac {1}{5}}\right)^{2}}}}={\frac {1}{\sqrt {26}}}\approx 0{,}196116135138184$

1.7   $\cos \beta ={\sqrt {1-\sin ^{2}\beta }}={\sqrt {1-\left({\frac {1}{\sqrt {26}}}\right)^{2}}}={\frac {5}{\sqrt {26}}}\approx 0{,}980580675690920$

Stumpfwinkeliges Dreieck HKP (2.0) mit eingebundenem rechtwinkeligen Dreieck B₁PH (2.1)

01-Quadratur-des Kreises-9-0-Berechnung-wiki

2.0  $\triangle {HKP}$

 Gegeben:

 $\angle {OKJ}=\alpha =45^{\circ }\;(aus\;1.0)$

 $\sin \alpha =\cos \alpha ={\frac {1}{\sqrt {2}}}\;(aus\;1.1)$

 ${\overline {HK}}={\overline {A_{1}N}}={\frac {5}{6}}r\;(aus\;1.2)$

2.1  $\triangle {B_{1}PH}$

 Gegeben:

 $\angle {B_{1}HP}=\angle {A_{1}NH}=\beta =\arctan \left({\frac {1}{5}}\right)\;(aus\;1.4)$

 $\sin \beta ={\frac {1}{\sqrt {26}}}\;(aus\;1.6)$

 $\cos \beta ={\frac {5}{\sqrt {26}}}\;(aus\;1.7)$

01-Quadratur-des Kreises-9-0-Berechnung-wiki

 2.1.1  $\angle {HPB_{1}}=\gamma$

Berechnung des arithm. Ausdrucks

$\gamma =90^{\circ }-\beta$

Mit dem Additionstheorem

$\sin(90^{\circ }-\beta )=\sin 90^{\circ }\cdot \cos \beta -\cos 90^{\circ }\cdot \sin \beta$

ergibt sich:

 2.1.2  $\sin \gamma =\sin \left(90^{\circ }-\beta \right)=1\cdot {\frac {5}{\sqrt {26}}}-0={\frac {5}{\sqrt {26}}}\approx 0{,}980580675690920$

Mit dem Additionstheorem

$\sin(90^{\circ }-\beta )=\sin 90^{\circ }\cdot \cos \beta -\cos 90^{\circ }\cdot \sin \beta$

ergibt sich:

 2.1.3  $\cos \gamma =\cos \left(90^{\circ }-\beta \right)=0+1\cdot {\frac {1}{\sqrt {26}}}={\frac {1}{\sqrt {26}}}\approx 0{,}196116135138184$

$\gamma =\arcsin \left({\frac {5}{\sqrt {26}}}\right)=\arccos \left({\frac {1}{\sqrt {26}}}\right)\approx 78{,}6900675259797869^{\circ }$

01-Quadratur-des Kreises-9-0-Berechnung-wiki

2.2   $\angle {HPK}=\delta =\alpha +\gamma$

Berechnung des arithm. Ausdrucks

$\delta =45^{\circ }+\gamma$

Mit dem Additionstheorem

$\sin \left(45^{\circ }+\gamma \right)=\sin 45^{\circ }\cdot \cos \gamma +\cos 45^{\circ }\cdot \sin \gamma$

ergibt sich:

 2.2.1  $\sin \delta =\sin \left(45^{\circ }+\gamma \right)={\frac {1}{\sqrt {2}}}\cdot {\frac {1}{\sqrt {26}}}+{\frac {1}{\sqrt {2}}}\cdot {\frac {5}{\sqrt {26}}}={\frac {3}{\sqrt {13}}}\approx 0{,}832050294337843$

 2.2.2  $\delta =180^{\circ }-\arcsin \left({\frac {3}{\sqrt {13}}}\right)=180^{\circ }-56,309932474020...^{\circ }\approx 123{,}6900675259797869^{\circ }$

2.3   ${\overline {HP}}$

Mit dem Sinussatz ergibt sich:

 2.3.1  ${\overline {HP}}={\frac {{\overline {HK}}\cdot \sin \alpha }{\sin \delta }}={\frac {5}{6}}r\cdot {\frac {\frac {1}{\sqrt {2}}}{\frac {3}{\sqrt {13}}}}=r\cdot {\frac {5{\sqrt {26}}}{36}}$

${\overline {HP}}\approx 0{,}708197154665664\cdot r$

Gleichschenkeliges Dreieck MFR

01-Quadratur-des Kreises-9-0-Berechnung-wiki

3.0  $\triangle {MFR}$

 Gegeben aus Zeichnung:

 ${\overline {MF}}={\overline {MR}}=r$

 ${\overline {FR}}={\overline {FS}}={\frac {1}{6}}r$

3.1  $\epsilon =\angle {RMF}$

 Mit dem Kosinussatz ergibt sich:

 3.1.1   $\cos \epsilon ={\frac {{\overline {FM}}^{2}+{\overline {MR}}^{2}-{\overline {FR}}^{2}}{2{\overline {FM}}\cdot {\overline {MR}}}}={\frac {2-\left({\frac {1}{6}}\right)^{2}}{2}}\Rightarrow \cos \epsilon ={\frac {71}{72}}$

$\epsilon =\arccos \left({\frac {71}{72}}\right)\approx 9{,}560383694398317^{\circ }$

 3.1.2   $\sin \epsilon ={\sqrt {1-\cos ^{2}\epsilon }}$

3.2  Höhe zur Seite ${\overline {FM}}$

 3.2.1   ${\overline {C_{1}R}}=r\cdot \sin \epsilon =r\cdot {\sqrt {1-\left({\frac {71}{72}}\right)^{2}}}=r\cdot {\frac {\sqrt {143}}{72}}$

${\overline {C_{1}R}}\approx 0{,}166086954765297\cdot r$

Rechtwinkeliges Dreieck HE₁T

01-Quadratur-des Kreises-9-0-Berechnung-wiki

4.0  $\triangle {D_{1}HT}$

  Gegeben:

 ${\overline {D_{1}T}}={\overline {FS}}={\frac {1}{6}}r\;(aus\;1.0)$

 ${\overline {D_{1}F}}={\overline {C_{1}R}}=r\cdot {\frac {\sqrt {143}}{72}}\;(aus\;3.2)$

4.1  ${\overline {D_{1}H}}={\overline {HF}}+{\overline {D_{1}F}}=r\cdot \left(1+{\frac {\sqrt {143}}{72}}\right)$

 ${\overline {D_{1}H}}\approx 1{,}166086954765297\cdot r$

4.2  Hypotenuse   ${\overline {HT}}=r\cdot {\sqrt {{\overline {D_{1}H}}^{2}+{\overline {D_{1}T}}^{2}}}=r\cdot {\sqrt {\left(1+{\frac {\sqrt {143}}{72}}\right)^{2}+{\frac {1}{36}}}}$

 ${\overline {HT}}\approx 1{,}177937419327352\cdot r$

4.3  $\angle {THD_{1}}=\zeta =\arcsin \left({\frac {\overline {D_{1}T}}{\overline {HT}}}\right)=\arcsin \left({\frac {\frac {1}{6}}{\sqrt {\left(1+{\frac {\sqrt {143}}{72}}\right)^{2}+{\frac {1}{36}}}}}\right)\Rightarrow \zeta =\arcsin \left({\frac {1}{6\cdot {\sqrt {{\frac {1}{36}}+\left(1+{\frac {\sqrt {143}}{72}}\right)^{2}}}}}\right)$

 $\zeta \approx 8{,}134090101448814^{\circ }$

Rechtwinkeliges Dreieck A₁HN

01-Quadratur-des Kreises-9-0-Berechnung-wiki

5.0  $\triangle {A_{1}E_{1}H}$

 Gegeben:

 ${\overline {A_{1}H}}={\frac {1}{6}}r\;(aus\;1.0)$

 $\sin \zeta =\left({\frac {1}{6\cdot {\sqrt {{\frac {1}{36}}+\left(1+{\frac {\sqrt {143}}{72}}\right)^{2}}}}}\right)\approx 0,141490255706317\;(aus\;4.3)$

5.1  $\tan \zeta ={\frac {\sin \zeta }{\sqrt {1-\sin ^{2}\zeta }}}=\left({\frac {\frac {1}{6\cdot {\sqrt {{\frac {1}{36}}+\left(1+{\frac {\sqrt {143}}{72}}\right)^{2}}}}}{\sqrt {1-\left({\frac {1}{6\cdot {\sqrt {{\frac {1}{36}}+\left(1+{\frac {\sqrt {143}}{72}}\right)^{2}}}}}\right)^{2}}}}\right)\Rightarrow \tan \zeta =r\cdot \left({\frac {12}{72+{\sqrt {143}}}}\right)$

  $\tan \zeta \approx 0{,}142928163277679$

5.2  ${\overline {A_{1}E_{1}}}={\overline {A_{1}H}}\cdot \tan \zeta =r\cdot {\frac {1}{6}}\cdot \left({\frac {12}{72+{\sqrt {143}}}}\right)=r\cdot \left({\frac {2}{72+{\sqrt {143}}}}\right)$

 ${\overline {A_{1}E_{1}}}\approx 0{,}0238213605462799\cdot r$

Stumpfwinkeliges Dreieck E₁HN

01-Quadratur-des Kreises-9-0-Berechnung-wiki

6.0  $\triangle {E_{1}HN}$

 Gegeben:

 ${\overline {A_{1}N}}={\frac {5}{6}}r\;(aus\;1.2)$

 ${\overline {HN}}=r\cdot {\sqrt {\frac {13}{18}}}\;(aus\;1.3)$

 ${\overline {HP}}=r\cdot {\frac {5{\sqrt {26}}}{36}}\;(aus\;2.3.1)$

 ${\overline {A_{1}E_{1}}}=r\cdot \left({\frac {2}{72+{\sqrt {143}}}}\right)\;(aus\;5.2)$

6.1  ${\overline {E_{1}N}}={\overline {A_{1}N}}-{\overline {A_{1}E_{1}}}=r\cdot \left({\frac {5}{6}}-\left({\frac {2}{72+{\sqrt {143}}}}\right)\right)$

${\overline {E_{1}N}}\approx 0{,}809511972787053\cdot r$

6.2:  ${\overline {NP}}={\overline {HN}}-{\overline {HP}}=r\cdot {\sqrt {\frac {13}{18}}}-r\cdot {\frac {5{\sqrt {26}}}{36}}\Rightarrow r\cdot {\frac {\sqrt {26}}{36}}$

  ${\overline {NP}}=r\cdot {\frac {\sqrt {26}}{36}}\approx 0{,}1416394309331329\cdot r$

Stumpfwinkeliges Dreieck NPV

01-Quadratur-des Kreises-9-0-Berechnung-wiki

7.0  $\triangle {NPV}\;ist\;{\mbox{ähnlich}}\;\triangle {E_{1}HN}\;(aus\;6.0)$

  Gegeben:

 ${\overline {HN}}=r\cdot {\sqrt {\frac {13}{18}}}\;(aus\;1.3)$

 ${\overline {E_{1}N}}=r\cdot \left({\frac {5}{6}}-\left({\frac {2}{72+{\sqrt {143}}}}\right)\right)\;(aus\;6.1)$

 ${\overline {NP}}=r\cdot {\frac {\sqrt {26}}{36}}\;(aus\;6.2)$

7.1  ${\overline {NV}}={\frac {{\overline {E_{1}N}}\cdot {\overline {NP}}}{\overline {HN}}}=r\cdot \left({\frac {\left({\frac {5}{6}}-\left({\frac {2}{72+{\sqrt {143}}}}\right)\right)\cdot {\frac {\sqrt {26}}{36}}}{\sqrt {\frac {13}{18}}}}\right)\Rightarrow {\overline {NV}}=r\cdot {\frac {348+5{\sqrt {143}}}{36\left(72+{\sqrt {143}}\right)}}$

 ${\overline {NV}}\approx 0{,}134918662131175\cdot r$

Rechtwinkeliges Dreieck LMV

01-Quadratur-des Kreises-9-0-Berechnung-wiki

8.0  $\triangle {LMV}$

  Gegeben:

 ${\overline {LN}}=r\cdot {\frac {1}{6}}\;(aus\;1.0)$

 ${\overline {LM}}={\overline {A_{1}N}}=r\cdot {\frac {5}{6}}\;(aus\;1.2)$

 ${\overline {NV}}=r\cdot {\frac {348+5{\sqrt {143}}}{36\left(72+{\sqrt {143}}\right)}}\;(aus\;7.1)$

8.1  ${\overline {LV}}={\overline {LN}}+{\overline {NV}}=r\cdot \left({\frac {1}{6}}+{\frac {348+5{\sqrt {143}}}{36\left(72+{\sqrt {143}}\right)}}\right)\approx 0{,}301585328797842\cdot r$

8.2   ${\overline {MV}}$ entspricht der konstruierten Hälfte der Seite $(s\cdot {\frac {1}{2}})$ des Quadrates.

  Hypotenuse ${\overline {MV}}={\sqrt {{\overline {LM}}^{2}+{\overline {LV}}^{2}}}=r\cdot {\sqrt {{\frac {25}{36}}+\left({\frac {1}{6}}+{\frac {348+5{\sqrt {143}}}{36\left(72+{\sqrt {143}}\right)}}\right)^{2}}}\;\approx 0{,}886226920709671881\cdot r$

Konstruierte Seite des Quadrates

$\mathbf {s=2r\cdot {\sqrt {{\frac {25}{36}}+\left({\frac {1}{6}}+{\frac {348+5{\sqrt {143}}}{36\left(72+{\sqrt {143}}\right)}}\right)^{2}}}\;\approx 1{,}77245384141934376\cdot r}$

Version 2

Näherungskonstruktion

1. Kreis um $M$ mit beliebigem Radius ${\overline {AM}}$.
2. Gerade durch $A$ und $M$ ergibt Schnittpunkt $B$.
3. Gerade senkrecht zu ${\overline {AB}}$ durch $M$ ergibt Schnittpunkte $C$ und $D$.
4. Strecken ${\overline {AE}}={\frac {1}{10}}\cdot {\overline {AM}}={\overline {AF}}={\overline {FG}}={\overline {GH}}={\overline {HI}}$ eintragen.
5. Kreis um $M$ durch $E$.
6. Strecken ${\overline {EJ}}={\overline {JA}}={\overline {FL}}$, Kreis um $M$ durch $J$ ergibt Schnittpunkt $K$.
7. Bestimmen der Funktionspunkte:

Es beginnt mit Punkt $N$, dessen Abstand zu Punkt $C$ ist gleich der Strecke ${\overline {GJ}}$. In der Darstellung beschrieben als $|CN|={\overline {GJ}}$. Auf diese Art und Weise werden auch die weiteren Funktionspunkte von $O$ als $|KO|={\overline {ML}}$ bis $W$ als $|CW|={\overline {BI}}$ (Reihenfolge siehe Kurzbeschreibung in der Darstellung) festgelegt.

8. Einzeichnen der Kreissekanten:

Es beginnt mit der Sekante ab $W$ durch $V$ bis sie die äußere Kreislinie in $Z_{1}$ schneidet. Die nächste Sekante läuft ab dem zuletzt erhaltenen Schnittpunkt $Z_{1}$ durch $U$ bis sie wieder die äußere Kreislinie in $A_{1}$ schneidet. Auf diese Art und Weise werden auch die Punkte von $B_{1}$ bis $H_{1}$ (Reihenfolge ist anhand des Verlaufs der Sekanten zu entnehmen) bestimmt.

9. Die letzte Sekante ${\overline {H_{1}E}}$ schneidet die Strecke ${\overline {CM}}$ in $I_{1}$ und liefert somit die Strecke ${\overline {I_{1}M}}={\frac {1}{2}}\cdot a$.
10. Konstruiere abschließend mittels der Strecke ${\overline {I_{1}M}}$ das Quadrat $A'B'C'D'$ mit Seite $a$.

• Somit ergibt sich:

Ein Quadrat mit einem nahezu gleichen Flächeninhalt wie der des gegebenen Kreises.

Fehler

Bezogen auf den Einheitskreis r = 1 [LE]

Der absolute Fehler der konstruierten Seite des gesuchten Quadrats ist mit der vorliegenden Konstruktion in GeoGebra nicht darstellbar, da das Ergebnis der konstruierten Seite in allen angezeigten fünfzehn Nachkommastellen mit dem Ergebnis der berechneten Seite übereinstimmt (siehe Weblinks → GeoGebra) .

• Konstruierte Seitenlänge des Quadrates mit z. B. $a=1{,}772453850905516\;[LE]$. → Die letzte Nachkommastelle kann sich von Konstruktion zu Konstruktion unterscheiden!
• Seitenlänge des Quadrates $a_{SOLL}={\sqrt {\pi }}=1{,}772453850905516\;027\ldots \;[LE]$.
• Absoluter Fehler der konstruierten Seitenlänge:

Bis zu den max. angezeigten 15 Nachkommastellen ist der absolute Fehler $F_{a}=a-a_{SOLL}=0{,}0\;[LE]$

• Flächeninhalt des konstruierten Quadrates $A=a^{2}=3{,}141592653589793\;141\ldots \;[FE]$.
• Flächeninhalt des Quadrates $A_{SOLL}=\pi =3{,}141592653589793\;238\ldots \;[FE]$
• Absoluter Fehler des Flächeninhalts des Quadrates $=F_{A}=a^{2}-a_{SOLL}^{2}=-9{,}67\ldots E-17\;[FE]$.

Beispiele um die Fehler zu verdeutlichen

• Bei einem Radius r = 1 Mrd.km (das Licht bräuchte für diese Strecke ca. 56 min) wäre der Fehler der konstruierten Seite des Quadrats < 1 mm.
• Bei einem Radius r = 1.000 km wäre der Fehler des Flächeninhalts des Quadrats < -1 cm².

Weblinks

• Geogebra
•  Quadratur des Kreises
• Quadratur des Kreises, Animation

Dreiteilung des Winkels 60°

01- Dreiteilung des Winkels 60°

• Näherungskonstruktion
• "Konstruktionsprinzip", "Konstruktion Winkel 0 > bis 180°" u. a. m. siehe Kapitel Dreiteilung des Winkels.
• Beginnt der Kreisbogen b um den Punkt M ab dem Punkt E und endet im Punkt B, ist der Punkt G auf der Hilfslinie g gut erkennbar. Somit kann bereits ein Winkel $\geqq$ 60° direkt gedrittelt werden.

Konstruktion

1. Zeichne durch den Punkt M eine Gerade.
2. Bestimme den beliebigen Punkt A auf dieser Gerade, es ergibt sich die Strecke MA als erster Winkelschenkel.
3. Konstruiere den Winkel 60° um den Punkt M entgegen dem Uhrzeigersinn, mittels je einem kurzen Kreisbogen um den Punkt A sowie um den Punkt M mit dem Radius gleich der Strecke MA, die beiden Kreisbogen schneiden sich im Punkt B
4. Verbinde den Punkt M mit dem Punkt B, es ergibt sich der zweite Winkelschenkel.
5. Konstruiere vom Winkel $\angle {AMB}$ die Winkelhalbierende W₁.
6. Konstruiere vom Winkel $\angle {AMW_{1}}$ die Winkelhalbierende W₂, die Länge der Strecke MW₂ etwas länger als $\mathbf {{\frac {1}{2}}r}$
7. Konstruiere vom Winkel $\angle {W_{2}MW_{1}}$ die Winkelhalbierende W₃, etwas länger als die Strecke MA.
8. Konstruiere vom Winkel $\angle {W_{2}MW_{3}}$ die Winkelhalbierende W₄, etwa gleich lang wie die Winkelhalbierende W₃.
9. Zeichne den Kreisbogen b um den Punkt M, ab dem Punkt B bis zur Winkelhalbierende W₄, es ergibt sich der Schnittpunkt E auf W₄ und der Schnittpunkt D auf W₃.
10. Zeichne eine gerade Hilfslinie g die über den Punkt E den Punkt D anvisiert (quasi ein Lineal an die Punkte E und D angelegt), aber nur bis zum Punkt E verläuft. Somit ist zwischen den Punkten E und D keine gerade Hilfslinie g und der Kreisbogen MED für den späteren Schnittpunkt H frei zugänglich.
11. Zeichne einen Halbkreis um den Punkt E mit dem Radius gleich dem Abstand |DE|, es ergibt sich auf der Hilfslinie g der Schnittpunkt F.
12. Konstruiere auf der Hilfslinie g die Strecke FG, sie ist ein Drittel der Strecke EF.
13. Zeichne einen Kreis um den Punkt G mit dem Radius gleich der Strecke EF, es ergibt sich auf dem Kreisbogen MED der Schnittpunkt H.
14. Verbinde den Punkt H mit dem Punkt M, die Winkelschenkel MH und MA schließen den Winkel $\mathbf {\beta } \approx \mathbf {{\frac {1}{3}}\alpha }$ ein.

• Somit ist der Winkel 60° nahezu gedrittelt.

Zusätzliche Approximationen herleitbar

• Neuneckseite
• Seite vom 36-Eck, Näherungskonstruktion Winkel 10°
• Näherungskonstruktion Winkel 5°

Fehler

• Die Fehler der Winkel $\mathbf {\beta }$ bzw. $\mathbf {\gamma }$ sind zu gering für eine korrekte Anzeige in GeoGebra, sie werden deshalb als exakt 20° bzw. 40° angezeigt.
• Neuneckseite, bei einem Radius r = MA = 100.000 km wäre der Fehler an der Sehne ca. 8,6 mm.

Berechnung

• Im Kapitel Neuneck, unter Berechnung sind zur Verifizierung des Konstruktionsprinzips alle Berechnungsschritte für die Dreiteilung des Winkels 60° aufgezeigt.

Weblinks

Neuneck in diesem Buch im Kapitel Polynomkonstruktionen

Dreiteilung des Winkels in diesem Buch im Kapitel Die drei antiken Probleme

Dreiteilung des Winkels in diesem Buch im Kapitel Die drei antiken Probleme

Drittel der Strecke in diesem Buch

Verdoppelung des Würfels

Version 1

1. Quadrat mit beliebiger Seitenlänge $a_{1}$, Ecken gegen den Uhrzeigersinn $A,B,C,$ und $D$.
2. Mittelpunkt $M$ des Quadrates mithilfe zweier kurzer Diagonalenabschnitte, Umkreis des Quadrates.
3. Mittelachse durch $M$ ergibt Schnittpunkte $E,I,J,$ und $F$.
4. Mittelachse senkrecht zu ${\overline {EF}}$ durch $M$ ergibt Schnittpunkte $G,K,L,$ und $H$.
5. Strecken ${\overline {IN}}={\frac {1}{10}}\cdot {\overline {IJ}},\;\;{\overline {IO}}={\overline {IN}}={\overline {NP}}={\overline {PQ}}$.
6. Strecken ${\overline {OR}}={\frac {1}{2}}\cdot {\overline {IO}}={\overline {ES}}$, Kreis um $M$ durch $S$ ergibt Schnittpunkt $T$.
7. Bestimmen der Funktionspunkte:

Es beginnt mit Punkt $U$, dessen Abstand zu Punkt $G$ ist gleich der Strecke ${\overline {IN}}$. In der Darstellung beschrieben als $|GU|={\overline {IN}}$. Auf diese Art und Weise werden auch die weiteren Funktionspunkte von $V$ als $|PV|={\overline {PH}}$ bis $F_{1}$ als $|BF_{1}|={\overline {MQ}}$ (Reihenfolge siehe Kurzbeschreibung in der Darstellung) festgelegt.

8. Einzeichnen der Kreissekanten:

Es beginnt mit der Sekante ab $F_{1}$ durch $E_{1}$ bis sie die äußere Kreislinie in $G_{1}$ schneidet. Die nächste Sekante läuft ab dem zuletzt erhaltenen Schnittpunkt $G_{1}$ durch $D_{1}$ bis sie wieder die äußere Kreislinie in $H_{1}$ schneidet. Auf diese Art und Weise werden auch die Punkte von $I_{1}$ bis $O_{1}$ (Reihenfolge ist anhand des Verlaufs der Sekanten zu entnehmen) bestimmt.

9. Letzte Sekante von $O_{1}$ bis $E$ schneidet die Mittelachse ${\overline {GH}}$ in $P_{1}$.
10. Ein kurzer Kreisbogen um $M$ mit Radius ${\overline {P_{1}M}}$ liefert mit ${\overline {P_{1}Q_{1}}}=a_{2}$ die Seitenlänge des gesuchten Würfels 2.

• Somit ergibt sich:

a) Die Strecke P₁Q₁, sie entspricht der Seitenlänge a₂ des Würfels 2.

b) Ein Würfel 2 mit einem Volumen, das im Vergleich zum gegebenen Würfel 1 nahezu doppelt so groß ist.

Fehler

Bezogen auf einem Würfel mit der Seitenlänge a₁ = 1 [LE]

• Konstruierte Seitenlänge des verdoppelten Würfels in GeoGebra $a_{2}=1{,}259921049894872\;[LE]$
• Seitenlänge des verdoppelten Würfels $a_{2\;SOLL}={\sqrt[{3}]{2}}=1{,}259921049894873164...\;[LE]$
• Absoluter Fehler der konstruierten Seitenlänge des verdoppelten Würfels $Fa_{2}=-1{,}16...E-15\;[LE]$
• Volumen des verdoppelten Würfels mit konstruierter Seitenlänge in GeoGebra $a_{2}{^{3}}=1{,}999999999999994453...\;[VE]$
• Volumen des verdoppelten Würfels $a_{2\;SOLL}{^{3}}=2{,}0\;[VE]$
• Absoluter Fehler des Volumens mit konstruierter Seitenlänge $F_{V}=a_{2}{^{3}}-a_{2\;SOLL}{^{3}}=-5{,}54...E-15\;[VE]$

Beispiel um den Fehler zu verdeutlichen

• Bei einem Würfel 1 mit der Seitenlänge a₁ = 1 Mrd. km (das Licht bräuchte für diese Strecke ca. 55 min) wäre der Fehler der konstruierten Seitenlänge a₂ des verdoppelten Würfels 2 ca. -1,2 mm.
• Bei einem Würfel 1 mit der Seitenlänge a₁ = 10 km wäre der Fehler des Volumens vom verdoppelten Würfels 2 ca. -5,5 dm³ oder ca. -5,5 Liter

Konstruktionsprinzip

• Näherungskonstruktion
• Die Hauptelemente sind ein Zahlenstrahl s₁, zwei darauf senkrecht stehende Teilerstrahlen s₂ und s₄, ein zu s₁ paralleler Scheitelstrahl s₃, zwei Diagonalstrahlen s₅ und s₆ und zwei Hilfsstrahlen s₇ und s₈. Näheres wird in der Konstruktion beschrieben.
• Von dem vorgegebenen Zähler bzw. Nenner (wenn keine Dezimalzahl) werden die Dezimalstellen in der Reihenfolge Einer, Zehner, Hunderter u. s. w. jeweils mittels Projektion mit dem Faktor ${\frac {1}{10}}$ bzw. falls die nächste Dezimalstelle eine "0" ist, mit dem Faktor ${\frac {1}{100}}$ verkleinert und auf einem Teilerstrahl s₂ oder s₄ geometrisch addiert oder subtrahiert.
• Zuerst wird der Nenner konstruiert, anschließend zum Punkt A des Teilerstrahls s₂ addiert und der sich dabei ergebende Schnittpunkt, z. B. T, Nenner, mit dem Punkt U des Zahlenstrahls s₁ (S₁ Würfel 1) verbunden, dabei ergibt sich die Verbindungsstrecke T, NennerU.

Der konstruierte Zähler wird ebenfalls zum Punkt A des Teilerstrahls s₂ addiert, dabei ergibt sich der Schnittpunkt, z. B. V, Zähler.

Die abschließende Parallele zur Verbindungstrecke T, NennerU erzeugt den Schnittpunkt W auf dem Zahlenstrahl s₁. Somit entspricht die Länge der Stecke AW exakt dem Wert des vorgegebenen Bruches.

• Ansatz: Ein Bruch der die gewünschte Näherung an $\mathbf {\sqrt[{3}]{2}}$ hat. Die Anwendung der Strahlensätze in kompakter Form.

Konstruktion

• Als Basiskonstruktion ist das Schema für die Konstruktion von Brüchen auf einen Strahl eingearbeitet.
• Alternative: Auf einem Ausdruck der Basiskonstruktion die Konstruktion manuell mit Schreibstift, Zirkel und Lineal fortsetzen.
• Wähle z. B. einen Dezimalbruch der die gewünschte Näherung an $\mathbf {\sqrt[{3}]{2}}$ hat. Die Qualität der Näherung ist einfach voraussehbar, wenn ein Dezimalbruch (Anzahl der Nullen im Nenner) eingesetzt wird.
• Im dargestellten Beispiel ist der Dezimalbruch ${\frac {S_{2}{\mbox{Würfel 2}}}{S_{1}{\mbox{Würfel 1}}}}={\frac {1.259.921.049.894.873.164.767}{1E+21}}$ gewählt.
• Einundzwanzig Nachkommastellen sind gleich deren des Wertes $\mathbf {\sqrt[{3}]{2}}$.

Nenner

1. Bestimme die Seite des Würfel 1 S₁ mittels der beliebigen Strecke AU.
2. Konstruiere den Würfel 1 so, dass die Vorderseite auf dem Zahlenstrahl s₁ und an dem Teilerstrahl s₂ anliegt.
3. Verbinde den Punkt T,Nenner mit dem Punkt U, somit ist der Nenner konstruiert.

Zähler

4. Verbinde den siebten Punkt des Teilerstrahls s₄ (Zahl 7, Einerstelle des Zählers vom Dezimalbruch) mit dem Scheitelpunkt N, es ergibt sich der Schnittpunkt 7 auf dem Hilfsstrahl s₇. Der Wert der Zahl 7 vom Teilerstrahl s₄ ist dadurch mit dem Faktor ${\frac {1}{10}}$ verkleinert.
5. Greife die Strecke J7 ab und addiere sie zum sechsten Teilungspunkt des Teilerstrahls s₂, es ergibt sich der Schnittpunkt 67.
6. Verbinde den Schnittpunkt 67 des Teilerstrahls s₂ mit dem Scheitelpunkt P, es ergibt sich der Schnittpunkt 67 auf dem Hilfsstrahl s₈. Es könnte alternativ mit den Scheitelpunkten O oder I verbunden werden. Damit aber die projizierten Zahlen (Schnittpunkte) zueinander einen gut erkennbaren Zwischenraum für das Abgreifen des Abstandes zum Scheitelstrahl s₃ haben, ist es vorteilhaft abfangs die Teilerstrahlen (s₂, s₄) und Hilfsstrahlen (s₇, s₈) in etwa gleichmäßig zu verwenden.
7. Greife die Strecke K67 ab und addiere sie zum siebten Teilungspunkt des Teilerstrahls s₄, es ergibt sich der Schnittpunkt 767.
8. Verbinde den Schnittpunkt 767 des Zahlenstrahls s₄ mit dem Scheitelpunkt H, es ergibt sich der Schnittpunkt 767 auf dem Teilerstrahl s₂.
9. Greife die Strecke C767 ab und addiere sie zum vierten Teilungspunkt des Teilerstrahls s₂, es ergibt sich der Schnittpunkt 4.767. Es ist bezüglich Übersicht im Folgenden vorteilhaft: Die Zifferngruppierung (Punkt oder Abstand) zu verwenden und ggf. lange Zahlen mittig mit "..." abzukürzen.
10. Setze diese Vorgehensweise bis zur Zahl 49.894.873.164.767 (angezeigt als 49.894...767 auf Teilerstrahl s₄) fort.

• Beachte: Die nächste Stelle des Zählers ist eine Null (0), deshalb muss der Wert der Zahl 49.894...767 vom Teilerstrahl s₄, vor der geometrischen Addition mit der übernächsten Dezimalstelle 1, mit dem Faktor ${\frac {1}{100}}$ verkleinert sein! In diesem Fall ist die erste Verkleinerung mit dem Faktor ${\frac {1}{10}}$ stets auf einem Teilerstrahl durchzuführen, da die auf einem Hilfsstrahl projizierten Zahlen nicht auf den benachbarten Hilfsstrahl und nicht auf die Teilerstrahlen projiziert werden können!

11. Verbinde den Schnittpunkt 49.894...767 des Teilerstrahls s₄ mit dem Scheitelpunkt H, es ergibt sich der Schnittpunkt 49.894...767 auf dem Teilerstrahl s₂. Der Wert der Zahl 49.894...767 vom Teilerstrahl s₄ ist nun mit dem Faktor ${\frac {1}{10}}$ verkleinert.
12. Verbinde den Schnittpunkt 49.894...767 des Teilerstrahls s₂ mit dem Scheitelpunkt I, es ergibt sich der Schnittpunkt 049.894...164.767 auf dem Teilerstrahl s₄. Der Wert der Zahl 49.894...767 vom Teilerstrahl s₄ ist nun mit dem Faktor ${\frac {1}{100}}$ verkleinert.
13. Greife die Strecke F049.894...164.767 ab und subtrahiere sie vom zweiten Teilungspunkt A des Teilerstrahls s₂, es ergibt sich der Schnittpunkt 1.049...767.
14. Setze diese Vorgehensweise fort bis der Zähler mit dem Schnittpunkt 1.259.921.049.894.873.164.767 auf dem Teilerstrahl s₄ konstruiert ist.
15. Greife die Strecke E1.259.921.049.894.873.164.767 ab und addiere sie zum zweiten Teilungspunkt A des Teilerstrahls s₂, es ergibt sich der Punkt V, Zähler.
16. Zeichne eine Parallele zur Strecke T,NennerU ab dem Punkt V, Zähler bis zum Zahlenstrahl s₁, es ergibt sich der Schnittpunkt W. Die Strecke AW ist die gesuchte Seite S₂ des Würfel 2.
17. Konstruiere den Würfel 2 so, dass die Vorderseite auf dem Zahlenstrahl s₁ und an dem Teilerstrahl s₂ anliegt.

• Somit ergibt sich:

Ein Würfel 2 mit einem Volumen, das im Vergleich zum gegebenen Würfel 1 nahezu doppelt so groß ist..

Berechnung

• Allgemein: Seite des Würfel 2 S₂ = S₁ • $\mathbf {\sqrt[{3}]{2}}$.
• Die Berechnung der konstruierten Seite des Würfel 2 S₂ geschieht, aufgrund des Konstruktionsprinzips, schrittweise durch die geometrischen Additionen bzw. Subtraktionen der einzelnen Zwischenergebnisse auf den Teilerstrahlen s₂ bzw. s₄.
• Der vorgegebene Dezimalbruch ${\frac {1.259.921.049.894.873.164.767}{1E+21}}$ wird auf dem Teilerstrahl s₄ und s₂ prinzipiell exakt dargestellt.

Fehler

Bezüglich des Ansatzes sind die Fehler bis zur 21. Nachkommastelle prinzipiell = 0 [LE bzw. VE]. Siehe hierzu auch die Abschnitte Berechnung und Weblinks (Animation).

Beispiele um den Fehler zu verdeutlichen

• Bei einem Würfel 1 mit S₁ = 1 Billiarde km (das Licht bräuchte für diese Strecke ca. 105,8 Jahre) wäre vom Würfel 2 der Fehler der Seite S₂ ≈ -0,21 mm.
• Bei einem Würfel 1 mit S₁ = 100 km wäre vom Würfel 2 der Fehler des Volumens ≈ -1,0 cm³

Weblinks

 Commons: Animation, Verdoppelung des Würfels – Album mit Bildern, Videos und Audiodateien

Weblinks

•   Quadrat
•  Würfelverdoppelung
•  GeoGebra
•  Einheitskreis
•  Mittelsenkrechte
•  Messabweichung