Neuneck

(Planimetrie/ Polygonkonstruktionen/ Neuneck)

Neuneck (Nonagon)

• Näherungskonstruktion für das regelmäßige Neuneck, auch mit Zirkel und Lineal ohne Maßeinteilung darstellbar.
• Einleitung und Erklärungen zu "Mathematische Zusammenhänge", "Konstruktionen" mit weiteren Näherungskonstruktionen u. a. m. sind in dem Artikel Neuneck enthalten.

Konstruktion

Besonderheit

• Die Darstellung zeigt eine Konstruktion bei gegebenem Umkreis. Eine Alternative bei gegebener Seite ist mit "alternativ" gekennzeichnet.

Konstruktion bei gegebenem Umkreis

1. Zeichne eine frei wählbare Strecke MJ.
2. Bestimme den Punkt S auf der Strecke MJ. In der Darstellung wurde hierfür die Strecke MJ halbiert. Prinzipiell ist die Lage des Punktes S bei gegebenem Umkreis frei wählbar.
3. Zeichne um den Punkt M einen Kreis durch den Punkt S, es ist der Umkreis des späteren Neunecks.
4. Ziehe einen kurzen Kreisbogen um den Punkt J mit dem Radius MJ.
5. Bestimme den Punkt B mit einem Abstand |SB|, der gleich lang ist wie die Strecke MS. Dies ist der erste Eckpunkt des entstehenden Neunecks.
6. Zeichne eine gerade Linie ab dem Punkt M bis zum kurzen Kreisebogen, es ergibt sich der Schnittpunkt K.
7. Verbinde den Punkt K mit dem Punkt J, somit entsteht das gleichseitige Dreieck MJK.
8. Konstruiere vom Winkel $\angle {JMK}$ die Winkelhalbierende W₁.
9. Konstruiere vom Winkel $\angle {JMW_{1}}$ die Winkelhalbierende W₂, mit einer Länge ca. drei Viertel der Strecke MJ.
10. Konstruiere vom Winkel $\angle {W_{2}MW_{1}}$ die Winkelhalbierende W₃, etwas länger als die Strecke MJ.
11. Konstruiere vom Winkel $\angle {W_{2}MW_{3}}$ die Winkelhalbierende W₄, mit einer Länge etwa gleich lang wie die Winkelhalbierende W₃.
12. Zeichne den Kreisbogen b um den Punkt M, ab dem Punkt K bis zur Winkelhalbierende W₄, es ergibt sich der Schnittpunkt O auf W₄ und der Schnittpunkt N auf W₃.
13. Zeichne eine gerade Hilfslinie g die über den Punkt O den Punkt N anvisiert (quasi ein Lineal an die Punkte O und N angelegt), aber nur bis zum Punkt O verläuft. Somit ist zwischen den Punkten O und N keine gerade Hilfslinie g und der Kreisbogen MON für den späteren Schnittpunkt R frei zugänglich.
14. Zeichne einen Halbkreis um den Punkt O mit dem Radius |NO|, es ergibt sich auf der Hilfslinie g der Schnittpunkt P.
15. Konstruiere auf der Hilfslinie g die Strecke PQ, sie ist ein Drittel der Strecke OP.
16. Zeichne einen Kreis um den Punkt Q mit dem Radius OP, es ergibt sich auf dem Kreisbogen MON der Schnittpunkt R.
17. Verbinde den Punkt R mit dem Punkt M, es ergibt sich der Schnittpunkt A auf dem Umkreis des entstehenden Neunecks.
18. Verbinde den Punkt A mit dem Punkt B, es ergibt sich die erste Seite des entstehenden Neunecks.
19. Trage die Strecke AB siebenmal entgegen dem Uhrzeigersinn auf dem Umkreis ab.
20. Verbinde die benachbarten Eckpunkte miteinander, somit ergibt sich das Neuneck ABCDEFGHI.

Fehler der ersten Seite

1.0  $Absoluter\;Fehler\;von\;{\overline {AB}}$

Gegeben:

 ${\overline {AB}}\approx \;r\cdot \;0{,}684040286737349\;[LE]\;(aus\;8.2\;der\;Berechnung)$

1.1  $Neuneckseite,\;s=r\cdot 2\cdot \sin \left({\frac {180^{\circ }}{9}}\right)\approx \;r\cdot \;0{,}684040286651337\;[LE]$

1.2  $Fehler\;absolut,\;F_{a}={\overline {AB}}-s=r\cdot 0{,}00000000008601...\approx \;r\cdot \;8,6E-11\;[LE]$

Beispiel zur Verdeutlichung

Bei einem Umkreisradius r = 100.000 km wäre der absolute Fehler der 1. Seite ca. 8,6 mm.

Konstruktion bei gegebener Seite

1. Zeichne eine frei wählbare Strecke MJ.
2. Konstruiere über und mittels der Strecke MJ ein gleichseitiges Dreieck und bezeichne den dritten Eckpunkt mit K.
3. Konstruiere vom Winkel $\angle {JMK}$ die Winkelhalbierende W₁.
4. Konstruiere vom Winkel $\angle {JMW_{1}}$ die Winkelhalbierende W₂, mit einer Länge ca. drei Viertel der Strecke MJ.
5. Konstruiere vom Winkel $\angle {W_{2}MW_{1}}$ die Winkelhalbierende W₃, etwas länger als die Strecke MJ.
6. Konstruiere vom Winkel $\angle {W_{2}MW_{3}}$ die Winkelhalbierende W₄, mit einer Länge etwa gleich lang wie die Winkelhalbierende W₃.
7. Zeichne den Kreisbogen b um den Punkt M, ab dem Punkt K bis zur Winkelhalbierende W₄, es ergibt sich der Schnittpunkt O auf W₄ und der Schnittpunkt N auf W₃.
8. Zeichne eine gerade Hilfslinie g die über den Punkt O den Punkt N anvisiert (quasi ein Lineal an die Punkte O und N angelegt), aber nur bis zum Punkt O verläuft. Somit ist zwischen den Punkten O und N keine gerade Hilfslinie g und der Kreisbogen MON für den späteren Schnittpunkt R frei zugänglich.
9. Zeichne einen Halbkreis um den Punkt O mit dem Radius |NO|, es ergibt sich auf der Hilfslinie g der Schnittpunkt P.
10. Konstruiere auf der Hilfslinie g die Strecke PQ, sie ist ein Drittel der Strecke OP.
11. Zeichne einen Kreis um den Punkt Q mit dem Radius OP, es ergibt sich auf dem Kreisbogen MON der Schnittpunkt R.
12. Verbinde den Punkt R mit dem Punkt M.
13. Konstruiere vom Winkel $\angle {RMK}$ die Winkelhalbierende W₅.
14. Zeichne auf der Winkelhalbierenden W₅ einen Kreis um den in der Lage frei wählbaren Punkt T mit einem Radius, der gleich der halben gegebenen Neuneckseite ist.
15. Konstruiere eine Senkrechte zur Winkelhalbierende W₅ durch den Punkt T, es ergibt sich auf dem Kreis um Punkt T der Schnittpunkt V.
16. Konstruiere eine Parallele zur Winkelhalbierende W₅ ab dem Punkt V bis zur Strecke MK, es ergibt sich der Schnittpunkt B. Dies ist der erste Eckpunkt des entstehenden Neunecks.
17. Zeichne um den Punkt M einen Kreis durch den Punkt B, es ist der Umkreis des entstehenden Neunecks. Es ergibt sich der Schnittpunkt A auf der Strecke MR.
18. Verbinde den Punkt A mit dem Punkt B, dies ist die erste Seite des entstehenden Neunecks.
19. Trage die Strecke AB siebenmal entgegen dem Uhrzeigersinn auf dem Umkreis ab.
20. Verbinde die benachbarten Eckpunkte miteinander, somit ergibt sich das Neuneck ABCDEFGHI.

Fehler des Umkreisradius

2.0  $Absoluter\;Fehler\;von\;{\overline {MS}}=r$

Gegeben:

 $s_{1}=1{,}0\;[LE]\;(aus\;9.0\;der\;Berechnung)$

 $r_{k}\approx 1{,}461902199897722\;[LE]\;(aus\;9.1\;der\;Berechnung)$

 $\;r\approx 1{,}461902200081543\;[LE]\;(aus\;10.1\;der\;Berechnung)$

2.1   $Fehler\;absolut,\;F_{a}=r_{k}-r=-0{,}000000000183821\ldots \approx -1{,}8E-10\;[LE]$

Beispiel zur Verdeutlichung

Bei einer Seitenlänge s₁ = 10.000 km wäre der konstruierte Umfangsradius r ≈ 14.629,0219989 km um ca. 1,8 mm zu kurz.

Berechnung

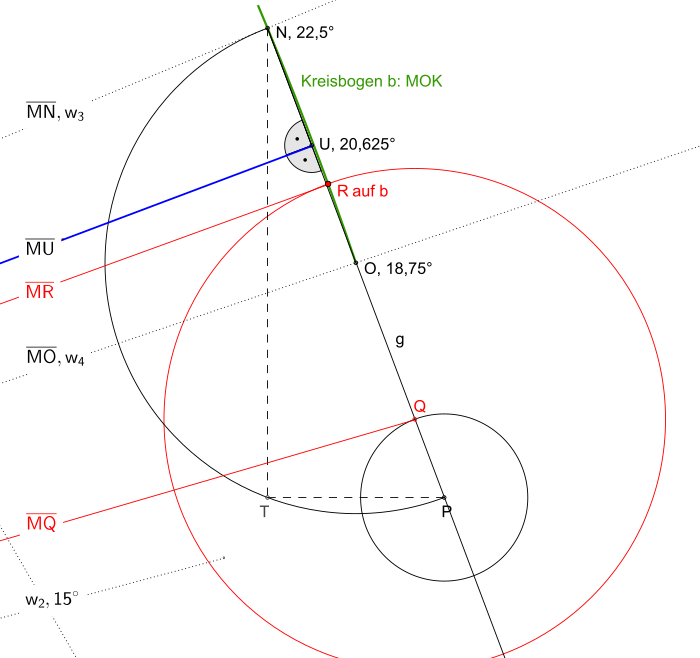
Kreissektor mit gleichseitigem Dreieck MJK

1.0  $Kreisssektor\;und\;\triangle {MJK}$

Gegeben aus Zeichnung:

 ${\overline {MS}}=Umkreisradius\;r=1[LE]$

 ${\overline {MJ}}={\overline {JK}}={\overline {KM}}={\overline {MN}}={\overline {MO}}=2r$

 $\angle {MKJ}=\alpha =60^{\circ }$

 $\angle {JML}=\gamma =30^{\circ }$

 $\angle {JMw_{2}}=\delta =15^{\circ }$

 $\angle {JMN}=\epsilon ={\frac {1}{2}}\cdot \left(\gamma +\delta \right)=22,5^{\circ }$

 $\angle {JMO}=\zeta ={\frac {1}{2}}\cdot \left(\delta +\epsilon \right)=18,75^{\circ }$

 $\angle {OMN}=\eta =\epsilon -\zeta =3,75^{\circ }$

1.1  ${\overline {NO}}={\overline {OP}}={\overline {QR}}$

1.2  ${\overline {NO}}=4r\cdot \sin \left({\frac {\eta }{2}}\right)\approx r\cdot 0{,}130876331287104$

1.3  ${\overline {PQ}}={\frac {4}{3}}r\cdot \sin \left({\frac {\eta }{2}}\right)\approx r\cdot 0{,}043625443762368$

Rechtwinkeliges Dreieck PNT

2.0   $\triangle {PNT}$

Gegeben:

• Der Punkt $U$ liegt mittig auf der Sekante ${\overline {NO}}$

 ${\overline {NO}}=4r\cdot \sin \left({\frac {\eta }{2}}\right)\approx r\cdot 0{,}130876331287104\;(aus\;1.2)$

 ${\overline {PQ}}={\frac {4}{3}}r\cdot \sin \left({\frac {\eta }{2}}\right)\approx r\cdot 0{,}043625443762368\;(aus\;1.3)$

2.1  ${\overline {NP}}=2\cdot {\overline {NO}}=8r\cdot \sin \left({\frac {\eta }{2}}\right)\approx r\cdot 0{,}261752662574209$

2.2  ${\overline {NQ}}={\overline {NP}}-{\overline {PQ}}={\frac {20}{3}}r\cdot \sin \left({\frac {\eta }{2}}\right)\approx r\cdot 0{,}218127218811840$

2.3  ${\overline {NU}}={\frac {1}{2}}\cdot {\overline {NO}}=2r\cdot \sin \left({\frac {\eta }{2}}\right)\approx r\cdot 0{,}065438165643552$

Rechtwinkeliges Dreieck MNU

3.0  $\triangle {MNU}$

Gegeben:

 ${\overline {MN}}=2r\;(aus\;1.0)$

 $\angle {JMN}=\epsilon ={\frac {1}{2}}\cdot \left(\gamma +\delta \right)=22,5^{\circ }\;(aus\;1.0)$

 $\angle {JMO}=\zeta ={\frac {1}{2}}\cdot \left(\delta +\epsilon \right)=18,75^{\circ }\;(aus\;1.0)$

 $\angle {OMN}=\eta =\epsilon -\zeta =3,75^{\circ }\;(aus\;1.0)$

3.1  $\angle {JMU}=\theta ={\frac {1}{2}}\cdot \left(\zeta +\epsilon \right)=20,625^{\circ }$

3.2  $\angle {UMN}=\iota ={\frac {1}{2}}\eta =1,875^{\circ }$

3.3  ${\overline {MU}}=cos\left(\iota \right)\cdot {\overline {MN}}=2r\cdot cos\left(\iota \right)\approx r\cdot 1{,}998929174952731$

Rechtwinkeliges Dreieck MQU

4.0  $\triangle {MQU}$

Gegeben:

 ${\overline {MU}}=cos\left(\iota \right)\cdot {\overline {MN}}=2r\cdot cos\left(\iota \right)\approx r\cdot 1{,}998929174952731\;(aus\;3.3)$

 ${\overline {NP}}=8r\cdot \sin \left({\frac {\eta }{2}}\right)\approx r\cdot 0{,}261752662574209\;(aus\;2.1)$

 ${\overline {PQ}}={\frac {4}{3}}r\cdot \sin \left({\frac {\eta }{2}}\right)\approx r\cdot 0{,}043625443762368\;(aus\;1.3)$

 ${\overline {NU}}=2r\cdot \sin \left({\frac {\eta }{2}}\right)\approx r\cdot 0{,}065438165643552\;(aus\;2.3)$

4.1  ${\overline {UQ}}={\overline {NP}}-{\overline {PQ}}-{\overline {NU}}={\frac {14}{3}}r\cdot \sin \left({\frac {\eta }{2}}\right)\approx r\cdot 0{,}152689053168288$

4.2  $\angle {QMU}=\kappa =arctan\left({\frac {\overline {UQ}}{\overline {MU}}}\right)={\frac {{\frac {14}{3}}r\cdot \sin \left({\frac {\eta }{2}}\right)}{2r\cdot cos\left(\iota \right)}}={\frac {{\frac {7}{3}}r\cdot \sin \left({\frac {\eta }{2}}\right)}{r\cdot cos\left(\iota \right)}}\approx 4{,}368080079657319^{\circ }$

4.3  ${\overline {MQ}}={\sqrt {{\overline {MU}}^{2}+{\overline {UQ}}^{2}}}={\sqrt {\left(2r\cdot cos\left(\iota \right)\right)^{2}+\left({\frac {14}{3}}r\cdot \sin \left({\frac {\eta }{2}}\right)\right)^{2}}}={\sqrt {\left(2r\cdot cos\left(1,875^{\circ }\right)\right)^{2}+\left({\frac {14}{3}}r\cdot \sin \left({\frac {3,75^{\circ }}{2}}\right)\right)^{2}}}\approx r\;\cdot \;2{,}004752302264455$

Stumpfwinkeliges Dreieck MQR

5.0  $\triangle {MQR}$

Gegeben:

 ${\overline {MQ}}={\sqrt {\left(2r\cdot cos\left(\iota \right)\right)^{2}+\left({\frac {14}{3}}r\cdot \sin \left({\frac {\eta }{2}}\right)\right)^{2}}}\approx r\;\cdot \;2{,}004752302264455\;(aus\;4.3)$

 ${\overline {QR}}={\overline {NO}}=4r\cdot \sin \left({\frac {\eta }{2}}\right)\approx r\cdot 0{,}130876331287104\;(aus\;1.2)$

 ${\overline {MR}}=2r\;(aus\;Zeichnung)$

 $\eta =3,75^{\circ }\;(aus\;1.0)$

 $\iota =1,875^{\circ }\;(aus\;3.2)$

Mit dem Kosinussatz ergibt sich:

5.1   $\angle {QMR}=\lambda =arccos\left({\frac {{\overline {MQ}}^{2}+{\overline {MR}}^{2}-{\overline {QR}}^{2}}{2\cdot {\overline {MR}}\cdot {\overline {MQ}}}}\right)=\left({\frac {\left(2r\cdot cos\left(\iota \right)\right)^{2}+\left({\frac {14}{3}}r\cdot \sin \left({\frac {\eta }{2}}\right)\right)^{2}+4r^{2}-\left(4r\cdot \sin \left({\frac {\eta }{2}}\right)\right)^{2}}{4r\cdot {\sqrt {\left(2r\cdot cos\left(\iota \right)\right)^{2}+\left({\frac {14}{3}}r\cdot \sin \left({\frac {\eta }{2}}\right)\right)^{2}}}}}\right)\Rightarrow arccos\left({\frac {4r^{2}\cdot \cos ^{2}\left(1.875^{\circ }\right)+{\frac {52}{9}}r^{2}\cdot \sin ^{2}\left({\frac {3.75^{\circ }}{2}}\right)+4r^{2}}{4r{\sqrt {4r^{2}\cdot cos^{2}\left(1.875^{\circ }\right)+{\frac {196}{9}}r^{2}\cdot sin^{2}\left({\frac {3.75^{\circ }}{2}}\right)}}}}\right)\approx 3{,}743080074412935^{\circ }$

Nebenwinkel JMR

6.0  $\angle {JMR}$

Gegeben:

 $\angle {JMU}=\theta ={\frac {1}{2}}\cdot \left(\zeta +\epsilon \right)=20,625^{\circ }\;(aus\;3.1)$

 $\angle {QMU}=\kappa \approx 4{,}368080079657319^{\circ }\;(aus\;4.2)$

 $\angle {QMR}=\lambda \approx 3{,}743080074412935^{\circ }\;(aus\;5.1)$

6.1   $\angle {JMR}=\mu =\angle {JMU}-\angle {QMU}+\angle {QMR}=\theta -\kappa +\lambda \approx 19{,}999999994755615^{\circ }$

Zentriwinkel RMK

7.0  $\angle {RMK}$

Gegeben:

 $\angle {JMR}=\mu \approx 19{,}999999994755615^{\circ }\;(aus\;6.1)$

7.1  $\angle {RMK}=\beta =60^{\circ }-\mu =60^{\circ }-19{,}999999994755615^{\circ }\approx 40{,}000000005244385^{\circ }$

Erste Seite des Neunecks

8.0  ${\overline {AB}}$

Gegeben:

 $\angle {RMK}=\beta =60^{\circ }-\mu \approx 40{,}000000005244385^{\circ }\;(aus\;7.1)$

8.1   $Sekante\;{\overline {KR}}=sin\left({\frac {\beta }{2}}\right)\;\cdot \;4r=sin\left({\frac {40{,}000000005244385^{\circ }}{2}}\right)\;\cdot \;4r\;\approx \;r\;\cdot \;1{,}368080573474698$

8.2   $\mathbf {{\overline {AB}}={\frac {\overline {KR}}{2}}={\frac {sin\left({\frac {\beta }{2}}\right)\cdot 4r}{2}}=sin\left({\frac {\beta }{2}}\right)\cdot 2r\approx \;r\cdot 0{,}684040286737349} \;[LE]$

Konstruierter Umkreisradius $r_{k}$ bei gegebener Seite s₁

9.0  $r_{k}={\overline {MS}}$

Gegeben:

 $\;s_{1}=1{,}0\;[LE]\;zum\;Beispiel$

 $\;\;\beta \approx 40{,}000000005244385^{\circ }\;(aus\;7.1)$

 $s_{1}=sin\left({\frac {\beta }{2}}\right)\cdot 2r_{k}\;(aus\;8.2)$

9.1   $\mathbf {r_{k}={\frac {s_{1}}{2\cdot sin\left({\frac {\beta }{2}}\right)}}={\frac {1}{2\cdot sin\left({\frac {\beta }{2}}\right)}}\approx 1{,}461902199897722\;[LE]}$

Umkreisradius $r$ bei gegebener Seite s₁

10.0  $r$

Gegeben:

 $s_{1}=1{,}0\;[LE]\;(aus\;9.0)$

 $\;\beta =40^{\circ }$

 $s_{1}=sin\left({\frac {\beta }{2}}\right)\cdot 2r$

10.1  $\mathbf {r={\frac {s_{1}}{2\cdot sin\left({\frac {\beta }{2}}\right)}}={\frac {1}{2\cdot sin\left({\frac {40^{\circ }}{2}}\right)}}\approx 1{,}461902200081543\;[LE]}$

Weblinks

Dreiteilung des Winkels 60° in diesem Buch im Kapitel Die drei antiken Probleme

Drittel der Strecke in diesem Buch im Kapitel Verschiedenes

Neuneck mit gegebener Seitenlänge

Winkelhalbierende

Konstruktion einer Parallelen durch einen gegebenen Punkt

Parallele

Kreiswinkel (Zentriwinkel)