Näherung 2

Als Die drei antiken Probleme oder Klassische Probleme der antiken Mathematik werden bezeichnet:
- die Quadratur des Kreises
- die Dreiteilung des Winkels
- die Verdoppelung des Würfels
Sie sind erwiesenermaßen nicht (exakt) als Konstruktion mit Zirkel und Lineal lösbar.
- Lösungskriterien, Historisches u. a. m. sind im Artikel Klassische Probleme der antiken Mathematik enthalten.
- In diesem Kapitel werden zu den drei klassischen Problemen Methoden aufgezeigt, mit denen außergewöhnlich genaue Näherungslösungen möglich sind. Die Approximationen sind auch mit Zirkel und Lineal ohne Maßeinteilung auf Format DIN A4 darstellbar.
Hilfsmittel
[Bearbeiten]Schema für die Konstruktion von Brüchen auf einen Strahl
[Bearbeiten]Verwendungszweck
[Bearbeiten]- Für Quadratur des Kreises, Verdoppelung des Würfels u. a. m., in denen ein Bruch als exakte Strecke benötigt wird.
- Vorzugsweise geeignet für Brüche > >
Konstruktionsprinzip
[Bearbeiten]- Eine Anwendung des dritten Strahlensatzes in Kombination mit Zahlenstrahlen.
- Die Hauptelemente sind ein Zahlenstrahl s1, zwei darauf senkrecht stehende Teilerstrahlen s2 und s4, ein zu s1 paralleler Scheitelstrahl s3, zwei Diagonalstrahlen s5 und s6 und zwei Hilfsstrahlen s7 und s8.
- Es sind echte und unechte Brüche sowie Dezimalbrüche, die im Schema Platz finden, einsetzbar.
- Tipp: Auf einem Ausdruck der Basiskonstruktion die entsprechende Konstruktion manuell mit Schreibstift, Zirkel und Lineal fortsetzen.
Konstruktion
[Bearbeiten]
- Die Lage des Zahlenstrahls s1 ist frei wählbar (siehe im Folgenden Quadratur des Kreises). Ist es bezüglich des Platzbedarfs möglich, zeichne z. B. durch den Punkt A den Zahlenstrahl s1. Er ist für die Darstellung des konstruierten Zählers und des konstruierten Nenners bestimmt.
- Zeichne den Teilerstrahl s2 durch den Punkt A senkrecht stehend zum Zahlenstrahl s1.
- Trage z. B. zwei gleichlange Strecken ab dem Punkt A nach unten auf dem Teilerstrahl s2 ab und bezeichne deren Endpunkte mit B bzw. C.
- Beachte: Die Position des Punktes A vom Strahl s1 auf dem Strahl s2 (Abstand zu Punkt C) ist frei wählbar.
- Zeichne durch den Punkt C den zum Zahlenstrahl s1 parallelen Scheitelstrahl s3.
- Trage die Strecke AB achtmal ab dem Punkt A nach oben auf dem Teilerstrahl s2 ab, es ergibt sich der Schnittpunkt D,10, der Teilerstrahl s2 ist somit in zehn gleiche Teile geteilt.
- Konstruiere die Strecke CE auf dem Scheitelstrahl s3 mittels eines Kreisbogens um C mit dem Radius gleich der Strecke CD,10.
- Zeichne den Teilerstrahl s4 ab dem Punkt E parallel zum Teilerstrahl s2.
- Trage die Strecke AB einmal ab dem Punkt E sowie achtmal ab dem Punkt 2 auf dem Teilerstrahl s4 ab, es ergeben sich die Schnittpunkte F und 10,G, der Teilerstrahl s4 ist somit in zehn gleiche Teile geteilt.
- Verbinde den Punkt B mit dem Punkt F.
- Zeichne einen zum größten Teil unterbrochenen Diagonalstrahl s5 ab dem Scheitelstrahl s3 durch den Punkt B bis zum Punkt 10,G, es ergibt sich auf dem Scheitelstrahl s3 der Scheitelpunkt H. Der Scheitelpunkt H ist für die Projektionsstrahlen bestimmt, die bei der Konstruktion des Zählers bzw. Nenners vom Teilerstrahl s4 ausgehen.
- Zeichne einen zum größten Teil unterbrochenen Diagonalstrahl s6 ab dem Scheitelstrahl s3 durch den Punkt F bis zum Punkt D,10, es ergibt sich auf dem Scheitelstrahl s3 der Scheitelpunkt I. Der Scheitelpunkt I ist für die Projektionsstrahlen bestimmt, die bei der Konstruktion des Zählers bzw. Nenners vom Teilerstrahl s2 ausgehen.
- Teile den Scheitelstrahl s3 in drei gleichlange Teile, es ergeben sich die Punkte J und K.
- Zeichne die Hilfsstrahlen s7 und s8 jeweils senkrecht stehend zum Scheitelstrahl s3 ab dem Punkt J bzw. ab dem Punkt K. Die beiden Hilfsstrahlen werden alternativ nur zur Lagebestimmung (Abstand zum Scheitelstrahl s3) der projizierten Zahl verwendet.
- Beachte: Die auf einem Hilfsstrahl projizierten Zahlen können nicht auf den benachbarten Hilfsstrahl und nicht auf die Teilerstrahlen projiziert werden!
- Konstruiere die Strecke LE gleich der Strecke EI auf dem Scheitelstrahl s3
- Verbinde den Punkt L mit dem Punkt 3 auf dem Teilerstrahl s4.
- Zeichne eine Parallele zur Strecke L3 ab dem Punkt F vom Teilerstrahl s4, es ergibt sich der Schnittpunkt M auf dem Scheitelstrahl s3.
- Konstruiere die Strecke NJ gleich der Strecke LM sowie die Strecke JO gleich der Strecke EM auf dem Scheitelstrahl s3, es entstehen die beiden Scheitelpunkte N und O.
- Konstruiere die Strecke KP gleich der Strecke LM sowie die Strecke KQ gleich der Strecke EM auf dem Scheitelstrahl s3, es entstehen die beiden Scheitelpunkte P und Q.
- Somit ist das Schema (exakt) konstruiert.
Weblinks
[Bearbeiten] Dritter Strahlensatz
Zahlenstrahl
Quadratur des Kreises
[Bearbeiten]Variante 1
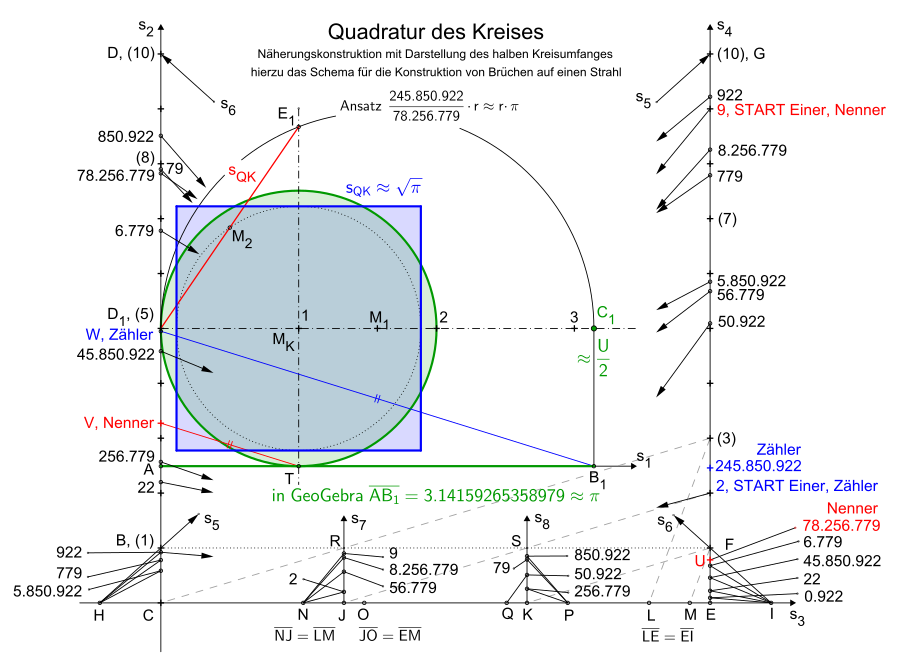
[Bearbeiten]Näherungskonstruktion mit Darstellung des halben Kreisumfangs
Konstruktionsprinzip
[Bearbeiten]- Die Hauptelemente sind ein Zahlenstrahl s1, zwei darauf senkrecht stehende Teilerstrahlen s2 und s4, ein zu s1 paralleler Scheitelstrahl s3, zwei Diagonalstrahlen s5 und s6 und zwei Hilfsstrahlen s7 und s8.
- Von dem vorgegebenen Nenner und Zähler werden die Dezimalstellen in der Reihenfolge Einer, Zehner, Hunderter u. s. w. jeweils mittels Projektion mit dem Faktor bzw. falls die nächste Dezimalstelle eine "0" ist, mit dem Faktor verkleinert und auf einem Teilerstrahl s2 oder s4 geometrisch addiert bzw. subtrahiert.
- Zuerst wird der Nenner konstruiert, anschließend zum Punkt A des Teilerstrahls s2 addiert und der sich dabei ergebende Schnittpunkt, z. B. V, Nenner, mit dem Punkt T des Zahlenstrahls s1 (Wert = 1) verbunden, dabei ergibt sich die Verbindungsstrecke V, NennerT.
- Der konstruierte Zähler wird ebenfalls zum Punkt A des Teilerstrahls s2 addiert, dabei ergibt sich der Schnittpunkt, z. B. W, Zähler.
- Die abschließende Parallele zur Verbindungstrecke V, NennerT erzeugt den Schnittpunkt B1 auf dem Zahlenstrahl s1. Somit entspricht die Länge der Stecke AB1 exakt dem Wert des vorgegebenen Bruches.
- Ansatz: Ein Bruch der die gewünschte Näherung an bzw. an hat. Die Anwendung der Strahlensätze in kompakter Form.
- Es sind sämtliche Brüche z. B. mit einer beliebigen Näherung an bzw. an einsetzbar.
Konstruktion
[Bearbeiten]- Als Basiskonstruktion ist das Schema für die Konstruktion von Brüchen auf einen Strahl eingearbeitet. Da für den Zahlenstrahl s1 der Abstand AC auf s2 frei wählbar ist, wurde er aus Gründen des Platzbedarfs (Einer des Zählers ist 2 ) nahe 2,5 gewählt.
- Wähle z. B. einen Dezimalbruch oder einen unechten Bruch der die gewünschte Näherung an hat.
- Im dargestellten Beispiel ist der unechte Bruch gewählt, dieser wurde schon 1770 von Johann Heinrich Lambert in seinem Buch "Beyträge zum Gebrauche der Mathematik und deren Anwendung" veröffentlicht.
- Fünfzehn Nachkommastellen sind gleich deren des Wertes .
Radius des Kreises
[Bearbeiten]- Bestimme den Radius r des Kreises mittels der beliebigen Strecke AT. Um die prinzipielle Genauigkeit des Konstruktionsprinzips (mithilfe GeoGebra) zu verdeutlichen, ist in der folgenden Darstellung der Radius r = 1 gewählt.
- Konstruiere den Mittelpunkt MK so, dass der anschließend eingezeichnete Kreis mit dem Radius r gleich der Strecke MKT, den Teilerstrahl s2 und den Zahlenstrahl s1 berührt.
Nenner
[Bearbeiten]- Verbinde den neunten Punkt des Teilerstrahls s4 (Zahl 9, START Einer, Nenner) mit dem Scheitelpunkt N des Hilfsstrahls s7, es ergibt sich darauf der Schnittpunkt 9. Der Wert der Zahl 9 vom Teilerstrahl s4 ist dadurch mit dem Faktor verkleinert.
- Greife die Strecke J9 ab und addiere sie zum siebten Teilungspunkt des Teilerstrahls s2, es ergibt sich darauf der Schnittpunkt 79.
- Verbinde den Schnittpunkt 79 des Teilerstrahls s2 mit dem Scheitelpunkt P des Hilfsstrahls s8, es ergibt sich darauf der Schnittpunkt 79. Es könnte alternativ mit dem Scheitelpunkt O des Hilfsstrahls s7 oder mit dem Scheitelpunkt I des Teilerstrahls s4 verbunden werden. Damit aber die projizierten Zahlen (Schnittpunkte) zueinander einen gut erkennbaren Zwischenraum für das Abgreifen des Abstandes zum Scheitelstrahl s3 haben, ist es vorteilhaft anfangs die Teilerstrahlen (s2, s4) und Hilfsstrahlen (s7, s8) in etwa gleichmäßig zu verwenden.
- Greife die Strecke K79 vom Hilfsstrahl s8 ab und addiere sie zum siebten Teilungspunkt des Teilerstrahls s4, es ergibt sich darauf der Schnittpunkt 779.
- Verbinde den Schnittpunkt 779 des Teilerstrahls s4 mit dem Scheitelpunkt H des Teilerstrahls s2, es ergibt sich darauf der Schnittpunkt 779.
- Setze diese Vorgehensweise, zuerst Projizieren, dann Abgreifen und schließlich Addieren, fort bis der Nenner mit dem Schnittpunkt 78.256.779 auf dem Teilerstrahl s4 konstruiert ist.
- Greife die Strecke EU (Nenner) ab und addiere sie zum Punkt A des Teilerstrahls s2, es ergibt sich darauf der Schnittpunkt V, Nenner. Somit ist der Nenner konstruiert.
- Verbinde den Schnittpunkt V, Nenner mit dem Punkt T des Zahlenstrahles s1, es ergibt sich die Strecke V, NennerT.
Zähler
[Bearbeiten]- Verbinde den zweiten Punkt des Teilerstrahls s4 (Zahl 2, START Einer, Zähler) mit dem Scheitelpunkt N des Hilfsstrahls s7, es ergibt sich darauf der Schnittpunkt 2.
- Greife die Strecke R2 ab (größere Zirkelöffnung) und subtrahiere sie vom dritten Teilungspunkt des Teilerstrahls s2, es ergibt sich darauf der Schnittpunkt 22.
- Verbinde den Schnittpunkt 22 des Teilerstrahls s2 mit dem Scheitelpunkt I des Teilerstrahls s4, es ergibt sich darauf der Schnittpunkt 22.
- Greife die Strecke F22 ab und subtrahiere sie vom zehnten Teilungspunkt des Teilerstrahls s4, es ergibt sich darauf der Schnittpunkt 922.
- Beachte: Die nächste Stelle des Zählers ist eine Null (0), deshalb muss der Wert der Zahl 922 vom Teilerstrahl s4, vor der geometrischen Addition mit der übernächsten Dezimalstelle 5, mit dem Faktor verkleinert sein! In diesem Fall ist die erste Verkleinerung mit dem Faktor stets auf einem Teilerstrahl durchzuführen, da die auf einem Hilfsstrahl projizierten Zahlen nicht auf den benachbarten Hilfsstrahl und nicht auf die Teilerstrahlen projiziert werden können!
- Verbinde den Schnittunkt 922 des Teilerstrahls s4 mit dem Scheitelpunkt H des Teilerstrahls s2, es ergibt sich darauf der Schnittpunkt 922.
- Verbinde den Schnittunkt 922 des Teilerstrahls s2 mit dem Scheitelpunkt I des Teilerstrahls s4, es ergibt sich darauf der Schnittpunkt 0.922. Der Wert der Zahl 922 vom Teilerstrahl s4 ist dadurch mit dem Faktor verkleinert.
- Greife die Strecke F0.922 ab (größere Zirkelöffnung) und subtrahiere sie vom sechsten Teilungspunkt des Teilerstrahls s4, es ergibt sich darauf der Schnittpunkt 50.922.
- Verbinde den Schnittpunkt 50.922 des Teilerstrahls s4 mit dem Scheitelpunkt Q des Hilfsstrahls s8, es ergibt sich darauf der Schnittpunkt 50.922. Es könnte alternativ mit dem Scheitelpunkt N des Hilfsstrahls s7 oder mit dem Scheitelpunkt H des Teilerstrahls s2 verbunden werden. Damit aber die projizierten Zahlen (Schnittpunkte) zueinander einen gut erkennbaren Zwischenraum für das Abgreifen des Abstandes zum Scheitelstrahl s3 haben, ist es vorteilhaft anfangs die Teilerstrahlen (s2, s4) und Hilfsstrahlen (s7, s8) in etwa gleichmäßig zu verwenden.
- Greife die Strecke K50.922 vom Hilfsstrahl s8 ab und addiere sie zum achten Teilungspunkt des Teilerstrahls s2, es ergibt sich der Schnittpunkt 850.922.
- Setze diese Vorgehensweise, zuerst Projizieren, dann Abgreifen und schließlich Addieren, fort bis der Zähler mit dem Schnittpunkt 245.850.922 auf dem Teilerstrahl s4 konstruiert ist.
- Greife die Strecke E245.850.922 (Zähler) und addiere sie zum Punkt A des Teilerstrahls s2, es ergibt sich darauf der Schnittpunkt W, Zähler. Somit ist der Zähler konstruiert.
- Ziehe eine Parallele zur Strecke V, NennerT bis auf den Zahlenstrahl s1, damit ergibt sich der Schnittpunkt B1.
- Errichte eine Senkrechte auf den Zahlenstrahl s1 ab dem Punkt B1 bis auf die Mittelachse des Kreises, es ergibt sich der Schnittpunkt C1.
- Halbiere die Strecke D1C1, dabei entsteht der Mittelpunkt M1.
- Zeichne über M1 den Thaleskreis ab C1, er schneidet die Mittelachse des Kreises in E1.
- Verbinde den Punkt D1 mit dem Punkt E1, die Strecke D1E1 entspricht der konstruierten Seitenlänge SQK des gesuchten Quadrates.
- Halbiere die Strecke D1E1, es ergibt sich der Schnittpunkt M2.
- Zeichne einen Kreis um den Mittelpunkt MK mit dem Radius MKM2.
- Konstruiere mithilfe der Seitenlänge SQK um den Mittelpunkt MK und mittels des Hilfskreises mit dem Radius MKM2 das gesuchte Quadrat.
- Somit ergibt sich:
- a) Ein Quadrat mit einem nahezu gleichen Flächeninhalt wie der vom gegebenen Kreis.
- b) Eine Strecke AB1 mit einer Länge, die nahezu gleich dem halben Umfang des Kreises ist.
Berechnung
[Bearbeiten]- Allgemein: Seite des Quadrates SQ = r •
- Die Berechnung der konstruierten Seite des Quadrates SQK geschieht, aufgrund des Konstruktionsprinzips, schrittweise durch die geometrischen Additionen bzw. Subtraktionen der einzelnen Zwischenergebnisse auf den Teilerstrahlen s2 bzw. s4.
- Der vorgegebene unechte Bruch wird auf dem Zahlenstrahl s1 prinzipiell exakt dargestellt.
Absoluter Fehler der konstruierten Seitenlänge des Quadrates FSQK
[Bearbeiten][LE]
Beispiele um die Fehler zu verdeutlichen
[Bearbeiten]- Bei einem Kreis mit Radius r = 100 Milliarden km (das Licht bräuchte für diese Strecke ca. 91 Stunden) wäre der Fehler der konstruierten Seitenlänge des Quadrates SQK ≈ 2,2 mm.
- Bei einem Kreis mit Radius r = 100 km wäre der Fehler der Fläche des Quadrates ≈ -0,781 mm2
Variante 2
[Bearbeiten]Näherungskonstruktion
[Bearbeiten]

Sie beruht auf der Näherung
Nach dem Ziehen des Einheitskreises ( [LE]) werden die x-Achse und die y-Achse eingetragen. Es folgen der Kreisbogen und die (nicht eingezeichnete) Mittelsenkrechte zwischen und mit Schnittpunkt . Nun wird das Lot von auf mit Fußpunkt gefällt. Das dadurch erzeugte rechtwinklige Dreieck hat wegen der Hypotenuse und des Winkels die Katheten und . Die Strecke wird in halbiert. Um den oben beschriebenen Ansatz für die Näherung zu erhalten, stellt man sich ein rechtwinkliges Dreieck mit der Hypotenuse und der kleinen Kathete vor. Mit dem Satz des Pythagoras gilt für die große Kathete
Die Länge der Kathete ist mit Zirkel und Lineal konstruierbar (siehe Animation, gleiches Konstruktions-Prinzip wie in Variante 1).
Weiter geht es mit dem Einzeichnen des rechtwinkligen Dreiecks anhand der jetzt bekannten Seiten. Hierzu wird zuerst der Punkt mithilfe einer Parallelen zur x-Achse auf die y-Achse projiziert, der Schnittpunkt ist . Der darauf folgende Kreis mit dem Radius schneidet die Parallele in und . Die Halbgerade ab durch den Kreismittelpunkt und die in errichtete Senkrechte schneiden sich in und ergeben damit das Dreieck . Der abschließende Kreis mit Radius ist der Inkreis des gesuchten Quadrates .
Fehler
[Bearbeiten]Bei einem Kreis mit Radius r = 1 [LE]:
- In GeoGebra konstruierte Seite des Quadrates [LE]
- Soll-Seite des Quadrates [LE]
- Absoluter Fehler E-12 [LE]
- Fläche des konstruierten Quadrates [FE]
- Soll-Fläche des Quadrates [FE]
- Absoluter Fehler E-12 [FE]
Verdeutlichung:
- 11 Nachkommastellen sind gleich denen von bzw. 10 Nachkommastellen sind gleich denen von .
- Bei einem Kreis mit dem Radius r = 1 Mio. km wäre der Fehler der Seite a ≈ 1,3 mm
- Bei einem Kreis mit dem Radius r = 1 km wäre der Fehler der Fläche A ≈ 5 mm2
Weblinks
[Bearbeiten] Quadratur des Kreises
Johann Heinrich Lambert: Beyträge zum Gebrauche der Mathematik und deren Anwendung Quadratur des Circuls, S. 157 Abgerufen am 2. Juli 2017.
Dreiteilung des Winkels
[Bearbeiten]- Einleitung und Erklärungen zu "Klassisches Problem", "Verallgemeinerung", "Nicht-klassische Verfahren" u. a. m. sind im Artikel Dreiteilung des Winkels enthalten.
Variante 1
[Bearbeiten]Konstruktionsprinzip
[Bearbeiten]- Näherungskonstruktion
- Den gegebenen Winkel mit vier Winkelhalbierenden verkleinern und den Kreisbogen MFG zwischen Winkelhabierende w3 und w4 mit einer Näherungslösung dritteln.
Konstruktion für Winkel > 0° bis 180°
[Bearbeiten]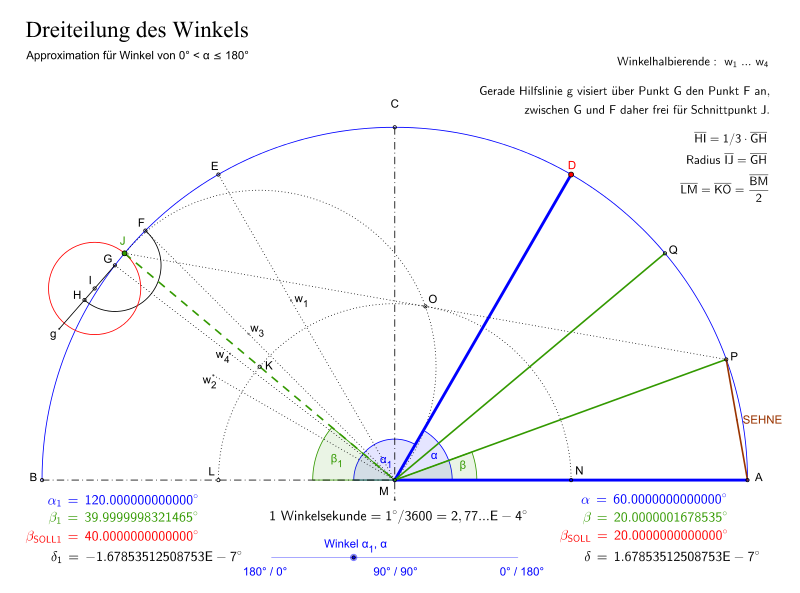
- Für Winkel < 90° ist, zur klaren Unterscheidung der Punkte die auf der geraden Hilfslinie g liegen, meist die Drittelung des Supplementwinkels vorteilhaft. Dies wird im folgenden Beispiel berücksichtigt.
- Zeichne durch den Punkt M eine Gerade.
- Zeichne um den Punkt M einen Halbkreis, es ergeben sich auf der Gerade die Schnittpunkte A und B, die Strecke MA ist der erste Winkelschenkel.
- Konstruiere eine Senkrechte zur Strecke AB ab Punkt M bis sie den Halbkreis schneidet, es ergibt sich der Schnittpunkt C.
- Konstruiere als Beispiel den Winkel = 60°, es ergibt sich der Schnittpunkt D auf dem Halbkreis MAB
- Verbinde den Punkt M mit dem Punkt D, es ergibt sich der zweite Winkelschenkel der mit der Strecke MB den Supplementwinkel = 120° einschließt.
- Konstruiere vom Winkel die Winkelhalbierende w1, es ergibt sich auf dem Halbkreis MAB der Schnittpunkt E.
- Konstruiere vom Winkel die Winkelhalbierende w2, die Länge der Strecke Mw2 etwas länger als
- Konstruiere vom Winkel die Winkelhalbierende w3, es ergibt sich auf dem Halbkreis MAB der Schnittpunkt F.
- Konstruiere vom Winkel die Winkelhalbierende w4, es ergibt sich auf dem Halbkreis MAB der Schnittpunkt G.
- Zeichne eine gerade Hilfslinie g die über den Punkt G den Punkt F anvisiert (quasi ein Lineal an die Punkte F und G angelegt), aber mit ihrer Länge, ca. Abstand |EF|, nur bis zum Punkt G verläuft und keine Verbindung der Punkte F und G herstellt. Somit ist zwischen diesen beiden Punkten der Halbkreis MAB für den späteren Schnittpunkt J frei zugänglich.
- Zeichne einen Halbkreis um den Punkt G mit dem Radius gleich dem Abstand |FG|, es ergibt sich auf der Hilfslinie g der Schnittpunkt H.
- Konstruiere auf der Hilfslinie g die Strecke HI, sie ist ein Drittel der Strecke GH.
- Zeichne einen Kreis um den Punkt I mit dem Radius gleich der Strecke GH, es ergibt sich auf dem Halbkreis MAB zwischen den Punkten F und G der Schnittpunkt J.
- Verbinde den Punkt J mit dem Punkt M, die Winkelschenkel JM und MB schließen den Winkel ein. Somit ist vorerst vom Supplementwinkel 120° ein approximiertes Drittel dargestellt. .
- Halbiere die Strecke JM, es ergibt sich darauf der Schnittpunkt K.
- Zeichne um den Punkt M einen Halbkreis der durch den Punkt K verläuft, es ergeben sich die Schnittpunkte L und N auf der Strecke AB.
- Zeichne um den Punkt K einen Halbkreis der vom Punkt M zum Punkt J verläuft, es ergibt sich der Schnittpunkt O mit dem Halbkreis MNL.
- Zeichne eine Gerade vom Punkt J durch den Punkt O bis zum Halbkreis MAB, es ergibt sich darauf der Schnittpunkt P.
- Verbinde den Punkt P mit dem Punkt M, die Winkelschenkel PM und MA schließen den Winkel ein.
- Trage die Strecke AP ab dem Punkt P einmal auf dem Halbkreis MAB ab, es ergibt sich darauf der Schnittpunkt Q. Somit ist der Winkel 60° nahezu gedrittelt.
Fehler
[Bearbeiten]- Der max. Winkelfehler von bzw. ist ca. 1,25E-6°, wenn der Winkel nahezu 0° bzw. nahezu 180° ist.
Beispiel um den Fehler zu verdeutlichen
[Bearbeiten]- Bei einem Radius r = MA = 100 km wäre der max. Fehler an der Sehne 2,2 mm
Berechnung
[Bearbeiten]- Im Kapitel "Neuneck", unter "Berechnung" sind zur Verifizierung des Konstruktionsprinzips alle Berechnungsschritte für die Dreiteilung des Winkels (Beispiel ) aufgezeigt. Für die Dreiteilung des oben dargestellten Supplementwinkels 120°, sind in den Formeln die entsprechenden Werte (u. a. Länge des Winkelschenkels ändert sich von 2r in r) und Bezeichnungen (Punkte, Winkel, Strecken etc.) einzusetzen.
Variante 2
[Bearbeiten]Konstruktionsprinzip
[Bearbeiten]- Näherungskonstruktion
- Ein paar Konstruktionselemente stammen aus Alberts' Konstruktion.
- Mit der stark vereinfachten Konstruktion wird folgendes erreicht:
- Der größte Teil der Konstruktion liegt in der unteren Hälfte des Kreises
- Eine praktikable Dreiteilung des Winkels ab nahe bis
- Die Animation (Schrittgröße ca. 3° bis 4°) zeigt alternativ die Konstruktion für Winkel > 0° bis 90° sowie die dazu spiegelbildliche Konstruktion ab 90° bis 180°. Aus Gründen der Übersichtlichkeit sind die Punkte ohne Beschriftung.
Konstruktion für Winkel > 0° bis 180°
[Bearbeiten]

- Kreis mit beliebigem Durchmesser um Mittelpunkt
- Winkelschenkel und Winkelschenkel schließen den Winkel im Scheitel ein, und den Ergänzungswinkel
- Kreis um mit Radius ; die Verlängerung des Winkelschenkels schneidet Kreis in
- Durchmesser mit und Verbindung des Punktes mit
- Punkt auf Kreis so, dass
- Strecke in halbieren, die anschließende Mittelsenkrechte von schneidet in ergibt
- Parallele zu ab erreicht Kreis in
- Parallele zu ab Punkt darauf so, dass
- Linie ab durch erreicht Kreis in anschließend Linie ab bis
- Parallele zu ab erreicht Kreis in
- Strecke über hinaus verlängern, Punkt darauf so, dass
- Linie ab durch erreicht Kreis in
- Bestimme Punkt so, dass Winkel Verbindung mit ergibt den Winkel
- Mittelsenkrechte von schneidet in verbinde mit
- Bestimme Punkt so, dass Winkel
- Abschließende Verbindung mit ergibt Winkel
- Der Winkel ist nahezu gleich einem Drittel des Winkels
- Der Winkel ist nahezu gleich einem Drittel des Winkels
Fehlerbetrachtung
[Bearbeiten]Eine Fehleranalyse, ähnlich Alberts' Konstruktion, ist nicht vorhanden.
Die dargestellte Konstruktion wurde mit der Dynamische-Geometrie-Software (DGS) GeoGebra GeoGebra angefertigt; darin werden in diesem Fall die Winkelgrade meist mit signifikanten dreizehn Nachkommastellen angezeigt. Die sehr kleinen Fehler des Winkels bzw. , sprich, die Differenzwerte aus bzw. werden von GeoGebra stets mit angezeigt.
Betrachtet man die Grafik in GeoGebra, in sehr kleinen Schritten, die zu- oder abnehmenden Winkelweiten des Winkels bzw. mithilfe des Schiebereglers oder der Animation, ist vereinzelt eine max. Abweichung vom SOLL-Wert bzw. ablesbar.
Verdeutlichung des absoluten Fehlers
[Bearbeiten]Der in GeoGebra ablesbare Differenzwert von max. entspricht einem absoluten Fehler der – nicht eingezeichneten – Sehne bzw. der sich wie folgt ergibt:
Hätten die Winkelschenkel die Länge gleich 1 Milliarde km (das Licht bräuchte für diese Strecke ≈ 56 Minuten, das ist etwas weniger als 7-mal die Entfernung Erde – Sonne), wäre der absolute Fehler der beiden – nicht eingezeichneten – Sehnen bzw. ≈ 1,7 mm.
Weblinks
[Bearbeiten]Neuneck in diesem Buch
Supplementwinkel oder Ergänzungswinkel
Dreiteilung einer Strecke in diesem Buch
Dreiteilung des Winkels 60° in diesem Buch
Alberts' Konstruktion: Näherung für Winkelweiten größer 0° bis 90°, mit Fehleranalyse
Verdoppelung des Würfels
[Bearbeiten]Eine relativ einfache Näherungskonstruktion, aber mit einer ebenfalls außergewöhnlichen Genauigkeit ist im Folgenden beschrieben.
- Einleitung, Erklärung und Weiterführungen sind im Artikel Würfelverdoppelung enthalten.
- ist die Kantenlänge des Ausgangswürfels, die des verdoppelten Würfels
Konstruktionsbeschreibung
[Bearbeiten]Es beginnt mit dem Einheitskreis mit Radius und dem Einzeichnen des Durchmessers . Als nächstes wird die zum Durchmesser senkrecht stehende Mittelachse eingetragen. Es folgt jeweils ein Kreisbogen mit Radius um und ; die Schnittpunkte sind und . Eine nicht eingezeichnete Mittelsenkrechte des Abstandes halbiert den Kreisbogen in . Eine Parallele zu ab ergibt die Strecke . Den Punkt bestimmt man mithilfe einer nicht eingezeichneten Mittelsenkrechten des Abstandes .
Weiter geht es mit dem Übertragen des Abstandes ab , dabei ergibt sich der Schnittpunkt . Eine Parallele zu ab ergibt die Strecke . Der Punkt wird mithilfe einer nicht eingezeichneten Mittelsenkrechten des Abstandes bestimmt. Die abschließende Verbindung des Punktes mit schneidet in und liefert somit die Strecke , deren Länge nahezu gleich dem Sollwert ist.
Fehler
[Bearbeiten]In GeoGebra werden max. 15 Nachkommastellen angezeigt.
Beispiel zur Verdeutlichung der Fehler
[Bearbeiten]- Bei einem Würfel 1 mit der Kantenlänge a1 = 1 Mrd. km (das Licht bräuchte für diese Strecke ca. 56 min.) wäre bezüglich der konstruierten Kantenlänge a2 des verdoppelten Würfels 2 kein Fehler evaluierbar.
- Somit liegt die Vemutung nahe, dass der absolute Fehler < 1 mm ist.
- Bei einem Würfel 1 mit der Kantenlänge a1 = 10 km wäre der Fehler des Volumens vom verdoppelten Würfels 2 vermutlich < 0,7 dm3 oder < 1 Liter.
Weblinks
[Bearbeiten] Commons: Animation, Verdoppelung des Würfels – Album mit Bildern, Videos und Audiodateien
Commons: Animation, Verdoppelung des Würfels – Album mit Bildern, Videos und Audiodateien- Quadrat
- GeoGebra
- Einheitskreis
- Mittelsenkrechte
- Messabweichung




























































































































![{\displaystyle F=2\cdot \sin \left({\frac {1\cdot 10^{-13}\mathrm {^{\circ }} }{2}}\right)=0{,}000\;000\;000\;000\;001\;745\ldots =1{,}745\ldots \cdot 10^{-15}\;[\mathrm {LE} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12684260ede34dd5c2cda172dd4e5032324a8a43)


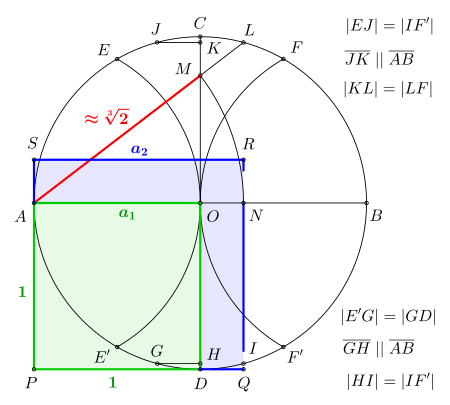















![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)
![{\displaystyle {\begin{alignedat}{2}{\text{in GeoGebra konstruierte Länge der Strecke }}\qquad {\overline {AM}}&=&&1{,}259921049894873\;[\mathrm {LE} ]\\-{\text{Sollwert }}\qquad -{\sqrt[{3}]{2}}&=-&&1{,}259921049894873\dots \;[\mathrm {LE} ]\\\hline {\text{absoluter Fehler in GeoGebra nicht evaluierbar }}\qquad F&=&&0{,}000000000000000\dots \;[\mathrm {LE} ]\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40521cdaf74849d920d7c9403ebbbd722919664e)