Optik

Aus Wikibooks

Band 10 des Werkes Einführung in die Theoretische Physik - Ein Lehrbuch in mehreren Bänden

Inhaltsverzeichnis

1 Motivation
2 Geometrische Optik
3 Optische Instrumente
4 Licht als elektromagnetische Welle
5 Die Ausbreitung des Lichts
- 5.1 Huygenssches Prinzip
- 5.2 Fermat'sche Prinzip
6 Polarisation
7 Interferenz
8 Grunderscheinungen der Beugung
- 8.1 Beugung am Spalt
- 8.2 Beugung am Gitter

[Bearbeiten] Motivation

Warum leuchtet der Himmel tagsüber blau, abends aber rot? Wieso sieht man nachts Sterne, tagsüber aber nicht? Wie funktioniert das Sehen weit entfernter Objekte? Ist Licht nun wellenförmig oder besteht es aus Teilchen?

Der Begriff Optik leitet sich aus dem griechischen Wort optike ab, Optik ist also die Lehre vom Sichtbaren. Eine der wichtigsten Größen innerhalb der Optik ist die Wellenlänge $λ$ . Sie ergibt eigentlich nur mit der Vorstellung, dass Licht sich wellenförmig ausbreitet, Sinn. Zur Beschreibung von verschiedenen Farbeindrücken bei Licht hat sich die Wellenlänge auch im Teilchenbild bewährt.

Im engeren Sinn ist Optik die Lehre der elektromagnetischen Strahlung im Wellenlängenbereich des sichtbaren Lichts (ca. 380nm bis 780nm). Im weiteren Sinne wird allerdings der Bereich vom Infraroten bis Ultravioletten mit dazu genommen. Des Weiteren spricht man auch von der Röntgenoptik, deren Wellenlängenbereich sich auf das der Röntgenstrahlung bezieht.

1675 wurde von dem dänischen Astronomen Olaus Römer über astronomische Messungen zum ersten Mal ein vernünftiger Wert für die Geschwindigkeit des Lichts gefunden. Über nichtastronomische Messungen gelang es erstmals Fizeau im Jahr 1849, annehmbare Werte für die Lichtgeschwindigkeit zu ermitteln, diese Messmethoden wurden später durch Foucault 1852 und dann noch von Michelson um 1930 verbessert. Seit dem Jahre 1983 liegt der heute gültige Wert der Lichtgeschwindigkeit bei

$c = 299.792.458\,\frac{\mathrm{m}}{\mathrm{s}}$

In den meisten Fällen ist allerdings der Wert von $c = 3 \cdot 10^8\,\tfrac{\mathrm{m}}{\mathrm{s}}$ vollkommen ausreichend.

[Bearbeiten] Geometrische Optik

Einfache Versuche zeigen, dass man in einer ersten Näherung gut davon ausgehen kann, dass Licht sich geradlinig als Strahl ausbreitet. Für erste Betrachtungen ist diese Annahme ausreichend (Grenze: Objekte, die das Licht begrenzen, haben eine Mindestgröße von etwa 100mal der Wellenlänge des verwendeten Lichts). Damit lassen sich Spiegel, Linsen und daraus zusammengesetzte Geräte (Mikroskop, Teleskop, usw.) beschreiben.

[Bearbeiten] Reflexion und Brechung

[Bearbeiten] Reflexionsgesetz

Einfallender und ausfallender Strahl bilden mit dem Lot, auch Grenzflächennormale genannt, gleiche Winkel. Außerdem bilden Einfallsstrahl und Lot eine Ebene, die Einfallsebene, in welcher auch der reflektierte Strahl liegt. Daraus resultiert:

$\alpha = \alpha'\$

Welcher Anteil der Energie des Strahls an der Grenzfläche reflektiert wird, hängt von den Brechzahlen der betreffenden Medien (und damit der Lichtgeschwindigkeit), dem Einfallswinkel sowie von der Polarisationsrichtung der Welle ab.

[Bearbeiten] Brechungsgesetz

Unter Umständen wird nicht die ganze Energie einer elektromagnetischen Welle reflektiert, sondern teilweise oder zur Gänze transmittiert, was bedeutet, dass der Strahl in das Medium eintritt. Bei diesem Übergang der Welle von einem Medium ins andere ändert sich die Ausbreitungsrichtung des Strahles sowie die Wellenlänge seiner, ihn beschreibenden Welle, wobei die Frequenz allerdings gleich bleibt. Das Verhältnis vom Sinus des Einfallswinkels zum Sinus des Brechungswinkels ist abhängig von den beiden Medien, zwischen denen der Übergang stattfindet. Die für beide Medien charakteristische Konstante n heißt Brechzahl. Wenn $n 1$ kleiner als $n 2$ ist, findet eine Brechung zum Lot statt, im umgekehrten Fall wird das Licht vom Lot weg gebrochen. Die Brechzahl des Vakuums ist als 1 definiert (näherungsweise gilt dieser Wert auch für Luft).

$n_1 \cdot \sin(\alpha) = n_2 \cdot \sin(\beta)$

[Bearbeiten] Totalreflexion

Nach dem Brechungsgesetz ist

$\sin (\beta) = \frac{n_1}{n_2} \cdot \sin(\alpha)$ .

Bei $n 1 > n 2$ , also an der Grenzfläche vom optisch dichteren zum dünneren Medium kann jedoch

$\frac{n_1}{n_2} \cdot \sin(\alpha) > 1$

werden. In diesem Fall gibt es keine reelle Lösung für den Winkel $\beta \$ , und es tritt keine Brechung auf. Der einfallende Strahl wird vollständig reflektiert; dieser Fall wird als Totalreflexion bezeichnet. Der Winkel $\alpha_T \$ , bei dem $\beta = 90^\circ$ wird, wird als Grenzwinkel für Totalreflexion bezeichnet.

$\alpha_T = \arcsin \left( \frac{n_2}{n_1} \right)$

[Bearbeiten] Dispersion

Wie erwähnt hängt die Geschwindigkeitsveränderung beim Übergang elektromagnetischer Strahlen von einem Medium in ein anderes vom Brechzahl n ab. Die Brechzahl eines Materials ist allerdings keine Konstante, sondern eine Funktion der Wellenlänge. Also:

$n = n ( \lambda )\$

Dies hat zur Folge, dass sich weißes Licht, welches ja aus allen für uns sichtbaren Farben, gleichbedeutend mit Wellenlängen, zusammensetzt, in die Farbfolge Rot, Orange, Gelb, Grün, Blau, Violett aufspaltet, sobald es durch ein Prisma geschickt wird. Das Licht wird dabei in sein Spektrum aufgespalten, und die nach dem Prisma sichtbar werdenden Bestandteile des weißen Lichtes sind nicht weiter aufspaltbar, eine Eigenschaft, die monochromatisch genannt wird. Ähnliche Vorgänge spielen auch in der Datenübertragung eine Rolle, weil auch hier Informationspakete weggeschickt werden, welche aus mehreren Wellen zusammengesetzt sind. Auch hier kommt es durch unterschiedliche Ausbreitungsgeschwindigkeit der Wellen in diesem Paket zu Dispersion, hierbei zerrinnt der abgeschickte Wellenberg und wird breiter.

[Bearbeiten] Spiegel

Ein Spiegel reflektiert Licht.

Die Entfernung von einem Objekt vor dem Spiegel zum Spiegel ist genau so groß wie die Entfernung vom Spiegel bis zu einem (gedachten) Objekt hinter dem Spiegel. Um das zu zeigen bringt man zwei Objekte in Deckung, wie zwei Bleistifte, einer vor und einer hinter dem Spiegel. Man verschiebt nun den Bleistift hinter dem Spiegel so, dass er mit seinem Spiegelbild übereinstimmt und misst die jeweiligen Abstände
Ein Spiegel vertauscht nicht rechts und links, wie man mit einem Bleistift vor dem Spiegel nachweisen kann. Die Spitze vom Bleistift verändert nur dann ihre Richtung, wenn sie mehr oder weniger direkt auf den Spiegel zeigt. Der Spiegel vertauscht vorne und hinten.
Wirft man einen Strahl schräg auf einen Spiegel, wird dieser im gleichen Winkel reflektiert wie er eingefallen ist. Beide Strahlen liegen in einer Ebene.

[Bearbeiten] Brechung an Grenzflächen

[Bearbeiten] Linsen

[Bearbeiten] Sammellinse

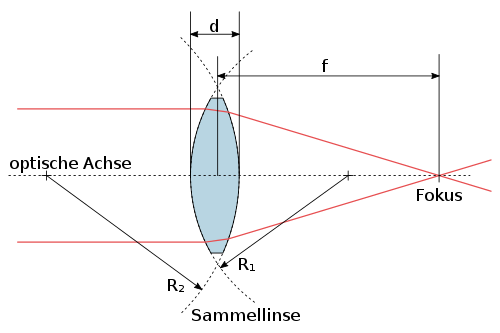
Mit speziellen Formen von Grenzflächen kann man nun mit der Brechung erreichen, dass Strahlen die von einem Punkt kommen, ins Unendliche abgebildet werden, das bedeutet, dass sie danach parallel verlaufen.

! Bild Sammellinse mit Fokos -> \infty !

in der geometrischen Optik sind die Vorgänge umkehrbar. Das bedeutet, mit der gleichen Linse kann man parallele Strahlen auf einen Punkt fokussieren.

man spricht deshalb bei dieser Linse von einer Sammellinse. Die wichtigste Größe ist die Brennweite f: das ist der Abstand zwischen dem Brennpunkt und Hauptebene der Linse.

[Bearbeiten] Zerstreuungslinse

[Bearbeiten] Linsenfehler

[Bearbeiten] chromatische Abberation

chromatische Abberation ist die durch Brechung erzeugter Farbsaum

[Bearbeiten] sphärische Abberation

sphärische Abberation ist durch Brechung erzeugte Randunschärfe

[Bearbeiten] Astigmatismnus

Der Astigmatismus ist ein Abbildungsfehler von Gegenstandspunkten, die seitlich versetzt zur optischen Achse liegen. Bei der Abbildung durch eine Sammellinse entstehen dabei zwei Bildpunkte.

Dieser Abschnitt soll in einem gesonderten Buch mit dem Titel theoretische Optik behandelt werden.

[Bearbeiten] Optische Instrumente

[Bearbeiten] Auge

[Bearbeiten] Lupe

[Bearbeiten] Kamera

[Bearbeiten] Objektiv

Ein Objektiv ist ein System aus Linsen, Mechanik, sowie in Sonderfällen auch Elektronik. Es dient normalerweise den Zweck durch reale Linsen den Eigenschaften einer idealen Linse so nahe wie möglich zu kommen. Da jede reale Linse verschiede Formen von Abberationen (Bildfehlern) aufweist, die aber durch die Kombination mehrere Linsen, zu Linsengruppen und Objektiven, abgemindert werden können. Die Vielfalt von Objektiven ist nahezu unbegrenzt. Sie reicht von winzigen Plastiklinsen-Objektiven in Handykameras, bis hin zu tonnenschweren Lithografieobjektiven, die zur Belichtung von Wafern in der Chipindustrie benötigt werden.

[Bearbeiten] Mikroskop

[Bearbeiten] Teleskop

[Bearbeiten] Licht als elektromagnetische Welle

Im Allgemeinen bestehen elektromagnetische Wellen aus gleichfrequenten, versetzt schwingenden elektrischen und magnetischen Wellen. Die Schwingungsrichtungen dieser Transversalwellen sind gegeneinander um $\tfrac{\pi}{2}$ gekippt. Zeitlich sind sie um eine viertel Periode verschoben.

Aus den Maxwellgleichungen folgt die Wellengleichung:

$\Delta E - \frac{1}{c^2}\frac{\partial}{\partial t^2}E = 0.$

mit

E(t): elektrische Feldstärke

Diese Gleichung für E(t) gilt allgemein für elektromagnetische Wellen, also auch für Funkwellen. Einen bestimmten Bereich der elektromagnetischen Wellen nennen wir Licht, da er vom menschlichen Auge registriert wird.

[Bearbeiten] Die Ausbreitung des Lichts

Aus der Beobachtung, das sich Licht geradlinig ausbreitet, werden in der geometrischen Optik die Gesetzmäßigkeiten des Lichtes mit Hilfe des Strahlenmodells beschrieben.

Die Lichtausbreitung erfolgt durch Lichtstrahlen. Diese Strahlen sind Lichtkegel aus infinitesimal kleinen Öffnungswinkeln.
Ein Lichtstrahl unterliegt den Gesetzen der Reflexion und der Brechung.

Streng physikalisch gesehen breitet sich Licht jedoch wellenförmig aus. Die Eigenschaften von Schwingungen und Wellen kommen bei Interferenz und Beugung zum Tragen.

[Bearbeiten] Huygenssches Prinzip

Es besagt dass von jedem Punkt entlang einer Wellenfront wieder eine Welle ausgeht. Diese Welle besitzt die gleiche Ausbreitungsgeschwindigkeit und die selbe Frequenz wie die ursprüngliche Wellenfront. Strahlen sind dabei Linien des Lichtes welche senkrecht auf die Wellenfronten stehen.

[Bearbeiten] Fermat'sche Prinzip

Nach dem Fermat'schen Prinzip breitet sich das Licht zwischen 2 definierten Punkten auf dem optisch kürzesten Weg aus. Die optische Weglänge $l opt$ ergibt sich hierbei aus der geometrischen Weglänge $l geo$ und der relativen optischen Dichte des Mediums im Vergleich mit der von Vakuum $n$ . $n$ ergibt sich aus dem Verhältnis der Ausbreitungsgeschwindigkeiten zueinander. Es gilt für die Werte $n 1$ , $n 2$ in den Medien 1 und 2 mit den Lichtausbreitungsgeschwindigkeit $c 1$ und $c 2$ :

$\frac{n_1}{n_2} = \frac{c_2}{c_1}$

Und für die optische Weglänge gilt:

$l_\mathrm{opt} = l_\mathrm{geo} \cdot n$

Im Allgemeinen ist zu beachten, dass die Ausbreitungsgeschwindigkeit von der Frequenz der elektromagnetischen Welle abhängen kann (Dispersion).

[Bearbeiten] Polarisation

Licht ist eine elektromagnetische Welle. Sowohl die elektrische, als auch die magnetische Feldstärke schwingen senkrecht zur Ausbreitungsrichtung: Sie schwingen nach oben/unten, oder links/rechts, wenn sich die Welle nach vorne ausbreitet.

! Bild !

Licht von der Sonne oder einer Glühlampe (oder Neonröhre) ist unpolarisiert, es schwingt in alle möglichen Richtungen, weil die Entstehung unkontrolliert in einem statistischen Prozess stattfindet, das Licht also durch Elektronen bzw. Atome unterschiedlichster Schwingungsrichtungen emittiert wird. Mit doppelbrechenden Kristallen oder speziellen Filtern kann man aus unpolarisiertem Licht aber (linear) polarisiertes Licht filtern; dabei wird Licht einer Polarisationsrichtung hindurchgelassen, und die senkrecht dazu polarisierten Anteile werden reflektiert oder absorbiert. Polarisiertes Licht schwingt nur noch in einer Richtung.

Fällt eine polarisierte elektromagnetische Welle mit der Amplitude (Feldstärke) $E_0 \$ auf einen Polarisator, dessen Polarisationsrichtung gegenüber der des Lichts um den Winkel $\alpha \$ verdreht ist, ist die Amplitude hinter dem Polarisator

$E = E_0 \cdot \cos \alpha$ .

Mit Hilfe spezieller Lichterzeuger (Laser) lässt sich ohne Filterung polarisiertes Licht erzeugen. Dies ist jedoch keine inhärente Eigenschaft eines Lasers.

Überlagern sich zueinander senkrecht polarisierte Lichtwellen gleicher Stärke und mit einer Phasenverschiebung von 90°, so entsteht zirkular polarisiertes Licht. Hierbei rotiert die elektrische Feldstärke senkrecht zur Ausbreitungsrichtung. Der Betrag der Feldstärke ist dabei zu jedem Zeitpunkt gleich. Je nach Drehrichtung, welche von der Phasenlage bestimmt wird, handelt es sich um rechts- bzw. links zirkularpolarisiertes Licht. Im allgemeinen Fall, also unterschiedliche Stärke der Lichtstrahlen und beliebige Phasenverschiebung, liegt elliptisch polarisiertes Licht vor.

Im Photonenbild existieren wegen der Helizität der Photonen nur zirkularpolarisite Photonen. Linear polarisiertes Licht besteht dann aus der Überlagerung von rechts- und links-zirkuar polarisierten Photonen.

[Bearbeiten] Interferenz

Es kommt zu Auslöschung durch Interferenz wenn zwei kohärente, linear polarisierte und um eine halbe Wellenlänge verschoben Lichtbündel aufeinander treffen. Hierbei stößt ein Wellenberg auf das betragsmäßig gleich große Wellental was zur Auslöschung führt.

[Bearbeiten] Allgemeines über Interferenz von Lichtwellen

[Bearbeiten] Kohärenz und Kohärenzbedingung

[Bearbeiten] Interferenz an planparallelen Platten

[Bearbeiten] Michelson Interferometer

[Bearbeiten] Grunderscheinungen der Beugung

Unter dem Begriff Beugungsphänomene werden all diejenigen Lichterscheinungen zusammengefasst, bei denen sich die Ausbreitung von Licht (i. a. aller Strahlung) nicht mehr mit Hilfe der Gesetze der geometrischen Optik erklärt werden können. Beugung tritt genau dann auf, wenn ein Hindernis (z. B. ein Spalt oder ein Schirm mit kreisförmigen Öffnungen) im Lichtweg steht. Daher tritt Beugung in der Optik grundsätzlich immer auf. Je nach den Umständen kann die Beugung allerdings vernachlässigt werden.

Es wird traditionell zwischen Fresnelscher und Fraunhoferscher Beugung unterschieden. Unterscheidungskriterium sind die Abstände von Lichtquelle und Beobachtungspunkt der Beugung von dem beugenden Objekt ausschlaggebend.

Zur Beschreibung dieser Phänomene geht man davon aus, dass Licht sich als Welle ausbreitet.

[Bearbeiten] Beugung am Spalt

[Bearbeiten] Beugung am Gitter