Physikalische Grundlagen der Nuklearmedizin/ Das Zerfallsgesetz
Einleitung
[Bearbeiten]Dies ist das dritte Kapitel des Wikibooks Physikalische Grundlagen der Nuklearmedizin
Wir haben den radioaktiven Zerfall von einem phänomenologischen Standpunkt aus im letzten Kapitel betrachtet. In diesem Kapitel werden wir einen allgemeineren analytischen Zugang wählen.
Der Grund hierfür ist, dass wir so eine Denkweise entwickeln können in der wir die Vorgänge quantitativ mathematisch fassen können. Wir werden uns mit den Konzepten der Zerfallskonstante und der Halbwertszeit sowie mit den für die Messung der Radioaktivität verwendeten Einheiten vertraut machen. Ferner besteht die Möglichkeit das erworbene Verständnis durch Übungen am Ende des Kapitels zu vertiefen.
Annahmen
[Bearbeiten]Üblicherweise beginnt man eine physikalische Analyse mit dem Aufstellen einiger vereinfachender Annahmen über das System. Dadurch können wir unwichtige Effekte, die das Verständnis erschweren loswerden. Manchmal kann es jedoch auch vorkommen, dass wir die Situation so stark vereinfachen, dass sie zu abstrakt und damit schwer verständlich wird. Daher werden wir versuchen das Thema des radioaktiven Zerfalls mit einem aus dem Alltag bekannten Phänomen in Beziehung zu setzten welches wir als Analogie benutzen und so hoffentlich die abstrakten Probleme umschiffen können. Wir werden hier die Herstellung von Popcorn als Analogie verwenden. Man denke also an einen Topf in den man Öl gibt, anschließend Mais hinzufügt, ihn dann auf einer Herdplatte erhitzt und schaut, was passiert. Der geneigte Leser mag dies auch praktisch ausprobieren wollen. Für den radioaktiven Zerfall betrachten wir eine Probe, die eine große Zahl radioaktiver Kerne enthält, die alle von der selben Art sind. Dies entspricht den noch nicht geplatzten Maiskörnern im Topf. Als zweites nehmen wir an, dass alle radioaktiven Kerne durch den gleichen Prozess zerfallen sei es nun Alpha-, Beta- oder Gamma-Zerfall. Anders ausgedrückt platzen die intakten Maiskörner zu bestimmten Zeitpunkten während des Heizprozesses. Drittens nehmen wir uns einen Moment lang Zeit, um uns darüber klar zu werden, dass wir die Vorgänge nur in einem statistischen Sinne beschreiben können. Wenn wir ein einzelnes Maiskorn betrachten, können wir dann vorhersagen wann es platzen wird? Nicht wirklich. Wir können uns jedoch überlegen dass eine große Anzahl von ihnen nach einer bestimmten Zeit geplatzt sein wird. Aber dies ist ungleich komplizierter als die Frage bezüglich eines einzelnen Maiskorns. Anstatt uns also mit einzelnen Einheiten zu beschäftigen, betrachten wir das System auf einer größeren Skala und hier kommt die Statistik ins Spiel. Wir können den radioaktiven Zerfall statistisch als „Ein Schuss“-Prozess betrachten, das heißt, wenn ein Kern zerfallen ist, so kann er nicht noch einmal zerfallen. In anderen Worten, wenn ein Maiskorn geplatzt ist kann es nicht noch einmal platzen.
Weiterhin ist die Zerfallswahrscheinlichkeit für noch nicht zerfallene Kerne zeitlich konstant. Anders ausgedrückt ist die Wahrscheinlichkeit für ein noch nicht geplatztes Maiskorn in der nächsten Sekunde zu platzen genauso groß wie in der vorherigen Sekunde.
Lassen wir uns diese Popcorn Analogie nicht zu weit treiben. Machen wir uns bewusst, dass die Rate mit der das Popcorn platzt über die Wärme die wir dem Topf zuführen kontrollieren können. Auf die Zerfallsprozesse von Kernen haben wir jedoch keine derartigen Einflussmöglichkeiten. Die Rate mit der Kerne zerfallen kann nicht durch Heizen der Probe beeinflusst werden. Auch nicht durch Kühlung, oder Erhöhung der Drucks oder durch Änderung der Gravitation (indem man die Probe in den Weltraum bringt), auch nicht durch Änderung irgendeiner anderen Eigenschaft seiner physikalischen Umgebung. Das einzige was die Halbwertszeit eines individuellen Kerns bestimmt scheint der Kern selbst zu sein. Aber im Mittel können wir sagen, dass der Kern innerhalb einer gewissen Zeitspanne zerfallen wird.
Gesetz des radioaktiven Zerfalls
[Bearbeiten]Führen wir nun einige Symbole ein um den Schreibaufwand zu reduzieren, den wir treiben müssen, um die Vorgänge zu beschreiben, und machen uns einige mathematische Methoden zu eigen, mit denen wir die Situation erheblich einfacher als zuvor beschreiben können.
Nehmen wir an wir hätten eine Probe eines radioaktiven Materials mit Kernen, welche zu einem bestimmten Zeitpunkt noch nicht zerfallen sind. Was passiert dann in einem kurzen Zeitabschnitt? Einige Kerne werden mit Sicherheit zerfallen. Aber wie viele?
Aufgrund unserer obigen Argumentation können wir sagen, dass die Anzahl der zerfallenden von der Anzahl der insgesamt vorhandenen Kerne abhängen wird und weiterhin von der Dauer der betrachteten kurzen Zeitspanne. In anderen Worten, je mehr Kerne da sind, um so mehr Kerne werden auch zerfallen. Und je länger die Zeitspanne ist, um so mehr Kerne werden zerfallen. Lassen wir uns diese Zahl der Kerne, die zerfallen mit und die Dauer des kurzen Zeitintervalls mit bezeichnen.
Somit haben wir begründet, dass die Anzahl der radioaktiven Kerne, die im Zeitintervall von bis zerfällt proportional zu und zu ist. Als Formel schreibt sich diese Tatsache wie folgt:
Das negative Vorzeichen deutet an, dass abnimmt.
Wandeln wir nun die proportionale Beziehung in eine Gleichung um, so können wir schreiben:
wobei die Proportionalitätskonstante λ Zerfallskonstante heißt.
Nach Division durch können wir diese Gleichung umschreiben zu:
Also beschreibt diese Gleichung den Vorgang für ein kurzes Zeitintervall . Um herauszufinden, was zu beliebigen Zeitpunkten los ist, können wir einfach die Vorgänge in kurzen Zeitintervallen addieren. Anders ausgedrückt müssen wir die obige Gleichung integrieren. Drücken wir dies etwas formaler aus so können wir sagen, dass in der Zeit von bis zu einem späteren Zeitpunkt die Anzahl der radioaktiven Kerne von auf gefallen sein wird, so dass:
Dieser letzte Ausdruck heißt Gesetz des radioaktiven Zerfalls. Es besagt, dass die Anzahl der radioaktiven Kerne exponentiell mit der Zeit abnimmt, wobei die Geschwindigkeit des Zerfalls durch die Zerfallskonstante λ festgelegt ist.
Bevor wir uns diese Gleichung näher anschauen betrachten wir noch einmal welche Mathematik wir oben benutzt haben. Zunächst haben wir die Integralrechnung verwendet um herauszufinden was über einen längeren Zeitraum geschieht, wobei wir wussten was über kurze Zeiträume geschieht. Zweitens verwendeten wir folgende Beziehung aus der Analysis:
wobei den natürlichen Logarithmus von x darstellt. Drittens verwendeten wir die Definition des Logarithmus also:
und damit
Kehren wir nun zum Gesetz des radioaktiven Zerfalls zurück. Das Gesetz sagt aus, dass die Anzahl der Kerne exponentiell abnimmt wobei die Rate durch die Zerfallskonstante festgelegt wird. Das Gesetz ist in der Abbildung unten als Graph dargestellt:

Aufgetragen ist die Anzahl radioaktiver Kerne gegenüber der Zeit t. Wir sehen, dass die Anzahl der radioaktiven Kerne von (der Anzahl der radioaktiven Kerne zum Zeitpunkt ) anfangs sehr schnell und später etwas langsamer abnimmt, also klassisch exponentiell verläuft.
Den Einfluss der Zerfallskonstante kann man an der folgenden Abbildung erkennen:
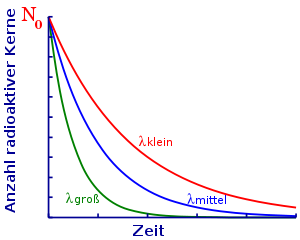
Alle drei Kurven werden durch Exponentialgesetze beschrieben, lediglich die Zerfallskonstanten sind unterschiedlich gewählt. Man beachte, dass die Kurve mit kleiner Zerfallskonstante relativ langsam und die Kurve mit großer Zerfallskonstante recht schnell abfällt.
Die Zerfallskonstante ist eine Eigenschaft des jeweiligen Radionuklids. Einige wie Uran-238 haben einen recht geringen Wert und das Material zerfällt daher langsam über einen langen Zeitraum. Andere Kerne wie Technetium-99m haben eine relativ hohe Zerfallskonstante und zerfallen daher schneller.
Es ist auch möglich das Zerfallsgesetz aus einer anderen Perspektive zu betrachten indem man den Logarithmus von Nt gegen die Zeit aufträgt. Anders ausgedrückt können wir von unserer obigen Analyse ausgehend die folgende Gleichung graphisch auftragen:
in anderer Form
Beachte, dass dieser Ausdruck eine einfache Gleichung der Form mit und ist. Die Gleichung beschreibt also eine Gerade mit der Steigung wie man in der folgenden Abbildung sieht. Eine solche Darstellung ist häufig hilfreich, wenn man einen Zusammenhang ohne die Komplikationen eines direkten exponentiellen Verhaltens verstehen möchte.

Halbwertszeit
[Bearbeiten]Die meisten von uns haben nicht gelernt instinktiv in logarithmischen oder exponentiellen Skalen zu denken, wenngleich viele natürliche Phänomene exponentiell verlaufen. Die meisten Denkweisen, die wir in der Schule erlernt haben basieren auf linearen Änderungen, dies macht das intuitive Verständnis des radioaktiven Zerfalls etwas schwieriger. Aus diesem Grund gibt es eine wichtige vom Zerfallsgesetz abgeleitete Größe die es uns leichter macht zu verstehen was passiert.
Diese Größe heißt Halbwertszeit und drückt die Länge der Zeit aus die es dauert, bis sich die Radioaktivität eines Radioisotops auf die Hälfte reduziert hat. Graphisch können wir dies wie folgt ausdrücken:

die benötigte Zeit ist die Halbwertszeit, für die gilt:
Man beachte, dass die Halbwertszeit nicht beschreibt wie lange ein Material radioaktiv bleibt, sondern lediglich die Länge der Zeit die es dauert bis sich seine Radioaktivität halbiert. Beispiele für Halbwertszeiten einiger Radioisotope sind in der Tabelle unten angegeben. Man beachte, dass einige von ihnen recht kurze Halbwertszeiten haben. Diese werden gerne für Zwecke der medizinischen Diagnostik verwendet, weil so ihre Radioaktivität nach der Anwendung am Patienten nicht sehr lange im Körper verweilt, was zu relativ geringen Strahlendosen führt.
| Radioisotop | Halbwertszeit (ca.) |
|---|---|
| 13 Sekunden | |
| 6 Stunden | |
| 8 Tage | |
| 1 Monat | |
| 30 Jahre | |
| 462 Tage | |
| 1620 Jahre | |
| 4.51 · 109 Jahre |
Diese kurzlebigen Radioisotope stellen jedoch ein logistisches Problem da, wenn sie an einem Ort verwendet werden sollen, der nicht in unmittelbarer Nähe einer Herstellungsanlage für Radioisotope liegt. Wenn wir zum Beispiel 99mTc für eine Untersuchung an einem Patienten 5.000 Kilometer von der nächsten Herstellungsanlage einsetzen möchten. Die Herstellungsanlage könnte sich zum Beispiel in Sydney und der Patient in Perth befinden. Nachdem wir das Isotop in einem Kernkraftwerk erzeugt haben würde es mit einer Halbwertszeit von 6 Stunden zerfallen. Würden wir als das Material in einen Transporter packen und zum Flughafen von Sydney fahren. Dann würde das Isotop zerfallen während der Transporter im Verkehr von Sydney fest steckt, dann noch mehr während auf den Flug nach Perth gewartet wird. Dann noch mehr wenn es nach Perth geflogen wird und so weiter. Wenn es endlich bei unserem Patienten ankommt, wird sich seine Radioaktivität sehr stark reduziert haben und möglicherweise für die Untersuchung nutzlos geworden sein. Und wie wäre es, wenn wir 81mKr anstelle von 99mTc für unseren Patienten verwenden würden? Im letzten Kapitel dieses Wikibooks werden wir sehen, dass diese logistischen Herausforderungen zu recht innovativen Lösungen Anlass gegeben haben. Mehr dazu jedoch später!
Aus der Tabelle ist ersichtlich, dass andere Isotope sehr lange Halbwertszeiten haben. Zum Beispiel hat 226Ra eine Halbwertszeit von mehr als 1.500 Jahren. Dieses Isotop wurde für therapeutische Anwendungen in der Medizin verwendet. Man denke an die damit verbundenen logistischen Probleme. Offensichtlich ist das Transport vom Herstellungsort zum Anwendungsort hierbei unproblematisch. Jedoch muss man beachten wie lange das Material an seinem Bestimmungsort gelagert werden muss. Man braucht einer Lagereinheit in der das Material sicher über einen langen Zeitraum gelagert werden kann. Aber wie lange? Eine Faustregel für Größen der Radioaktivität in der Medizin besagt, dass die Radioaktivität für ca. 10 Halbwertszeiten erheblich sein wird. Somit bräuchten wir eine sichere Umgebung zur Lagerung von 226Ra über einen Zeitraum von ca. 16.000 Jahren. Diese Lagereinrichtung müsste sicher gegen nicht vorhersehbare Ereignisse, wie Erdbeben, Bombenangriffe usw. aufgebaut sein und von unseren Nachfahren als solche erkennbar sein. Eine in der Tat ausgesprochen delikate Aufgabe.
Beziehung zwischen Zerfallskonstante und Halbwertszeit
[Bearbeiten]Auf Basis des oben gesagten kann man erahnen, dass es eine Beziehung zwischen Halbwertszeit und Zerfallskonstante geben müsste. Ist die Zerfallskonstante klein, so sollte die Halbwertszeit groß sein und entsprechend sollte bei großer Zerfallskonstante die Halbwertszeit klein sein. Aber wie genau sieht nun diese Beziehung aus?
Wir können diese Frage sehr leicht beantworten indem wir die Definition der Halbwertszeit in das Zerfallsgesetz einsetzen. Dieses Gesetz besagt dass zu jeder beliebigen Zeit t:
und aus der Definition der Halbwertszeit wissen wir, dass:
genau dann wenn
Wir können daher das Radioaktive Zerfallsgesetz umschreiben indem wir Nt und t wie folgt ersetzen:
Somit:
und
Diese letzten beiden Gleichungen drücken die Beziehung zwischen Halbwertszeit und Zerfallskonstante aus. Diese sind sehr nützlich zur Lösung von Rechenaufgaben im Gebiet der Radioaktivität und bilden meist den ersten Schritt zu deren Lösung.
Einheiten der Radioaktivität
[Bearbeiten]Die SI (oder auch metrische) Einheit der Radioaktivität ist nach Henri Becquerel, als Ehrung für seine Entdeckung der Radioaktivität, das Becquerel mit dem Symbol Bq. Das Becquerel ist definiert als die Menge einer radioaktiven Substanz die zu einer Zerfallsrate von einem Zerfall pro Sekunde führt. In der medizinischen Diagnostik stellt ein 1 Bq eine recht geringe Menge an Radioaktivität dar. In der Tat ist es einfach sich seine Definition mit Hilfe des englischen Begriffs bugger all (zu Deutsch: rein gar nichts) zu merken. Daher werden das Kilobecquerel (kBq) sowie das Megabecquerel (MBq) häufiger verwendet. Die traditionelle (und heute veraltete) Einheit der Radioaktivität ist nach Marie Curie benannt und heißt Curie mit dem Symbol Ci. Das Curie ist definiert als die Menge einer radioaktiven Substanz die zu einer Zerfallsrate von 3.7 ·1010 Zerfällen pro Sekunde führt. In anderen Worten 37 Tausend Millionen Zerfälle pro Sekunde, was wie man sich denken kann eine erhebliche Menge an Radioaktivität darstellt. Für Zwecke der medizinischen Diagnostik werden daher das Millicurie (mCi) und das Mikrocurie (µCi) häufiger verwendet.
-
Marie Curie
-
Henri Becquerel
Warum also zwei Einheiten? Im Wesentlichen kommt es es hier wie auch sonst bei der Frage nach Maßeinheiten darauf an in welchem Teil der Welt man sich befindet. Der Kilometer wird zum Beispiel in Australien und Europa gerne als Entfernungseinheit verwendet, wohingegen man in den USA bevorzugt die Meile benutzt. So wird man in einem amerikanischen Lehrbuch häufig das Curie als Einheit der Radioaktivität und in einem australischen sehr wahrscheinlich das Becquerel und in einem europäischen häufig beide Einheiten antreffen. Daher ist es sinnvoll beide Einheiten zu kennen.
Übungen
[Bearbeiten]Unten sind drei Übungsaufgaben angegeben die dabei helfen sollen das Verständnis des in diesem Kapitel behandelten Stoffs zu vertiefen. Die erste ist ziemlich einfach und übt die Anwendung des Zerfallsgesetzes sowie das Verständnis des Begriffs Halbwertszeit. Die zweite Aufgabe ist erheblich schwieriger und beschäftigt sich mit der Berechnung Anzahl der in einer Probe radioaktiven Materials pro Zeiteinheit zerfallenden Kerne und verwendet das Gesetz des radioaktiven Zerfalls. Die dritte Aufgabe ist der zweiten sehr ähnlich, fragt jedoch aus einem leicht anderen Blickwinkel.
Bevor man sich an die Fragen macht möge man sich diese Seite anschauen, die einem einige einfache Rechnungen abnehmen kann.
Aufgabe 1
(a) Die Halbwertszeit von 99mTc beträgt 6 Stunden. Nach welcher Zeit ist noch ein sechzehntel der ursprünglichen Menge des Radioisotops vorhanden?
(b) Verifiziere dein Ergebnis auf einem anderen Weg.
Lösung:
(a) Ausgehend von der ober erhaltenen Beziehung zwischen der Zerfallskonstante und der Halbwertszeit können wir nun die Zerfallskonstante wie folgt berechnen.
Wir wenden nun das Zerfallsgesetz an,
die können wir in folgende Form umschreiben:
Gefragt ist nun wann auf ein sechzehntel ihres Wertes zurückgegangen ist, das bedeutet:
Somit haben wir
was wir nach auflösen müssen. Eine Möglichkeit dies zu tun ist im folgenden angegeben:
Es wird also 24 Stunden dauern bis nur noch ein sechzehntel der ursprünglichen Radioaktivität vorhanden ist.
(b) Eine Möglichkeit die Antwort zu verifizieren benutzt die Definition der Halbwertszeit. Wir wissen aus der Aufgabenstellung, dass 99mTc eine Halbwertszeit von 6 Stunden hat. Daher ist nach sechs Stunden noch die Hälfte der Radioaktivität vorhanden. Nach 12 Stunden noch ein viertel, nach 18 Stunden noch ein achtel und nach 24 Stunden bleibt genau ein sechzehntel übrig. Und wir kommen zu selben Zahlenwert wie in (a). Also stimmt unser Ergebnis.
Man beachte dass dieser Ansatz sinnvoll ist da wir uns mit dem relativ einfachen Fall zu tun haben in dem Radioaktivität halbiert, geviertelt und so weiter wird. Aber mal angenommen die Frage wäre gewesen wie lange es dauert bis die Radioaktivität auf ein Zehntel ihres ursprünglichen Wertes gefallen ist. Die deutlich aufwendigere Ableitung im mathematischen Weg der in Teil (a) beschritten wurde, kann auch diese Frage leicht beantworten.
Aufgabe 2
Berechne die Radioaktivität von einem Gramm 226Ra, die Halbwertszeit betrage 1620 Jahre und die Avogadrozahl sei 6,023 · 1023.
Lösung:
Wir können genau wie bei Übung 1(a) ansetzen indem wir die Zerfallskonstante aus der Halbwertszeit mit Hilfe der folgenden Gleichung berechnen:
Man beachte, dass wir als Dauer eines Jahres 365,25 Tage angesetzt haben um für Schaltjahre zu kompensieren, als wir von 'pro Jahr' auf 'pro Sekunde' umrechneten. Ferner mussten wir in 'pro Sekunde' umrechnen, das die Einheit der Radioaktivität als Anzahl der pro Sekunde zerfallenden Kerne definiert ist.
Als zweites berechnen wir wie viele Kerne 1 g 226Ra enthält:
Als drittes müssen wir das Zerfallsgesetz in eine Form bringen in der wir die Anzahl der pro Zeiteinheit zerfallenden Kerne ablesen können. Wir können dies erreichen in dem wir die Gleichung wie folgt ableiten:
Der Grund dafür hier den Absolutbetrag zu verwenden ist, dass wir das Minuszeichen loswerden wollen, da wir ja wissen dass wir es mit einer zeitlich abnehmenden Größe zu tun haben. Wir können nun die Daten, die wir für λ und N oben abgeleitet haben einsetzen:
Also ist die Radioaktivität einer Probe von einem Gramm Radium-226 ungefähr 1 Ci.
Diese Antwort ist nicht verwunderlich, da die Definition des Curie ursprünglich auf der Radioaktivität von 1 g Radium-226 beruhte.
Übung 3
Was ist die minimale Masse eines 99mTc Strahlers, der eine Radioaktivität von 1 MBq hat. Nimm an, dass die Halbwertszeit 6 Stunden beträgt und die Avogadrozahl 6,023·1023 ist.
Lösung
Wir gehen von der Beziehung zwischen Halbwertszeit und Zerfallskonstante aus:
Zweitens sagt uns die Frage, dass die Radioaktivität 1 MBq beträgt. Daher haben wir wegen 1 MBq = 1 · 106 Zerfälle pro Sekunde:
Schließlich kann die Masse dieser Kerne wie folgt berechnet werden:
In anderen Worten also lediglich etwas mehr als fünf Pikogramm 99mTc werden benötigt um eine Million Gamma-Strahlen pro Sekunde ab zu strahlen. Dieses Ergebnis zeigt nochmal einen wichtigen Punkt den man über den Strahlenschutz lernen sollte. Nämlich, dass man radioaktive Materialien genauso behandeln sollte wie krankheitserregende Bakterien.





















































