Introduction and motivation – Serlo

We now come to an important topic in higher mathematics: complex numbers. With Complex Analysis, there exists a whole area (worth an entire lecture course) that deals with complex numbers and functions on the complex numbers. Complex numbers are also used in physics. They are used to describe vibrations or electrical resistance. Besides the motivation we want to deal with the intuition behind the complex numbers. Furthermore we will also learn about properties of complex numbers.

Motivation (historical)

Why consider complex numbers? The most common motivation is defining a solution to equations like $x^{2}=-1$. This equation is not solvable using real numbers. One extends the set (actually field) of real numbers and defines the "new number" $\mathrm {i}$ as a solution of the above equation.

The beginning of the complex numbers was marked by the findings of the Italian mathematicians Niccolò Fontana Tartaglia. (1500-1557) and Gerolamo Cardano (1501-1576). Basically, however, it was not about the solution of equations of the form $x^{2}=-1$ with negative radicals, but about the solution of cubic equations. At this time methods for the solution of linear and quadratic equations were already known. However, this was not yet the case for cubic equations, i.e. equations of the form $ax^{3}+bx^{2}+cx+d=0$ with $a,b,c,d\in \mathbb {R}$. Tartaglia found a solution formula for special cubic equations of the form $x^{3}=cx+d$ with $c>0$ and $d>0$:

$x={\sqrt[{3}]{{\frac {d}{2}}+{\sqrt {{\frac {d^{2}}{4}}-{\frac {c^{3}}{27}}}}}}+{\sqrt[{3}]{{\frac {d}{2}}-{\sqrt {{\frac {d^{2}}{4}}-{\frac {c^{3}}{27}}}}}}$

Cardano, who was given the formula by Tartaglia, realised that for certain values of $c$ and $d$ the formula contained a root with negative radicals. Thus, for $c=15$ and $d=4$:

${\begin{aligned}x&={\sqrt[{3}]{{\frac {4}{2}}+{\sqrt {{\frac {4^{2}}{4}}-{\frac {15^{3}}{27}}}}}}+{\sqrt[{3}]{{\frac {4}{2}}-{\sqrt {{\frac {4^{2}}{4}}-{\frac {15^{3}}{27}}}}}}\\[0.5em]&={\sqrt[{3}]{2+{\sqrt {-121}}}}+{\sqrt[{3}]{2-{\sqrt {-121}}}}\end{aligned}}$

Such roots as ${\sqrt {-121}}$ were considered "not resolvable" at that time. One could not imagine that the square of a number could be a negative result. However, it was already known that every cubic function always has an intersection with the $x$ axis and thus a root.

Rafael Bombelli, a student of Cardano, came to the conclusion that he simply had to define a new type of number, which gives a negative number when being squared. He introduced the numbers $+{\sqrt {-1}}$ and $-{\sqrt {-1}}$, which he regarded as a new sign. For example he determined ${\sqrt {-121}}=11\cdot {\sqrt {-1}}$. By applying the existing arithmetic laws to these new numbers (with the peculiarity that ${\sqrt {-1}}\cdot {\sqrt {-1}}=-1$), he came to the following result:

${\begin{aligned}(2+{\sqrt {-1}})^{3}&=2^{3}+3\cdot 2^{2}\cdot {\sqrt {-1}}+3\cdot 2\cdot \left({\sqrt {-1}}\right)^{2}+\left({\sqrt {-1}}\right)^{3}\\&=8+12\cdot {\sqrt {-1}}+6\cdot (-1)-{\sqrt {-1}}\\&=2+11\cdot {\sqrt {-1}}\\&=2+{\sqrt {-121}}\end{aligned}}$

Thus, formally speaking, ${\sqrt[{3}]{2+{\sqrt {-121}}}}=2+{\sqrt {-1}}$. Analogously, ${\sqrt[{3}]{2-{\sqrt {-121}}}}=2-{\sqrt {-1}}$. Bombelli could hence use Cardano's formula to find the solution $x=4$ of the equation $x^{3}=15\cdot x+4$:

${\begin{aligned}x&={\sqrt[{3}]{2+{\sqrt {-121}}}}+{\sqrt[{3}]{2-{\sqrt {-121}}}}\\[0.3em]&=\left(2+{\sqrt {-1}}\right)+\left(2-{\sqrt {-1}}\right)=4\end{aligned}}$

Using roots of negative numbers (i.e.imaginary numbers) as an intermediate tool, it was finally possible to construct real-valued solutions to the above equation. Interestingly, Bombelli dismissed his discovery as "useless". The newly created type of number was still the subject of numerous discussions later on, as this type of number could be used to explain interesting phenomena in analysis, such as the "Eulerian formula" named after the famous mathematician Leonard Euler. It was only Euler who introduced the symbol for the imaginary unit $\mathrm {i}$ in 1777. They seemingly have no correspondence in real life. (How would you measure a distance of ${\sqrt {-1}}$ miles?) Thus the name "imaginary" numbers. But actually, with some work, one can describe real life-phenomena with them. So they are technically not different from real numbers - just parts of models in our brains which describe and predict the outside world ;)

Deriving the imaginary unit

At the school, the "set of feasible numbers" has been constantly expanded. Starting with the natural numbers, first the integers were introduced, then the rational came and finally the real numbers. With each expansion, new arithmetical operations could be carried out: The transition to the integers allowed subtractions like $2-5$, in the rational numbers arbitrary divisions like $2\div 5$ were possible and in the real numbers any root of positive numbers like ${\sqrt {2}}$ could be calculated.

Each extension allowed for solving new equations. For instance, $x+5=2$ can be solved in the integers, which is not yet the case in the natural numbers. Equations like $5x-2=0$ require for the solution the transition to the rational numbers and equations like $x^{2}-2=0$ the transition to the real numbers.

We now consider the equation $x^{2}+9=0$. In school we would say that this equation has no solution because we are not allowed to take a root of the negative number $-9$. Is it possible that by extending our set of numbers this equation becomes solvable? After all, previously unsolvable equations could already be solved by introducting new numbers.

Let us assume that we may take roots from negative numbers. Then $x={\sqrt {-9}}$ is a solution of the equation $x^{2}+9=0$. If we assume that we can apply the calculation rules of the root known to us, we obtain

${\begin{aligned}x={\sqrt {-9}}={\sqrt {9\cdot (-1)}}={\sqrt {9}}\cdot {\sqrt {-1}}=3\cdot {\sqrt {-1}}\end{aligned}}$

We can transfer our solution to a product of the real number $3$ with ${\sqrt {-1}}$. This trick can be applied to any root of a negative number. Each of these roots can be represented as the product of a real number with ${\sqrt {-1}}$. So if we know what ${\sqrt {-1}}$ is, we can calculate the root of any negative number.

Now in the new set of imaginary numbers, our known calculation rules of the root cannot apply. Otherwise we would get the following contradiction:

$-1=\left({\sqrt {-1}}\right)^{2}={\sqrt {-1}}\cdot {\sqrt {-1}}={\sqrt {(-1)\cdot (-1)}}={\sqrt {1}}=1$

We must therefore be careful when we take roots of negative numbers. Nevertheless, the equation ${\sqrt {-9}}=3\cdot {\sqrt {-1}}$ shows us a possible important connection. From a solution of the equation $x^{2}+1=0$ (namely ${\sqrt {-1}}$) we can obtain a solution of the equation $x^{2}+9=0$ (namely ${\sqrt {-9}})$. We can show this connection even without using "root rules":

${\begin{aligned}&&x^{2}+9&=0\\[0.3em]\iff {}&&{\frac {x^{2}}{9}}+{\frac {9}{9}}&=0\\[0.3em]\iff {}&&\left({\frac {x}{3}}\right)^{2}+1&=0\\[0.3em]&&&\ {\color {OliveGreen}\left\downarrow \ z={\frac {x}{3}}\right.}\\[0.3em]\iff {}&&z^{2}+1&=0\end{aligned}}$

The connection $z={\tfrac {x}{3}}\iff x=3z$ privides us with a solution for $x^{2}+9=0$, if a solution of $z^{2}+1=0$ is known. We only have to multiply it by $3$. This connection has already been indicated with ${\sqrt {-9}}=3\cdot {\sqrt {-1}}$. In an analogous way we should be able to solve other quadratic equations, if we know a solution for the equation $z^{2}+1=0$.

Let us now introduce $\mathrm {i}$ as a solution of the equation $x^{2}+1=0$. What this number is, we do not know. We simply imagine that such a number exists. Appropriately $\mathrm {i}$ is called imaginary number or imaginary unit in mathematics. With this we can also give a solution of the equation $x^{2}+9=0$. As we derived it above, such a solution is $3\cdot \mathrm {i}$.

The complex plane

What is the imaginary unit?

How can we visualize the imaginary number $\mathrm {i}$? Let us first take a step back and look at the real numbers. These can be visualized as dots on the real line:

The real number line with numbers from -3 to +3

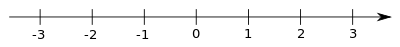
The imaginary unit $\mathrm {i}$ does not lie on the real number line, since $\mathrm {i}$ is not a real number. However, we can find out where $\mathrm {i} ^{2}=-1$ is by means of the property $\mathrm {i}$. First we illustrate the operation of multiplication with $-1$. If we multiply any number $x\in \mathbb {R}$ by $-1$, it is reflected at $0$ to $-x$:

This plane shows a reflection of x at 0.

This reflection is the same in the plane as a $180^{\circ }$ rotation of $x$ around the origin:

This plane shows a rotation of x by 180 degrees around 0.

So the operation $x\mapsto (-1)\cdot x$ is a $180^{\circ }$-rotation. Now $\mathrm {i} ^{2}=-1$ so we can translate the operation $x\mapsto (-1)\cdot x$ into $x\mapsto \mathrm {i} \cdot (\mathrm {i} \cdot x)$. The multiplication of $x$ by $\mathrm {i}$ thus corresponds to an operation which, if applied twice, causes a $180^{\circ }$ rotation.

So we have to think about how we can divide a $180^{\circ }$-rotation into two identical operations. It is obvious that these operations are two $90^{\circ }$-rotations. We conclude that by multiplying $\mathrm {i} \cdot x$ the number $x$ is rotated by $90^{\circ }$. This allows us to consider where $\mathrm {i}$ is located. The value is $\mathrm {i} =\mathrm {i} \cdot 1$. So $\mathrm {i}$ results from a $90^{\circ }$-rotation of $1$. The imaginary number is located straight above the origin at a distance $1$ from the real line:

This plane shows a rotation of x by 90 degrees around 0, which is equivalent to multiplication by i.

Note that we could have turned both clockwise and counterclockwise to determine the position of $\mathrm {i}$. We choose here the anti-clockwise rotation, since angles in Mathematics are always given in this direction of rotation. Now we know where $\mathrm {i}$ lies. But where is $2\mathrm {i}$, $3\mathrm {i}$, $\ldots$? If we multiply $\mathrm {i}$ by $2$ or $3$, these points are rotated by $90^{\circ }$. Thus, like $\mathrm {i}$, they lie perpendicular to the zero, but have the distance $2$ or $3$ from the origin:

This plane shows a rotation of 1,2,x,a by 90 degrees around 0, which is equivalent to multiplication by i.

Now let us choose any positive real number $a$. Where is $a\cdot \mathrm {i}$ on the plane? Just as for $2$ and $3$, our number $a$ undergoes a $90^{\circ }$ rotation when multiplying $\mathrm {i} \cdot a$. The result $\mathrm {i} \cdot a=a\cdot \mathrm {i}$ is straight above $0$. The distance to the origin remains invariant. This means that $a\cdot \mathrm {i}$ is as far from the zero as $a$.

Negative numbers $b$ on the other hand are on the real line to the left of the zero. If we rotate the number by $90^{\circ }$ around the zero, it lands exactly below the origin. As with the positive numbers, the distance from the zero remains the same when the number is rotated. If we connect the newly found points $\mathrm {i}$, $a\cdot \mathrm {i}$, $b\cdot \mathrm {i}$, $\ldots$, a straight line is formed. It is perpendicular to the real line and passes through the zero.

Let us consider any $x$ in $\mathbb {R}$. Then $x\cdot \mathrm {i}$ lies on this straight line. If we have a point on the straight line, then there is a real number $x$, with $x\cdot \mathrm {i}$ being exactly this point. So the following applies: The straight line contains exactly the numbers $x\cdot \mathrm {i}$ where $x$ is a real number:

This plane shows a rotation of 1,2,x,a by 90 degrees around 0, which is equivalent to multiplication by i.

Deriving $a+b\,\mathrm {i}$

We have two straight lines, the real line and the newly constructed ("imaginary") straight line. The two lines form two axes of a coordinate system. The real line is then naturally called the real axis and the line perpendicular to it is called the imaginary axis. What do the points inside the coordinate system correspond to? For the point $(5,0)$ we have to go five whole steps from the zero to the right. So $(5,0)$ describes the real number $5$. This works similarly with $(-2,0)$. To reach this point we have to go two steps to the left along the real axis to $-2$. If we go three steps upwards from zero we reach $3\mathrm {i}$. Thus the point $(0,3)$ corresponds to the number $3\mathrm {i}$. If we want to reach $-4\mathrm {i}$, we have to go four steps down to the point $(0,-4)$.

Complex plane with 5 points

And which number describes $(5,3)$? To reach the point $(5,3)$, we can first take $5$ steps to the right and then $3$ steps up. Here we use the well-known vector calculation (syllabus in most high schools around the world) in the plane $\mathbb {R} \times \mathbb {R} =\mathbb {R} ^{2}$ to obtain $(5,3)=(5,0)+(0,3)$. As we have already found out, $(5,0)$ corresponds to the number $5$ and $(0,3)$ describes $3\mathrm {i}$. Consequently, $(5,3)$ represents the number $5+3\mathrm {i}$. But we can also first take $3$ steps upwards and then $5$ steps to the right to reach $(5,3)$. Then we get as a corresponding number $3\mathrm {i} +5$. It should not matter if we first move to the right and then up or the other way round. Therefore $5+3\mathrm {i} =3\mathrm {i} +5$ must apply. By convention one always writes this number as $5+3\mathrm {i}$ ("real part first").

In the same way, we can proceed for any real numbers $a,b\in \mathbb {R}$ to find the corresponding number to the point $(a,b)$ in the complex plane. We go to the right by $a$ and upwards by $b$. For $(a,b)$ we get the corresponding number $a+b\,\mathrm {i}$.

Although there is a plus here, we cannot further simplify the formula. We can not transform $a+b\,\mathrm {i}$ into a simpler expression (of purely real numbers or purely multiple of $\mathrm {i}$ without the plus), as the tuple $(a,b)$ cannot be expressed with only 1 coordinate. However, the expression $a+b\,\mathrm {i}$ can be used for calculations. If we calculate with $a+b\,\mathrm {i}$, we treat the plus as usual.

But why would we also need numbers of the form $a+b\,\mathrm {i}$? Let us first remember why we introduced $\mathrm {i}$. We wanted to solve the equation $x^{2}+1=0$. Since this equation has no real solution, we needed $\mathrm {i}$. Let us now look at the equation $x^{2}-2x+2=0$. Using the second binomial formula we can transform the equation:

${\begin{array}{rrl}&0&=x^{2}-2x+2=(x^{2}-2x+1)+1\\&&=(x-1)^{2}+1\\\iff {}&(x-1)^{2}&=-1\end{array}}$

The conversion to $(x-1)^{2}=-1$ makes clear that no real number can fulfil this equation. If $x$ is a real number, then $x-1$ is also real and $(x-1)^{2}\neq -1$. Let us now try to solve this equation with the help of complex numbers. We know that $\mathrm {i} ^{2}=-1$. So we look for an $x$ such that $x-1=\mathrm {i}$. If we had such an $x$, then $(x-1)^{2}=\mathrm {i} ^{2}=-1$ and we would have solved the equation. The result is $x=1+\mathrm {i}$. Our solution is in the form $a+b\,\mathrm {i}$ with real numbers $a$ and $b$! Therefore it makes sense that we not only consider numbers of the form $b\,\mathrm {i}$ but also $a+b\,\mathrm {i}$. In this way, additional previously unsolvable quadratic equations can be solved.

We call $a+b\,\mathrm {i}$ a general complex number. We call the set of all those complex numbers $\mathbb {C}$. The set of all $a+b\,\mathrm {i}$ exactly corresponds to the set of all points on the 2D-plane which is spanned by the real and imaginary axis. This plane is mathematically called complex plane:

The complex plane

We have "equated" the complex numbers with the plane using the equation $(a,b){\hat {=}}a+b\,\mathrm {i}$. (Mathematically, we have constructed a bijection between both sets, which assigns $(a,b)$ to $a+b\,\mathrm {i}$). Now we can calculate with complex numbers as we are used to with vectors from the plane. Besides addition (which is possible for vectors as well as for complex numbers), we can also multiply with complex numbers (which we cannot do with vectors!). We can even show that the complex numbers with their addition and multiplication form a field. The structure for calculating in complex numbers is thus similar to what we are used to from real numbers.