Linear combinations

The main property of vectors is that one can take linear combinations with them. In this chapter you will learn exactly what this is.

Motivation of the term linear combination

Paths on a map

Let's look at the following map:

Treasure Map with path drawn

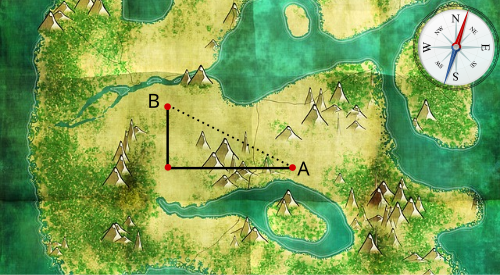
Our goal is to make it from our starting point $A$ to the end point $B$. Of course, there are an infinite number of ways to do this. If we want to get from $A$ to $B$ by the shortest route, we walk along the straight line connecting the two points. Another possibility is to walk three steps westwards from the starting point $A$ until we reach the level of the end point $B$ and then walk two steps northwards in the direction of $B$.

If $w$ is the standard vector towards the west ("vector = marching direction + distance", "standard" means that the distance is 1) and $n$ is the standard vector towards the north, then $\overrightarrow{AB}$ can be represented by the following weighted sum of $w$ and $n$:

$\overrightarrow{AB}=3w+2n$

Decomposing forces

In the following, we will look at an example from physics. Consider the illustration with a ball on an inclined plane. We assume that the ball does not encounter any relevant friction.

Ball on an inclined plane

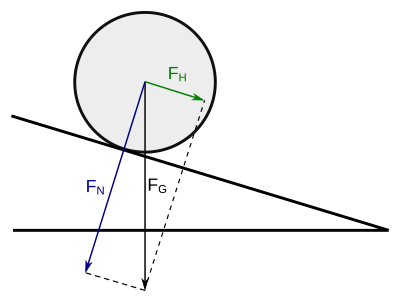
The gravitational force acting on our ball is perpendicular to the horizontal (it points down). However, the ball cannot simply fall downwards through the inclined plane. The plane prevents it from doing so. For this reason, we have to decompose the weight force $\overrightarrow{F_G}$ into two parts: one part is perpendicular to the inclined plane and gets countered by the plane itself (normal force $\overrightarrow{F_N}$) and one part is parallel to the inclined plane (downward force $\overrightarrow{F_H}$). The force $\overrightarrow{F_H}$ accelerates the ball.Both components have to add up to $\overrightarrow{F_G}$:

$\begin{array}{cc}\overrightarrow{F_G}& =\overrightarrow{F_H}+\overrightarrow{F_N}\\ & =1\cdot \overrightarrow{F_H}+1\cdot \overrightarrow{F_N}\end{array}$

The weight force is thus a simply weighted sum of two components.

Decomposing a vector within a plane

Consider any vector $\overrightarrow{v}=(v_x,v_y{)}^T$ with $v_x,v_y\in ℝ$ in the plane. We can then represent each such vector as

$\overrightarrow{v}=v_x\cdot \left(\begin{array}{c}1\\ 0\end{array}\right)+v_y\cdot \left(\begin{array}{c}0\\ 1\end{array}\right)$

This shows that we can interpret any vector of ${ℝ}^2$ as a weighted sum of the two standard (normalized) vectors $(1,0{)}^T$, $(0,1{)}^T$.

Definition of the linear combination

We have seen that in many examples we can represent vectors as a sum of other vectors with prefactors. We want to generalise our observation and call these sums linear combinations:

Definition (Linear combination)

Let $V$ be an $F$-vector space with $F$ a field. Each sum ${\alpha }_1{v}_1+\mathrm{...}+{\alpha }_n{v}_n={\sum }_{i=1}^n{\alpha }_i{v}_i$ with $v_1,\mathrm{...},v_n\in V$ and ${\alpha }_1,\mathrm{...},{\alpha }_n\in F$ is called a linear combination. If the vector $v\in V$ can be written as $v={\alpha }_1{v}_1+\mathrm{...}+{\alpha }_n{v}_n={\sum }_{i=1}^n{\alpha }_i{v}_i$, then we say that $v$ is a linear combination of the vectors $v_1,\mathrm{...},v_n$ with coefficients ${\alpha }_1,\mathrm{...},{\alpha }_n$ .

Examples

Example (Linear combination)

The vector $(-2,7,3{)}^T\in {ℝ}^3$ can be written as

$\left(\begin{array}{c}-2\\ 7\\ 3\end{array}\right)=-2\cdot \left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)+7\cdot \left(\begin{array}{c}0\\ 1\\ 0\end{array}\right)+3\cdot \left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)$

In other words, the vector $(-2,7,3{)}^T$ is a linear combination of the vectors $(1,0,0{)}^T$, $(0,1,0{)}^T$ and $(0,0,1{)}^T$ with coefficients $-2$, $7$ and $3$.

Example (Calculation of centre of gravity)

Let us now consider another typical example from physics. The figure shows three particles in ${ℝ}^3$ with masses $m_1$, $m_2$ and $m_3$, which can be described by the respective position vectors $\overrightarrow{x_1}$, $\overrightarrow{x_2}$ and $\overrightarrow{x_3}$:

Three masses in space whose positions are described by three vectors.

What is their centre of gravity? The total mass is $M=m_1+m_2+m_3$. Then the centre of gravity vector $\overrightarrow{S}$ of the system can be determined from the three mass particles by a linear combination:

$\overrightarrow{S}=\frac{m_1}{M}\cdot \overrightarrow{x_1}+\frac{m_2}{M}\cdot \overrightarrow{x_2}+\frac{m_3}{M}\cdot \overrightarrow{x_3}$

The vector $\overrightarrow{S}$ is a weighted sum of the individual location vectors $\overrightarrow{x_1}$, $\overrightarrow{x_2}$, $\overrightarrow{x_3}$ and thus a linear combination of these vectors.

System of equations as linear combination

We consider the following (arbitrarily chosen) system of equations

$\begin{array}{cc}2x+4y-8z& =6\\ -x+9y+3z& =1\\ 5x+2y-4z& =3\end{array}$

Such a system of equations can be rewritten using vectors and scalars as:

$\left(\begin{array}{c}2\\ -1\\ 5\end{array}\right)\cdot x+\left(\begin{array}{c}4\\ 9\\ 2\end{array}\right)\cdot y+\left(\begin{array}{c}-8\\ 3\\ -4\end{array}\right)\cdot z=\left(\begin{array}{c}6\\ 1\\ 3\end{array}\right)$

This notation makes it clear that solving a system of equations basically amounts to determining the correct coefficients $x,y,z$ of a linear combination.

Linear combination as a standard form

We want to show that we can take the linear combination as a kind of standard form for arbitrary combinations of vectors. Any succession of operations such as stretching and addition of vectors can be seen as a linear combination. For this purpose, we consider as examples two arbitrary vectors $v$ and $w$ as well as the scalars $\alpha$, $\beta$, $\lambda$ and $mu$. Let us take the following conjunction of $v$ and $w$:

$\beta \cdot (\alpha (v+\mu w)+\lambda v)$

By applying the vector space axioms step by step, we can transform the above conjunction into a linear combination:

$\begin{array}{cc}& \beta (\alpha (v+\mu w)+\lambda v)\\ & \downarrow \text{distributive law for vectors }\\ =& \beta (\alpha v+\alpha (\mu w))+\lambda v)\\ & \downarrow \text{associative law for scalars }\\ =& \beta (\alpha v+(\alpha \mu )w)+\lambda v)\\ & \downarrow \text{distributive law for vectors }\\ =& \beta (\alpha v)+\beta (\alpha \mu )w+\beta (\lambda v)\\ & \downarrow \text{associative law for scalars }\\ =& (\beta \alpha )v+(\beta \alpha \mu )w+(\beta \lambda )v\\ & \downarrow \text{commutative law }\\ =& (\beta \alpha )v+(\beta \lambda )v+(\beta \alpha \mu )w\\ & \downarrow \text{distributive law for scalars }\\ =& (\beta \alpha +\beta \lambda )v+\beta \alpha \mu w\end{array}$

At the end of the transformation we get a linear combination of the vectors $v$ and $w$. We have noted in each case which vector space axioms were used in the respective steps. With this example, it is easy to see that this procedure can be applied to all combinations of vectors. Thus the linear combination is a kind of standard form for arbitrary links of vectors.