Linear independence – Serlo
Motivation
[Bearbeiten]Basic motivation
[Bearbeiten]Maybe, you learned about vectors in school, where they were drawn as arrows in the plane or in space. Both a plane and space are vector spaces. But how do they differ?
A spontaneous answer could be: "The plane is two-dimensional and the space is three-dimensional". But this brings us immediately to further questions:
- What is the dimension of a vector space?
- How can we define it?
In the definition of the vector space the term "dimension" does not occur...
Intuition of a dimension
[Bearbeiten]
The term "dimension" describes in how many independent directions geometric objects can be extended in a space. The objects can also move in just as many independent directions in space ("degrees of freedom of motion").
The plane has two dimensions - the width and the length. It is flat, no object of the plane can reach out of it "into height". A sphere as a three-dimensional object cannot be part of the plane. In contrast, the space with length, width and height has three dimensions. A sphere can thus be part of space.
We summarize: The dimension intuitively corresponds to the number of independent directions into which a geometric object can expand or move. So, for the definition of dimension, we need to answer the following questions:
- What is a direction in a vector space?
- When are two directions independent?
- How can the number of independent directions be determined?
Derivation of the Definition
[Bearbeiten]
What is a direction within a vector space?
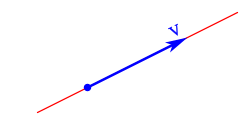
[Bearbeiten]Let's take the vector space of the plane as an example. We can represent a direction with an arrow:

Now an arrow is nothing but a vector. So with the help of vectors, directions can be represented. Here we must not use the zero vector. As an arrow of length zero it has no direction. We can generalize this to arbitrary vector spaces:
Every vector not equal to the zero vector represents a direction in a vector space.
The direction in which the vector points is , that is, the span of the vector . To this span belong all extensions of the direction vector and thus describes the straight line, which is spanned by :
From the line to the plane
[Bearbeiten]To get from the straight line to the plane, we need not only one vector but several, more precisely at least two vectors (). This is intuitively obvious, because a plane can be spanned unambiguously only with two vectors. Therefore we need a further, linearly independent vector. What does "independent" mean in this case? First, we notice that the new vector must not be the zero vector. This vector does not give any direction. Furthermore, the new vector must also not be a multiple of the original vector, i.e. . This also holds for reflections of straight line vectors, represented by multiplicatioin with a negative factor.
-
The vector is a stretched version of the vector with a positive stretching factor. This vector is not pointing in a direction independent of .
-
The vector is a stretched version of the vector with a positive stretching factor (which includes a reflection). This vector is not pointing in a direction independent of .
-
The direction of is independent of . Both vectors together span a plane.
We conclude: The new vector is independent of the direction vector exactly when the latter is not on the straight line. So we need for all real numbers . Hence, the new vector must not be in the span of the other one. The two spans have only the zero point as intersection.
From the plane to space
[Bearbeiten]We have just seen that we can characterize a plane by two independent vectors. Now we want to go from the plane to space. Here, we also have to add an independent direction. But what is a direction independent of the plane?
The new vector must not be the zero vector, because this vector does not indicate a direction. The new vector must also not lie in the plane, because in that case, no new direction would be described. Only if the new vector does not lie in the plane, it will point in a new, independent direction:
-
The vector lies in the plane spanned by and . Hence, does not point into a direction spanned by and .
-
The vector does not lie in the plane spanned by and . All three vectors span the entire space, which means that points into a direction independent of and .
How can we formulate this insight mathematically? Let and be the two direction vectors spanning the plane. This plane is then equal to the set . Hence, the plane is the set of all sums for real numbers . In order for the new vector not to be in the plane, it must be for all . Thus, in independent of <ma
Question: We had first required that the new vector must not be the zero vector. Why is it sufficient that for all ? And why does this imply ?
For we have . Since also for the new vector shall not be equal to , we have .
Question: Is it sufficient that is no multiple of or ?
No, take for example . If is independent of , then is neither a stretched version of , nor one of . However, this vector lies in the plane spanned by and , so it does not point into a direction independent of and .
A first criterion for linear independence
[Bearbeiten]Let's summarize: To describe a straight line we needed a vector not being the zero vector. In the transition from the straight line to the plane, we had to add a vector independent of . Independence of from means that does not lie in the line described by . So we need to have for all .
In the second step, we added a new direction to the plane, which is independent of the two vectors and . Here independence manifests itself in the fact that is not in the plane spanned by and . Hence, we need for all real numbers and . We can generalise this to an arbitrary number of vectors (but it is not so easy to visualize anymore):
The vector is independent of the vectors , if for all .
In the above description, the sum appears. Such a sum is called linear combination of the vectors to . We may also say that is linearly independent if . The description can be changed to:
The vector is independent of the vectors , if cannot be written as a linear combinationof the vectors to .
Here we have clarified when a vector is independent of other vectors. Is this sufficient to describe the independence of vectors?! Take the following three vectors , and as an example:

Since no vector is a multiple of another vector, the three vectors, seen in pairs, point in independent directions. For example is independent of and is independent of . So the three vectors are not independent of each other because they all lie in one plane. We have and so is independent of and . Accordingly, we have to impose linear independence between , and :
- is independent of and : We have for all .
- is independent of and : We have for all .
- is independent of and : We have for all .
It should be emphasised at this point that it is necessary to require all three conditions. If we were to waive the last two conditions, the first requirement would guarantee that the vector is linearly independent of the vectors and , but it is not clear from this requirement that and are linearly independent of each other. This does not have to be fulfilled, which would mean that the three vectors would again not be linearly independent of each other.
Therefore, none of the three vectors must be able to be represented as a linear combination of the other two vectors. Otherwise at least one of the vectors is dependent on the other vectors. We can generalise this to any number of vectors:
Definition (Second criterion for linear independence)
Some vectors to are linearly independent if none of the vectors can be written as a linear combination of the other vectors. This means that the following must apply:
- for all .
- for all .
- ...
- for all .
So to are linearly independent, if for all and .
From the first criterion to the formal definition
[Bearbeiten]With our first criterion, which we found above, we have already found a suitable definition for linear independence of vectors. In the following, we will try to find a more concise equivalent criterion, with which we can examine the linear independence of vectors more easily.
Vectors are independent if no vector can be represented as a linear combination of the other vectors. From this we will derive another criterion for linear independence, which is less computationally demanding. Let us take vectors , to from a vector space that are not independent. So there is one vector that can be represented by the others. Let be this vector. There are thus stretching factors (scalars) to , such that
We can transform this equation by computing on both sides ( is the zero vector of the vector space ):
This is a so-called nontrivial linear combination of the zero vector. A nontrivial linear combination of the zero vector is a linear combination with the result where at least one coefficient is not equal to . For we would trivially . This is the so-called trivial linear combination of the zero vector, where all coefficients are equal to . You can always form this trivial linear combination, no matter which vectors to you choose. So it does not carry information. If to are dependent, there is at least one non-trivial linear combination of the zero vector (as we saw above) in addition to the trivial linear combination. So:
If to are linearly dependent, then the zero vector can be represented by at least one non-trivial linear combination of to .
In other words:
linearly dependent There exists a non-trivial linear combination of using
Now we can apply the principle of contraposition: holds if and only if . So:
There is no non-trivial linear combination of using are linearly independent
With this we have found a criterion for linear independence. If the zero vector can only be represented trivially by a linear combination of to , then these vectors are linearly independent. However, this criterion can also be used as a definition of linear independence. To do this, we need to show the converse direction of the above implication. If there is a non-trivial linear combination of the zero vector, then the vectors under consideration are linearly dependent.
So let to be vectors for which there exists a non-trivial linear combination of the zero vector. This means, there are coefficients (scalars) to , such that where at least one of the coefficients to is not . Let be this coefficient. Then
Since we can multiply both sides by . Then,
On both sides we can now add :
Thus can be represented as a linear combination of the other vectors and hence the vectors to are linearly dependent. This proves taht the following definition of linear independence is equivalent to the first one:
Definition (Second criterion for linear independence)
The vectors are linearly independent if the only linear combination of them resulting in the zero vector is the trivial linear combination, i.e. if we have with , the must hold for all .
If there is at least one non-trivial linear combination of the zero vector, the considered vectors are linearly dependent.
Definition of a family
[Bearbeiten]We have talked above about a several vectors being linearly independent. But what is this "collection" of vectors from a mathematical point of view? We already know the notion of a set. So it is obvious to understand also as a set. Does this view intuitively fit linear independence? Actually, it turns out problematic, if we have two equal vectors with . Both point in the same direction and span no two independent directions. Thus they are intuitively linearly dependent. And indeed, one can be written as a linear combination of the other as . Thus the vectors are also strictly mathematically linearly dependent. However, a set may only contain different elements. That is, the set containing and is . So the set contains only one element and does not capture duplications of vectors.
So we need a new mathematical term that also captures duplications. This is the concept of family:
Definition (family)
A family of elements from a set consists of an index set , such that every index gets assigned an element .
If a finite set, we call it a finite family.
If , then one cally a sub-family of . Conversely, is them called a super-family of .
Formally, a family can be seen as a mapping of the index set into the set . In contrast to sets, elements may occur more than once in families, namely if they belong to different indices.
If the set is countable, the elements of the family can be numbered: . However, the index set may also be overcountable, e.g. . In this case cannot be written as a sequence . The term family thus contains all sequences, and includes even larger "collections" of mathematical objects.
So when we say the vectors and are linearly dependent we can express it by saying that the family with is linearly dependent.
Often one writes (with slight abuse of notation) if the are elements of and it is clear from the context what the index set looks like. Similarly, means that there is an with .
With this we can rewrite the second definition of linear independence:
Definition (Second criterion for linear independence, new version)
The family of vectors is linearly independent if the only linear combination representing the zero vector is the trivial linear combination, i.e. if with , then for all .
General definition of linear independence
[Bearbeiten]Motivation
[Bearbeiten]We have learned above two definitions for the fact that finitely many vectors are linearly independent:
- A somewhat unwieldy: vectors are independent if no vector can be written as a linear combination of the others. So must not occur.
- A somewhat more compact one: The zero vector can only be represented as a trivial linear combination. So implies .
So far we have only considered finitely many vectors. What happens with infinitely many vectors? Can there even be an infinite number of linearly independent vectors? We would need a vector space that has infinitely many linearly independent directions. We know intuitively that the vector space has at most two and the at most three independent directions. So we need a much "bigger" vector space to get infinitely many independent directions. So we consider a vector space where every vector has infinitely many coordinates: with . Accordingly, corresponds to a real sequence and is the sequences vector space, or sequence space.
In we have the linearly independent unit vectors . We can continue this construction and obtain for the vectors with the at the -th place and otherwise .
The infinitely many vectors form a family . This family intuitively represents "infinitely many different directions" in and is thus intuitively linearly independent. So it makes sense to define linear independence for infinitely many vectors in such a way that is a linearly independent family. The "somewhat unwieldy definition 1." above would be suitable for this in principle: We could simply copy it and say "a family of vectors is linearly independent if no can be written as a linear combination of the others". In fact, in none of the can be written as a linear combination of the other vectors. Therefore, the definition already makes sense at this point. However, there are infinitely many and thus infinitely many conditions!
We prefer to consider the "somewhat more compact definition 2.": "Vectors are linearly independent if can only be represented by the trivial linear combination." What does this formulation mean explicitly in this example? We are given a linear combination of . Linear combinations are finite, that is, we have finitely many vectors and such that
We now have to show that all , since then the linear combination of above is trivial. This works in exactly the same way as in , except that here we have to compare infinitely many entries.
What do we have to do now to get a general definition for general families and general vector spaces? The "somewhat more compact definition 2." carries over almost literally: "A family of vectors is linearly independent if can only be represented by the trivial linear combination." For the written out implication, we can make use of our language of families: We replace the double indices by the word "sub-family".
Definition
[Bearbeiten]Definition (Linear dependence and independence of vectors)
Let be a field, be a -vectorspace and a family of vectos from .
is called linearly independent, if for every finite sub-family and all with the following holds:
A family is called linearly dependent, if it is not linearly independent.
Warning
Linear combinations of elements of a set always consist of finitely many summands, even if the set is infinite.
E.g. the family is linearly independent in the vector space , although . This is because the exponential function is not a finite linear combination of the monomials.
Hint
You may often find the term "linearly independent set" instead of "linearly independent family". We have already considered above that it makes more sense to use families here, because unlike sets, families also cover duplications of elements. From every set one can construct the family . Thus the term "linearly (in)dependent" carries over to sets. Linearly independent families do not contain a vector twice. Families without double elements correspond to sets via the above construction. If we want to have a family of linearly independent vectors (e.g. in the preconditions of a set), we can also ask for a set of linearly independent vectors. If we want to test whether a family of vectors is linearly independent, we cannot first convert it into a set. Because there, doublings disappear and cause linear dependence.
Hint
The definition of linear (in)dependence refers to subfamilies of a vector space. These may contain vectors several times and may even be overcountable.
For finite families, we alternatively talk about the elements, i.e. the statement "The family is linearly (in)dependent" becomes " are linearly (in)dependent".
Implications of the definition
[Bearbeiten]Re-formulating the definition for finite sub-families
[Bearbeiten]We have a definition of linear independence for arbitrary subfamilies of a vector space . Does this agree with our old definition for finite subfamilies? Intuitively, they should agree for finite subfamilies, since we derived the general definition from our old definition. The following theorem actually proves this:
Theorem (Linear independence for finitely many vectors)
- The vectors are linearly independent if and only if with implies .
- The vectors are linearly dependent if and only if there are to not all equal to , such that .
Proof (Linear independence for finitely many vectors)
We first prove the first statement. We have to establish an equivalence.
Let be linearly independent. By the defintion of linear independence we obtain that for every finite sub-family of and for all scalars with we have:
is a finite sub-family of itself. Therefore for all from , we get that for all .
Conversely, assume that for all from it follows that . We would like to show that is linearly independent. So let be a finite sub-family of . That means . Let with be scalars with
We extend this sum so that it covers all . This is done by defining for all . Then
It follows from our premise that and hence for all . So is linearly independent.
The second statement is exactly the logical contraposition of the first. For we have shown with the two statements
" is linearly independent"
""
The second point is the statement . But this is equivalent to and thus equivalent to the first statement.
Reducing the definition to finite sub-families
[Bearbeiten]We have defined linear independence for any family of vectors, so also for infinitely many vectors. But in the definition we only need to show a statement for finite subfamilies : For all with we need the following:
In the previous theorem we have seen that this statement is exactly linear independence of .
Theorem (Criterion with finitely many sub-families)
- A family is linearly independent if and only if every finite sub-family is linearly independent.
- A family is linearly dependent if and only if it contains a finite linearly dependent sub-family .
Proof (Criterion with finitely many sub-families)
First we prove the first statement. We have to establish an equivalence. Let be a linearly independent family of vectors from . We show that every finite sub-family of is linearly independent.
Let for this be a finite sub-family of . From our definition of linear independence it follows that for all scalars with the following holds:
Using the previous theorem , we get that is linearly independent.
Conversely, let every finite subfamily of be linearly independent. We show that . Let for this a finite subfamily of . We want to show that for all scalars with the following holds:
According to our premise, is linearly independent. So it follows again with the previous theorem that for all scalars with
holds.
The second statement is exactly the logical contraposition of the first. For we have shown with the two statements
" is linearly independent"
"every finite sub-family of is linearly independent"
The second point is the statement . But this is equivalent to and thus equivalent to the first statement.
Overview
[Bearbeiten]The following properties can be derived from the definition of linear independence with a few proof steps. Let be a field and a -vector space:
- Every sub-family of a family of linearly independent vectors is linearly independent. Conversely, every super-family of a family of linearly dependent vectors is again linearly dependent.
- Let be a single vector. Then is linearly independent if and only if . So "almost always". Conversely, every family (no matter how large) is linearly dependent as soon as it contains the zero vector.
- Let . The vectors and are linearly dependent if and only if there is a with the property or .
- If a family of vectors is linearly dependent, one of them can be represented as a linear combination of the others.
Sub-families of linear independent vectors are linearly independent
[Bearbeiten]A linearly independent family remains linearly independent if you take away vectors. Linear dependence, on the other hand, is preserved if you add more vectors. Intuitively, the addition of vectors tends to "destroy" linear independence and cannot be restored by adding more vectors.
Theorem
- Every sub-family of a family of linearly independent vectors is again linearly independent.
- Every super-family of a family of linearly dependent vectors is again linearly dependent.
Proof
We start with the first statement. Let be a family of linearly independent vectors from and any sub-family of . Let and with
Since , the vectors are also in . And as is linearly independent, we have that . So is linearly independent.
From this we deduce the second statement. Let a family of linearly dependent vectors from and any super-family of . Assume taht is linearly independent. Then, we have with the previous statement that also , as a sub-family of , is linearly independent. But this is a contradiction because is linearly dependent.
Families including the zero vector are linearly independent
[Bearbeiten]When is a family with exactly one vector linearly independent? This question is easy to answer: whenever this vector is not the zero vector. Conversely, every family with the zero vector is linearly dependent. Including the one that contains only the zero vector itself.
Theorem (Families including the zero vector are linearly independent)
- The zero vector is linearly dependent.
- If is linearly dependent, then .
- A family of vectors containing the zero vector is always linearly dependent.
Proof (Families including the zero vector are linearly independent)
- We have that . There is therefore a non-trivial linear combination of the vector , which has as a result. Hence, is linearly independent.
- If is linearly dependent, then there are with . Since , there is a multiplicative inverse . Multiplying the equation by we get . So must be the zero vector .
- This assertion follows simply from 1. and the theorem about the linear dependence of superfamilies of linearly dependent families.
Two vectors are linearly dependent if one is a stretched version of the other
[Bearbeiten]When is a family with two vectors linearly independent? We can answer the question by saying when the opposite is the case. So when are two vectors linearly dependent? Linear dependence of two vectors holds if and only if both "lie on a straight line", i.e. one vector is a stretched version of the other.
Theorem
Let . The vectors and are linearly dependent if and only if there is a with or .
Proof
We need to prove the following two implications:
- and are linearly dependent
- and are linearly dependent
Proof step: First implication
If one of the two vectors is the zero vector, then according to the previous theorem, and are linearly dependent. So let and . Further, let be chosen such that . This is w.l.o.g. possible, because if it cannot be done, we swap the labels of the two vectors. So we use instead of and instead of . According to the premise, there must exist a , such that the equation with the new labels holds.
Now we have that . So we have the zero vector represented as a non-trivial linear combination. This means that and are linearly dependent.
Proof step: Second implication
Let and be linearly dependent. Then, by definition, there is a non-trivial linear combination of the zero vector. Thus there exist such that and are both nonzero and the equation holds. We consider teh case where . Then, from the equation we conclude
However, if , then we need to have . Analogously to the calculation above you can then get with .
With linear dependence, one vector is a linear combination of the others
[Bearbeiten]For finitely many vectors, we started with the definition that vectors are linearly dependent if one of the vectors can be written as a linear combination of the others (first definition). We have already seen that this definition is equivalent to the null vector being able to be written as a linear combination of the vectors (second definition). For the general definition with possibly infinitely many vectors, we have used the version with the zero vector (the second) as our definition. And one can indeed show that even in the general case the first definition is equivalent to it:
Theorem
Let be a -vector space and let be linearly dependent vectors, but being linearly independent. Then, there exist such that .
How to get to the proof?
Because of the linear dependence of there exist not equal to , such that . We want to write as a linear combination of the . That means, we want to solve the equation for . We can transform this equation into
Now we want to divide by . This only works if . So we show that the case cannot occur. Suppose . Then, we have
We know that are linearly independent. So all are equal to . Hence, all are equal to . That is a contradiction. Therefore cannot occur.
Proof
Since are linearly dependent, there exist with , where not all are equal . Hence,
We first show . Assume that . Then, we would have
By linear independence of we have for all . But this is not possible, since are not all equal to 0. So we have . We can hence divide by and the linear combination we are looking for is
now set . Then, , which is what we wanted to show.
Linear independence and unique linear combinations
[Bearbeiten]In this section, we will take a closer look at the connection between linear independence and linear combinations. To do this, we recall what it means that the vectors are linearly dependent or independent. Suppose the vectors are linearly dependent. From our definition of linear independence, we know that there must then be a non-trivial zero representation, since at least one scalar for some . We illustrate this with the following example
Example (Linear independence and non-trivial representation of 0)
Let us consider the vectors . These are linearly dependent, since
By transforming this equation we obtain a representation of the zero vector:
In addition to this representation, there is also the so-called trivial representation of the zero vector, in which every pre-factor is equal to zero:
Because of the linear dependence, the zero vector can be represented in two ways via a linear combination.
Regardless of whether the considered family of vectors is linearly independent or not, there is always the trivial zero representation, in which all scalars have the value :
In case of linear dependence of the vectors, the representation of the zero is no longer unambiguous. We can summarise our results so far in a theorem and generalise them:
Theorem (Linear independence and unique linear combination)
Let be a vector space and .
All linear combinations of vectors from are unique linearly independent.
Proof (Linear independence and unique linear combination)
We show the contraposition:
There is a linear combination of vectors from that is not unique is linearly dependent.
"" We assume there was a , such that at least two different representations of are possible using vectors from :
Let with and with and . Subtraction of the two equations gives
Since the representations of are different, there is at least one factor for . Hence, the vectors are linearly dependent by definition and thus is also linearly dependent.
"" If is linearly independent, then contains a linearly independent subset .
Then, apart from the trivial representation of zero , there is at least one more: because of the linear dependence, there are factors that are not all zero, with
So we have shown that there are then two representations of as linear combinations of these vectors. Thus linear combinations are not unique.
Exercises
[Bearbeiten]Exercise 1
[Bearbeiten]Exercise (Linear independence)
Show that the vectors are linearly independent.
Solution (Linear independence)
We have to show that the zero vector can only be represented trivially by the given vectors. This means that the following equation with the real numbers only has the solutions :
This implies:
Now, two column vectors are equal if every component is equal. So the following equations must hold:
We hence have . Plugging this into , we obtain . With this we have shown that from the equation we get that all coefficients , and are equal to . Thus, the three vectors are linearly independent.
Exercise 2
[Bearbeiten]Exercise (Linear dependence)
Show that the following set of four vectors is linearly dependent:
Solution (Linear dependence)
By definition, the vectors and are linearly dependent if and only if we can find a nontrivial linear combination of zero. Such a combination is for example given by
Therefore the vectors are linearly dependent.
Solution (Lineare dependence, alternative)
Vectors are linearly dependent if one of them can be represented as a linear combination of the other ones. Now the vector can be represented as a linear combination of the others:
Thus the vectors are linearly dependent.
Exercise 3
[Bearbeiten]Exercise (Trigonometrical polynomials)
Let with for all . That means, is a -preiodic function. We consider the set of -preiodic functions. These form an -vector space.
Are the functions linearly independent?
How to get to the proof? (Trigonometrical polynomials)
We investigate how to write the zero function as a linear combination of the three functions. To do this, we determine the values of in the equation . We can do this by inserting three different values for and then solving the resulting system of equations.
Values for which we explicitly know the exact values of the cosine are suitable for this - for example and . For those, we know and .
Solution (Trigonometrical polynomials)
Let , such that
for all . We would like to establish . Plugging in for the values and , we obtai the following system of equations for :
The system of equations can now be solved in different ways. We transform the first equation and get . We can substitute this into the second equation and get , so . If we now substitute our results into the third equation, we have . This is equivalent to . From the other equations, we conclude .
Thus we have uniquely determined the coefficients and . That is, there is no non-trivial linear combination of the . The functions are therefore linearly independent.
Exercise 4
[Bearbeiten]Exercise (Linear (in-)dependence?)
Prove or disprove the following statement:
Let . The set is linearly dependent if and only if each of the vectors is a linear combination of the other two.
How to get to the proof? (Linear (in-)dependence?)
For the set to be linearly dependent, it is sufficient if two of the three vectors are multiples of each other, while the third can be linearly independent of the two. With this consideration we can construct a counterexample.
Solution (Linear (in-)dependence?)
The statement is not correct. We consider the set
Then we can represent the zero vector as a non-trivial linear combination of the three vectors:
Thus the set is linearly dependent. However, the vector is not a linear combination of the other two.
Exercise 5
[Bearbeiten]Exercise (Linearly independent vectors in )
Prove: Within the vector space of -tuples over the field , the vectors , up to are linearly independent.
Solution (Linearly independent vectors in )
We have to show that we can uniquely represent the zero vector as a linear combination of the vectors . So let us consider the linear combination of the vectors with for . We need to have
We can interpret this as a linear system of equations as
Thus we have shown that the are uniquely determined and . After defining the linear independence, we have shown that the vectors are linearly independent.
Exercise 6
[Bearbeiten]Exercise (Linearly independent vectors and endomorphisms)
Let be a field and an endomorphism of the -vector space . Let , such that for a fixed natural number , we have: for and . Here, means that the -fold application of onto the vector . Prove that then the vectors are linearly independent.
How to get to the proof? (Linearly independent vectors and endomorphisms)
We need to show that for with
we already have . We can try to get the individual from this equation: We know that . If we now apply to this equation, we get
We have thus eliminated one summand. With this we have reduced our problem to a case with summands. That is, by proceeding with induction, we can now infer the statement.
Solution (Linearly independent vectors and endomorphisms)
We perform an induction over to iterate the idea of reducing the number of vectors one-by-one.
Theorem whose validity shall be proven for the :
If with for all and , then is linearly independent.
1. Base case:
We need to show that and are linearkly independent, if and hold. That means we have to show that for with we already have . Now,
Since , we have . So by choice of and , we also have . With the same argument, we now have .
1. inductive step:
2a. inductive hypothesis:
If with for all and , then is linearly independent.
2b. induction theorem:
If with for all and , then is linearly independent.
2b. proof of induction step:
Let , such that . Then,
Applying the induction assumption to , we get that . Hence, . Since , we also have . So is linearly independent.























































































































































![{\displaystyle {\begin{aligned}0_{V}&=\sum _{j\in J}\lambda _{j}\cdot v_{j}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ {\text{add }}0_{V}\right.}\\[0.3em]&=\sum _{j\in J}\lambda _{j}\cdot v_{j}+0_{V}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ 0_{V}=\sum _{i\in J\setminus \{1,\ldots ,n\}}0\cdot v_{i}\right.}\\[0.3em]&=\sum _{j\in J}\lambda _{j}\cdot v_{j}+\sum _{i\in J\setminus \{1,\ldots ,n\}}0\cdot v_{i}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ 0=\lambda _{i}\right.}\\[0.3em]&=\sum _{j\in J}\lambda _{j}\cdot v_{j}+\sum _{i\in J\setminus \{1,\ldots ,n\}}\lambda _{i}\cdot v_{i}\\[0.3em]&=\sum _{k\in \{1,\ldots ,n\}}\lambda _{k}\cdot v_{k}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/640ae5b9c3ed6f1f5b3deb8753eb5ea8d2cdc4c7)





































![{\displaystyle {\begin{aligned}\beta \cdot w&=-\alpha \cdot v&&\\[0.3em]&\ {\color {OliveGreen}\downarrow {\text{multiply both sides with }}\beta ^{-1}}\\[0.3em]w&=\,\beta ^{-1}\cdot (-\alpha \cdot v)&&\\[0.3em]&\ {\color {OliveGreen}\downarrow {\text{associative law of scalar multiplication}}}\\[0.3em]&=\,-(\beta ^{-1}\alpha )\cdot v&&\\[0.3em]&\ {\color {OliveGreen}\downarrow {\text{set }}{\lambda \colon =-(\beta ^{-1}\alpha )}}\\[0.3em]&=\,\lambda \cdot v\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4881a296552b400318f7a40be7f26ac21e5a86f)


















































![{\displaystyle {\begin{aligned}&\rho _{1}\cdot {\begin{pmatrix}1\\1\\0\end{pmatrix}}+\rho _{2}\cdot {\begin{pmatrix}0\\1\\0\end{pmatrix}}+\rho _{3}\cdot {\begin{pmatrix}0\\1\\1\end{pmatrix}}={\begin{pmatrix}0\\0\\0\end{pmatrix}}\\[0.3em]&\quad {\color {OliveGreen}\left\downarrow \ {\text{scalar multiplication}}\right.}\\[0.3em]\implies &{\begin{pmatrix}\rho _{1}\\\rho _{1}\\0\end{pmatrix}}+{\begin{pmatrix}0\\\rho _{2}\\0\end{pmatrix}}+{\begin{pmatrix}0\\\rho _{3}\\\rho _{3}\end{pmatrix}}={\begin{pmatrix}0\\0\\0\end{pmatrix}}\\[0.3em]&\quad {\color {OliveGreen}\left\downarrow \ {\text{vector addition}}\right.}\\[0.3em]\implies &{\begin{pmatrix}\rho _{1}\\\rho _{1}+\rho _{2}+\rho _{3}\\\rho _{3}\end{pmatrix}}={\begin{pmatrix}0\\0\\0\end{pmatrix}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8f114c95cd875eb550911ae6e1091bf473a0295)































![{\displaystyle {\begin{aligned}x={\frac {\pi }{2}}&:&\lambda _{1}-\lambda _{3}&=0\\[0.3em]x=\pi &:&\lambda _{1}-\lambda _{2}+\lambda _{3}&=0\\[0.3em]x=0&:&\lambda _{1}+\lambda _{2}+\lambda _{3}&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1400d8d1e5652d95c5e39023edf85b6996ae5c3d)
































![{\displaystyle {\begin{aligned}0=F(0)&=F(\lambda _{0}v+\lambda _{1}F(v)+\dots +\lambda _{n}F^{n}(v))\\[0.3em]&=\lambda _{0}F(v)+\lambda _{1}F^{2}(v)+\dots +\lambda _{n}F^{n+1}(v)\\[0.3em]&=\lambda _{0}F(v)+\lambda _{1}F^{2}(v)+\dots +\lambda _{n-1}F^{n}(v).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1de9590d8f7252c3de95aa4ce5260e12d74a3a3c)









![{\displaystyle {\begin{aligned}0=F(0)&=F(\lambda \cdot v+\mu \cdot F(v))\\[0.3em]&=\lambda \cdot F(v)+\mu \cdot F^{2}(v)\\[0.3em]&=\lambda \cdot F(v)\\[0.3em]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac174efa65a06223304484fe6dfa30f23df5d9b6)








![{\displaystyle {\begin{aligned}0=F(0)&=F(\lambda _{0}\cdot v+\lambda _{1}\cdot F(v)+\dots +\lambda _{n+1}\cdot F^{n+1}(v))\\[0.3em]&=\lambda _{0}\cdot F(v)+\lambda _{1}\cdot F^{2}(v)+\dots +\lambda _{n+1}\cdot F^{n+2}(v)\\[0.3em]&=\lambda _{0}\cdot F(v)+\dots +\lambda _{n}\cdot F^{n+1}(v)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3251b14e68e28324427e37a60597e2dc2fe1290c)



