Sequences – Serlo
The sequence is one of the most important terms in analysis. On the basis of sequences we will define the term of the limit value later. This in turn allows us to introduce all important concepts of analysis like derivative and continuity.
Sequences in "everyday life"
[Bearbeiten]Maybe, you can think of some examples from your everyday life, where "things line up" as a sequence...
Question: What examples of sequences do you know?
There is no uniquely correct answer to this. Let me give you some examples:
Think of customers queuing anywhere in some well-defined order.
Or think of the order of things you do after getting up: 1. brushing your teeth, 2. taking a shower, 3. getting dressed, 4. making coffee, 5. drinking that coffee, ...
You may also think of sequences that get longer over time. An example which our German colleagues like is the sequence of the nations that won the World Cup (both men and women): 1 Uruguay, 2 Italy, 3 Italy, 4 Uruguay, 6 Germany, ...
All examples have in common that the order of the elements of a sequence is exactly defined. There is an exactly defined order of the sequence elements, which has to be considered. After getting up you should make coffee before drinking it (the reverse order would be suboptimal ![]() ).
).
In addition, one or more objects can appear several times in a sequence. In the sequence of the soccer world champions, some nations appear more than once because they won the soccer world championship more than once. This distinguishes a sequence from a set. For a set it does not make sense to ask how often an element occurs in the set, as it may occur at most once. One can only ask whether an object is an element of a set or not.
Furthermore, you can number the individual sequence members of a sequence. You can say who was the first president of the USA, the second president and so on. So you can assign one or more numbers to each element of a sequence, which indicate at which position this object occurs in the sequence.
Many of the sequences known in everyday life are finite, but infinite sequences are imaginable too. If soccer world championships would be played for all eternity, the sequence of soccer world champions would be infinite.
Formal definition
[Bearbeiten]Let us now turn to the concept of a sequence in mathematics. The big difference to the notion of sequences in everyday life is, that in mathematics a sequence is always infinitely long. In mathematics there are also "finite sequences", but mathematicians call them"tuples" instead of sequences. ("finite = tuple", "infinite = sequence")
A sequence is thus an infinite sequence of objects. Here stands for the object in the first place, for the object in the second place and so on. For sequences there is the abbreviated notation . This is the (intuitive) definition of a sequence:
A sequence is an infinite ordered arrangement of elements:
This definition is only intuitive, because we did not define the term "infinite ordered arrangement" exactly. This has to be done for an exact (non-intuitive) definition.
Example (sequence)
The sequence of real numbers is:
The sequence of powers of 2 is:
Exercise (for understanding): Write the following sequences in the above form within one bracket
- The sequence of square numbers
- The sequence of positive odd numbers
Important terms
[Bearbeiten]The single elements of a sequence are mathematically called sequence elements. They are enumerated by a natural number . This natural number is called index. For example, is the sequence element of index .
For a sequence with elements from the set , a sequence elements must be an element of the set . For instance, take the sequence . The sequence member is identical to or , namely the number .
If you refer to the whole sequence, you write . Two short notations for are and . Often the letter is used as an index variable. But every letter can be used as index variable as long as it has no other meaning in the respective context. For instance, , , or are common, as well.
In real analysis, we consider sequences of real numbers. These special sequences are called real-valued sequences. In the following overview and in the following table all essential terms concerning the components of sequences are summarized:
| term | notation | definition |
|---|---|---|
| sequence | or | A sequence is an infinite arrangement of objects. |
| sequence element | A sequence element is one specific element within a sequence, standing at some position. | |
| index | The index is that position, i.e. a natural number. |
Warning
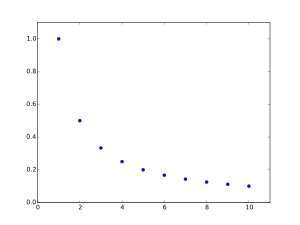
Some students tend to imagine a real sequence as a continuous function (especially if they want to draw it). This is not a good intuition, because a real sequence consists only of a sequence of single real numbers and not a continuously drawn line. This is demonstrated by the following comparison of the harmonic sequence with the function with . Notice that in contrast to the function there are only discrete values (single points) in the graph for the harmonic sequence:
-
The harmonic sequence defined by , takes discrete values.
-
Compare the continuous function . Its domain are the real positive numbers.
The intuition with dots (left side) is better for understanding sequences.
Definition as a function
[Bearbeiten]Definition
[Bearbeiten]Above we have intuitively defined the sequence as an infinite arrangement of objects. The term of a function will allow us to make a mathematically precise definition: We take the set of natural numbers and assign to each natural number an object (where the objects come from some set in which the sequence takes its values). Thus we get an infinite and numbered arrangement of objects, as the following sketch illustrates:
So a sequence is mathematically a function For instance, we could write the sequence of Presidents of the US as such a function:
(For English monarchs, the situation is not so easy as there are different houses with different sequences.)
The function assigns to any natural number the corresponding -th sequence element:
Definition (sequence)
A sequence with values in the set is a map
we write instead of .
The definition above only uses mathematical terms, so it serves as a mathematically exact definition. Hence, it is used in textbooks as definition for a sequence.
Remarks
[Bearbeiten]For a sequence with sequence elements from the set the short form stands for a function . So sequences are nothing else than functions.
Let us take the two sequences and . Strictly speaking, both sequences are different, because the target sets are and , i.e. different and therefore the functions are different, as well. But their "short spellings" do not differ: and . This distinction becomes obvious, if you call a sequence in the natural numbers and a sequence in the real numbers.
To make clear that a sequence is a mapping from the natural numbers into the set , we say that is a sequence in . Sometimes also the notation is used.
Question: Why is the sequence not defined as a set ? What differs a sequence and a set?
There are two reasons: Toking the soccer world champion sequence (starting from 1990)
The map is defined by
- In a sequence an element can occur several times. In a set, this is not allowed. Brazil is several times soccer world champion, France (2020) is not. If you look at the sequence , you can see this. If you only know the set of soccer world champions , there is no way to tell whether Brazil is a multiple soccer world champion.
- In a sequence there is an order of elements. The objects in a set do not have an order. In the sequence , we can read out which country has won the third soccer world championship since 1990: . If we only know the set of soccer world champions , there is no way to tell which country has won the third soccer world championship since 1990.
Kinds of sequences
[Bearbeiten]

Folgen können beliebige Objekte als Folgenglieder besitzen. So sind reelle Folgen Folgen von reellen Zahlen. Dies ist auch der Typ der meisten Folgen, die uns in der Analysis begegnen werden. There is aber auch möglich, Folgen von komplexen Zahlen zu haben, welche komplexe Folgen genannt werden. Aber auch Folgen von Mengen oder Folgen von Funktionen sind möglich.
In den letzten Kapiteln haben wir bereits Intervallschachtelungen kennengelernt. Since Intervalle Mengen sind, sind Intervallschachtelungen Beispiele für Folgen von Mengen. Die folgende Tabelle listet einige Beispiele für Folgen auf:
Sequences can have any objects as sequence elements. There are real-valued sequences , which are sequences in the real numbers. Most sequences, which we encounter in real analysis will be of this type. Taking sequences of complex numbers, we get complex-valued sequences. But also sequences of sets or sequences of functions are possible (see the two figures).
In the last articles, we already learned about nested intervals. Since intervals are sets, nested intervals are an example for sequences of sets. The following table lists some examples of sequences:
| kind of sequences | explicit law | the first elements |
|---|---|---|
| real sequence | ||
| complex sequence | ||
| sequence of sets | ||
| sequence of intervals | ||
| sequence of functions |
The explicit law is the formula with which a sequence element can be expressed directly, if just the index is given. There is also a recursive law, which states what an element is in terms of the previous elements. In the next chapter, we will discuss the different laws for sequences in more detail.






























































![{\displaystyle M_{n}=\left[-{\tfrac {1}{n}},\,{\tfrac {1}{n}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd674047fa658c5ca4452399ad9d4d4bc816c968)
![{\displaystyle \left[-1,\,1\right],\,\left[-{\tfrac {1}{2}},\,{\tfrac {1}{2}}\right],\,\left[-{\tfrac {1}{3}},\,{\tfrac {1}{3}}\right],\,\left[-{\tfrac {1}{4}},\,{\tfrac {1}{4}}\right],\,\ldots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/df59b58109d8b75a087b6ba8d4ae3f1b8206f73d)



