Union and intersection of vector spaces – Serlo

Motivation

We know various operations to construct a new set from given sets. If $(U_{i})_{i\in I}$ is a family of sets, we can, for example, form the average $\bigcap _{i\in I}U_{i}$ or the union $\bigcup _{i\in I}U_{i}$. Assume that the $U_{i}$ are also subspaces of a larger vector space $V$. This means that the $U_{i}$ are non-empty subsets of $V$, which are closed under addition and scalar multiplication. Are the average and the union of $U_{i}$ then also subspaces of $V$?

Intersection of vector spaces

Is the intersection of subspaces of a vector space again a subspace? To answer this question, let us first consider the case of two subspaces and look at examples in $\mathbb {R} ^{3}$.

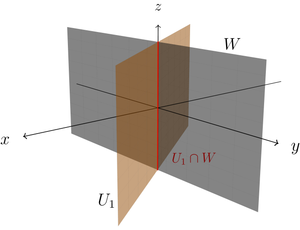
1. Let us first look at the two planes $U_{1}=\operatorname {span} \{(2,1,0)^{T},(0,0,1)^{T}\}$ and $W=\operatorname {span} \{(0,2,0)^{T},(0,0,-1)^{T}\}$ (the y-z-plane). In the image we can see that its intersection is the z-axis $\operatorname {span} \{(0,0,1)^{T}\}$, i.e. a subspace of $\mathbb {R} ^{3}$.
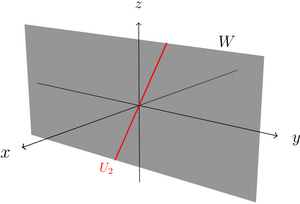
2. The second image shows that the intersection of the line $U_{2}=\operatorname {span} \{(0,1,2)^{T}\}$ with the y-z plane $W$ is also a line, namely $U_{2}$.
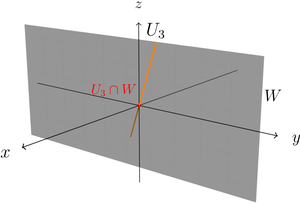
3. If we intersect the y-z plane $W$ with the line $U_{3}=\operatorname {span} \{(1,1,1)^{T}\}$ instead, we see that the intersection only contains the zero vector. This is also a subspace of $\mathbb {R} ^{3}$.

• 
  Intersection of two planes
• 
  Intersection of a plane with a line
• 
  Intersection of a plane with a line

In the examples, the intersection of the two subspaces is always a subspace of $\mathbb {R} ^{3}$. We now show that this also applies to general subspaces of any vector space.

Theorem (Intersection of vector spaces)

Let $U$ and $W$ be two subspaces of a vector space $V$. The intersection $U\cap W=\{v\in V:v\in U\land v\in W\}$ of $U$ and $W$ is a subspace of $V$.

Proof (Intersection of vector spaces)

First, we have to establish the three subspace criteria:

Proof step: $U\cap W$ is not empty

Since $U$ and $W$ are subspaces, we have $0_{V}\in U$ and $0_{V}\in W$. Thus, $0_{V}\in U\cap W$, and therefore $U\cap W\neq \emptyset$.

Proof step: $U\cap W$ is closed under addition.

Let now $v,w\in U\cap W$ be arbitrary. Then $v,w\in U$ and $v,w\in W$ apply. As the subspaces $U$ and $W$ are closed under addition, we get $v+w\in U$ and $v+w\in W$. This also means $v+w\in U\cap W$.

Proof step: $U\cap W$ is closed under scalar multiplication.

Let $\lambda \in K$ and $v\in U\cap W$ be arbitrary. Then we have $v\in U$ and $v\in W$. Since the subspaces $U$ and $W$ are closed under scalar multiplication, we obtain$\lambda \cdot v\in U$ and $\lambda \cdot v\in W$. Thus, also $\lambda \cdot v\in U\cap W$.

Hint

We have seen that $U\cap W$ is a subspace of $V$. Because $U\cap W\subseteq U$, the intersection is also a subspace $U$. From this we get $\dim(U\cap W)\leq \dim(U)$. Similarly, $\dim(U\cap W)\leq \dim(W)$ follows from $U\cap W\subseteq W$. This makes intuitively sense: if we intersect one subspace with another, its dimension cannot possibly become larger.

We have shown that the intersection of two subspaces is again a subspace. However, at no point in the proof is it relevant that there are only two or finitely many subspaces involved. In fact, the statement applies to any family of subspaces.

Exercise (Arbitrary intersection of vector spaces)

Let $I$ be an arbitrary index set and $(U_{i})_{i\in I}$ a family of subspaces of a vector space $V$. Then, the intersection $\bigcap _{i\in I}U_{i}$ is a subspace of $V$.

Solution (Arbitrary intersection of vector spaces)

Let $i\in I$ and let $U_{i}$ be subspaces of the $K$-vector space $V$. The intersection $U:=\bigcap _{i\in I}U_{i}$ of all vector spaces $U_{i}$ is again a vector space.

Proof step: $U$ is not empty.

Since the $U_{i}$ are subspaces, we have $0\in U_{i}$ for all $i\in I$ and therefore $0\in U$. Thus $U$ is not empty.

Proof step: $U$ is closed under Addition.

Let $v,w\in U$. Then $v,w\in U_{i}$ holds for all $i\in I$. Because the $U_{i}$ are vector spaces, they are closed under addition and hence $v+w\in U_{i}$ is valid for all $i\in I$. This means $v+w\in U$.

Proof step: $U$ is closed under scalar multiplication.

Let $w\in U$ and $\lambda \in K$. Then $w\in U_{i}$ holds for all $i\in I$. Since the $U_{i}$ are vector spaces, they are closed under scalar multiplication and $\lambda \cdot w\in U_{i}$ is valid for all $i\in I$. Hence $\lambda \cdot w\in U$.

Union of vector spaces

Is the union of subspaces of a vector space a vector space again? Let us first look at an example.

Example (Coordinate axis cross is not a subspace)

Let $V=\mathbb {R} ^{2}$. We choose the coordinate axes $U=\operatorname {span} \{(1,0)^{T}\}$ and $W=\operatorname {span} \{(0,1)^{T}\}$ as subspaces. Their union is the axis cross in $\mathbb {R} ^{2}$. Based on the figure, we can already surmise that this is not a subspace of $\mathbb {R} ^{2}$: There are two "directions", but at the same time $U\cup W$ is not the two-dimensional plane. And indeed, the two vectors $(1,0)^{T}$ and $(0,1)^{T}$ are in $U\cup W$, but their sum $(1,1)^{T}$ is not in the union. Therefore, $U\cup W$ is not a subspace of $\mathbb {R} ^{2}$.

Union of two lines in two-dimensional real space

So we see that the union of two subspaces is generally not a subspace. Is this always the case?

Example (Union of vector spaces is again a vector space)

We consider the two subspaces $U=\operatorname {span} \{(1,1,2)^{T}\}$ and $V=\operatorname {span} \{(0,1,1)^{T},(1,0,1)^{T}\}$ of $\mathbb {R} ^{3}$. As $(1,1,2)^{T}=(0,1,1)^{T}+(1,0,1)^{T}\in V$ we have $U\subseteq V$. Therefore $U\cup V=V$ and the union of the two subspaces is again a subspace.

Union of a line with a plane in three-dimensional space

The union of two subspaces is therefore in some cases, but not always, a subspace. In the example, $U$ was contained in $W$, so that $U\cup W=W$ was a subspace. This always works: If two subspaces are given and one of them is contained in the other, then the union is equal to the larger of the two, i.e. a subspace again.

This is indeed the only case in which the union of two subspaces is again a subspace, as the first example with the coordinate axes makes clear: If $U\nsubseteq W$ and $W\nsubseteq U$, then the union will not be closed under addition. There will then always exist two vectors $u,w$ with $u\in U\setminus W$ and $w\in W\setminus U$. The sum $u+w$ thus contains a part that is not in $U$ and therefore cannot be in $U$: Otherwise, $w=u+w-u\in U$ would also be true. The same applies to $u+w\notin W$.

We therefore have the following criterion for determining when the union of two subspaces is a subspace.

Theorem (Condition for the union of two vector spaces to be a vector space again)

Let $V$ be a vector space over a field $K$ and let $U$ and $W$ be two subspaces of $V$. Then $U\cup W$ is a subspace of $V$ if and only if $U\subseteq W$ or $W\subseteq U$ holds.

Proof (Condition for the union of two vector spaces to be a vector space again)

Proof step: If $U\cup W$ is a subspace of $V$, then we have $U\subseteq W$ or $W\subseteq U$.

We prove the statement by contradiction: Assume that neither $U\subseteq W$ nor $W\subseteq U$ is true. We show that $U\cup W$ is then not a subspace of $V$. Instead, we find two elements $u,w\in U\cup W$, so that $u+w\notin U\cup W$:

Since $U\nsubseteq W$, there exists an element $u\in U$ that is not contained in $W$. Similarly, since $W\nsubseteq U$, there exists a $w\in W$ that is not contained in $U$.

Thus, $u,w\in U\cup W$. But the sum $u+w$ is neither in $U$ nor in $W$: If $u+w\in U$, then $w=(u+w)+(-u)\in U$, in contradiction to the choice of $w$. Here we have used the fact that $u\in U$ implies also $-u\in U$ and that $U$ is closed under addition. In the same way, you can see that $u+w$ does not lie in $W$.

Therefore, $u+w\notin U\cup W$ applies. This means that the union $U\cup W$ is not closed under addition, i.e. it is not a subspace.

Proof step: If $U\subseteq W$ or $W\subseteq U$, then $U\cup W$ is a vector space

If $W\subseteq U$, then $U\cup W=U$, so the union is a subspace. Similarly, it follows from $U\subseteq W$ that $U\cup W=W$ is a subspace.

The proof of the theorem shows that the property of being a subspace fails due to addition. The scalar multiplication on $V$ was not relevant in the proof. In fact, $U\cup W$ is always closed under scalar multiplication, even if the union is not a subspace: If $\lambda \in K$ and $x\in U\cup W$, say $x\in U$, then $\lambda x\in U\subseteq U\cup W$ holds, since $U$ is closed under scalar multiplication as a subspace. The case $x\in W$ is analogous.

Since $V$ is a vector space and $U,W$ are subspaces, $(V,+)$ forms a group and $(U,+),(W,+)$ subgroups. We have thus effectively shown that $U\cup W$ is a subgroup of $V$ if and only if $U\subseteq W$ or $W\subseteq U$ holds. There is a more general statement about (not necessarily commutative) groups. The proof is quite analogous to the proof for subspaces that we have seen above.

Theorem (Union of subgroups)

Let $G$ be a group and $U,H$ subgroups. Then $U\cup H$ is a subgroup of $G$ if and only if $U\subseteq H$ or $H\subseteq U$ holds.

The union of subspaces $U$ and $W$ is generally not a subspace. However, you can define the smallest subspace that contains $U\cup W$. This subspace is the subspace sum $U+W$.