Volumes on rings – Serlo
Extensive quantities
[Bearbeiten]"Measuring" in the sense of measure theory means quantify: What is asked is not "what value has ...?", "how fast/hot/bright is ...?", but "how much of ...?", "how big/heavy/numerous is ...?". So we are interested in quantities that change with the size of the underlying system: doubling the system doubles the quantity. In physics, quantities with this property are called extensive quantities. An example is mass: if we join two systems of boxes and with mass and , the resulting system has the larger mass . By contrast, quantities that do not change with the size of the underlying system are also called intensive. For example, temperature is an intensive quantity: pouring two liquids of one temperature together does result in the same temperature, and not the sum of the temperatures.
So whenever we quantify something in measure theory, we are measuring an extensive quantity. Other examples of such quantities are:
Example (Extensive quantities)
- geometric volumes: the length of a distance, the area of a plane or surface, the volume of a geometrical object, ... even volumes of objects of non-integer dimension are conceivable (fractals).
- the energy contained in a physical system
- the amount of matter (how many atoms?)
- the electric charge on a field
- but also: the probability of events. If more possible results of a random experiment belong to an event, then the probability that the event occurs increases.
So we can understand the measure theory as a mathematical theory of measuring extensive quantities.
Volume-measuring functions
[Bearbeiten]How can we grasp the measuring of such quantities mathematically? Obviously, by measuring a quantity, an assignment is described: A certain object (geometric body, event, accumulation of things) gets assigned exactly one "volume". Thus, the measuring of a quantity can be described by a function. The domain of definition of this function contains the objects to be measured. These can be understood as subsets of a huge set . For example, (physical) objects. such as cubes, cuboids, spheres, cones, etc. can be seen as subsets of :
Example (Geometric objects as subsets of )
For example, cuboids can be described by sets of the form , where . It is often more clever to use half-open intervals of the form instead of closed intervals: The "half-open cuboids" formed from these can be joined disjointly and without gaps.
A sphere with center at the origin and radius is represented by the set .
Likewise, one can consider subsets of when measuring an extensive quantity counting objects. So the domain of definition will be a set system of subsets of a large basic set (to be determined more precisely in each case) and the function will be a function on sets. The function values correspond to the volumes assigned to these sets and are scalars in . For now, let us call such a function a volume-measuring function.
Definition (Volume-measuring function)
We formalize the measurement of an extensive quantity via a function on a system of subsets of a basic set with values in . Such a function
that describes the measurement of an extensive quantity, is called a volume-measuring function (on ).
From a mathematical point of view, a volume-measuring function is nothing more than a function on sets with values in . We investigate which further properties a volume-measuring function should have in order to be able to describe the measurement of an extensive quantity in a meaningful way.
Which properties shall a volume-measuring function have?
[Bearbeiten]Non-negativity
[Bearbeiten]It makes intuitive sense to require non-negativity of volume-measuring functions. After all, how should a negative volume be interpreted? Admittedly, there are situations in which one also allows negative numbers as dvalues of a volume-measuring function (signed measures). One example is the measurement of a total charge, which is composed of positive and negative parts. Sometimes the range of values is generalized even further, so that also complex numbers can appear as function values (complex measures) or certain linear mappings (spectral measures). However, all these cases arise as generalizations from the non-negative real situation, so we will restrict ourselves to the real case at the being. Moreover, infinity should also be allowed as a function value in certain cases: For instance, the geometric volume of should be infinite. So we require: a volume-measuring function maps to .
Monotonicity
[Bearbeiten]Volume-measuring functions are intended to formalize the measurement of extensive quantities. Extensive quantities are characterized by the fact that they increase with increasing size of the underlying system. For example, when determining the number of atoms in a sample of matter, one should count more atoms after adding a certain amount of the matter. This property should also be found in volume-measuring functions: enlarging a geometric object makes it gain more volume. Mathematically, this can be described by the term monotonicity of a function on sets:
Definition (Monotonic functions on sets)
A function is called monotonic, if for all sets with , we have that .
We will demand a volume-measuring function to be monotonic: larger sets have larger volumes.
Sub-additivity
[Bearbeiten]

The monotonicity of the volume-measuring function guarantees that the value for a given set is always less than or equal to the value for any superset . But is this also true if the superset is a union of several sets? Intuitively, this should be the case: If a set is covered by sets , then the volume-measuring function evaluated on should in no case yield a value larger than for the sum of the contents of the covering sets.
Mathematically expressed: for a volume-measuring function and sets it should hold that:
In particular, this property should be satisfied if the union of the covering sets itself is no longer in the domain of definition . But this property is not yet expressed by the monotonicity!
Example
Consider the base set and the set system . Let the function be defined by and . Obviously, is monotonic. However, monotonicity no longer holds for finite covers! We have , but
Thus, the property of functions on sets that monotonicity is preserved even in the case of finite covers has to be required additionally. We call it sub-additivity:
Definition ((finite) sub-additive function on sets)
A function is called (finitely) subadditive if for all and arbitrary sets it holds that:
If the covering of the set consists of only one set , this property corresponds exactly to monotonicity. So we can take sub-additivity as a generalization of monotonicity and replace the requirement of monotonicity of volume-measuring functions by this generalized version: measuring functions must be sub-additive.
Additivity
[Bearbeiten]The properties of monotonicity or more generally of sub-additivity required so far make only an "approximate" statement: the function values of a sub-additive function on sets may be above the "real" value. As an example:
Example (Sub-additivity for outer approximations)
Let and . The function with and is obviously sub-additive. However, the function value of the quantity is only an upper bound for the exact value: To be expected would be .

Obviously, for a volume-measuring function to be "exact", this property must be additionally required: If a set is exactly covered by finitely many, pairwise disjoint sets , then the function value of the volume-measuring function evaluated at is said to be equal to the sum of the function values for the individual .
It is hence important whether the sets within a union are pairwise disjoint. To make explicit the pairwise disjointness within a union, we introduce a new notation:
Definition (Disjoint union)
A union of sets is called disjoint if the are pairwise disjoint, and we write
The above formulated condition of "exactness" of a function on sets is called (finite) additivity: for an exact covering of a set, decomposition and reassembly does not change its volume:
Definition ((finite) additive function on sets)
A function is called (finitely) additive if for all and all pairwise disjoint sets with it holds that:
We fix this desirable property of a volume-measuring function to be exact by demanding: volume-measuring functions must be additive.
Warning
In the definition of additivity, we imposed the restrictive condition that the union of also lies in the set system , so that the left-hand side of the equation makes sense. This was not necessary the case for sub-additivity, because it was only a matter of covering (and not decomposing) a set.
It is important to note that due to this limiting condition, the additivity is even more dependent on the domain of definition (i.e., a set system), than the sub-additivity. In particular, the additivity of a function on sets does not in general follow from its sub-additivity or monotonicity. A counter-example is a function on sets, whose domain of definition does not contain disjoint sets:
Example (An additive, but non-monotone function on sets)
Let be a set system and a function on sets with and . Then is additive, but not sub-additive, not even monotonic.
However, we will see later that additivity implies sub-additivity if the domain of definition has "a sufficiently good structure".
Last, the additivity of volume-measuring functions makes it desirable that holds: Because of additivity, must hold, and this condition is only satisfiable for or . If now , then due to monotonicity would have to hold for all sets . To exclude this pathological case, one additionally demands: For volume-measuring functions, must hold.
Conclusion
[Bearbeiten]Let us recap the properties that a volume-measuring function should have in order to meaningfully describe the measurement of an extensive quantity:
- Such a function should map to . In most cases, this makes sense. But we can still generalize to further extended ranges of values.
- It should be sub-additive. We derived sub-additivity as an improved form of monotonicity that is preserved even in the presence of finite covers. In particular, any sub-additive function on sets is also monotonic. The monotonicity itself reflects the characteristic property of extensive quantities to grow with increasing size of the system under consideration.
- It should be additive. Additivity corresponds to the property of a volume-measuring function to be "exact" and to be compatible with decomposing measured objects into finitely many parts and reassembling them.
- It should assign the value zero to the empty set. This makes intuitive sense and also serves to exclude the case that the volume-measuring function is constantly infinite.
Rings: the domain of definition
[Bearbeiten]In the considerations about additivity a difficulty has already appeared: Whether a set function is additive also depends on its domain of definition. The more sets are contained in the definition range, the more set ocmbinations we have to check for additivity, so it gets more difficult. After all, how large can a system containing subsets of be made(as the domain of definition of a volume-measuring function) without destroying its additivity? Indeed, the answer is not generally "the power set " (whichh would be the largest possible set system). We have to stop before! An example where this happens is the elementary geometric volume on the :
The volume problem
[Bearbeiten]The goal is to define an additive set function that describes the elementary geometric volume in . The problem of defining this function on all of is also called the volmue problem. And it will turn out to be unsolvable!
Definition (The volume problem)
We are looking for a "content function" defined on the power set with the following properties:
- finite additivity
- motion invariance: for any motion and for all it holds that . (A motion is an affine-linear transformation of the form with and orthogonal linear component , i.e., a rotation, reflection, or translation in space.)
- Normalizedness:
However, Hausdorff, Banach and Tarski were able to prove that such a measure cannot be found:
- The volume problem is unsolvable for the if . (Hausdorff, 1914)
- The volume problem is solvable for the and the , but it is not uniquely solvable. (Banach, 1923)
The first case looks somewhat paradox: we would expect such a volume naturally to exist (why should subsets of the for do not have a volume?) However, this is not the case! Building on Hausdorff's result, Banach and Tarski showed the following theorem, which is also known as reflecting the "Banach-Tarski paradox":
Theorem (Theorem of Banach and Tarski (1924))
Let and let be bounded sets with nonempty interior. Then there are sets and motions such that is the disjoint union of sets and is the disjoint union of the sets .
This theorem makes vividly clear that the volume problem on the cannot be solvable for . The implications would be absurd: it follows from the theorem that a sphere (think of a pea or an orange) can be suitably divided into finitely many parts and assembled into a sphere the size of the sun. (Of course, this does not work in real life, simply because physical bodies are not continuous sets of points, but are composed of atoms. The quantities of such a decomposition are extremely complex and can best be illustrated as "point clouds", which in general cannot be stated explicitly).
Warning
Although the volume problem is intractable for , not all volume-measuring functions make problems if we want to define it on the whole power set. It depends on the desired properties of the measurement function and on the basic set under consideration whether this is possible. For the volume problem, we only chose too strong requirements: it is the invariance of motion that causes difficulties for . However, for "simpler" measurement functions, it may well be possible to define them on the whole power set. An example is the measurement function over a set which is constant zero. Also, reducing the base set may make our life easier.
Rings of sets
[Bearbeiten]So, in general, we cannot hope to define an additive set function on the whole power set. This makes it necessary to think more carefully about the set system , which is to serve as the domain of definition of volume-measuring functions. Mathematicians spent some considerable time on defining classes of such set systems and therefore, the literature on measure theory provides a whole zoo of such set systems: Semi-rings, rings, -rings (pronounced "sigma-rings"), algebras, -algebras, Dynkin systems, monotonous classes, ... You may find an overview in this article
Intuitively, the domain of an additive (and subadditive) volume-measuring function should be stable under the following set operations: the disjoint union of finitely many sets "" and its counterpart, forming differences of sets "". Moreover, if one has the difference operation available, one can make arbitrary unions "artificially" disjoint: if and are (not necessarily disjoint) sets, then , where the two united sets on the right-hand side of the equation are again in . So one can forget about disjointness and speak of arbitrary finite unions. Finally, to exclude trivial cases, we require and can now define:
Definition (Ring of sets)
Let be a set. A set system is called ring of sets (or ring for short) if:
Hint
- For every ring we have : By condition 1 there is at least one element , and by 3 it also holds that .
- In point 2, we can use induction to extend the stability of the set system from 2 to any finite number of sets.
Examples for rings of sets
[Bearbeiten]Over a base set there are always the two rings and .
Example (Countable subsets)
The system of countable subsets of is a ring:
- Since the empty set is countable, is nonempty.
- If are two countable sets, then their union is also countable, so holds.
- If are countable, then because their difference is also countable and holds.
This is already an example containing a lot of sets. Especially, for finite , the ring can be chosen to be all of the power set . For base sets with infinitely many points, such as , one can also easily construct rings:
Example (Finite subsets)
The set system of finite subsets of is a ring:
- The empty set is finite, so is nonempty.
- If are finite, then so is their union, i.e., .
- If are finite, then because of so is their difference, i..e, .
Another important example of a ring in case is the following:
Example (Ring of cuboids)

Consider the set system
of the axis-parallel cuboids in . (The intervals in the product may be open, half-open, or closed.) The ring of cuboids in is defined as the ring generated by , that is, the smallest ring containing . Its elements are so-called cuboids, i.e. finite unions of axis-parallel cuboids in . One can specify this ring explicitly: It is the intersection of all set rings over containing the cuboids . (Compare also the article on generated -algebras.)
Volumes on rings
[Bearbeiten]We have now found some properties that a volume-measuring functions should satisfy in order to meaningfully describe the measurement of an extensive quantity: non-negativity, subadditivity (especially monotonicity) and additivity. As natural domains of definition of such functions we juts defined rings.
Additivity is sufficient on rings
[Bearbeiten]Above, we noticed that from the additivity of a volume-measuring function, the subadditivity does not follow in general. And not even its monotonicity - at least not if nothing else is known about the domain of definition . But if the set system is a ring, then the monotonicity and the subadditivity already follow from the additivity and non-negativity of the volume-measuring function. The reason is that by cut-stability of the set system, one can easily make unions "artificially" disjoint and thus exploit the property of additivity. When proving this statement, it is clever to first show the somewhat simpler property of monotonicity and then subadditivity.
Theorem (Additive, non-negative functions defined on rings of sets are monotonous)
Let be a ring over the base set and let be an additive and nonnegative function (on sets). Then is monotone.
Proof (Additive, non-negative functions defined on rings of sets are monotonous)
Let be such that . The idea is to determine the "more" of over : Since is a ring, and it due to additivity,
where in the last step we exploited the non-negativity of .
Theorem (Additive,non-negative functions defined on rings of sets are sub-additive)
Using the notion of the previous theorem, is subadditive.
Proof (Additive,non-negative functions defined on rings of sets are sub-additive)
Let besuch that . We make the union of "artificially" disjoint:
Thus, each is formed by taking out all the elements already contained in the sets . Note that the are also in the ring , as it is stable under difference and union.
Thus also holds for all and it follows from additivity and the (already proven) monotonicity of :
Definition
[Bearbeiten]Thus, one can characterize the monotonicity and subadditivity of a volume-measuring function defined on a ring by its non-negativity and additivity alone. So we can now summarize all the properties that a measurement function should possess in the following definition:
Definition (Volume on a ring)
Let be a ring over the set . A nonnegative function is called volume function on (or volume, for short) if:
- ,
- is additive.
We call the value of a set the volume of .
The condition makes intuitive sense and also serves to exclude the pathological case .
Hint
Sometimes, volumes are defined on other set systems, for example on so-called semi-rings or algebras.
Examples
[Bearbeiten]Example
Let be the ring of all finite subsets of and let be the function
which counts the number of elements of a set . Contents:
- The empty set contains no elements, so .
- Let be disjoint. Because of disjointness, the number of elements in the union is the sum of the number of elements in and and it holds that .
One can also consider this volume on the entire power set . Then one only has to consider that the additivity holds even if one or both of the disjoint sets contain infinitely many elements.
Example
For any subset , we define
This is a volume on :
- The empty set is finite, so .
- If and are disjoint, then if the sets are both finite. If either or both sets are infinite, additivity also holds: if w.l.o.g. is infinite, then .
A particularly important example is the so-called elementary geometric volume:
Example (Geometric volume of cuboids)
We already know the ring of cuboids, whose elements are finite unions of axis-parallel cuboids in . (An axis-parallel cuboid in is a product of intervals, each open, half-open, or closed.) One can show that any such cuboid can be written as a disjoint union of cuboids.
One can show that the function so defined is a volume on the ring of cuboid bodies . This includes showing that is well-defined, so that the value does not depend on the chosen decomposition of the cuboid into disjoint cuboids.
Further properties of volumes
[Bearbeiten]We collect properties of volumes. In the following, let be a ring (in particular closed under differences and finite unions) and let be a volume.
Theorem (Subtractivity)
Volumes are subtractive: Let with and . Then holds.
Proof (Subtractivity)
By additivity, holds. Because of we can subtract on both sides of the equation and get the result.
Warning
One cannot do without the condition ! If holds, one gets the undefined expression . This cannot be sensibly defined. For example, if is the elementary geometric volume on that assigns to each interval its length, then for the value "" is . But for and one gets "".
Another property of finite volumes (i.e. for all sets ) is the so-called inclusion-exclusion principle. It is important in probability theory (where ), and traces the volumes of a union of sets to a sum of volumes of intersections. Note that for a ring and , we also have . Finite intersections of sets from thus lie again in .
Theorem (Inclusion-exclusion-Principle)
Let the content be finite and let , . Then
Proof (Inclusion-exclusion-Principle)
What does this formula even mean? We first make clear what it means for small :
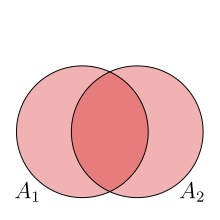
- For we have
OK, this is obvious.
- For we have
So the formula tells us: if we want to calculate the volume of a union, we first add the measures (=areas) of and . However, we have counted the overlap "twice" and must subtract it again.

- For we have
A slightly more complicated case: We add, first all 3 measures. Here, the "double overlap areas" , and were counted twice. The "triple overlap area" even three times! Subtracting the three "double-overlaps" removes the duplication in the . But the measure of has been subtracted three times, that is, once too many. So we have to add it back at the end.
Here an induction over begins to appear: The step in can be generalized to higher . Our induction can then simply be started with .
Theorem whose validity shall be proven for the :
1. Base case:
For we obviously have .
1. inductive step:
2a. inductive hypothesis:
2b. induction theorem:
2b. proof of induction step:
In the step , the measure must be added to the union on the left-hand side - but minus the sets that are already included. So we have

To the first term on the right (corresponding to the 3 circles in the figure) we can apply the induction assumption, because the union goes only up to :
In the third term on the right (corresponding to the red area in the figure), it makes no difference whether we intersect with the whole union, or first intersect all sets individually and then take the union. In both cases, everything outside is "cut away" from the union:
Substituting the first and third terms on the right yields:
What does the complicated expression on the right-hand side mean? And does it actually correspond to the induction assertion? The right-hand side consists of 3 sums, whose summands already have the desired form from the induction assertion (including the correct signs).
- The first term now contains all summands in which does not occur.
- The second term contains all summands in which but no other occurs.
- The third term contains all summands in which and at least one other occurs.
So, in total, we have covered each summand from the induction assertion exactly once. This is because each summand contains either or not and either one of the terms or not. So
which establishes the induction assertion.











![{\displaystyle [a_{1},b_{1}]\times [a_{2},b_{2}]\times [a_{3},b_{3}]\subseteq \mathbb {R} ^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5322ada035f64bb968be0b1187fa9e9a2bd48268)

![{\displaystyle (a_{i},b_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ddb403df05aa19b9e997798ba95d48a9fa37d6d)








![{\displaystyle [0,\infty ]:=\mathbb {R} _{0}^{+}\cup \{\infty \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7de5951aac33f2684875448f3eef9010e627eb2)

















![{\displaystyle \mu :{\mathcal {C}}\rightarrow [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06d2b7a145e4a8689a51cd6eee53f5a81a2a7946)

























![{\displaystyle [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52088d5605716e18068a460dec118214954a68e9)




![{\displaystyle \mu :{\mathcal {P}}(\mathbb {R} ^{n})\rightarrow [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c45afcc0119aba183bf15e4cab27ad15322386fd)






![{\displaystyle \mu ([0,1]^{n})=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd8a6af2484d737fa4a63167a8350a5f571f4923)



































![{\displaystyle \mu :{\mathcal {P}}(\Omega )\supseteq {\mathcal {R}}\rightarrow [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a22f3f88e061e20d916c80815c6bfee16ec54c3)












![{\displaystyle \mu :{\mathcal {R}}\to [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad7b11383d04db361504135058e7751dc669c823)













![{\displaystyle \mu \colon {\mathcal {R}}\to [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bf1de550ba65db8deccc44e5f6d49e83186aaff)







![{\displaystyle A=(-\infty ,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/854508b0a3aeab8a9e04ac56e77ce140c49be3d9)
































