Statistik: Approximation von Verteilungen
Approximation: Approximation heißt Näherung, wie ja beispielsweise Alpha Proxima Centauri der uns am nächsten gelegene Stern ist. Wir wollen also Verteilungswerte, bei deren Berechnung wir heftige Unlustgefühle entwickeln, mit Hilfe anderer Verteilungen annähern. Sie werden nun mit Recht einwenden, dass das ja heutzutage mit der Entwicklung schneller Rechner eigentlich überflüssig sei. Nun hat man aber nicht immer einen Computer dabei (etwa in einer Klausur) oder es fehlt die Software zur Berechnung. MS-Excel bietet zwar solche Funktionen, aber die Umsetzung ist etwas verquer, so dass häufig ein erhöhter Verstehensaufwand betrieben werden muss. Bei bestimmten Funktionswerten, wie großen Binomialkoeffizienten gehen schon mal Taschenrechner in die Knie.
Approximation diskreter Verteilungen durch diskrete Verteilungen
Die Wahrscheinlichkeitsfunktion der Hypergeometrischen Verteilung sieht so aus:
Haben wir als Anwendung eine Kiste mit 10 Ü-Eiern gegeben, von denen 3 den gesuchten Obermotz enthalten, kann man etwa die Wahrscheinlichkeit, bei 5 Versuchen zwei Obermotze zu erhalten, leicht errechnen - naja, relativ leicht.
Aber betrachten wir den Fall: In einer Sendung von 500 speziellen Chips sind 100 Stück defekt. Bei der Eingangskontrolle werden 20 Chips getestet. Wenn jetzt die Wahrscheinlichkeit verlangt wird, dass genau 10 defekte Chips gezogen werden, erhält man
Spüren Sie schon Unlustgefühle? Vielleicht können wir uns hier die Berechnung mit der Binomialverteilung erleichtern. Vergleichen wir die beiden Verteilungen, fällt auf, dass beide den gleichen Erwartungswert haben: EX = nθ. Nur in den Varianzen unterscheiden sie sich,
- Binomialverteilung: und hypergeometrische Verteilung:
nämlich im Korrekturfaktor. Wird nun N sehr groß, ist der Korrekturfaktor fast Eins und wir erhalten approximativ die Varianz der Binomialverteilung. Wie groß ist jetzt ein großes N? Das kommt darauf an, wie genau wir die Näherung haben wollen. Für die Approximation der Hypergeometrischen Verteilung durch die Binomialverteilung gibt es mehrere empfohlene Faustregeln, je nach Geschmack der Autoren. Eine der einfacheren Faustregeln, die man sich auch einigermaßen merken kann, ist
ist. Da in unserem Beispiel diese Voraussetzungen erfüllt sind, berechnen wir die gesuchte Wahrscheinlichkeit als
Wir haben also das Modell ohne Zurücklegen durch ein Modell mit Zurücklegen angenähert. Man könnte so argumentieren: Wenn etwa 10000 Kugeln in einer Urne sind, macht es kaum einen Unterschied, ob beim 2. Versuch noch 9999 oder 10.000 Kugeln übrig sind. Analoges gilt für die Zahl der Kugeln 1. Sorte. Deshalb genügt auch die Angabe des Anteils θ dieser Kugeln an der Gesamtheit der Kugeln:
Noch eine Bemerkung: Stellt man sich allerdings bei der Berechnung dieser Binomialkoeffizienten ein bisschen dumm an, protestiert die Software, weil man einen Überlauf erhält. Man kann allerdings hier mit der Stirling-Formel noch etwas ausrichten. Oder man logarithmiert die Fakultäten.
Für sehr kleines θ (oder sehr kleines 1-θ) und sehr großes n ist die Binomialverteilung wiederum annähernd Poisson-verteilt. Es ist nämlich die Poissonverteilung die Grenzverteilung der Binomialverteilung für n → ∞ und θ → 0. Die Berechnung der Poissonverteilung ist einfacher als die Berechnung der Binomialverteilung. Eine Faustregel wäre hier etwa, dass eine binomialverteilte Zufallsvariable durch die Poisson-Verteilung angenähert werden kann, wenn θ ≤ 0,05 und n ≥ 50 ist. Dann ist
Über den Umweg der Binomialverteilung kann dann auch die hypergeometrische Verteilung gegebenenfalls mit der Poisson-Verteilung approximiert werden:
ist.
Weiter unten folgt eine tabellarische Zusammenfassung ausgewählter Approximationen.
Approximation diskreter Verteilungen durch die Normalverteilung
Was ist nun aber, wenn wir wissen wollen, wie groß die Wahrscheinlichkeit ist, dass höchstens 15 defekte Chips gefunden werden: P(X ≤ 15)? Hier müssen wir auf die oben beschriebene Weise 16 Wahrscheinlichkeiten ermitteln und addieren. Spätestens hier wünscht man sich eine Möglichkeit, so etwas schneller errechnen zu können. Es wäre doch angesagt, wenn man da die Normalverteilung verwenden könnte.
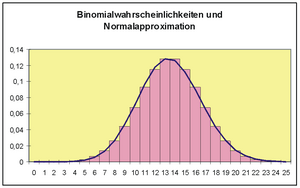
Vergleichen wir die Grafiken der Binomialverteilungen. Es wurden hier die Wahrscheinlichkeiten als benachbarte Säulen dargestellt, was ja am optischen Erklärungswert nichts ändert.
Wir können deutlich erkennen, dass die Binomialverteilung für θ = 0,5 symmetrisch ist. Hier passt sich die Normalverteilung am besten an. Je weiter θ von 0,5 abweicht, desto schlechter ist die Anpassung der Normalverteilung. Die so gut wie immer verwendete Faustregel ist, dass man mit der Normalverteilung approximieren darf, wenn
ist. Dürfen heißt natürlich nicht, dass es sonst verboten ist, sondern dass sonst die Anpassung unbefriedigend ist.
Eine Normalverteilung hat den Erwartungswert μ und die Varianz σ2. Wie soll man diese Parameter bei der Approximation ermitteln? Nun wissen wir ja, dass der Erwartungswert der Binomialverteilung und ihre Varianz
- und
sind, also nehmen wir doch einfach diese Parameter für die Normalverteilung, also
- und .
Etwas fehlt uns noch: Wir nähern hier eine diskrete Verteilung durch eine stetige Verteilung an. Diskrete und stetige Verteilungen sind zwei völlig unterschiedliche Konzepte. Wir betrachten hier das Beispiel einer Binomialverteilung mit n = 45 und θ = 0,3.
Nähern wir P(X ≤ 12) = B(12|45;0,3) durch Φ(12|45·0,3; 45·0,3·0,7) an, wird nur die halbe Säule addiert, denn die stetige Verteilung kennt keine Säulen. Soll die ganze Säule einbezogen werden, müssen wir bis 12,5 gehen, also P(X ≤ 12) = B(12|45;0,3) durch Φ( 12,5|45·0,3; 45·0,3·0,7).
 |
 |
Den addierten Wert 0,5 nennt man Stetigkeitskorrektur.
Speziell gilt für die Wahrscheinlichkeit P(X = a):
P(X = a) = b(a|n;θ) ≈ Φ(a+0,5|nθ; nθ(1-θ)) - Φ(a -0,5|nθ; nθ(1-θ)).

Approximation stetiger Verteilungen durch die Normalverteilung
Jetzt haben wir also auch noch stetige Funktionen, die wir mit der Normalverteilung annähern wollen. Was gibt es denn da für welche? Nun, welche die man oft braucht, etwa für Schätzen und Testen, als da wären die χ2-Verteilung, die F-Verteilung und die t-Verteilung.
Nehmen wir uns doch mal die χ2-Verteilung vor. Ein Blick auf ihre Dichtefunktion verrät, dass diese mit wachsendem n immer symmetrischer wird, sich also der Normalverteilung annähert. Wir wissen, dass die χ2-Verteilung eine Summe von Zufallsvariablen, nämlich standardnormalverteilten, quadrierten, ist und wir erinnern uns (gell?), dass nach dem zentralen Grenzwertsatz sich die Verteilung einer Summe von Zufallsvariablen der Normalverteilung annähert. Betrachten wir die mit n Freiheitsgraden χ2-verteilte Zufallsvariable X. Wir bilden eine neue Zufallsvariable
Eine gängige Faustregel besagt für die Approximation für die Wahrscheinlichkeit P(Y ≤ y):
Die Dichtefunktion t-Verteilung dagegen hat eine ähnliche Form wie die Standardnormalverteilung, denn auch sie ist symmetrisch bezüglich der Null. Hier genügt eine einfache Faustregel: Wenn n > 30 ist, kann man die Verteilungswerte der t-Verteilung annähernd mit Hilfe der Standardnormalverteilung bestimmen:
Tabelle der Approximationen
| Gesuchte Verteilung | Approximation durch | ||
| Binomial | Poisson | Normal | |
| Binomial |
--- | |
|
| Hypergeometrische |
|
über Binomialverteilung | |
| Poisson |
--- | --- | |
| χ2-Verteilung → |
--- | --- | |
| t-Verteilung |
--- | --- | |
| F-Verteilung |
--- | --- | |












































