Die Idee der Integralrechnung ist es, ganz allgemein krummlinig begrenzte Flächen zu berechnen, also etwa die Fläche zwischen dem Graph einer Funktion und der x-Achse.
Wir vereinbaren folgende Notation:
∫
a
b
f
(
x
)
d
x
{\displaystyle \int \limits _{a}^{b}f(x)\,\mathrm {d} x}
ist das bestimmte Integral der Funktion f nach [der Variablen] x [in den Grenzen] von a bis b. Es soll den Flächeninhalt zwischen Kurve und Achse wie in der Abb. oben S bezeichnen. Das (Integrations-) Differential dx gibt an, nach welcher Variablen integriert wird; es hat in der Regel nur symbolische Bedeutung.
Es handelt sich hierbei um ein Riemann-Integral (nach B. Riemann). Es gibt auch noch verallgemeinerte Integralbegriffe.
Die Integralrechnung beschäftigt sich mit der Berechnung solcher Integrale.
Um nun einem Integral systematisch "zu Fläche zu rücken", nähert man es durch sog. Ober- und Untersummen immer genauer an.
Gesucht ist der Flächeninhalt zwischen einer Normalparabel und der x-Achse zwischen x=0 und 1, also
∫
0
1
x
2
d
x
.
{\displaystyle \int _{0}^{1}x^{2}\,\mathrm {d} x.}
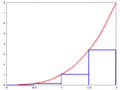
Die vierten Ober- und Untersummen graphisch dargestellt:
4. Untersumme
4. Obersumme
Die Flächen der Rechtecke lassen sich nun einfach berechnen, sodass wir eine obere und eine untere Schranke für den Flächeninhalt haben:
∫
0
1
x
2
d
x
{\displaystyle \int _{0}^{1}x^{2}\mathrm {d} x}
>
R
1
{\displaystyle >R_{1}\,}
+
R
2
{\displaystyle +R_{2}\,}
+
R
3
{\displaystyle +R_{3}\,}
+
R
4
{\displaystyle +R_{4}\,}
=
1
4
⋅
0
2
{\displaystyle ={\frac {1}{4}}\cdot 0^{2}}
+
1
4
⋅
(
1
4
)
2
{\displaystyle +{\frac {1}{4}}\cdot \left({\frac {1}{4}}\right)^{2}}
+
1
4
⋅
(
2
4
)
2
{\displaystyle +{\frac {1}{4}}\cdot \left({\frac {2}{4}}\right)^{2}}
+
1
4
⋅
(
3
4
)
2
,
denn jedes Rechteck ist
1
4
lang und so hoch
{\displaystyle +{\frac {1}{4}}\cdot \left({\frac {3}{4}}\right)^{2},\qquad {\text{denn jedes Rechteck ist }}{\tfrac {1}{4}}{\text{ lang und so hoch}}}
=
0,218
75
{\displaystyle =0{,}21875\,}
Analog lässt sich die Obersumme berechnen:
∫
0
1
x
2
d
x
{\displaystyle \int _{0}^{1}x^{2}\mathrm {d} x}
<
R
1
{\displaystyle <R_{1}\,}
+
R
2
{\displaystyle +R_{2}\,}
+
R
3
{\displaystyle +R_{3}\,}
+
R
4
{\displaystyle +R_{4}\,}
+
1
4
⋅
(
1
4
)
2
{\displaystyle +{\frac {1}{4}}\cdot \left({\frac {1}{4}}\right)^{2}}
+
1
4
⋅
(
2
4
)
2
{\displaystyle +{\frac {1}{4}}\cdot \left({\frac {2}{4}}\right)^{2}}
+
1
4
⋅
(
3
4
)
2
{\displaystyle +{\frac {1}{4}}\cdot \left({\frac {3}{4}}\right)^{2}}
+
1
4
⋅
(
4
4
)
2
{\displaystyle +{\frac {1}{4}}\cdot \left({\frac {4}{4}}\right)^{2}}
=
0,468
75
{\displaystyle =0{,}46875\,}
Damit gilt:
0,218
75
<
∫
0
1
x
2
d
x
<
0,468
75
{\displaystyle 0{,}21875<\int _{0}^{1}x^{2}\mathrm {d} x<0{,}46875}
Hier erhält man allgemein für die n-te Untersumme
U
n
{\displaystyle U_{n}}
U
n
=
1
n
⋅
0
2
+
1
n
⋅
(
1
n
)
2
+
1
n
(
2
n
)
2
+
1
n
⋅
(
3
n
)
2
+
⋯
+
1
n
⋅
(
n
−
1
n
)
2
{\displaystyle U_{n}={\frac {1}{n}}\cdot 0^{2}+{\frac {1}{n}}\cdot \left({\frac {1}{n}}\right)^{2}+{\frac {1}{n}}\left({\frac {2}{n}}\right)^{2}+{\frac {1}{n}}\cdot \left({\frac {3}{n}}\right)^{2}+\cdots +{\frac {1}{n}}\cdot \left({\frac {n-1}{n}}\right)^{2}}
und die n-te Obersumme
O
n
{\displaystyle O_{n}}
O
n
=
1
n
⋅
(
1
n
)
2
+
1
n
(
2
n
)
2
+
1
n
⋅
(
3
n
)
2
+
⋯
+
1
n
⋅
(
n
n
)
2
{\displaystyle O_{n}={\frac {1}{n}}\cdot \left({\frac {1}{n}}\right)^{2}+{\frac {1}{n}}\left({\frac {2}{n}}\right)^{2}+{\frac {1}{n}}\cdot \left({\frac {3}{n}}\right)^{2}+\cdots +{\frac {1}{n}}\cdot \left({\frac {n}{n}}\right)^{2}}
Um nun zu dem exakten Wert des Integrals zu kommen, definiert man formal
∫
1
2
x
2
d
x
=
lim
n
→
∞
U
n
=
lim
n
→
∞
O
n
{\displaystyle \int _{1}^{2}x^{2}\mathrm {d} x=\lim _{n\to \infty }U_{n}=\lim _{n\to \infty }O_{n}}
falls diese gleich sind.
Wir führen dies einmal für die Obersummen durch:
O
n
=
1
n
⋅
(
1
n
)
2
+
1
n
(
2
n
)
2
+
1
n
⋅
(
3
n
)
2
+
⋯
+
1
n
⋅
(
n
n
)
2
|
klammere
1
n
aus, quadriere die
B
r
u
¨
c
h
e
{\displaystyle \left.O_{n}={\frac {1}{n}}\cdot \left({\frac {1}{n}}\right)^{2}+{\frac {1}{n}}\left({\frac {2}{n}}\right)^{2}+{\frac {1}{n}}\cdot \left({\frac {3}{n}}\right)^{2}+\cdots +{\frac {1}{n}}\cdot \left({\frac {n}{n}}\right)^{2}\qquad \right|{\text{ klammere }}{\tfrac {1}{n}}{\text{ aus, quadriere die }}\mathrm {Br{\ddot {u}}che} }
=
1
n
[
1
2
n
2
+
2
2
n
2
+
3
2
n
2
+
⋯
n
2
n
2
]
|
klammere
1
n
2
aus
{\displaystyle =\left.{\frac {1}{n}}\left[{\frac {1^{2}}{n^{2}}}+{\frac {2^{2}}{n^{2}}}+{\frac {3^{2}}{n^{2}}}+\cdots {\frac {n^{2}}{n^{2}}}\right]\qquad \qquad \qquad \right|{\text{ klammere }}{\tfrac {1}{n^{2}}}{\text{ aus}}}
=
1
n
[
1
n
2
⋅
(
1
2
+
2
2
+
3
2
+
⋯
+
n
2
)
]
mit
1
2
+
2
2
+
3
2
+
.
.
.
+
n
2
=
1
6
n
(
n
+
1
)
(
2
n
+
1
)
{\displaystyle ={\frac {1}{n}}\left[{\frac {1}{n^{2}}}\cdot \left(1^{2}+2^{2}+3^{2}+\cdots +n^{2}\right)\right]\qquad {\text{ mit }}1^{2}+2^{2}+3^{2}+...+n^{2}={\tfrac {1}{6}}n(n+1)(2n+1)}
=
1
n
[
n
(
n
+
1
)
(
2
n
+
1
)
6
n
2
]
|
Klammer weg,
1
n
hebt sich auf
{\displaystyle =\left.{\frac {1}{n}}\left[{\frac {n(n+1)(2n+1)}{6n^{2}}}\right]\qquad \qquad \qquad \right|{\text{ Klammer weg, }}{\tfrac {1}{n}}{\text{ hebt sich auf}}}
=
(
n
+
1
)
(
2
n
+
1
)
6
n
2
{\displaystyle ={\frac {(n+1)(2n+1)}{6n^{2}}}}
=
2
n
2
+
3
n
+
1
6
n
2
{\displaystyle ={\frac {2n^{2}+3n+1}{6n^{2}}}}
=
2
n
2
6
n
2
+
3
n
6
n
2
+
1
6
n
2
{\displaystyle ={\frac {2n^{2}}{6n^{2}}}+{\frac {3n}{6n^{2}}}+{\frac {1}{6n^{2}}}}
=
1
3
+
1
2
n
+
1
6
n
2
{\displaystyle ={\frac {1}{3}}+{\frac {1}{2n}}+{\frac {1}{6n^{2}}}}
Davon lässt sich nun der Grenzwert bilden:
lim
n
→
∞
O
n
=
lim
n
→
∞
1
3
+
1
2
n
+
1
6
n
2
=
1
3
.
{\displaystyle \lim _{n\to \infty }O_{n}=\lim _{n\to \infty }{\frac {1}{3}}+{\frac {1}{2n}}+{\frac {1}{6n^{2}}}={\frac {1}{3}}.}
Für die Untersummen erhält man
U
n
=
O
n
−
1
n
⋅
1
2
{\displaystyle U_{n}=O_{n}-{\frac {1}{n}}\cdot 1^{2}}
und damit analog ebenfalls
lim
n
→
∞
U
n
=
1
3
.
{\displaystyle \lim _{n\to \infty }U_{n}={\frac {1}{3}}.}
Damit ist:
∫
0
1
x
2
d
x
=
1
3
.
{\displaystyle \int \limits _{0}^{1}x^{2}\mathrm {d} x={\frac {1}{3}}.}
∫
a
b
f
(
x
)
d
x
=
lim
n
→
∞
U
n
(
x
)
=
lim
n
→
∞
∑
i
=
1
n
f
(
x
i
−
1
)
Δ
x
i
=
lim
n
→
∞
O
n
(
x
)
=
lim
n
→
∞
∑
i
=
1
n
f
(
x
i
)
Δ
x
i
{\displaystyle \int \limits _{a}^{b}f(x)\mathrm {d} x=\lim _{n\to \infty }U_{n}(x)=\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i-1})\Delta x_{i}=\lim _{n\to \infty }O_{n}(x)=\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i})\Delta x_{i}}
heißt bestimmtes Integral von f über [a,b]. Die
Δ
x
{\displaystyle \Delta _{x}}
Δ
x
=
b
−
a
n
{\displaystyle \Delta x={\tfrac {b-a}{n}}}
Man nennt
f
{\displaystyle f}
Integrand und
a
,
b
{\displaystyle a,b}
Integrationsgrenze .
Eigenschaften des bestimmten Integrals [ Bearbeiten ] Sind die Integrationsgrenzen gleich, erhält man eine „flächenlose“ Strecke:
∫
a
a
f
(
x
)
d
x
=
0
{\displaystyle \int \limits _{a}^{a}f(x)\mathrm {d} x=0}
Intervalladditivität (
a
≤
b
≤
c
{\displaystyle a\leq b\leq c}
∫
a
c
f
(
x
)
d
x
=
∫
a
b
f
(
x
)
d
x
+
∫
b
c
f
(
x
)
d
x
{\displaystyle \int \limits _{a}^{c}f(x)\mathrm {d} x=\int \limits _{a}^{b}f(x)\mathrm {d} x+\int \limits _{b}^{c}f(x)\mathrm {d} x}
Durch Verdopplung der Funktion werden alle Rechtecke doppelt so groß, allgemein:
∫
a
b
k
⋅
f
(
x
)
d
x
=
k
⋅
∫
a
b
f
(
x
)
d
x
{\displaystyle \int \limits _{a}^{b}k\cdot f(x)\mathrm {d} x=k\cdot \int \limits _{a}^{b}f(x)\mathrm {d} x}
Addition der Funktionen ergibt Addition der Integralwerte:
∫
a
b
(
f
(
x
)
+
g
(
x
)
)
d
x
=
∫
a
b
f
(
x
)
d
x
+
∫
a
b
g
(
x
)
d
x
{\displaystyle \int \limits _{a}^{b}(f(x)+g(x))\mathrm {d} x=\int \limits _{a}^{b}f(x)\mathrm {d} x+\int \limits _{a}^{b}g(x)\mathrm {d} x}
Bestimmung eines Integrals nach dem Hauptsatz der Analysis [ Bearbeiten ] Der Hauptsatz der Differential- und Integralrechnung führt die Berechnung eines bestimmten Integrals zurück auf das Finden der Stammfunktion von
f
{\displaystyle f}
F
(
x
)
{\displaystyle F(x)}
F
′
(
x
)
{\displaystyle F'(x)}
f
{\displaystyle f}
∫
a
b
f
(
x
)
d
x
=
F
(
b
)
−
F
(
a
)
:=
F
(
x
)
|
a
b
{\displaystyle \int \limits _{a}^{b}f(x)\mathrm {d} x=F(b)-F(a):=F(x){\Big |}_{a}^{b}}
wobei
F
(
x
)
=
∫
f
(
x
)
d
x
{\displaystyle F(x)=\int f(x)\mathrm {d} x}
[ Bearbeiten ] An dieser Stelle sei noch ein Beispiel für eine nicht (in diesem, riemannschen Sinne) integrierbare Funktion gegeben:
f
(
x
)
=
{
1
wenn
x
irrational
0
wenn
x
rational
{\displaystyle f(x)={\begin{cases}1&{\text{ wenn }}x{\text{ irrational}}\\0&{\text{ wenn }}x{\text{ rational}}\end{cases}}}
In jedem Intervall ist der kleinste Wert 0, da in jedem Intervall eine rationale Zahl liegt; damit ist jede Untersumme 0. Gleichzeitig ist in jedem Intervall der größte Wert 1, womit jede Obersumme 1 ist.
Wie die Mathematikweisheit "Das Differenzieren ist ein Handwerk, das Integrieren eine Kunst" bereits feststellt, gibt es kein allgemeines Verfahren zur (exakten) Bestimmung eines Integrals, also insbesondere der Stammfunktion. Es gibt Verfahren, wie etwa die partielle Integration oder Substitution, mit denen man – allerdings auch nur mit einem guten "mathematischen Auge" – zum Integral findet. Genaueres siehe Analysis: Integrationsregeln, Stammfunktion .
Weitere Integralbegriffe sind etwa das Lebesgue-Integral und das Stieltjes-Integral.
Hauptartikel Analysis: Integralrechnung: Anwendungen 

























![{\displaystyle =\left.{\frac {1}{n}}\left[{\frac {1^{2}}{n^{2}}}+{\frac {2^{2}}{n^{2}}}+{\frac {3^{2}}{n^{2}}}+\cdots {\frac {n^{2}}{n^{2}}}\right]\qquad \qquad \qquad \right|{\text{ klammere }}{\tfrac {1}{n^{2}}}{\text{ aus}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d75f8032bf8a9893e1a74fdb49a526fdc827bf41)
![{\displaystyle ={\frac {1}{n}}\left[{\frac {1}{n^{2}}}\cdot \left(1^{2}+2^{2}+3^{2}+\cdots +n^{2}\right)\right]\qquad {\text{ mit }}1^{2}+2^{2}+3^{2}+...+n^{2}={\tfrac {1}{6}}n(n+1)(2n+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee282267f30ae8c45f0c72e1b0698543b022ac19)
![{\displaystyle =\left.{\frac {1}{n}}\left[{\frac {n(n+1)(2n+1)}{6n^{2}}}\right]\qquad \qquad \qquad \right|{\text{ Klammer weg, }}{\tfrac {1}{n}}{\text{ hebt sich auf}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfe3dbff20d8271403da629eac6a4945bf4422cf)






















