Analysis: Einführung in die Funktionentheorie und Potenzfunktionen
In der Analysis wird häufig mit Funktionen gearbeitet. Was eine Funktion ist, lässt sich am besten erklären mit einigen Beispielen.
1. Die Zeit, die benötigt wird, um mit einem bestimmten elektrischen Wasserkocher (kaltes) Wasser zum Kochen zu bringen, ist abhängig von der Wassermenge. Statt 'ist abhängig von', kann man auch sagen: 'ist eine Funktion von'. Nennt man die benötigte Zeit y und die Wassermenge x, dann notiert man:
und sagt: y ist eine Funktion von x. Die Funktion ist in diesem Fall eine sehr einfache, namentlich
denn die Zeit ist proportional zur Wassermenge. Misst man die Zeit in Minuten und die Wassermenge in Liter, dann gilt für einen Wasserkocher mit a=7 (Liter pro Minute) :
Man kann nun z.B. berechnen, dass es 3,5 Minuten dauert, um einen halben Liter Wasser zum Kochen zu bringen, und 10,5 Minuten für 1,5 Liter.
2. Der Benzinverbrauch eines bestimmten Fahrzeugs wird gemessen während einen standardisierten Fahrt. Der Verbrauch y ist eine Funktion (ist abhängig) von der Geschwindigkeit x:
Bekannt ist, dass der Verbrauch mit wachsender Geschwindigkeit überproportional ansteigt. Eine Möglichkeit für die Funktion wäre:
Misst man den Verbrauch in Liter pro 100 Km, und der Geschwindigkeit in Kilometern pro Stunde, dann gilt für ein bestimmtes Auto: Damit kann man berechnen, dass bei einer Geschwindigkeit von km/Stunde, der Verbrauch gleich
- Liter pro 100 Km ist.
3. Bei der Geburt ihres Enkelkindes haben die Großeltern ein Sparkonto eröffnet mit 1000 Euro Startguthaben. Jeden Monat überweisen sie 50 Euro aufs Konto. Wie viel nach einiger Zeit auf dem Konto steht, hängt von dem Zeitverlauf ab. Der Saldo y ist eine Funktion der verstrichenen Zeit x:
worin x die Anzahl der vergangen Monate ist. Nach 70 Monaten befindet sich auf dem Konto ein Betrag von
4. Einige Mitarbeiter einer Firma nehmen sich vor, zusammen mit einem gemeinsamen Auto zur Arbeit zu fahren. Es gibt ein Angebot eines Gebrauchtwagens für 3600 Euro, den sie kaufen möchten. Weil sie sich die Kosten teilen, hängt der Betrag y, den jeder einzeln bezahlen muss, von der Anzahl x der Teilnehmer ab.
definiert für x = 1, 2, 3, 4, und 5. Der Betrag y hat nur die möglichen Werte 3600, 1800, 1200, 900 und 720 Euro.
5. Es muss bei eine Funktion nicht unbedingt um Zahlen handeln. Der Preis der Artikel im Supermarkt y ist zwar eine Zahl, aber er ist eine Funktion der Artikel x. Jeder Mensch hat einen Vater. Der Vater y einer Person ist eine Funktion der Person x.
| Eine Funktion ist ein Vorschrift, wie man den Funktionswert bestimmen kann anhand des Wertes des Arguments. Das Argument wird auch x-Wert genannt und der Funktionswert y-Wert. Die Menge aller x-Werte heisst Definitionsbereich, die Zusammenfassung der y-Werte Wertebereich. |
Formell heisst es:
| Eine Funktion ist eine eindeutige Zuordnung, wobei ein x-Wert genau einem y-Wert zugeordnet ist. |
Lineare Funktionen
[Bearbeiten]Darstellung linearer Funktionen
[Bearbeiten]Errechnen von Argumenten und Darstellung von Graphen anhand von Wertetabellen
[Bearbeiten]| Eine lineare Funktion ist eine eindeutige Zuordnung der Form y=mx+n, wobei n der Achsenabschnitt und m die Steigung der Funktionsgeraden ist. |
Beispiele:

1. Gegeben ist die lineare Funktion y=x
Um Werte zu ermitteln erstellt man eine Wertetabelle. Hierbei setzt man für x = beliebige Werte innerhalb des Definitionsbereiches ein und errechnet y. So erhält man die Tabelle:
| x | 0 | 1 | 2 | 3 | 4 | 5 | ... |
| y | 0 | 1 | 2 | 3 | 4 | 5 | ... |
Nun kann man diese erhaltenen geordneten Zahlenpaare in ein kartesisches Koordinatensystem einzeichnen. Es entsteht ein linearer Graph. Lineare Graphen sind (in kartesischen Koordinatensystemen) immer Geraden, d. h. sie haben weder Anfangs- noch Endpunkt, wenn der Wertebereich nicht eingeschränkt wurde. Bei Polarkoordinaten trifft dies nicht zu!

2. Gegeben ist die lineare Funktion y=4x+1
Um eine Wertetabelle anzufertigen, werden auch hier für x nacheinander Werte des Definitionsbereiches eingesetzt. Je kleiner Δx, desto mehr y-Werte erhält man, was für nichtlineare Funktionen ein genaueres Zeichnen des Funktionsgraphen ermöglicht.
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 1 | 5 | 9 | 13 | 17 | 21 |
Bei einer linearen Funktionsgleichung reicht es aus, zwei y-Werte zu errechnen und eine Gerade dadurch zu zeichnen.
Darstellung von Graphen anhand der Funktionsgleichung
[Bearbeiten]
Wenn man eine Funktionsgleichung gegeben hat, muss man nicht erst alle y-Werte ausrechnen, um einen Graphen zeichnen zu können. Nur anhand der gegebenen Glieder des Funktionsterms kann man den Graph ableiten. Da lineare Funktionen die Form y=mx+n haben geht man wie folgt vor:
- Man geht vom Nullpunkt aus n „Schritte“ auf der y-Achse entlang und markiert sich den Punkt.
- Man geht vom Nullpunkt aus einen „Schritt“ nach rechts. Das macht man immer!
- Man geht m „Schritte“ auf der gedachten Achse x=1 entlang (das ist eine vertikale Linie durch die Stelle x=1) und markiert sich den Punkt.
- Verbinde beide markierte Punkte und du hast den zugehörigen Graphen der Funktion erhalten.
Bei der Funktion y=2x+3 sieht das dann so aus:
- Gehe 3 Einheiten an der y-Achse nach oben. Mache den ersten Punkt.
- Eine Einheit nach rechts,
- und weitere 2 Einheiten nach oben. Mache hier den zweiten Punkt.
- Man verbindet die beiden erhaltenen Punkte.
Beispiele:
1. Gegeben ist die Funktionsgleichung y=-5x+3. Zeichne den Graphen!
Man kann durch diese Form m und n ableiten. Daraus folgt: m=-5 und n=3. Somit kann man wie oben beschrieben vorgehen und den Graphen einzeichnen.

2. Gegeben ist der Term 3x-4y=-5. Zeichne den Graphen!
Hier ist nur ein Term mit zwei Variablen gegeben, d. h. es muss nach einer Variablen umgestellt werden. Um die Form y=mx+n zu erhalten, muss man y von den anderen Gliedern isolieren.
Nun haben wir y erstmal isoliert. Hier reicht das aber noch nicht, denn wir müssen den Term noch umstellen, damit man die Form y=mx+n erhält.
Anschließend leitet man wieder die Glieder n und m ab und zeichnet den Graphen ein.
Eigenschaften linearer Funktionen
[Bearbeiten]Um lineare Funktionen charakterisieren zu können, betrachtet man verschiedene Eigenschaften. Wenn man diese Eigenschaften auflistet, nennt man das eine Kurvendiskussion.

Beispiel: Gegeben sei die Funktion y=2,5x+1,5
Definitions- und Wertebereich
Als erstes betrachtet man immer den Gültigkeitsbereich (Zahlenbereich) der Argumente und der Funktionswerte.
- Definitionsbereich: x ∈ R (sprich: x ist Element der Reellen Zahlen)
- Wertebereich: y ∈ R (sprich: y ist Element der Reellen Zahlen)
Bei Funktionen höheren Grades können die y- und x-Werte auch begrenzt sein.
Monotonie
Man unterscheidet bei der Monotonie linearer Funktionen zwischen (streng) monoton steigend und (streng) monoton fallend. Man legt fest:
- Ein Graph ist monoton steigend, wenn die den Argumenten zugehörigen Funktionswerte größer werden.
- Streng monoton steigend nennt man einen Graphen, wenn aus
- x1<x2 folgt, dass y1<y2 ist
- für alle x, x ∈ R
- Ein Graph ist monoton fallend, wenn die den Argumenten zugehörigen Funktionswerte kleiner werden.
- Analog folgt:
- Streng monoton fallend nennt man einen Graphen, wenn aus
- x1<x2 folgt, dass y1>y2 ist
- für alle x, x ∈ R
Somit ist der hier "diskutierte" und abgebildete Graph (streng) monoton steigend, man schreibt wie folgt:
- für alle x, x ∈ R, ist der Graph (streng) monoton steigend.
Nullstelle
| Die Nullstelle ist die Abszisse des Schnittpunktes des Graphen mit der x-Achse. |
Jede lineare Funktion der Form (n>0)x+m besitzt genau eine Nullstelle. Kurz kann man sagen, die Nullstelle ist der Schnittpunkt des Graphen mit der x-Achse. Wenn man den Graphen darstellt, kann man häufig die Nullstelle anhand der Abbildung erahnen. Bei Funktionen, wo der Graph nicht genau eine Einheit schneidet, ist es oft schwierig die Nullstelle exakt zu bestimmen. Man kann diese aber mit der Funktionsgleichung errechnen:
Da die Nullstelle die Abszisse des Schnittpunktes mit der x-Achse ist, können wir den Schnittpunkt mit den Koordinaten (x;0) beschreiben, deswegen setzen wir für y=0 und für x=x0ein.
Da wir nur die Abszisse suchen, wird x0 allein geschrieben.
Schnittpunkte mit der y-Achse
Um den Schnittpunkt (0;y0) mit der y-Achse zu ermitteln können, gehen wir wie bei der Nullstelle vor! Dabei ersetzen wir aber x durch 0 und errechnen y0.
- Py(0;1,5)
Hier erhalten wir zum Schluss den Schnittpunkt, somit wird er in der Form Py(0;y) dar.
Quadratische Funktionen
[Bearbeiten]| Eine Funktion mit der Gleichung y=ax2+bx+c mit R als Definitionsbereich nennt man eine quadratische Funktion. |
- Aufgabe
- Die Funktion y=x2 ist im Intervall -2,5 <x<2,5 grafisch darzustellen. Lege dafür eine Wertetabelle an!
| x | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 |
| y (=x2) | 6,25 | 4 | 2,25 | 1 | 0,25 | 0 | 0,25 | 1 | 2,25 | 4 | 6,25 |
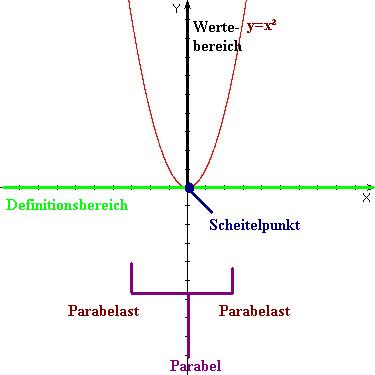
Kurvendiskussion der quadratischen Funktion y=x²
- Definitionsbereich: x є R
- Wertebereich: y є R, y>0
- Der Wertebereich muss eingeschränkt werden, da es keine negativen Funktionswerte gibt.
- Monotonie: für alle x<0 monoton fallend und für alle x>0 monoton steigend
- Nullstelle(n): x0=0
- Schnittpunkt mit der y-Achse: Py(0;0)
- Scheitelpunkt: S(0;0)
- größter und kleinster Funktionswert
- ymin=0
- ymax=→ ∞ (sprich: gegen unendlich)
- Symmetrieachse: y-Achse
- Öffnung: nach oben
- Verlauf: vom II. zum I. Quadranten
Die Funktion y=x² ist die Kurzform der Form y=ax²+bx+c=. Um deutlich zu machen, dass diese Gleichung wirklich eine typische quadratische Funkion darstellt, kann man auch schreiben: 1x²+0x+0. Man kann a und b noch direkt charakterisieren. „a“ stellt die Lage der Parabeläste und „b“ die Verschiebung auf der y-Achse dar.
Formen quadratischer Funktionen
[Bearbeiten]Quadratische Funktionen der Form y=(x-d)²
[Bearbeiten]
Beispiel:
Gegeben sind die Funkionen y=x², y=(x-3)² und y=(x+2)². Lege eine Wertetabelle an, zeichne die Graphen in ein Koordinatensystem und triff eine Aussage über die Scheitelpunkte der Graphen.
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y=x² | 4 | 1 | 0 | 1 | 4 | 9 |
| y=(x-3)² | 25 | 16 | 9 | 4 | 1 | 0 |
| y=(x+2)² | 0 | 1 | 4 | 9 | 16 | 25 |
Beim Einzeichnen muss man beachten, dass der Graph immer um d an der x-Achse verschoben wird. So kann man folgende Scheitelpunkte ablesen:
- y=x² --> S(0;0)
- y=(x-3)² --> S(3;0)
- y=(x+2)² --> S(-2;0)
Anhand dieser Werte kann man die Scheitelpunktkoordinaten verallgemeinern:
| Wenn y=(x-d)², dann hat der Scheitelpunkt die Koordinaten S(d;0). |

- Aufgabe
- Führe eine geeignete Kurvendiskussion für die Gleichung y=(x+4)² durch und stelle den Graphen in einem Koordinatensystem dar.
- Definitionsbereich: x є R
- Wertebereich: y є R, y>0
- Monotonie: für x<-4 monton fallend, für x>-4 monoton steigend
- Nullstelle(n): x1/2=-4
- Schnittpunkt mit der y-Achse: Py(0;16)
- Scheitelpunkt: S(-4;0)
- ymin=0; ymax= → ∞
Quadratische Funktionen der Form y=x²+px+q
[Bearbeiten]Man kann mit der Binomischen Formel Gleichungen der Form y=(x+d)² in Gleichungen der Form x²+px+q (Normalform) umformen.
(a+b)² = a²+2ab+b² = x²+px+q
- Aufgabe
- Gegeben sind die Funktionen y1=(x-2)², y2=(x-2)²-1,5 und y3=(x-2)²+1,5. Zeiche die Gleichungen in ein Koordinatensystem ein, forme sie in die Normalform um, gib die Scheitelpunkte an, verallgemeinere eine Scheitelpunktform, errechne die Nullstellen und lege eine Regel für die Feststellung deren Anzahl fest!

- Die zweite und dritte Funktion ist in der Form y=(x-d)²+e dargestellt, diese nennt man auch Scheitelpunktform. Man formt sie mit Hilfe der binomischen Formel zur Normalform um und addiert b mit e. So entstehen folgende Lösungen für die Normalform:
- y1=(x-2)² --> y1=x²-4x+4
- y2=(x-2)²-1,5 --> y2=x²-4x+2,5
- y3=(x-2)²+1,5 --> y3=x²-4x+5,5
- Da wir schon die Scheitelpunktform gegeben haben, ist es leicht diese zu bestimmen. Es gilt:
Wenn y=(x-d)²+e, dann hat der Scheitelpunkt die Koordinaten S(d;e).
- So lauten die Scheitelpunkte:
- S1(2;0)
- S2(2;-1,5)
- S3(2;1,5)
- Die Nullstellen sind bei quadratischen Funktionen nicht so einfach zu berechnen. Eine quadratische Funktion kann abhängig von e, eine, zwei oder keine Nullstelle besitzen. Um die Nullstellen schnell feststellen zu können, benötigt man die Normalform der quadratischen Gleichung. Vorab kann man durch die Diskriminante die Anzahl der Nullstellen bestimmen, mit folgender Gleichung: D=(p/2)²-q.
- Die Gleichung für die Errechnung der Nullstellen lautet wie folgt:
x1/2= -(p/2)± √D
- Wir ermitteln zuerst die Diskriminanten und errechnen anschließend die Nullstellen.
- Für die Gleichung y1=x²-4x+4
- D=(p/2)²-q
- D=(-4/2)²-4
- D=0 --> eine Nullstelle
- x1= -(-4/2)± √0
- x1=2
- L={2}
- Für die Gleichung y2=x²-4x+2,5
- D=(p/2)²-q
- D=(-4/2)²-2,5
- D=2,5 --> zwei Nullstellen
- x1/2= -(-4/2)± √2,5
- x1≈3,58
- x2≈0,42
- L≈{0,42;3,58}
- Für die Gleichung y3=x²-4x+5,5
- D=(p/2)²-q
- D=(-4/2)²-5,5
- D=-1,5 --> keine Nullstelle, da die Wurzel aus negativen Zahlen nicht definiert ist.
- L={}
- Für die Gleichung y1=x²-4x+4
- Durch diese Beispielrechnungen kann man nun folgende Regeln für die Feststellung der Nullstellen mit Hilfe der Diskriminante treffen:
- Wenn D<0, dann keine Nullstelle.
- Wenn D=0, dann eine Nullstelle.
- Wenn D>0, dann zwei Nullstellen.
- Weitere Ableitungen und Festlegungen im Zusammenhang der Aufgabe:
- Mit Hilfe des Wertes von "e" kann man auch die Anzahl der Nullstellen bestimmen, sodass gilt:
- Wenn e>0, dann keine Nullstellen.
- Wenn e=0, dann eine Nullstelle.
- Wenn e<0, dann zwei Nullstellen.
- Somt kann man auf das Verhältnis zwischen "e" und "D" schließen: e=-D
- Ableitung weiterer Scheitelpunktkoordinaten durch "D" und "e": S((-p/2);(-(p/2)²+q))
- Mit Hilfe des Wertes von "e" kann man auch die Anzahl der Nullstellen bestimmen, sodass gilt:
Quadratische Gleichungssysteme
[Bearbeiten]Begriff der quadratischen Gleichung
[Bearbeiten]| Gleichungen, die man auf die Form ax²+bx+c=0 (a≠0) zurückführen kann, heißen quadratische Gleichungen. Man nennt ax² das quadratische Glied, bx das lineare Glied und c das absolute Glied. Eine quadratische Gleichung besitzt keine, eine oder zwei Lösungen. |
Grafisches Lösen quadratischer Gleichungssysteme
[Bearbeiten]Man kann quadratische Gleichungssysteme grafisch mit Hilfe der Normalparabel (y=x²) und einer Geraden lösen.

Beispiel: Gegeben ist die Gleichung x²-2x-5=0. Entwickle ein Gleichungssystem und löse es grafisch!
-->Man teilt diese Gleichung in eine lineare und eine quadratische Gleichung auf. So erhält man die folgenden beiden Gleichungen:
- y=x² (Normalparabel)
- y=2x+5 (Gerade, weil linear)
Nun zeichnet man die beiden Graphen in ein Koordinatensystem ein und liest die Schnittpunkte der Normalparabel mit der Geraden ab. Die x-Werte der erhaltenen geordneten Zahlenpaare sind die Lösungen der Gleichung.
L={-1,5;3,4}
Rechnerisches Lösen quadratischer Gleichungen
[Bearbeiten]Beim Lösen quadratischer Gleichungen unterscheidet man drei Fälle.
- Lösen durch Wurzelziehen
- Lösen durch quadratische Ergänzung
- Lösen mit Hilfe der Lösungsformel
Zu jedem Fall wird ein Beispiel aufgelistet.
Lösen durch Wurzelziehen
x² = 7 I√
|
Lösen durch quadratische Ergänzung
x²+6x=0 IRückführung auf eine binomische Formel mit: +(6/2)²
|
Lösen mit Hilfe der Lösungsformel
x²-7x+6=0
|
Weitere Potenzfunktionen
[Bearbeiten]Potenzfunktionen mit negativen ganzzahligen Exponenten
[Bearbeiten]| Festlegung: y = x-n 2|n (2 ist Teiler von n, n ist also gerade) |
Aufgabe:Zeichne den Graphen der Funktion y = x-2 in ein Koordinatensystem ein. Lege dazu eine Wertetabelle an und führe anschließend eine Kurvendiskussion durch!
| x | -3 | -2 | -1 | -0,7 | -0,5 | 0 | 0,5 | 0,7 | 1 | 2 | 3 |
| y (=x-2) | 0,11 | 0,25 | 1 | 2,04 | 4 | n.d. | 4 | 2,04 | 1 | 0,25 | 0,11 |

Kurvendiskussion:
- Definitionsbereich: x є R; x ≠ 0
- Wertebereich: y є R; y>0
- Nullstellen: keine
- Schnittpunkte mit der y-Achse: keine
- Symmetrie: axialsymmetrisch zur y-Achse (y-Achse = Symmetrieachse)
- Monotonie:
- monoton steigend bei x<0
- monoton fallend bei x>0
- Verhalten im Unendlichen: asymptotisch, x-Achse und y-Achse sind Asymptoten
| Asymptoten sind Geraden, an die sich ein Graph anschmiegt. Asymptoten, die senkrecht zur x-Achse verlaufen, heißen auch Polgeraden. Die Stelle xp, in der die Polgerade die x-Achse schneidet, heißt Polstelle. |
| Festlegung: y = x-n 2 |
Aufgabe:Zeichne den Graphen der Funktion y = x-1 in ein Koordinatensystem ein. Lege dazu eine Wertetabelle an und führe anschließend eine Kurvendiskussion durch!
| x | -3 | -2 | -1 | -0,7 | -0,5 | 0 | 0,5 | 0,7 | 1 | 2 | 3 |
| y (=x-1) | -0,33 | -0,5 | -1 | -1,43 | -2 | n.d. | 2 | 1,43 | 1 | 0,5 | 0,33 |

Kurvendiskussion:
- Definitionsbereich: x є R; x ≠ 0
- Wertebereich: y є R; y ≠ 0
- Nullstellen: keine
- Schnittpunkte mit der y-Achse: keine
- Symmetrie: Punktsymmetrisch zum Ursprung 0
- Monotonie: Für alle x, außer x ≠ 0 monoton fallend.
- Verhalten im Unendlichen: asymptotisch, x-Achse und y-Achse sind Asymptoten
- Polstelle: xp=0
Potenzfunktionen mit gebrochenen Exponenten
[Bearbeiten]Auf Potenzfunktionen mit gebrochenen Exponenten hat ein Faktor k eine wichtige Auswirkung! Diese Potenzfunktionen haben die Bildungsvorschrift:
y = x1/n * k
| Wenn k > 1, dann wird der Graph zur y-Achse gestreckt. | Wenn 0 < k < 1, dann wird er Graph zur y-Achse gespiegelt. | Wenn k < 0, dann wird der Graph an der x-Achse gespiegelt. |
























