Benutzer:Stabacs/ Mengenlehre
Mengenlehre
[Bearbeiten]Geschichtliches
[Bearbeiten]Nach der Definition des Mathematikers Georg Cantor, der als Begründer der Mengenlehre gilt, ist eine Menge "eine Zusammenfassung von bestimmten wohl unterschiedenen Objekten der Anschauung oder des Denkens, welche die Elemente der Menge genannt werden, zu einem Ganzen".
Grundlage
[Bearbeiten]Die Definition von Cantor klingt heute etwas geschwollen. Es ist der sogenannte naive Standpunkt. Kurz gesagt ist eine Menge nach dem naiven Standpunkt eine Zusammenfassung unterscheidbarer Objekte wobei diese Objekte als Elemente bezeichnet werden. Das unterscheidbar in obigem Satz ist wichtig, weil in einer Menge kein Element doppelt vorkommen darf. So ein Objekt kann also zum Beispiel eine Zahl sein, ein Wort oder eben alles Andere, was voneinander unterscheidbar ist.
Angeben einer Menge
[Bearbeiten]Im Prinzip gibt es drei verschiedene Möglichkeiten eine Menge anzugeben:
- durch explizites Aufzählen aller Elemente, die in der Menge enthalten sind, und zwar in geschweiften Klammern. Zum Beispiel oder oder aber auch sowas wie . Die Elemente müssen bei so einer Aufzählung deutlich voneinander getrennt sein, deswegen verwendet man üblicherweise einen Beistrich zwischen den Elementen. Bei Zahlen ist aber (gerade wenn am Computer geschrieben wird) auch einfach nur ein Leerzeichen denkbar. Wenn mit der Hand geschrieben wird, sind Zwischenräume aber eher ungünstig, weil die meistens mit der Zeit so eng werden, dass nicht mehr wirklich gesagt werden kann, ob es noch eine Lücke ist oder nicht.
- durch implizites Aufzählen aller Elemente, welche in der Menge enthalten sind. Dabei werden charakteristische Elemente der Menge angegeben und dem Leser durch "..." angezeigt, dass es mehr als die angegeben Elemente gibt, die einer bestimmten Form genügen. So kann man zum Beispiel die Menge aller Primzahlen durch angeben.
- durch Definieren ihrer Eigenschaft, z.B. mittels Damit wären alle ganzen Zahlen größer als 50 in enthalten. Also
Um ein Element einer Menge anzuzeigen, schreibt man . Beispiele:
Die leere Menge
[Bearbeiten]ist die sogenannte leere Menge. Sie kann verschieden definiert werden. Hier ein paar Beispiele:
Relationen und Operationen auf Mengen
[Bearbeiten]| Symbol | Bedeutung | Beispiel |
|---|---|---|
| m ist Element von M. | ||
| M ist Teilmenge von N, das heißt, jedes Element von M ist auch Element von N. | und | |
| M ist echte Teilmenge von N, das heißt, M ist Teilmenge von N, aber nicht gleich N. | , aber nicht: | |
| Vereinigung von M und N: die Menge aller Elemente, die Element von M oder N (oder beiden) sind | ||
| Schnittmenge von M und N: die Menge aller Elemente, die Element sowohl von M als auch von N sind | ||
| Mengendifferenz von M und N: die Menge aller Elemente, die Element von M sind, aber nicht Element von N | ||
| Symmetrische Differenz von M und N: die Menge aller Elemente, die Element der Vereinung sind, aber nicht Element des Durchschnitts . Mit anderen Worten |
Zu einer gegebenen Menge heißt die Kardinalität von . Für eine endliche Menge mit Elementen gilt gerade .
Die Menge aller Teilmengen von wird als Potenzmenge bezeichnet:
Falls endlich, gilt .
Für zwei Mengen ist die Menge aller geordneten Paare mit und das kartesische Produkt von und . Man schreibt dies als
und es gilt: . Falls schreibt man auch abkürzend , bzw. allgemeiner .
Mengenlehre 2
[Bearbeiten]Beschreibungen von Mengen
[Bearbeiten]- Beschreibung durch Aufzählung der Elemente:
Die Elemente stehen in einer geschweiften Klammer und sind durch Komma getrennt.
Beispiel: M = { a, b, c }. - Beschreibung durch eine Eigenschaft:
Die Elemente werden durch ein Zeichen (meist ein Buchstabe) repräsentiert, nach einem Längsstrich wird die Eigenschaft angegeben: { x | x hat die Eigenschaft E }.
Beispiel: M = { t | t ist ein Wikibook }. - Ob Elemente zur Menge gehören oder nicht, wird wie folgt ausgedrückt:
x ∈ M anstelle von "x ist Element von M".
x ∉ M anstelle von "x ist nicht Element von M". - Gleichheit von Mengen: Die Mengen A und B sind genau dann gleich, A = B, wenn sie die gleichen Elemente haben.
M = N ⇔ Für alle x gilt: (x ∈ M ⇔ x ∈ N).
Der Doppelpfeil besagt, dass die vor und nach ihm angegebenen Aussagen äquivalent sind, d. h. sich gegenseitig implizieren (A ⇔ B steht also für "sowohl A⇒B als auch B⇒A ").
Teilmengen
[Bearbeiten]- Definition
- A ist Teilmenge (Untermenge) der Menge B ⇔ Für alle x gilt: (x ∈ A ⇒ x ∈ B).
Man nennt B dann eine Obermenge von A.
- Symbolisch wird dies durch A ⊂ B bzw. B ⊃ A ausgedrückt.
- Rechenregeln
- Seien M, N und O Mengen. Dann gilt:
- M ⊂ M
- M ⊂ N und N ⊂ M ⇒ M = N
- M ⊂ N und N ⊂ O ⇒ M ⊂ O
Beispiel - Beweis zu 2:
Vorausgesetzt sei M ⊂ N und N ⊂ M. Aus der obigen Definition von "Teilmenge" folgt sofort:
Falls x ∈ M, so gilt wegen M ⊂ N auch x ∈ N, und
falls x ∈ N, so gilt wegen N ⊂ M auch x ∈ M, also zusammengefasst:
"Wenn x ∈ M, so auch x ∈ N" und "wenn x ∈ N, so auch x ∈ M". Damit ist gezeigt:
"x ∈ M genau dann, wenn x ∈ N". Dies aber ist genau die Definition der Gleichheit von Mengen.
Vereinigung und Durchschnitt von Mengen
[Bearbeiten]- Definitionen
- A ∩ B := { x | x ∈ A und x ∈ B } heißt Durchschnitt der Mengen A und B.
A ∪ B := { x | x ∈ A oder x ∈ B } heißt Vereinigung der Mengen A und B.
Das "Oder" wird bei der Vereinigung im Sinne eines nicht ausschließenden Oder (lat.: vel - daher auch das Zeichen ) gebraucht, d. h. es muss mindestens eine der beiden Aussagen zutreffen, evtl. können auch beide zutreffen.
Beispiel: { A, B, C, D } ∪ { B, D, F, G } = { A, B, C, D, F, G }.
Vielleicht ist dir das Zeichen ":=" aufgefallen. Es soll bedeuten, dass hier die Gleicheit nach Definition gilt und nicht etwa errechnet oder bewiesen wurde.
Leere Mengen, disjunkte Mengen
[Bearbeiten]- Definition
- Die Menge, die keine Elemente enthält, heißt leere Menge. Symbol: .
In der Mathematik betrachtet man formal auch die "Zusammenfassung von nichts" als Menge! Das mag seltsam anmuten, hat aber etwas damit zu tun, wie in der Logik Subjunktion bzw. Implikation festgelegt sind. Danach hat man jetzt ⊂ M für alle Mengen M.
- Definition
- Zwei Mengen A und B, für die gilt A ∩ B = , heißen disjunkt (punktfremd)
Verallgemeinerte Definition von Vereinigung und Durchschnitt
[Bearbeiten]Um Durchschnitt und Vereinigung einer größeren Anzahl (sogar unendlich vieler) Mengen darstellen zu können, lässt man in den folgenden Definitionen beliebige Mengen als Indexmengen zu:
- Definitionen
- I sei eine nicht-leere Menge, und für jedes i ∈ I sei eine Menge gegeben. Dann ist
- a) der (verallgemeinerte) Durchschnitt der Mengen über alle i ∈ I definiert als
.
- b) die (verallgemeinerte) Vereinigung der Mengen über alle i ∈ I definiert als
.
Mit diesen so definierten Verallgemeinerungen lassen sich jetzt z. B. folgende Sachverhalte prägnant darstellen:
Für alle sei . Dann gilt: und .
An dieser Stelle wird erstmals in diesem Buch das Symbol für die Menge der natürlichen Zahlen verwendet. Diese Zahlen werden später im Kapitel Natürliche Zahlen ausführlich besprochen.
Differenz von Mengen, Komplement
[Bearbeiten]Eine andere Möglichkeit, neue Mengen zu erzeugen, bietet die Wegnahme von Elementen aus einer Menge.
- Definition
- A\B := { x | x ∈ A und x ∉ B }
heißt die Differenz der Mengen A und B.
Falls B ⊂ A gegeben ist, so liegt damit automatisch eine weitere Menge fest, nämlich die Menge derjenigen Elemente von A, die nicht zu B gehören. Hierzu folgende
- Definition
- Ist B ⊂ A, so heißt A\B das Komplement von B bezüglich A.
Potenzmenge
[Bearbeiten]Man kann auch Mengen wieder als Elemente auffassen und sie zu einer neuen "Menge von Mengen" zusammenfassen. Diese erhält dann einen eigenen Namen.
- Definition
- Es sei R eine Menge. Dann nennt man
die Potenzmenge von R.
Zwei Beispiele sollen die Definition verdeutlichen:
; die Potenzmenge einer Menge ist also stets nicht-leer! Sie enthält ja mindestens die leere Menge als Element.
.
Eine Teilmenge einer Potenzmenge nennt man auch Mengensystem oder Mengenfamilie.
Relationen
[Bearbeiten]- Paarmengen und kartesisches Produkt (Kreuzprodukt)
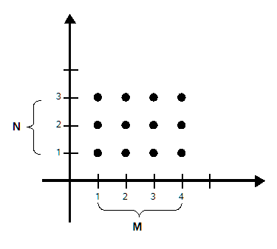
Wie allgemein bekannt lässt sich die Lage eines Punktes in der Ebene durch zwei Zahlen beschreiben. Dazu benutzt man ein rechtwinkliges (kartesisches) Koordinatensystem mit einer x-Achse und y-Achse, die senkrecht aufeinander stehen. Bezeichnet man beispielsweise mit x1 den Abstand eines Punktes P1 von der y-Achse (dieser ist negativ, wenn P1 links der Y-Achse liegt) und mit y1 man den Abstand eines Punktes P1 von der x-Achse (dieser ist negativ, wenn P1 unterhalb der der X-Achse liegt), so wird durch das Zahlenpaar (x1, y1) die Lage des Punktes im Koordinatensystem beschrieben. Bei dem Zahlenpaar (x1, y1) ist die Reihenfolge wesentlich. So beschreiben beispielsweise die Zahlenpaare (1,2) und (2,1) unterschiedliche Punkte im Koordinatensystem, es gilt also (1,2) ≠ (2,1).
Diese Paarbildung wird mit den folgenden Definitionen auf allgemeine Mengen erweitert:
- Definitionen
Sind M und N Mengen und ist x∈M und y∈N
- geordnetes Paar:
(x,y) heißt geordnetes Paar. - Gleichheit von geordneten Paaren
Zwei geordnete Paare "(x1, y1) und (x2, y2) sind gleich" ⇔ "x1 = x2 und y1 = y2" - Paarmenge
Die Paarmenge (kartesisches Produkt, Kreuzprodukt) von M und N wird wie folgt definiert:
M×N := { (x,y) | x ∈ M und y ∈N }
Normalerweise spricht man nur von Paaren (statt von geordneten Paaren), die Reihenfolge der Elemente ist aber wesentlich.
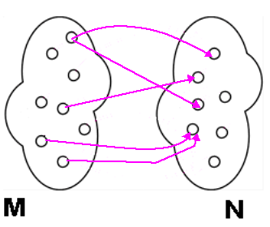
In vielen mathematischen Sachverhalten stehen Objekte in bestimmten Zusammenhängen z. B. "10 ist größer als 5". Der Zusammenhang "10 ist größer als 5" kann auch in der ungewöhnlichen Weise "(10,5) steht in der Relation größer" dargestellt werden. Das Beispiel zeigt aber, wie der Begriff der Relation auf den Mengenbegriff zurückgeführt werden kann.
Definition Relation
[Bearbeiten]- M und N seien Mengen
R heißt eine "Relation zwischen M und N" ⇔ " R ⊂ M×N "
Ist M=N, so heißt R eine Relation auf M
- Gilt (x,y)∈R dann "erfüllen x und y die Relation R" oder "stehen in der Relation R". Oft wird hierfür auch "xRy" geschrieben.
Beispiel:
ist eine Relation auf und definiert die oben erwähnte "Größer-Relation".
Äquivalenzrelation
[Bearbeiten]Viele Probleme lassen sich vereinfachen, indem man Objekte, die gewissen gemeinsamen Kriterien genügen, als äquivalent betrachtet, obwohl sie sich hinsichtlich anderen Kriterien unterscheiden können. Hierzu benutzt man in der Mathematik die Äquivalenzrelation.
- Definitionen
Seien M eine Menge und eine Relation auf M
- Äquivalenzrelation:
ist eine Äquivalenzrelation auf M, wenn für alle x,y,z∈M gilt:
- Reflexivität:
- Symmetrie: ⇒
- Transitivität: und ⇒
- Äquivalenzklasse
Sei R eine Äquivalenzrelation auf M. Die Menge der zu x∈M äquivalenten Elemente von M - nennt man die Äquivalenzklasse oder Faser von x bezüglich . Das Element x heißt Repräsentant von [x].
Beispiel:
Die oben erwähnte Gleichheitsrelation ΔM:= { (x,x) | x∈ M } ist die "klassische" Äquivalenzrelation. Reflexivität, Symmetrie und Transitivität sind die bekannten Eigenschaften der Gleichheit. Außerdem gilt für alle x,y ∈ M: "(x,y) ∈ ΔM ⇔ x=y". Die Äquivalenzklassen von M bezüglich ΔM sind also Mengen mit genau einem Element, d.h. [x]={x}.
In diesem Zusammenhang der Hinweis, dass eine Menge eine "Zusammenfassung wohl unterschiedener Objekte" ist.
Beispiel und Übung:
Etwas spannender ist schon die Entscheidung, ob es sich bei der Relation
um eine Äquivalenzrelation handelt. Es ist also zu prüfen, ob R auf der Menge reflexiv, symmetrisch und transitiv ist.
- Satz
- Sei eine Äquivalenzrelation auf M, dann gilt
- Beweis
- Sei . Dann ist und , und wegen der Transitivität und der Symetrie gilt daher . Für jedes gilt daher und wegen der Transitivität auch . Daraus folgt . Ganz analog zeigt man . Damit gilt .
- Dass gilt ist klar.
Bemerkung: Dieser Satz besagt, dass Äquivalenzklassen disjunkt oder gleich sein müssen. D.h. eine Äquivalenzrelation auf der Menge M, bildet eine disjunkte Partition der Menge M.
Ordnungsrelation
[Bearbeiten]Mengen kann man über die Teilmengenbeziehung "⊂" der Größe nach ordnen. Solche Ordnungen werden durch Eigenschaften wie Reflexivität, Antisymmetrie und Transitivität charakterisiert. Dies führt zu der sehr allgemeinen Definition der Ordnungsrelation
Definition - Ordnungsrelation
[Bearbeiten]Seien M eine Menge und R eine Relation auf M
- Ordnungsrelation:
R ist eine Ordnungsrelation auf M, wenn für alle x,y,z∈M gilt:
- Reflexivität: (x,x)∈R
- Antisymmetrie: (x,y)∈R und (y,x)∈R ⇒ x=y
- Transitivität: (x,y)∈R und (y,z)∈R ⇒ (x,z)∈R
- Ist R eine Ordnungsrelation auf M, so heißt das Paar (M,R) eine geordnete Menge und R eine Ordnung auf M. Die Namensgebung ist hier leider nicht sehr einheitlich. Man sagt statt Ordnung auch Halbordnung, Partialordnung oder teilweise Ordnung.
- Statt (x,y)∈ R schreibt man oft xRy, und auch, wie sicherlich vertraut, x≤y [sprich x kleiner oder gleich y].
- (M,R) ist linear (total) geordnet, wenn für alle x,y∈M gilt: "(x,y)∈R oder (y,x)∈R"
Definition - Kette
[Bearbeiten]- Eine nicht-leere Teilmenge K⊂M einer geordneten Menge (M,≤) heißt Kette von (M,≤), falls (K, ≤ ∩ K × K) eine total Ordnung ist.
Die vertraute Schreibweise "≤" könnte zu dem Fehlschluss verleiten, dass die Definition nur "gut bekannte" geordnete Mengen, wie z. B. die natürlichen Zahlen beschreibt. Das ist nicht der Fall, der Begriff ist viel allgemeiner. Das sollen die folgenden Beispiele verdeutlichen:
Beispiel:
Die oben erwähnte Gleichheitsrelation ΔM:= { (x,x) | x∈ M } ist eine Ordnungsrelation auf M.
Wie schon gesagt ist ΔM eine Äquivalenzrelation, also ist sie reflexiv und transitiv. Falls (x,y)∈ΔM und (y,x)∈ΔM folgt aus der Definition der Gleicheitsrelation x=y, d. h. auch die Antisymmetrie ist erfüllt.
Beispiel und Übung:
Potenzmenge:
Sei M eine Menge und die Potenzmenge von M. Durch
U ≤ V := U ⊂ V ⊂ M
wird eine Ordnungsrelation auf definiert. Beweisen lässt sich dies mit den Rechenregeln der Teilmengenbeziehung.
Zum Schluss dieses Abschnitts noch eine Übungsaufgabe, bei der vielleicht erst mit dem "zweiten Blick" klar wird, was hier eigentlich definiert wird:
Übungsaufgabe:
Zeige:
Sei M eine Menge und ≤ eine Ordnung auf M.
Für jede Teilmenge N⊂M wird durch
≤N := ≤ ∩ (N×N)
eine Ordnung auf N definiert. ≤ läßt sich also auf Teilmengen N einschränken.
Hinweise:
Es wird vorausgesetzt, dass M eine Menge und (M,≤) eine geordnete Menge ist.
Sei nun N eine Teilmenge von M. (N×N) ist dann eine Relation auf N, bei der alle Elemente von N miteinander in Beziehung stehen, d. h. für alle x,y∈N gilt (x,y)∈ (N×N).
"≤" steht als Symbol für die vorausgesetzte Ordnungsrelation, d. h. "≤" symbolisiert eine Relation oder Teilmenge von (M×M), also insbesondere ist "≤" eine Paarmenge.
Aus den beiden Paarmengen ≤ und (N×N) wird dann der Durchschnitt "≤ ∩ (N×N)" gebildet. Dieser Durchschnitt ist wieder eine Paarmenge. Und genau für diese Paarmenge soll gezeigt werden, dass sie eine Ordnungsrelation, d. h. reflexiv, antisymmetrisch und transitiv, ist.
Im Folgenden werden ausgezeichnete Elemente geordneter Mengen bezüglich gegebener Teilmengen beschrieben. Diese Begriffe werden in der Analysis und auch vielen anderen Gebieten der Mathematik häufig verwendet.
Maximum - Minimum
[Bearbeiten]- Definition
- (M,≤) sei eine geordnete Menge und N eine Teilmenge von M
- "x heißt Maximum oder größtes Element von N" :⇔ "x∈N und ∀y∈N gilt y≤x"
- "x heißt Minimum oder kleinstes Element von N" :⇔ "x∈N und ∀y∈N gilt x≤y"
- Satz
- Eine Teilmenge einer geordneten Menge besitzt höchstens ein Maximum (Minimum)
- Beweis
- Seien also a und b Maxima von N. Dann gilt a,b∈N und a≤b (b ist Maximum) sowie b≤a (b ist Maximum. Daraus folgt wegen der Antisymmetrie der Ordnungsrelation sofort a=b.
Eine geordnete Menge muss kein Maximum oder Minimum besitzen, z.B. die Menge , besitzt weder ein Maximum noch ein Minimum, obwohl sie geordnet ist.
Da Maximum und Minimum einer Teilmenge N eindeutig bestimmt sind (vorausgesetzt sie existieren!) definiert man weiter:
- Definition
- Sei N eine Teilmenge einer geordneten Menge (M,≤) und x sei ein Maximum von N, so setzt man: max N := x (min N := x)
Obere Schranke - untere Schranke
[Bearbeiten]Im Allgemeinen existieren zu einer Teilmenge N einer geordneten Menge (M,≤) weder Minimum noch Maximum. Für solche Teilmengen N ist die obige Definition nicht anwendbar. Mit der folgenden Definition erweitert man Menge der "möglichen Elemente" indem man auch Elemente der Menge M zuläßt.
- Definition
- (M,≤) sei eine geordnete Menge und N eine Teilmenge von M
- "x heißt obere Schranke von N (in M)" :⇔ "x∈M und ∀y∈N gilt y≤x"
- "x heißt untere Schranke von N (in M)" :⇔ "x∈M und ∀y∈N gilt x≤y"
- Sei := { x | x ist obere Schranke von N (in M) }.
"N heißt nach oben beschränkt" :⇔ " , d. h. N hat (mindestens) eine obere Schranke" - Sei := { x | x ist untere Schranke von N (in M) }.
"N heißt nach unten beschränkt" :⇔ " , d. h. N hat (mindestens) eine untere Schranke" - "N heißt beschränkt" :⇔ "N ist nach oben und unten beschränkt"
Supremum - Infimum
[Bearbeiten]Falls ein minimales Element der Menge := { x | x ist obere Schranke von N (in M) } existiert, so ist es nach dem oben bewiesenen Satz eindeutig und dieses Element nennt man dann Supremum von N. Die Existenz eines solchen Elementes ist jedoch keinesfalls gesichert und im "Einzelfall" nachzuweisen. Erst nachdem dieser Nachweis geglückt ist, dürfen also die folgende Definitionen benutzt werden:
- Definition
- (M,≤) sei eine geordnete Menge und N eine Teilmenge von M
- "x heißt Supremum oder kleinste obere Schranke oder sup N von N (in M)" :⇔ "x:= min " .
- "x heißt Infimum oder größte untere Schranke oder inf N von N (in M)" :⇔ "x:= max "
- Satz
- (M,≤) sei eine geordnete Menge, N eine Teilmenge von M und x∈ M. Dann gilt:
- x = max N ⇔ x∈ und x∈N ⇔ x = sup N und x∈N
- x = min N ⇔ x∈ und x∈N ⇔ x = inf N und x∈N
Sup N muss im Gegensatz zum max N nicht zur Teilmenge N gehören. Ein Beispiel hierzu ist die Menge N := { x | x ∈ , 1 < x < 2 } ( steht für die Menge der reellen Zahlen). Später werden wir solche Beispiele genauer untersuchen.
Wohlordnung
[Bearbeiten]Zum Schluss diese Abschnitts wird noch der Begriff der Wohlordnung eingeführt. Ein Beispiel für eine wohlgeordnete Menge sind die natürlichen Zahlen mit der "natürlichen" Ordnung. Dagegen sind die "normalen" Ordnungen der ganzen oder positiven reellen Zahlen nicht wohlgeordnet.
- Definition
- Eine Ordnung ≤ auf einer Menge M heißt Wohlordnung ⇔ ∀ L ⊂ M mit existiert min L.
Zahlenmengen
[Bearbeiten]Die natürlichen Zahlen
[Bearbeiten]sind die sogenannten natürlichen Zahlen. Es sind alle ganzen Zahlen von Eins anfangend. Das folgende Axiomensystem von Giuseppe Peano beschreibt alle Eigenschaften dieser Menge.
Axiomensystem von G. Peano
[Bearbeiten]- ist eine natürliche Zahl
- Jede natürliche Zahl hat einen eindeutig bestimmten Nachfolger .
- ist kein Nachfolger einer natürlichen Zahl
- Für jede Menge , die und mit auch jeden Nachfolger enthält, gilt .
Beweisprinzip der vollständigen Induktion
[Bearbeiten]Das Axiomensystem von G. Peano führt auf das sehr wichtige Beweisprinzip der vollständigen Induktion: sei eine Aussage, in der eine natürliche Zahl vorkommt. Wenn dann
- ist wahr
- Falls wahr ist, ist auch wahr
gilt, ist die Aussage für jede natürliche Zahl wahr.
Häufig gebrauchte Varianten
- Man startet bei . Die Aussage ist dann allerdings nur für wahr.
- Falls wahr sind, ist auch wahr.
Die Ganzen Zahlen
[Bearbeiten]Die Ganzen Zahlen sind eine Erweiterung der natürlichen Zahlen um deren negative Gegenstücke. Also zum Beispiel: .
Aufbau der ganzen Zahlen
[Bearbeiten]Hier soll beschrieben werden, wie man aus gewinnt.
Die rationalen Zahlen
[Bearbeiten]Die Rationalen Zahlen oder Brüche sind alle Zahlen, die sich als Bruch schreiben lassen. Also:
Aufbau der rationalen Zahlen
[Bearbeiten]Die reellen Zahlen
[Bearbeiten]Die reellen Zahlen bestehen aus den rationalen und den irrationalen Zahlen. Auf die Definition kommen wir noch später zu sprechen, jedoch einige Beispiele für irrationale Zahlen:
- allgemein:
- (Die Kreiszahl Pi)
- (Die eulersche Zahl)
Die komplexen Zahlen
[Bearbeiten]Die komplexen Zahlen sind eine gedanklich geschaffene Zahlenmenge, um mit Zahlen rechnen zu können die in der Menge der Reellen Zahlen nicht existieren. Man kann sie als eine Art Hilfsmittel betrachten, mit denen bestimmte Berechnungen (z.B. in der Elektrotechnik) gelöst werden können. Ohne die Komplexen Zahlen wäre dies häufig nicht, oder nur mit erheblich größerem Aufwand möglich.
Eine komplexe Zahl Z hat immer die folgende Form:
a und b sind jeweils reelle Zahlen. a heißt Realteil, b Imaginärteil. i wird als Imaginäre Einheit bezeichnet.
Die Imaginäre Einheit i ist die Zahl, die aus der folgenden Gleichung resultiert: Daraus folgt, dass i den Wert haben müsste. Die Wurzel von negativen Zahlen ist jedoch nicht definiert. Deshalb wird der Buchstabe i als Platzhalter verwendet. (In der Elektrotechnik wird statt "i" der Buchstabe "j" verwendet.) Es gelten dieselben Rechenregeln wie für die Reellen Zahlen. Übrigens kann jede reelle Zahl auch als komplexe Zahl angegeben werden. Hierbei ist der Imaginärteil einfach 0.
Ist der Imaginärteil des Ergebnisses einer komplexen Berechnung nicht Null, so muss das Ergebnis je nach Anwendungsgebiet speziell interpretiert werden.
Beispiele:
- (3 ist der Realteil, 2 der Imaginärteil.)
Weitere häufig benutzte Mengen
[Bearbeiten]Wikipedia zu Mengen
[Bearbeiten]Die Menge ist eines der wichtigsten und grundlegenden Konzepte der Mathematik. Man fasst im Rahmen der Mengenlehre einzelne Elemente (beispielsweise Zahlen) zu einer Menge zusammen. Eine Menge muss kein Element enthalten (diese Menge heißt die „leere Menge“). Bei der Beschreibung einer Menge geht es ausschließlich um die Frage, welche Elemente in ihr enthalten sind. Es wird nicht danach gefragt, ob ein Element mehrmals enthalten ist, oder ob es eine Reihenfolge unter den Elementen gibt.
Begriff und Notation von Mengen
[Bearbeiten]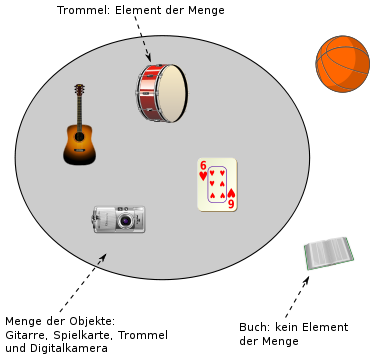
Der Begriff Menge geht auf Bernard Bolzano und Georg Cantor zurück. In Bolzanos Manuskripten aus den Jahren zwischen 1830 bis 1848 heißt es: „Inbegriffe nun, bey welchen auf die Art, wie ihre Theile mit einander verbunden sind, gar nicht geachtet werden soll, an denen somit Alles, was wir an ihnen unterscheiden, bestimmt ist, sobald nur ihre Theile [selbst] besimmt sind, verdienen es eben um dieser Beschaffenheit willen, mit einem eigenen Nahmen bezeichnet zu werden. In Ermangelung eines andern tauglichen Wortes erlaube ich mir das Wort Menge zu diesem Zwecke zu brauchen;“[1]. Cantor beschrieb eine Menge „naiv“ als eine Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens zu einem Ganzen beschrieb. Die Objekte der Menge heißen Elemente der Menge. Weder der Begriff Menge noch der Begriff Element werden im mathematischen Sinn definiert; sie werden auch nicht als oder in Axiomen definiert. Die moderne Mengenlehre und damit ein Großteil der Mathematik basiert auf den Zermelo-Fraenkel-Axiomen, Neumann-Bernays-Gödel-Axiomen oder anderen Axiomensystemen. Wir haben ein natürliches, intuitiv richtiges Verständnis für Mengen; allerdings führt der Begriff „die Menge aller Mengen, die sich nicht selbst als Element enthalten“ zu einem Widerspruch, der Russell’schen Antinomie; ebenso wie „die Menge aller Mengen“.
Eine Veranschaulichung des Mengenbegriffs, die Richard Dedekind zugeschrieben wird, ist das Bild eines Sackes, der gewisse (als Einzelne abgrenzbare) Dinge enthält. Nützlich ist diese Vorstellung zum Beispiel für die leere Menge: ein leerer Sack. Die leere Menge ist also nicht „nichts“, sondern der Inhalt eines Behältnisses, das keine der für es als Inhalt vorgesehenen Dinge enthält. Das „Behältnis“ selbst verweist nur auf die bestimmte zu zählende Sorte und Art von Elementen.
Endliche Mengen können (insbesondere wenn sie relativ wenig Elemente haben) durch Aufzählen ihrer Elemente (aufzählende Mengenschreibweise) angegeben werden, etwa M = {blau, gelb, rot}, wobei es wie gesagt nicht auf eine Reihenfolge ankommt oder darauf, ob ein Element mehr als einmal genannt wird. D.h. es gilt: {blau, gelb, rot} = {blau, blau, gelb, rot} [2]
Oft ist es ungünstig oder (bei unendlichen Mengen) unmöglich, die Elemente einer Menge aufzuzählen. In diesen Fällen gibt es eine andere Notation, in der die Elemente einer Menge durch eine Eigenschaft festgelegt werden, zum Beispiel M = { x | x ist eine Grundfarbe }.
Weiterhin prägte Dedekind das Synonym des Systems zu welchem er Elemente zusammenfasste, diese Bezeichnung ist heute noch teilweise üblich, so nennt man eine „Menge von Vektoren“ auch kurz ein Vektorsystem.
Andere Schreibweisen
[Bearbeiten]Andere Schreibweisen für Mengen können als Abkürzungen für die intensionale Notation angesehen werden:
- die aufzählende Schreibweise M = { blau, gelb, rot } kann als eine Abkürzung für die umständlichere Schreibweise M = { x | x = blau oder x = gelb oder x = rot } verstanden werden.
- bei der elliptischen Schreibweise werden nur einige Elemente als Beispiele aufgeführt, etwa: M = { 3, 6, 9, 12, …, 96, 99 }. Sie ist nur verwendbar, wenn das Bildungsgesetz aus diesen Beispielen oder aus dem Zusammenhang klar ist. Hier ist offenbar die Menge gemeint, die sich intensional als M = { x | x ist eine durch 3 teilbare Zahl zwischen 1 und 100 } schreiben lässt. Diese Schreibweise wird häufig für unendliche Mengen angewendet. So beschreibt G = { 4, 6, 8, 10, … } die Menge der geraden, natürlichen Zahlen, die größer sind als 2 (also das obige Beispiel G).
- Neue Mengen kann man auch durch Mengenoperationen bilden, wie aus A und B die Schnittmenge . Diese kann intensional geschrieben werden als M = { x | x ist in A und x ist in B }
- ferner gibt es noch die induktive Definition von Mengen.
Grundlegende Beziehungen zwischen Mengen
[Bearbeiten]Die Dinge, die in einer Menge enthalten sind, heißen Elemente. Ist ein Objekt Element einer Menge , so schreibt man dafür formal: . Die Verneinung ( ist kein Element von ) schreibt man als: . Historisch geht das Symbol zurück auf den griechischen Buchstaben ε als Anfangsbuchstabe von εστί.[3]
Gleichheit von Mengen und Extensionalität
[Bearbeiten]Gleichheit
[Bearbeiten]Zwei Mengen heißen gleich, wenn sie dieselben Elemente enthalten.
Diese Definition bezeichnet die Extensionalität und damit die grundlegende Eigenschaft von Mengen. Formal:
Tatsächlich muss eine Menge aber meist intensional beschrieben werden. Das heißt: Es wird eine Aussageform angegeben (mit einer Objektvariablen , die eine wohlbestimmte Definitionsmenge haben sollte), sodass genau dann gilt, wenn zutrifft. Dafür schreibt man dann:
Zu jeder Menge gibt es viele verschiedene Aussageformen , die diese beschreiben. Die Frage, ob zwei gegebene Aussageformen und dieselbe Menge beschreiben, ist keineswegs trivial. Im Gegenteil: Viele Fragestellungen der Mathematik lassen sich in dieser Form formulieren: „Sind und die gleiche Menge?“
Viele Gleichheitsbeweise benutzen die Äquivalenz .
Extensionalität
[Bearbeiten]Vorlage:Hauptartikel Wenn zwei Mengen dieselben Elemente enthalten, so sind sie gleich. Auf die Art und Weise, wie die Zugehörigkeit der Elemente zu den Mengen beschrieben ist, kommt es dabei nicht an. Die für Mengen charakteristische Eigenschaft, dass es auf die Art der Beschreibung nicht ankommt, nennt man ihre Extensionalität (von lateinisch extensio = Ausdehnung; betrifft den Umfang des Inhaltes).
Unendliche Mengen müssen aber meist „intensional“ (beschreibende Mengenschreibweise) beschrieben werden (von lateinisch intensio = Spannung; betrifft die Merkmale des Inhaltes). Das heißt: Eine Menge wird durch eine bestimmte Bedingung oder Eigenschaft beschrieben, die alle Elemente der Menge (und nur diese) erfüllen: beispielsweise G:= { x | x ist eine gerade natürliche Zahl und größer als 2 }, gelesen „sei G die Menge aller x, für die gilt: x ist eine gerade natürliche Zahl und größer als 2“, oder kürzer: „sei G die Menge aller geraden natürlichen Zahlen > 2“.
Es ist teilweise schwer zu entscheiden, ob zwei intensional beschriebene Mengen gleich sind. Dafür muss festgestellt werden, ob die Eigenschaften aus den intensionalen Beschreibungen logisch äquivalent sind (wenn die eine Eigenschaft wahr ist, ist es auch die andere, und umgekehrt).
Aus der Extensionalität folgt unmittelbar, dass es nur eine leere Menge gibt: Jede andere Menge, die die gleichen (also keine) Elemente enthält, wäre dieser gleich.
Teilmenge
[Bearbeiten]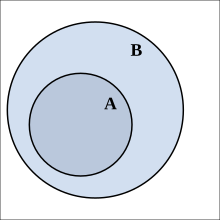
Eine Menge heißt Teilmenge einer Menge , wenn jedes Element von auch Element von ist.
wird dann Obermenge (selten: Übermenge) von genannt. Formal:
- .
ist echte Teilmenge von (oder ist echte Obermenge von ), wenn Teilmenge von ist, aber von verschieden, also jedes Element aus auch Element von ist, aber (mindestens) ein Element in existiert, das nicht in enthalten ist.
Die Relation „ist Teilmenge von“ bildet eine Halbordnung. Die Relation „echte Teilmenge“ ist eine strenge Halbordnung.
Es gibt zwei Notationen:
- für „Teilmenge“ und für „echte Teilmenge“ oder
- für „Teilmenge“ und für „echte Teilmenge“.
In diesem Artikel wird das erstgenannte System verwendet, es sind jedoch beide weit verbreitet.
Die Negation der Relationen , und kann durch das durchgestrichene jeweilige Relationssymbol bezeichnet werden, also zum Beispiel durch . Außerdem ist es möglich, die Reihenfolge der beiden Argumente zu vertauschen, wenn dabei auch das Relationssymbol umgedreht wird. So kann also anstelle von auch , anstelle von auch und anstelle von auch geschrieben werden. Auch ein gleichzeitiges Durchstreichen und Umdrehen dieser Relationssymbole ist denkbar.
Wenn alle Elemente in einer Menge auch in einer zweiten Menge enthalten sind, so nennt man Menge eine Teilmenge von Menge . Die Menge enthält dann mindestens so viele Elemente wie die Menge . Für Teilmengen wird das Zeichen verwendet.
Formal: Es gilt , wenn aus folgt, dass ist.
Nach dieser Definition ist jede Menge auch Teilmenge von sich selbst: . Der Unterstrich in dem Zeichen soll das andeuten, indem er an ≤ erinnert. Eine echte Teilmenge von ist eine Teilmenge, die nicht selbst ist, geschrieben .
- Hinweis
Die Notation der Teilmengenrelation ist uneinheitlich, die beiden folgenden Möglichkeiten sind heute üblich, wobei die erste der ursprünglich von Bertrand Russell (vgl. Principia Mathematica) eingeführten entspricht:
- steht für „Teilmenge“, für „echte Teilmenge“
- steht für „Teilmenge“, für „echte Teilmenge“.
Durchschnitt (Schnittmenge, Schnitt)
[Bearbeiten]
Vorlage:Hauptartikel Die Schnittmenge zweier Mengen und besteht aus allen Elementen, die in jeder der beiden Mengen enthalten sind (also sowohl in als auch in ). Die Schnittmenge von und wird geschrieben.
Formal: Es gilt genau dann, wenn und .
Besitzen zwei Mengen kein gemeinsames Element, heißen sie elementfremd oder disjunkt. Ihre Schnittmenge ist die leere Menge.
Leere Menge
[Bearbeiten]Vorlage:Hauptartikel Die Menge, die kein Element enthält, heißt leere Menge. Sie wird mit oder auch bezeichnet. Aus der Extensionalität der Mengen folgt, dass es nur eine leere Menge gibt: Jede „andere“ leere Menge enthält dieselben Elemente (nämlich keine), ist also gleich. Folglich sind und verschieden, da letztere Menge eine andere Menge als Element enthält. Die leere Menge ist Teilmenge einer jeden Menge.
Schnittmenge
[Bearbeiten]
Gegeben ist eine nichtleere Menge von Mengen. Die Schnittmenge (auch Durchschnittsmenge) von ist die Menge der Elemente, die in jeder Elementmenge von enthalten sind. Formal:
- .
Ist eine Paarmenge, also , so schreibt man für gewöhnlich
und liest dies: geschnitten mit (oder: Der Durchschnitt von und ) ist die Menge aller Elemente, die sowohl in als auch in enthalten sind.
Diese Schreibweise lässt sich leicht auf den Durchschnitt aus endlich vielen Mengen verallgemeinern.
Abweichende Schreibweise für den Durchschnitt aus beliebig vielen Mengen:
Die Elemente der Menge , die ja selbst wieder Mengen sind, werden mit bezeichnet. Es wird eine „Indexmenge“ (Lambda) eingeführt, sodass ist. Die Schnittmenge wird dann geschrieben als:
- ,
also die Menge aller Elemente, die in sämtlichen Mengen enthalten sind.
Eine ältere Bezeichnung für den Durchschnitt ist inneres Produkt oder Produkt erster Art. Dieses wird dann auch als
- oder .
geschrieben. Insbesondere die letzte Schreibweise ist von vielen Autoren für das kartesische Produkt (siehe unten) reserviert.
Vereinigungsmenge
[Bearbeiten]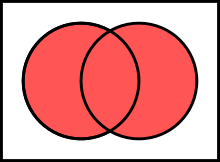
Dies ist der zur Schnittmenge duale Begriff: Die Vereinigungsmenge von ist die Menge der Elemente, die in mindestens einer Elementmenge von enthalten sind. Formal:
- .
Im Gegensatz zu ist auch dann erklärt, wenn leer ist, und zwar ergibt sich .
Für schreibt man wieder
und liest dies: vereinigt mit (oder: Die Vereinigung von und ) ist die Menge aller Elemente, die in oder in enthalten sind. Das „oder“ ist hier nicht-ausschließend zu verstehen. Die Vereinigung umfasst auch die Elemente, die in beiden Mengen enthalten sind.
Unter Verwendung einer geeigneten Indexmenge schreibt man:
- .
Diese Schreibweise ist auch für die Vereinigung endlich vieler Mengen geeignet.
Als ältere Bezeichnung hierfür wird zuweilen noch die Summe verwendet und dann geschrieben
- oder .
Vorsicht: Der Begriff Summe wird heute auch für die disjunkte Vereinigung von Mengen benutzt.
Differenz und Komplement
[Bearbeiten]
Die Differenz wird gewöhnlich nur für zwei Mengen definiert: Die Differenzmenge (auch Restmenge) von und ist die Menge der Elemente, die in , aber nicht in enthalten sind. Formal:
Ist , so heißt die Differenz auch Komplement von in . Dieser Begriff wird vor allem dann verwendet, wenn eine Grundmenge ist, die alle in einer bestimmten Untersuchung in Frage stehenden Mengen umfasst. Diese Menge muss dann im Folgenden nicht mehr erwähnt werden, und
heißt einfach das Komplement von . Andere Schreibweisen für sind , oder .
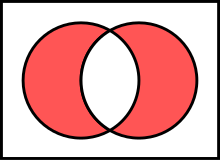
„A ohne B“ vereinigt „B ohne A“
Die Menge
wird gelegentlich als symmetrische Differenz von und bezeichnet. Es handelt sich um die Menge aller Elemente, die jeweils in einer, aber nicht in beiden Mengen liegen. Bei Verwendung des ausschließenden Oder (XOR oder ) kann man dafür auch
schreiben.
Kartesisches Produkt
[Bearbeiten]Die Produktmenge oder das kartesische Produkt, in älterer Terminologie auch Verbindungsmenge oder Produkt zweiter Art, soll hier ebenfalls zunächst als Verknüpfung von zwei Mengen definiert werden:
Die Produktmenge von und ist die Menge aller geordneten Paare, deren erstes Element aus und deren zweites Element aus ist.
Die Elemente des kartesischen Produkts sind also keine Elemente der Ausgangsmengen, sondern komplexere Objekte, nämlich geordnete Paare. Formal:
Unter der Verwendung von n-Tupeln lässt sich der Begriff leicht für die Verknüpfung endlich vieler Mengen verallgemeinern:
Die Produktbildung ist weder kommutativ noch assoziativ. So sind , und drei verschiedene Mengen, nämlich , sowie . Aufgrund Bijektionen wie und der daraus folgenden Isomorphie werden diese Mengen oft nicht unterschieden. Die Assoziativität bis auf Isomorphie erlaubt es, beliebige Produktmengen aus einer endlichen Anzahl von Mengen mit der Menge der -Tupel zu identifizieren und ohne Rücksicht auf die konkrete Klammerung mit zu bezeichnen.
Für die Produktmenge beliebig vieler Mengen, die durch die Indexmenge benannt werden, schreibt man oder, wenn diese Notation schon für „Produkte erster Art“ verwendet wird, . Für die Definition einer solchen Produktmenge wird ein allgemeiner Funktionsbegriff benötigt. Sie ist die Menge aller Funktionen, die jedem Indexelement ein Element der Menge zuordnen. Formal:
Ob ein solches kartesisches Produkt nicht leer ist, das heißt ob es überhaupt stets solche Funktionen wie auf der rechten Seite dieser Definitionsgleichung angegegeben gibt, hängt eng mit dem Auswahlaxiom zusammen.
Für das Mengenprodukt aus identischen Faktoren gibt es abkürzende Schreibweisen:
- Anstelle des -fachen endlichen Mengenprodukts schreibt man auch .
- Das unendliche Mengenprodukt ist kanonisch isomorph zur Menge aller Abbildungen . In Analogie zum endlichen Fall wird dafür die Schreibweise benutzt.
Die Mengen und sind nicht notwendig gleich, aber wegen der Bijektion mit , , zueinander isomorph. Die Definition der zweistelligen Produktmenge ist also mit der Definition der Produktmenge beliebig vieler Mengen konsistent, weshalb für eine endliche nichtleere Produktmenge in der Regel auch nicht zwischen und unterschieden wird.
Potenzmenge
[Bearbeiten]Vorlage:Hauptartikel Die Potenzmenge von ist die Menge aller Teilmengen von .
Die Potenzmenge von enthält immer die leere Menge und die Menge . Somit ist , also eine einelementige Menge. Die Potenzmenge einer einelementigen Menge ist , enthält also zwei Elemente. Allgemein gilt: Besitzt genau Elemente, so hat die Elementanzahl . Dies motiviert auch die Schreibweise anstelle .
Bei unendlichen Mengen ist der Begriff nicht unproblematisch: Es gibt nachweislich kein Verfahren, das alle Teilmengen auflisten könnte. (Siehe dazu: Cantors zweites Diagonalargument.) Bei einem axiomatischen Aufbau der Mengenlehre (etwa ZFC) muss die Existenz der Potenzmenge durch ein eigenes Potenzmengenaxiom gefordert werden.
Konstruktive Mathematiker betrachten deshalb die Potenzmenge einer unendlichen Menge als einen grundsätzlich unabgeschlossenen Bereich, zu dem – je nach Fortgang der mathematischen Forschung – immer noch neue Mengen hinzugefügt werden können.
Vereinigung (Vereinigungsmenge)
[Bearbeiten]
Die Vereinigungsmenge aus zwei Mengen und erhält man, indem man alle Elemente zusammenfasst, die in der einen oder in der anderen Menge enthalten sind (oder möglicherweise auch in beiden). Das Zeichen dafür ist .
Formal: Es gilt , wenn oder ; das oder ist hier nicht ausschließend zu verstehen, x ist also auch in der Vereinigung, wenn es in A und in B liegt. Um darzustellen, dass die vereinigten Mengen disjunkt sind, verwendet man auch das Zeichen .
Zwar wird die Vereinigung durch den Junktor (oder) definiert - die Verwendung der Zeichen ist in diesem Fall intuitiv.
- die disjunkte Vereinigung darf jedoch nicht mit der Mengenoperation verwechselt werden,
- die durch den Junktor (ausschließendes oder) definiert wird, also der symmetrischen Differenz - die Verwendung der Zeichen ist in diesem Fall kontraintuitiv.
Für die Verwendung dieser Zeichen gibt es jedoch keine allgemein anerkannten Konventionen, es ist also im Einzelfall zu prüfen, ob ein Autor mit nicht doch die symmetrische Differenz ![]() meint.
meint.
Differenz (Differenzmenge)
[Bearbeiten]
Die Differenz zweier Mengen erhält man, indem man alle Elemente zusammenfasst, die in A, aber nicht in B enthalten sind. Das Zeichen dafür ist . Die Differenz ist im Gegensatz zu Schnitt und Vereinigung weder kommutativ noch assoziativ.
Formal: Es gilt , wenn und .
Beispiele für Mengenoperationen
[Bearbeiten]Wir betrachten die Mengen , und . Es gelten:
- ,
- , ,
- , ,
- Für die Komplemente bezüglich gilt , , , .
- , , ,
- , ,
- = 3, = = 2, = 0, = 1
- , , ,
- , ,
- ,
Konkretere Beispiele sind hier nochmals benannt.
- Die Menge aller zweistelligen „Schnapszahlen“ lautet . 33 ist ein Element dieser Menge, 23 ist es nicht.
- Die Menge der natürlichen Zahlen ist eine echte Teilmenge der Menge der ganzen Zahlen .
Weitergehende Begriffe
[Bearbeiten]- Teilmengen der reellen Geraden, der Ebene oder des dreidimensionalen euklidischen Raumes werden aus historischen Gründen oder, um einen Hinweis auf die darin enthaltenen Elemente zu geben, oft Punktmengen genannt. Dieser Begriff bezeugt die geometrische Herkunft der Mengenlehre.
- In der modernen Mathematik werden die Zahlenbereiche rein mit den Methoden der Mengenlehre (mit der leeren Menge als einzigem Grundbaustein) schrittweise aufgebaut, von den natürlichen Zahlen über die ganzen Zahlen und die rationalen Zahlen zu den reellen Zahlen (und evtl. weiter zu den komplexen Zahlen und noch darüber hinaus).
- In der Schule hat die Mengenlehre unter dem Schlagwort Neue Mathematik zeitweise große Bedeutung erlangt.
- Bei unendlichen Mengen treten besondere Phänomene hinsichtlich der üblichen Ordnungsrelationen auf.
- Zur Veranschaulichung der Beziehungen zwischen Mengen dienen Mengendiagramme.
- Beziehungen zwischen den Elementen einer Menge und denen einer anderen werden durch „Zuordnungen“ (Relationen) beschrieben, eindeutige Zuordnungen durch „Abbildungen“ (Funktionen).
Literatur
[Bearbeiten]- Klaus Kursawe: Mengen, Zahlen, Operationen. Scripta Mathematica. Aulis Verlag Deubner, Köln 1973, ISBN 3-7614-0176-0.
- Hans-Dieter Gerster: Aussagenlogik, Mengen, Relationen. Studium und Lehre Mathematik. Franzbecker, Hildesheim 1998, ISBN 3-88120-287-0.
- Adolf Fraenkel: Einleitung in die Mengenlehre. Springer, Berlin/Heidelberg/New York 1928, Dr. Martin Sändig oHG, Walluf 1972 (Repr.), ISBN 3-500-24960-4.
- Erich Kamke: Mengenlehre. 6. Aufl. Walter de Gruyter, Berlin 1969.
- Paul R. Halmos: Naive Mengenlehre. Vandenhoeck & Ruprecht, Göttingen 1968, ISBN 3-525-40527-8.
- H. Schinköthe: Mengen und Längen, Lehrbuch der elementaren Grundlagen mathematischen Denkens und seiner Entwicklung für die Bereiche: Kindergarten, Vorschule, Grundschule, Sonderschule, Rechenschwächetherapie. RESI, Volxheim 2000 (Libri/BoD), ISBN 3-8311-0701-7.
- Oliver Deiser: Einführung in die Mengenlehre. Die Mengenlehre Georg Cantors und ihre Axiomatisierung durch Ernst Zermelo. 3. Auflage. Springer Verlag, Berlin, Heidelberg 2010, ISBN 978-3-642-01444-4 (DOI:10.1007/978-3-642-01445-1).
Einzelnachweise
[Bearbeiten]- ↑ Bernard Bolzano: Einleitung zur Grössenlehre und erste Begriffe der allgemeinen Grössenlehre. In: Jan Berg (Hrsg.): Bernard-Bolzano-Gesamtausgabe, Hg. von Eduard Winter et al.. Reihe II, A, Band 7, Friedrich Frommann Verlag, Stuttgart, Bad Cannstatt 1975, ISBN 3-7728-0466-7, S. 152.
- ↑ http://www.ti.inf.uni-due.de/fileadmin/public/teaching/mast/slides/ss2011/grundlagen-2x2.pdf Abgerufen am 18. November 2011
- ↑ So erklärt in Bertrand Russell, Alfred North Whitehead: Principia Mathematica. 1 Auflage. Cambridge University Press, Cambridge 1910–1913 (Online-version der Universität Michigan; Stand: 2011-10-23; S. 26). und bereits früher bei Peano
Aus Wikipedia über Mengenlehre / Geschichte
[Bearbeiten]Die Mengenlehre ist das grundlegende Teilgebiet der Mathematik. Die gesamte Mathematik, wie sie heute üblicherweise gelehrt wird, ist in der Sprache der Mengenlehre formuliert und baut auf den Axiomen der Mengenlehre auf. Alle mathematischen Objekte, die in Teilbereichen wie Algebra, Analysis, Geometrie, Stochastik oder Topologie behandelt werden, um nur einige wenige zu nennen, sind Mengen. Gemessen daran ist die Mengenlehre eine recht junge Wissenschaft; erst nach der Überwindung der Grundlagenkrise der Mathematik zu Beginn des 20. Jahrhunderts konnte die Mengenlehre ihren heutigen, zentralen und grundlegenden Platz in der Mathematik einnehmen.
Geschichte
[Bearbeiten]19. Jahrhundert
[Bearbeiten]
Die Mengenlehre wurde von Georg Cantor in den Jahren 1874 bis 1897 begründet. Statt des Begriffs Menge benutzte er anfangs Wörter wie „Inbegriff“ oder „Mannigfaltigkeit“; von Mengen und Mengenlehre sprach er erst später. 1895 formulierte er folgende Mengendefinition:
- Unbekannt: „Unbekannt“
Cantor klassifizierte die Mengen, insbesondere die unendlichen, nach ihrer Mächtigkeit. Für endliche Mengen ist das die Anzahl ihrer Elemente. Er nannte zwei Mengen äquivalent (gleichmächtig), wenn sie sich bijektiv aufeinander abbilden lassen. Die Mächtigkeit oder Kardinalzahl einer Menge M ist nach Cantor die Äquivalenzklasse der zu M äquivalenten (gleichmächtigen) Mengen. Er beobachtete wohl als Erster, dass es verschiedene unendliche Mächtigkeiten gibt. Die Menge der natürlichen Zahlen und alle dazu gleichmächtigen Mengen heißen nach Cantor abzählbar, alle anderen unendlichen Mengen heißen überabzählbar.
- Wichtige Ergebnisse von Cantor
- Die Mengen der natürlichen, der rationalen (Cantors erstes Diagonalargument) und der algebraischen Zahlen sind abzählbar und damit gleichmächtig.
- Die Menge der reellen Zahlen hat größere Mächtigkeit als die der natürlichen Zahlen, ist also nichtabzählbar (Cantors zweites Diagonalargument).
- Die Menge aller Untermengen einer Menge M (ihre Potenzmenge) hat stets größere Mächtigkeit als M, das ist auch als Satz von Cantor bekannt.
- Von je zwei Mengen ist mindestens eine gleichmächtig zu einer Untermenge der anderen. Das wird mit Hilfe der von Cantor ausführlich behandelten Wohlordnung bewiesen.
- Es gibt überabzählbar viele Mächtigkeiten.
Cantor benannte das Kontinuumproblem: Gibt es eine Mächtigkeit zwischen derjenigen der Menge der natürlichen und der Mächtigkeit der Menge der reellen Zahlen? Er selbst versuchte es zu lösen, blieb aber erfolglos. Später stellte sich heraus, dass die Frage grundsätzlich nicht entscheidbar ist.
Neben Cantor war auch Richard Dedekind ein wichtiger Wegbereiter der Mengenlehre. Er sprach von Systemen statt von Mengen und entwickelte 1872 eine mengentheoretische Konstruktion der reellen Zahlen[1] und 1888 eine verbale mengentheoretische Axiomatisierung der natürlichen Zahlen.[2]
Giuseppe Peano, der Mengen als Klassen bezeichnete, schuf bereits 1889 den ersten formalen Klassenlogik-Kalkül als Basis für seine Arithmetik mit den Peano-Axiomen, die er erstmals in einer präzisen mengentheoretischen Sprache formulierte. Er entwickelte damit die Grundlage für die heutige Formelsprache der Mengenlehre und führte viele heute gebräuchliche Symbole ein, darunter das Symbol für das Elementprädikat, das als „ist Element von“ verbalisiert wird.[3]
Eine andere mengentheoretische Begründung der Arithmetik versuchte Gottlob Frege wenig später in seinem Kalkül von 1893. In diesem entdeckte Bertrand Russell 1902 einen Widerspruch, der als Russellsche Antinomie bekannt wurde. Dieser Widerspruch und auch andere Widersprüche entstehen aufgrund einer uneingeschränkten Mengenbildung, weshalb die Frühform der Mengenlehre später als naive Mengenlehre bezeichnet wurde. Cantors Mengendefinition beabsichtigt aber keine solche naive Mengenlehre, wie sein Beweis der Allklasse als Nichtmenge durch die zweite Cantorsche Antinomie belegt.[4]
Cantors Mengenlehre wurde von seinen Zeitgenossen in ihrer Bedeutung kaum erkannt und keineswegs als revolutionärer Fortschritt angesehen, sondern stieß bei manchen Mathematikern, etwa bei Leopold Kronecker, auf Ablehnung. Noch mehr geriet sie in Misskredit, als Antinomien bekannt wurden, so dass etwa Henri Poincaré spottete: „Die Logik ist gar nicht mehr steril – sie zeugt jetzt Widersprüche.“
20. Jahrhundert
[Bearbeiten]Im 20. Jahrhundert setzten sich Cantors Ideen immer mehr durch; gleichzeitig vollzog sich innerhalb der sich entwickelnden Mathematischen Logik eine Axiomatisierung der Mengenlehre, mittels derer zuvor herrschende Widersprüche überwunden werden konnten.
1903/1908 entwickelte Bertrand Russell seine Typentheorie, in der Mengen stets einen höheren Typ als ihre Elemente haben, damit problematische Mengenbildungen unmöglich würden. Er wies den ersten Ausweg aus den Widersprüchen und zeigte in den Principia Mathematica von 1910–1913 auch ein Stück der Leistungsfähigkeit der angewandten Typentheorie. Letztlich erwies sie sich aber als unzulänglich für Cantors Mengenlehre und konnte sich auch wegen ihrer Kompliziertheit nicht durchsetzen.
Handlicher und erfolgreicher war dagegen die von Ernst Zermelo 1907 entwickelte axiomatische Mengenlehre, die er gezielt zur widerspruchsfreien Begründung der Mengenlehre von Cantor und Dedekind schuf. Abraham Fraenkel bemerkte 1921, dass dazu zusätzlich sein Ersetzungsaxiom nötig sei. Zermelo fügte es in sein Zermelo-Fraenkel-System von 1930 ein, das er kurz ZF-System nannte. Er konzipierte es auch für Urelemente, die keine Mengen sind, aber als Mengenelemente in Frage kommen und Cantors „Objekte unserer Anschauung“ einkalkulieren. Die heutige Zermelo-Fraenkel-Mengenlehre ist dagegen nach Fraenkels Vorstellung eine reine Mengenlehre, deren Objekte ausschließlich Mengen sind.
Viele Mathematiker setzten aber statt auf eine konsequente Axiomatisierung auf eine pragmatische Mengenlehre, die Problem-Mengen mied, so etwa die oft aufgelegten Mengenlehren von Felix Hausdorff ab 1914 oder von Erich Kamke ab 1928. Nach und nach wurde es immer mehr Mathematikern bewusst, dass die Mengenlehre eine unentbehrliche Grundlage für die Strukturierung der Mathematik ist. Das ZF-System bewährte sich in der Praxis, weshalb es heute als Basis der modernen Mathematik von der Mehrheit der Mathematiker anerkannt ist; keinerlei Widersprüche konnten mehr aus dem ZF-System abgeleitet werden. Die Widerspruchsfreiheit konnte allerdings nur für die Mengenlehre mit endlichen Mengen nachgewiesen werden, aber nicht für das komplette ZF-System, das Cantors Mengenlehre mit unendlichen Mengen enthält; nach Gödels Unvollständigkeitssatz von 1931 ist ein solcher Nachweis der Widerspruchsfreiheit prinzipiell nicht möglich. Gödels Entdeckungen steckten nur Hilberts Programm, die Mathematik und Mengenlehre auf eine nachweislich widerspruchsfreie axiomatische Basis zu stellen, eine Grenze, aber hinderten den Erfolg der Mengenlehre in keiner Weise, so dass von einer Grundlagenkrise der Mathematik, von der Anhänger des Intuitionismus sprachen, in Wirklichkeit nichts zu spüren war.
Die endgültige Anerkennung der ZF-Mengelehre in der Praxis zog sich allerdings noch über längere Zeit hin. Die Mathematiker-Gruppe mit Pseudonym Nicolas Bourbaki trug wesentlich zu dieser Anerkennung bei; sie wollte die Mathematik auf der Basis Mengenlehre einheitlich neu darstellen und setzte dies ab 1939 in zentralen Mathematikgebieten erfolgreich um. In den 1960er Jahren wurde es dann allgemein bekannt, dass sich die ZF-Mengenlehre als Grundlage der Mathematik eignet. Es gab sogar einen vorübergehenden Zeitraum, in dem die Mengenlehre in der Grundschule behandelt wurde.
Parallel zur Erfolgsgeschichte der Mengenlehre blieb jedoch die Diskussion der Mengenaxiome in der Fachwelt aktuell. Es entstanden auch alternative axiomatische Mengenlehren, etwa 1940 die Neumann-Bernays-Gödel-Mengenlehre, die ZF auf Klassen verallgemeinert, oder 1955 die Ackermann-Mengenlehre, die neu an Cantors Mengendefinition anknüpfte.
- ↑ Richard Dedekind: Stetigkeit und irrationale Zahlen. Braunschweig 1872.
- ↑ Richard Dedekind: Was sind und was sollen die Zahlen? Braunschweig 1888.
- ↑ Giuseppe Peano: Arithmetices Principia nova methodo exposita. Turin 1889
- ↑ Brief von Cantor an Dedekind vom 31. August 1899, in: Georg Cantor: Gesammelte Abhandlungen mathematischen und philosophischen Inhalts. ed. E. Zermelo, Berlin 1932, S. 448.




































































![{\displaystyle [x]:=\lbrace y\in M\mid x\sim y\rbrace }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9577f7f99d949ad7e14c56a4ac5996c272dc7cce)

![{\displaystyle [x]\cap [y]\not =\emptyset \Leftrightarrow [x]=[y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4c9905e338a0c83b12fe93b4d92dcd9fe8fabc0)
![{\displaystyle z\in [x]\cap [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/815ef00d294b6a9fdaaa892145581fbd553be9f1)
![{\displaystyle a\in [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05b02437c238452a7cd8dbb82cd1cd934c8e380b)


![{\displaystyle [x]\subseteq [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4044b09c892280324baed37803bc2090935cedf8)
![{\displaystyle [y]\subseteq [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac2e8afc1de2256507f713d34dc61c6cc7c3b7a5)
![{\displaystyle [x]=[y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c34866e2a1216182b168dc1e272b0b02f1aab3a)
![{\displaystyle [x]=[y]\Rightarrow [x]\cap [y]\not =\emptyset }](https://wikimedia.org/api/rest_v1/media/math/render/svg/822eeb31d5b2bcc0479b358f32b09edceed25b66)






























![{\displaystyle {\sqrt[{q}]{p}}\ \mathrm {mit} \ q\in \mathbb {N} \ \mathrm {und} \ p\ \mathrm {Primzahl} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb7aaa7caeb31dad8f80ecccf26bd123794cb575)

































































































































































