Das Mehrkörperproblem in der Astronomie/ Enge Begegnungen von Massenpunkten/ Indiviuelle Zeitskalen pro Massenpunkt

Konstruktion

Wie soeben diskutiert, lässt sich jedem Mitglied eines Mehrkörpersystems eine eigene dynamische Zeitskala zuordnen. Auf alle Massenpunkte die kleinste im Ensemble auftretende Skala anzuwenden, würde jedoch viel zu lange Rechenzeiten nach sich ziehen. Wielen (1967) ^[1] und Aarseth (1985) ^[2] entwickelten daher ein Verfahren, dass es erlaubt, individuelle dynamische Zeitskalen beizubehalten. Die Autoren benutzten hierbei als grundlegende Lösungsmethode das Mehrschrittverfahren nach Adams-Bashforth und Adams-Moulton. Makino und Aarseth (1992) ^[3] legten dar, dass auch die auf Hermite-Polynome beruhenden Lösungsformeln für eine objektspezifische Behandlung der dynamischen Zeitskala geeignet sind. Hut und andere (1995) ^[4] zeigten schließlich, dass dies auch für das Leapfrog-Verfahren möglich ist.

Ganz allgemein lassen sich auf dem Prädiktor-Korrektor-Prinzip beruhende Verfahren am besten auf individuelle Zeitschritte hin erweitern, da man durch einfaches Einsetzen aktueller Werte in Lösungsformeln direkt zum nächsten Zustand gelangen kann. Hingegen ist das Runge-Kutta-Verfahren für eine Dynamisierung der Zeitschritte sehr unhandlich, da es etliche Zwischenstufen benötigt, um einen Schritt abzuarbeiten.

Die Verwendung individueller dynamischer Zeiten und damit auch Zeitschritte $Δ t_{i}$ hat zwangsläufig zur Folge, dass jeder Massenpunkt auch zu individuellen Zeitpunkten $t_{i}$ betrachtet wird. Man geht nun folgendermaßen vor:

1) Jeder Körper hat zu seinem Zeitpunkt $t_{i}$ einen Zeitschritt $Δ t_{i}$ . Man greife denjenigen heraus, für welchen $t_{i} + Δ t_{i}$ den niedrigsten Wert hat (zweiter roter Kreis).

2) Man extrapoliere für alle Massenpunkte ihre momentanen Positionen ${\vec{x}}_{n}$ hin zu den für den Zeitpunkt $t_{i} + Δ t_{i}$ gültigen Positionen ${\vec{x}}_{n + 1}$ (türkise Kreise). Dazu verwende man den Prädiktor. Unabhängig von der Wahl der grundlegenden Lösungsformeln bestimme man für das in Schritt 1 gewählte Objekt mit der gleichen Methode auch die Geschwindigkeit ${\vec{v}}_{n + 1}$ für diesen Zeitpunkt. Verwendet man als Lösungsmethode die Hermite-Polynome, muss man für alle Körper die extrapolierten Geschwindigkeiten ermitteln.

3) Aus den Positionen ${\vec{x}}_{n + 1}$ gewinne man mittels des Gravitationsgesetzes die Beschleunigung ${\vec{a}}_{n + 1}$ , welche zur Zeit $t_{i} + Δ t_{i}$ auf den ausgewählten Körper wirkt. Im Falle der Hermite-Polynome als fundamentales Lösungsschema wird auch der Ruck ${\vec{j}}_{n + 1}$ zum neuen Zeitpunkt benötigt (was erklärt, warum dann auch die Geschwindigkeiten aller Mitglieder des Ensembles extrapoliert werden müssen).

4) Man verbessere die Position ${\vec{x}}_{n + 1}$ des gerade untersuchten Massenpunktes mit Hilfe des Korrektors (dritter roter Kreis). Im Falle des Leapfrog- bzw. Mehrschrittverfahrens braucht man hierzu nur die extrapolierte Geschwindigkeit ${\vec{v}}_{n + 1}$ . Werden die Hermite-Polynome verwendet, geht auch die extrapolierte Beschleunigung ${\vec{a}}_{n + 1}$ in die Korrektur ein. Anschließend verbessere man auf die gleiche Weise die Geschwindigkeit ${\vec{v}}_{n + 1}$ des herausgegriffenen Objekts mittels der Beschleunigung ${\vec{a}}_{n + 1}$ und bei Benutzung der Hermite-Polynome auch mittels des Rucks ${\vec{j}}_{n + 1}$ . Zuletzt aktualisiere man den Zeitschritt $Δ t_{i}$ auf Grundlage des neuen Verhältnisses $v_{n + 1} / a_{n + 1}$ bzw. $a_{n + 1} / j_{n + 1}$ .

5) Nur der in Schritt 1 ausgewählte Körper wird versetzt, alle anderen bleiben auf ihren Positionen ${\vec{x}}_{n}$ zu ihren Zeitpunkten $t_{i}$ . Nun kehre man zu Schritt 1 zurück.

Prädiktor-Korrektor-Verfahren mit variablen Zeitschritten

Sowohl die Hermite-Polynome- als auch Leapfrog-Methode stellen wie bereits erläutert jeweils ein Einschrittverfahren dar. Damit können die für feste Schritte erarbeiteten Lösungsformeln unverändert auch für dynamische Zeitintervalle übernommen werden. Die nachfolgenden C-Codes sind so auch ohne detaillierte Schilderungen verständlich und im Vergleich zu denjenigen für konstante Schritte kaum umfangreicher.

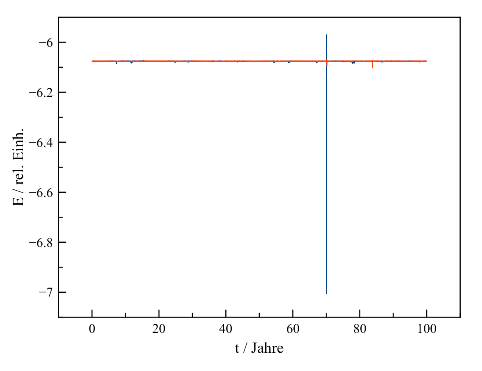
Beispiel mit Hermite-Polynome-Verfahren

Um den Effekt dynamischer Zeitschritte zu demonstrieren, sei abermals das im letzten Kapitel eingeführte Drei-Körper-System herangezogen. Um dieses so genau wie möglich zu modellieren, wird auf eine Glättung der Gravitation verzichtet, der Plummerradius also auf 0 gesetzt. Um hinsichtlich der Energieerhaltung stabile Resultate zu erzielen, darf man die Schrittweite höchstens auf 0.5% des Verhältnisses Beschleunigung / Ruck einstellen, muss also deutlich unter der von Aarseth und Hoyle (1964) empfohlenen Obergrenze von 3% bleiben.

Simulation eines Drei-Körper-Systems mit dem Hermite-Polynome-Verfahren über einen Zeitraum von 100 Jahren mit individuellen dynamischen Zeitschritten pro Massenpunkt. Die Schrittweite beträgt 3% bzw. 0.5% des Verhältnisses Beschleunigung / Ruck (blaue bzw. rote Kurve) des jeweiligen Körpers

Zwar reicht die Festlegung $Δ t$ = 0.03 $a / j$ bereits aus, um trotz der nach 70 Jahren auftretenden Beinahe-Kollision das Ensemble zusammenzuhalten, was gegenüber den bislang benutzten festen Schritten von 1 Tag bereits eine deutliche Verbesserung darstellt. Die Verletzung der Energieerhaltung ist mit mehr als 10% des Absolutwertes aber nach wie vor erheblich. Mit Schritten von 0.005 $a / j$ hingegen wird dieses Ereignis korrekt behandelt, so dass von diesem Zeitpunkt an die beiden Lösungen sich immer weiter auseinander entwickeln.

Nach 83 Jahren kommt es bei der auf feinerer Schrittweite beruhenden Lösung zu einer weiteren, extrem engen Begegnung, bei der sich zwei Körper bis auf weniger als 1 Million km nähern. Auch dieses Mal gelingt es, ein abruptes Auseinanderfliegen des Systems zu vermeiden. Ein genauer Blick auf die Energieerhaltung zeigt aber, dass trotz z.T. extrem kleiner Zeitschritte immer noch ein wenn auch relativ geringer Fehler von etwa einem halben Prozent der Gesamtenergie auftritt.

Testrechnungen, bei denen die Schrittweite anhand des Verhältnisses Geschwindigkeit / Beschleunigung bestimmt wurde, lassen im Vergleich zum Kriterium Beschleunigung / Ruck keinen signifikanten Unterschied erkennen.

Verletzung der Energieerhaltung durch eine Simulation eines Drei-Körper-Systems mit dem Hermite-Polynome-Verfahren über einen Zeitraum von 100 Jahren mit individuellen dynamischen Zeitschritten pro Massenpunkt. Die Schrittweite beträgt 3% bzw. 0.5% des Verhältnisses Beschleunigung / Ruck (blaue bzw. rote Kurve) des jeweiligen Körpers

Die folgenden Abbildungen zeigen sehr eindrucksvoll die Anpassung der zeitlichen Schrittweiten an die aktuellen Gegebenheiten. Zumeist liegen die $Δ t_{i}$ in einer Größenordnung zwischen 1/1000 und 1/10 Jahr, also bei mehreren Stunden bis zu 1 Monat. Wiederholt stellen sich jedoch kurzzeitig außerordentlich kleine Schritte ein, bis herunter zu 1 / 10000000 Jahr entsprechend nur wenigen Sekunden! Betrachtet man die Abstände der Massenpunkte zu ihren nächsten Nachbarn, so zeigt sich, dass diese Momente exakt mit solchen extremer Annäherungen zusammenfallen. Zwar dominieren Distanzen von einer Größenordnung von 1 bis 10 Astronomischen Einheiten. Mehrmals jedoch kommen zwei Körper sich außerordentlich nahe, bis auf wenige 1/1000 Astronomische Einheiten entsprechend einigen 100000 km.

Bei solchen Minimalabständen ist es streng genommen nicht mehr zulässig, die drei Objekte als Massenpunkte zu betrachten. Selbst wenn große Körper nicht miteinander kollidieren, verformen sie sich bei genügend engen Passagen durch wechselseitig ausgeübte Gezeitenkräfte gegenseitig und verändern damit auch ihre Gravitationsfelder. Zudem wird dabei ein Teil der Energie des Mehrkörpersystems in Wärme umgewandelt, so dass die Summe von kinetischer und potentieller Energie nicht mehr erhalten bleibt, sondern vielmehr abnimmt. Wie später erläutert wird, spielen solche Prozesse in den dichten Kernregionen von Kugelsternhaufen durchaus eine signifikante Rolle.

Leider ist es nicht praktikabel, extrem enge Vorübergänge zweier Massenpunkte auf jeden Fall immer korrekt wiedergeben zu wollen. Insbesondere bei komplexen, aus tausenden oder gar Millionen von Objekten bestehenden Systemen treten derartige Ereignisse sehr häufig auf und führen dazu, dass sich die Simulation aufgrund der dann notwendigen sehr kleinen Zeitschritte ständig daran festbeißt. In der Praxis ist man gezwungen, auch bei Verwendung dynamischer Zeitschritte mit einem endlichen Plummerradius zu arbeiten und so wie schon im letzten Unterkapitel angedeutet effektive Untergrenzen für die dynamische Zeitskala sicherzustellen.

Beispiel mit Leapfrog-Verfahren

Die geringere relative Genauigkeit des Leapfrog-Verfahrens macht sich erwartungsgemäß durch eine im Vergleich zu den Hermite-Polynomen etwas schlechtere Energieerhaltung bemerkbar. Bei nahen Vorübergängen zweier Massenpunkte treten Verletzungen des Energiesatzes etwas häufiger auf. Die relativen Fehler, die während der Simulation des schon wiederholt als Testobjekt verwendeten Dreikörpersystems auftreten, bleiben mit einigen 0.01 bis 0.1% aber weiterhin recht gering. Allerdings beobachtet man zusätzlich eine kleine Drift, welche etwa 0.03% dr Gesamtenergie ausmacht.

Trotz nur kleiner Abweichungen hinsichtlich der Gesamtenergie liefert die Leapfrog-Methode eine völlig andere Lösung als das Hermite-Polynome-Verfahren. Die Ursache hierfür liegt jedoch nicht nur in der unterschiedlichen Präzision der beiden Ansätze. Wie später aufgezeigt wird, sind die Orbits innerhalb von Mehrkörperensembles in der Regel äußerst sensibel selbst gegenüber kleinsten Störungen und somit generell nicht prognostizierbar. Für Systeme wie Sternhaufen, Galaxien oder gar noch größere Strukturen muss man für einen Vergleich mit Beobachtungen daher kollektive Eigenschaften wie z.B. die Dichte als Funktion des Abstandes zum Zentrum betrachten.

In dieser Hinsicht ist das Leapfrog-Verfahren trotz seiner nominell etwas schlechteren Stabilität brauchbar, wie z.B. Quinn und andere (1997) ^[5] anhand von Stern- und Galaxienhaufen dargelegt haben. Es bietet gegenüber den Hermite-Polynomen zudem den Vorteil eines wesentlich geringeren Rechenaufwands, da nur Beschleunigungen, nicht aber Rucks betrachtet werden müssen (weshalb die dynamische Schrittweite nun auf dem Verhältnis $v / a$ anstatt $a / j$ beruht). Vor allem für Simulationen mit sehr vielen Massenpunkten wird es daher in der Praxis häufig eingesetzt.

C-Code: Variable Zeitschritte mit Hermite-Polynome-Verfahren

Da der Code für individuelle Zeitskalen mit demjenigen für konstante Schrittweite über weite Passagen identisch ist, können alle bisher definierten Variablen und Prozeduren übernommen werden. Neu sind die Double tneu und tneumin, um den kleinsten soeben vorkommenden Wert $t_{i} + Δ t_{i}$ zu bestimmen. Die unsigned Integer stern gibt an, welcher Körper diesen Minimalwert aufweist, also als nächstes zu simulieren ist. Die Double gamma bezeichnet den Bruchteil des Verhältnisses $| \vec{a} | / | \vec{j} |$ , welcher als dynamische Zeitskala verwendet wird. Neu ist schließlich auch die Double epsilon für den Plummerradius.

Um jedem Massenpunkt eigene Zeitpunkte zuzuordnen, müssen diese zusätzlich zu den bisher verwendeten Größen vorgehalten werden. Dazu dient das Array tau. Ein weiteres Array tdyn definiert die dynamischen Zeitskalen der Objekte. Beide Arrays enthalten Double.

/* Globale Variablen */

unsigned int N;
double epsilon;
double *m;
double ***r;
double ***v;
double ***a;
double ***j;
double s[3];
double c[3];
double *tau;
double *tdyn;

unsigned int i,k;
unsigned int stern;

double t,dt,dt2,dt3,dt4,dt5;
double T;
double tneu,tneumin;
double gamma;

/* Initialisierung aller Massenpunkte aus Anfangspositionen und -geschwindigkeiten  */
/* Beschleunigungen und Rucks                                                       */
/* Zeitpunkte und dynamische Zeitskalen                                             */

t = 0;
for (i = 0;i < N;i ++)
{
  tau[i] = 0;
  ruck (i,N,epsilon,m,r[0],v[0],a[0][i],j[0][i]);
  tdyn[i] = gamma * betrag (a[0][i]) / betrag (j[0][i]);
}

while (t < T)
{

/* Bestimmung des Massenpunkts mit dem kleinsten neuen Zeitpunkt t + delta t */

  tneumin = T;
  for (i = 0;i < N;i ++)
  {
    tneu = tau[i] + tdyn[i];
    if (tneu < tneumin)
    {
      tneumin = tneu;
      stern = i;
    }
  }

  /* Prädiktor-Schritt                                                                                            */
  /* Erste Näherung für neue Positionen nach dem Schema rneu = ralt + valt * dt + aalt * dt2 / 2 + jalt * dt3 / 6 */ 
  /* Erste Näherung für neue Geschwindigkeiten nach dem Schema vneu = valt + aalt * dt + jalt * dt2 / 2           */
  /* Wie bisher für alle Körper, aber nun mit individuellen Zeitschritten dt                                      */

  for (i = 0;i < N;i ++)
  {
    dt = tneumin - tau[i];
    dt2 = pow (dt,2);
    dt3 = pow (dt,3);
    for (k = 0;k < 3;k ++)
    {
      r[1][i][k] = r[0][i][k] + v[0][i][k] * dt + a[0][i][k] * dt2 / 2 + j[0][i][k] * dt3 / 6;
      v[1][i][k] = v[0][i][k] + a[0][i][k] * dt + j[0][i][k] * dt2 / 2;
    }
  }

  /* Korrektor-Schritt - nur einmal durchlaufen                                                    */
  /* Beschleunigung und Ruck an vorläufig neuen Positionen                                         */
  /* Verbesserung der neuen Positionen und Geschwindigkeiten durch Einsetzen in die Lösungsformeln */
  /* Jetzt nur für den Körper mit dem kleinsten neuen Zeitpunkt mit seinem Zeitschritt dt          */

  dt = tneumin - tau[stern];
  dt2 = pow (dt,2);
  dt3 = pow (dt,3);
  dt4 = pow (dt,4);
  dt5 = pow (dt,5);
  ruck (stern,N,epsilon,m,r[1],v[1],a[1][stern],j[1][stern]);
  for (k = 0;k < 3;k ++)
  {
    s[k] = (- 6 * (a[0][stern][k] - a[1][stern][k]) - (4 * j[0][stern][k] + 2 * j[1][stern][k]) * dt) / dt2;
    c[k] = (12 * (a[0][stern][k] - a[1][stern][k]) + 6 * (j[0][stern][k] + j[1][stern][k]) * dt) / dt3;
    r[1][stern][k] += s[k] * dt4 / 24 + c[k] * dt5 / 120;
    v[1][stern][k] += s[k] * dt3 / 6 + c[k] * dt4 / 24;
  }

  /* Aktualisierung des soeben simulierten Objekts */
  /* Verbesserte Position und Geschwindigkeit      */
  /* Beschleunigung und Ruck                       */
  /* Zeitpunkt und dynamische Zeitskala            */

  for (k = 0;k < 3;k ++)
  {
    r[0][stern][k] = r[1][stern][k];
    v[0][stern][k] = v[1][stern][k];
    a[0][stern][k] = a[1][stern][k];
    j[0][stern][k] = j[1][stern][k];
  }
  tau[stern] = tneumin;
  tdyn[stern] = gamma * betrag (a[0][stern]) / betrag (j[0][stern]);

  /* Aktualisierung der verflossenen simulierten Zeit */

  t = tneumin;
}

C-Code: Variable Zeitschritte mit Leapfrog-Verfahren

Die Struktur der C-Codes für Leapfrog- und Hermite-Polynome-Methode ist fast völlig gleich, nur die Lösungsformeln unterschieden sich. Dementsprechend haben die hier verwendeten Variablen exakt die gleiche Bedeutung wie oben.

/* Globale Variablen */

unsigned int N;
double epsilon;
double *m;
double ***r;
double ***v;
double ***a;
double *tau;
double *tdyn;

unsigned int i,k,z;
unsigned int stern;

double t,dt,dt2;
double T;
double tneu,tneumin;
double gamma;

/* Initialisierung aller Massenpunkte aus Anfangspositionen und -geschwindigkeiten  */
/* Beschleunigungen                                                                 */
/* Zeitpunkte und dynamische Zeitskalen                                             */

t = 0;
for (i = 0;i < N;i ++)
{
  tau[i] = 0;
  beschleunigung (i,N,epsilon,m,r[0],a[0][i]);
  tdyn[i] = gamma * betrag (v[0][i]) / betrag (a[0][i]);
}

while (t < T)
{

/* Bestimmung des Massenpunkts mit dem kleinsten neuen Zeitpunkt t + delta t */

  tneumin = T;
  for (i = 0;i < N;i ++)
  {
    tneu = tau[i] + tdyn[i];
    if (tneu < tneumin)
    {
      tneumin = tneu;
      stern = i;
    }
  }

  /* Prädiktor-Schritt                                                                           */
  /* Erste Näherung für neue Positionen nach dem Schema rneu = ralt + valt * dt + aalt * dt2 / 2 */ 
  /* Wie bisher für alle Körper, aber nun mit individuellen Zeitschritten dt                     */ 
  /* Erste Näherung für neue Geschwindigkeiten nach dem Schema vneu = valt + aalt * dt           */ 
  /* Nur für den Körper mit dem kleinsten neuen Zeitpunkt mit seinem Zeitschritt dt              */

  for (i = 0;i < N;i ++)
  {
    dt = tneumin - tau[i];
    dt2 = pow (dt,2);
    for (k = 0;k < 3;k ++)
    {
      r[1][i][k] = r[0][i][k] + v[0][i][k] * dt + a[0][i][k] * dt2 / 2;
      if (i == stern)
      v[1][i][k] = v[0][i][k] + a[0][i][k] * dt + j[0][i][k];
    }
  }

  /* Korrektor-Schritt - drei Mal durchlaufene Iteration                                           */
  /* Beschleunigung an vorläufig neuen Positionen                                                  */
  /* Verbesserung der neuen Positionen und Geschwindigkeiten durch Einsetzen in die Lösungsformeln */
  /* Jetzt nur für den Körper mit dem kleinsten neuen Zeitpunkt mit seinem Zeitschritt dt          */

  dt = tneumin - tau[stern];
  for (z = 0;z < 3;z ++)
  {
    beschleunigung (stern,N,epsilon,m,r[1],a[1][stern]);
    for (k = 0;k < 3;k ++)
    {
      r[1][stern][k] = r[0][stern][k] + (v[0][stern][k] + v[1][stern][k]) * dt / 2;
      v[1][stern][k] = v[0][stern][k] + (a[0][stern][k] + a[1][stern][k]) * dt / 2;
    }
  }

  /* Aktualisierung des soeben simulierten Objekts */
  /* Verbesserte Position und Geschwindigkeit      */
  /* Beschleunigung                                */
  /* Zeitpunkt und dynamische Zeitskala            */

  for (k = 0;k < 3;k ++)
  {
    r[0][stern][k] = r[1][stern][k];
    v[0][stern][k] = v[1][stern][k];
    a[0][stern][k] = a[1][stern][k];
  }
  tau[stern] = tneumin;
  tdyn[stern] = gamma * betrag (v[0][stern]) / betrag (a[0][stern]);

  /* Aktualisierung der verflossenen simulierten Zeit */

  t = tneumin;
}

Mehrschrittverfahren mit variablen Zeitschritten (für Fortgeschrittene)

Modifikation der Lösungsformeln

Das Mehrschrittverfahren nach Adams-Bashforth und Adams-Moulton hat wie die Leapfrog-Methode gegenüber den Hermite-Polynomen den Vorteil, dass man als Größe höchter Ordnung lediglich die Beschleunigung berücksichtigen muss. Die Einführung variabler Zeitschritte hat aber zur Folge, dass auf Grund unterschiedlicher Differenzen zwischen verschiedenen zurückliegenden Zeitpunkten die für konstante Zeitschritte abgeleiteten Formeln nicht mehr gelten. Der Rechenaufwand ist dadurch auch ohne Ruck erheblich, die Programmierung sehr viel aufwendiger. Zwar lassen sich alle wesentlichen Fakten weiterhin zumeist ohne höhere Mathematik darstellen, doch wendet sich dieser Abschnitt dennoch an fortgeschrittene Leser. Wie für feste Schrittweiten wird zunächst der Fall zweier zurückliegender Zeitpunkte $t_{n - 1}$ und $t_{n}$ behandelt.

Adams-Bashforth-Formel für zwei zurückliegende Zeitpunkte

Um die modifizierte Adams-Bashforth-Formel zu gewinnen, wird nun der Ansatz

{\vec{x}}_{n + 1} = {\vec{x}}_{n} + {\vec{v}}_{n} (t_{n + 1} - t_{n}) + \frac{1}{2} {\vec{a}}_{n} (t_{n + 1} - t_{n})^{2}

benutzt. Abermals wird die Beschleunigung $a_{n}$ auf die Geschwindigkeiten ${\vec{v}}_{n}$ und ${\vec{v}}_{n - 1}$ zurückgeführt. Es gilt ${\vec{a}}_{n} = ({\vec{v}}_{n} - {\vec{v}}_{n - 1}) / (t_{n} - t_{n - 1})$ . Durch Einsetzen erhält man als zunächst unhandlich erscheinendes Ergebnis:

{\vec{x}}_{n + 1} = {\vec{x}}_{n} + {\vec{v}}_{n} (t_{n + 1} - t_{n}) + \frac{1}{2} \frac{{\vec{v}}_{n} - {\vec{v}}_{n - 1}}{t_{n} - t_{n - 1}} (t_{n + 1} - t_{n})^{2}

Dieses vereinfacht sich jedoch sehr, wenn man das Verhältnis $α_{n + 1} = (t_{n + 1} - t_{n}) / (t_{n} - t_{n - 1})$ des neuesten zum letzten Zeitschritt einführt:

{\vec{x}}_{n + 1} = {\vec{x}}_{n} + ((1 + \frac{1}{2} α_{n + 1}) {\vec{v}}_{n} - \frac{1}{2} α_{n + 1} {\vec{v}}_{n - 1}) (t_{n + 1} - t_{n})

Analog hierzu liefern die Beschleunigungen ${\vec{a}}_{n}$ und ${\vec{a}}_{n - 1}$ die Geschwindigkeit ${\vec{v}}_{n + 1}$ . Für den Sonderfall einer festen Schrittweite wird $α_{n + 1} = 1$ , womit man die schon im letzten Kapitel erläuterte spezielle Formel erhält.

Adams-Moulton-Formel für zwei zurückliegende Zeitpunkte

Die Herleitung der modifizierten Adams-Moulton-Formel erfordert auch mit nur zwei zurückliegenden Ereignissen viel algebraische Rechenarbeit, wobei sich aber das Verhältnis $α_{n + 1}$ erneut als entscheidendes Maß für die Modifikation erweist. Man startet mit dem Ansatz

{\vec{x}}_{n + 1} = {\vec{x}}_{n} + {\vec{v}}_{n} (t_{n + 1} - t_{n}) + \frac{1}{2} {\vec{a}}_{n} (t_{n + 1} - t_{n})^{2} + \frac{1}{6} {\vec{j}}_{n} (t_{n + 1} - t_{n})^{3}

Relativ einfach ist der Beschleunigungsterm zu behandeln. Wie bisher wird die Beschleunigung ${\vec{a}}_{n}$ durch die Geschwindigkeiten ${\vec{v}}_{n + 1}$ und ${\vec{v}}_{n - 1}$ ausgedrückt gemäß ${\vec{a}}_{n} = ({\vec{v}}_{n + 1} - {\vec{v}}_{n - 1}) / (t_{n + 1} - t_{n - 1})$ . Auf den ersten Blick ist hier von $α_{n + 1}$ nichts zu sehen. Doch kann man den Nenner schreiben als $(t_{n + 1} - t_{n}) + (t_{n} - t_{n - 1})$ . Klammert man jetzt noch $t_{n} - t_{n - 1}$ aus, so liegt für ${\vec{a}}_{n}$ die gewünschte Form vor:

{\vec{a}}_{n} = \frac{{\vec{v}}_{n + 1} - {\vec{v}}_{n}}{(1 + α_{n + 1}) (t_{n} - t_{n - 1})}

Die Multiplikation mit $(t_{n + 1} - t_{n})^{2}$ erlaubt es, $α_{n + 1}$ ein weiteres Mal zu verwenden:

\frac{1}{2} {\vec{a}}_{n} (t_{n + 1} - t_{n})^{2} = \frac{1}{2} \frac{α_{n + 1}}{1 + α_{n + 1}} ({\vec{v}}_{n + 1} - {\vec{v}}_{n - 1}) (t_{n + 1} - t_{n})

Der Ruckterm ist anspruchsvoller. ${\vec{j}}_{n}$ wird wie gehabt durch ${\vec{a}}_{n + 1 / 2}$ und ${\vec{a}}_{n - 1 / 2}$ ersetzt. Es ist ${\vec{j}}_{n} = ({\vec{a}}_{n + 1 / 2} - {\vec{a}}_{n - 1 / 2}) / (t_{n + 1 / 2} - t_{n - 1 / 2})$ . Die beiden Zwischenzeiten lassen sich durch $t_{n + 1 / 2} = 1 / 2 (t_{n + 1} + t_{n})$ und $t_{n - 1 / 2} = 1 / 2 (t_{n} + t_{n - 1})$ auf die gewohnten ganzzahligen Zeitpunkte zurückführen, wodurch der Nenner die Gestalt $1 / 2 (t_{n + 1} - t_{n - 1})$ erhält. Die Zwischenbeschleunigungen können wie schon bekannt durch ${\vec{a}}_{n + 1 / 2} = ({\vec{v}}_{n + 1} - {\vec{v}}_{n}) / (t_{n + 1} - t_{n})$ und ${\vec{a}}_{n - 1 / 2} = ({\vec{v}}_{n} - {\vec{v}}_{n - 1}) / (t_{n} - t_{n - 1})$ ausgedrückt werden. Durch eine ähnliche Umformung der Nenner wie für den Beschleunigungsterm erhält man:

{\vec{j}}_{n} = \frac{2}{(1 + α_{n + 1}) (t_{n} - t_{n - 1})} (\frac{{\vec{v}}_{n + 1} - {\vec{v}}_{n}}{t_{n + 1} - t_{n}} - \frac{{\vec{v}}_{n} - {\vec{v}}_{n - 1}}{t_{n} - t_{n - 1}})

Die Multiplikation mit $(t_{n + 1} - t_{n})^{3}$ bringt eine enorme Vereinfachung mit sich:

\frac{1}{6} {\vec{j}}_{n} (t_{n + 1} - t_{n})^{3} = \frac{1}{3} \frac{α_{n + 1}}{1 + α_{n + 1}} ({\vec{v}}_{n + 1} - (1 + α_{n + 1}) v_{n} + α_{n + 1} {\vec{v}}_{n - 1}) (t_{n + 1} - t_{n})

Fasst man schließlich alle Terme zusammen, so gewinnt man als durchaus noch überschaubares Resultat:

{\vec{x}}_{n + 1} = {\vec{x}}_{n} + (\frac{5}{6} \frac{α_{n + 1}}{1 + α_{n + 1}} {\vec{v}}_{n + 1} + (1 - \frac{1}{3} α_{n + 1}) {\vec{v}}_{n} + \frac{α_{n + 1}}{1 + α_{n + 1}} (\frac{1}{3} α_{n + 1} - \frac{1}{2}) {\vec{v}}_{n - 1}) (t_{n + 1} - t_{n})

Entsprechend liefern die Beschleunigungen ${\vec{a}}_{n + 1}$ , ${\vec{a}}_{n}$ und ${\vec{a}}_{n - 1}$ einen verbesserten Wert für ${\vec{v}}_{n + 1}$ . Mit festen Zeitschritten geht obige Beziehung ebenfalls in das bereits im letzten Kapitel dargestellte Ergebnis über.

Iterationsformeln für beliebige Anzahl zurückliegender Zeitpunkte

Für mehr als zwei zurückliegende Zeitpunkte werden mit variabler zeitlicher Schrittweite die Formeln nach Adams-Bashforth und Adams-Moulton so komplex, dass eine direkte algebraische Darstellung nicht mehr angebracht ist. Nach Lopez und Romay (2010) ^[6] können diese jedoch durch ein iteratives Verfahren ausgewertet werden. Berücksichtigt man die $k + 1$ letzten Zeitpunkte von $t_{n}$ bis zurück nach $t_{n - k}$ , so lautet die Adams-Bashforth-Formel:

({\vec{x}}_{n + 1})_{A B} = {\vec{x}}_{n} + (t_{n + 1} - t_{n}) (g_{0} (n) β_{0} (n) Φ_{0} (n) + ... + g_{k - 1} (n) β_{k - 1} (n) Φ_{k - 1} (n))

Die Korrektur nach Adams-Moulton gewinnt man durch:

({\vec{x}}_{n + 1})_{A M} = ({\vec{x}}_{n + 1})_{A B} + (t_{n + 1} - t_{n}) g_{k} (n) Φ_{k} (n + 1)

$(n)$ bedeutet, dass die entsprechenden Terme für den Zeitpunkt $t_{n}$ zu betrachten sind. Alle Terme $g_{j} (n)$ , $β_{j} (n)$ und $Φ_{j} (n)$ gehen wie nun dargelegt jeweils aus einem Iterationsschema hervor. Am einfachsten schaut dieses für $β_{j} (n)$ aus. Es gilt die Vorschrift:

β_{0} (n) = 1

β_{j} (n) = β_{j - 1} (n) \frac{t_{n + 1} - t_{n + 1 - j}}{t_{n} - t_{n - j}}

Die ersten beiden Iterationen liefern damit:

β_{1} (n) = α_{n + 1}

β_{2} (n) = \frac{1 + α_{n + 1}}{1 + α_{n}} α_{n + 1} α_{n}

Je mehr zurückliegende Zeitpunkte berücksichtigt werden, umso mehr Verhältnisse $α$ zwischen aufeinanderfolgenden Schritten gehen in die Modifikation der originalen Lösungsformeln ein.

Für $Φ_{j} (n)$ ist die Iteration weit aufwendiger. Sie enthält die zurückliegenden Geschwindigkeiten und lautet:

Φ_{0} (n) = v_{n}

Φ_{j} (n) = Φ_{j - 1} (n) - β_{j - 1} (n - 1) Φ_{j - 1} (n - 1)

Für die ersten beiden Stufen erhält man:

Φ_{1} (n) = v_{n} - v_{n - 1}

Φ_{2} (n) = v_{n} - (1 + α_{n}) v_{n - 1} + α_{n} v_{n - 2}

Um einen Term $Φ_{j} (n)$ zu berechnen, muss man sich im Allgemeinen durch alle Terme gemäß des Schemas $Φ_{j - 1} (n - 1)$ , $Φ_{j - 2} (n - 2)$ usw. durchhangeln, bis man ein $Φ_{0} (n - k)$ erreicht hat.

Ähnlich schwierig gestaltet sich die Bestimmung von $g_{j} (n)$ . Es gilt folgender Algorithmus:

g_{j} (n) = c_{j, 1} (n)

c_{j, q} (n) = c_{j - 1, q} (n) - c_{j - 1, q + 1} (n) \frac{t_{n + 1} - t_{n}}{t_{n + 1} - t_{n + 1 - j}}

c_{0, q} (n) = \frac{1}{q}

Um $c_{j, q} (n)$ für ein bestimmtes $j$ zu bestimmen, muss man sukzessiv $c_{j - 1, q + 1}$ , $c_{j - 2, q + 2}$ usw. durchlaufen, bis man bei einem $c_{0, k + 1}$ angekommen ist. Die ersten beiden $g_{j} (n)$ lauten:

g_{1} (n) = \frac{1}{2}

g_{2} (n) = \frac{1}{2} - \frac{1}{6} \frac{α_{n + 1}}{1 + α_{n + 1}}

Um den Rechenaufwand in begrenzen, schlug Aarseth (1985) ^[2] vor, zwar für den gerade untersuchten Körper (mit dem kleinsten $t_{n + 1}$ ) die letzten 5 Zeitpunkte (von $t_{n - 4}$ bis $t_{n}$ ) zu berücksichtigen. Um die für die Adams-Moulton-Korrektur erforderlichen Positionen aller übrigen Massenpunkte zum Zeitpunkt $t_{n + 1}$ zu berechnen, sollten dagegen die letzten drei Zeitpunkte (von $t_{n - 2}$ bis $t_{n}$ ) genügen.

Praktisches Vorgehen

Die iterative Berechnung der Koeffizienten der Adams-Bashforth- und Adams-Moulton-Formeln lässt sich durch die Wahl eines geeigneten Schemas deutlich vereinfachen. Zuerst bestimmt man alle erforderlichen Zeitdifferenzen, danach die Terme $β_{j} (n)$ , zuletzt die $Φ_{j} (n)$ . Unabhängig von den $β_{j} (n)$ und $Φ_{j} (n)$ folgen aus den Zeitdifferenzen direkt die $g (n)$ .

Zeitdifferenzen

Die Konstruktion beginnt mit der Bestimmung aller für die nachfolgenden Berechnungen erforderlichen Zeitdifferenzen. Hierbei stellt sich bei der Entwicklung des Gesamtschemas heraus, dass nur Differenzen der Art $t_{n} - t_{n - j}$ (zwischen aktuellem und einem zurückliegenden Zeitpunkt) und $t_{n + 1} - t_{n + 1 - j}$ (zwischen einem neuen und bezüglich diesem zurückliegenden Zeitpunkt) benötigt werden. Die mit jedem weiter zurückliegenden Zeitpunkt zusätzlich benötigten Differenzen sind nachfolgend für $k$ von 0 bis 4 zusammengestellt.

(\begin{matrix} 0 & t_{n + 1} - t_{n} & - \\ 1 & t_{n + 1} - t_{n - 1} & t_{n} - t_{n - 1} \\ 2 & t_{n + 1} - t_{n - 2} & t_{n} - t_{n - 2} \\ 3 & t_{n + 1} - t_{n - 3} & t_{n} - t_{n - 3} \\ 4 & t_{n + 1} - t_{n - 4} & t_{n} - t_{n - 4} \end{matrix})

Bevor man mit dem Mehrschrittverfahren arbeiten kann, muss man wie schon erwähnt zunächst mit einem Einschrittverfahren mit konstanter Schrittweite $Δ t$ Eingangswerte festlegen. Damit nimmt die Tabelle der Zeitdifferenzen folgende Anfangsgestalt an:

(\begin{matrix} 0 & t_{n + 1} - t_{n} & - \\ 1 & t_{n + 1} - t_{n - 1} & Δ t \\ 2 & t_{n + 1} - t_{n - 2} & 2 Δ t \\ 3 & t_{n + 1} - t_{n - 3} & 3 Δ t \\ 4 & t_{n + 1} - t_{n - 4} & 4 Δ t \end{matrix})

Nach der Bewegung eines Massenpunktes hin zu einer neuen Position muss die Tabelle aktualisiert werden. Dabei nimmt die bisherige Differenz $t_{n} - t_{n - 1}$ den Wert von $t_{n + 1} - t_{n}$ an, die Differenz $t_{n} - t_{n - 2}$ bekommt den Wert von $t_{n + 1} - t_{n - 1}$ usw. Hierbei muss man mit dem ältesten Wert beginnen und sich Schritt für Schritt bis zum Jüngsten durcharbeiten. Der bisherige Zeitpunkt $t_{n - 4}$ bekommt also den Wert $t_{n - 3}$ zugewiesen, $t_{n - 3}$ den Wert $t_{n - 2}$ usw.

Beta-Terme

Mit gegebenen Zeitdifferenzen können die $β$ -Terme ermittelt werden. Aus dem Aufbau des gesamten Algorithmus folgt, dass lediglich Ausdrücke des Typs $β_{j} (n)$ eingehen. Die mit jedem älteren Zeitpunkt hinzutretenden Terme seien wieder als Matrix dargestellt.

(\begin{matrix} 0 & β_{0} (n) \\ 1 & β_{1} (n) \\ 2 & β_{2} (n) \\ 3 & β_{3} (n) \\ 4 & β_{4} (n) \end{matrix})

Zu Beginn der Simulation nimmt diese eine besonders einfache Form an. Im Zähler und Nenner der Konstruktionsformel für die $β$ -Terme werden jeweils gleich viele Zeitpunkte übersprungen. Da die Startwerte auf konstanter Schrittweite beruhen, folgt daraus, dass alle diese Terme am Anfang gleich 1 sind.

Zur Berechnung der $β_{j} (n)$ beginnt man mit $β_{0} (n)$ , gefolgt von $β_{1} (n)$ , $β_{2} (n)$ usw. Da nur Terme mit einer einzigen zeitlichen Referenz (nämlich $t_{n}$ ) gebraucht werden, besteht kein Bedarf für ein spezielles Aktualisierungsschema.

Phi-Terme

Nun stehen alle erforderlichen Informationen für die $Φ$ -Terme bereit. Um die Simulation in Gang zu setzen, muss man jetzt in der Tat alle Ausdrücke bestimmen, die anhand der vorgehaltenen Zeitpunkte gebildet werden können. Nachfolgende Tabelle zeigt die für die Adams-Bashforth-Formel erforderlichen Terme.

(\begin{matrix} 0 & Φ_{0} (n) \\ 1 & Φ_{0} (n - 1) & Φ_{1} (n) \\ 2 & Φ_{0} (n - 2) & Φ_{1} (n - 1) & Φ_{2} (n) \\ 3 & Φ_{0} (n - 3) & Φ_{1} (n - 2) & Φ_{2} (n - 1) & Φ_{3} (n) \\ 4 & Φ_{0} (n - 4) & Φ_{1} (n - 3) & Φ_{2} (n - 2) & Φ_{3} (n - 1) & Φ_{4} (n) \end{matrix})

Zur Auswertung muss man die Matrix zeilenweise durchgehen. Man startet also mit $Φ_{0} (n) = v_{n}$ und $Φ_{0} (n - 1) = v_{n - 1}$ . Letzteres gestatten den Schritt $Φ_{1} (n) = Φ_{0} (n) - Φ_{0} (n - 1)$ . Weiter geht es mit $Φ_{0} (n - 2) = v_{n - 2}$ , was $Φ_{1} (n - 1) = Φ_{0} (n - 1) - Φ_{0} (n - 2)$ und schließlich $Φ_{2} (n) = Φ_{1} (n) - Φ_{1} (n - 1)$ ermöglicht (man erinnere sich, das anfänglich alle $β$ -Terme gleich 1 sind).

Für die Adams-Moulton-Formel werden zusätzlich die Terme des Typs $Φ_{j} (n + 1)$ benötigt. Man muss dazu mit $Φ_{0} (n + 1)$ beginnen und nacheinander alle $Φ_{j} (n + 1)$ bis herauf zu $j = k + 1$ ermitteln.

Nach erfolgter Initialisierung kommt man mit den Komponenten der Art $Φ_{j} (n)$ und $Φ_{j} (n + 1)$ aus, Glieder für weiter zurückliegende Zeitreferenzen werden dann nicht weiter benötigt. Kennt man die neue Position und Geschwindigkeit des momentan betrachteten Objekts, so aktualisiert man zunächst die $Φ_{j} (n + 1)$ gemäß der soeben vorgestellten Reihenfolge. Anschließend aktualisiert man die $Φ_{j} (n)$ . Hierbei bekommt $Φ_{0} (n)$ einfach den Wert von $Φ_{0} (n + 1)$ , $Φ_{1} (n)$ denjenigen von $Φ_{1} (n + 1)$ usw.

g-Terme

Für diese gibt es wie für die $β$ -Terme keine eigentliche Initialisierung und dementsprechend keine Aktualisierung. Die in den Formeln von Adams-Bashforth und Adams-Moulton auftretenden $g (n)$ beruhen auf Koeffizienten $c_{j, q}$ , welche als Referenz allesamt auf einen neuen Zeitpunkt $t_{n + 1}$ zugreifen. Untenstehende Tabelle gibt die für die Adams-Bashforth-Formel erforderlichen Koeffizienten an.

(\begin{matrix} 0 \\ 1 & c_{0, 2} \\ 2 & c_{0, 3} & c_{1, 2} \\ 3 & c_{0, 4} & c_{1, 3} & c_{2, 2} \\ 4 & c_{0, 5} & c_{1, 4} & c_{2, 3} & c_{3, 2} \end{matrix})

Wie bei den $Φ$ -Termen muss man die volle Matrix zeilenweise bearbeiten. Der Startpunkt lautet $g_{0} (n) = 1$ , gefolgt von $c_{0, 2} = 1 / 2$ und $g_{1} (n) = g_{0} (n) - c_{0, 2}$ . Die nächste Zeile beginnt mit $c_{0, 3} = 1 / 3$ . Dies gestattet $c_{1, 2} = c_{0, 2} - c_{0, 3}$ und damit $g_{2} (n) = g_{1} (n) - c_{1, 2} (t_{n + 1} - t_{n}) / (t_{n + 1} - t_{n - 1})$ .

Für die Adams-Moulton-Formel muss obiges Schema noch um eine Zeile erweitert werden. Gemäß dem hier dargestellten Beispiel startet diese mit $c_{0, 6}$ , gefolgt von $c_{1, 5}$ bis hin zu $c_{4, 2}$ , woraus letzendlich $g_{5} (n)$ folgt.

Beispiel des Drei-Körper-Systems

Wendet man das Mehrschrittverfahren mit individuellen Zeitschritten auf das schon mehrfach in diesem Buch behandelte Drei-Körper-System an, so stellt man gegenüber der Hermite-Polynome-Methode eine weitere, aber recht geringfügige Steigerung der Güte der Simulation fest. Um nicht zusätzlich noch Rucks berechnen zu müssen, wird wie für die Leapfrog-Methode das Verhältnis Geschwindigkeit / Beschleunigung als Maß für die Schrittweite herangezogen. Mit einem $Δ t$ von 0.03 $v / a$ wird die enge Begegnung nach 70 Jahren etwas besser modelliert als durch das Hermite-Polynome-Verfahren, jedoch tritt nach wie vor eine deutliche Verletzung der Energieerhaltung mit etwa 5% des absoluten Wertes auf. Bei einer Schrittweite von 0.005 $v / a$ ist überhaupt kein Vorteil zugunsten der Mehrschritt-Methode zu erkennen.

C-Code: Variable Zeitschritte mit Mehrschrittverfahren

Für das Mehrschrittverfahren wird der Code bei Einbeziehung individueller Zeitschritte wesentlich umfangreicher, zudem treten insbesondere für die Berechnung der Koeffizienten der Lösungsformeln zahlreiche neue Variablen hinzu.

Die für die einzelnen Massenpunkte auch schon für feste Zeitschritte benötigten Variablen für Position, Geschwindigkeit und Beschleunigung werden einfach übernommen. Neu sind dagegen die Arrays tau und tauneu für vergangene und neue Zeitpunkte. Ersteres ist als Array von Zeigern zweidimensional, um für jeden Körper die 5 letzten Zeitpunkte, zu denen er simuliert wurde, festzuhalten. Letzteres ist nur eindimensional, um den jeweils neuesten Zeitpunkt anzugeben.

Die für das Lösungsschema erforderlichen Zeitdifferenzen werden durch dtauneu0 bis dtauneu4 und dtau01 bis dtau04 dargestellt. Erstere beziehen sich auf Differenzen $t_{n + 1} - t_{n + 1 - j}$ , letztere auf solche $t_{n} - t_{n - j}$ . Die Ziffer 0 steht also für den Zeitpunkt $t_{n}$ , die Ziffer 1 für $t_{n - 1}$ usw. Im Prinzip könnte man diese Variablen (sowie die nachfolgend diskutierten) weiter durch Arrays zusammenfassen, doch wurde zugunsten einer übersichtlicheren Darstellung der Zusammenhänge darauf verzichtet. Alle Zeitdifferenzen erfordern lediglich eindimensionale Arrays (ein Wert für jeden Massenpunkt).

beta00 bis beta40 repräsentieren die $β_{j} (n)$ . Die erste Ziffer steht für dem Index $j$ . Die 0 bedeutet, daß der Term als Referenz den Zeitpunkt $t_{n}$ verwendet. beta00 wird als Konstante deklariert (weil dessen Wert stets gleich 1 ist), die übrigen Beta-Variablen als eindimensionale Arrays (abermals ein Wert pro Objekt).

Für die eigentliche Simulation werden von den $Φ$ -Termen nur die $Φ_{j} (n + 1)$ und $Φ_{j} (n)$ gebraucht, sowohl für die Geschwindigkeit als auch die Beschleunigung. Die übrigen Elemente der $Φ$ -Matrix treten nur bei der Initialisierung in Erscheinung und werden dort als lokale Variablen deklariert. Die $Φ_{j} (n + 1)$ werden durch phi0neuv bis phi5neuv bzw. phi0neua bis phi5neua dargestellt, die $Φ_{j} (n)$ durch phi00v bis phi40v bzw. phi00a bis phi40a. Wieder steht die erste Ziffer für $j$ , "neu" bzw. die zweite Ziffer für die Zeitreferenz. Neue Phi-Werte für Zeitpunkte n+1 müssen nur für den gerade zu bewegenden Massenpunkt für jede kartesische Komponente bestimmt werden. Dementsprechend sind die dafür erforderlichen Variablen einfache Vektorarrays. Alte Phi-Werte für Zeitpunkte n dagegen müssen für das ganze Ensemble bekannt sein, so dass für die dazugehörigen Variablen Arrays von Zeigern (also wieder zweidimensionale Arrays) erforderlich sind.

g1 bis g5 schließlich beziehen sich auf die g-Terme. g1 und g2 sind immer gleich 1 bzw. 1/2 und werden somit als Konstanten deklariert. g2 bis g4 müssen für alle Massenpunkte gegeben sein und dementsprechend als eindimensionale Arrays definiert werden. g5 hingegen wird nur für den aktuell bearbeiteten Körper als einfache Double benötigt

Die c-Terme c12, c13, c14 und c15 sind mit Werten von 1/6, 1/12, 1/20 und 1/30 ebenfalls Konstanten, die restlichen c-Glieder c22, c23, c24, c32, c33 und c42 hingegen wiederum Variablen. Die beiden Ziffern stehen jetzt für die Indizes $j$ und $q$ . c22, c23 und c32 müssen für das ganze System als eindimensionale Arrays zur Verfügung stehen, c24, c33 und c42 jedoch bloß für das soeben simulierte Objekt als einfache Double.

Die Koeffizienten für die Formeln nach Adams-Bashforth werden durch ABv und ABa für Geschwindigkeit und Beschleunigung angegeben, diejenigen für die Formeln nach Adams-Moulton entsprechend durch AMv und AMa. Letztere sind nur für den soeben zu bewegenden Massenpunkt für jede kartesische Komponente erforderlich, so dass sie lediglich als einfache Vektorarrays deklariert werden müssen. Erste müssen für jeden Massenpunkt in Form von (effektiv zweidimensionalen) Arrays von Zeigern gegeben sein.

Die Variablen tdyn, stern, t, dt, tneu, tneumin, T, gamma und epsilon haben die gleichen Bedeutungen wie in den Codes für das Hermite-Polynome- und Leapfrog-Verfahren.

/* Globale Variablen */

unsigned int i,j,k;
unsigned int stern;
unsigned int N;
unsigned int ordnung;

double *m;
double **r;
double **rneu;
double ***v;
double **vneu;
double ***a;
double **aneu;
double **tau;
double *tauneu;
double *tdyn;

double *dtauneu0,*dtauneu1,*dtauneu2,*dtauneu3,*dtauneu4;
double *dtau01,*dtau02,*dtau03,*dtau04;

const double beta00 = 1; double *beta10,*beta20,*beta30,*beta40;	

double phi0neuv[3],phi1neuv[3],phi2neuv[3],phi3neuv[3],phi4neuv[3],phi5neuv[3];
double **phi00v,**phi10v,**phi20v,**phi30v,**phi40v;

double phi0neua[3],phi1neua[3],phi2neua[3],phi3neua[3],phi4neua[3],phi5neua[3];
double **phi00a,**phi10a,**phi20a,**phi30a,**phi40a;

const double c12 = 0.166666666667; const double c13 = 0.0833333333333;
const double c14 = 0.05; const double c15 = 0.0333333333333;
double *c22,*c23,c24;
double *c32,c33;
double c42;

const double g0 = 1; const double g1 = 0.5; double *g2,*g3,*g4,g5;

double **ABv,**ABa;
double AMv[3],AMa[3];		

double t,dt;
double tneu,tneumin;
double T;

double gamma;
double epsilon;

/* Berechnung der ersten Zustände des Systems mittels des Runge-Kutta-Verfahrens */

rungekutta ();

/* Initialisierung der für die Lösungsformeln gebrauchten Terme */

ABMinitial ();

while (t < T)
{

/* Bestimmung des Massenpunkts mit dem kleinsten neuen Zeitpunkt t + delta t */

  tneumin = T;
  for (i = 0;i < N;i ++)
  {
    tneu = tau[0][i] + tdyn[i];
    if (tneu < tneumin)
    {
      tneumin = tneu;
      stern = i;
    }
  }

/* Prädiktor-Schritt                                                       */
/* Generieren neuer Positionen durch Extrapolation nach Adams-Bashforth    */
/* Wie bisher für alle Körper, aber nun mit individuellen Zeitschritten dt */

  for (i = 0;i < N;i ++)
  {

/* Neue Zeitdifferenzen */

    tauneu[i] = tneumin;
    dtauneu0[i] = tauneu[i] - tau[0][i];
    dtauneu1[i] = tauneu[i] - tau[1][i];
    dtauneu2[i] = tauneu[i] - tau[2][i];
    dtauneu3[i] = tauneu[i] - tau[3][i];
    dtauneu4[i] = tauneu[i] - tau[4][i];

/* Beta-Terme */

    beta10[i] = beta00 * dtauneu0[i] / dtau01[i];
    beta20[i] = beta10[i] * dtauneu1[i] / dtau02[i];
    beta30[i] = beta20[i] * dtauneu2[i] / dtau03[i];
    beta40[i] = beta30[i] * dtauneu3[i] / dtau04[i];

/* g- und c-Terme */

    g2[i] = g1 - c12 * dtauneu0[i] / dtauneu1[i];
    c22[i] = c12 - c13 * dtauneu0[i] / dtauneu1[i];
    g3[i] = g2[i] - c22[i] * dtauneu0[i] / dtauneu2[i];
    c23[i] = c13 - c14 * dtauneu0[i] / dtauneu1[i];
    c32[i] = c22[i] - c23[i] * dtauneu0[i] / dtauneu2[i];
    g4[i] = g3[i] - c32[i] * dtauneu0[i] / dtauneu3[i];

/* Neue Positionen durch modifizierte Formel nach Adams-Bashforth */

    for (k = 0;k < 3;k ++)
    {
      ABv[i][k] = g0 * beta00 * phi00v[i][k] +
                  g1 * beta10[i] * phi10v[i][k] +
                  g2[i] * beta20[i] * phi20v[i][k] +
                  g3[i] * beta30[i] * phi30v[i][k] +
                  g4[i] * beta40[i] * phi40v[i][k];
      rneu[i][k] = r[i][k] + ABv[i][k] * dtauneu0[i];
    }
  }

/* Prädiktor-Schritt                                                              */
/* Generieren neuer Geschwindigkeiten durch Extrapolation nach Adams-Bashforth    */
/* Nur für den Körper mit dem kleinsten neuen Zeitpunkt mit seinem Zeitschritt dt */
/* Keine zusätzlichen Koeffizienten-Berechnungen erforderlich                     */

  for (k = 0;k < 3;k ++)
  {
    ABa[stern][k] = g0 * beta00 * phi00a[stern][k] +
                    g1 * beta10[stern] * phi10a[stern][k] +
                    g2[stern] * beta20[stern] * phi20a[stern][k] +
                    g3[stern] * beta30[stern] * phi30a[stern][k] +
                    g4[stern] * beta40[stern] * phi40a[stern][k];
    vneu[stern][k] = v[0][stern][k] + ABa[stern][k] * dtauneu0[stern];
  }

/* Korrektor-Schritt - nur einmal durchlaufen                                                     */
/* Beschleunigung an vorläufig neuen Positionen                                                   */
/* Verbesserung der neuen Positionen und Geschwindigkeiten durch Interpolation nach Adams-Moulton */
/* Jetzt nur für den Körper mit dem kleinsten neuen Zeitpunkt mit seinem Zeitschritt dt           */

  beschleunigung (stern,N,epsilon,m,rneu,aneu[stern]);

  for (k = 0;k < 3;k ++)
  {

/* Zusätzlich benötigte g- und c-Terme */

    c24 = c14 - c15 * dtauneu0[stern] / dtauneu1[stern];
    c33 = c23[stern] - c24 * dtauneu0[stern] / dtauneu2[stern];
    c42 = c32[stern] - c33 * dtauneu0[stern] / dtauneu3[stern];
    g5 = g4[stern] - c42 * dtauneu0[stern] / dtauneu4[stern];

/* Neue Phi-Terme für Geschwindigkeit */

    phi0neuv[k] = vneu[stern][k];
    phi1neuv[k] = phi0neuv[k] - beta00 * phi00v[stern][k];
    phi2neuv[k] = phi1neuv[k] - beta10[stern] * phi10v[stern][k];
    phi3neuv[k] = phi2neuv[k] - beta20[stern] * phi20v[stern][k];
    phi4neuv[k] = phi3neuv[k] - beta30[stern] * phi30v[stern][k];
    phi5neuv[k] = phi4neuv[k] - beta40[stern] * phi40v[stern][k];

/* Korrigierte Position durch modifizierte Formel nach Adams-Moulton */

    AMv[k] = g5 * phi5neuv[k];
    rneu[stern][k] = r[stern][k] + (ABv[stern][k] + AMv[k]) * dtauneu0[stern];

/* Neue Phi-Terme für Beschleunigung */

    phi0neua[k] = aneu[stern][k];
    phi1neua[k] = phi0neua[k] - beta00 * phi00a[stern][k];
    phi2neua[k] = phi1neua[k] - beta10[stern] * phi10a[stern][k];
    phi3neua[k] = phi2neua[k] - beta20[stern] * phi20a[stern][k];
    phi4neua[k] = phi3neua[k] - beta30[stern] * phi30a[stern][k];
    phi5neua[k] = phi4neua[k] - beta40[stern] * phi40a[stern][k];

/* Korrigierte Geschwindigkeit durch modifizierte Formel nach Adams-Moulton */

    AMa[k] = g5 * phi5neua[k];
    vneu[stern][k] = v[0][stern][k] + (ABa[stern][k] + AMa[k]) * dtauneu0[stern];
  }

/* Aktualisierung des soeben simulierten Objekts */

  ABMaktuell ();

/* Aktualisierung der verflossenen simulierten Zeit */

  t = tneumin;
}

Die Runge-Kutta-Prozedur zur Initialisierung der Simulation unterscheidet sich in keiner Weise vom einfachen Mehrschrittverfahren mit konstanten Zeitschritten. Nach der Bestimmung der anfänglchen Geschwindigkeiten und Beschleunigungen müssen darüber hinaus lediglich die dazugehörigen dynamischen Zeitskalen der Massenpunkte berechnet werden. Die Prozedur wird daher hier nicht nochmals wiedergegeben.

Bei der Initialisierung der in die Lösungsformeln eingehenden Terme ist es entscheidend, die richtige Reihenfolge einzuhalten. Die $Φ$ -Terme für weiter zurückliegende Zeitpunkte $t_{n - 1}$ bis $t_{n - 4}$ werden nur an dieser Stelle benötigt. Die erste Ziffer im Variablennamen gibt abermals den Index $j$ an, die zweite Ziffer die Zeitreferenz.

void ABMinitial (void)
{
  double phi01,phi11,phi21,phi31;
  double phi02,phi12,phi22;
  double phi03,phi13;
  double phi04;

  for (i = 0;i < N;i ++)
  {

/* Zeitpunkte */

    for (j = 0;j < 5;j ++)
    tau[j][i] = (4 - j) * dt;

/* Zeitdifferenzen */

    dtau01[i] = dt;
    dtau02[i] = 2 * dt;
    dtau03[i] = 3 * dt;
    dtau04[i] = 4 * dt;

/* Phi-Terme */

    for (k = 0;k < 3;k ++)
    {

/* Für Geschwindigkeiten */

      phi00v[i][k] = v[0][i][k];

      phi01 = v[1][i][k];
      phi10v[i][k] = phi00v[i][k] - phi01;

      phi02 = v[2][i][k];
      phi11 = phi01 - phi02;
      phi20v[i][k] = phi10v[i][k] - phi11;

      phi03 = v[3][i][k];
      phi12 = phi02 - phi03;
      phi21 = phi11 - phi12;
      phi30v[i][k] = phi20v[i][k] - phi21;

      phi04 = v[4][i][k];
      phi13 = phi03 - phi04;
      phi22 = phi12 - phi13;
      phi31 = phi21 - phi22;
      phi40v[i][k] = phi30v[i][k] - phi31;

/* Für Beschleunigungen */

      phi00a[i][k] = a[0][i][k];

      phi01 = a[1][i][k];
      phi10a[i][k] = phi00a[i][k] - phi01;

      phi02 = a[2][i][k];
      phi11 = phi01 - phi02;
      phi20a[i][k] = phi10a[i][k] - phi11;

      phi03 = a[3][i][k];
      phi12 = phi02 - phi03;
      phi21 = phi11 - phi12;
      phi30a[i][k] = phi20a[i][k] - phi21;

      phi04 = a[4][i][k];
      phi13 = phi03 - phi04;
      phi22 = phi12 - phi13;
      phi31 = phi21 - phi22;
      phi40a[i][k] = phi30a[i][k] - phi31;
    }
  }
}

Nachdem ein Massenpunkt bewegt wurde, müssen sämtliche für diesen definierte Größen aktualisiert werden. Auch hier kommt es auf die genaue Reihenfolge an. Zunächst werden Position, Geschwindigkeit und Beschleunigung aktualisiert, dann folgen Zeitpunkte und Zeitdifferenzen. Endlich werden die $Φ_{j} (n + 1)$ abgearbeitet und ganz zuletzt die $Φ_{j} (n)$ .

void ABMaktuell (void)
{

/* Positionen, Geschwindigkeiten und Beschleunigungen */

  for (k = 0;k < 3;k ++)
  {
    r[stern][k] = rneu[stern][k];
    v[0][stern][k] = vneu[stern][k];
    a[0][stern][k] = aneu[stern][k];
  }

/* Zeitpunkte und dynamische Zeitskalen */

  for (j = 4;j > 0;j --)
  tau[j][stern] = tau[j-1][stern];
  tau[0][stern] = tauneu[stern];
  tdyn[stern] = gamma * betrag (v[0][stern]) / betrag (a[0][stern]);

/* Zeitdifferenzen */

  dtau01[stern] = dtauneu0[stern];
  dtau02[stern] = dtauneu1[stern];
  dtau03[stern] = dtauneu2[stern];
  dtau04[stern] = dtauneu3[stern];

/* Phi-Terme */

  for (k = 0;k < 3;k ++)
  {

/* Für Geschwindigkeiten */

    phi0neuv[k] = vneu[stern][k];
    phi1neuv[k] = phi0neuv[k] - beta00 * phi00v[stern][k];
    phi2neuv[k] = phi1neuv[k] - beta10[stern] * phi10v[stern][k];
    phi3neuv[k] = phi2neuv[k] - beta20[stern] * phi20v[stern][k];
    phi4neuv[k] = phi3neuv[k] - beta30[stern] * phi30v[stern][k];

    phi00v[stern][k] = phi0neuv[k];
    phi10v[stern][k] = phi1neuv[k];
    phi20v[stern][k] = phi2neuv[k];
    phi30v[stern][k] = phi3neuv[k];
    phi40v[stern][k] = phi4neuv[k];

/* Für Beschleunigungen */

    phi0neua[k] = aneu[stern][k];
    phi1neua[k] = phi0neua[k] - beta00 * phi00a[stern][k];
    phi2neua[k] = phi1neua[k] - beta10[stern] * phi10a[stern][k];
    phi3neua[k] = phi2neua[k] - beta20[stern] * phi20a[stern][k];
    phi4neua[k] = phi3neua[k] - beta30[stern] * phi30a[stern][k];

    phi00a[stern][k] = phi0neua[k];
    phi10a[stern][k] = phi1neua[k];
    phi20a[stern][k] = phi2neua[k];
    phi30a[stern][k] = phi3neua[k];
    phi40a[stern][k] = phi4neua[k];
  }
}

Einzelnachweise

↑ Wielen R., Dynamical evolution of star cluster models, in: Veröffentlichung des Astronomischen Recheninstituts Heidelberg Nr.19, 1967
↑ ^2,0 ^2,1 Aarseth S.J., in: Multiple Time Scales, Hrsg. Brackbill und Cohen, Academic Press, New York S.377 ff, 1985
↑ Makino J., Aarseth S.J., On a Hermite integrator with Ahmad-Cohen-scheme for gravitational many-body problems, in: Publications of the Astronomical Society of Japan Band 44, S.141 ff, 1992
↑ Hut P., Makino J., McMillan S., Building a better Leapftog, in: The Astrophysical Journal 443, S.L93 ff, 1995
↑ Quinn T., Katz N., Stadel J., Lake G., Time stepping N-body simulations, in: eprint arXiv:astro-ph/9710043 (unter http://arxiv.org/abs/astro-ph/9710043), 1997
↑ Lopez D.J und Romay J.G., Implementing Adams methods with preassigned stepsize ratios, in: Mathematical Problems in Engineering Band 2010, 2010

[1] Wielen R., Dynamical evolution of star cluster models, in: Veröffentlichung des Astronomischen Recheninstituts Heidelberg Nr.19, 1967

[Aarseth-2] 2,0 ^2,1 Aarseth S.J., in: Multiple Time Scales, Hrsg. Brackbill und Cohen, Academic Press, New York S.377 ff, 1985

[3] Makino J., Aarseth S.J., On a Hermite integrator with Ahmad-Cohen-scheme for gravitational many-body problems, in: Publications of the Astronomical Society of Japan Band 44, S.141 ff, 1992

[4] Hut P., Makino J., McMillan S., Building a better Leapftog, in: The Astrophysical Journal 443, S.L93 ff, 1995

[5] Quinn T., Katz N., Stadel J., Lake G., Time stepping N-body simulations, in: eprint arXiv:astro-ph/9710043 (unter http://arxiv.org/abs/astro-ph/9710043), 1997

[6] Lopez D.J und Romay J.G., Implementing Adams methods with preassigned stepsize ratios, in: Mathematical Problems in Engineering Band 2010, 2010

[1]

[2]

[3]

[4]

[5]

[6]