Das Mehrkörperproblem in der Astronomie/ Hierarchische Algorithmen/ Räumliche Hierarchie

Idee

Um die in einem Mehrkörpersystem herrschenden Kräfte exakt zu bestimmen, muss man wie schon mehrfach erwähnt sämtliche Massenpaare individuell betrachten, wodurch der Rechenaufwand quadratisch mit der Anzahl $N$ der Mitglieder wächst. Dieser rapide Anstieg wird jedoch vermieden, wenn man stattdessen nur die in der näheren Umgebung eines Körpers sich befindlichen Nachbarn exakt behandelt, weiter entfernte Massenpunkte hingegen zu Gruppen zusammenfasst und anstelle der Einzelobjekte nur noch die Schwerpunkte dieser Cluster zur Kräfteberechnung heranzieht. Je weiter eine solche Gruppe entfernt ist, umso größer darf deren räumliche Ausdehnung sein, ohne die von ihr ausgehende Gravitation zu ungenau abzuschätzen. Auf Grundlage dieser Idee lässt sich ein Algorithmus entwickeln, dessen Rechenaufwand in der gewünschten Größenordnung $NlogN$ liegt.

Um Gruppen von Massenpunkten zu definieren, die je nach Entfernung unterschiedlich groß gehalten werden können, wird gemäß dem Verfahren von Barnes und Hut (1986) ^[1] das Ensemble in Würfel (Oktanten) verschiedener Kantenlänge $a/2^{n}$ eingeteilt, wobei $n$ nun unterschiedliche Raumebenen darstellt. Im Gegensatz zur Konstruktion der Zeithierarchie startet man jetzt nicht auf der niedrigsten, sondern der höchsten Ebene (welche nun aber umgekehrt durch $n=0$ gekennzeichnet ist und nicht durch den höchsten vorkommenden Wert von $n$ ). Um das System auf der obersten Ebene mit 8 Würfeln der Kantenlänge $a$ sicher zu überdecken, muss $a$ sich nach dem Abstand des fernsten Körpers vom Gesamtschwerpunkt des Ensembles richten.

Für jeden dieser Würfel wird die Anzahl der darin sich befindlichen Objekte ermittelt. Ist mehr als ein solches in einem Oktanten vorhanden, wird dieser in 8 kleinere Würfel der Größe $a/2$ unterteilt, es tritt die Raumebene $n=1$ hinzu. Im nächsten Schritt werden diese kleineren Kuben überprüft. Findet sich in einem solchen trotz der kleineren Kantenlänge erneut mehr als ein Massenpunkt, erfolgt für diesen eine neuerliche Aufteilung in noch kleinere Würfel mit einer Ausdehnung von nunmehr $a/4$ entsprechend der Ebene $n=2$ . Dieses Verfahren wird solange fortgesetzt, bis in jedem Oktanten nur noch ein Körper anzutreffen ist.

Konstruktion einer Raumhierarchie nach dem Barnes-Hut-Algorithmus

Rücken im Verlauf einer Simulation Massenpunkte eng zusammen, so werden dort u.U. sehr kleine Würfel benötigt, um auf ein Objekt pro solchem zu kommen, d.h. eventuell müssen gleich mehrere Raumebenen angelegt werden. Entfernen sie sich wieder voneinander, sind solch kleine Oktanten und entsprechend tiefe Ebenen nicht mehr erforderlich.

Zwischen Raum- und Zeithierarchie besteht ein fundamentaler Unterschied. Bei letzterer genügt es, die Zeitebenen und die dazugehörigen dynamischen Zeitschritte der einzelnen Körper zu kennen. Hingegen ist für die räumliche Hierarchie die Kenntnis allein der Ebenen und der Dazugehörigkeiten der Massenpunkte zu den entsprechenden Würfeln unzureichend. Wie nachfolgend diskutiert wird, müssen für jeden belegten Kubus auch die Positionen und sofern die Simulation auf dem Hermite-Polynome-Verfahren beruht, auch die Geschwindigkeiten ihrer Schwerpunkte bekannt sein, welche sich mit jedem Simulationsschritt ändern.

Nach jeder Ausführung des Prädiktors muss daher die Raumhierarchie aktualisiert werden. Zunächst überprüft man, ob durch den Prädiktor zumindest ein Massenpunkt bezogen auf die niedrigste Raumebene in einen anderen Würfel überwechselt. Ist das nicht der Fall, können die momentan definierten Oktanten beibehalten werden, nur die Positionen und gegebenenfalls die Geschwindigkeiten ihrer Schwerpunkte müssen neu berechnet werden. Ansonsten muss das hierarchische Gitter selbst neu aufgebaut werden.

Prozeduren im Würfelgitter

Einordnung der Massenpunkte

Die Einstufung der Massenpunkte in die Raumhierarchie ist viel anspruchsvoller als deren Zuordnung zur Zeithierarchie. Bei letzterer genügt es, für jeden Körper nur die Zeitebene vorzuhalten, auf welcher er sich tatsächlich befindet. Im Falle der Raumhierarchie jedoch muss für jedes Objekt nicht nur die Lage bezüglich der tatsächlichen, sondern auch aller darüber liegenden Ebenen bekannt sein. Befindet sich nämlich ein Körper nahe an einem Massenpunkt, dessen Beschleunigung bestimmt werden soll, muss jener als Einzelobjekt oder bestenfalls als zu einer Gruppe geringer Ausdehnung (die schon mit einem kleinen Würfel überdeckt werden kann) zugehörig betrachtet werden. Ist der gleiche Körper weit von einem anderen Massenpunkt entfernt, darf er von diesem aus gesehen als Mitglied eines weiträumigen Clusters (der nur von einem großen Oktanten abgedeckt wird) aufgefasst werden. Betrachtet man in obiger Abbildung z.B. den Massenpunkt oben rechts, so ist dessen nächster Nachbar als Einzelobjekt zu behandeln. Aus der Sicht des Massenpunktes unten links dürfen die beiden Körper oben rechts hingegen zu einer Gruppe zusammengefasst werden. Je nach Perspektive ist ein Objekt somit unterschiedlichen Raumebenen zugehörig.

Die Lage eines Massenpunktes in der Raumhierarchie kann durch ganzzahlige kartesische Koordinaten angegeben werden. Auf der höchsten Ebene sind nur 2*2*2 Würfel vorhanden, die möglichen Werte pro Koordinate also 0 oder 1. Auf der nächsten Ebene existieren 4*4*4 Kuben, so dass sich der mögliche Wertebereich von 0 bis 3 erstreckt. Allgemein weist eine Ebene $n$ $2^{n+1}*2^{n+1}*2^{n+1}$ Oktanten auf, so dass jede Koordinate Werte von 0 bis $2^{n+1}-1$ annehmen kann. In obigem zweidimensionalen Beispiel hat der Massenpunkt rechts oben auf der Ebene 0 die Position (1,1), auf der Ebene 1 die Lage (3,2) und auf seiner niedrigsten Ebene 2 die Koordinaten (7,5).

Die Einordnung der Massenpunkte in das Würfelgitter beruht auf folgenden Algorithmus, für welchen zunächst nur die Struktur erläutert wird. Der dazugehörige C-Code wird im letzten Abschnitt dieses Unterkapitels angegeben.

Start auf höchster Ebene e = 0
while (zumindest zwei Massenpunkte im gleichen Würfel)
{
  Berechnung der Positionen aller Körper i im Würfelgitter bezüglich der aktuell betrachteten Ebene e
  for (i = 0;i < N;i ++)
  {
    if (Ebene des Körpers i = aktuell betrachtete Ebene e)
    {
      Neuer Würfel für Körper i
      for (j = i + 1;j < N;j ++)
      {
        if (Körper j im gleichen Würfel wie Körper i)
        {
          Aufnahme des Körpers j in den Würfel von Körper i
          Verschieben beider Körper i und j auf die nächsttiefere Ebene
        }
      }
    }
  }
  if (zumindest ein Paar i,j mit gemeinsamem Würfel auf aktuell betrachteter Ebene gefunden)
  Analyse auf nächsttieferer Ebene
  e++
}

Zu Beginn auf der obersten Ebene, wird für den ersten Massenpunkt $i$ sogleich ein Würfel der Kantenlänge $a$ angelegt. Die Positionen aller anderen Objekte $j$ auf der aktuell untersuchten Ebene werden mit derjenigen des Körpers $i$ verglichen. Bei gleicher Position (d.h. Zugehörigkeit zum gleichen Oktanten wie Massenpunkt $i$ ) wird $j$ zum Kubus von $i$ hinzugefügt, gleichzeitig beide Körper $i$ und $j$ der nächsttieferen Ebene zugeordnet. Solche Objekte $j$ werden von der laufenden $i$ -Schleife nicht mehr bearbeitet, da diese nur Massenpunkte berücksichtigt, welche der aktuell analysierten Ebene angehören. Dies bedeutet aber, dass nicht alle möglichen Paare $i,j$ geprüft werden müssen, um die Mitglieder des Ensembles in die Raumhierarchie einzuordnen.

Bleibt ein Körper in seinem Würfel allein, wird er nicht auf die nächsttiefere Ebene geschoben. Geht der Algorithmus zur nächsten Ebene über, so wird ein solches Einzelobjekt nicht mehr von der $i$ -Schleife beachtet, da es im Vergleich zur aktuellen Ebene um eine Stufe zurückgeblieben ist. Hingegen erfasst der Algorithmus nun solche Massenpunkte, welche auf der Ebene zuvor von der $j$ -Schleife um eine Stufe nach unten versetzt wurden.

Auf jeder Ebene werden für alle belegten Würfel laufende Nummer, Masse, die Position und eventuell auch die Geschwindigkeit des Schwerpunkts festgehalten, zudem auch die laufende Nummer des jeweils übergeordneten Würfels auf der nächsthöheren Ebene. Um die Schwerpunkte der Oktanten schnell neu berechnen zu können, wird für jeden auch eine Liste mit den Nummern der enthaltenen Massenpunkte angelegt.

Bestimmung von Beschleunigung und Ruck

Um die auf einen Körper ausgeübte Beschleunigung und für das Hermite-Polynome-Verfahren auch den Ruck zu ermitteln, werden jetzt nur die Massenpunkte in dessen unmittelbarer Umgebung als Einzelobjekte betrachtet. Von einer gewissen Entfernung an werden alle in einem Würfel sich befindlichen Objekte kollektiv behandelt, indem die Gesamtmasse des Oktanten sowie die Position und gegebenenfalls auch die Geschwindigkeit dessen Schwerpunkts zur Berechnung herangezogen werden anstatt die entsprechenden Größen der individuellen Mitglieder. Diese Näherung ist zulässig, sofern die Kantenlänge $a/2^{n}$ eines solchen Würfels nicht zu groß ist im Vergleich zu seiner Entfernung $r$ von dem soeben untersuchten Körper, d.h. das Verhältnis zwischen den beiden Längenskalen einen gewissen Wert $\alpha$ nicht überschreitet:

{\frac {a/2^{n}}{r}}<\alpha

Je kleiner dieser Schwellwert gesetzt wird, umso genauer werden die Kräfte zwischen den Mitgliedern eines Mehrkörpersystems bestimmt, umso größer ist jedoch auch der Rechenaufwand. Der hierarchische Algorithmus greift dann erst auf recht tiefer Ebene, da ein im Vergleich zur Kantenlänge eines Kubus erheblicher Abstand desselben verlangt wird. Als Folge davon werden weiterhin viele in der Umgebung eines Körpers sich befindliche Massenpunkte individuell betrachtet, und selbst zu größeren Entfernungen hin zumeist nur kleine Würfel, die lediglich wenige Objekte zu einer Gruppe zusammenfassen. Mit $\alpha$ = 0 wird auf eine Gruppenbildung komplett verzichtet.

Umgekehrt bedeutet ein großer Schwellwert, dass nur noch wenige Massenpunkte in der unmittelbaren Umgebung eines Körpers einzeln behandelt werden. Mit zunehmendem Abstand geht das Verfahren zügig zu Würfeln großer Kantenlänge über, die viele Objekte enthalten können. Die nun sehr effiziente Gruppenbildung und damit kürzere Rechenzeit ist jedoch mit einem größeren Fehler bei der Berechnung der Kräfte im Ensemble erkauft.

Gemäß Barnes und Hut (1986) ^[1] sollte $\alpha$ maximal auf 1 gesetzt werden. Den Autoren zufolge werden dann die auf die einzelnen Mitglieder eines Mehrkörpersystems einwirkenden Kräfte mit einer relativen Genauigkeit von 1% bestimmt.

Das Vorgehen bei der Berechnung der auf einen Körper einwirkenden Beschleunigung und des Rucks wird wie der Algorithmus zur Einordnung der Massenpunkte in die räumliche Hierarchie zunächst rein qualitativ vorgestellt.

for (e = 0;e < Anzahl der Ebenen;e ++)
{
  for (o = 0;o < Anzahl der belegten Oktanten auf Ebene e;o ++)
  {
    if (übergeordneter Oktant bereits abgearbeitet)
    dann auch aktueller Oktant abgearbeitet
    else
    {
      Betrachte Abstand r zwischen aktuellem Oktant und Körper i
      if (Kantenlänge (a / 2^e) / r < alpha oder Oktant enthält nur 1 Massenpunkt)
      {
        Bestimme Beschleunigung und Ruck, welche der aktuelle Oktant auf Körper i ausübt
        aktueller Oktant abgearbeitet
      }
    }
  }
}

Aus der Sicht eines Körpers $i$ werden beginnend mit der höchsten Ebene die gesamte Hierarchie und innerhalb jeder Ebene alle belegten Würfel abgearbeitet. Zuerst wird für den gerade betrachteten Oktanten geprüft, ob der darüber liegende bereits in die Berechnung eingegangen ist. In diesem Fall kann der aktuelle Kubus einfach übergangen und sogleich als abgearbeitet gekennzeichnet werden. Ansonsten wird der Abstand $r$ zwischen dessen Schwerpunkt und dem Körper $i$ ermittelt. Ist $r$ im Vergleich zur Kantenlänge $a/2^{n}$ des Würfels groß genug, so werden alle darin vorhandenen Massenpunkte wie soeben beschrieben als Kollektiv behandelt und dieser wiederum als abgearbeitet markiert. Kann der Oktant wegen einer im Vergleich zu $r$ zu großen Kantenlänge nicht abgearbeitet werden, erfasst der Algorithmus auf der nächsttieferen Ebene dessen Teilwürfel. Enthält ein Kubus nur 1 Massenpunkt, kann er natürlich unabhängig von seiner Größe und Entfernung berücksichtigt werden. Auf diese Weise werden auch diejenigen Objekte einbezogen, welche sich nicht zu Gruppen zusammenfassen lassen, weil sie sich entweder in der unmittelbaren Umgebung des Körpers $i$ oder in Bereichen geringer Dichte aufhalten.

Die Aussagen von Barnes und Hut (1986) ^[1] über die Genauigkeit ihres Verfahrens gelten nur im Mittel. Im Einzelfall hängt der durch die Gruppenbildung bewirkte Fehler stark von der Verteilung der Massenpunkte in einem Würfel ab. Als Beispiele seien die in folgender Skizze dargestellten Fälle diskutiert, in denen jeweils drei Massenpunkte der Masse $m$ durch ihren Schwerpunkt ersetzt werden.

Abschätzung des Fehlers der Kräfteberechnung in einem Mehrkörpersystem durch den Barnes-Hut-Algorithmus. Drei Massenpunkte in der Mitte und an den Seitenflächen eines Würfels der Kantenlänge $d$ und der Entfernung $r$ werden durch ihren Schwerpunkt ersetzt. Die Massenpunkte stehen einmal hinter-, einmal nebeneinander

Im ersten Fall stehen diese hintereinander und üben die Beschleunigungen $Gm/(r-d/2)^{2}$ , $Gm/r^{2}$ und $Gm/(r+d/2)^{2}$ auf. Mit $\alpha =d/r$ lauten diese $Gm/(r^{2}(1-\alpha /2)^{2})$ , $Gm/r^{2}$ und $Gm/(r^{2}(1+\alpha /2)^{2})$ . Ersetzt man die Körper durch ihren Schwerpunkt, so ergibt sich die genäherte Beschleunigung $3Gm/r^{2}$ . Vergleicht man den exakten Wert $a$ mit der Näherung $a_{BH}$ , so gilt folgendes Verhältnis:

{\frac {a}{a_{BH}}}={\frac {1}{3}}\left({\frac {1}{(1-{\frac {\alpha }{2}})^{2}}}+1+{\frac {1}{(1+{\frac {\alpha }{2}})^{2}}}\right)

Im zweiten Fall sind die Massenpunkte nebeneinander postiert. Die Beschleunigungen sind nun $Gm/(r^{2}+d^{2}/4)$ , $Gm/r^{2}$ und wiederum $Gm/(r^{2}+d^{2}/4)$ bzw. $Gm/(r^{2}(1+\alpha ^{2}/4))$ , $Gm/r^{2}$ und nochmals $Gm/(r^{2}(1+\alpha ^{2}/4))$ . Der Vergleich mit der Näherung liefert nun:

{\frac {a}{a_{BH}}}={\frac {1}{3}}\left(1+{\frac {2}{1+{\frac {\alpha ^{2}}{4}}}}\right)

Stehen die Massenpunkte hintereinander, so wird durch eine Gruppenbildung die von diesen ausgeübte Beschleunigung mit einer im Vergleich zur Entfernung zunehmenden Größe des Würfels weit unterschätzt. Mit $\alpha$ = 0.5 liegt der relative Fehler bei knapp 20%, mit $\alpha$ = 1 aber schon bei etwa 80%. Die Ursache für diese erhebliche Abweichung liegt in der $1/r^{2}$ -Abhängigkeit der Gravitation. Liegt der Schwerpunkt eines Oktanten weiter entfernt als ein individueller Massenpunkt, so wird mit der Gruppenbildung die vom einzelnen Körper ausgehende Kraft unterschätzt. Liegt der Schwerpunkt näher als ein Einzelobjekt, so verhält es sich umgekehrt. Die $1/r^{2}$ -Abhängigkeit sorgt jedoch dafür, dass der Fehler im ersten Fall deutlich schwerer wiegt als im letzteren.

Liegen die Massenpunkte nebeneinander, so verhält sich das Verfahren wesentlich stabiler. Mit $\alpha$ = 0.5 und 1 finden sich nun relative Fehler von einigen % und etwas mehr als 10%. Mit einer Gruppenbildung wird die ausgeübte Beschleunigung leicht überschätzt, da die Entfernung zum Schwerpunkt etwas geringer ist als zu den Mittelpunkten der seitlichen Flächen des Würfels.

Gemäß den hier erörterten Beispielen scheint der Fehler des Barnes-Hut-Algorithmus deutlich höher zu liegen als von den Autoren ursprünglich selbst genannt. In einer weiteren Arbeit aus dem Jahr 1989 ^[2] geben diese in der Tat an, dass bei einer geringen Anzahl von Massenpunkten pro Würfel (weniger als 10) mit einem relativen Fehler der Kraft von bis zu 10% gerechnet werden muss. Für die Genauigkeit des Verfahrens ist nicht allein $\alpha$ entscheidend, sondern auch die Zahl der Objekte pro Würfel. Je größer diese ist, umso geringer ist der durch Inhomogenitäten bewirkte Fehler bei der Kräfteberechnung. Vor allem im dichten Zentralbereich eines Mehrkörpersystems sind somit zuverlässige Ergebnisse zu erwarten. Man kann zudem davon ausgehen, dass die dort sich befindlichen Massenpunkte von allen Seiten von Würfeln mit relativ vielen Einzelkörpern umgeben sind und sich die pro Oktant eingeführten Fehler so in erheblichem Maße gegenseitig aufheben. Finden sich mehr als 1000 Massenpunkte pro Würfel, ist selbst mit einem $\alpha$ von 1 ein relativer Fehler der Kraft von nur einigen 0.1% gegeben.

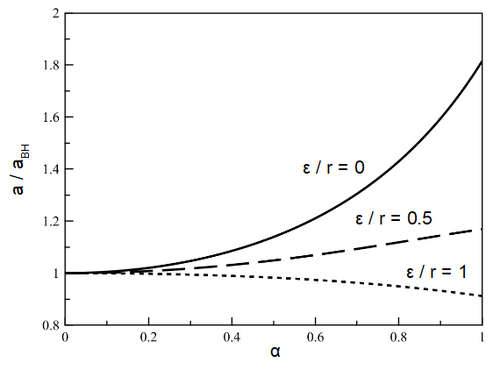
Wird die Anziehungskraft gemäß der Methode von Aarseth geglättet, wirkt sich dies zusätzlich stabilisierend auf den Barnes-Hut-Algorithmus aus. Dessen relativer Fehler hängt jetzt auch davon ab, wie weit ein Oktant im Vergleich zum Plummerradius $\epsilon$ entfernt ist, also vom Verhältnis $\beta =\epsilon /r$ . Betrachtet man obiges Beispiel abermals für den ungünstigsten Fall hintereinander stehender Massenpunkte, so gilt:

{\frac {a}{a_{BH}}}={\frac {1}{3}}(1+\beta ^{2})^{3/2}\left({\frac {1-\alpha /2}{((1-\alpha /2)^{2}+\beta ^{2})^{3/2}}}+{\frac {1}{(1+\beta ^{2})^{3/2}}}+{\frac {1+\alpha /2}{((1+\alpha /2)^{2}+\beta ^{2})^{3/2}}}\right)

Beträgt der Abstand des Oktanten das doppelte des Plummerradius, so tritt bei einem $\alpha$ von 0.5 ein relativer Fehler von nur noch circa 3% Prozent in Erscheinung. Wird ein $\alpha$ gleich 1 zugelassen, steigt bei unveränderter Glättung der Gravitation die Abweichung auf immerhin noch etwa 15%. Ist $\epsilon$ der Distanz des Würfels gleich, so liegen die entsprechenden relativen Fehler nur noch bei circa 2% und 10%. Zudem kehrt der durch die Gruppenbildung begangene Fehler bei der Kräfteberechnung jetzt seine Richtung um: Diese liefert jetzt größere Beschleunigungen als die exakte Betrachtung, da für Abstände kleiner als der Plummerradius Aarseth's Glättungsformel eine um so geringere Kraft liefert, je geringer die Entfernung zwischen zwei Massenpunkten ist. Gerade dann, wenn eine stark inhomogene Verteilung von Massenpunkten gleichzeitig von sehr kleinen Abständen zwischen einzelnen Körpern (d.h. in der Größenordnung des Plummerradius) begleitet wird, erweist sich für ein geglättetes Gravitationsgesetz das Barnes-Hut-Verfahren also als recht stabil.

{\displaystyle \epsilon } — Abschätzung des Fehlers der Kräfteberechnung in einem Mehrkörpersystem durch den Barnes-Hut-Algorithmus für das Szenario dreier hintereinander stehender Massenpunkte für verschiedene Plummerradien $\epsilon$ im Vergleich zur Entfernung $r$ des Würfels. Die drei Kurven entsprechen von oben nach unten den Fällen $\epsilon /r$ gleich 0, 0.5 und 1

Insgesamt wird die Genauigkeit einer Mehrkörpersimulation mittels hierarchischer Kräfteberechnung zumeist von deren Fehlern dominiert und nicht von der Wahl der Lösungsformel für die sukzessive Berechnung von zurückgelegten Strecken und Geschwindigkeiten. Auch dies rechtfertigt, das nominell ungenauere Leapfrog-Verfahren den Hermite-Polynomen vorzuziehen.

Abschließend sei als praktisches Beispiel ein weiteres Mal das schon wiederholt besprochene Drei-Körper-System herangezogen. Der Parameter $\alpha$ wird auf 0.1 gesetzt, d.h. aus der Sicht eines Massenpunktes die beiden übrigen Objekte erst dann zu einer Gruppe zusammengefasst, wenn der überdeckende Würfel mindestens 10 Mal kleiner ist als dessen Entfernung. Obwohl damit bei der Berechnung der von einem solchen Paar ausgehenden Gesamtkraft lediglich ein geringer Fehler in der Größenordnung von zumeist nur 0.1% begangen wird, sind die Auswirkungen der Näherung bereits drastisch. Die originalen und die genäherten Bahnen weichen im Laufe der Zeit immer mehr voneinander ab, bis schließlich jede Ähnlichkeit verschwunden ist. Für die Bearbeitung von Problemen, wo es auf eine möglichst exakte Vorhersage der einzelnen Orbits ankommt (z.B. der Frage nach der Langzeitstabilität der Planetenbahnen), ist der Barnes-Hut-Algorithmus also völlig ungeeignet. Erfolgreich kann er dagegen bei aus sehr vielen Einzelobjekten bestehenden Systemen eingesetzt werden, wo die genaue individuelle Bahn eines Körpers in der Regel nicht von Bedeutung ist. Bei Kugelsternhaufen oder Galaxien beispielsweise ist es meist ausreichend, wenn großräumige Eigenschaften wie z.B. die Verteilung der Dichte oder die Häufigkeit von Geschwindigkeiten richtig modelliert werden. Welche Auswirkungen hierbei unterschiedliche Einstellungen von $\alpha$ haben, wird im Praxiskapitel gezeigt.

Simulation eines Drei-Körper-Systems mit dem Hermite-Polynome-Verfahren über einen Zeitraum von 100 Jahren mit hierarchischen Zeitschritten pro Massenpunkt bei gleichzeitiger Verwendung des Barnes-Hut-Algorithmus. Die Festlegung der Zeitschritte beruht auf einer dynamischen Zeitskala von 0.5% des Verhältnisses Beschleunigung / Ruck. Die Zusammenfassung einzelner Massenpunkte zu einem Gesamtobjekt erfolgt unter der Maßgabe $\alpha$ = 0.1 (rote Kurve). Die Näherung ist mit der auf exakter Kräfteberechnung beruhenden Lösung (blaue Kurve) zunächst fast deckungsgleich. Wegen der unterschiedlichen auf jeweils einen Massenpunkt einwirkenden Kräfte entwickeln sich die Bahnen im Laufe der Zeit jedoch immer weiter auseinander

Aktualisierung der Raumhierarchie

Nach jeder Anwendung des Prädiktors muss die Raumhierarchie aktualisiert werden. Da die Massenpunkte durch eine einmalige Anwendung der Prognoseformel nur kurze Strecken zurücklegen, bleiben diese selbst auf der niedrigsten Raumebene oft allesamt in ihren aktuellen Würfeln. Für viele Simulationsschritte genügt es somit, die Schwerpunkte der momentan definierten Oktanten neu zu bestimmen. Dazu dient das folgende Verfahren, dessen Code wiederum im letzten Abschnitt dieses Unterkapitels gegeben wird.

for (e = Anzahl der Ebenen - 1;e > 0;e --)
{
  for (o = 0;o < Anzahl der belegten Oktanten auf Ebene e;o ++)
  {
    Summiere für Schwerpunktberechnung über alle im aktuellen Oktanten vorhandenen Massenpunkte i
    sofern diese nicht schon abgearbeitet sind
    Markiere jeden vorhandenen Massenpunkt i als abgearbeitet
  }

  if (e > 0)
  {
    for (o = 0;o < Anzahl der belegten Oktenten auf Ebene e;o ++)
    {
      Betrachte die soeben aktualisierten Oktanten auf Ebene e selbst als Massenpunkte
      Addiere sie zu ihren übergeordneten Oktanten auf Ebene e - 1 hinzu
    }
  } 
}

Die Neuberechnung der Würfelschwerpunkte startet im Gegensatz zu den bisher vorgestellten Algorithmen auf der untersten Raumebene. Zuerst werden die kleinsten Kuben aktualisiert, indem über die dort vorhandenen Massenpunkte $i$ (auf der niedrigsten Ebene zwangsläufig immer nur einer pro Würfel) aufsummiert wird, wobei jeder Körper $i$ als abgearbeitet markiert wird. Die Oktanten können nun selbst als Massenpunkte angesehen und zu den ihnen übergeordneten Würfeln addiert werden. Dieses Prinzip wird auf allen Ebenen wiederholt. Massenpunkte $i$ , welche tiefer eingeordnet sind als die momentan abgearbeitete Ebene, müssen somit nicht nochmals individuell berücksichtigt werden. Auf jeder Ebene wird der Inhalt eines Oktanten jeweils an seinen übergeordneten Würfel weitergereicht.

C-Code: Raumhierarchie mit Hermite-Polynome-Verfahren

Alle bisher eingeführten Variablen werden übernommen, doch treten für die Raumhierarchie zahlreiche neue hinzu. Die unsigned Integer e und o dienen im Folgenden dazu, Raumebenen und belegte Würfel (Oktanten) innerhalb einer solchen abzuzählen. Nebene gibt die Anzahl der Raumebenen, das eindimensionale Array Noktant die Anzahl belegter Kuben pro Ebene an.

Für jeden Massenpunkt wird seine tiefste Raumebene durch das einfache Array ebene_raum angezeigt. Das zweidimensionale Array status_raum listet die entsprechenden Koordinaten im Würfelgitter auf (wobei als Datentyp aber unsigned Long anstatt unsigned Integer verwendet wird). Der erste Index des Arrays bezieht sich erwartungsgemäß auf den Körper, der zweite auf die Koordinate. Als weiteres zweidimensionales Array hält nr_raum für jedes Objekt auf jeder Raumebene die Nummer des Würfels vor, in welchem es sich befindet. Hier bezieht sich der erste Index auf die Ebene und erst der zweite auf den Massenpunkt.

Bei den Variablen, welche verschiedene Größen der belegten Oktanten bezeichnen, bezieht sich der erste Index stets auf die Ebene, der zweiter auf den Würfel und bei Vektorgrößen ein dritter auf die Koordinate. Die zweidimensionalen Arrays No (für unsigned Integer) und Mo (für Double) geben auf jeder Ebene für jeden Kubus die Anzahl dort vorhandener Körper und deren Gesamtmasse an. Die dreidimensionalen Arrays ro und vo (wieder für Double) halten die Schwerpunktpositionen und -geschwindigkeiten der Oktanten vor. Das einfache Array Ao liefert pro Raumebene die Kantenlänge der Würfel. nruebero und flago stellen wieder zweidimensionale Arrays für unsigned Integer dar. nruebero kennzeichnet auf jeder Ebene für jeden Würfel die Nummer des übergeordneten Oktanten. flago zeigt an, ob ein Würfel im Laufe einer Kräfteberechnung bereits erfasst wurde oder nicht.

Um die in einem Oktanten vorhandenen Massenpunkte festzuhalten, wird das dreidimensionale Array nrobjekto für unsigned Integer eingeführt. Ein weiteres Mal repräsentieren die ersten beiden Indizes Raumebene und Würfel. Der dritte Index dient nun dazu, die Nummern der im Kubus sich befindlichen Körper aufzulisten. Um festzustellen, ob ein Einzelobjekt bei einer Neuberechnung der Schwerpunktpositionen und -geschwindigkeiten der Oktanten bereits einbezogen wurde, dient das eindimensionale Array flag.

Als letzte Variable ist alpha zu nennen, das für die Gruppenbildung entscheidende Verhältnis zwischen Kantenlänge und Entfernung eines Würfels zu dem zu simulierenden Massenpunkt.

/* Alte globale Variablen */

unsigned int i,k;
unsigned int N;
 
double *m;
double ***r;
double ***v;
double ***a;
double ***j;
double s[3];
double c[3];
double *tdyn;
int *ebene_zeit;
unsigned int potenz[16];
double *status_zeit;
 
double t,dt,dt2,dt3,dt4,dt5;
double dtmin;
unsigned long Z;
double tdynmin;
double T;
 
double gamma;
double epsilon,epsilon2,epsilon3;

/* Neue globale Variablen */

unsigned int e,o;
unsigned int Nebene;
unsigned int *Noktant;

unsigned int *ebene_raum;
unsigned long **status_raum;
unsigned int **nr_raum;

unsigned int **No;
double **Mo;
double ***ro;
double ***vo;
double *Ao;
unsigned int **nruebero;
unsigned int **flago;
unsigned int ***nrobjekto;
unsigned int *flag;

double alpha;

Der Hauptcode bleibt - auch mit Einbeziehung der Zeithierarchie - fast unverändert gültig. Während der Ausführung des Prädiktors wird nun aber überprüft, ob dadurch die Massenpunkte bezogen auf die unterste Raumebene in ihren Würfeln bleiben oder nicht. Dies geschieht mittels der lokalen unsigned Integer status_raum_neu, die immer um 1 hochgezählt wird, sobald ein Übergang eines Körpers zu einem anderen Oktanten festgestellt wird. Im allerersten Simulationsschritt erfolgt diese Prüfung noch nicht, da die Raumhierarchie an sich erst einmal angelegt werden muss. Der Prädiktorschritt sieht nun folgendermaßen aus:

    status_raum_neu = 0;
    for (i = 0;i < N;i ++)
    {
      dt = t - status_zeit[i] + dtmin;
      dt2 = pow (dt,2);
      dt3 = pow (dt,3);
      for (k = 0;k < 3;k ++)
      {
        r[1][i][k] = r[0][i][k] + v[0][i][k] * dt + a[0][i][k] * dt2 / 2 + j[0][i][k] * dt3 / 6;
        if (t > 0 && (unsigned long) floor ((r[1][i][k] + Ao[0]) / Ao[Nebene-1]) != status_raum[i][k])
        status_raum_neu ++;
        v[1][i][k] = v[0][i][k] + a[0][i][k] * dt + j[0][i][k] * dt2 / 2;
      }
    }

Halten sich alle Körper des Ensembles weiterhin in ihren bisherigen Würfeln auf (was durch status_raum_neu = 0 erkannt wird), so reicht vor dem Korrektorschritt eine Neuberechnung der Oktantenschwerpunkte aus. Anderenfalls muss die Raumhierarchie neu konstruiert werden. Dementsprechend lauten die nächsten Anweisungen:

    if (t > 0 && status_raum_neu == 0)
    updatehierarchie (N,m,r[1],v[1]);
    else
    {
      speicherfreigabehierarchie ();
      raumhierarchie (N,m,r[1],v[1]);
    }

Für die Neudefinition der Raumhierarchie dient eine gesonderte Prozedur, welche mit raumhierarchie (N,m,r[1],v[1]) aufgerufen wird. Übergeben werden dieser die Anzahl der Objekte, deren Massen uund die mittels des Prädiktors vorhergesagten Positionen und Geschwindigkeiten.

Für die Konstruktion des Würfelgitters ist eine dynamische Speicherverwaltung zwingend erforderlich, da zu Beginn weder die Anzahl der Raumebenen noch die Anzahl der belegten Oktanten pro Ebene bekannt sind. Deshalb sind die entsprechenden Anweisungen im nachfolgenden Code mit angegeben. Bevor eine neue Hierarchie definiert werden kann, muss der von der bisherigen belegte Speicher freigegeben werden, was wiederum durch eine eigene, hier nicht weiter ausgeführte Prozedur geschehen kann.

Die lokalen Variablen innerhalb der Prozedur haben folgende Bedeutung. Die Double abstand gibt die Entfernung eines Körpers vom Koordinatenursprung (Schwerpunkt des Gesamtsystems) an. Die unsigned Integer gleich zählt ab, wie oft auf der gerade analysierten Raumebene zwei Körper innerhalb des gleichen Würfels gefunden wurden. i und j zählen die Massenpunkte selbst ab.

void raumhierarchie (unsigned int N, double *m, double **r, double **v)
{
  double abstand;
  unsigned int gleich;
  unsigned int i,j;

/* Kantenlänge eines Würfels auf Ebene 0 gleich Abstand des fernsten Massenpunkts vom Ursprung */

  Ao = malloc (sizeof (double));
  Ao[0] = 0;
  for (i = 0;i < N;i ++)
  {
    ebene_raum[i] = 0;
    abstand = betrag (r[i]);
    if (Ao[0] < abstand)
    Ao[0] = abstand;
  }

/* Speicherzuweisung und Initialisierung des ersten Würfels auf Ebene 0 */
/* Anzahl der Würfel pro Ebene                                          */

  Noktant = malloc (sizeof (double));

/* Anzahl der Massenpunkte pro Würfel */

  No = malloc (sizeof (double *));
  No[0] = malloc (sizeof (double));
  No[0][0] = 0;

/* Masse pro Würfel */

  Mo = malloc (sizeof (double *));
  Mo[0] = malloc (sizeof (double));
  Mo[0][0] = 0;

/* Schwerpunktposition pro Würfel */

  ro = malloc (sizeof (double **));
  ro[0] = malloc (sizeof (double *));
  ro[0][0] = malloc (3 * sizeof (double));
  for (k = 0;k < 3;k ++)
  ro[0][0][k] = 0;

/* Schwerpunktgeschwindigkeit pro Würfel */

  vo = malloc (sizeof (double **));
  vo[0] = malloc (sizeof (double *));
  vo[0][0] = malloc (3 * sizeof (double));
  for (k = 0;k < 3;k ++)
  vo[0][0][k] = 0;

/* Nummer des übergeordneten Oktanten pro Würfel */

  nruebero = malloc (sizeof (unsigned int *));
  nruebero[0] = malloc (sizeof (unsigned int));
  nruebero[0][0] = 0;

/* Zur späteren Berechnung von Beschleunigung und Rucks verwendetes Flag pro Würfel */

  flago = malloc (sizeof (unsigned int *));
  flago[0] = malloc (sizeof (unsigned int));

/* Nummer des Würfels in welchem sich ein bestimmter Massenpunkt aufhält */

  nr_raum = malloc (sizeof (unsigned int *));
  nr_raum[0] = malloc (N * sizeof (int));

/* Liste vorhandenen Massenpunkte pro Würfel */

  nrobjekto = malloc (sizeof (unsigned int **));
  nrobjekto[0] = malloc (sizeof (unsigned int *));
  nrobjekto[0][0] = malloc (sizeof (unsigned int));

/* Start des Algorithmus */

  gleich = 65535;
  e = 0;

/* Anlegen einer neuen Ebene, falls auf letzter Ebene zumindest 1 Würfel mit mehr als 1 Massenpunkt vorhanden */

  while (gleich > 0)
  {

/* Kantenlänge eines Würfels auf Ebene e halb so groß wie auf Ebene e-1 */

    if (e > 0)
    {
      Ao = realloc (Ao,(e + 1) * sizeof (double));
      Ao[e] = Ao[e-1] / 2;
    }

/* Für alle Massenpunkte Umrechnen der (kontinuierlichen) kartesischen in (diskrete) Gitterkoordinaten */

    for (i = 0;i < N;i ++)
    {
      for (k = 0;k < 3;k ++)
      status_raum[i][k] = (unsigned int) floor ((r[i][k] + Ao[0]) / Ao[e]);
    }

    if (e > 0)
    {

/* Speicherzuweisung und Initialisierung des ersten Würfels auf Ebene e */
/* Folgt dem gleichen Schema wie auf Ebene 0                            */
/* Man beachte, dass bereits e Ebenen vorhanden sind                    */

      Noktant = realloc (Noktant,(e + 1) * sizeof (double));
      No = realloc (No, (e + 1) * sizeof (double *));
      No[e] = malloc (sizeof (double));
      No[e][0] = 0;
      Mo = realloc (Mo, (e + 1) * sizeof (double *));
      Mo[e] = malloc (sizeof (double));
      Mo[e][0] = 0;
      ro = realloc (ro, (e + 1) * sizeof (double **));
      ro[e] = malloc (sizeof (double *));
      ro[e][0] = malloc (3 * sizeof (double));
      for (k = 0;k < 3;k ++)
      ro[e][0][k] = 0;
      vo = realloc (vo, (e + 1) * sizeof (double **));
      vo[e] = malloc (sizeof (double *));
      vo[e][0] = malloc (3 * sizeof (double));
      for (k = 0;k < 3;k ++)
      vo[e][0][k] = 0;
      nruebero = realloc (nruebero, (e + 1) * sizeof (unsigned int *));
      nruebero[e] = malloc (sizeof (unsigned int));
      nruebero[e][0] = 0;
      flago = realloc (flago, (e + 1) * sizeof (unsigned int *));
      flago[e] = malloc (sizeof (unsigned int));
      nr_raum = realloc (nr_raum, (e + 1) * sizeof (unsigned int *));
      nr_raum[e] = malloc (N * sizeof (int));
      nrobjekto = realloc (nrobjekto, (e + 1) * sizeof (unsigned int **));
      nrobjekto[e] = malloc (sizeof (unsigned int *));
      nrobjekto[e][0] = malloc (sizeof (unsigned int));
    }
    Noktant[e] = 0;

/* Abarbeiten aller Massenpunkte */

    gleich = 0;
    for (i = 0;i < N;i ++)
    {

/* Anlegen eines Würfels für Massenpunkt i falls                                                     */
/* dieser auf Ebene e-1 die Ebene e zugewiesen bekommen hat (dort nicht allein in seinem Würfel war) */

      if (ebene_raum[i] == e)
      {

/* Hinzufügen des Massenpunkts i zu dem neuen Würfel  */
/* Aufnahme in die Liste der Massenpunkte des Würfels */

        if (No[e][Noktant[e]] > 0)
        nrobjekto[e][Noktant[e]] = realloc (nrobjekto[e][Noktant[e]], 
                                            (No[e][Noktant[e]] + 1) * sizeof (unsigned int *));
        nrobjekto[e][Noktant[e]][No[e][Noktant[e]]] = i;

/* Aktualisierte Anzahl der Massenpunkte im Würfel */

        No[e][Noktant[e]] ++;

/* Aktualisierte Masse */

        Mo[e][Noktant[e]] += m[i];

/* Aktualisierte Schwerpunktposition und -geschwindigkeit */

        for (k = 0;k < 3;k ++)
        {
          ro[e][Noktant[e]][k] += m[i] * r[i][k];
          vo[e][Noktant[e]][k] += m[i] * v[i][k];
        }

/* Nummer des übergeordneten Würfels */

        if (e > 0)
        nruebero[e][Noktant[e]] = nr_raum[e-1][i];

/* Vorhalten der Nummer des neuen Würfels für den Massenpunkt i */

        nr_raum[e][i] = Noktant[e];

/* Abarbeiten aller Massenpunktpaare */

        for (j = i + 1;j < N;j ++)
        {

/* Vergleich der Gitterkoordinaten für das Paar (i,j)                              */
/* Falls Koordinaten identisch und auch Massenpunkt j auf Ebene e                  */
/* Verschieben beider auf nächsttiefere Ebene, da im aktuellen Würfel nicht allein */

          if (status_raum[j][0] == status_raum[i][0] && status_raum[j][1] == status_raum[i][1] &&
              status_raum[j][2] == status_raum[i][2] && ebene_raum[j] == e)
          {
            ebene_raum[i] = e + 1;
            ebene_raum[j] = e + 1;

/* Abzählen der Ereignisse, dass Paare innerhalb des gleichen Würfels gefunden wurden */

            gleich ++;

/* Hinzufügen des Massenpunktes j zu dem gleichen Würfel wie Massenpunkt i */
/* Folgt dem gleichen Schema wie für Massenpunkt i                         */

            nrobjekto[e][Noktant[e]] = realloc (nrobjekto[e][Noktant[e]],
                                                (No[e][Noktant[e]] + 1) * sizeof (unsigned int *));
            nrobjekto[e][Noktant[e]][No[e][Noktant[e]]] = j;

            No[e][Noktant[e]] ++;
            Mo[e][Noktant[e]] += m[j];
            for (k = 0;k < 3;k ++)
            {
              ro[e][Noktant[e]][k] += m[j] * r[j][k];
              vo[e][Noktant[e]][k] += m[j] * v[j][k];
            }
            nr_raum[e][j] = Noktant[e];
          }
        }

/* Nach Ende der j-Schleife Speicherzuweisung und Initialisierung des nächsten Würfels auf Ebene e */
/* Folgt abermals dem gleichen Schema wie die vorherigen Zuweisungen                               */
/* Man beachte, dass bereits Noktant[e] Würfel auf Ebene e vorhanden sind                          */

        Noktant[e] ++;
        No[e] = realloc (No[e], (Noktant[e] + 1) * sizeof (double));
        No[e][Noktant[e]] = 0;
        Mo[e] = realloc (Mo[e], (Noktant[e] + 1) * sizeof (double));
        Mo[e][Noktant[e]] = 0;
        ro[e] = realloc (ro[e], (Noktant[e] + 1) * sizeof (double *));
        ro[e][Noktant[e]] = malloc (3 * sizeof (double));
        for (k = 0;k < 3;k ++)
        ro[e][Noktant[e]][k] = 0;
        vo[e] = realloc (vo[e], (Noktant[e] + 1) * sizeof (double *));
        vo[e][Noktant[e]] = malloc (3 * sizeof (double));
        for (k = 0;k < 3;k ++)
        vo[e][Noktant[e]][k] = 0;
        nruebero[e] = realloc (nruebero[e], (Noktant[e] + 1) * sizeof (unsigned int));
        nruebero[e][Noktant[e]] = 0;
        flago[e] = realloc (flago[e], (Noktant[e] + 1) * sizeof (unsigned int));
        nrobjekto[e] = realloc (nrobjekto[e], (Noktant[e] + 1) * sizeof (unsigned int *));
        nrobjekto[e][Noktant[e]] = malloc (sizeof (unsigned int));
      }
    }

/* Nach Ende der i-Schleife Abschluss der Berechnung von Schwerpunktposition und -geschwindigkeit */
/* für jeden Würfel auf Ebene e                                                                    */

    for (o = 0;o < Noktant[e];o ++)
    {
      for (k = 0;k < 3;k ++)
      {
        ro[e][o][k] /= Mo[e][o];
        vo[e][o][k] /= Mo[e][o];
      }
    }

/* Anlegen einer neuen Ebene, falls auf letzter Ebene zumindest 1 Würfel mit mehr als 1 Massenpunkt vorhanden */

    if (gleich > 0)
    e ++;
  }
  Nebene = e + 1;
}

Die Aktualisierung der Schwerpunkte einer schon vorgegebenen Hierarchie von Oktanten geschieht durch eine Prozedur updatehierarchie (N,m,r[1],v[1]), welcher die gleichen Werte übergeben werden wie der Raumhierarchie-Prozedur. Die lokale unsigned Integer n zählt die in einem Würfel vorhandenen Körper ab.

void updatehierarchie (unsigned int N, double *m, double **r, double **v)
{
  unsigned int n;

  /* Initialisierung der Schwerpunkte nur für Positionen und Geschwindigkeiten        */
  /* Gesamtmassen der belegten Oktanten bei gleich gebliebener Hierarchie unverändert */

  for (e = 0;e < Nebene;e ++)
  {
    for (o = 0;o < Noktant[e];o ++)
    {
      for (k = 0;k < 3;k ++)
      {
        ro[e][o][k] = 0;
        vo[e][o][k] = 0;
      }      
    }
  }

  for (i = 0;i < N;i ++)
  flag[i] = 0;

  /* Aktualisierung der Schwerpunkte der Oktanten auf aktueller Ebene e                    */
  /* Betrachte individuelle Mitglieder des Ensembles als Massenpunkte innerhalb der Würfel */

  for (e = Nebene - 1;e > 0;e --)
  {
    for (o = 0;o < Noktant[e];o ++)
    {
      for (n = 0;n < No[e][o];n ++)
      {

  /* Individueller Massenpunkt muss nur berücksichtigt werden */
  /* falls nicht schon auf tieferer Ebene abgearbeitet        */

        if (flag[Nr_objekt_o[e][o][n]] == 0)
        {
          for (k = 0;k < 3;k ++)
          {
            ro[e][o][k] += m[nrobjekto[e][o][n]] * r[nrobjekto[e][o][n]][k];
            vo[e][o][k] += m[nrobjekto[e][o][n]] * v[nrobjekto[e][o][n]][k];
          }

  /* Markiere individuellen Massenpunkt nach Addieren zu seinem Würfel als abgearbeitet */

          flag[nrobjekto[e][o][n]] = 1;
        }
      }
    }

    for (o = 0;o < Noktant[e];o ++)
    {
      for (k = 0;k < 3;k ++)
      {
        ro[e][o][k] /= Mo[e][o];
        vo[e][o][k] /= Mo[e][o];
      }
    }

  /* Aktualisierung der Schwerpunkte der übergeordneten Oktanten auf Ebene e - 1                  */
  /* Betrachte Oktanten auf Ebene e wiederum als Massenpunkte innerhalb der übergeordneten Würfel */
  /* An dieser Stelle KEINE Division von Positions- und Geschwindigkeitswerten mit Oktantenmassen */
  /* Noch fehlende individuelle Mitglieder des Ensembles werden auf nächster Ebene hinzuaddiert   */

    if (e > 0)
    {
      for (o = 0;o < Noktant[e];o ++)
      {
        for (k = 0;k < 3;k ++)
        {
          ro[e-1][nruebero[e][o]][k] += Mo[e][o] * ro[e][o][k];
          vo[e-1][nruebero[e][o]][k] += Mo[e][o] * vo[e][o][k];
        }
      }
    }
  }
}

Alle übrigen Simulationsanweisungen laufen ab wie bisher. Die Bestimmung von Beschleunigung und Ruck erfolgt nun jedoch mit einer modifizierten Prozedur ruckhierarchie (i,epsilon,r[1][i],v[1][i],a[1][i],j[1][i]), welche sich die Raumhierarchie zu Nutze macht. Dieser werden wie der Standardprozedur die Nummer des untersuchten Körpers, der Plummerradius sowie sämtliche vorläufige Positionen und Geschwindigkeiten übergeben. Die Anzahl der Massenpunkte und deren Massen tauchen hingegen als Übergabeparameter hier nicht auf, da ja jetzt nicht über die einzelnen Mitglieder des Ensembles summiert wird, sondern über die von diesen belegten Würfel. Zurückgegeben werden wie üblich Beschleunigung und Ruck, welche wie bisher in den Korrektor eingesetzt werden, um verbesserte Positionen und Geschwindigkeiten zu erhalten. Im Vergleich zum bisherigen Vorgehen werden keine neuen lokalen Variablen benötigt.

void ruckhierarchie (unsigned int objekt, double epsilon, double *r, double *v, double *a, double *j)
{

/* Lokale Variablen */

  unsigned int k;
  double dr[3];
  double d,d2,d3,d5,d6,d8;
  double dv[3];
  double skalar;

/* Initialisierung von Beschleunigung und Ruck */

  for (k = 0;k < 3;k ++)
  {
    a[k] = 0;
    j[k] = 0;
  }

/* Initialisierung aller Würfel als unbearbeitet */

  for (e = 0;e < Nebene;e ++)
  {
    for (o = 0;o < Noktant[e];o ++)
    flago[e][o] = 0;
  }

/* Berechnung von Beschleunigung und Ruck */
/* Abarbeiten aller Raumebenen            */

  for (e = 0;e < Nebene;e ++)
  {

/* Abarbeiten aller belegten Würfel innerhalb einer Ebene */

    for (o = 0;o < Noktant[e];o ++)
    {

/* Betrachte Würfel o falls                                                        */
/* 1) Übergeordneter Würfel von o noch nicht betrachtet UND                        */
/* 2) o enthält objekt nicht                                                       */
/* 1) wird sichergestellt durch                                                    */
/* a) Aktuelle Ebene = 0 -> kein übergeordneter Würfel vorhanden                   */
/* b) Sonst: Flag des übergeordneten Würfels steht auf 0                           */
/* 2) wird sichergestellt durch                                                    */
/* a) Aktuelle Ebene tiefer als Ebene des objekt -> objekt in seinem Würfel allein */
/* b) Sonst: o nicht Nummer des Würfels, in welchem objekt sich befindet           */

      if ((e == 0 || e > 0 && flago[e-1][nruebero[e][o]] == 0) &&
          (ebene_raum[objekt] < e || ebene_raum[objekt] >= e && nr_raum[e][objekt] != o))
      {

/* Abstand zwischen Würfel o und objekt */

        for (k = 0;k < 3;k ++)
        dr[k] = ro[e][o][k] - r[k];
        d = betrag (dr);

/* Betrachte Würfel o falls                                         */
/* Verhältnis Kantenlänge / Entfernung erfüllt alpha-Kriterium ODER */
/* o enthält nur einen Massenpunkt                                  */                   

        if (Ao[e] / d < alpha || No[e][o] == 1)
        {

/* Markieren von Würfel o als abgearbeitet */

          flago[e][o] = 1;

/* Geschwindigkeitsdifferenz zwischen Würfel o und objekt */

          for (k = 0;k < 3;k ++)
          dv[k] = vo[e][o][k] - v[k];

/* Weitere Berechnungen analog zur Standardprozedur */

          skalar = skalarprodukt (dr,dv);
          if (d > 2 * epsilon)
          {
            d3 = pow (d,3);
            d5 = pow (d,5);
          }
          else
          {
            d2 = pow (d,2) + 4 * epsilon2;
            d6 = pow (d2,3);
            d8 = pow (d2,4);
          }

          for (k = 0;k < 3;k ++)
          {
            if (d > 2 * epsilon)
            {
              a[k] += G * Mo[e][o] * dr[k] / d3;
              j[k] += G * Mo[e][o] * (dv[k] / d3 - 3 * skalar * dr[k] / d5);
            }
            else
            {
              a[k] += G * Mo[e][o] * 64 * epsilon3 * dr[k] / d6;
              j[k] += G * Mo[e][o] * 64 * epsilon3 * (dv[k] / d6 - 6 * dr[k] * skalar / d8);
            }
          }
        }
      }
          
/* Würfel o automatisch abgearbeitet, falls schon dessen übergeordneter Würfel abgearbeitet */

      if (e > 0 && flago[e-1][nruebero[e][o]] == 1)
      flago[e][o] = 1;
    }
  }
}

Der Barnes-Hut-Algorithmus kann selbstverständlich auch mit dem Leapfrog-Verfahren kombiniert werden. In diesem Fall werden nur die Schwerpunktpositionen der Würfel benötigt, nicht aber auch deren Geschwindigkeiten. Für jeden Massenpunkt muss dann lediglich die von der Hierarchie ausgeübte Beschleunigung bestimmt werden, nicht aber auch der Ruck. Die entsprechenden Codes sind hier nicht weiter aufgelistet, sie können aus den gegebenen Prozeduren durch Fortlassen der nicht erforderlichen Berechnungen leicht abgeleitet werden.

Einzelnachweise

↑ ^1,0 ^1,1 ^1,2 Barnes J., Hut P., A hierarchical O(N log N) force-calculation algorithm, in: Nature Band 324, S.446 ff., 1986
↑ Barnes J., Hut P., Error analysis of a tree code, in: The Astrophysical Journal Supplement Series Band 70, S.389 ff, 1989

[Barnes_und_Hut_1986-1] 1,0 ^1,1 ^1,2 Barnes J., Hut P., A hierarchical O(N log N) force-calculation algorithm, in: Nature Band 324, S.446 ff., 1986

[2] Barnes J., Hut P., Error analysis of a tree code, in: The Astrophysical Journal Supplement Series Band 70, S.389 ff, 1989

[1]

[2]