Das Mehrkörperproblem in der Astronomie/ Praktische Beispiele/ Großräumige Strukturen im Kosmos

Galaxien stellen keineswegs die oberste Ebene kosmischer Strukturbildung dar, sie schließen sich zu noch größeren Einheiten in Form von Galaxienhaufen und Superhaufen zusammen. Um diese Gebilde zu verstehen, erweist sich das im letzten Kapitel eingeführte Konzept dunkler Halos und Subhalos wiederum als sehr hilfreich. Wie nachfolgend gezeigt wird, bildet die dunkle Materie noch großräumigere Verdichtungen aus, welche sich als Träger der Galaxienhaufen erweisen, so wie die kleineren Halos und Subhalos große und kleine Galaxien repräsentieren.

Die Superhaufen wiederum zeigen ebenfalls keine gleichförmige Verteilung, sondern ordnen sich entlang von Filamenten an. Diese umschließen gewaltige nahezu leere Bereiche, welche kaum Galaxien enthalten. Auf dieser größten bekannten Skala für Mehrkörpersysteme kommt ein Phänomen ins Spiel, welches für die bisherigen Betrachtungen bedeutungslos war: Die Expansion des Universums. Die Bewegungen der Galaxien relativ zueinander sind nicht allein durch die wechselseitig ausgeübten Anziehungskräfte bestimmt, sondern auch dadurch, dass der Raum selbst sich ausdehnt. In den letzten Jahren hat sich herausgestellt, dass zum Verständnis dieser Ausdehnung neben der dunklen Materie eine noch mysteriösere Komponente benötigt wird, welche als dunkle Energie bezeichnet wird.

Wie Simulationen von Galaxien sind auch solche von großräumigen kosmischen Strukturen sehr aufwendig. Galaxienhaufen, Superhaufen und die von letzteren gebildeten Filamente stellen abermals Objekte sehr unterschiedlicher Ausdehnung dar, so dass wiederum Millionen von Testmassen benötigt werden, um die im Vergleich zu Filamenten viel kleineren Galaxienhaufen noch nachweisen zu können. Extrem hochaufgelösten Simulationen wie die am Ende des Kapitels vorgestellte Bolshoi-Simulation gelingt es sogar, die Bildung individueller Galaxien inmitten der Großstrukturen darzustellen. Die Anzahl der dabei beteiligten Massenpunkte erreicht hier die Größenordnung von Milliarden.

Die Expansion des Universums

Charakteristische Eigenschaften

Im Jahr 1922 beschrieb Wirtz , dass damals (auch vom Autor selbst) oft noch als "Nebel" bezeichnete Galaxien sich mit umso höherer Geschwindigkeit von uns entfernen, je lichtschwächer sie erscheinen. 1924 stellte er fest, dass eine solche Abhängigkeit für die Radialgeschwindigkeit auch bezüglich der Winkeldurchmesser von "Spiralnebeln" vorliegt. Indem Wirtz diese als Kriterium für deren Entfernungen deutete (je weiter eine Galaxie entfernt ist, umso kleiner erscheint sie in der Regel dem Beobachter), gelangte er zu der Erkenntnis, dass "Spiralnebel" sich umso rascher von uns entfernen, je weiter entfernt diese sind. Durch Anwendung seiner Daten auf das kosmologische Modell von de Sitter (welches später in diesem Abschnitt noch erläutert wird) erkannte er zudem, dass die Bewegung der Galaxien weg von uns eine Ausdehnung des Universums anzeigt.

Die Wirtz zur Verfügung stehenden Messungen reichten noch nicht aus, um den Zusammenhang zwischen Radialgeschwindigkeit und Entfernung einer Galaxie quantitativ durch eine Gesetzmäßigkeit darzustellen. Dies unternahm erstmalig im Jahr 1929 Hubble , welcher herausfand, dass die Radialgeschwindigkeit $v_{r}$ einer Galaxie zu ihrer Entfernung $r$ direkt proportional ist:

$v_{r}=Hr$

Die Proportionalitätskonstante $H$ wird Hubble zu Ehren Hubble-Konstante genannt. Hubble selbst gab eine Zunahme von $v_{r}$ um 500 km/s pro 1 Million Parsec an, was später jedoch erheblich korrigiert werden musste. Moderne Arbeiten, wie z.B. auch die bereits im Galaxienkapitel zitierte von Ling und anderen (2010) , gehen von etwa 70 km/s pro 1 Million Parsec aus, d.h. die Galaxien entfernen sich im Allgemeinen weit langsamer von uns fort als ursprünglich von Hubble angenommen. Damals standen nur Beobachtungen sehr naher Galaxien zur Verfügung, deren Bewegungen - wie man erst nachträglich erkannte - jedoch sehr stark durch die Zugehörigkeit zum lokalen Galaxienhaufen beeinflusst werden.

Wie in diesem Abschnitt noch ausführlich diskutiert wird (und anhand kosmologischer Modelle rasch klar wurde), ist die Hubble-Konstante in Wahrheit nicht konstant, sondern verändert sich im Laufe der Zeit. Dies hat zur Folge, dass der lineare Zusammenhang zwischen $v_{r}$ und $r$ nur bis zu Entfernungen von etwa 1 Milliarde Parsec gültig ist. Wegen der zwar sehr großen, aber doch endlichen Lichtgeschwindigkeit sieht man ein Objekt niemals so, wie es aktuell beschaffen ist, sondern wie es ausgesehen hat, als es das soeben eintreffende Licht ausgesandt hat. Je weiter ein Objekt entfernt ist, umso mehr liegt dieser Zeitpunkt der Lichtaussendung zurück. Für sehr ferne Galaxien gewinnt man demgemäß ein Bild, welches tatsächlich vor Milliarden Jahren vorlag, als die Hubble-Konstante noch einen deutlich anderen Wert aufwies als heute.

Hubbles Gesetz einer direkten Proportionalität zwischen Radialgeschwindigkeit und Entfernung einer Galaxie lässt sich durch eine Kugeloberfläche veranschaulichen, welche gleichmäßig aufgeblasen wird. Man betrachte eine Kugel mit Radius $R$, auf deren Fläche sich irgendwo ein Beobachter befindet (roter Punkt). Man nehme weiterhin zwei Punkte A und B mit Abständen $d$ und 2$d$ vom Beobachter (auf einer Kugeloberfläche bedeutet der "Abstand" zweier Punkte die Länge des Großkreisbogens, welcher diese miteinander verbindet).

Darstellung der Ausdehnung des Universums durch das Modell einer aufgeblasenen Kugelfläche

Die Kugel werde nun im Verlauf einer Zeit $t$ auf das Doppelte ihrer ursprünglichen Größe aufgeblasen. Damit verdoppeln sich auch die Entfernungen von A und B zum Beobachter auf 2$d$ bzw. 4$d$. Punkt A bewegt sich mit der Geschwindigkeit $d/t$, der doppelt so weit entfernte Punkt B mit der doppelten Geschwindigkeit 2$d/t$ vom Beobachter weg. Der Effekt ist vom Standort auf der Kugeloberfläche unabhängig und gilt für beliebige Beobachter und Orte A und B.

Auf den ersten Blick steht die Zunahme der Radialgeschwindigkeit mit der Entfernung zur Relativitätstheorie in Widerspruch. Auch unter Berücksichtigung der Zeitabhängigkeit der Hubble-Konstante treten ab einer gewissen Entfernung Geschwindigkeiten auf, welche die Lichtgeschwindigkeit übersteigen. Die "Flucht" der Galaxien weg von uns aufgrund der Expansion des Universums stellt jedoch keine Bewegung von einem Raumpunkt zum nächsten dar, sondern es ist der Raum selbst, welcher sich ausdehnt. In obigem Modell der Kugeloberfläche bleiben die Punkte A und B auf ihren Plätzen, ihre Längen- und Breitengrade ändern sich nicht. Die Lichtgeschwindigkeit stellt nur dann die Obergrenze dar, wenn ein Objekt sich von einem Raumpunkt zu einem anderen bewegt, in obigen Bild A und B also zu anderen Längen- und Breitengraden wandern.

Objekte, die aufgrund der Ausdehnung des Kosmos mit Überlichtgeschwindigkeit sich von uns wegbewegen, bleiben jedoch unsichtbar, da selbst das in unsere Richtung von diesen abgestrahlte Licht nach "außen" mitgerissen wird. Daraus folgt, dass das Universum nur bis zu einer gewissen Maximalentfernung beobachtbar ist. Der Wert dieses Horizonts ist unmittelbar mit dem zeitlichen Verhalten der Hubble-Konstanten verknüpft.

Darstellung in der Mehrkörpersimulation

Als Zusatzbeschleunigung

Der Mehrkörper-Pionier Aarseth wandte seine frühen Computersimulationen in den 1960-Jahren auch schon auf kosmologische Fragestellungen an. Um die Expansion des Universums zu beschreiben, führte er 1963 folgendes Konzept ein.

Berücksichtigung der Expansion des Universums in einer Mehrkörpersimulation auf Grundlage einer Zusatzbeschleunigung

Auf jedes Mitglied eines Ensembles wirken zwei Beschleunigungen, die durch die übrigen Körper ausgeübte Gravitationsbeschleunigung ${\vec {g}}$ sowie eine Expansionsbeschleunigung ${\vec {e}}$. Die Gravitationsbeschleunigung wird berechnet wie üblich, wobei analog zur Simulation von Galaxien mit einem Plummerradius des Typs $\epsilon =R/{\sqrt {N}}$ gearbeitet wird. Die Expansionsbeschleunigung ${\vec {e}}_{i}$ eines Körpers $i$ ist erwartungsgemäß mit der Hubble-Konstante verknüpft, wobei ${\vec {r}}_{i}$ sein aktueller Ort ist:

${\vec {e}}_{i}=H^{2}{\vec {r}}_{i}$

Mit diesem Ansatz einer Zusatzbeschleunigung verändern sich die Ortskoordinaten der Körper allein schon durch die Expansion, so dass mit zunehmender Ausdehnung des Kosmos deren Wertebereiche sich immer mehr erweitern. Dies aber ist inkonsistent mit dem soeben skizzierten Bild der aufgeblasenen Kugeloberfläche, wo die Koordinaten der Einzelobjekte von der Ausdehnung des Universums unberührt bleiben.

Aarseths Methode erlaubt jedoch eine sehr einfache Abschätzung, in wieweit ein Mehrkörpersystem mit einer Gesamtmasse $M$ und einer charakteristischen Ausdehnung $R$ durch die Ausdehnung des Universums gestört wird. Dazu vergleicht man die Schwerebeschleunigung $GM/R^{2}$ am Rand des Ensembles mit der Änderung der Expansionsbeschleunigung $H^{2}R$ von dessen Zentrum bis zum Rand (für die Stabilität des Systems ist nicht die absolute Expansionsbeschleunigung relevant, sondern nur, in wieweit sich diese zwischen dessen Mitgliedern unterscheidet). In folgender Tabelle sind verschiedene Typen von Mehrkörpersystemen sehr unterschiedlicher Größe und Masse zusammengefasst, wobei Massen in Sonnenmassen, Strecken in Parsec und Zeiten in Jahren gegeben sind. Wie schon erwähnt, gilt mit diesen Einheiten G = 4.49814 10^-15. Die Hubble-Konstante nimmt dann den Wert H = 7.16 10^-11 an.

System	Masse	Ausdehnung	$e/g$
Bahn der Erde um Sonne	1	1 / 206265	1.3 10-22
Plejaden	690	2.5	2.6 10-8
Bahn der Sonne um galaktisches Zentrum	1.06 1011	8300	6.1 10-6
Lokale Galaxiengruppe	2 1012	106	5.7 10-1
Virgo-Haufen	1015	2.5 107	1.8 101

Die Störung der Planetenbahnen durch die kosmische Expansion liegt weit unter der Nachweisgrenze. Die Orbits der Sterne in Haufen und auch in Galaxien werden ebenfalls nur in sehr geringfügigem Maß durch diesen Vorgang beeinflusst. Anders verhält es sich dagegen für die Bewegung der Galaxien untereinander. Schon auf der Ebene kleiner Galaxienhaufen wie der lokalen Gruppe darf die Ausdehnung des Universums nicht mehr vernachlässigt werden. Sehr große Strukturen wie etwa der Virgo-Superhaufen werden in hohem Maße durch die Expansion dominiert.

Aarseths Modell gibt auch einen ersten Hinweis auf die Bevorzugung filamentartiger Strukturen auf den größten Skalen des Kosmos. Ein aus der Frühphase des Kosmos mit unregelmäßiger Gestalt hervorgegangenes genügend großes Mehrkörperensemble wurde seitdem in Richtung seiner größten Abmessung weit stärker auseinandergezogen als in Richtung seiner kleinsten Ausdehnung und dementsprechend abgeflacht.

Durch mitbewegte Koordinaten

Eine mit dem Bild der aufgeblasenen Kugeloberfläche übereinstimmende Beschreibung gewinnt man, indem man Ortskoordinaten ${\vec {x}}_{i}$ einführt, welche der Expansion folgen. Man stellt sich den Raum aus beliebig kleinen Elementen aufgebaut vor, die entsprechend der Expansion des Universums ebenfalls gedehnt werden.

Berücksichtigung der Expansion des Universums in einer Mehrkörpersimulation auf Grundlage mitbewegter Koordinaten

Wie gewünscht, ändern sich solche Koordinaten ${\vec {x}}_{i}$ eines Körpers durch die Ausdehnung des Kosmos nicht, sondern allein durch die auf ihm von anderen Massen ausgeübte Schwerebeschleunigung ${\vec {g}}$. Um diese zu bestimmen, muss man jedoch zunächst weiterhin von den physikalischen Koordinaten ${\vec {r}}_{i}$ ausgehen, welche auch durch die Expansion modifiziert werden. Die beiden Koordinatensätze werden über den sogenannten Skalenfaktor $a(t)$ miteinander verknüpft.

${\vec {r}}_{i}=a(t){\vec {x}}_{i}$

$a(t)$ gibt an, wie groß das Weltall zu einer bestimmten Zeit $t$ im Vergleich zu einer gewissen Ausgangssituation $t$ = 0 ist. Um Strukturen kosmischen Ausmaßes deuten zu können, muss man die zeitliche Entwicklung dieses Faktors (d.h. des Expansionsverhaltens) verstehen, was im nachfolgenden Abschnitt ausführlich dargelegt wird.

Um ${\vec {g}}$ im mitbewegten (aufgeblasenen) Koordinatensystem darzustellen, schreibt man das Newtonsche Gravitationsgesetz zuerst in den ortsfesten (physikalischen) Koordinaten ${\vec {r}}_{i}$ auf. Vereinfachend wird hier angenommen, dass alle Probekörper einer Simulation die gleiche Masse $m$ aufweisen.

${\vec {g}}=Gm\sum \limits _{j\neq i}{\frac {{\vec {r}}_{j}-{\vec {r}}_{i}}{|{\vec {r}}_{j}-{\vec {r}}_{i}|^{3}}}$

Anschließend rechnet man die Schwerebeschleunigung in die Koordinaten ${\vec {x}}_{i}$ um, was leider nur mit Kenntnissen der Differentialrechnung möglich ist. Es stellt sich heraus, dass auch jetzt gegenüber dem originalen Newtonschen Gesetz Zusatzglieder auftauchen (also in obiger Formel nicht einfach nur die ${\vec {r}}_{i}$ durch $a{\vec {x}}_{i}$ ersetzt werden). Der Vorteil gegenüber dem ursprünglichen Ansatz von Aarseth besteht darin, dass diese Extrabeschleunigungen unmittelbar aus der Definition der Koordinaten folgen und nicht mehr Ad-hoc eingeführt werden müssen. Zudem enthalten diese jetzt nicht nur die Hubble-Konstante $H$, sondern auch einen sogenannten Beschleunigungsparameter $q$. Während $H$ nur angibt, wie schnell sich der Kosmos zu einem bestimmten Zeitpunkt ausdehnt, liefert $q$ zusätzlich die Information, ob diese Expansion auch einer zeitlichen Änderung unterliegt. Aarseth's einfaches Modell einer Zusatzkraft in ortsfesten Koordinaten gilt nur für eine statische Ausdehnung, wohingegen der auf mitbewegten Koordinaten beruhende Ansatz auch auf eine mögliche Beschleunigung oder Abbremsung derselben Rücksicht nimmt.

Einschub für Fortgeschrittene: Newtonsches Gravitationsgesetz in mitbewegten Koordinaten

Wie soeben angedeutet, lautet im ortsfesten Koordinatensystem in einem Ensemble identischer Testmassen die auf einen Körper einwirkende Gravitationsbeschleunigung:

${\frac {d^{2}{\vec {r}}_{i}}{dt^{2}}}=Gm\sum \limits _{j\neq i}{\frac {{\vec {r}}_{j}-{\vec {r}}_{i}}{|{\vec {r}}_{j}-{\vec {r}}_{i}|^{3}}}$

Mit Hilfe der Produktregel folgen aus der Definition der mitbewegten Koordinaten ${\vec {r}}_{i}=a(t){\vec {x}}_{i}$ die entsprechenden Umrechnungsformeln zwischen den beiden Koordinatensätzen für Geschwindigkeiten und Beschleunigungen.

${\frac {d{\vec {r}}_{i}}{dt}}={\frac {da}{dt}}{\vec {x}}_{i}+a{\frac {d{\vec {x}}_{i}}{dt}}$

${\frac {d^{2}{\vec {r}}_{i}}{dt^{2}}}={\frac {d^{2}a}{dt^{2}}}{\vec {x}}_{i}+2{\frac {da}{dt}}{\frac {d{\vec {x}}_{i}}{dt}}+a{\frac {d^{2}{\vec {x}}_{i}}{dt^{2}}}$

Setzt man diese Vorschriften in die ortsfeste Formulierung des Newtonschen Gravitationsgesetzes ein, so erhält man dessen Darstellung in mitbewegten Koordinaten (wobei zusätzlich noch alle Terme durch $a$ dividiert werden).

${\frac {1}{a}}{\frac {d^{2}a}{dt^{2}}}{\vec {x}}_{i}+{\frac {2}{a}}{\frac {da}{dt}}{\frac {d{\vec {x}}_{i}}{dt}}+{\frac {d^{2}{\vec {x}}_{i}}{dt^{2}}}={\frac {Gm}{a^{3}}}\sum \limits _{j\neq i}{\frac {{\vec {x}}_{j}-{\vec {x}}_{i}}{|{\vec {x}}_{j}-{\vec {x}}_{i}|^{3}}}$

Der Ausdruck $(da/dt)/a$ entspricht genau der Hubble-Konstante, denn er normiert die Änderung des Skalenfaktors mit der Zeit (entsprechend der Expansionsgeschwindigkeit) auf den Skalenfaktor selbst (entsprechend dem Abstand zum Beobachter). $d^{2}a/dt^{2}$ beschreibt die Beschleunigung von $a$. Anstelle dieser wird in der Kosmologie oft der schon erwähnte Parameter $q$ benutzt, welcher die Beschleunigung sowohl auf den Skalenfaktor als auch auf die Hubble-Konstante normiert.

$q=-a{\frac {d^{2}a/dt^{2}}{(da/dt)^{2}}}=-{\frac {d^{2}a/dt^{2}}{aH^{2}}}$

Unter Verwendung von $H$ und $q$ nimmt das Gravitationsgesetz schließlich folgende Gestalt an.

${\frac {d^{2}{\vec {x}}_{i}}{dt^{2}}}={\frac {Gm}{a^{3}}}\sum \limits _{j\neq i}{\frac {{\vec {x}}_{j}-{\vec {x}}_{i}}{|{\vec {x}}_{j}-{\vec {x}}_{i}|^{3}}}+qH^{2}{\vec {x}}_{i}-2H{\frac {d{\vec {x}}_{i}}{dt}}$

In der Praxis wird auch für kosmologische Simulationen die Gravitation mittels eines Plummerradius geglättet. $\epsilon$ wird wie die Positionen der Testmassen im mitbewegten Koordinatensystem betrachtet, d.h. der tatsächliche physikalsche Plummerradius $a\epsilon$ der Ausdehnung des Universums angepasst.

Zeitabhängigkeit

Beschleunigungsgleichung

Ein dynamisches Modell des ganzen Weltalls erfordert wie schon angedeutet die Kenntnis der Zeitabhängigkeit der Expansion, d.h. für alle drei Parameter $a$, $H$ und $q$. Die entsprechenden Zusammenhänge lassen sich nur mittels der Allgemeinen Relativitätstheorie korrekt herleiten, worauf hier verzichtet wird. Die wesentlichen Kerngedanken können auch anhand des folgenden Newtonschen Modells erörtert werden.

Es werde eine Kugel mit Radius $r$ betrachtet, deren Masse $M$ mit der Dichte $\rho$ gleichmäßig über das ganze Volumen verteilt ist. Die Bewegung der Teilchen in einem solchen als homogenes Fluid betrachtetes Universum ist allein durch die Expansion bestimmt, so dass deren mitbewegte Koordinaten sich nicht ändern, d.h. allein der Skalenfaktor von der Zeit abhängt.

Vergleichbar der Diskussion des Newtonschen Gravitationsgesetzes gibt man die Beschleunigung $g$, welche ein Körper an der Oberfläche der Kugel erfährt, zuerst in ortsfesten Koordinaten an:

$g=-{\frac {GM}{r^{2}}}$

Dann überträgt man auch diese Beziehung in mitbewegte Koordinaten. Nach einigen weiteren Umformungen gewinnt man erwartungsgemäß als Resultat, dass die im Kosmos vorhandene Masse infolge der von ihr ausgehenden Gravitation eine negative Beschleunigung desselben zur Folge hat, seiner Ausdehnung also entgegenwirkt. Die Abbremsung ist dabei der Dichte des Weltalls direkt proportional.

Gemäß Friedmann, welcher die Expansion auf Grundlage der Allgemeinen Relativitätstheorie betrachtete, bremst auch der im Fluid herrschende Druck $p$ die Expansion. Auf den ersten Blick erscheint dies paradox, da ein unter Druck stehendes Gas dazu neigt, sich auszudehnen. Um der Expansion zu folgen, muss dieses jedoch Arbeit verrichten, was aufgrund der Energieerhaltung aber nur in endlichem Maße möglich ist.

An Friedmanns Darstellung der Beschleunigung des Universums fällt zudem auf, dass diese auch einen positiven Anteil enthält, die sogenannte kosmologische Konstante $\Lambda$ als eine der Gravitation entgegengesetzte Kraft. Sie wurde ursprünglich von Einstein möglicherweise aus rein weltanschaulichen Gründen eingeführt, um ein seinen Vorstellungen entsprechendes statisches Modell mit verschwindender Beschleunigung zu erhalten.

In den letzten 20 Jahren hat man allerdings erkannt, dass $\Lambda$ tatsächlich eine Existenzberechtigung besitzt. Supernovae des Typs Ia zeigen einen sehr stabilen Zusammenhang zwischen ihrer Maximalleuchtkraft und der Schnelligkeit des anschließenden Helligkeitsabfalls, so dass mit solchen auch sehr große Entfernungen zuverlässig bestimmt werden können. Beobachtungen z.B. von Reiss und anderen (1998) oder Perlmutter und anderen (1998) zeigten, dass bei gegebener Fluchtgeschwindigkeit einer Galaxie die scheinbare Helligkeit einer dort aufleuchtenden Supernova geringer - d.h. deren Entfernung größer ist - als man angesichts der seit dem Urknall wirkenden Massenanziehung erwarten würde. Eine überproportionale Entfernung im Vergleich zur Fluchtgeschwindigkeit bedeutet jedoch eine unerwartete Expansion. Diese aber erfordert wiederum, dass das Universum eine Komponente enthält, welche der Schwerkraft entgegen gerichtet ist. Dieser merkwürdige Bestandteil ist bis heute noch rätselhafter geblieben als die dunkle Materie und wird als dunkle Energie bezeichnet.

Einschub für Fortgeschrittene: Beschleunigungsgleichung der kosmischen Expansion

Wie schon skizziert, sind im Modell der homogenen, expandierenden Kugel die mitbewegten Koordinaten eines Teilchens von der Zeit unabhängig. Aus $r=ax$ folgt so unmittelbar $dr/dt=a$ $dx/dt$ und $d^{2}r/dt^{2}=a$ $d^{2}x/dt^{2}$.

Für ein an der Oberfläche der Kugel sich befindliches Teilchen herrscht in ruhenden Koordinaten eine Schwerebeschleunigung $d^{2}r/dt^{2}=-GM/r^{2}$. In mitbewegten Koordinaten gilt damit für die Beschleunigung des Skalenfaktors:

${\frac {d^{2}a}{dt^{2}}}=-{\frac {GM}{x^{3}a^{2}}}$

Ersetzt man die Masse der Kugel durch deren Dichte gemäß $M=4\pi \rho r^{3}/3=4\pi \rho x^{3}a^{3}/3$, so fällt $x^{3}$ heraus und es ergibt sich die Newtonsche Beschleunigungsgleichung:

${\frac {1}{a}}{\frac {d^{2}a}{dt^{2}}}=-{\frac {4\pi }{3}}G\rho$

Die vollständige Friedmannsche Beschleunigungsgleichung lautet:

${\frac {1}{a}}{\frac {d^{2}a}{dt^{2}}}=-qH^{2}=-{\frac {4\pi G}{3c^{2}}}(\rho c^{2}+3p)+{\frac {\Lambda c^{2}}{3}}$

Bei der zu $\rho$ proportionalen Abbremsung des Kosmos muss selbstverständlich berücksichtigt werden, dass mit dem Skalenfaktor automatisch auch die Dichte einer Zeitabhängigkeit unterworfen ist. Dabei muss man zusätzlich bedenken, dass nicht nur die sichtbare und dunkle Materie zu $\rho$ beiträgt, sondern wegen der Äquivalenz von Energie und Masse auch die im All vorhandene Strahlung.

Das zeitliche Verhalten der Materiedichte ist unmittelbar einsichtig. $\rho _{M}$ ist umgekehrt proportional zum Volumen des Universums, so dass gilt:

$\rho _{M}\sim {\frac {1}{a^{3}}}$

Den Trend für die durch die Strahlung repräsentierte Dichte $\rho _{S}$ kann man mittels eines sehr einfachen Modells verständlich machen, wonach der Kosmos nur Strahlung enthält und die Zahl seiner Lichtquanten konstant bleibt. Deren Anzahldichte folgt wie die Materiedichte einer Proportionalität $1/a^{3}$. Expandiert das Universum, wird jedoch auch die Wellenlänge $\lambda$ der Lichtquanten dem Skalenfaktor folgend gedehnt, d.h. es gilt $\lambda \sim a$. Da Lichtquanten einen Impuls und damit auch eine Masse $m=hc/\lambda$ aufweisen, gilt wegen der Dehnung der Wellenlänge $m\sim 1/a$. Die der Strahlung entsprechende Masse fällt also umgekehrt proportional zum Skalenfaktor ab, womit zusammen mit dem Verhalten der Anzahldichte der Lichtquanten resultiert:

$\rho _{S}\sim {\frac {1}{a^{4}}}$

Im heutigen Kosmos ist der Beitrag von $\rho _{S}$ gegenüber der Materiedichte unbedeutend. Rechnet man jedoch in die Vergangenheit zu einem immer kleineren Skalenfaktor zurück, so findet man wegen der für die Strahlungsdichte steileren Abhängigkeit von $a$ einen Zeitpunkt, von welchem an die Strahlung über die Materie dominiert. Diese Strahlungsära wird im nächsten Unterkapitel noch ausführlicher beschrieben.

Mit fortschreitender Expansion dünnt das Weltall immer mehr aus, wodurch zugleich dessen Abbremsung durch Strahlung und Materie immer schwächer wird. Dies lässt bereits erahnen, dass eine gewisse Mindestdichte erforderlich ist, um die Ausdehnung in endlicher Zeit zum Stehen zu bringen. Diese Dichte wird kritische Dichte genannt und nachfolgend weiter diskutiert.

Auch die kosmologische Konstante wird oft durch ein Dichteäquivalent $\rho _{\Lambda }$ gemäß $\Lambda =8\pi G\rho _{\Lambda }/c^{2}$ ausgedrückt. Gemäß heutiger Vorstellung dünnt die dunkle Energie im Gegensatz zu Materie und Strahlung nicht aus, d.h. $\rho _{\Lambda }$ ist konstant. Dies wiederum hat zur Folge, dass mit fortschreitender Expansion des Weltalls die dunkle Energie immer stärker dominiert, so dass die durch diese ausgeübte Beschleunigung schließlich der Abbremsung durch die Schwerkraft überwiegt. In der Frühphase des Universums hingegen spielte $\rho _{\Lambda }$ kaum eine Rolle.

Der Druck wiederum ist wie die Materie- und Strahlungsdichte von der Zeit abhängig, für ein auf Massenpunkte anstatt einer kontinuierlichen Massenverteilung beruhendes Modell jedoch per Definition gleich 0. Ein realistisches Modell muss aber zumindest den von der Strahlung ausgeübten Druck $p_{S}$ berücksichtigen, um den Übergang von der Strahlungs- zur Materieära korrekt zu beschreiben. $p_{S}$ ist der Strahlungsdichte direkt proportional, es ist $p_{S}=c^{2}\rho _{S}/3$. Der von der Materie ausgeübte Druck kann hingegen in der Tat zumeist vernachlässigt werden.

Formell lässt sich auch der dunklen Energie ein Druck zuordnen gemäß $p_{\Lambda }=-c^{2}\rho _{\Lambda }$. Das Minuszeichen steht dabei für die abstoßende, der Schwerkraft entgegenwirkenden Kraftrichtung.

Bewegungsgleichung

Das Modell der sich ausdehnenden homogenen Kugel erlaubt nicht nur Aussagen über die Beschleunigung der Expansion, sondern auch über diese selbst, indem es eine Beziehung zwischen der Hubble-Konstanten und anderen fundamentalen Größen herstellt. Legt man ein weiteres Mal das Newtonsche Gravitationsgesetz zugrunde, zeigt sich, dass das Quadrat von $H$ wie die Abbremsung der Dichte des Kosmos proportional ist. Mit fortschreitender Ausdünnung desselben nähert sich in einem Newtonschen Weltall die Hubble-Konstante stetig dem Wert 0 an, was gleichbedeutend ist mit einer fortschreitend verlangsamten Ausdehnung.

Im Rahmen der Allgemeinen Relativitätstheorie tritt abermals die kosmologische Konstante in Erscheinung. Da die entsprechende Dichte sich nicht ändert, verschwindet für einen solchen Kosmos mit zunehmender Zeit die Hubble-Konstante nicht, sondern verharrt letztendlich auf einem gleichbleibenden Niveau. Für einen Raum, der permanent anschwillt, entspricht ein konstantes $H$ größer als 0 einer beschleunigten Expansion, denn mit immer größeren Entfernungen $r$ treten immer höhere Fluchtgeschwindigkeiten $Hr$ auf.

Als neuer, noch nicht genannten Beitrag, taucht in der Allgemeinen Relativitätstheorie die Krümmung $k$ auf, welche die Geometrie des Modells charakterisiert. Dabei ist zu beachten, dass die Relativitätstheorie aufgrund der Verknüpfung von Raum und Zeit ein vierdimensionales Konzept darstellt, so dass hier nicht von gekrümmten Flächen, sondern Räumen die Rede ist.

Der einfachste Fall $k$ = 0 entspricht einem Universum, dessen Geometrie sich wie in einer Ebene verhält. Die kürzeste Verbindung zwischen zwei Punkte ist eine Gerade, die Winkelsumme in einem Dreieck beträgt 180 Grad. In Analogie zur Ebene spricht man von einem flachen Raum, in welchem die Euklidische Geometrie gilt.

Geometrie in einer Ebene. Die Seiten eines Dreiecks sind Geradenstücke, die Winkelsumme beträgt 180 Grad

$k$ > 0 stellt ein Modell mit einem sogenannten positiv gekrümmten Raum dar, welcher durch die Riemannsche Geometrie gekennzeichnet ist. Die kürzeste Verbindung zwischen zwei Punkten ist nun keine Gerade, sondern eine krumme, als Geodäte bezeichnete Kurve. Die Winkelsumme in einem Dreieck, dessen Seiten von solchen Geodäten gebildet werden, ist größer als 180 Grad. Ein anschauliches Beispiel ist die schon ganz zu Beginn dieses Kapitels erwähnte Kugeloberfläche. Die kürzeste Verbindung zwischen zwei Orten ist dort ein Bogen auf einem Großkreis (ein Kreis, dessen Umfang dem der Kugel entspricht). Ein positiv gekrümmter Kosmos weist eine kleinere Hubble-Konstante auf als ein flacher, d.h. dehnt sich langsamer aus.

Geometrie auf einer Kugeloberfläche. Die Seiten eines Dreiecks sind Segmente von Großkreisen, die Winkelsumme übersteigt 180 Grad

$k$ < 0 gibt ein Weltall mit einem negativ gekrümmten Raum wieder, welcher durch die Geometrie von Lobatschewski beschrieben wird. Auch hier ist die kürzeste Verbindung zwischen zwei Punkten durch eine krumme Geodäte gegeben, doch ist die Winkelsumme in einem Dreieck jetzt kleiner als 180 Grad. Ein zweidimensionales Beispiel ist die Fläche eines Sattels, auf welcher die kürzeste Verbindung zwischen zwei Orten durch ein Hyperbelstück dargestellt wird. Bei negativer Krümmung ist die Hubble-Konstante größer im Vergleich zu einem flachen Raum entsprechend einer schnelleren Expansion.

Geometrie auf einer Satteloberfläche. Die Seiten eines Dreiecks sind Segmente von Hyperbeln, die Winkelsumme unterschreitet 180 Grad

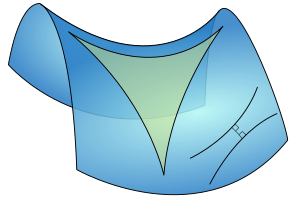
Einschub für Fortgeschrittene: Bewegungsgleichung der kosmischen Expansion

In mitbewegten Koordinaten lautet die Newtonsche Beschleunigungsgleichung:

${\frac {d^{2}a}{dt^{2}}}=-{\frac {GM}{x^{3}a^{2}}}$

Multipliziert man diese auf beiden Seiten mit $da/dt$ und integriert jeweils über die Zeit, so gewinnt man den Ausdruck:

${\frac {1}{2}}\left({\frac {da}{dt}}\right)^{2}={\frac {GM}{x^{3}a}}+C$

Ersetzt man ein weiteres Mal die Masse durch die Dichte, erhält man:

$\left({\frac {1}{a}}{\frac {da}{dt}}\right)^{2}={\frac {8\pi }{3}}G\rho +C$

Um die Integrationskonstante zu bestimmen, ist man erneut auf die Allgemeine Relativitätstheorie angewiesen. Gemäß Friedmann lautet die vollständige Gleichung:

$\left({\frac {1}{a}}{\frac {da}{dt}}\right)^{2}=H^{2}={\frac {8\pi }{3}}G\rho -{\frac {kc^{2}}{a^{2}}}+{\frac {\Lambda c^{2}}{3}}$

Krümmung und Dichte

Die Geometrie des Weltalls folgt unmittelbar aus dessen mittleren Dichte. Auf Grundlage der Bewegungsgleichung der kosmischen Expansion lässt sich darlegen, dass für ein flaches Universum eine sogenannte kritische Dichte $\rho _{C}$ erforderlich ist, und diese wiederum folgendermaßen aus der Hubble-Konstanten abgeleitet werden kann:

$\rho _{C}={\frac {3H^{2}}{8\pi G}}$

Überwiegt die mittlere Dichte der kritischen, liegt ein positiv gekrümmter Kosmos vor. Umgekehrt zieht eine kleinere mittlere Dichte einen negativ gekrümmten Raum nach sich.

Gegenwärtig geht man von einem flachen Universum aus. Die schon zitierten Arbeiten von Reiss und anderen (1998) bzw. Perlmutter und anderen (1998) legen nahe, dass die der dunklen Energie entsprechende Dichte etwa 70% der kritischen beträgt. Für einen flachen Kosmos muss dann die Dichte der dunklen und sichtbaren Materie zusammen bei circa 30% des kritischen Niveaus liegen. Die dunkle Energie stellt demgemäß schon heute den Löwenanteil der gesamten Dichte des Weltalls.

Einschub für Fortgeschrittene: Krümmung und Dichte

Um den Zusammenhang zwischen Krümmung und Dichte des Weltalls zu erkennen, drückt man die Friedmann-Gleichung in einer normierten Form aus, indem man die Werte der zeitabhängigen Größen zu einem beliebigen Zeitpunkt mit den gegenwärtigen vergleicht (letztere werden fortan mit einem Index 0 gekennzeichnet). Vernachlässigt man die Strahlung, so besteht zwischen beliebigen Dichten $\rho$ und der heutigen $\rho _{0}$ der Zusammenhang $\rho =(a_{0}/a)^{3}\rho _{0}$. Aus der Bewegungsgleichung folgt, dass der Ausdruck $\rho _{C}=3H^{2}/8\pi G$ ebenfalls die Dimension einer Dichte hat. Das Verhältnis zwischen der tatsächlichen Dichte $\rho$ und $\rho _{C}$ wird für beliebige Zeiten mit $\Omega$ bzw. für die Gegenwart mit $\Omega _{0}=8\pi G\rho _{0}/3H_{0}^{2}$ gekennzeichnet. Die der kosmologischen Konstante entsprechende Dichte wird ebenfalls $\rho _{C}$ gegenübergestellt, die entsprechenden Verhältnisse lauten $\Omega _{\Lambda }$ bzw. $\Omega _{\Lambda 0}=\Lambda c^{2}/3H_{0}^{2}$. Setzt man die $\Omega$ in die Bewegungsgleichung ein, so nimmt diese folgende Gestalt an:

$H^{2}=H_{0}^{2}\left(\Omega _{0}\left({\frac {a_{0}}{a}}\right)^{3}-{\frac {kc^{2}}{H_{0}^{2}a^{2}}}+\Omega _{\Lambda 0}\right)$

Die Friedmann-Gleichung lässt sich weiter vereinfachen, indem man sie für die heutigen Verhältnisse betrachtet. Dann gilt einfach $H=H_{0}$ und $a=a_{0}$ und somit

${\frac {kc^{2}}{H_{0}^{2}a_{0}^{2}}}=\Omega _{0}+\Omega _{\Lambda 0}-1$

Dies ist genau der gesuchte Zusammenhang zwischen Krümmung und Dichte. Man betrachte zuerst ein Modell ohne kosmologische Konstante, also mit $\Omega _{\Lambda 0}$ = 0. Um die Krümmung verschwinden zu lassen, muss dann $\Omega _{0}$ exakt gleich 1 sein, d.h. die Dichte $\rho _{0}$ genau dem kritischen Wert $\rho _{C0}=3H_{0}^{2}/8\pi G$ entsprechen.

Wird die kosmologische Konstante berücksichtigt, so wird für eine ebene Geometrie für die Materie nur ein $\Omega _{0}=1-\Omega _{\Lambda 0}$ und dementsprechend eine Dichte $\rho =\rho _{C0}(1-\Omega _{\Lambda 0})$ benötigt. Ersetzt man in der Bewegungsgleichung die Krümmung durch die heutigen Dichteverhältnisse, so lautet diese schließlich:

$H^{2}=H_{0}^{2}\left(\Omega _{0}\left({\frac {a_{0}}{a}}\right)^{3}+(1-\Omega _{0}-\Omega _{\Lambda 0})\left({\frac {a_{0}}{a}}\right)^{2}+\Omega _{\Lambda 0}\right)$

Lösungen der Bewegungsgleichung

Im Folgenden seien die von Friedmann gefundenen Lösungen der Bewegungsgleichung qualitativ skizziert, wobei zunächst die kosmologische Konstante außer Acht gelassen wird.

Für ein flaches Universum zeigte er, dass ein solches bis in alle Ewigkeit expandiert. Seine Ausdehnung wird mehr und mehr abgebremst, kommt aber erst nach unendlich langer Zeit zum Stehen. Der einem solchen Kosmos zu Beginn mitgegebene Schub und die Gravitation halten einander exakt die Waage.

Ein Weltall negativer Krümmung dehnt sich angesichts seiner geringeren Dichte erst recht für alle Zeit aus. Die Schwerkraft kann die anfänglich mitgelieferte Bewegungsenergie nicht vollständig ausgleichen, so dass die Expansion sich zwar auch in diesem Fall verlangsamt, aber nie gänzlich zum Stillstand kommt. Im Extremfall einer von Anfang an verschwindenden Materiedichte findet überhaupt keine Abbremsung statt. Ein solches Modell liefert eine Ausdehnung mit konstanter Geschwindigkeit, d.h. eine lineare Aufblähung des Raumes mit der Zeit.

In einem Kosmos positiver Krümmung überwiegt die Gravitation der kinetischen Energie. Die Ausdehnung kommt nach endlicher Zeit zum Erliegen, so dass der Raum ein endliches Maximalvolumen annimmt. Danach kontrahiert ein solches Universum, bis sein Volumen wieder den Wert 0 erreicht. Dieser Zyklus von Expansion und Kontraktion wird beliebig oft durchlaufen.

Qualitative Abhängigkeit des Skalenfaktors von der Zeit in Abhängigkeit von der Zeit. Für die am steilsten ansteigende Kurve ist eine kosmologische Konstante $\Lambda$ > 0 angenommen, für alle übrigen $\Lambda$ = 0. Die den Kurven zugrundeliegenden Dichten werden jeweils als ein Vielfaches $\Omega$ der kritischen Dichte ausgedrückt

In Modellen mit kosmologischer Konstante steht der Schwerkraft nicht nur die initial dem Weltall mitgelieferte Bewegungsenergie, sondern auch die dunkle Energie entgegen. Wegen ihrer merkwürdigen Eigenschaft, im Gegensatz zur dunklen und sichtbaren Materie nicht auszudünnen, wird deren abstoßende Kraft im Vergleich zur Gravitation umso stärker, je weiter der Kosmos sich ausdehnt. Infolgedessen stellt sich nicht nur eine fortwährende Expansion ein, sondern diese wird auch noch immer weiter beschleunigt.

Allen Lösungen Friedmanns ist gemeinsam, dass sie mit einem Raumvolumen gleich 0 starten. Im Falle positiver Krümmung und ohne kosmologische Konstante tritt dies zudem zyklisch immer wieder auf. Dies legt nahe, dass das Universum aus einem Zustand verschwindender Ausdehnung, d.h. unendlicher Dichte heraus entstanden ist. Diese Vorstellung widerspricht jedoch einer fundamentalen Aussage der Quantenmechanik. Gemäß der sogenannten Heisenbergschen Unschärferelation ist es nicht möglich, Ort und Impuls eines Teilchens gleichzeitig mit beliebiger Genauigkeit zu bestimmen, wodurch ein verschwindendes Volumen ausgeschlossen ist. Dieser Widerspruch zwischen Allgemeiner Relativitätstheorie und Quantenmechanik konnte bis heute nicht aufgelöst werden.

Da das Weltall flach zu sein scheint, seien die entsprechenden Lösungen Friedmanns ausführlicher dargestellt, sowohl ohne als auch mit kosmologischer Konstante $\Lambda$. Dabei bedeuten im Folgenden $H_{0}$ der heutige Wert der Hubble-Konstante (70 km/s pro Mpc) und $\Omega _{0}$ bzw. $\Omega _{\Lambda 0}$ die heutigen Anteile der Materie bzw. dunklen Energie an der Gesamtdichte des Weltalls (0.3 bzw. 0.7). Weiterhin wird zwecks Vereinfachung der Formeln die Abkürzung $\omega =3H_{0}{\sqrt {\Omega _{\Lambda 0}}}/2$ benutzt. Der gegenwärtige Skalenfaktor wird auf 1 gesetzt, d.h. die Ausdehnung des Kosmos $a(t)$ zu einem beliebigen Zeitpunkt auf die momentane normiert. Damit gilt:

$\Lambda =0\Rightarrow a(t)=\left({\frac {3}{2}}H_{0}t\right)^{2/3}$

$\Lambda >0\Rightarrow a(t)=\left({\frac {\Omega _{0}}{\Omega _{\Lambda 0}}}\right)^{1/3}(\sinh(\omega t))^{2/3}$

Beide Modelle liefern einen Wert für die Zeit $t_{0}$, welche seit der Entstehung des Kosmos ($a$ = 0) verstrichen ist. Einsetzen von $a$ = 1 und Auflösen nach der Zeit liefern:

$\Lambda =0\Rightarrow t_{0}={\frac {2}{3H_{0}}}$

$\Lambda >0\Rightarrow t_{0}={\frac {1}{\omega }}\operatorname {arcoth} {\frac {1}{\sqrt {\Omega _{\Lambda 0}}}}$

Ohne kosmologische Konstante ergibt sich mit der gegenwärtigen Hubble-Konstanten ein Weltalter von etwa 9.3 Milliarden Jahren. Dies widerspricht jedoch den heutigen Vorstellungen über die Entwicklung der Sterne, welche für Kugelsternhaufen ein Alter von bis zu fast 13 Milliarden Jahren anzeigen. Hingegen erhält man mit kosmologischer Konstante ein $t_{0}$ von circa 13.4 Milliarden Jahren, was mit den Entwicklungsmodellen der Kugelsternhaufen gut übereinstimmt. Das hohe Alter dieser Objekte ist so ein weiterer Hinweis auf die Existenz einer dunklen Energie. Das zeitliche Verhalten des Skalenfaktors in einem falchen Universum ist in untenstehender Abbildung zusammengefasst.

Lösung der Friedmann-Gleichung für ein flaches Universum. Dargestellt ist die Abhängigkeit des Skalenfaktors $a$ von der Zeit mit bzw. ohne kosmologische Konstante (durchgezogene bzw. gestrichelte Kurve). Die gepunktete Linie stellt den heutigen auf 1 normierten Zustand dar

Aus der Definition der Hubble-Konstanten (Anstieg der Fluchtgeschwindigkeit mit der Entfernung, wobei erstere wiederum das Anwachsen des Raums mit der Zeit darstellt) folgt für beide hier diskutierten Fälle deren Zeitabhängigkeit $H(t)$:

$\Lambda =0\Rightarrow H(t)=H_{0}{\frac {t_{0}}{t}}$

$\Lambda >0\Rightarrow H(t)=H_{0}{\sqrt {\Omega _{\Lambda 0}}}\coth(\omega t)$

Wie schon geschildert, kommt für ein flaches Weltall ohne kosmologische Konstante die Expansion mehr und mehr zum Stillstand, was sich in einer mit fortschreitender Zeit immer mehr dem Wert 0 annähernden Hubble-Konstanten manifestiert. Unter Einbeziehung der dunklen Energie strebt die Hubble-Konstante stattdessen gegen einen nicht verschwindenden Wert, was eine permanente Beschleunigung bedeutet. Auch $H(t)$ seit hier graphisch wiedergegeben.

Lösung der Friedmann-Gleichung für ein flaches Universum. Dargestellt ist die Abhängigkeit der Hubble-Konstanten $H$ von der Zeit mit bzw. ohne kosmologische Konstante (durchgezogene bzw. gestrichelte Kurve). Die gepunktete Linie stellt den heutigen Zustand dar

Zuletzt sei die Zeitabhängigkeit des Beschleunigungsparameters $q(t)$ genannt:

$\Lambda =0\Rightarrow q={\frac {1}{2}}$

$\Lambda >0\Rightarrow q(t)={\frac {1}{2}}(1-3(\tanh(\omega t))^{2})$

Mit $\Lambda$ = 0 ist $q$ von der Zeit unabhängig. Der positive Wert steht für die Abbremsung eines solchen Universums. Im Falle $\Lambda >0$ ist der Beschleunigungsparameter nur für eine gewisse Zeit nach der Entstehung des Kosmos positiv. Im Laufe der Zeit gewinnt die dunkle Energie im Vergleich zur beobachtbaren und dunklen Materie mehr und mehr die Oberhand, wodurch die anfänglich abgebremste Expansion schließlich in eine beschleunigte Ausdehnung umschlägt.

Lösung der Friedmann-Gleichung für ein flaches Universum. Dargestellt ist die Abhängigkeit des Beschleunigungsparameters $q$ von der Zeit mit bzw. ohne kosmologische Konstante (durchgezogene bzw. gestrichelte Kurve)

Die Lösungen mit kosmologischer Konstante enthalten stets sogenannte Hyperbelfunktionen. Während die trigonometrischen Funktionen aus auf dem Einheitskreis $x^{2}+y^{2}=1$ beruhenden geometrischen Konstruktionen hervorgehen, entstehen die Hyperbelfunktionen in analoger Weise aus der Einheitshyperbel $x^{2}-y^{2}=1$. Sie sind unter der Wikipedia ausführlich beschrieben.

Anfangsbedingungen

Wie für die Simulation eines Planetensystems, eines Sternhaufens oder einer Galaxie müssen auch für ein Modell des Weltalls als Ganzes Startbedingungen für die Verteilung der Materie und ihre charakteristischen Geschwindigkeiten festgelegt werden. Die aus der Friedmann-Gleichung folgende Vorstellung eines extrem dichten Anfangszustands lässt erwarten, dass das frühe Universum sich von den heute beobachtbaren Strukturen noch viel dramatischer unterschied als ein Sternhaufen oder eine Galaxie nach der Bildung erster Sterne von der jetztigen Gestalt. Angesichts der gleichzeitig zutage tretenden Widersprüche mit der Quantentheorie stellt sich dabei die Frage, in wie weit dieser Anfangszustand überhaupt rekonstruierbar ist und bis heute sichtbare Spuren hinterlassen hat.

Die kosmische Hintergrundstrahlung

Wie im letzten Unterkapitel dargelegt, ist die Dichte der Strahlung $\rho _{S}$ im Universum umgekehrt proportional zur vierten Potenz des Skalenfaktors $a$. Daraus lässt sich ableiten, dass mit kleinerem Skalenfaktor auch eine höhere Temperatur $T$ des Strahlungsfeldes einhergeht. $\rho _{S}$ ist nämlich der vierten Potenz von $T$ proportional, woraus wegen $\rho _{S}\sim 1/a^{4}$ nmittelbar folgt

$T\sim {\frac {1}{a}}$

Die der Strahlung entsprechende Temperatur ist umgekehrt proportional dem Skalenfaktor. Der Kosmos war ursprünglich also nicht nur äußerst dicht, sondern auch extrem heiß. Mit den Konsequenzen eines solchen glühenden Urzustands befassten sich im Detail erstmals Alpher (1948) sowie Alpher und andere (1948) (diese Forschergruppe wurde von Gamow geleitet, welcher dem Doktoranden Alpher als Hauptautor den Vortritt ließ), sie nannten diesen in Anlehnung an Aristoteles' Idee einer Urmaterie Ylem. Als eine der bedeutsamsten Folgen dieses Ylems sagten die Autoren die Existenz eines homogenen Strahlungshintergrunds voraus, der infolge der fortschreitenden Ausdehnung des Weltalls sich seitdem immer weiter abgekühlt hat und dessen heutige Temperatur nur noch bei etwa 3 K liegen sollte. Tatsächlich stießen Penzias und Wilson (1965) bei Arbeiten an einer Hornantenne völlig unbeabsichtigt auf ein nicht behebbares Störsignal, das laut Dicke und anderen (1965) die von obigen Autoren geforderten Eigenschaften erfüllte.

Die von Penzias und Wilson entdeckte sogenannte kosmische Hintergrundstrahlung wurde in den letzten Jahrzehnten mit Hilfe von Satelliten mit hoher Genauigkeit vermessen. Der Cosmic Background Explorer COBE, die Wilkinson Microwave Anisotropy Probe WIMAP und das Planck-Weltraumteleskop bestimmten nicht nur das Spektrum und die Temperatur der Strahlung, sondern auch deren Verteilung am Himmel. Dabei stellte sich heraus, dass der Mikrowellenhintergrund nicht völlig gleichmäßig ist. Allerdings betragen die Schwankungen um die mittlere Temperatur von circa 2.7 K nur wenige hunderttausendstel K, wie Hinshaw und andere (2009) aufgezeigt haben.

Kartierung der kosmischen Hintergrundstrahlung durch Hinshaw und anderer (2009) auf Grundlage der Messungen der Wilkinson Microwave Anisotropy Probe WIMAP. Die dunkelblauen Gebiete sind 0.0002 K kühler, die roten 0.0002 K heißer als im Durchschnitt

Die Entstehung der Hintergrundstrahlung kann man sich folgendermaßen klar machen. Rechnet man in die Vergangenheit zurück, so erreicht man aufgrund der stetig ansteigenden Temperatur des Strahlungsfeldes einen Zeitpunkt, bis zu dem kein nach außen hin elektrisch neutraler Wasserstoff, sondern nur ein aus freien Elektronen und Protonen bestehendes Plasma existieren konnte. In ionisierter Materie kann sich Licht jedoch aufgrund der sogenannten Thomson-Streuung nicht frei ausbreiten. Man kann sich diese als eine Abfolge elastischer Stöße der Lichtquanten an den geladenen Teilchen des Plasmas vorstellen, wodurch die Richtung der Lichtausbreitung bei unveränderter Wellenlänge ständig geändert wird. In der Regel stoßen sich die Lichtquanten dabei an Elektronen, da diese aufgrund ihrer viel geringeren Masse bei einer gegebenen Temperatur sich viel rascher bewegen als die Protonen. Der Kosmos war, solange er als Plasma vorlag, ein undurchsichtiger gleißender Nebel. Die Hintergrundstrahlung gibt genau jenen Moment wieder, als Elektronen und Protonen sich vereinigten und fortan elektromagnetische Strahlung ungehindert durch die Thomson-Streuung den Raum durchqueren konnte.

Um das Alter des Universums zu diesem Zeitpunkt zu bestimmen, muss man als erstes seine damalige Größe im Vergleich zur gegenwärtigen betrachten. Um Wasserstoff ionisieren zu können, ist eine Temperatur von etwa 3000 K erforderlich. Als die Hintergrundstrahlung entstand, war das Weltall somit etwa 1100 Mal heißer und dementsprechend kleiner als heute. Setzt man diesen Skalenfaktor in die soeben gegebene Lösung der Friedmann-Gleichung ein, so liefert diese ein damaliges Weltalter von ungefähr 460000 Jahren. Jedoch berücksichtigt diese Berechnung neben der dunklen Energie nur die Materie, nicht aber den Dichteanteil der Strahlung. Letztere hatte zu jener Zeit jedoch viel mehr Gewicht, wohingegen der Beitrag der dunkle Energie noch vernachlässigbar war.

Aus dem momentanen Wert der Hubble-Konstante, der flachen Geometrie und der kosmologischen Konstante folgt, dass die Materiedichte gegenwärtig bei ungefähr 2.8 $\cdot$ 10^-27 kg/m³ liegt. Die Temperatur der Hintergrundstrahlung liefert eine Strahlungsdichte von etwa 4.5 $\cdot$ 10^-31 kg/m³. Das Verhältnis $\rho _{M}:\rho _{S}$ der beiden Komponenten ist also heute circa 6200:1. Geht man zur Zeit der Entstehung der Hintergrundstrahlung zurück, so nimmt $\rho _{M}$ um einen Faktor (1100)³, $\rho _{S}$ aber um das (1100)⁴-fache zu. Das Verhältnis der beiden Dichten lag damals somit 1100 mal niedriger bei nur knapp 6:1.

Gemäß Bennett und anderen (2003) entstand die Hintergrundstrahlung etwa 380000 Jahre nach dem durch $a$ = 0 definierten Urknall, d.h. das Modell einer expandierenden Kugel ohne Strahlung stimmt zum Zeitpunkt der Rekombination mit der exakten Theorie noch einigermaßen überein. Der Kosmos war gerade noch genügend stark von der Materie dominiert, um das vereinfachte Konzept anwenden zu dürfen. Noch früher aber war die Dichte der Strahlung (weit) höher als diejenige der Materie, so dass für diese Epoche das simple Szenario definitiv versagt.

Die fast gleichförmige Temperatur der Hintergrundstrahlung zeigt, dass das soeben durchsichtig gewordene Universum noch sehr homogen war und nur äußerst geringe Dichteunterschiede aufwies. Dabei entsprechen, wie z.B. Schneider (2008) erörtert hat, Gebiete höherer Temperatur Bereichen geringerer Dichte und umgekehrt. Lichtquanten, die aus Gebieten höherer Dichte entkamen, erlitten durch die dort herrschende stärkere Gravitation eine größere Rotverschiebung entsprechend einer Strahlung niedrigerer Temperatur.

Die Rekonstruktion der damaligen Dichteverteilung aus der heute sichtbaren Temperaturverteilung ist mit einigen Problemen behaftet, da die ursprünglichen Eigenschaften der Lichtquanten der Hintergrundstrahlung durch nachträgliche Prozesse oft verfälscht wurden. Auch nach der Bildung neutralen Wasserstoffs waren (und sind auch heute noch) freie Elektronen vorhanden. Lichtquanten, die solche Elektronen passierten, verloren durch Thomson-Streuung ihre ursprüngliche Bewegungsrichtung. Gleiches widerfuhr Lichtquanten bei engen Vorübergängen an sehr massereichen Objekten wie etwa Galaxien oder gar Galaxienhaufen infolge der Lichtablenkung durch starke Gravitationsfelder. Beide Prozesse bewirkten eine Verschmierung ursprünglich vorhandener Ungleichmäßigkeiten der Hintergrundstrahlung, so dass diese jetzt glatter erscheint, als es der einstigen Dichteverteilung entspricht. Beim Durchlaufen von Galaxien(haufen) traten zudem wiederholt Blau- und Rotverschiebungen auf, welche in der Summe nicht immer sich gegenseitig aufhoben und somit die Temperatur des Strahlungsfeldes störten.

Dichteverteilung

Schon wenige Jahre nach der Entdeckung der Hintergrundstrahlung hatte Zeldovich (1970) die Idee, das gerade durchsichtig gewordene Universum als ein Gas zu beschreiben, dessen homogene Dichteverteilung durch Schallwellen geringfügig gestört wurde, und die Entwicklung solcher Störungen aufgrund der Schwerkraft zu beobachten. Darauf aufbauend, stellten Efstathiou und andere (1985) den frühen Kosmos durch Testmassen gleicher Masse $m$ dar, welche im ungestörten Zustand ein regelmäßiges Würfelgitter bildeten. Die Schallwellen wurden durch Versetzungen der Testmassen gegenüber dem idealen Gitter modelliert.

Als erstes stellt sich bei diesem Konzept die Frage nach der Größe einer solchen Testmasse. Um die Gravitation als alleinige Kraft zu betrachten, d.h. den Gasdruck vernachlässigen zu dürfen, muss $m$ wesentlich größer als die sogenannte Jeans-Masse sein. Letztere gibt an, welche Masse eine Gaswolke höchstens aufweisen darf, damit sie aufgrund des ihr innewohnenden Drucks - welcher wiederum von der Temperatur und Dichte des Gases abhängt - der Schwerkraft standhalten kann. Unmittelbar nach der Vereinigung der Elektronen mit den Protonen zu neutralem Wasserstoff betrug diese mehrere 100000 Sonnenmassen. Testmassen einer Größenordnung von 100 Millionen Sonnenmassen (wie sie bei der nachfolgend erörterten Bolshoi-Simulation zur Anwendung kamen) sind für eine N-Körper-Simulation des frühen Weltalls ohne Berücksichtigung des Gasdrucks also zulässig.

In der Praxis ist $m$ auch durch die verfügbare Rechenkapazität nach unten begrenzt. Geringe Testmassen erlauben, kleinräumige Strukturen zu modellieren, erfordern aber umgekehrt eine größere Anzahl von Testobjekten und dementsprechend einen höheren Rechenaufwand.

Als nächstes sind die Abmessungen des Würfelgitters zu diskutieren (siehe nächste Abbildung). Im ungestörten Zustand haben benachbarte Testmassen in jeder Richtung einen Abstand $a$ voneinander, welcher entsprechend der Dichte $\rho$ des frühen Universums und der Masse $m$ gewählt werden muss. Wie soeben geschildert, beläuft sich die gegenwärtige Dichte des Kosmos auf etwa 2.8 $\cdot$ 10^-27 kg/m³ bzw. 1.4 $\cdot$ 10^-7 Sonnenmassen pro Kubikparsec. Als die Hintergrundstrahlung entstand, war $\rho$ wie ebenfalls schon besprochen um das 1100³-fache höher, entsprechend ungefähr 54 Sonnenmassen pro Kubikparsec. Mit Testobjekten von 100 Millionen Sonnenmassen ist ein Abstand $a=(m/\rho )^{1/3}$ von circa 123 Parsec zum jeweils nächsten Nachbarn erforderlich.

Die Ausdehnung $L$ des gesamten Gitters ist wie $m$ durch den maximal akzeptierten Rechenaufwand begrenzt. In jeder Richtung gibt es $L/a+1$ Testmassen, insgesamt also $(L/a+1)^{3}$.

Modellierung des homogenen Universums nach der Rekombination durch ein Ensemble von Testteilchen gleicher Masse, welche ein regelmäßiges Würfelgitter bilden, beruhend auf Efstathiou und anderen (1985)

Der entscheidende Gedanke besteht nun darin, vor Beginn einer Simulation die regelmäßige Anordnung der Testobjekte durch Schallwellen zu stören, was zunächst eindimensional dargestellt werden soll. In nachfolgender Abbildung läuft eine solche Welle mit einer Amplitude $a/2$ und einer Länge $8a$ durch das Gitter und versetzt jede Testmasse um einen Betrag $\Delta x$, wodurch sich lokale Schwankungen der Dichte ausbilden.

Störung eines eindimensionalen Ensembles von Teilchen mit ursprünglich regelmäßiger Anordnung durch eine Schallwelle

Bei der Einführung solcher Wellen müssen wie eben angedeutet sowohl deren Amplituden als auch Längen festgelegt werden. In einem kontinuierlichen Medium wie einem Gas kann die Wellenlänge $\lambda$ an und für sich beliebige Werte annehmen. Eine Computersimulation stützt sich jedoch stattdessen nur auf ein Ensemble endlich vieler Testmassen, die ungestört nur bestimmte diskrete Positionen einnehmen. Damit aber sind auch die möglichen $\lambda$ auf wenige diskrete Werte beschränkt. Die größtmögliche Wellenlänge ist durch die Gesamtausdehnung $L$ des Gitters gegeben, die kleinstmögliche beträgt $2a$. Allgemein sind Wellenlängen $L/k$ möglich, wobei $k$ eine ganze Zahl, die sogenannte Wellenzahl darstellt. $k$ umfasst einen Wertebereich von 1 bis $k_{max}=L/2a$ (hier und im Folgenden wird angenommen, dass $L$ ein geradzahliges Vielfaches von $a$ ist).

Mathematisch lässt sich die Störung $\Delta x$, welche eine Testmasse durch eine Welle der Länge $L/k$ erleidet, einfach durch eine trigonometrische Funktion wiedergeben. $A_{k}$ stellt dabei deren Amplitude und $\phi _{k}$ deren Phase dar.

$\Delta x=A_{k}\cos \left({\frac {2\pi kx}{L}}+\phi _{k}\right)$

Da Wellen der zulässigen $k$ gleichzeitig in Erscheinung treten können, muss über alle diese summiert werden:

$\Delta x=\sum _{k=-k_{max}}^{k_{max}}A_{k}\cos \left({\frac {2\pi kx}{L}}+\phi _{k}\right)$

Der Fall $k=0$ wird aus der Summe ausgeschlossen. Die Summierung sowohl über positive als auch negative Wellenzahlen erklärt sich dadurch, dass sowohl nach rechts als auch nach links laufende Wellen berücksichtigt werden sollen.

Es lohnt sich, die mathematische Behandlung der Schallwellen mit der Analyse der Planetenbewegungen zu vergleichen. Tatsächlich kommt hier exakt die gleiche Technik - die Fourieranalyse - zum Einsatz. Der Unterschied besteht darin, dass für die Planetenbahnen nach einer zeitlichen Periodizität gesucht wird, für die Schallwellen hingegen nach einem periodischen Verhalten im Raum.

Die Phasen der einzelnen Wellenmoden können als Zufallsereignisse betrachtet werden und müssen daher nicht explizit definiert werden. Für jedes $\phi _{k}$ wird schlicht eine Zufallszahl zwischen 0 und 2$\pi$ generiert. Um die Amplituden zu bestimmen, sind dagegen zusätzliche theoretische Überlegungen erforderlich. Ganz allgemein ist $A_{k}$ eine Funktion der Wellenzahl und nimmt mit zunehmendem $k$ ab, d.h. je kürzer die Wellenlänge, umso kleiner die Amplitude. Efstathiou und andere nahmen an, dass unter den Bedingungen eines flachen Kosmos mit kalter dunkler Materie sich Dichteschwankungen herausbildeten, die einer Gaußschen Normalverteilung folgten. Um solche Störungen mit Schallwellen zufälliger Phase nachzubilden, müssen deren Amplituden folgende Beziehung erfüllen.

$A_{k}={\frac {\alpha }{2\pi k}}$

Die Amplitude ist demgemäß umgekehrt proportional der Wellenzahl. $\alpha$ ist ein freier Parameter, welcher an und für sich anhand der durch die Verteilung der kosmischen Hintergrundstrahlung angezeigten Dichteschwankungen festgelegt werden kann. Faktisch ist $\alpha$ jedoch durch die endliche räumliche Auflösung der Simulation nach unten beschränkt. Um mittels des hier vorgestellten Verfahrens normalverteilte Dichtefluktuationen erzeugen zu können, darf $\alpha$ nicht wesentlich kleiner als der Abstand $a$ benachbarter Testmassen im ungestörten Zustand sein. Das aber bedeutet, dass eine Simulation nicht mit den tatsächlich beobachteten extrem geringen Dichteunterschieden unmittelbar nach der Rekombination gestartet werden kann.

Glücklicherweise lässt sich dieses Problem umgehen. Zeldovich entwickelte ein Näherungsverfahren, das die zeitliche Verstärkung kleiner Dichteschwankungen durch Gleichungen beschreibt, welche durch Standardverfahren ohne die Notwendigkeit einer N-Körper-Simulation gelöst werden können. Dieses ist brauchbar, solange lokale Dichtedifferenzen kleiner als die mittlere Dichte bleiben. Die so für eine gewisse Zeit nach der Rekombination vorhergesagten stärkeren Amplituden können anschließend der Festlegung der Anfangsbedingungen der eigentlichen Mehrkörpersimulation dienen.

Ein realitätsnahes Modell muss selbstverständlich alle drei Raumdimensionen berücksichtigen. Aus der Verschiebung $\Delta x$ einer Testmasse wird damit ein Verschiebungsvektor $\Delta {\vec {r}}=(\Delta x,\Delta y,\Delta z)$, an Stelle der Wellenzahl k tritt der Wellenvektor ${\vec {k}}_{r}=(k_{x},k_{y},k_{z})$, dessen einzelne Komponenten weiterhin Werte von 1 bis $L/2a$ aufweisen können. Für die Bestimmung einer jeden Verschiebungskomponente muss nun eine Dreifachsumme gebildet werden, welche über alle Komponenten des Wellenvektors läuft (wobei der Nullvektor ausgeschlossen ist).

${\begin{pmatrix}\Delta x\\\Delta y\\\Delta z\end{pmatrix}}=\sum _{k_{x}=-k_{max}}^{k_{max}}\sum _{k_{y}=-k_{max}}^{k_{max}}\sum _{k_{z}=-k_{max}}^{k_{max}}A_{k}{\frac {1}{|{\vec {k}}|}}{\begin{pmatrix}k_{x}\\k_{y}\\k_{z}\end{pmatrix}}\cos \left({\frac {2\pi {\vec {k}}\cdot {\vec {x}}}{L}}+\phi _{\vec {k}}\right)$

Das Produkt $kx$ in der Cosinus-Funktion wird durch das Skalarprodukt von Orts- und Wellenvektor ersetzt. Jede Welle hat wieder eine Zufallsphase, welche nun aber für alle möglichen Kombinationen des Tripels $(k_{x},k_{y},k_{z})$ erzeugt werden muss. Ebenso existiert für jedes Tripel eine Amplitude, welche nun dem Betrag des Wellenvektors umgekehrt proportional ist.

$A_{\vec {k}}={\frac {\alpha }{2\pi |{\vec {k}}|}}$

Abschließend sei ein Beispiel für die Methode von Efstathiou und anderen gezeigt. Untenstehende Abbildung zeigt ein zweidimensionales Ensemble mit einer Ausdehnung von 14 $a$. Damit können die Komponenten des Wellenvektors Werte von 1 bis 7 annehmen. $\alpha$ ist auf $a$ gesetzt. Tatsächlich liefert der Algorithmus erhebliche lokale Dichteschwankungen.

Störung eines zweidimensionalen Ensembles von Teilchen mit ursprünglich regelmäßiger Anordnung durch ein Spektrum von Schallwellen. Wellenlängen, Phasen und Amplituden folgen dem Modell von Efstathiou und anderen (1985)

Schon Zeldovich erkannte, dass sich derartige Störungen unter dem Einfluss der Schwerkraft trotz der Expansion des Weltalls weiter verstärkten, so dass sein eigenes nur für schwache Fluktuationen gültiges Verfahren nicht mehr zulässig war. Efstathiou und andere konnten in Simulationen mit bis zu 64³ = 262144 Testobjekten tatsächlich die Entstehung filamentartiger Strukturen aus anfänglich sehr geringen Dichteschwankungen beobachten. Moderne auf Milliarden von Testmassen beruhende Simulationen, wie sie im letzten Abschnitt dieses Kapitels behandelt werden, haben diese Ergebnisse erheblich verfeinert und die Richtigkeit von Zeldovich' Idee eindrucksvoll bestätigt.

Geschwindigkeitsverteilung

Die mittlere Anfangsgeschwindigkeit der Testmassen in obigem Würfelgitter ist gleich 0. Infolge der Schallwellen erleiden diese jedoch nicht nur eine Störung der Position, sondern auch der Geschwindigkeit. Die Geschwindigkeit, mit der Teilchen unter der Einwirkung einer Schallwelle sich hin- und herbewegen, wird als Schallschnelle bezeichnet und darf nicht mit der Schallgeschwindigkeit verwechselt werden. Letztere gibt an, wie schnell sich die in der Schallwelle vorhandene Energie ausbreitet. Die Amplitude der Schallschnelle $V$ ist mit der Amplitude $A$ der Auslenkung und der Frequenz $f$ der Schwingung folgendermaßen verknüpft:

$V=2\pi fA$

Die Frequenz kann durch die Wellenlänge $\lambda$ und die Schallgeschwindigkeit $c$ gemäß $f=c/\lambda$ ausgedrückt werden. Für die Wellenlänge gilt im eindimensionalen Gitter wiederum $\lambda =L/k$. Die Amplitude der Auslenkung folgt gemäß dem hier benutzten Modell der Beziehung $A=\alpha /2\pi k$. Einsetzen in obige Formel liefert:

$V={\frac {\alpha c}{L}}$

Die Amplitude der Schallschnelle ist für normalverteilte Dichteschwankungen von der Wellenzahl $k$ unabhängig, was auch für die dreidimensionale Erweiterung gilt. Für das obige Beispiel eines zweidimensionalen gestörten Gitters wurde $\alpha$ = $a$ und $L$ = 14 $a$ verwendet, so dass sich hierfür $V$ = $c$ / 14 ergibt.

Um die Schallgeschwindigkeit nach der Rekombination abzuschätzen, wird das frühe Universum als ideales Gas behandelt. Die Gastheorie zeigt, dass die Schallgeschwindigkeit folgendermaßen von der Temperatur $T$, der molaren Masse $M_{mol}$ und dem Adiabatenkoeffizienten $\kappa$ abhängt, wobei $R$ die universelle Gaskonstante bedeutet:

$c={\sqrt {\frac {\kappa RT}{M_{mol}}}}$

Aufgrund der hohen Temperatur von etwa 3000 K lag das Gas damals in atomarer, nicht molekularer Form vor, so dass $\kappa$ = 5/3 war. Die molare Masse folgt aus den beiden Komponenten Wasserstoff und Helium (die ebenfalls kurz nach dem Urknall entstandenen geringen Mengen von Lithium werden hier vernachlässigt), deren Massenanteile etwa 75% bzw. 25% betrugen (also im Verhältnis 3:1 standen). Da ein Wasserstoffatom eine etwa 4 Mal kleinere Masse hat als ein Heliumatom, folgt aus dem Massenverhältnis, dass erstere ungefähr 12 Mal häufiger waren als letztere. Aus diesem Verhältnis folgt für das Gasgemisch aus den individuellen molaren Massen (1.008 g / Mol für Wasserstoff unf 4.003 g / Mol für Helium) eine molare Masse von circa 1.24 g pro Mol. Zusammen mit der Gaskonstante von 8.314 J / (Mol K) liefern diese Angaben eine Schallgeschwindigkeit von etwa 5.8 km/s für den gerade durchsichtig gewordenen Kosmos. Für das obige gestörte zweidimensionale Gitter wäre demnach eine Amplitude der Schallschnelle von circa 410 m/s anzusetzen.

Die Geschwindigkeit während einer Schwingung ist hinsichtlich ihrer Zeitabhängigkeit gegenüber der Auslenkung um 90 Grad phasenverschoben, so dass zur Beschreibung der Geschwindigkeitsstörung $\Delta {\vec {v}}$ anstelle der Cosinus- Sinusfunktionen treten. Die eindimensionale Beschreibung lautet:

$\Delta v={\frac {\alpha c}{L}}\sum _{k=-k_{max}}^{k_{max}}\sin \left({\frac {2\pi kx}{L}}+\phi _{k}\right)$

Für die dreidimensionale Darstellung gilt:

${\begin{pmatrix}\Delta v_{x}\\\Delta v_{y}\\\Delta v_{z}\end{pmatrix}}={\frac {\alpha c}{L}}\sum _{k_{x}=-k_{max}}^{k_{max}}\sum _{k_{y}=-k_{max}}^{k_{max}}\sum _{k_{z}=-k_{max}}^{k_{max}}{\frac {1}{|{\vec {k}}|}}{\begin{pmatrix}k_{x}\\k_{y}\\k_{z}\end{pmatrix}}\sin \left({\frac {2\pi {\vec {k}}\cdot {\vec {x}}}{L}}+\phi _{\vec {k}}\right)$

Endlichkeit und Grenzenlosigkeit des Kosmos

Bei allen bisher behandelten Systemen - vom Planetensystem bis hin zu Galaxien - ist es zulässig, dass einzelne Mitglieder dem Ensemble entkommen. Für das Universum als Ganzes ist dies jedoch nicht möglich, da es gemäß der Friedmann-Gleichung einen endlichen, durch den Skalenfaktor definierten Raum umfasst. Zugleich hat es wie die Oberfläche einer Kugel dennoch keine Grenzen. Jeder Körper - egal wo er sich befindet - ist stets von allen Seiten von benachbarten Massen umgeben. Um diese fundamentalen Eigenschaften zu berücksichtigen, müssen an dem hier vorgestellten Konstrukt eines Würfelgitters einige wesentliche Änderungen vorgenommen werden. Im Folgenden wird dabei der Weg nachgezeichnet, den die Autoren der Bolshoi-Simulation (russisch: bolshoi = groß) Klypin und andere (2011) gegangen sind, welche wiederum auf dem Algorithmus von Kravtsov und anderen (1997) ruht.

Berücksichtgung der Endlichkeit

Werden für eine Simulation des Weltalls mitbewegte, der Expansion folgende Koordinaten verwendet, so bleibt die Kantenlänge $L$ des hier den Raum darstellenden Würfels unverändert. Die Endlichkeit des Kosmos verlangt, dass in diesem Modell kein einziger Massenpunkt einen Koordinatenwert größer als $L$ / 2 bzw. kleiner als $-L$ / 2 aufweist. In der Praxis kann infolge enger Begegnungen einzelner Körper untereinander aber nicht vermieden werden, dass Massenpunkte gelegentlich diese Grenzen überschreiten. Um solche Ausreißer in den Würfel zurückzubeordern, wendeten die Autoren der Bolshoi-Simulation folgenden recht willkürlich erscheinenden, aber einfach zu handhabenden Trick an.

Behandlung der Endlichkeit des Raumes in der Bolshoi-Simulation von Klypin und anderen (2011)

Verlässt ein Massenpunkt den Würfel, lässt man diesen auf der gegenüberliegenden Seite einfach wieder eintreten. In der Skizze hat der nach außen gewanderte Körper eine x-Koordinate kleiner als $-L$ / 2. Um diesen wieder im Würfel unterzubringen, erhält er einen neuen x-Wert $x+L$. Tritt umgekehrt eine x-Position größer als $L$ / 2 auf, wird diese durch $x-L$ ersetzt. Die y- und z-Koordinate bleiben in beiden Fällen unverändert. Ist eine der letzteren von einer Grenzverletzung betroffen, wird völlig analog vorgegangen.

Berücksichtigung der Grenzenlosigkeit

Im Würfelmodell sind nur Körper, die sich relativ nahe am Koordinatenursprung aufhalten, mehr oder weniger gleichmäßig von Nachbarn umgeben. Massenpunkte nahe der Seitenflächen weisen nur in Richtung des Zentrums Nachbarn auf. Solche Randlagen stehen jedoch im Widerspruch zur Grenzenlosigkeit des Kosmos. Um diesen Konflikt aufzulösen, verwendeten Klypin und andere ein Modell, in welchem der Original-Würfel in allen Richtungen im Prinzip unendlich viele Ebenbilder hat. Um die Kraft zu berechnen, welche auf einen Original-Körper einwirkt, werden diese Ebenbilder wie reale Massenpunkte behandelt.

Behandlung der Grenzenlosigkeit des Raumes in der Bolshoi-Simulation von Klypin und anderen (2011)

In der Praxis muss man nur solche Ebenbilder berücksichtigen, welche sich in einem Würfel der Kantenlänge 2 $L$ um den Koordinatenursprung befinden. Diese werden definiert, indem die originalen Koordinaten $(x,y,z)$ eines Massenpunkts bei negativen Ausgangswerten um $L$ vergrößert und bei positiven um $L$ verringert werden. In dreidimensionaler Darstellung hat jeder Körper 7 Ebenbilder. 3 Ebenbilder entstehen, indem jeweils nur 1 Koordinate geändert wird, 3 weitere durch simultane Änderung von 2 Koordinaten und das letzte durch gleichzeitige Änderung aller 3 Koordinaten. Sind z.B. alle drei Koordinaten negativ, so lauten die Ebenbilder $(x+L,y,z),(x,y+L,z),(x,y,z+L),(x+L,y+L,z),(x+L,y,z+L),(x,y+L,z+L)$ und $(x+L,y+L,z+L)$.

Um die auf eine reale Testmasse ausgeübte Schwerkraft zu bestimmen, wird um diese ein Würfel der Kantenlänge $L$ aufgespannt. Nur reale Körper und Ebenbilder innerhalb dieses Würfels werden berücksichtigt, alle anderen ignoriert. Auf einen Probekörper mit einer x-Koordinate $x$ lässt man also nur solche Massenpunkte einwirken, deren x-Werte zwischen $x-L/2$ und $x+L/2$ liegen. Entsprechend wird mit der y- und z-Koordinate verfahren.

Simulationsbeispiele

Eine Beschreibung der Bolshoi-Simulation soll dieses Kapitel und damit auch das Buch beschließen. Es handelt sich um die bislang umfangreichste Nachbildung der Strukturbildung im Universum. Sie beruht auf einem Würfelgitter mit nicht weniger als 2048³ = 8589934592 Körpern, wobei jeder einzelne eine Masse von etwa 200 Millionen Sonnenmassen aufweist. Durch diese enorme Anzahl kommt die schon im Galaxienkapitel angesprochene Eigenschaft der dunklen Materie, sich zu Halos sehr unterschiedlicher Größe und Masse zu verdichten, hervorragend zur Geltung. Dank der relativ geringen Masse pro Testobjekt können auch kleine Materiekonzentrationen bis herab zu circa 20 Milliarden Sonnenmassen nachgewiesen werden, was einer Zwerggalaxie von der Größenordnung der Großen Magellanschen Wolke entspricht. Andererseits wird nicht nur die Bildung großer Galaxien, sondern auch von weiträumigen Galaxienhaufen sichtbar - es finden sich Halos bis hin zu einer Größenordnung von 1000 Billionen Sonnenmassen entsprechend etwa 1000 Galaxien vom Ausmaß der Milchstraße.

Die Bolshoi-Simulation beeindruckt nicht nur durch die Anzahl der Massenpunkte, sondern auch die betrachtete Zeitspanne, welche sich von der Frühzeit des Kosmos bis zur Gegenwart erstreckt. Sie startet zu einem Zeitpunkt, als die Schwankungsbreite der ursprünglich extrem geringen Dichteunterschiede bereits auf etwa 8.6% der mittleren Dichte angewachsen war. Mittels der Theorie von Zeldovich (1970) kommen die Autoren der Simulation zu dem Schluß, dass das Universum damals circa 80 Mal kleiner war als heute. Gemäß dem in diesem Kapitel vorgestellten Modell eines flachen Kosmos mit einem heutigen Anteil der dunklen Energie von ungefähr 70% an der Gesamtdichte entspricht ein solcher Skalenfaktor einem Zeitpunkt von etwa 24 Millionen Jahre nach dem Urknall.

Für die Bolshoi-Simulation seien nicht nur die wichtigsten Resultate, sondern auch die erforderliche Rechnerkapazität genannt. Klypin und andere (2011) führten sie auf dem sogenannten Pleiades-Computer am NASA Ames Research Center durch. Dieser war mit 13824 Core-Prozessoren und einem RAM-Speicher von circa 13 Terabyte ausgestattet. Die insgesamt gelieferte Datenmenge belief sich auf ungefähr 100 Terabyte.

Eine exzellente Statistik - für jede betrachtete Epoche wurden im Mittel etwa 10 Millionen Halos gefunden - erlaubt sehr detaillierte Aussagen über die Häufigkeit und Verteilung dieser Objekte und entsprechend zuverlässige Vergleiche mit Beobachtungen. Kleine Verdichtungen sind - wie auch schon im Galaxienkapitel angedeutet - wesentlich häufiger anzutreffen als große. Die Bildung großer Halos beansprucht viel Zeit, so dass solche im jungen Universum sehr selten oder gar nicht vorhanden sind. Zum Zeitpunkt eines Skalenfaktors von 1/11 gegenüber dem heutigen (Weltalter circa 500 Millionen Jahre) finden sich in der Bolshoi-Simulation Halos nur bis zu einer Größenordnung von 100 Milliarden Sonnenmassen, d.h. die Entstehung von Systemen wie der Milchstraße ist noch nicht abgeschlossen. Erst bei einem Skalenfaktor von 1/7 (ungefähr 900 Millionen Jahre nach dem Urknall) überschreiten manche Verdichtungen die für große Galaxien erforderliche Massenskala von 1 Billion Sonnenmassen. Stark bevölkerte Galaxienhaufen treten erst ab einem Skalenfaktor von 1/3.5 (Weltalter etwa 4 Milliarden Jahre) in Erscheinung, in Form von Halos mit bis zu einigen 10 Billionen Sonnenmassen.

Die gute Auflösung (100 Massenpunkte für die kleinsten Verdichtungen, mehrere Millionen für die größten) gestattet sogar eine genaue Analyse der inneren Struktur der Halos, welche sich ebenfalls im Laufe der Zeit verändert. Kleine Verdichtungen stammen oft noch aus der Frühzeit des Kosmos. Sie hatten so viel Zeit, sich zu ihren Zentren hin weiter zu konzentrieren. Vor allem sehr große Halos sind in der Regel weit jünger, so dass sie ungeachtet ihrer enormen Massen sich längst nicht in gleichem Maße weiter verdichten konnten. Im frühen Weltall war der Anschauung entsprechend in großen Halos, sofern solche überhaupt existierten, die Materie stärker zur Mitte hin konzentriert als in kleinen. Mit fortschreitendem Alter des Kosmos hat sich dies mehr und mehr umgekehrt. Kleine Verdichtungen werden heute von sehr alten Objekten mit sehr dichten Zentralregionen dominiert. Bei großen Halos überwiegen dagegen vergleichsweise junge Systeme mit weniger dichten Zentren. Die seltenen alten großen Halos fallen in der Statistik kaum ins Gewicht. Dieser Befund der Bolshoi-Simulation stimmt gut mit der Tatsache überein, dass Zwerggalaxien noch stärker von der dunklen Materie beherrscht erscheinen als große Sternsysteme.