Einführung in die Systemtheorie/ Druckversion
Dynamische Systeme
[Bearbeiten]Methoden der Systemtheorie
[Bearbeiten]Schwerpunkt der Systemtheorie ist die Behandlung der verschiedenen dynamischen Systeme, deren Signale, die verschiedenen mathematischen Beschreibungen als Systemmodelle und die Systemberechnung. Folgende detaillierte Aufgabenbereiche und Systemdefinitionen sind damit verbunden:
- Definition dynamischer Systeme als Modell,
- Definition von Ein- und Mehrgrößensystemen,
- Identifikation der Systemstruktur,
- Verhalten linearer und nichtlinearer Systeme,
- Zeitverhalten: Systeme mit Zeitinvarianz und Zeitvarianz,
- Arten der mathematischen Beschreibung des Systemverhaltens:
- Gewöhnliche Differenzialgleichung im Zeitbereich f(t)
- Übertragungsfunktion im komplexen Frequenzbereich F(s)
- Systemdarstellung im Zustandsraum f(t)
- Zeitdiskrete Systembeschreibung und Systemberechnung f(k*Δt)
- Modellbildung eines Systems,
- Definition geeigneter Testsignale,
- Allgemeine Definition der Systemstabilität
Zum wirklichen Verständnis des Zeitverhaltens der dynamischen Systeme sind die Kenntnisse der gängigen mathematischen Berechnungsmethoden erforderlich. Dazu gehören die Kenntnisse der Entstehung und Lösung der gewöhnlichen Differenzialgleichung, die Anwendung der Laplace-Transformation, die Systembeschreibung mit der Übertragungsfunktion, für fachlich Fortgeschrittene die Systembehandlung im Zustandsraum und nicht zuletzt die numerische Berechnung dynamischer Systeme mit der diskreten Zeit Δt.
Totzeitbehaftete und nichtlineare dynamische Systeme und deren zugehörige Signale lassen sich zu einem vernünftigen Aufwand nur numerisch berechnen, alle anderen genannten mathematischen Beschreibungen sind nur bedingt brauchbar. Ist einer Übertragungsfunktion G(s) die transzendente Funktion des Totzeitgliedes multiplikativ angehängt, dann kann das Gesamtsystem nicht mehr algebraisch behandelt werden. [transzendent (Mathematik): über das algebraische hinausgehend].
Dieses vorliegende Kapitel "Dynamische Systeme" zeigt mit seinen Unterkapiteln vereinfacht den Einstieg in die mathematischen Beschreibungen, um den vorgezogenen Begriff "Dynamisches System" verstehen zu können.
Definition dynamisches System
[Bearbeiten]Ein dynamisches System ist eine abgegrenzte zeitabhängige Funktionseinheit, die durch ihre Signaleingänge und Signalausgänge in einer Wechselwirkung mit der Umwelt steht. Das System kann beispielsweise ein mechanisches Gebilde, ein elektrisches Netzwerk aber auch ein biologischer Vorgang oder ein Bestandteil der Volkswirtschaft sein. Es hat mindestens einen Signaleingang und einen Signalausgang.
Dynamische Systeme werden mit Hilfe mathematischer Werkzeuge als Modelle eines realen Übertragungssystems beschrieben. Damit lässt sich für gegebene Eingangssignale der Verlauf der Ausgangssignale von einem bestimmten Zeitpunkt t = 0 = t(0) an für t > t(0) bestimmen. Ebenso eignen sich die Modelle zur Systemanalyse.
Systeme lassen sich in nichttechnische, natürliche oder künstliche - von Menschenhand geschaffene Einrichtungen - einteilen. Dennoch zeigen diese unterschiedlichen Systeme bei ähnlichen Strukturen als Modelle prinzipiell ähnliche mathematische Eigenschaften.
Ein technisches dynamisches System enthält einen oder mehrere Energiespeicher, die konzentriert oder räumlich verteilt angeordnet sind. Häufig werden bei Systemberechnungen zur Vereinfachung konzentrierte Energiespeicher angenommen. Systembeispiele: Feder-Masse-Dämpfungssystem, Elektrischer Schwingkreis.
Dynamische Systeme mit konzentrierten Systemspeichern enthalten Variablen als Funktion der Zeit. Dynamische Systeme mit räumlicher Verteilung der Systemspeicher enthalten Variablen als Funktionen der Zeit und des Ortes.
Das Ausgangs- Eingangsverhalten dieser Systeme kann linear, kontinuierlich nichtlinear, diskontinuierlich nichtlinear, zeitinvariant, zeitvariant und totzeitbehaftet sein. Dies gilt für Eingrößen- und Mehrgrößensysteme.
Ferner können die internen Energiespeicher Anfangswerte enthalten, wenn das Signalverhalten eines Systems zu einem bestimmten Zeitpunkt innerhalb eines Einschwingvorgangs für betrachtete werden sollen.
Statische lineare oder nichtlineare Systeme haben keine Energiespeicher und damit kein Zeitverhalten. Das Ausgangs- Eingangsverhalten wird durch algebraische oder transzendente (Trigonometrische oder exponentielle) Funktionen oder Wertetabellen beschrieben.
Viele technische dynamische Systeme enthalten Komponenten von mechanischen, elektrischen, elektronischen, hydraulischen und fluidischen (Fluidik = Elemente mit pneumatischer bzw. hydraulischer Hilfsenergie) Elementen. Bei gleicher Systemstruktur gelten die gleichen mathematischen Systembeschreibungen.
- Systeme mit konzentrierten und verteilten Energiespeichern
- Ein technisches dynamisches System enthält einen oder mehrere Energiespeicher, die konzentriert oder räumlich verteilt angeordnet sind. Häufig werden bei Systemberechnungen zur Vereinfachung konzentrierte Energiespeicher angenommen.
- Das zeitliche Verhalten des dynamischen Systems ist durch die inneren Systemgrößen bestimmt, die als Energiespeicher vorhanden sind und sich nicht sprunghaft ändern können. Sie bedeuten zum Beispiel "Spannung an einem Kondensator", "Strom in einer Induktivität", bei einem "Feder-Masse-Dämpfungssystem die potentiellen und kinetischen Energieanteile". Diese dynamischen Systemteile entsprechen den konzentrierten Energiespeichern.
- Dynamische Systeme mit konzentrierten Systemspeichern enthalten Variablen als Funktion der Zeit.
- Dynamische Systeme mit räumlicher Verteilung der Systemspeicher enthalten verteilte Systemparameter. Bei diesen Systemen sind die Variablen nicht nur Funktionen der Zeit sondern auch vom Ort. (Beschreibung durch partielle Differenzialgleichungen oder Näherungsmodelle)
- Beispiele für kontinuierliche Systeme mit räumlich verteilten Energiespeichern stellen elektrische Leitungen im Rahmen der Leitungstheorie dar oder ein anderes Beispiel der Thermodynamik ist die räumliche oder flächenmäßige Wärmeenergie-Ausbreitung als Folge eines Energiesprunges in einem homogenen Medium (Metall, Flüssigkeit, Stein usw.).
- System mit Anfangswerten
- Technische dynamische Systeme besitzen Speicher (Gedächtnis) der Materie, der Energie oder der Information. Die Gedächtniswirkung bezieht sich auf einen transienten Einschwingvorgang des Systems als Folge einer vorangegangenen Eingangserregung. Zu einem festgelegten beliebigen Zeitpunkt t = t0 innerhalb des Einschwingvorgangs hat das System, das mehrere Energiespeicher enthalten kann, einen oder mehrere sogenannte Anfangswerte in den Speichern.

- Die Anfangswerte y01...y0n sind die inneren Systemgrößen eines dynamischen Systems während eines Einschwingvorgangs zu einem beliebigen Zeitpunkt t0, zu dem das System betrachtet werden soll. Die Lösung einer systembeschreibenden Differenzialgleichung je nach Anzahl der Differenziale der Systemordnung beruht immer auf Anwendung von Integrationsfunktionen. Ein einzelner Anfangswert ist der Ausgangswert jeder der möglichen Integratoren, die zur Lösung der Differenzialgleichung zum Zeitpunkt t0 notwendig sind.
- Im Zustandsraum betrachtet, sind die Anfangswerte die Zustandsvariablen x1...xn eines dynamischen Systems zum Zeitpunkt t0 in dem Signalflussplan der "Regelungsnormalform" dargestellt. Dabei entsprechen die jeweiligen Ausgänge der Integratoren zum Zeitpunkt t0 den Zustandsvariablen und sind gleichzeitig die Anfangswerte.
- Die bis in die 1960-er Jahre bevorzugte Lösung einer systembeschreibenden Differenzialgleichung durch einen Analogrechner ähnelt sehr stark der Regelungsnormalform des Zustandsraumes. Die Ausgangswerte der Integratoren zum beliebig wählbaren Zeitpunkt t0 während des Einschwingvorgangs sind die Anfangswerte. Der Signalflussplan als mathematisches Modell eines Analogrechners ist heute in gleicher Weise gültig. Die Berechnung des Signalflussplans wird numerisch durchgeführt und bezieht sich auf die explizite (deutlich, eindeutig) Form der Differenzialgleichung, bei der die höchste Ableitung der Ausgangsgröße y(t) von der Gleichung freigestellt wird.
- Die Integratoren des Modells starten mit dem Rechenprogramm bei der Eingangserregung z.B. u(t) = 0 von den eingestellten Anfangswerten. Siehe Signalflussplan an der Summenstelle für die höchste Ableitung . Die Lösung der Differenzialgleichung für y(t) wird so erzwungen.
- Befindet sich das System nach genügend langer Zeit im Ruhezustand - d. h. der Einschwingvorgang ist abgeschlossen und das System-Eingangssignal hat den Wert Null - dann sind auch die Anfangswerte zu einem wählbaren Zeitpunkt t0 gleich Null.
- Hat das System eine Eingangserregung u(t) > 0, und der Einschwingvorgang ist nach genügend langer Zeit abgeschlossen, dann nimmt die Ausgangsgröße y(t) = x1(t) entsprechend der Proportionalverstärkung K den Wert der Eingangsgröße u(t) * K an. Zwingend notwendig ist dazu, dass die Variable x2(t) laut Signalflussplan den Wert Null annimmt, anderenfalls könnte sich kein statischer Wert für y(t) ergeben.
- Eingangserregung und Anfangswerte
- In der Systemtheorie ist es üblich, den Beginn des Beobachtungszeitraumes eines dynamischen Vorganges formal bei t = 0 festzulegen, daher sind Testsignale am Eingang des Systems für den Zeitraum t < 0 gleich Null. Zu dem bestimmten Zeitpunkt t0 , ab dem man das Verhalten des dynamischen Systems betrachten möchte, können die Energiespeicher des Systems Anfangswerte enthalten. Erhält das System zu diesem definierten Zeitpunkt t0 eine Erregung, überlagern sich die Anfangswerte und die Wirkung der Eingangserregung für den Zeitraum .
- Ist die Eingangserregung zum Zeitpunkt t0 gleich Null, ist das System mit Anfangswerten sich selbst überlassen und die Ausgangsgröße strebt zeitlich - ein stabiles System vorausgesetzt - einen Wert gegen Null bzw. die Ruhelage an. Handelt es sich um ein instabiles System (z.B. um ein System mit Rückkopplung), wird je nach Systemordnung zwischen monotoner und oszillatorischer Instabilität unterschieden. Dabei strebt die System-Ausgangsgröße zeitlich einen Maximalwert an. (Siehe Kapitel "Systemtheorie/ Übertragungsfunktion")
- Für die Analyse und Ermittlung des Eingangs- Ausgangsverhalten von Systemen der regelungstechnischen Anlagen ist häufig das Systemverhalten ohne Anfangswerte von Interesse. Die Systemspeicher befinden sich bei t0 im Ruhezustand und haben den Wert Null.
- Mathematisches Modell
- Das dynamische System ist meist ein mathematisches Modell eines realen Übertragungssystems, welches mit Hilfe mathematischer Werkzeuge für gegebene Eingangssignale den Verlauf der Ausgangssignale von einem bestimmten Zeitpunkt t(0) = 0 an für t > t(0) bestimmt. Die häufigsten mathematischen Systembeschreibungen sind die Differenzialgleichung, die Übertragungsfunktion, der Frequenzgang und die zeitdiskrete Differenzengleichung. Enthalten die Systeme eine Totzeit (Transportzeit, Getriebespiele), Begrenzungseffekte oder andere Nichtlinearitäten kommt für die Systemberechnung praktisch nur die zeitdiskrete Differenzengleichung in Verbindung mit logischen Funktionen als Systembeschreibung infrage.
- Ausnahmsweise werden auch physikalische materielle Modelle verwendet. Beispiele: Hydraulischer Strömungskanal im verkleinerten Maßstab, Regelkreisnachbildung mit einem Analogrechner.
- Alle diese Systeme können sich linear, kontinuierlich nichtlinear, diskontinuierlich nichtlinear, zeitinvariant, zeitvariant und totzeitbehaftet als Eingrößen- und Mehrgrößensystem verhalten.
- Statisches System
- Im Gegensatz zu den dynamischen Systemen hat ein statisches System im Sinne der Systemtheorie verschwindend kleine Energiespeicher und damit angenähert kein Zeitverhalten, sondern wird durch das Eingangs-Ausgangsverhalten des Systems definiert. Dieses Verhalten kann proportional, kontinuierlich linear, kontinuierlich nichtlinear oder diskontinuierlich (gebrochene Funktion) auftreten und wird – soweit möglich – durch eine mathematische Modellbeschreibung oder durch Wertetabellen angenähert beschrieben.
- System mit verzögerndem und voreilendem Ausgangsverhalten
- Allgemein reagieren dynamische Systeme ohne Hilfsenergie bzw. ohne Verstärker, die aus mehreren Systemteilen bestehen können, signaltechnisch je nach System-Übertragungsverhalten mit einem meist verzögertem Signal des Systemausgangs. Enthält das System einen "Energieverstärker", kann statt einer verzögernden Wirkung eine vorauseilende Signalwirkung erreicht werden. Beispiele dafür sind die in der Regelungstechnik eingesetzten PD- und PID-Regler, aber auch gewollte Frequenzgang-Korrekturen des Systemverhaltens.
Einführung der mathematischen Systembeschreibung
[Bearbeiten]Übersicht der mathematischen Systembeschreibung
[Bearbeiten]
Ein dynamisches System hat ein Zeitverhalten und soll als Vereinfachung als ein System mit konzentrierten Energiespeichern beschrieben werden. Sind die physikalischen Komponenten eines beispielsweise schwingfähigen Systems - wie Feder-Masse-Dämpfungssystem - oder elektrisch - Kapazität-Induktivität-Widerstandssystem bekannt, können diese Systeme mit einer gewöhnlichen Differenzialgleichungen mit konstanten Koeffizienten beschrieben werden.
Da dieses genannte System zwei Energiespeicher (z.B. Feder und Masse) enthält, wird es durch eine gewöhnliche Differenzialgleichung zweiter Ordnung beschrieben.
Je nach vorhandenen Informationen und Systemverhalten eines dynamischen Systems existieren noch verschiedene andere mathematische Systembeschreibungen, die sich zur Systemanalyse, Systemidentifikation und Systemberechnung besser eignen.
Zum Verständnis der verschiedenen Arten der Systeme und des Systemverhaltens sind mathematische Beschreibungen von Teilsystemen, die in verschiedensten Strukturen auftreten können, erforderlich. Dazu gehört die Kenntnis der wichtigsten Begriffe der Systembeschreibung, die gewöhnliche Differenzialgleichung und Laplace-Übertragungsfunktion, die aus der Differenzialgleichung mittels der Laplace-Transformation bestimmt werden kann. Beide Methoden setzen lineare dynamische Systeme voraus. Weitere Systembeschreibungen wie die Differenzengleichungen und die Systembeschreibungen im Zustandsraum werden aus den Differenzialgleichungen abgeleitet.
Obwohl die Übertragungsfunktion G(s) eine Systembeschreibung linearer Systeme im komplexen Frequenzbereich s = δ + jω darstellt, kennzeichnet sie an Hand der symbolischen Darstellung einfacher algebraischer Gleichungen das charakteristische Systemverhalten im Zeitbereich. Es existieren nur 6 verschiedene Formen einfacher oder mehrfacher Kombinationen davon.
Totzeitbehaftete nichtlineare dynamische Übertragungssysteme lassen sich meist in statische nichtlineare Systeme und dynamische lineare Systeme aufteilen und beschreiben. Das Zeitverhalten dieser Systeme kann nur numerisch errechnet werden, weil Nichtlinearitäten Unikate sind, die mit logischen Programmbefehlen oder Datentabellen beschrieben werden können.
Nachfolgend findet eine Kurzdarstellung dieser Systembeschreibungen statt.
Einführung der Systembeschreibung mit Differenzialgleichungen
[Bearbeiten]Die wichtigste mathematische Systembeschreibung ist die Differenzialgleichung, welche die speziellen physikalischen Grundgesetze des zeitlichen Verhaltens eines bestimmten dynamischen Systems beschreibt. Mit den Differenzialgleichungen lassen sich viele dynamische Systeme aus der Technik, Natur und Gesellschaft darstellen. Viele scheinbar sehr verschiedene physikalische Probleme lassen sich mit der Differenzialgleichung jedoch formal identisch berechnen.
Eine systembeschreibende Differenzialgleichung ist durch die Differentiale der Energiespeicher und der Ein-Ausgangssignale bestimmt. Die Differenzialgleichung eines dynamischen Systems beschreibt den Zusammenhang zu jedem Zeitpunkt zwischen der Ausgangsgröße y(t) und der Eingangsgröße u(t). Die Ordnung der Differentialgleichung ist durch die Ordnung der höchsten vorkommenden Ableitung gegeben.
Andere bekannte Systembeschreibungen der dynamischen Systeme lassen sich von den Differenzialgleichungen entwickeln, wie die Übertragungsfunktion mit dem komplexen Frequenzbereich f(s), der Frequenzgang f(jω), die Zustandsraumdarstellung und die für die numerische Berechnung benötigten Differenzengleichungen.
Mathematische Modelle der dynamischen Systeme werden je nach Kenntnis und Verfügbarkeit der Systemparameter durch verschiedene mathematische Beschreibungsmethoden gekennzeichnet, bzw. angenähert.

Nichtlineare dynamische Systeme können zur einfacheren Berechnung auch durch Modelle in Kombinationen von nichtlinearen Systemen ohne Zeitverhalten und linearen dynamischen Systemen aufgeteilt werden, z.B. nach dem Hammerstein-Modell. Nichtlineare statische Modelle sind meist Unikate.
Die Berechnung dynamischer Systeme dient der Kenntnis des Ausgangs-Eingangsverhaltens und der Systemanalyse. Je nach Art des dynamischen Systems eignen sich verschiedene mathematische Beschreibungs- und Berechnungsverfahren:
Gewöhnliche Differenzialgleichung höherer Ordnung mit konstanten Koeffizienten
[Bearbeiten]- Eine Differentialgleichung ist eine Gleichung, die eine oder mehrere Ableitungen einer unbekannten Funktion enthält. Die Bezeichnung "gewöhnlich" bezieht sich darauf, dass die gesuchte Funktion nur von einer Variablen abhängt. Es wird nur nach einer Variablen abgeleitet. Eine lineare gewöhnliche Differenzialgleichung enthält die gesuchte Funktion und deren Ableitungen nur in der ersten Potenz. Die gesuchte Funktion darf auch nicht in Argumenten von Winkelfunktionen, Logarithmen usw. erscheinen, anderenfalls wird die Differenzialgleichung nichtlinear. Nichtlineare Differenzialgleichungen mit den verschiedenen Arten der Nichtlinearität sind nur in sehr seltenen Ausnahmefällen analytisch lösbar. Solche dynamischen Systeme können mittels der numerischen zeitdiskreten Methoden beschrieben und berechnet werden.
- Die häufigsten mathematischen Systembeschreibungen linearer Systeme sind gewöhnliche Differenzialgleichungen mit konstanten Koeffizienten. Zur Aufstellung der Differenzialgleichungen höherer Ordnung werden Bilanzgleichungen der Energie / Materie-Speicher benötigt. Systeme mit konzentrierten Speichern erfordern für jede Speicherfunktion eine Differenzialgleichung 1. Ordnung. Diese Differenzialgleichungen mit den Anfangsbedingungen = Null können am einfachsten über die Laplace-Transformation gelöst werden.
- Bei dynamischen Systemen in Form ausgeführter technischer Anlagen stehen Differentialgleichungen selten zur Verfügung. Das Systemverhalten muss erst noch analysiert und dann formuliert werden.
- Beispiel einer gewöhnliche Differenzialgleichung n-ter Ordnung mit konstanten Koeffizienten a und b für ein System mit dem Ausgangssignal y(t) und Eingangssignal u(t):
Differenzialgleichung höherer Ordnung mit variablen Koeffizienten
[Bearbeiten]- Sind diese Koeffizienten oder nur ein Koeffizient dieser Differenzialgleichung variabel, dann ändert sich das Zeitverhalten des dynamischen Systems, d.h. eine Sprungantwort des Systems für einen gegebenen Eingangssprung nimmt einen anderen zeitlichen Verlauf. Dieses Verhalten wird leicht verständlich, wenn man die Laplace-transformierte Differenzialgleichung als Übertragungsfunktion betrachtet.
- Sind die Koeffizienten zeitabhängig, führt dieses zu zeitvariantem Systemverhalten, d.h. das Zeitverhalten des Systems ist zu unterschiedlichen Zeitpunkten für t > t0 unterschiedlich. Systembeispiel: Wenn bei einer beschleunigten Rakete die Masse des Treibstoffs sich ändert.
Partielle Differenzialgleichung
[Bearbeiten]- Bei partiellen Differenzialgleichungen hängt die gesuchte Funktion von mehreren Variablen ab. Es wird nach mehreren Variablen abgeleitet. Die Anwendung dieser Gleichung erfolgt z.B. bei dynamischen Systemen mit Zeit- und Ortskoordinaten.
- Systembeispiel: Signalübertragung bei langen elektrischen Leitungen oder Wärmefluss in homogenen Medien.
Beispiel der Entstehung einer Differenzialgleichung mit elektrischen Bauelementen
[Bearbeiten]
- L = Induktivität, C = Kondensator, R = Widerstand, UC = Spannung am Kondensator = Ausgangsgröße, UE = Eingangsspannung
Es können Zeitkonstanten wie T1 = R * C und T2² = L * C eingeführt werden mit y(t) = Ausgangsgröße, u(t) = Eingangsgröße.
oder in allgemeiner Koeffizienten-Darstellung:
Einführung der konventionellen Lösung einer gewöhnlichen Differenzialgleichung
[Bearbeiten]Die Lösung einer Differenzialgleichung (DGL) erfolgt immer durch Integration und ist eine Funktion, nicht ein Wert. Natürlich kann auch ein bestimmter Wert der Ausgangsgröße für eine bestimmte Zeit errechnet werden.
Die Lösung der Differenzialgleichung ist die Ausgangsgröße y(t) in Abhängigkeit der Art und Größe des gegebenen Eingangssignals u(t). Eingangssignale sind häufig Testsignale wie die Sprung- und Impulsfunktion, die charakteristische Signalantworten des Systems hervorrufen, die der Systemdiagnose dienen können.
Die gewöhnliche Differenzialgleichung (DGL) beschreibt ein lineares Übertragungssystem mit n Energiespeichern durch n Ableitungen der Systemausgangsgröße y(t) und m Ableitungen der Eingangsgröße u(t) des Systems. Die Lösung einer DGL erfolgt durch Integration. Jede unbestimmte Integration ergibt Integrationskonstanten Cn, deren Anzahl durch die Ordnung n der DGL festgelegt ist.
Für ein gegebenes Eingangssignal an dem linearen dynamischen System mit Anfangswerten ergibt sich als Lösung der systembeschreibenden gewöhnlichen DGL eine Addition aus zwei Lösungsanteilen, der homogenen und partikulären Lösung, die einen Funktionsverlauf f(t) der Ausgangsgröße des Systems darstellen. Die konventionelle Lösung einer inhomogenen DGL besteht aus der allgemeinen Lösung der homogenen DGL mit der Ausgangsgröße yH(t) mit der Eingangsgröße u(t) = 0 sowie einer speziellen partikulären Lösung der inhomogenen DGL yP(t) mit u(t) ≠ 0.
Inhomogene DGL = DGL mit u(t) ≠ 0)
- Bei der homogenen Lösung der DGL liegen Anfangswerte vor. Die Systemeingangsgröße u(t) ist dabei gleich Null. Das System ist sich selbst überlassen und strebt einen stabilen Ruhezustand an, Systemstabilität vorausgesetzt.
- Bei der partikulären Lösung der DGL sind die Anfangswerte gleich Null und die Systemeingangsgröße u(t) ≠ Null.
- Die Summe der beiden Ausgangs-Teilgrößen y(t) = yH(t) + yP(t) ergibt die Gesamtlösung.
Differenzialgleichung mit Anfangswerten
[Bearbeiten]Die Anfangsbedingungen beschreiben einen speziellen Zustand des Übertragungssystems. Die homogene (charakteristische) DGL beschreibt das Verhalten ohne Eingangsgröße (für u(t) = 0), das sogenannte Eigenverhalten, d. h. das System bleibt ausgehend von den Anfangswerten sich selbst überlassen.
Sind alle Anfangswerte der homogenen DGL gleich Null, ist die Lösung der DGL für yH(t) auch gleich Null. Mit dem Lösungsansatz ergibt sich ein universelles Lösungsverfahren für die homogene Lösung der DGL-en beliebiger Ordnungen mit konstanten Koeffizienten.
Die partikuläre Lösung der DGL eines Systems höherer Ordnung (> 2. Ordnung) über das Faltungsintegral gestaltet sich schwierig. Einfacher wird die Lösung über die Laplace-Transformation und noch einfacher und übersichtlicher mit Hilfe der numerischen Berechnung.
Definition Anfangswertproblem
[Bearbeiten](Anfangswertproblem = Differenzialgleichung mit ihren zugehörigen Anfangswerten)
Das eigentliche Anfangswertproblem besteht darin, mit den gegebenen Anfangswerten y0 und y'0 ... y(n)0 und den Eigenwerten λn (Nullstellen) der DGL die Integrationskonstanten Cn zu berechnen. Die Anfangswerte werden in die Lösungsgleichung anstelle von yH(t) eingesetzt. Dabei werden die Terme der DGL entsprechend der Ordnung differenziert und dann die Gleichungen für t = 0 berechnet. Damit ergeben sich entsprechend der Ordnung n der DGL n Gleichungen, aus denen die Integrationskonstanten errechnet werden können.
Die Berechnung der Integrationskonstanten ist leider sehr umständlich, gehört aber zur klassischen Lösung der DGL.
Anwendung dynamisches System mit Anfangswerten
[Bearbeiten]Der Zustand eines dynamischen Systems (z.B. Regelstrecke) ist durch den Energiegehalt der im System enthaltenen Energiespeicher bestimmt. Zu einem beliebigen Zeitpunkt t = t0, der als Anfangszustand der Ausgangsgröße y(t) bezeichnet wird, folgt die Ausgangsgröße y(t) in Abhängigkeit des Anfangszustandes und des Eingangssignals u(t) für t>t0 für beliebig lange Zeiten. Dazu wird die Vorgeschichte des Systems für t < 0 nicht benötigt.
Verzichtet man auf die Berechnung einer DGL mit Anfangswerten eines Übertragungssystems, kann mit Hilfe der Übertragungsfunktion G(s) und Laplace-Transformationstabellen die Lösung der Differenzialgleichung für gegebene Eingangssignale im Zeitbereich bestimmt werden.
Ist die Übertragungsfunktion G(s) als Laplace-transformierte Differenzialgleichung gegeben, so ist die Berechnung des System-Ausgangssignals y(t) für ein gegebenes Eingangssignal Y(s) bei Anwendung der inversen Laplace-Transformation immer eine partikuläre Lösung. Die partikuläre Lösung der Differenzialgleichung ist in der Regelungstechnik meist von hauptsächlichem Interesse.
In der Regelungstechnik werden häufig Übertragungssysteme durch Aufzeichnung der Sprungantwort analysiert. Dabei wird meistens vorausgesetzt, dass sich das System in Ruhe befindet. Es gibt aber Anwendungen, bei denen die Speicher "Anfangswerte" haben oder das System bei Anfangswerten getestet werden sollen, um spezielle Aussagen zu treffen.
Numerische Lösung der Differenzialgleichung mit Anfangswerten
[Bearbeiten]Für viele dynamische Systeme sind nicht immer die physikalischen Einzelkomponenten bekannt und damit kann auch keine Differenzialgleichung aufgestellt werden. Außerdem ist die Lösung einer gewöhnlichen Differenzialgleichung höherer Ordnung schwierig.
Mit Hilfe von Testsignalen und Aufzeichnung der Systemreaktion kann ein dynamisches System identifiziert werden. Bei linearen Systemen wird vorzugsweise die Übertragungsfunktion G(s) als Funktion der komplexen Frequenz s benutzt. Die Zerlegung in Teilsysteme - Linearfaktoren - entspricht der kleinsten Systemeinheit G(s) der gewöhnlichen Differenzialgleichungen 1. Ordnung.
Die numerische Berechnung bezieht sich auf ein konstantes kleines Zeitintervall Δt, der diskreten Zeit. Für dieses Zeitintervall wird an Hand von Differenzengleichungen rekursiv (Rekursion = zurücklaufen) das Systemausgangssignal mit der Folge (k*Δt) neu berechnet und bildet damit einen fein gestuften Signalverlauf als Funktion der Zeit.
Es bestehen mehrere Methoden der Bildung von Differenzengleichungen. Die einfachste Methode ist das Verfahren nach dem "Euler-Streckenzugverfahren", das mit 4 verschiedenen Differenzengleichungen sämtliche lineare Übertragungssysteme approximieren (annähern) kann.
Bei der numerischen Berechnung eines Übertragungssystems mit Anfangswerten oder ohne Anfangswerte ergibt sich das Anfangswertproblem nicht. Die numerische Berechnung bezieht sich dabei auf den Signalflussplan der Regelungsnormalform des Zustandsraumes. Dies entspricht im Prinzip dem Signalflussplan des Analogrechners. Die numerische Integration bezieht sich dabei auf ein bestimmtes Integral. Die Integrationsgrenzen beginnen mit den jeweiligen Anfangswerten bei t0 und enden mit der gewünschten Betrachtungsdauer der rekursiven Berechnungsfolgen kMAX*Δt. Die Integratoren werden zu Beginn der Berechnung auf die gewünschten Anfangswerte gesetzt. Die System-Ausgangsgröße y(t) entspricht immer der Addition der homogenen und partikulären Lösung der DGL.
Sind keine Anfangswerte des Systems gegeben, so können die Systemteile numerisch durch Anwendung von Differenzengleichungen sehr einfach gelöst werden.
→ Siehe das ausführliche Kapitel "Einführung in die Systemtheorie/ Numerische Berechnung dynamischer Systeme".
→ Siehe das ausführliche Kapitel "Einführung in die Systemtheorie/ Gewöhnliche Differenzialgleichungen".
Einführung der Systembeschreibung mit der Übertragungsfunktion G(s)
[Bearbeiten]Der Begriff Übertragungsfunktion hat verschiedene Bedeutungen und kennzeichnet allgemein die Abhängigkeit des Ausgangssignals Y eines Übertragungssystems G von dessen Eingangssignal U.
Neben dem Begriff Laplace-Übertragungsfunktion G(s) - in der Regelungstechnik vereinfacht "Übertragungsfunktion" genannt - existiert auch der Begriff der "Z-Übertragungsfunktion", die aus der Übertragungsfunktion G(s) entstanden ist. Während Differenzialgleichungen für kontinuierliche Signale mit der Laplace-Transformation gelöst werden können, hat die Z-Transformation für zeitdiskrete Signale bei abgetasteten Signalfolgen eine ähnliche Bedeutung. Die Anwendung der Z-Übertragungsfunktion bei abgetastete Signalfolgen ist nicht zwingend, es können auch zur numerischen Systemberechnung Differenzengleichungen des Systems verwendet werden. Die Z-Übertragungsfunktion ist nicht Gegenstand dieses Kapitels.
Die Übertragungsfunktion G(s) eines linearen dynamischen Systems g(t) entsteht z. B. aus der Laplace-Transformation einer systembeschreibenden gewöhnlichen Differenzialgleichung. Sie ist in der Regelungstechnik die häufigste Darstellungsform des Eingangs- und Ausgangsverhaltens von linearen Übertragungssystemen im komplexen Frequenzbereich.
Die Übertragungsfunktion G(s) ist eine abstrakte nicht messbare Größe und beschreibt das mathematische Verhalten eines linearen zeitinvarianten Systems im Frequenzbereich mit der komplexen Variable s. Sie wird nach der Zerlegung der Zähler- und Nennerpolynome durch Nullstellenbestimmung in Produktterme (Linearfaktoren) erfolgreich eingesetzt für Systemanalyse, Systemsynthese, Systemstabilität und erlaubt die algebraische Behandlung von beliebig geschalteten rückwirkungsfreien Teilsystemen.
Die Übertragungsfunktion G(s) beschreibt das Verhältnis der Ausgangsgröße Y(s) zu der Eingangsgröße U(s) im Bildbereich, ist unabhängig von seinen Signalen und gültig in einem linearen und zeitinvarianten System (d. h., das Systems zeigt zu jeder Zeit - bei gleicher Erregung - das gleiche Verhalten).
Die allgemeine Form der Übertragungsfunktion G(s) lautet in Polynomdarstellung:
Beispiel einer Übertragungsfunktion G(s) der 3. Ordnung mit den Koeffizienten ai und bi in Polynomdarstellung mit n > m
Definition der Systemgrößen:
- G(s) ist die Laplace-Transformierte von g(t). Die symbolische Schreibweise lautet:
- G(s) beschreibt das dynamische System mit einer Gleichung in Form einer gebrochen-rationalen Funktion unter der Voraussetzung, dass die internen Energiespeicher des dynamischen Systems gleich Null sind (d. h. verschwindende Anfangsbedingungen). Die Übertragungsfunktion kann über die Laplace-Transformation der systembeschreibenden gewöhnlichen Differenzialgleichung entstehen. Andere Entstehungsweisen sind die empirische Messung und Auswertung des Frequenzgangs , die Systemanalyse mit Hilfe der Impuls- oder der Sprungantwort oder die Bildung des Impedanzverhältnisses des unbekannten linearen Systems.
- Y(s) ist das Systemausgangssignal,
- U(s) ist das Eingangssignal, welches als Testsignal häufig die Funktion eines Signalsprungs, eines Signalimpulses oder einer sinusförmigen Erregung hat.
- Die komplexe Frequenz ist eine unabhängige Variable des Laplace- oder Bildbereichs. Sie tritt mit einem ganzzahligen Exponenten als Potenz im Zähler und Nenner einer Übertragungsfunktion auf, ist aber nur ein Symbol für eine vollzogene Transformation einer Ableitung bestimmter Ordnung n oder eines Integrals der gewöhnlichen Differenzialgleichung. Die Variable s in verschiedenen Darstellungsarten der Übertragungsfunktion kann beliebig algebraisch behandelt werden, enthält aber keinen Zahlenwert.
- bi = Koeffizienten des Zählers, ai = Koeffizienten des Nenners.
- n und m bedeuten jeweils den Grad des Nennerpolynoms und des Zählerpolynoms (Ordnung des Systems). In der Produktdarstellung bedeutet n die Anzahl der Pole im Nenner, m die Anzahl der Nullstellen im Zähler. Sind alle Koeffizienten der Polynomdarstellung in der geordneten Reihenfolge vorhanden, positiv und die Systemordnung n > m, handelt es sich um ein asymptotisch stabiles Übertragungssystem.
Wird die Übertragungsfunktion der Polynomdarstellung in die Produktdarstellung gebracht, können sämtliche Systemeigenschaften wie die Kriterien der Stabilität, Pole, Nullstellen, Verstärkung und Zeitkonstanten aus der Übertragungsfunktion abgeleitet werden. Durch die Rücktransformation mittels der inversen Laplace-Transformation kann das zeitliche Verhalten eines Übertragungssystems als Funktion des Eingangssignals berechnet werden.
Entstehung der Übertragungsfunktion
[Bearbeiten]Die Übertragungsfunktion G(s) beschreibt nach der Systemtheorie die mathematische Beziehung zwischen einem dynamischen System und den zugehörigen Ein- und Ausgangssignalen im sogenannten s-Bereich. Elektrische, mechanische, biologische und andere dynamische Systeme können durch die gleiche Form der Übertragungsfunktion beschrieben werden, wenn die Anzahl und die Struktur der Systemspeicher identisch sind.

Es bestehen mehrere Wege, die zu einer Übertragungsfunktion G(s) führen:
- Laplace-Transformation der systembeschreibenden gewöhnlichen Differenzialgleichung,
- aus dem Signalverhältnis Y(s) / U(s), wenn dieses bekannt ist.
- durch Messen des Frequenzgangs G(jω),
- Spannungsteiler aus einem rückwirkungsfreien Impedanzverhältnis, (Beispiel: RC-beschalteter Operationsverstärker),
- durch Systemidentifikation mittels Sprung- oder Impulsantwort
Die "klassische" Entstehungsweise der Übertragungsfunktion ergibt sich über die Laplace-Transformation der systembeschreibenden Differenzialgleichung mit konstanten Koeffizienten. Das Ergebnis ist eine Polynomgleichung mit der komplexen Frequenz s, die als Stellvertreter für jeden Differentialquotienten steht. Diese Transformation erfolgt nach dem Differentiationssatz der Laplace-Transformation. Der Grad, d.h. die Ordnung des Differentialquotienten entspricht dem Exponenten von s.
Enthält die Differenzialgleichung auch Ableitungen der Systemeingangsgröße, dann entsteht durch die Transformation eine gebrochene rationale Funktion G(s) als Quotient mit Polynomen im Nenner und Zähler. Sind keine Ableitungen der Eingangsgröße gegeben, existiert nach der Transformation nur ein Nennerpolynom der Übertragungsfunktion. Im Zähler der Übertragungsfunktion steht für diesen Fall die Verstärkung K, die auch die Größe 1 betragen kann.
Laplace-Transformation einer linearen gewöhnlichen Differenzialgleichung
[Bearbeiten]Die Übertragungsfunktion entsteht durch die Laplace-Transformation, eine Integraltransformation, aller zeitabhängigen Terme der System-Differenzialgleichung und beschreibt das Übertragungsverhalten im sogenannten Bild- oder Frequenzbereich (s-Bereich) mit der der komplexen Variablen s.
Die Übertragungsfunktion eines Systems entsteht z.B. durch Austausch der zeitabhängigen Terme einer systembeschreibenden Differentialgleichung mit den Laplace-Transformierten. Voraussetzung ist, dass die Anfangsbedingung des Systems Null ist.
Je nach Grad der Ableitungen einer Funktion x(t) entstehen mit Hilfe des Laplace-Differentiationssatzes nach der Transformation folgende Laplace-Transformierte:
Der Grad der Ableitung im Zeitbereich und die zugehörige Transformierte im Bildbereich kann in dieser Weise beliebig fortgesetzt werden. Der Laplace-Operator s entspricht also der 1. Ableitung einer Funktion f(t), s² entspricht der 2. Ableitung einer Funktion f(t) und so weiter.
Für das Integral gilt die Laplace-Transformierte:
Das dynamische Verhalten von linearen Übertragungssystemen (LZI-Systeme) wird durch gewöhnliche Differenzialgleichungen beschrieben. Der Wert der Ordnung n gibt die höchste Ableitung der Ausgangsgröße y(t) und damit allgemein die Anzahl der Energiespeicher des Übertragungssystems wieder.
Eine allgemein geordnete gewöhnliche Differenzialgleichung n-ter Ordnung lautet wie folgt:
- (mit y(t) als Ausgangssignal und u(t) als Eingangssignal)
Falls die Koeffizienten und alle konstant sind, ist die Laplace-Transformation ausführbar. Allgemein gilt für die Signale u(t) und y(t) mit den zu Null gesetzten Anfangsbedingungen:
- für alle
Damit lautet die Laplace-Transformierte der Übertragungsfunktion als Polynomgleichung:
Die Polynomgleichung kann so umgestellt werden, dass ein Verhältnis der Ausgangsgröße Y(s) zur Eingangsgröße U(s) gebildet werden kann. Der Rest der Terme der Polynomgleichung entspricht dem Übertragungssystem G(s) in Form einer gebrochen-rationalen Funktion, also einem Verhältnis aus Zähler und Nenner.
- Die Übertragungsfunktion als eine rational gebrochene Funktion in Polynom-Darstellung lautet
.
Für die Anwendung der Übertragungsfunktion zur Systemberechnung wird der Zustand der Energiespeicher des dynamischen Systems zum Zeitpunkt t = 0 als energiefrei angesehen. Damit werden die Anfangswerte des Systems zu Null.
Eine wesentliche nützliche Eigenschaft der Laplace-Übertragungsfunktion besteht darin, dass zwischen allen Komponenten ein algebraischer Zusammenhang besteht. Ein weiterer Vorteil besteht darin, dass mit Hilfe von Laplace-Transformationstabellen die Umwandlung vom s-Bereich in den Zeitbereich überführt werden kann und somit eine gewöhnliche Differenzialgleichung gelöst werden kann.
Definition Nullstellen und Pole
[Bearbeiten]Ein lineares zeitinvariantes Übertragungssystem ohne Totzeit ist durch Pole, Nullstellen und Proportionalitätsfaktoren der Übertragungsfunktion vollständig bestimmt.
Die Ermittlung der Pole und Nullstellen der Polynome einer Übertragungsfunktion erlaubt die Umwandlung der Polynomdarstellung in eine Produktdarstellung. Die Übertragungsfunktion in der Produktdarstellung führt bei einem gegebenen Eingangssignal über die Laplace-Rücktransformation direkt zu einer Lösung im Zeitbereich. Die Produktdarstellung einer Übertragungsfunktion entspricht einer multiplikativ angeordneten Reihendarstellung von Teilsystemen (Elementarsystemen, Linearfaktoren), wobei ein Teilsystem nicht durch nachfolgende Teilsysteme belastet sein darf.
Zur Nullstellenbestimmung eines Polynoms mit Zahlenwerten werden die Polynome des Zählers und des Nenners der Übertragungsfunktion jeweils gleich Null gesetzt. Bei der Darstellung der Übertragungsfunktion als eine rational gebrochene Funktion werden die Nullstellen des Zählerpolynoms, die das Polynom zu Null machen, als Nullstellen bezeichnet. Die Nullstellen des Nennerpolynoms bezeichnet man als Pole .
Polynome des 2. Grades können mit Hilfe der bekannten "pq-Gleichung" zur Lösung von gemischt-quadratischen Gleichungen gelöst werden. Es existieren noch weitere Verfahren zur Nullstellenbestimmung von Polynomen höheren Grades.
In dieser allgemeinen Darstellung ist noch nicht definiert, um welche Art von elementaren Produkten (= Linearfaktoren) es sich bei der Übertragungsfunktion handelt. Das Systemverhalten wird erst deutlich, wenn Zahlenwerte für die Nullstellen, Pole und Verstärkung vorliegen.
Ein Polynom hat so viele Nullstellen (bzw. Pole), wie es dem höchsten Grad der Ordnung entspricht. Je nach Größe und Anzahl der Koeffizienten der Polynome ergeben sich bei der Pol- Nullstellenbestimmung für die zu bestimmenden Werte der Pole und Nullstellen unterschiedliche mathematische Formen für und , die Null, ± reell und ± konjugiert komplex sein können.
Die Werte von Polen und Nullstellen stabiler Elementarsysteme sind immer negativ. Positive Werte von Polen und Nullstellen führen zur monotonen oder oszillatorischen Instabilität des Gesamtsystems. Pole und Nullstellen haben die Maßeinheit einer Frequenz.
Die Pole bestimmen das Zeitverhalten des Systems, Nullstellen die Systemamplituden. Sind alle Realteile der Pole eines zeitinvarianten dynamischen Systems negativ und von Null verschieden, so ist das Übertragungsverhalten asymptotisch stabil. Bei einem Produktterm mit einem Pol, dessen Realteil und Imaginärteil Null ist, verhält sich das Gesamtsystem semistabil (integrierendes Verhalten).
Linearfaktoren
[Bearbeiten]Sind die Nullstellen bzw. die Pole eines Polynoms bekannt, kann das Zähler- und Nennerpolynom in Produktterme (Linearfaktoren) zerlegt werden. Weil die Nullstellen aus zu Null gesetzten Polynomen berechnet werden, muss sichergestellt werden, dass keine Faktoren gekürzt worden sind. Es empfiehlt sich eine Prüfung vorzunehmen, ob die Pol- Nullstellendarstellung (= Produktdarstellung) durch Ausmultiplizieren auch mit dem Polynom identisch ist.
Eine Nullstelle des Zählerpolynoms sn oder ein Pol des Nennerpolynoms sp kann bei asymptotischer Stabilität des Teilsystems folgende drei Formen von Zahlenwerten einnehmen:
- {sn; sp} = 0, (Absolutglied des Polynoms fehlt),
- {sn; sp} = (reeller Wert der Pole und Nullstellen),
- {sn; sp} = (konjugiert komplexer Wert der Pole oder Nullstellen).
Bezeichnet man den Realteil einer Nullstelle oder eines Poles mit und den Imaginärteil mit , dann ergeben sich bei Übertragungsfunktionen in der Produktdarstellung bei reellen und konjugiert komplexen Nullstellen und Polen unterschiedliche Gleichungen, die durch die Größe der Zahlenwerte der Koeffizienten der Polynomdarstellung bestimmt werden. Die angegebenen drei Formen der Linearfaktoren können einfach und mehrfach auftreten.
In der linearen Regelungstechnik und Systemtheorie ist es eine willkommene Tatsache, dass praktisch alle vorkommenden regulären (stabilen) Übertragungsfunktionen bzw. Frequenzgänge von Regelkreisgliedern auf drei Grundformen geschrieben bzw. zurückgeführt werden können. Die Linearfaktoren haben eine völlig unterschiedliche Bedeutung, je nachdem ob sie im Zähler oder im Nenner einer Übertragungsfunktion stehen.
Stehen die Linearfaktoren im Zähler, haben sie eine differenzierende Wirkung, stehen sie im Nenner, haben sie eine verzögernde (speichernde) Wirkung:
Typ Linearfaktor (Zeitkonstanten-Darstellung) Bedeutung im Zähler Bedeutung im Nenner
Nullstelle "Absolutglied fehlt"Differenzierer, D-Glied Integrator, I-Glied
Nullstelle "reelle Zahl"PD1-Glied Verzögerung, PT1-Glied PD2-Glied: für 0 < D < 1
mit konjugiert komplexen NullstellenSchwingungsglied PT2-Glied: für 0 < D < 1
mit konjugiert komplexen Polen
- Dabei ist T die Zeitkonstante, s die komplexe Frequenz, D der Dämpfungsgrad.
- Beispiel einer Übertragungsfunktion der Polynomdarstellung und der Zerlegung in die Pol-Nullstellen-Darstellung mit reellen Linearfaktoren:
- Sind in der Polynomdarstellung alle Ableitungen und zugehörige Koeffizienten lückenlos mit positivem Vorzeichen vorhanden, stellt die Übertragungsfunktion für die Exponenten n > m ein zeitverzögerndes asymptotisch stabiles System dar. Werden negative Werte der Pole und Nullstellen eingesetzt, entstehen positive Linearfaktoren.
- Das Gesamtsystem wird als "globales proportionales Systemverhalten" bezeichnet.
- Beispiel: Bestimmung des Pols eines Linearfaktors im Nennerpolynom:
- Beispiel einer Übertragungsfunktion der Polynomdarstellung ohne Absolutglied im Nennerpolynom und der Zerlegung in die Pol-Nullstellen-Darstellung mit reellen Linearfaktoren:
- Der Term der gewöhnlichen Differenzialgleichung oder eines transformierten Polynoms im Zähler und Nenner der Übertragungsfunktion mit den Koeffizienten und wird allgemein als Absolutglied bezeichnet. Für oder gilt:
- Linearfaktor ohne Absolutglied des Polynoms im Nenner, Pol .
- Fehlt das Absolutglied a0 im Nennerpolynom (a0 = 0), kann die Variable s aus dem Nennerpolynom ausgeklammert werden. Dieses Gesamtverhalten des Systems wird als "globales integrierendes Systemverhalten" bezeichnet. Fehlt das Absolutglied b0 im Zählerpolynom (b0 = 0), kann die Variable s aus dem Zählerpolynom ausgeklammert werden. Dieses Gesamtverhalten des Systems wird als "globales differenzierendes Systemverhalten" bezeichnet.
- Beispiel einer Übertragungsfunktion in der Pol-Nullstellen-Darstellung mit einem konjugiert komplexen Pol im Nennerpolynom:
- Bei dynamischen Systemen 2. Ordnung (z.B. Feder-Masse-Dämpfungssystem) oder bei Systemen 1. Ordnung, die eine positive Rückführung enthalten (Regelkreise), kann ein Energieaustausch stattfinden. Solche Systeme mit konjugiert komplexen Lösungen der Pole und Nullstellenkönnen können in einem Gesamtsystem enthalten sein und treten immer paarweise - meist im Nenner der Übertragungsfunktion - mit einem identischen Realteil auf.
- und , oder zusammengefasst
- Die Polynome mit konjugiert komplexen Nullstellen werden zur einfacheren Berechenbarkeit zu quadratischen Termen zusammengefasst, in denen nur reelle Koeffizienten auftreten. Deshalb lässt sich ein Elementarsystem 2. Ordnung mit konjugiert komplexen Polen und Nullstellen nicht in 2 Linearfaktoren 1. Ordnung mit nur reellen Koeffizienten zerlegen.
- Wird der Klammerausdruck mit den komplexen Größen im Nenner aufgelöst, entsteht:
- und
- Wenn Zahlenwerte vorliegen, können mit verschiedenen Methoden, wie mit der pq-Formel für Systeme 2. Ordnung, oder fertige im Internet verfügbare Programme bis 4. Ordnung mit dem Aufruf - "Nullstellen (Lösungen) von Polynomen bestimmen" - die Pole und Nullstellen bestimmt werden.
- Für Systeme mit Polynomen 2. Ordnung der Form errechnen sich die Nullstellen bzw. die Pole:
- Wenn das Polynom 2. Ordnung in die Form zur Lösung einer gemischt quadratischen Gleichung gebracht wird, lassen sich die Nullstellen für p und q durch Faktorenvergleich bestimmen. wird positiv, wenn negative Realteile von oder vorliegen.
- Die Pol- Nullstellendarstellung der Übertragungsfunktion für ein asymptotisch stabiles System enthält immer positive Zahlenwerte, was voraussetzt, dass die Pole und Nullstellen negative Realteile enthalten.
Zeitkonstantendarstellung
[Bearbeiten]Es existieren 2 faktorielle Darstellungsformen, die Pol-Nullstellen-Darstellung und die Zeitkonstanten-Darstellung. Die Zeitkonstanten-Darstellung hat einen höheren Anschauungswert und den Vorteil, dass bei Änderung der Zeitkonstante sich die Systemverstärkung nicht ändert.
Bei der Zeitkonstantendarstellung wird der Produktterm s - sn so umgestellt, dass der Reziprokwert 1/sn = T gebildet wird.
Der Produktterm in der Zeitkonstanten-Darstellung mit negativem Wert der Polstelle sP (Term im Nenner asymptotisch stabiles System) lautet damit:
- .
Bei der Zeitkonstanten-Darstellung des Linearfaktors werden die zwei Terme positiv dargestellt. Dies setzt voraus, dass die Realanteile der zugehörigen Nullstellen und Pole negativ sind.
- Rechenbeispiel einer Übertragungsfunktion G(s) 3. Ordnung mit konjugiert komplexen Polen im Nenner
Gegeben:
- Übertragungsfunktion 3. Ordnung in Polynomdarstellung
Gesucht:
- Übertragungsfunktion in der Pol- Nullstellendarstellung.
- Übertragungsfunktion in der Zeitkonstanten-Darstellung.
Lösung: Bestimmung der Nullstellen und Polstellen der Polynome:
durch Anwendung eines Rechenprogrammes aus dem Internet.
[Suchbegriff: "Nullstellen (Lösungen) von Polynomen" unter Google]:Nullstelle:
Polstelle:
Polpaar:
Bei einem Polynom mit konjugiert komplexen Polen im Nenner einer Übertragungsfunktion handelt es sich um ein
Teilsystem mit der Bezeichnung -Schwingungsglied.Bestimmung der Linearfaktoren aus den Polen und Nullstellen:
Nullstellen und Pole Linearfaktoren Nullstelle: Polstelle: Polpaar:
mit
mit
- Übertragungsfunktion in der Pol- Nullstellen-Darstellung
- Übertragungsfunktion in der Zeitkonstanten-Darstellung
Anmerkung: Ein zu Null gesetztes Polynom kann beliebig mit Zahlen multipliziert oder dividiert werden, die Nullstellen sind immer identisch. Faktoren von zerlegten Polynomen in Produkte müssen berücksichtigt werden, anderenfalls sind Polynom und Produkte nicht identisch.
Negative reelle Pole und Nullstellen bedeuten Systemstabilität des betreffenden Übertragungsgliedes im s-Bereich. Negative konjugiert komplexe Polpaare bedeuten Systemstabilität als schwingendes Übertragungsglied innerhalb eines bestimmten Dämpfungsbereichs D.
Die Art der Pole einer Übertragungsfunktion bestimmt das Zeitverhalten eines Systems. Nullstellen der Übertragungsfunktion haben nur Einfluss auf die Systemamplituden.
Darstellungsformen der Übertragungsfunktion
[Bearbeiten]Aus der Laplace-Transformation einer systembeschreibenden Differenzialgleichung entsteht die Grundform der Übertragungsfunktion G(s) in Polynom-Darstellung. Daraus lassen sich weitere bekannte Schreibweisen der Übertragungsfunktionen errechnen, die unterschiedliche Eigenschaften für die Berechnung der Ausgangsgröße y(t) im Zeitbereich des Übertragungssystems G(s) bei gegebenem Eingangssignal U(s) aufweisen. Alle Formen der Übertragungsfunktionen sind mathematisch bei Rückrechnung mit der Polynomdarstellung identisch.
Die Übertragungsfunktion stellt sich in 4 mathematische Schreibweisen mit gleichem mathematischen Inhalt dar.
- Polynomdarstellung
- Produktdarstellung (Linearfaktoren)
- Zeitkonstantendarstellung
- Partialbruchdarstellung
Diese nicht mehr aufspaltbare Produkte in Zeitkonstantendarstellung sind: (Ts), (Ts+1) und (T2s + 2DTs + 1)KK. Sie haben ein völlig unterschiedliches Übertragungsverhalten, ob sie im Nenner (integrierend, verzögernd) oder Zähler (differenzierend) einer Übertragungsfunktion stehen.
Übertragungsfunktion Darstellungsform im s-Bereich Polynom-Darstellung Pol-Nullstellen-Darstellung
(Produktdarstellung)
s = Laplace-Operator, sn = Zahlenwert der Nullstelle, sp = Zahlenwert der PolstelleZeitkonstanten-Darstellung
Für reelle Linearfaktoren 1. Grades mit Absolutglied und negativen Pol- Nullstellen.Partialbruch-Darstellung
Für reelle Linearfaktoren 1. Grades mit Absolutglied.
Die Zerlegung der Zähler- und Nennerpolynome der Übertragungsfunktion in je eine Produktform (Linearfaktoren) gestattet eine einfache detaillierte Interpretation des Systemverhaltens und der Bestimmung der Koeffizienten des Übertragungssystems. Diese Zerlegung in Linearfaktoren erfolgt durch die Bestimmung der Nullstellen der Polynome.
Die Linearfaktoren, als kleinste Systemeinheit der Produktdarstellung der Polynome, haben konträre Signaleigenschaften, je nachdem, ob sie im Zähler oder im Nenner der Übertragungsfunktion stehen. Stehen sie im Zähler, haben sie eine differenzielle voreilende Signalwirkung des Systemausgangs, stehen sie im Nenner haben sie eine integrierende bzw. verzögernde Signalwirkung.
Linearfaktoren mit gleichen Zeitkonstanten und gleicher Verstärkung im Zähler und Nenner können sich theoretisch zum Übertragungsverhalten G(s) = 1 kompensieren. In der Regelungstechnik wird dieses Verhalten zum Reglerentwurf in einem Regelkreis als sogenannte Pol- Nullstellenkompensation genutzt.
Die Übertragungsfunktion:
eines dynamischen Übertragungssystems kann einfache und mehrfache Linearfaktoren im Zähler und Nenner enthalten. Derartige Systeme beschreiben das Frequenzverhalten mit der komplexen Frequenz mit einem Systemeingang und einen Systemausgang .
Darstellung der Übertragungsfunktion als Produktterme (Linearfaktoren)
[Bearbeiten]Der eigentliche Vorteil der Produkt-Darstellung von Übertragungsfunktionen G(s) mittels Nullstellenbestimmung liegt darin, dass praktisch alle vorkommenden regulären (stabilen) und nichtregulären (instabilen) Übertragungsfunktionen bzw. Frequenzgänge von Übertragungsgliedern G auf folgende drei Grundformen 1. und 2. Ordnung geschrieben bzw. zurückgeführt werden können. Stehen die Grundglieder im Zähler, haben sie eine differenzierende Wirkung, stehen sie im Nenner, haben sie eine verzögernde (speichernde) Wirkung:
Typ Übertragungsfunktion Bedeutung im Zähler Bedeutung im Nenner
Linearfaktor ohne AbsolutgliedDifferenzierer, D-Glied Integrator, I-Glied
Linearfaktor mit AbsolutgliedPD-Glied Verzögerung, PT1-Glied PD2-Glied: für 0 < D < 1
mit konjugiert komplexen NullstellenSchwingungsglied PT2-Glied:
für 0 < D < 1
mit konjugiert komplexen PolenNichtphasenminimales (nichtreguläres) System
PD-Glied mit positiver Nullstelle
(hat keine technische Bedeutung)Instabile Verzögerung PT1-Glied
mit einer positiven PolstelleNichtphasenminimales (nichtreguläres) System
PD-Glied 2. Ordnung
mit einer negativen und positiven Nullstelle
(hat eine Bedeutung als Vorfilter i. d. Regelungstechnik)Instabiles Schwingungsglied PT2-Glied
mit einer negativen und positiven Polstelle
Dabei ist T die Zeitkonstante, s die komplexe Frequenz bzw. die Laplace-Variable, D der Dämpfungsgrad.
- Prinzipielle Anwendung der Übertragungsfunktion für den Reglerentwurf
Die Übertragungsfunktion des geschlossenen Regelkreises ergibt sich durch algebraische Berechnung der Regelkreiskomponenten für die Kreis-Schließbedingung. Die sich so ergebenden Polynome der Übertragungsfunktion werden durch Bestimmung der Pole und Nullstellen in die Produktdarstellung überführt. Die Lage der Pole im s-Diagramm bestimmt die Stabilität des Regelkreises.
Rechenbeispiel zur Bestimmung der Übertragungsfunktion aus der systembeschreibenden Differenzialgleichung

Dämpfung D = 0,125.
Differenzialgleichung 3. Ordnung gegeben:
Gesucht
- Übertragungsfunktion in Zeitkonstantendarstellung,
- Beschreibung des Systemverhaltens im Zeitbereich,
- Sprungantwort des Systems im Zeitbereich
Die Polynomgleichung ergibt sich durch die Anwendung der Laplace-Transformation der Differenzialgleichung.
Durch Ausklammern des Verhältnisses von Ausgangs- zum Eingangssignal der Polynomgleichung entsteht die Übertragungsfunktion.
Die verbleibenden Terme der Polynomgleichung bilden die Übertragungsfunktion G(s).
Bestimmung der Nullstellen und Polstellen der Polynome durch Anwendung eines Rechenprogrammes aus dem Internet.
[Suchbegriff: "Nullstellen (Lösungen) von Polynomen unter Google]:Nullstelle:
Polstelle:
Polpaar:
Bildung der Produktdarstellung der Übertragungsfunktion:
Reelle Pole und Nullstellen bilden Linearfaktoren 1. Ordnung.
Konjugiert komplexe Polpaare bilden Linearfaktoren 2. Ordnung. Sie lassen sich nicht weiter aufspalten.Allgemeine Form der Produktdarstellung mit Linearfaktoren 1. Ordnung:
Werden negative Zahlenwerte der Nullstellen und Polstellen in diese Gleichung eingesetzt, werden die Produkte (Linearfaktoren) positiv und die Übertragungsfunktion verhält sich im Zeitbereich stabil. Der noch nicht bekannte Produktterm mit dem Linearfaktor 2. Ordnung kann errechnet werden, in dem das ursprüngliche Nennerpolynom durch den Term mit dem bekannten reellen Pol (s+0,5) dividiert wird. Das gesuchte Ergebnis ergibt sich durch normales Bruchrechnen, bei dem jeder Produktterm nacheinander durch den Diviser dividiert wird.
Damit entsteht die Übertragungsfunktion G(s) aus der systembeschreibenden Differenzialgleichung in Zeitkonstantendarstellung:
Das PD1-Glied im Zähler der Übertragungsfunktion kompensiert sich mit dem PT1-Glied im Nenner der Übertragungsfunktion zu 1.
Aus der Differenzialgleichung 3. Ordnung entsteht (zufällig oder gewollt) durch Kompensation ein Übertragungssystem 2. Ordnung, das als PT2-Schwingungsglied oder PT2KK-Glied (kk = konjugiert komplex)) bezeichnet wird.Übertragungsfunktion G(s) der systembeschreibenden Differenzialgleichung in Zeitkonstantendarstellung:
Aus der allgemeinen Übertragungsfunktion G(s) des schwingfähigen Verzögerungsgliedes mit konjugiert komplexem Polpaar lassen sich weitere Kennwerte des Systems ermitteln:Wenn das Nennerpolynom der oben genannten Form für die Dämpfung D einen Wert 0<D<1 aufweist, hat es konjugiert komplexe Pole. Diese Form des PT2-Gliedes bezeichnet man als Schwingungsglied. Schwingungsglieder entstehen durch Energieaustausch von zwei speicherfähigen Verzögerungsgliedern 1. Ordnung, wie Feder-Masse-Systeme, LC-Schwingkreis.
Allgemeine Form der Übertragungsfunktion der Schwingungsgleichung in Zeitkonstantendarstellung:Durch Koeffizientenvergleich lassen sich folgende Werte aus der Schwingungsgleichung ermitteln.
Zeitkonstante T:
Dämpfungswert D:
Aus der Polynomdarstellung einer Übertragungsfunktion 2. Ordnung kann nicht erkannt werden, ob es sich um ein schwingfähiges System (Schwingungsglied) oder um ein System mit 2 Verzögerungsgliedern je 1. Ordnung handelt. Ergibt die Nullstellenbestimmung anstelle von konjugiert komplexen Polen zwei reelle Pole, dann lautet die Übertragungsfunktion in Zeitkonstantendarstellung:Beispiel der Übertragungsfunktion in Zeitkonstantendarstellung mit reellen Polen und der Verstärkung K:
Testsignale
[Bearbeiten]Den Testsignalen ist gemeinsam, dass sie zum Zeitpunkt t = 0 beginnen und bei t < 0 eine Amplitude = 0 aufweisen. Es wird das Testsignal im s-Bereich als Eingangsgröße U(s) an einem Übertragungssystem und die Systemantwort als Ausgangsgröße Y(s) in der nachfolgenden Tabelle dargestellt. Zur Unterscheidung der Funktion der Signale werden sie mit den Zeichen δ (Impulsfunktion), Ϭ (Sprungfunktion), a (Rampenfunktion) und (Sinusfunktion) indiziert.
Die Ausgangsgröße y(t) eines linearen dynamischen Systems kann für ein gegebenes Eingangssignal u(t) bestimmt werden, wenn berechnet wird und in Laplace-Transformationstabellen für Y(s) z. B. in Zeitkonstanten-Darstellung die korrespondierende Gleichung der Zeitfunktion ermittelt wird.
Die Laplace-Transformation der Standard-Eingangssignale f(t) wie Impuls-, Sprung-, Rampen- und Sinusfunktionen stellen sich wie folgt dar:
Eingangssignal u(t) Zeitverhalten des Eingangssignals Bildbereich Impulsfunktion δ
(Stoßfunktion, Deltaimpuls)Normierter Impuls = Impulsdauer = Sprungfunktion σ Einheitssprung:
Anstiegsfunktion A
(Rampe)Anstiegsfunktion: Sinusfunktion
Berechnungsbeispiel für ein PT1-Verzögerungsglied mit einem Eingangssignal als Sprungfunktion
[Bearbeiten]
Für die Berechnung des Zeitverhaltens von Übertragungssytemen G(s) mit der Übertragungsfunktion müssen die Eingangssignale (Testsignale) u(t) für den s-Bereich definiert werden.
Gegeben:
- Übertragungsfunktion:
- Eingangssignal als normierte Sprungfunktion 1(t):
Gesucht:
- Suchfunktion im s-Bereich der Laplace-Transformationstabellen:
- Übergangsfunktion (Sprungantwort) im Originalbereich:
- Die Gleichung zur Berechnung des Zeitverhaltens des PT1-Gliedes kann direkt aus den Laplace-Transformationstabellen abgelesen werden. Die Transformationstabellen sind gelegentlich für die Übertragungsfunktionen des s-Bereiches in der Pol-Nullstellen-Darstellung oder in der Zeitkonstanten-Darstellung ausgeführt. Algebraisch sind beide Darstellungsarten identisch. Der Faktor K unterliegt nicht der Transformation und ist deshalb im s-Bereich wie auch im Zeitbereich gültig.
- Mit dem Einsetzen verschiedener Werte für t in die Gleichung ergibt sich ein geschlossener Funktionsverlauf für y(t).
Anmerkung: Bei Übertragungsfunktionen G(s) mit konjugiert komplexen Polen oder Nullstellen können die zugehörigen korrespondierenden Zeitfunktionen sehr aufwendig sein und erfordern für die Lösungen im Zeitbereich gute trigonometrische Kenntnisse. Einfacher bei solchen Systemen ist die numerische Berechnung mit der diskreten Zeit .
→ Siehe das ausführliche Hauptkapitel "Einführung in die Systemtheorie/ Übertragungsfunktion".
Einführung Frequenzgang
[Bearbeiten]Der Frequenzgang ist ein Spezialfall der Übertragungsfunktion. Er beschreibt das Ausgangs- Eingangs- Signalverhalten eines Übertragungssystems für ausschließlich periodische sinusförmige Eingangssignale. Setzt man für die komplexe Variable den Realteil zu Null, so geht die komplexe Übertragungsfunktion G(s) in den komplexen Frequenzgang
über, der physikalisch interpretiert und gemessen werden kann.
Beide mathematischen Begriffe der Übertragungsfunktion und des Frequenzgangs unterscheiden sich nur durch die Entstehungsweise. Sie können je nach Aufgabenstellung als Übertragungsfunktion im s-Bereich oder als Frequenzgang mit geschrieben werden.
Die bekanntesten Anwendungen des Frequenzgangs eines dynamischen Systems sind die grafischen Stabilitätsanalysen mittels des Bode-Diagramms und der Ortskurve des Frequenzgangs der vom amerikanischen Physiker Harry Nyquist entwickelten Stabilitätskriterien. Diese Verfahren dienen heute mehr dem Verständnis von Teilgebieten der Systemtheorie, sind aber keine Alternativen zur numerischen Berechnung eines Regelkreises, bei dem tabellarisch das innere Teil-Systemverhalten für jede Berechnungsfolge y(k•Δt) dargestellt und grafisch der zeitliche Signalverlauf verschiedener Ausgangsgrößen für eine beliebige Eingangsgröße gezeigt wird.
Ein wichtiges Anwendungsgebiet bei der experimentelle Systemidentifikation ist das Bode-Diagramm, in dem für ein unbekanntes dynamisches System durch eine frequenzvariable Einspeisung der Frequenzgang messtechnisch aufgenommen wird. Durch Bestimmung der Asymptoten an den Eckfrequenzen im Bode-Diagramm kann die Übertragungsfunktion G(s) des Systems ermittelt werden.
Einführung "Zeitdiskrete Systemmodelle"
[Bearbeiten]Relativ einfache Übertragungssystem-Strukturen mit nichtlinearen Elementen, Begrenzungseffekten und Totzeitsystemen sind durch konventionelle Rechenmethoden im kontinuierlichen Zeitbereich nicht mehr geschlossen lösbar. Abhilfe bietet die numerische Berechnung im diskreten Zeitbereich Δt. Derartige Modellberechnungen insbesondere bei Systemen höherer Ordnung, linear oder nichtlinear, ohne und mit Anfangswerten sind besonders anschaulich verständlich, weil sie das Zeitverhalten einer Kette von Einzelsystemen für einen kleinen Zeitschritt tabellarisch beschreiben, so wie sich das Übertragungssystem auch in der Realität als Kette von Einzelsystemen darstellt.
Für die Berechnung des Eingangs-Ausgangsverhaltens von Übertragungssystemen oder der Simulation von Regelkreisen bieten sich käufliche Rechenprogramme an. Mit den bekannten Programmen wie MATLAB und Simulink stehen umfangreiche Befehlssätze für die theoretische Modellierung von dynamischen Systemen und vielen speziellen regelungstechnischen Befehlen zur Verfügung.
Alternativ können mit selbst erstellten beliebigen Rechenprogrammen für Differenzengleichungen mit der diskreten Zeit Δt (auch Abtastzeit TA) in Verbindung mit logischen Operationen sehr effizient lineare und nichtlineare System-Simulationen durchgeführt werden.
Nichtlineare Übertragungssysteme sind häufig Unikate. In Kombination mit linearen dynamischen Systemen können sie meist als zeitunabhängiges Übertragungssystem vom zeitabhängigen Übertragungssystem abgetrennt und mit logischen Befehlen wie WENN-DANN-Sonst-Anweisungen oder mit Tabellenanweisungen beschrieben werden.
Systembeschreibungen: Differenzialgleichungen, Übertragungsfunktionen und Differenzengleichungen
[Bearbeiten]Die mathematischen Beschreibungen linearer dynamischer Systeme mit Differenzialgleichungen, Übertragungsfunktionen und Differenzengleichungen sind untereinander austauschbar, wenn sie nur je ein totzeitfreies lineares dynamisches System mit konstanten Koeffizienten im Zeitbereich, im komplexen Frequenzbereich und numerisch im zeitdiskreten Bereich beschreiben sollen. Jede mathematische Form der Beschreibungen kann in die jeweils andere Form der partikulären Lösung der DGL, der Übertragungsfunktion (Lösung ist immer partikulär) und der numerisch lösbaren Differenzengleichung übertragen werden.
Die Lösungswege der mathematischen Gleichungen für den Verlauf des Ausgangssignals bei einem gegebenen Eingangssignal sind wie folgt höchst unterschiedlich und von unterschiedlichen Schwierigkeitsgraden:
Systembeschreibung Mathematische Lösung im Zeitbereich Kommentar Differenzialgleichung 1. Gesamtlösung = Homogene Lösung + Partikuläre Lösung
2. Homogene Lösung:
3. Partikuläre Lösung für der DGL über das Faltungsintegral.1. Homogene Lösung bezieht sich nur auf Anfangswerte,
partikuläre Lösung nur auf Eingangssignale.
2. Umständliche Berechnung der Integrationskonstanten C.
3. Partik. Lösung mit Faltungsintegral > 2. Ordnung sehr schwierig.Übertragungsfunktion Mit Hilfe der inversen Laplace-Transformationstabellen
oder der Anwendung der Partialbruchzerlegung.* Kann aufwendige trigonometrische Berechnung bei Schwingungsgliedern bedeuten.
* Die Partialbruchzerlegung erfordert Spezialkenntnisse und Übung .Differenzengleichung Die numerische Berechnung erfolgt schrittweise im Abstand der diskreten Zeit Δt.
Die Gleichung wird mit Berechnungsfolgen wiederholt berechnet.
Jede Ausgangsgröße wird zur nächsten Berechnungsfolge zur Eingangsgröße .* Relativ einfach, insbesondere auch bei Systemen höherer Ordnung.
* Das Gleichungssystem kann leicht erweitert werden für
nichtlineare Funktionen und Totzeitsysteme.
* Ergebnis: Tabellarische Darstellung aller Berechnungsfolgen.
* Berechnung von Anfangswerten über die Regelungsnormalform.
Lineare Übertragungsglieder werden gerne bevorzugt als Übertragungsfunktionen G(s) möglichst in Zeitkonstantendarstellung benannt, weil sie als mathematisches Modell sehr einfach und übersichtlich dargestellt werden können, obwohl sie sich nicht auf den Zeitbereich sondern auf den komplexen Frequenzbereich beziehen.
Die Übertragungsfunktion G(s) entsteht durch die Laplace-Transformation von gewöhnlichen systembeschreibenden Differenzialgleichungen. Durch die Zerlegung der Polynome der Übertragungsfunktion im Zähler und Nenner als Linearfaktoren lässt sich nachweisen, dass lineare Übertragungssysteme nur 3 Formen von Linearfaktoren und deren Vielfache je im Zähler und Nenner der Polynomgleichung enthalten.
Für das einfachste Verfahren der der numerischen Berechnung - das "Euler-Streckenzugverfahren" - werden nur zwei Formen von Differenzengleichungen 1. Grades - Linearfaktor mit und ohne Absolutglied - je im Zähler oder Nenner der Übertragungsfunktion benötigt. Für diese 4 Formen der Übertragungsfunktionen in Zeitkonstantendarstellung, die den Differenzialgleichungen 1. Ordnung entsprechen, können zeitdiskrete Differenzengleichungen erstellt werden. Alle linearen Systeme G(s) beliebiger Ordnung - auch solche mit konjugiert komplexen Polen und Nullstellen (Beispiel Schwingungsglieder) - können mit diesen vier Arten von Differenzengleichungen berechnet werden.
Ein technisches lineares dynamisches System ohne Totzeit kann durch Teilsysteme (Linearfaktoren 1. Ordnung) vollständig beschrieben werden. Die Teilsysteme können beliebig multiplikativ, additiv oder zurückgekoppelt vermascht sein.
Tabelle der regulären (phasenminimalen) Übertragungsfunktionen 1. Ordnung in Zeitkonstanten-Darstellung :
| Übertragungsfunktion G(s) |
|||||
|---|---|---|---|---|---|
| Übergangsfunktion y(t) (Sprungantwort) |
 |
 |
 |
 |

|
| Benennung | P-Glied | I-Glied | D-Glied | PD1-Glied | PT1-Glied |
Anmerkung: Bei Linearfaktoren ohne Absolutglied wie das D-Glied und das I-Glied entsprechen die Zeitkonstanten T und 1/T dem Proportionalitätsfaktoren K.
Für jedes dieser genannten zeitabhängigen Teilsysteme kann eine Differenzengleichung erstellt werden.
Verfahren der numerischen Berechnung mit Differenzengleichungen
[Bearbeiten]Viele technische Übertragungssysteme bzw. Modelle der Übertragungssysteme verarbeiten kontinuierliche Eingangssignale und liefern auch kontinuierliche Ausgangssignale, dennoch können diese Übertragungssysteme aus linearen und nichtlinearen Teilsystemen bestehen.
Zeitdiskrete lineare dynamische Systeme sind dadurch gekennzeichnet, dass die inneren Systemzustände nur zu einzelnen Zeitpunkten definiert sind und an den Ein- und Ausgängen zeitdiskrete Signale auftreten. Sie spielen im Rahmen der Informationstechnik und digitalen Signalverarbeitung eine bedeutende Rolle und werden in Form von Berechnungsfolgen beschrieben.
Berechnungsfolgen mit der Folge berechnen eine Gleichung mit der Ausgangsgröße aus einem alten Zustand zu einem neuen Zustand der Ausgangsgröße mit dem zeitlichen Abstand der diskreten Zeit .
Für jedes Teilsystem ist die Ausgangsgröße die Eingangsgröße des nachfolgenden Systems. Parallelgeschaltete Systeme werden hintereinander berechnet, haben aber das gleiche Eingangssignal, deren Ausgangssignale werden addiert.
Diese Art der schrittweisen Berechnung eines Systems mit der Annäherung an die analytische Funktion des Systems wird als rekursiv (lat.: recurrere: zurücklaufen) bezeichnet. Die Genauigkeit der Annäherung an die analytische Funktion steigt mit dem Verhältnis des Quotienten der dominanten Systemzeitkonstante zur diskretisierten Zeit Δt.
Die den Übertragungsfunktionen G(s) zugehörigen Differenzengleichungen berechnen die Systemausgangsgröße im Zeitbereich für definierte Zeitintervalle für eine gegebene Eingangsgröße . Als vereinfachte Schreibweisen für zeitdiskrete Signale gelten die Indizierungen für die aktuelle Größe und für eine zurückliegenden Folge .
Genauigkeit der numerischen Berechnung und numerische Stabilität:
- Numerische Stabilität
- Zur Vermeidung der numerischen Instabilität kann die Verstärkung nicht unbegrenzt hoch gewählt werden, wenn es auch theoretisch bei stetig wirkenden Regelkreisen bis zu zwei Verzögerungsgliedern möglich wäre.
- Bedingung: Bei sehr großer Kreisverstärkung K einer Regelkreisnachbildung muss kleiner als sein.
- ist das Produkt aller Einzelverstärkungen, ist die dominante Systemzeitkonstante.
- Genauigkeit der numerischen Simulation
- Die Genauigkeit steigt mit kleiner werdendem Zeitintervall gegenüber der dominanten Systemzeitkonstante . Der Approximationsfehler im Vergleich zur analytische Funktion beträgt .
- Das Zeitintervall muss kleiner als die kleinste zu berechnende Systemzeitkonstante betragen. Anderenfalls treten zusätzliche Fehler auf.
Andere Methoden der numerischen Berechnung bedienen sich zur besseren Approximation z. B. an Stelle des Rechteck-Verfahrens (Explizites Eulerverfahren) des Trapezflächenverfahrens (Heun-Verfahren), des Mehrschrittverfahrens (Runge-Kutta-Verfahren) und anderer Verfahren.
Grund der aufwendigeren Approximationsverfahren ist die erzielbare höhere Genauigkeit und damit Reduzierung der Rekursionsfolgen, was bei langsamen Rechnern bei Echtzeitberechnungen erforderlich sein kann.
Schreibweise der Differenzengleichungen
[Bearbeiten]Differenzengleichungen entstehen durch lineare gewöhnliche Differenzialgleichungen, deren Differentialquotienten durch Differenzenquotienten ersetzt werden.
Bei der Anwendung zur Lösung einer Differenzialgleichung über die Übertragungsfunktion mit Hilfe der inversen Laplace-Transformation wird die analytische Lösung im Zeitbereich über den Suchbegriff in der Laplace-Transformationstabelle in Operatorenschreibweise gefunden.
Allgemein gilt für die inverse Transformation vom s-Bereich in den Zeitbereich der Suchbegriff:
Die numerische Berechnung einer Differenzengleichung eines Teilsystems (Linearfaktor) bedeutet eine Annäherung an die analytische Funktion des Systems und wird stets in Operatorenschreibweise dargestellt. Sie wird anders als im Umgang mit der Übertragungsfunktion schrittweise mit der Berechnungsfolge k immer neu berechnet, wobei die Ausgangsgröße des Teilsystems im nächsten Zeitzyklus die Eingangsgröße des gleichen Teilsystems ist. Die Differenzengleichungen als Beschreibung der Teilsysteme können nach einem Signalflussplan beliebig vermascht werden, die Struktur der Differenzengleichung für ein Teilsystem darf nicht verändert werden.
Beispiel einer Differenzengleichung eines Integrationsgliedes (I-Glied):
Der Integrationsalgorithmus lautet:
Differenzengleichung der Integration (I-Glied):
Beispiel der Entstehungsweise einer Differenzengleichung eines Verzögerungsgliedes (PT1-Glied)
[Bearbeiten]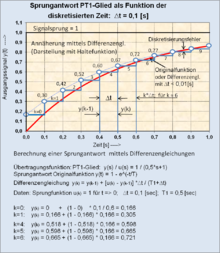
- Übertragungsfunktion des PT1-Gliedes
- Zugehörige Differenzialgleichung
Der Differenzialquotient der Differenzialgleichung wird durch den Differenzenquotient ersetzt mit folgendem Ansatz:
Diese Gleichung wird nach y(k) aufgelöst. Die Differenzengleichung des PT1-Gliedes lautet:
Differenzengleichung des PT1-Gliedes in vereinfachter Schreibweise mit identischer mathematischer Funktion:
Die tabellarische Form der numerischen Lösung erlaubt auch die Berechnung nichtlinearer statischer Systeme, indem die nichtlineare Beziehung als Wertetabelle der Tabellenspalte der Folge k zugeordnet wird. Ebenso ist die Berechnung der Totzeit eines Systems durch Verschiebung der Zeilen mit geeigneten Programmbefehlen möglich.
→ Siehe das ausführliche Kapitel "Einführung in die Systemtheorie/ Numerische Berechnung dynamischer Systeme".
Digitale Systemberechnung online
[Bearbeiten]Offline-Berechnungen sind beispielsweise Simulationen eines Modells eines dynamischen Systems, bei dem in Abhängigkeit eines Eingangssignals das Ausgangsverhalten des Systems bei verschiedenen Parametern untersucht wird. Das Zeitverhalten des Rechners - die Rechenzeit - hat dabei keinen Einfluss auf das Rechenergebnis.
In technischen Prozessen, in denen ein Signal nicht kontinuierlich sondern zeitdiskret ist, bezeichnet man als Abtastung eines Zahlenwertes mit dem Zeittakt TA. Derartige Systeme lassen sich nicht mit kontinuierlichen mathematischen Methoden wie die Differenzialgleichung im Zeitbereich oder mit der Übertragungsfunktion im komplexen Frequenzbereich beschreiben.
Anstelle von kontinuierlichen Signalen treten die mathematischen Methoden der zeitdiskreten Signale. Die Verfahren der Behandlung kontinuierlicher Signale ändern sich zu Verfahren der zeitdiskreten Behandlung wie folgt:
- Kontinuierliches Signal → abgetastetes Signal
- Differenzialgleichung → Differenzengleichung
- Laplace-Transformation → Z-Transformation
- Übertragungsfunktion G(s) → Z-Übertragungsfunktion G(z)
Wird ein Digitalrechner für die Steuerung eines realen stetigen Prozesses in einem Eingrößensystem eingesetzt, so werden 2 Schnittstellen benötigt. Das stetige Eingangssignal erfordert einen Analog-Digitalwandler (AD-Wandler), das digitale Ausgangssignal des Digitalrechners entweder eine Digitalanzeige oder ein Digital-Analogwandler (DA-Wandler). Mit einem Zeittakt werden Rechner und Schnittstellen synchronisiert. Der Digitalrechner simuliert mit Hilfe von Differenzengleichungen das dynamische System.
Bei Echtzeitberechnungen, beispielsweise mit einem programmierbaren digitalen Regler, der auf eine Hardware-Regelstrecke wirkt, wird die Diskretisierungszeit ∆t durch die "Abtastzeit" TA ersetzt, mit der das meist analoge Ausgangssignal der Regelstrecke über Analog-Digitalwandler erfasst wird. Der Abtastung des Ausgangssignals ist üblicherweise ein Halteglied (Sample-and-Hold-Schaltung) nachgeschaltet, so dass ein gestufter Verlauf des Ausgangssignals entsteht. Hat das Halteglied kein Zeitverhalten, wird es als Halteglied 0. Ordnung bezeichnet.
Bei schnellen Übertragungssystemen wie Regelstrecken spielen die Systemgeschwindigkeiten des Rechners, der A/D-Wandler, die Sample-and-Hold-Schaltung, wie auch die verwendeten Differenzengleichungen beziehungsweise deren Approximations-Algorithmen eine große Rolle.
Für die Durchführung der zeitdiskreten Rechenvorgänge am Digitalrechner wird eine spezielle Form der Laplace-Transformation, die Z-Transformation verwendet.
Kurzbeschreibung Zustandsraumdarstellung
[Bearbeiten]
Die Zustandsgrößen eines linearen dynamischen Systems beschreiben den inneren Bewegungsablauf des Systems.
Die Zustandsraumdarstellung bezieht sich auf ein Zustandsraummodell, welches meist ein Schema der Regelungsnormalform oder der Beobachtungsnormalform beschreibt. Es symbolisiert die überführte Differenzialgleichung n-ter Ordnung in n-gekoppelte Zustands-Differentialgleichungen erster Ordnung. Dabei werden sämtliche Beziehungen der Zustandsgrößen, der Eingangsgrößen und Ausgangsgrößen in Form von Matrizen und Vektoren dargestellt. Das Zustandsraummodell wird vereinfacht durch die zwei Zustandsgleichungen – der Zustandsdifferenzialgleichung und der Ausgangsgleichung – beschrieben.
Das Zustandsraummodell kann für nicht sprungfähige Systeme direkt aus den Koeffizienten der systembeschreibenden Differenzialgleichung oder der zugehörigen Übertragungsfunktion erstellt werden. Es gilt als ingenieurtechnisch geeignete Methode der Analyse und Synthese dynamischer Systeme im Zeitbereich und ist besonders effizient bei der regelungstechnischen Behandlung von Mehrgrößensystemen, nichtlinearen und zeitvariablen Übertragungssystemen.
Die Zustandsvariablen beschreiben physikalisch den Energiegehalt der in einem technischen dynamischen System enthaltenen Speicherelemente. Sie bedeuten z. B. Spannung an einem Kondensator, Strom in einer Induktivität, bei einem Feder-Massesystem die potentiellen und kinetischen Energieanteile. Die Anzahl der Zustandsvariablen des Zustandsvektors ist die Dimension des Zustandsraumes. Im Zustandsvektor zum beliebigen Zeitpunkt t(0) sind alle Informationen des dynamischen Übertragungssystems enthalten.
Wesentliche Begriffe zum Verständnis der Beschreibung eines Übertragungssystems im Zustandsraum sind das Zustandsraummodell und die angewandte Normalform, nach der die Zustandsgleichungen und zugehörigen Matrizen / Vektoren ausgelegt sind.
Bei den Zustandsbeschreibungen mit Normalformen nehmen die Zustandsgleichungen besonders einfache und zweckmäßige Formen für bestimmte Berechnungen an. Für die Normalformen wird von der Systembeschreibung des linearen Übertragungssystems durch die Differenzialgleichung oder zugehörige Übertragungsfunktion ausgegangen.

Die bekannteste Normalform ist die Regelungsnormalform, welche grafisch die Lösung einer Differenzialgleichung beschreibt.
Die Signalstruktur der Regelungsnormalform stellt sich als ein stetiges zeitkontinuierliches System dar, dass mit der Eingangsgröße u(t) die Lösung der Differentialgleichung y(t) wiedergibt und gleichzeitig die Zustandsvariablen zeigt.
Das Blockschaltbild der Regelungsnormalform zeigt die Umsetzung und Lösung der Differenzialgleichung in die physikalischen analogen Signalflüsse der Zustandsgrößen einschließlich der Ausgangsgröße bei gegebener Eingangsgröße. Man kann sie als eine Weiterentwicklung der in der Analogrechentechnik bekannten Verfahren zur Lösung einer Differentialgleichung n-ter Ordnung mit n Integratoren betrachten. Die Signalflüsse können bei Kenntnis der Koeffizienten der Zustandsvariablen direkt mittels numerischer Berechnung für beliebige Eingangssignale ermittelt und grafisch dargestellt werden.
Enthält die systembeschreibende Differenzialgleichung keine Differentiale der Eingangsgröße, bzw. die zugehörige Übertragungsfunktion hat nur Pole aber keine Nullstellen, so werden die Koeffizienten der Regelungsnormalform laut dargestelltem Blockschaltbild b1 und b2 zu Null.
Die Regelungsnormalform muss nicht zwingend in die Form von Matrizen und Vektoren dargestellt werden.
Zustandsdifferenzialgleichung und Ausgangsgleichung
[Bearbeiten]Das Zustandsraummodell wird anhand der dargestellten Signalflüsse durch 2 Gleichungen beschrieben, die Zustandsdifferenzialgleichung und die Ausgangsgleichung (auch Ausgabegleichung).
Die Zustandsdifferenzialgleichung ist eine Vektordifferenzialgleichung 1. Ordnung, die die Systemdynamik beschreibt. Sie gibt an, wie das Eingangssignal u(t) die einzelnen Speicher beeinflusst und wie diese Speicher miteinander verkoppelt sind.
Die algebraische Ausgangsgleichung beschreibt, wie das Ausgangssignal y(t) mit den Systemzuständen verbunden ist.
- Gleichungen des Zustandsraummodells:
Gleichung Bei Eingrößensystemen Bei Mehrgrößensystemen Zustandsdifferenzialgleichung
(auch Zustandsgleichung)Ausgangsgleichung
d = 0 für n > m
= 0 für n > m
Zustandsregelung
[Bearbeiten]
Ein Übertragungssystem in der Regelungsnormalform mit ihren Zustandsvariablen kann als Regelstrecke in einen Regelkreis eingebunden werden.
Durch die Zustandsrückführung kann keine stationäre Genauigkeit der Regelgröße zum Sollwert erreicht werden. Deshalb wird mit einem Vorfilter die Anpassung der Führungsgröße an die stationäre Ausgangsgröße hergestellt.
Für anspruchsvolle Regelaufgaben mit Systemen im Zustandsraum kann die Einführung eines überlagerten Regelkreises für den Zustandsregelkreis mit einer Ausgangsrückführung erforderlich sein. Damit sind sämtliche stationären Probleme für die Übereinstimmung der Führungsgröße mit der Regelgröße und konstante Störanteile ausgeschaltet. Das Vorfilter entfällt.
Die Zustandsregelung mit der Rückführung der Zustandsvariablen ist vergleichbar mit einer Kaskadenregelung.
Die Kaskadenregelung besteht aus hierarchisch hintereinander geschachtelten Folgeregelkreisen, die innerhalb eines überlagerten Regelkreises liegen. Diese effiziente Reglerstruktur der Kaskadenregelung ist möglich, wenn einzelne Signalgrößen von Teilsystemen einer Regelstrecke messbar sind. Diese Teilsysteme mit Verzögerungen niedriger Ordnung sind einfacher und schneller regelbar. Die Ausgangsrückführungen der Teilregelkreise entsprechen angenähert den Zustandsvariablen.
Kaskadenregler sind Hilfsgrößen-Regler innerhalb einer Folgekette. Sie erfüllen wie die Zustandsregler eine bessere Dynamik der Regelgröße und tragen zur Verbesserung des Störverhaltens bei.
→ Siehe den ausführlichen Wikipedia-Artikel Zustandsraumdarstellung
Einführung "Eingrößen- und Mehrgrößensysteme"
[Bearbeiten]
Es kann ein Signal oder es können mehrere Eingangssignale auf das System einwirken. Das System antwortet mit einem oder mit mehreren Ausgangssignalen. Diese mit einem Eingangs- und Ausgangssignal behafteten Systeme werden als Klasse der Eingrößensysteme, die mit mehreren Eingangs- und Ausgangssignalen werden als Mehrgrößensysteme bezeichnet.
Bei vielen technischen Prozessen müssen mehrere physikalische Größen gleichzeitig geregelt werden, wobei diese Größen voneinander abhängig sind. Bei Änderung einer Eingangsgröße (Stellgröße u(t)) wird zusätzlich eine andere Ausgangsgröße (Regelgröße y(t)) oder auch alle anderen Ausgangsgrößen beeinflusst.
Bei Mehrgrößen-Regelstrecken sind die Eingangsgrößen und Ausgangsgrößen untereinander verkoppelt. Im Regelkreis sind die r Eingangsgrößen der Regelstrecke U1(s) bis Ur(s) die Stellgrößen des Systems, die entsprechend dem Kopplungsgrad mehr oder weniger auf die verschiedene Anzahl m der Regelgrößen Y1(s) bis Ym(s) einwirken können.
Beispiele von einfachen Mehrgrößensystemen:
- Bei der Dampferzeugung sind Druck und Temperatur gekoppelt,
- Bei Klimaanlagen sind Temperatur und Luftfeuchtigkeit gekoppelt.
Für den einfachen Fall der Verkopplung einer Regelstrecke mit 2 Eingängen und 2 Ausgängen treten die häufigsten symmetrischen Verkopplungsarten in P- und V-Kanonische Form|kanonischer Struktur auf. Bei der P-kanonischen Struktur wirkt ein Eingang der Strecke über ein Koppelelement auf den nicht zugehörigen Ausgang der Strecke. Bei der V-kanonischen Struktur wirkt ein Ausgang der Strecke über ein Koppelelement auf den nicht zugehörigen Eingang der Strecke.
Je nach Art der gekoppelten Regelstrecken können für den Reglerentwurf 3 Konzepte gewählt werden:
- Dezentrale Regelung
- Jedem Stell- und Regelgrößenpaar wird ein eigener Regler zugeordnet. Die auf diesen Regelkreis durch die Kopplung einwirkenden Störungen werden durch den Regler kompensiert. Dieses Verfahren ist bei schwacher Kopplung oder bei langsamen Koppelsystemen gegenüber der Hauptregelstrecke akzeptabel.
- Regelung mit Entkopplung
- Jedem Stell- und Regelgrößenpaar wird ein Hauptregler und für die Kopplungen zwischen den Stell- und Regelgrößen je ein Entkopplungsregler zugeordnet. Es ist Aufgabe der Entkopplungsregler, den Einfluss der anderen Stellgrößen auf die jeweilige Regelgröße zu eliminieren oder zumindest zu reduzieren.
- Echte Mehrgrößenregelung
- Der Mehrgrößenregler hat so viele Eingänge wie Regelgrößen und so viele Ausgänge wie Stellgrößen. Die Kopplungen zwischen den Komponenten werden in einem einheitlichen Reglerkonzept berücksichtigt. Der Entwurf der Mehrgrößenregler erfolgt über die Matrizen- Vektorrechnung.
→ Siehe Wikipedia-Artikel Regler: Abschnitt Regler für Mehrgrößensysteme
→ Siehe Wikipedia-Artikel Regelstrecke: Abschnitt Mehrgrößensysteme
Quellen
[Bearbeiten]
Beschreibung linearer Prozesse im Zeitbereich
[Bearbeiten]Beschreibung linearer und nichtlinearer Prozesse im Zeitbereich
[Bearbeiten]- Normung der Signalbezeichnungen
Die bis zum Jahr 2009 gültige Norm DIN 19226 Leittechnik; Regelungstechnik und Steuerungstechnik wurde zurückgezogen und durch DIN IEC 60050-351 ersetzt.
Das deutsche Institut für Normung hat in der DIN EN 60027-6 sämtliche Begriffe und Formelzeichen für die Signale in Regelkreisen festgelegt.

Diese Normen wurden in der deutschen Fachliteratur der Regelungstechnik kaum verwendet. Es darf vermutet werden, dass der Einfluss durch das aus den USA stammende mathematische Verfahren der „Zustandsraumdarstellung“ von dynamischen Systemen den Zwang zu einer gemischten Vereinheitlichung von Signalbezeichnungen mit der Regelungstechnik geführt hat.
Zunehmend wird für die Eingangs- Ausgangsbezeichnung eines Systems anstelle von X und Y oder „Xe“ für das Eingangssignal und „Xa“ für das Ausgangssignal in der Fachliteratur der modernen Systemtheorie als Eingangsgröße „U“ und als Ausgangsgröße „Y“ verwendet.
Für die Systemtheorie werden nachfolgend, wie auch in der Regelungstechnik, die Signalgrößen des dargestellten Blockschaltbildes verwendet:
Systembeschreibung
[Bearbeiten]Die nachfolgenden Systembeschreibungen setzen die Kenntnisse der mathematischen Werkzeuge wie Differenzialgleichung, Laplace-Transformation und Übertragungsfunktion voraus. Diese Kenntnisse werden erst in späteren Kapiteln dargestellt. Gewöhnliche systembeschreibende Differenzialgleichungen können jederzeit in die anschaulicheren Übertragungsfunktionen und wieder zurück gewandelt werden. Übertragungsfunktionen behandeln keine Anfangswerte der physikalischen Systemspeicher.
Ein reales dynamisches System kann durch das Aufstellen von Differenzialgleichungen modelliert werden. Dazu werden für die Energie-/Materie-Speicher zunächst Bilanzgleichungen benötigt.
Für jeden konzentrierten Speicher entsteht eine Differenzialgleichung erster Ordnung mit der Ableitung der Ausgangsgröße y(t). Das Verhalten eines linearen Systems wird vollständig durch die Lösung der Differenzialgleichung wiedergegeben.
- Beispiele für Differenzialgleichungen erster Ordnung
Die Lösung einer linearen, inhomogenen Differenzialgleichung mit konstanten Koeffizienten setzt sich immer aus den Anteilen der homogenen und der partikulären Lösung zusammen.
- Die homogene Lösung bezieht sich auf die Anfangswerte der Systemspeicher. Die Eingangsgröße der Differenzialgleichung ist dabei zu Null gesetzt. Sind die Anfangswerte Null, ist auch die Lösung der Differenzialgleichung die Ausgangsgröße yH(t) = 0.
- Die partikuläre Lösung yP(t) bezieht sich auf eine von Null verschiedene Eingangsgröße u(t) bei denen die Systemspeicher den Wert Null haben. Diese Lösung des Eingangs- Ausgangsverhaltens eines Systems interessiert in den meisten Anwendungsfällen.
- Durch die Laplace-Transformation der systembeschreibenden Differenzialgleichung linearer Übertragungssysteme werden Systeme bei verschwindenden Anfangsbedingungen vom Zeitbereich in den sogenannten Bildbereich (s-Bereich) mit der komplexen Frequenz s übertragen.
- Das Produkt der Übertragungsfunktion mit dem Laplace-transformierten Eingangssignal U(s) ergibt das Ausgangssignal Y(s) des Systems. Mit der inversen Laplace-Transformation entsteht die gesuchte Lösung der Ausgangsgröße y(t) eines Übertragungssystems als Funktion der Eingangsgröße u(t) im Zeitbereich. Sie entspricht der partikulären Lösung der dem System zugehörigen Differenzialgleichung. Die partikuläre Lösung einer Differenzialgleichung über den Umweg der Laplace-Transformation ist einfacher als die direkte Lösung mit dem Faltungsintegral.
- Signale und Übertragungsfunktionen im s-Bereich können entsprechend ihrer Systemstruktur (Reihenschaltung, Parallelschaltung, Rückkopplungsschaltung) beliebig algebraisch behandelt werden.
- Durch die Analyse der Pole und Nullstellen der Übertragungsfunktion ergeben sich wichtige Aussagen über das Systemverhalten wie Eigendynamik, Stabilität und Zeitverhalten.
Testsignale
[Bearbeiten]
Den nichtperiodischen (deterministischen) Testsignalen kommt in der Regelungstechnik eine zentrale Bedeutung zu. Mit ihrer Hilfe ist es möglich, ein Übertragungssystem zu testen, auf Stabilität zu prüfen oder Eigenschaften des Systems durch Ermittlung der Kennwerte zu analysieren.
Den Testsignalen ist gemeinsam, dass sie zum Zeitpunkt t = 0 beginnen und bei t < 0 eine Amplitude = 0 aufweisen. Es wird das Testsignal als Eingangsgröße u(t) an einem Übertragungssystem angelegt und die Systemantwort als Ausgangsgröße y(t) aufgezeichnet und analysiert. Anhand der Kenndaten können mathematische Modelle geschaffen werden. Die häufig verwendete Darstellungsform eines Modells ist die Übertragungsfunktion im s-Bereich mit der komplexen Frequenz s.
Zur Unterscheidung der Funktion der Testsignale werden sie mit den Zeichen δ (Impuls), Ϭ (Sprung), a (Anstieg) und s (Sinus) indiziert.
Der theoretische Deltaimpuls (δ-Impuls, Dirac-Impuls) für t = 0 mit unendlich großer Amplitude ist technisch nicht realisierbar. An seiner Stelle wird ein Rechteckimpuls mit der Impulsfläche
1 = Amplitude · Zeit definiert. In der Praxis genügt ein Wert für die Impulsbreite von Δt = 1 % bis 10 % der dominanten Zeitkonstante des zu prüfenden Übertragungssystems.
Die Differentiation der Sprungfunktion entspricht der Impulsfunktion. Die Integration einer Sprungfunktion entspricht der Anstiegsfunktion. Die Differentiation der Sprungantwort eines linearen Übertragungssystems entspricht der Impulsantwort.

Die Sinusfunktion gehört zur Gruppe der periodischen Signale. Die frequenz-variable Einspeisung eines linearen Übertragungssystems erlaubt die Aufnahme des Amplituden- und Phasengangs des Systems. Mit Hilfe des Bode-Diagramms kann die Übertragungsfunktion des Systems bestimmt werden.
| Begriff Testsignal Xe(t) |
Zeitverhalten des Testsignals | Bildbereich | Systemantwort Xa(t) |
|---|---|---|---|
| Impulsfunktion δ oder Stoßfunktion, Deltaimpuls |
Normierter Impuls = Impulsbreite = Hauptanwendung: Erkennung des Systems, der Ordnung und der Stabilität |
Impulsantwort oder Gewichtsfunktion | |
| Sprungfunktion σ |
Einheitssprung: Hauptanwendung: Erkennung des Systems |
|
Sprungantwort oder Übergangsfunktion |
| Anstiegsfunktion oder Rampe |
Anstiegsfunktion: Gradient: Hauptanwendung: Bestimmung der Nachlaufeigenschaften |
Anstiegsantwort oder Rampenantwort | |
| Sinusfunktion s |
Hauptanwendung: Aufnahme des Amplituden- und Phasengang eines Systems |
|
Frequenzgang |
Linearitätseigenschaften
[Bearbeiten]
Die Linearität eines dynamischen Systems bedeutet, dass die systembeschreibende Differenzialgleichung linear ist. Eine lineare Differenzialgleichung enthält die gesuchte Funktion und deren Ableitungen nur in der ersten Potenz. Es dürfen keine Produkte der gesuchten Funktion und ihrer Ableitungen auftreten. Das heißt, die Koeffizienten müssen konstant sein.
Die symbolische Operatorenschreibweise lautet für ein lineares dynamisches System F mit dem Eingangssignal u(t) und Ausgangssignal y(t):
Der lineare Operator F ist die Operation, für die sich aus dem gegebenen Eingangssignal u(t) das Verhalten des Ausgangssignals y(t) ergibt.
Die Linearität eines Übertragungssystems bedeutet für alle Systembeschreibungen:
- Lineare Kennlinien,
- Lineare Gleichungen,
- Lineare Differenzialgleichungen.
- Lineares statisches System
Ein statisches System F mit dem Eingangssignal u und dem Ausgangssignal y hat einen linearen Zusammenhang mit y = F(u) wenn folgende Beziehung gilt:
- Superpositionsprinzip:
- Verstärkungsprinzip
- Lineares dynamisches System

Ein dynamisches System verhält sich linear, wenn die Wirkungen zweier linear überlagerter Eingangssignale sich am Ausgang des Systems in gleicher Weise linear überlagern.
Wird für ein Eingangssignal
die dargestellte Signalkombination gesetzt, so fordert das Superpositionsprinzip, dass die Ausgangsgröße des linearen Systems sich wie folgt darstellen lässt:
- Superpositionsprinzip
- Verstärkungsprinzip
Hierbei sind u1(t) und u2(t) beliebige Eingangssignale und K eine beliebige Konstante.
Nichtlineares Übertragungssystem
[Bearbeiten]Die lineare Systemeigenschaft ist häufig nicht gegeben, da viele zusammenwirkende Systeme z. B. in der Regelungstechnik bei Ventil-Kennlinien, Stellgrößenbegrenzungen oder Schaltvorgängen keine Linearität aufweisen.
Ein nichtlineares System kann entweder in Form nichtlinearer statischer Kennlinien oder in Form nichtlinearer Operationen wie Multiplikation oder Division von Variablen in algebraischen Gleichungen und Differentialgleichungen auftreten.
Ein nichtlineares dynamisches System 2. Ordnung entsteht beispielsweise durch ein Feder-Masse-Dämpfer-System, wenn das Federsystem oder der Dämpfer ein nichtlineares Verhalten hat. Anhand der Vielzahl der Formen nichtlinearer Systeme ist es schwierig, diese in bestimmte Klassen einzuordnen. Nichtlineare Systeme kann man als einzigartig einstufen.
Folgende Beziehungen ergeben sich bei nichtlinearen Systemen:
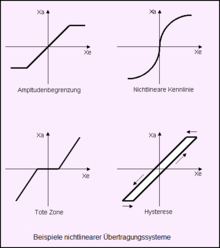
- Wird ein nichtlineares Übertragungssystem in einem festen Arbeitspunkt betrieben, dann kann das nichtlineare Verhalten des Systems durch ein lineares Modell für die nähere Umgebung des Arbeitspunktes ersetzt werden.
- Jeder nichtlineare Zusammenhang kann im Kleinsignalverhalten näherungsweise linear beschrieben werden. Die Näherung wird umso besser, je kleiner der Differenzenquotient y(t) zu u(t) am Arbeitspunkt ist.
- Ist eine nichtlineare Funktion als grafische Kennlinie gegeben, dann kann durch Anlegen einer Tangente im gewünschten Arbeitspunkt die Steigung der Tangente für die linearisierte Beziehung bestimmt werden
- Ein nichtlineares dynamisches System mit kontinuierlich fallender oder steigender Kennlinie kann auch durch Einbindung in einen eigenen Regelkreis linearisiert und damit auch in seinem dynamischen Verhalten verbessert werden.
- Nichtlineare Differenzialgleichungen lassen sich meist nur numerisch lösen. Wenn ein Übertragungssystem in Teilsysteme zerlegt werden kann und das nichtlineare Verhalten einzelner Systeme als analytische Gleichung oder Wertetabelle vorliegt, kann relativ einfach das Verhalten eines nichtlinearen dynamischen Systems berechnet werden.
Nachteilige Eigenschaften nichtlinearer Systeme
[Bearbeiten]Im Gegensatz zu den linearen dynamischen Systemen haben die nichtlinearen dynamischen Systeme folgende nachteiligen Eigenschaften:
- Für nichtlineare Systeme gilt das Superpositionsprinzip allgemein nicht.
- Für nichtlineare Systeme gilt das Verstärkungsprinzip allgemein nicht.
- Es existiert keine geschlossenen Theorie der mathematischen Behandlung wie bei den linearen Systemen.
- Funktionsblöcke eines Übertragungssystems können in der Reihenfolge nicht vertauscht werden.
- Die Betrachtung im Frequenzbereich ist nicht mehr so einfach möglich.
- Die Laplace-Transformation ist nicht mehr anwendbar.

Es sind nichtlineare statische Systeme und nichtlineare dynamische Systeme zu unterscheiden. Gelingt es, von einem dynamischen nichtlinearen System einen Block als nichtlineare statische Funktion (Kennlinienverhalten) und einen Block als lineares dynamisches System zu trennen, entstehen die sogenannten Hammerstein-Strukturen Hammerstein-Modell oder die Wiener-Struktur Wiener-Modell als Modelle der Systembeschreibung.
Diese beiden Modelle unterscheiden sich nur durch die Reihenfolge der Funktionsblöcke, haben aber bei größeren Eingangssignalen unterschiedliche Eigenschaften. Für die regelungstechnischen Belange ist das Hammerstein-Modell vorzuziehen, weil die Stellgröße des Reglers meist durch Begrenzungseffekte oder der Regler als sogenannter Kennlinienregler ein nichtlineares Verhalten hat.
Schwingungseigenschaften beliebiger Systeme bei sinusförmiger Erregung
[Bearbeiten]Bei einem nichtlinearen statischen System kann die Übertragungskennlinie als eine in weiten Grenzen sich ändernde Verstärkung angesehen werden. Das System antwortet auf ein sinusförmiges Eingangssignal meist mit einer Verzerrung der Schwingung des Eingangssignals gleicher Frequenz und einer Phasenverschiebung. Lediglich ein symmetrisches Zweipunkt-Element (Zweipunktregler) ohne Hysterese, ohne Totzone und Signalbegrenzung antwortet auf eine sinusförmige Eingangsschwingung mit einer Rechteckschwingung der gewählten Rechteck-Amplitude u(t) der gleichen Frequenz ohne eine Phasenverschiebung.
- Ein lineares dynamisches System antwortet auf ein sinusförmiges Eingangssignal u(t) = uMAX * sin(ωt) im eingeschwungenen Zustand immer mit der gleichen Frequenz, lediglich die Amplitude des Ausgangssignals y(t) wird verändert.
- Ein angeregtes lineares System mit konjugiert komplexen Polen schwingt immer sinusförmig.
- Ein angeregtes nichtlineares System z.B. ein Regelkreis mit einem Zweipunktregler als nichtlineare Kennlinie schwingt meistens – je nach Ordnung der Regelstrecke und damit des Tiefpass-Verhaltens – nicht sinusförmig oder bei höherer Ordnung der Regelstrecke gut angenähert sinusförmig.
- Wird ein nichtlineares statisches System mit einem sinusförmigen Eingangssignal e(t) erregt, kann sich die Frequenz und das Frequenzspektrum des Ausgangssignals u(t) völlig verändern.
- Beispiel: Nichtlinearität mit quadratischer oder exponentieller Kennlinie:
- Für eine sinusförmige Erregung mit quadratischer Kennlinie des Systems antwortet das System mit einer doppelten sinusförmigen Frequenz und Gleichanteil (verschobener Arbeitspunkt), das System mit exponentieller Kennlinie antwortet mit einem sinusähnlichen Impuls mit großem Oberwellenanteil.
- Sogenannte Kennlinienregler antworten bei einer sinusförmiger Erregung mit Rechteckschwingungen gleicher Frequenz und meist einer nacheilenden Phasenverschiebung φ zur Eingangsschwingung. Eine Ausnahme bildet der Zweipunktregler. Er antwortet auf eine sinusförmige Erregung mit einer Rechteckschwingung gleicher Frequenz ohne Phasenverschiebung.
Methoden der mathematischen Behandlung nichtlinearer Systeme
[Bearbeiten]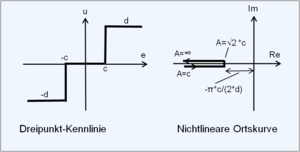
- Harmonische Balance
- Im Zustand der Dauerschwingung eines nichtlinearen dynamischen Regelsystems wird das nichtlineare statische System als lineares Übertragungsglied N(A) (A = Eingangsamplitude eMAX) betrachtet. Voraussetzung für das lineare dynamische System (Regelstrecke) ist das Tiefpass-Verhalten 2. und höherer Ordnung, bei dem die Ausgangsgröße y(t) eine angenäherte harmonische Sinusschwingung ist. Aus der Gleichung der Harmonischen Balance lassen sich die unbekannten Systemgrößen, die Amplitude A der Eingangsschwingung e(t) und die Frequenz der Dauerschwingung ω = 2*π*f bestimmen.
- Die Harmonische Balance ist ein sehr anschauliches Verfahren der Systemanalyse, das aber nicht auf die Stabilität der Ruhelage, sondern auf die Instabilität der Ruhelage, also auf stabile Dauerschwingungen zielt. Nur durch Schlussfolgerungen können daraus stabile Regelkreise bestimmt werden.
→ Siehe Wikipedia-Artikel: Harmonische Balance
- Direkte Methode von Ljapunow.[1]
- Mit den Stabilitätssätzen von Ljapunow ergibt sich ein breites Anwendungsfeld für die Stabilitätsuntersuchung und der Reglersynthese.
- Die Sätze lauten:
- Stabilität im Kleinen,
- Asymptotische Stabilität im Kleinen,
- Asymptotische Stabilität im Großen,
- Globale asymptotische Stabilität.
- Zustandsebene [2]
- Die Darstellung in der Zustandsebene ist für die Analyse und Reglersynthese geeignet, beschränkt sich aber auf Systeme 2. Ordnung. Die zeitoptimale Regelung ist gut behandelbar.

- Fuzzy-Systeme
- Fuzzy-Systeme, wie die Fuzzy-Logik und Fuzzy-Regler, sind für die experimentelle Modellierung nichtlinearer Systeme und für die Regler-Synthese mit geringem mathematischen Aufwand geeignet.
→ Siehe Wikipedia-Artikel: Fuzzy-Regler
- Numerische Berechnung
- Die numerische rekursive Berechnung eines nichtlinearen dynamischen Systems nach dem Euler-Streckenzug-Verfahren mit der diskreten Zeit Δt und der Berechnungsfolge k = (0, 1, 2, 3, ... kMAX) erlaubt als einfachstes Verfahren das Zeitverhalten sämtlicher vorkommenden nichtlinearen und totzeitbehafteten Systeme zu bestimmen.
- Die statische Nichtlinearität kann mit logischen Programm-Befehlen oder Wertetabellen berechnet, die Linearfaktoren der linearen Teilsysteme können mit Differenzengleichungen berechnet werden.
→ Siehe das ausführliche Hauptkapitel "Einführung in die Systemtheorie/ Numerische Berechnung dynamischer Systeme".
- Alternativ, soweit verfügbar, kommen numerischen Rechenprogramme wie kostenfreie GNU Octave oder kommerzielle Varianten wie MATLAB mit Simulink zur Anwendung.
Einführung in die Regelungstechnik
[Bearbeiten]Ein Regelkreis wie auch eine Regelstrecke sind dynamische Systeme. Es gelten die gleichen mathematischen Systembeschreibungen. Eine Regelstrecke ist immer stabil, wenn seine Einzelsysteme stabil sind, d.h. die Pole der Einzelsysteme haben einen negativen Realteil. Systeme mit Integratoren (I-Glieder) sind grenzstabil, ihre Pole liegen im Ursprung (Realteil = 0) des s-Diagramms (s-Ebene). Zwei Integratoren in einer Regelstrecke führen zur monotonen Instabilität. Dennoch können instabile Regelstrecken mit geeigneten Reglern zum stabilen Regelkreisverhalten gebracht werden.
Ein besonderes Phänomen der Stabilität eines offenen (aufgeschnittenen) Regelkreises tritt auf, wenn der Regelkreis geschlossen wird.
Eine der Regelstrecke nicht angepasste zu hohe Kreisverstärkung führt bei Regelstrecken mit Verzögerungsgliedern ab 3. Ordnung oder gar mit Totzeitverhalten zur oszillatorischen Instabilität. Bedingt durch das Zeitverhalten der Regelstrecke wird über den Soll-Istwert-Vergleich dem Regler eine verspätete Regeldifferenz zugeführt. Reduziert sich diese nacheilende Phasenverschiebung der Regelgröße des offenen Regelkreises um einen Wert kleiner als -180°, ergibt sich am Soll-Istwert-Vergleich anstelle einer Gegenkopplung eine Mitkopplung und der geschlossene Regelkreis wird bei einer Kreisverstärkung > 1 instabil.
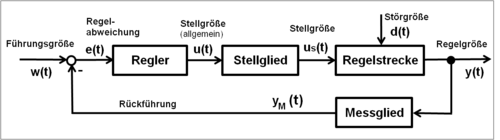
Prinzip der Regelung
[Bearbeiten]Durch die Subtraktion der negativen Rückführung der Regelgröße y(t) von der Führungsgröße w(t) entsteht die Regeldifferenz e(t), die auf den Regler wirkt. Es ist Aufgabe des Reglers, das Zeitverhalten der Regelgröße bezüglich des statischen und dynamischen Verhaltens gemäß den vorgegebenen Anforderungen festzulegen. Zur Erfüllung widersprechender Anforderungen wie gutes Führungs- und Störverhalten sind gegebenenfalls aufwändigere Regelkreisstrukturen erforderlich.
Regelkreismodell
[Bearbeiten]Die Aufgabe eines mathematisches Modells eines realen dynamischen Prozesses oder eines noch zu projektierenden technischen Prozesses dient dem Erkennen und der Vorhersage des Systemverhaltens.
Das mathematische Modell eines Regelkreises beschreibt alle äußeren Einflussgrößen wie Störgrößen und Eingangssignale auf den geschlossenen Wirkungsablauf des Regelkreises. Das Verhalten der Ausgangsgrößen wie die Regelgrößen sowie auch interessante Zwischengrößen (Stellgrößen) als Funktion der Eingangssignale und der Parameter von Regler und Regelstrecke sind von besonderem Interesse.
Je nach Lastenheft der regelungstechnischen Aufgabenstellung ist für die Bestimmung eines geeigneten Reglers das mathematische Modell der Regelstrecke erforderlich.
Mathematische Modelle können bei einfachen linearen physikalischen Systemen durch eine gewöhnliche Differenzialgleichung exakt eine Regelstrecke beschreiben (= Theoretische Modellbildung).
In den meisten Anwendungsfällen haben Übertragungssysteme (Regelstrecken) auch nichtlineare Komponenten und sind totzeitbehaftet. Für solche Systeme wird experimentell durch geeignete Testsignale die Systemantwort aufgezeichnet und ein mathematisches Modell gesucht, das den gemessenen Verlauf der Ausgangsgröße y(t) reproduziert (= Experimentelle Prozessanalyse). Ein derartig definiertes Modell ist durch Anwendung numerischer Verfahren einfach berechenbar. Sind nichtlineare Teilsysteme im Gesamtsystem enthalten, müssen diese getrennt erfasst und durch Wertetabellen definiert werden.
Global-proportionale Regelstrecken höherer Ordnung mit Totzeit lassen sich relativ genau durch Modelle als PT2-Tt-Glieder beschreiben. Global-integrale Regelstrecken lassen sich ebenso durch PT2-Tt-I-Glieder beschreiben.
Zum Modellverständnis eines dynamischen Systems müssen die wichtigsten Begriffe der inneren Systemspeicher verstanden werden.
Anforderung an einen Regelkreis
[Bearbeiten]- Der Regelkreis muss stabil sein.
- Die Stabilität des Regelkreises mit linearen zeitinvarianten Übertragungssystemen hängt von der Ordnung und den Parametern der Strecke, von der Struktur des Reglers und von den Parametern des Reglers ab.
- Wird eine Steuerstrecke aus linearen zeitinvarianten Systemen in Verbindung mit einem Regler zu einem Regelkreis gestaltet, dann werden in Bezug zum Verhalten der Steuerstrecke folgende Vorteile gewonnen:
- Die Regelgröße y(t) stellt sich auf das Niveau des Sollwertes w(t) ein,
- Störgrößen werden minimiert,
- Die dominante Zeitkonstante der Regelgröße verringert sich ungefähr um den Faktor der Kreisverstärkung.
- Bei Vorhandensein differenzierender PD-Glieder im Regler wird die Verstärkung um einen dynamischen Anteil noch zusätzlich erhöht. Dabei kann die Stellgröße u(t) sehr große Werte annehmen. Dies ergibt sich aus der Berechnung der Schließbedingung des offenen Regelkreises mit der Signalflussalgebra des Regelkreises.

- Eine zu einer Regelstrecke umfunktionierte Steuerstrecke lässt sich ohne Energiezufuhr nicht schneller machen. Dieses Beispiel zeigt den Effekt der gerätetechnischen Signalbegrenzung der Stellgröße y(t), die häufig als Schnittstelle von Steuersignalen und Steuerenergie fungiert (z. B. Stellantriebe, Ventile, usw.). Es ist Ermessenssache, ob die Leistungsschnittstelle zum Regler oder zur Regelstrecke gehört.
- Die Übertragungsfunktion dieses Beispiels eines einfachen Regelkreises enthält keinen Hinweis auf eine Signalbegrenzung und ist deshalb falsch, wenn eine Signalbegrenzung vorliegt. Übertragungsfunktionen gelten nur für lineare zeitinvariante Systeme.
- Man kann durchaus Signalbegrenzungen ignorieren und kommt zu einem stabilen Regelkreis. Jedoch entspricht das Übergangsverhalten der Regelgröße y(t) bei Signalbegrenzungen nicht der Übertragungsfunktion des Regelkreises.
- Ein wichtiges Verfahren der Bestimmung der Stabilität ist die Analyse des Nennerpolynoms der Übertragungsfunktion des Regelkreises, ob die Pole (Nullstellen des Nenners, die die Gleichung zu Null machen) in der linken s-Halbebene liegen.
- Der Regelkreis soll ein gutes Führungsverhalten und Störverhalten aufweisen.
- Werden keine besonderen regelungstechnischen Maßnahmen getroffen, sind dies widersprechende Anforderungen.
- Der Regelkreis soll sich robust verhalten.
- Unter „robust“ versteht man den Einfluss der schleichenden Änderungen der Parameter von Regler und Regelstrecke auf die Dynamik des Regelkreises. Diese durch innere und äußere Umwelteinflüsse wie z. B. Alterung, Reibung, Korrosion entstehenden Parameteränderungen müssen innerhalb eines zugelassenen Toleranzbereiches liegen. Das Verhalten der Robustheit wird auch mit Einfluss der „inneren Störgrößen“ eines Regelkreises bezeichnet.
Auslegungsstrategie
[Bearbeiten]In Bezug auf die gewünschte Stabilität des Regelkreises und weiteren Anforderungen der Dynamik der Regelgröße sind folgende Auslegungsstrategien des Reglers zu betrachten:
- Analyse eines gegebenen Regelkreises:
- Erfüllt die Regelgröße die Anforderungen nach Stabilität, Einschwingverhalten (Regelgüte), Störverhalten?
- Regelstrecke ist gegeben:
- Synthese der Reglereigenschaften, welche der Regler gemäß der Anforderungen erfüllen muss.
- Regelstrecke ist gegeben, erhöhte Dynamikforderungen der Regelgröße:
- Ist der höhere Aufwand eines Zustandsreglers mit Nutzung der inneren Systemgrößen (Zustandsvariablen) mit der Zustandsrückführung gegenüber einem konventionellen Regler mit Ausgangsrückführung vertretbar?
Spezialregler für gegebene bekannte und unbekannte Regelstrecken
[Bearbeiten]- Kombinierter Regler mit Vorsteuerung oder Vorfilter,
- Regler mit Störgrößenaufschaltung,
- Kaskadenregler: Einzelne Teilsysteme der Regelstrecke sind messbar:
- Kaskadenregler sind Hilfsgrößen-Regler für einen Folgeregelkreis. Sie erfüllen eine bessere Dynamik der Regelgröße und tragen zur Verbesserung des Störverhaltens bei.
- Regelstrecke mit Totzeit: Smith-Prädiktor eliminiert Totzeit.
- Mathematisches Modell der totzeitbehafteten Regelstrecke durch Smith-Prädiktor mit „Totzeit Vorhersage“.
- Regelstrecke unbekannt oder ändert sich:
- Adaptiver Regler erforderlich, der die Regelstrecke identifizieren und in bestimmten Grenzen optimal regeln kann.
- Regelkreis mit Rückführung der Zustandsvariablen,
- Verbesserte dynamische Regeleigenschaften gegenüber Regelkreisen mit Ausgangsrückführung. Vergleichbar mit Kaskadenreglern.
→ Siehe den ausführlichen Wikipedia-Artikel: Regelungstechnik
→ Siehe den ausführlichen Wikipedia-Artikel: Regelkreis
→ Siehe den ausführlichen Wikipedia-Artikel: Regler
→ Siehe den ausführlichen Wikipedia-Artikel: Regelstrecke
Groß- und Kleinsignalverhalten
[Bearbeiten]- Großsignale sind wirklich gemessene Signale
- Beispiel: Maximaler Sollwertsprung an einer Regeleinrichtung. Gemessene Sprungantwort der Regler-Stellgröße und der Regelgröße. Analyse der Problematik häufig vorkommender Stellgrößenbegrenzung, die zu nichtlinearem Verhalten führen.
- Kleinsignalverhalten
- Kleine Signalabweichungen um den Arbeitspunkt eines linearen Übertragungssystems müssen sich nicht proportional und identisch mit großen Signalabweichungen verhalten.
- Beispiel: Für kleine Sollwert-Änderungen an einer Regeleinrichtung müssen nicht zwangsläufig Stellgrößenbegrenzungen auftreten.
Einzelnachweise
[Bearbeiten]- ↑ Fachbuch Heinz Unbehauen „Regelungstechnik II“, Nichtlineare Regelsysteme, Kapitel: Stabilitätstheorie nach Ljapunow", 9. Auflage 2006
- ↑ Fachbuch Heinz Unbehauen „Regelungstechnik II“, Nichtlineare Regelsysteme, Kapitel: „Analyse nichtlinearer Regelsysteme in der Phasenebene“ und „Untersuchung von Relaisregelsystemen mit der Methode der Phasenebene“, 9. Auflage 2006
Zeitverhalten elementarer Übertragungsglieder der Übertragungsfunktion
[Bearbeiten]Zeitverhalten elementarer Übertragungsglieder
[Bearbeiten]Systeme mit konzentrierten und verteilten Parametern
[Bearbeiten]Dynamische Systeme ohne räumliche Ausdehnung der Systemspeicher haben konzentrierte Systemparameter. Die System-Ausgangssignale sind nur zeitabhängig.
Dynamische Systeme mit räumlicher Verteilung der Systemspeicher enthalten verteilte Systemparameter. Bei diesen Systemen sind die Variablen nicht nur Funktionen der Zeit sondern auch vom Ort. (Beschreibung durch partielle Differenzialgleichungen)
Die nachfolgenden Systembeschreibungen beziehen sich auf Systeme mit konzentrierten Parametern.
Zeitinvarianz
[Bearbeiten]Ein dynamisches Übertragungssystem ist zeitinvariant, wenn es sich über die Zeit nicht ändert. D.h. die Systemantwort y(t+t0) auf ein identisches Eingangssignal u(t+t0) ist von t0 unabhängig. Die Koeffizienten der mathematischen Systembeschreibung sind konstant (zeitlich unveränderlich, invariant).
Zeitvarianz
[Bearbeiten]Ein zeitvariantes System verhält sich zu verschiedenen Zeitpunkten unterschiedlich. Bei technischen Systemen liegt der Grund dafür meist in zeitabhängigen Parameterwerten, zum Beispiel durch Änderung der Koeffizienten der Energiespeicher [zeitabhängige Koeffizienten der Ableitungen y(t)]. Bei vielen Prozessen sind die Auswirkungen der Zeitvarianz so klein oder langsam, dass diese Systeme näherungsweise als zeitinvariant behandelt werden können.
Beispiel für ein typisches zeitvariantes Verhalten ist eine startende Rakete, deren Masse sich durch den verbrauchten Treibstoff ändert. Häufig spielt bei kleineren Massen der mechanische Verschleiß eine Rolle.
Kausalität
[Bearbeiten]Eine wichtige Eigenschaft dynamischer Systeme ist ihre Kausalität. Sie besagt, dass der Wert der Eingangsgröße zur Zeit t = t(0) das Verhalten des Systems nur für künftige Zeitpunkte t ≥ t(0) beeinflussen kann.
Eine Eingangsgröße zum Zeitpunkt t = t0 kann nur den gegenwärtigen und den zukünftigen Verlauf t ≥ t0 der Ausgangsgröße beeinflussen.
Ordnung der Übertragungsfunktion
[Bearbeiten]Blockschaltbilder erlauben eine übersichtliche Darstellung von dynamischen Prozessen und deren Signalflüsse.
Die häufigste Darstellungsform für das Eingangs- Ausgangsverhalten eines linearen Übertragungssystems ist die Übertragungsfunktion. Sie ist eine abstrakte nicht messbare mathematische Beschreibung für das Verhalten eines linearen zeitinvarianten Systems im Frequenzbereich mit der komplexen Variable s.
Der mathematische Begriff einer gebrochenen rationalen Funktion ist definiert als Quotient zweier Polynome, wobei die Ordnung des Systems im Nenner höher als im Zähler sein muss. Solche Systeme sind technisch realisierbar und entsprechen dem Eingangs- Ausgangsverhalten eines Übertragungssystems im sogenannten s-Bereich (Bildbereich).
Eine systembeschreibende gewöhnliche Differenzialgleichung kann mit der Laplace-Transformation in eine Übertragungsfunktion zunächst in Polynom-Darstellung als gebrochene rationale Funktion geschrieben werden. Durch Bestimmung der Nullstellen im Zähler und Nenner dieser Funktion kann die Polynomdarstellung in eine Produkt-Darstellung mit Linearfaktoren überführt werden. Ein Linearfaktor ist ein Term, in dem die Variable s nur den Grad 1 hat, d. h. keinen höheren Exponenten als 1 besitzt. Quadratische Linearfaktoren mit konjugiert komplexen Nullstellen haben den Grad 2.
Die Übertragungsfunktion in Polynom-Darstellung wird mit Hilfe der Nullstellenbestimmung nach folgender Gleichung in die Produkt-Darstellung überführt.
Produktdarstellung der Übertragungsfunktion:
Sind die Werte der Nullstellen bzw. der Pole der Linearfaktoren negativ, dann sind die Produktterme positiv und das System ist stabil. Systeme mit negativen Linearfaktoren im Nenner (mit positiven Polen) streben nach einer Systemerregung exponentiell einen theoretisch unendlich großen Wert an .
Die gleiche Übertragungsfunktion in Zeitkonstanten-Darstellung mit Tvi = - 1 / s0i. Dabei ändert sich der Verstärkungsfaktor infolge der Division mit den Nullstellen.
In der Produkt-Darstellung der Übertragungsfunktion können folgende Terme 1. Ordnung und 2. Ordnung mit konjugiert komplexen Nullstellen mehrfach auftreten:
- Produktterme 1. Ordnung (Linearfaktoren): s-s1 oder in Zeitkonstanten-Darstellung umgerechnet: T*s+1
- Linearfaktoren ohne Absolutglied : s - 0 = s, in Zeitkonstanten-Darstellung: T*s
- Produktterme 2. Ordnung (mit konjugiert komplexen Nullstellen): s2 + p*s + q,
- In Zeitkonstanten-Darstellung: T2*s2+2*D*T*s+1
Diese 3 nicht mehr aufspaltbaren Teilsysteme (Linearfaktoren bzw. quadratischer Linearfaktor) haben ein völlig unterschiedliches Übertragungsverhalten im Zeit- und Bildbereich, ob sie im Nenner oder Zähler der Übertragungsfunktion stehen. Komplizierteste lineare Systeme höherer Ordnung setzen sich aus diesen Teilsystemen zusammen.
Linearfaktoren haben differenzierendes Verhalten, wenn sie im Zähler der Übertragungsfunktion stehen und integrierendes oder zeitverzögerndes Verhalten, wenn sie im Nenner stehen. Sie werden auch als phasenminimale oder reguläre Systeme bezeichnet.
Phasenminimumsysteme sind rationale Übertragungsfunktionen G(s) ohne Totzeit, die nur Pole und Nullstellen in der linken s-Halbebene haben:
Übertragungsglieder als Blockstruktur im Signalflussplan
[Bearbeiten]Übertragungssysteme können aus Teilsystemen als Blöcke zusammengefasst werden. Es gilt das Superpositionsprinzip. Die Systeme in Produktdarstellung können in der Reihenfolge beliebig verschoben werden. Die Systemausgänge dürfen nicht durch nachfolgende Systemeingänge belastet werden (Rückwirkungsfreiheit).
- Parallelschaltung:
- Reihenschaltung:
- Gegenkopplung oder Rückkopplung:
- Gegenkopplung ohne Teilsystem in der Rückführung:
- Bei einem Regelkreis, der in dem Gegenkopplungszweig kein statisches oder dynamisches Teilsystem enthält, wird das System G2(s) = 1.
- Damit lautet die Übertragungsfunktion des geschlossenen Regelkreises:
- Mitkopplung:
- Eine Mitkopplung ist eine positive additiv wirkende Rückführung des Signalausgangs auf den Systemeingang. Sie führt je nach Größe der Verstärkung von G1(s) zur monotonen Instabilität oder zu einem Hysterese-Effekt.
- Gleichung der Übertragungsfunktion der Mitkopplung:
- Mit G1(s) als offener Regelkreis werden beliebige algebraische Zusammenführungen der Teilsysteme des Reglers und der Regelstrecke verstanden.
Lineare Systeme mit verzögerndem Verhalten
[Bearbeiten]Die nachstehenden Teilsysteme können beliebig im Zähler und Nenner einer Übertragungsfunktion G(s) entsprechend der Gesamtsystemstruktur multiplikativ und / oder additiv kombiniert werden.
- Integrierglied, Kurzform: I-Glied:
- Verzögerungsglied, Kurzform: PT1-Glied:
- Schwingungsglied, Kurzform: PT2-GliedKK mit konjugiert komplexen Polen.
Lineare Systeme mit differenzierendem Verhalten
[Bearbeiten]- Differenzierglied, Kurzform: D-Glied
- Proportional wirkendes D-Glied, Kurzform: PD1-Glied
- Proportional wirkendes D-Glied 2. Ordnung mit konjugiert komplexen Polen, Kurzform: PD2-GliedKK
- Beispiel eines realisierbaren Übertragungssystems 3. Ordnung (Anzahl Pole > Nullstellen)
Beschreibung einer Übertragungsfunktion G(s) als gebrochene rationale Funktion in Produktdarstellung mit der Verstärkung K:
Die systembeschreibende Differenzialgleichung dieser Systeme zeigt Stabilität an, wenn alle Koeffizienten der einzelnen Terme positiv sind. (Mindestvoraussetzung der Stabilität). Die Übertragungsfunktionen dieser linearen Grundsysteme sind stabil, wenn die Vorzeichen der zugehörigen Nullstellen negativ sind.
Gleiche stabile Pole und Nullstellen der 3 Grundformen lassen sich in der Produktform (= Reihenschaltung der Systeme) gegeneinander kürzen und vereinfachen damit die Berechnung des Gesamtsystems. In der Produktform der Zeitkonstanten-Darstellung im Zähler und Nenner können die Teilsysteme gegeneinander gekürzt werden, wenn die Zeitkonstanten TV = T sind.
Globales P-, I-, D-Systemverhalten
[Bearbeiten]Wenn in einer systembeschreibenden Differenzialgleichung oder in der zugehörigen Übertragungsfunktion aus der geschlossenen Reihenfolge der Ableitungen bestimmte Koeffizienten fehlen, bzw. zu Null gesetzt sind, ergibt sich für das Gesamtverhalten im Zeitbereich folgendes typische Verhalten für den Linearfaktor ohne Absolutglied:

- Globales P-Verhalten
Im stationären Zustand ergibt diese Form der Übertragungsfunktion nach einem Eingangssprung für das Ausgangssignal mit der Verstärkung K ein P-Verhalten im Zeitbereich, weil alle Linearfaktoren vollständig sind:
Nach dem Einschwingvorgang nach genügend langer Zeit ist die Ausgangsgröße:
- Globales I-Verhalten
Im stationären Zustand ergibt diese Form der Übertragungsfunktion nach einem Eingangssprung u(t) für das Ausgangssignal ein stetig wachsendes Ausgangssignal im Zeitbereich. Der Linearfaktor ohne Absolutglied befindet sich im Nenner.
Nach dem Eingangssprung und genügend langer Zeit ist die Ausgangsgröße:
- Globales D-Verhalten
Im stationären Zustand ergibt diese Form der Übertragungsfunktion nach einem Eingangssprung u(t) für die Ausgangsgröße y(t) den Wert 0. Der Linearfaktor ohne Absolutglied befindet sich im Zähler.
Das Ausgangssignal y(t) lautet:
Stabilität
[Bearbeiten]
- Ein dynamisches lineares oder nichtlineares System kann stabil oder instabil (monoton instabil oder oszillatorisch instabil) sein.
- Ein Regelkreis bestehend aus linearen oder nichtlinearen instabilen Teilsystemen kann mit geeigneten Reglern zum stabilen Verhalten gebracht werden.
- In einem Regelkreis mit einem Teilsystem mit Totzeit versagen die meisten Stabilitätskriterien, mit Ausnahme des grafischen Nyquist-Kriteriums für den "aufgeschnittenen" Regelkreis. Abhilfe: Numerische Berechnung des Systemverhaltens des Regelkreises für ein gegebenes Eingangssignal und tabellarische Darstellung der Berechnungsfolgen des Ausgangssignals im diskreten Zeitbereich.
- Der Übertragungsfunktion eines Systems kann die transzendente Funktion des Totzeitgliedes multiplikativ angehängt werden zu . Diese Form der Übertragungsfunktion als Gesamtsystem ist nur für Frequenzgang-Analysen geeignet. Eine algebraische Berechnung mit dieser Gleichungsform ist nicht möglich.
Die nachfolgenden Beschreibungen beziehen sich auf Systembeschreibungen der Übertragungsfunktion als gebrochen-rationale Funktion, die sich laut Definition immer linear verhalten muss.
Interne Stabilität:
[Bearbeiten]Wenn die Übertragungsfunktion eines Übertragungssystems oder eines Regelkreises vorliegt:
Die Pole einer Übertragungsfunktion bestimmen die Stabilität und die Geschwindigkeit der Systembewegung. Die Nullstellen einer Übertragungsfunktion haben nur Einfluss auf die Amplituden des Systems.
| Ein Übertragungssystem ist intern stabil, wenn alle (Teil-)Übertragungsfunktionen nur Pole in der linken s-Halbebene haben. |

Asymptotische Stabilität:
[Bearbeiten]Bedeutung: Das Ausgangssignal eines linearen dynamischen Systems im Zeitbereich strebt nach einer "Einschwingzeit" als Folge eines Eingangssignals einen stabilen Zustand auf das Niveau des Eingangssignals mit der Verstärkung K * u(t) an.
Bedingungen der asymptotischen Stabilität:
|
Bedeutung der Pole für das Systemverhalten bei einfachen Polen und konjugiert komplexen Polenpaaren:
- Lage aller Pole des Übertragungssystems in der linken s-Halbebene:
- System ist asymptotisch stabil.
- Lage eines Poles des Übertragungssystems in der rechten s-Halbebene:
- System ist monoton instabil.
- Lage eines Poles des Übertragungssystems auf der imaginären Achse (Realteil = 0) der s-Ebene:
- System ist grenzstabil.
- Lage mehrfacher Pole auf der imaginären Achse der s-Ebene:
- System ist instabil.
- Konjugiert komplexe Polpaare mit negativem Realteil:
- System ist asymptotisch stabil, die Schwingneigung ist von der Dämpfung D abhängig.
- Konjugiert komplexe Polpaare mit einem Realteil gleich oder größer Null:
- System verhält sich monoton instabil oder oszillatorisch instabil.
Externe Stabilität (BIBO-Stabilität)
[Bearbeiten]Wenn die Hardware eines Übertragungssystems bzw. eines Regelkreises oder eines genauen Modells mit dem Eingangs- und Ausgangssignal vorliegt:
| Ein Übertragungssystem gilt als extern stabil, wenn jedes beliebige beschränkte Eingangssignal an dem System auch ein beschränktes Ausgangssignal hervorruft. (BIBO-Stabilität) |
Lineare phasenminimale und nichtphasenminimale Übertragungssysteme
[Bearbeiten]- Phasenminimumsystem (reguläres System)
Bei stabilen dynamischen Übertragungssystemen sind die Koeffizienten der systembeschreibenden gewöhnlichen Differenzialgleichung positiv bzw. die Nullstellen und Pole der Übertragungsfunktion negativ.
- Phasenminimumsysteme sind Übertragungssysteme ohne Totzeit, bei denen die Übertragungsfunktion G(s) nur Pole und Nullstellen in der linken s-Halbebene hat.
- Für einen gegebenen Amplitudengang hat das Phasenminimumsystem eine minimale Phasenverschiebung. Die Kenntnis des Amplitudengangs genügt, um auf die Übertragungsfunktion des Systems schließen zu können.
- Nicht alle Phasenminimumsysteme sind stabil. Sie erfüllen alle den Begriff der "Internen Stabilität" aber nicht alle sind "Extern stabil".
- Nichtphasenminimumsystem (nichtreguläres System)
Ein dynamisches Übertragungssystem hat ein nichtminimales Phasenverhalten, wenn es eine Totzeit enthält oder die Pole oder Nullstellen der Übertragungsfunktion in der rechten Seite der s-Halbebene liegen. Der Phasenverlauf des Übertragungssystems ist betragsmäßig größer, als es bei einem phasenminimalen System mit gleichem Amplitudengang wäre.
Zusammenfassung der Eigenschaften der Nichtphasenminimumsysteme:
- Nichtphasenminimumsysteme enthalten eine Totzeit oder Pole oder Nullstellen in der rechten s-Halbebene.
- Nichtphasenminimumsysteme mit Polen in der rechten s-Halbebene sind instabile Systeme. Dieses System reagiert auf ein Eingangssignal mit einem unbeschränkten Ausgangssignal.
- Nichtphasenminimumsysteme mit Polen in der rechten s-Halbebene und Phasenminimumsysteme sind relativ leicht zu regeln.
- Nichtphasenminimumsysteme mit Nullstellen in der rechten s-Halbebene (Allpass-Systeme) sind stabile Systeme aber sehr schwierig zu regeln.
- Nullstellen in Phasenminimumsystemen und Nichtphasenminimumsystemen haben Einfluss auf die Amplituden der Ausgangssignale. Pole bestimmen das Zeitverhalten.
Nichtphasenminimum-Verhalten wird durch Totzeitglieder oder Allpassglieder in Serie mit Phasenminimumsystemen verursacht. Dieses Verhalten kann durch Differenzbildung von phasenminimalen Systemen oder durch positive Rückkopplung in einem Regelkreis entstehen. In der Natur können nichtphasenminimale Systeme entstehen, wenn z. B. auf die Lage einer Masse Beschleunigungskräfte einwirken, wie sie durch die Gravitation oder durch den Magnetismus hervorgerufen werden. Die Lage der Masse wird zunehmend beschleunigt und wächst progressiv bis zu einer natürlichen Begrenzung. Klassische Beispiele solcher Systeme sind: Invertiertes Pendel, Magnetschwebekörper, Laufkatze am Hebekran.
Ein nichtminimalphasiges System ist immer zerlegbar in eine Reihenschaltung bestehend aus Phasenminimumsystem und Allpass.
Instabile nichtphasenminimale Systeme beziehen sich auf Verzögerungsglieder 1. und 2. Ordnung:
Allpassglieder
[Bearbeiten]Allpassglieder sind multiplikative Kombinationen von instabilen PD1-Gliedern (positive Nullstelle im Zähler) und stabilen PT1-Gliedern (negativer Pole im Nenner) der Übertragungsfunktion.
Sie reagieren auf einen Eingangssprung u(t) zunächst mit einem Sprung entgegengesetzter Polarität, um sich dann asymptotisch auf das Niveau des Sprungs einzustellen.
Allpassglieder können durch Subtraktion eines PT1-Gliedes von einem DT1-Glied entstanden sein (= Parallelschaltung zweier Übertragungsfunktionen).
Allpassglieder sind Systeme, die für alle Frequenzen einen konstanten Amplitudengang haben. Lediglich die Phase eilt mit unterschiedlicher Abhängigkeit von ω nach.
Die Sprungantwort des Allpassgliedes im Zeitbereich nach der inversen Laplace-Transformation lautet:
Totzeitglied
[Bearbeiten]Das Totzeitglied verschiebt ein Eingangssignal u(t) um den Betrag der Totzeit Tt, ohne das Signal zu verformen.
Beispiel von Totzeitsystemen: Fördermengen mit dem Transportband, Lange Gasdruckleitungen, Spiel in Getriebeübersetzungen, Umschaltvorgänge bei Ventilen und andere Schaltvorgänge und Signallaufzeiten.
Im Gegensatz zu den linearen dynamischen Übertragungssystemen kann ein Totzeitsystem nicht mit einer gewöhnlichen Differenzialgleichung, sondern nur mit einer partiellen Differenzialgleichung beschrieben werden. Laufzeitglieder oder Totzeitglieder gehören zu der Klasse der Systeme mit verteilten Parametern. Sie haben keine konzentrierten Speicher und keine Pole und Nullstellen in der endlichen s-Ebene.
Einen wesentlich einfacheren Zusammenhang zwischen der Ein- und Ausgangsgröße eines Totzeitsystems gewinnt man durch die Darstellung der Totzeit mit der Übertragungsfunktion.
Zeitverhalten des Totzeitgliedes:
Sprungantwort:
Übertragungsfunktion des Totzeitgliedes:
Die Beziehung des Eingangs- und Ausgangsverhaltens des Totzeitsystems wird durch den Verschiebesatz der Laplace-Transformation wiedergegeben:
Für Übertragungssysteme mit einem Totzeitglied wird dem linearen System G1(s) die transzendente Funktion des Totzeitgliedes multiplikativ beigefügt:

Diese Darstellungsform eines Totzeitgliedes bzw. Kombinationen linearer dynamischer Systeme mit einem Totzeitverhalten als Übertragungsfunktion eignet sich für Analysen der Stabilität nur im Frequenzbereich. Dabei kommen grafische Stabilitätsverfahren wie das Bode-Diagramm oder die Ortskurve des Frequenzgangs zur Anwendung.
- Beispiel
Gegeben: System mit 4 Verzögerungsgliedern je T = 1 s und Totzeitglied Tt = 2 s
Das grafische Beispiel eines Verzögerungssystems mit Totzeit zeigt den numerisch berechneten Verlauf der Ausgangsgröße y(t) für einen Eingangssprung
und Rücksprung u(t) = 0.
Padé-Approximation
[Bearbeiten]Ein Totzeitglied kann als ein Allpassglied unendlicher Ordnung zu einem System mit gebrochener rationaler Übertragungsfunktion angenähert werden. Dieses Verfahren ist unter der Padé-Approximation bekannt. Die Genauigkeit der Annäherung hängt von der Ordnung des Allpassgliedes ab.
Padé-Approximation 1. und 2. Ordnung:
Der Nachteil dieser Form der Polynomdarstellung 2. Ordnung ist die erforderliche zusätzliche Rechenarbeit zur faktoriellen Darstellung. Für jede Änderung des Wertes der Totzeit müssen für die faktorielle Darstellung die Nullstellen und Pole berechnet werden. Je nach Größe der Totzeit können auch konjugiert komplexe Pole und Nullstellen entstehen.
Folgende Gleichung der modifizierten Padé-Approximation erlaubt die Berechnung der Annäherung an die Totzeit durch gleiche Allpassglieder beliebiger Ordnung n:

Die Padé-Approximation der Totzeit bringt bereits bei drei identischen Allpassgliedern (n = 3) gute Ergebnisse der Totzeit-Annäherung.
Der Allpass mit einem PD-Glied im Zähler mit einer positiven Nullstelle kann wie folgt in bekannte Teilsysteme 1. Ordnung als PT1-Glied und D-Glied zerlegt werden:
Beispiel von drei identischen Allpassgliedern in Reihenschaltung mit dem Proportionalfaktor K:
Für die numerische Berechnung (Eulersches Streckenzug-Verfahren) ergeben sich pro Allpass folgende drei Gleichungen, die hintereinander pro Berechnungsfolge zu berechnen sind:
(Jedes Ausgangssignal y(k) ist das Eingangssignal u(k) der nächsten Gleichung innerhalb einer Folge)
Für die numerische Berechnung der Reihenschaltung von 3 Allpässen sind damit 9 Gleichungen pro Berechnungsfolge erforderlich.
Bei Anwendung der Tabellenkalkulation durch die INDEX-Anweisung: „INDEX (Bezug: Spalte; Bereich)“ wird ein Index verwendet, um aus einem Bezug einen Wert zu wählen. Damit ist für die exakte Totzeit-Berechnung nur eine Gleichung pro Berechnungsfolge erforderlich.
Mathematische Modelle eines technischen dynamischen Systems
[Bearbeiten]Mathematische Modelle eines technischen dynamischen Systems
[Bearbeiten]Die Aufgabe eines mathematischen Modells eines realen dynamischen Prozesses dient dem Erkennen und der Vorhersage des Systemverhaltens bei messtechnisch erfassbaren System-Einflussgrößen. Dazu zählen z.B. durch rechnergesteuerte Simulation:
- Systemverhalten bei kritischen Umgebungsbedingungen, bestimmten Testsignalen, Störsignalen,
- Optimierung des Reglers bei geregelten Systemgrößen,
- Zerstörungsfreie Systemprüfung im Anlagenbau, in der verfahrenstechnischen Industrie, in der Chemieindustrie bei Großsignalverhalten.
Dynamische Systeme mit konzentrierten Parametern als Eingrößen- und Mehrgrößensysteme können sich linear, nichtlinear, zeitinvariant, zeitvariant und global-proportional, -integral und -differenzial verhalten. Systeme mit konzentrierten Parametern (Feder-Masse-System) haben im Gegensatz zu Systemen mit verteilten Parametern (z. B. Wärmefluss im homogenen Medium) keine räumliche Ausdehnung.
Häufig wird für die lineare Systembeschreibung als sogenannte Bewegungsgleichung die systembeschreibende gewöhnliche Differenzialgleichung mit konstanten Parametern verwendet. Viele ausgeführte technische dynamische Systeme enthalten nichtlineare, totzeitbehaftete und begrenzende Komponenten, so dass mit der Beschreibung der Differenzialgleichung nur eine Annäherung an das tatsächliche Verhalten eines realen Systems sein kann. Die meisten Prozesse sind mit dynamischen Systemen nichtlinear, so dass lineare Annäherungen getroffen werden müssen.
Gut angepasste Modelle aus vermischten linearen und nichtlinearen Systemen können nur numerisch definiert und mit Computern berechnet werden.
Begriffsklärungen der konträren Eigenschaften mathematischer Modelle dynamischer Übertragungssysteme:
[Bearbeiten]| Modell-Eigenschaften | Eigenschaft 1 | Eigenschaft 2 | Kommentar |
|---|---|---|---|
| Modell-Erstellung | analytisch | experimentell | Analytisch durch Differenzialgleichungen und Übertragungsfunktionen experimentell meistens durch die Systemsprungantwort. |
| Modell-Darstellung | parametrisch | nicht- parametrisch |
Parametrisch in Form einer Differenzialgleichung entweder analytisch oder experimentelle Identifikation. Die Sprungantwort ist ein nichtparametrisches dynamisches Modell |
| Modellverhalten | linear | nichtlinear | Ein lineares System muss der Linearitätseigenschaft des „Superpositionsprinzips“ entsprechen. Nichtlineare Systeme können im Arbeitspunkt linearisiert werden oder durch Wertetabellen numerisch berechnet werden. |
| Modellverhalten | dynamisch | statisch | Ein dynamisches Modell enthält Energiespeicher, die das Zeitverhalten bestimmen. Ein statisches Modell kat kein Zeitverhalten. Es kann in einem dynamischen Modell enthalten sein, wenn die zeitlichen Ableitungen der Ein- und Ausgangsgrößen des Modells (Differenzialgleichung) zu Null gesetzt werden. |
| Darstellung der Parameter | konzentriert | verteilt | Dynamische Systeme ohne räumliche Ausdehnung der Systemspeicher haben konzentrierte Systemparameter. Beispiel: Masse, Kondensator! Die System-Ausgangssignale sind nur zeitabhängig. Dynamische Systeme mit räumlicher Verteilung der Systemspeicher enthalten verteilte Systemparameter. Beispiel: Wärmefluss in einem homogenen Medium, Spannungsabfall in elektrischen Leitungen. Bei diesen Systemen sind die Variablen nicht nur Funktionen der Zeit sondern auch von Ortskoordinaten abhängig. (Beschreibung durch partielle DGL) |
| Zeitabhängigkeit der Parameter |
zeitinvariant | zeitvariant | Zeitinvariante Systeme werden durch gewöhnliche DGL mit konstanten Koeffizienten beschrieben. Bei zeitvarianten Systemen hat die gewöhnliche DGL keine konstanten Parameter. Beispiel: Die Masse einer Rakete reduziert sich während des Antriebs. |
| Beschreibungsform des Modellverhaltens |
kontinuierlich | diskret | Die Differenzialgleichung f(t) oder die Übertragungsfunktion F(s) beschreiben kontinuierliche Funktionen. Differenzengleichungen beschreiben zeitdiskrete Darstellungen für ein kleines Zeitintervall Δt. Durch rekursive Berechnung addiert sich für jede Berechnungs- folge k ein neuer Wert Δy(k) zum alten Wert y(k-1). Damit entsteht ein gebrochener Zeitverlauf für y(k*Δt). Alle Berechnungsgrößen treten im zeitlichen Abstand Δt auf. |
| Modellordnung | exakt | reduziert | Die Systemidentifikation kann theoretisch anhand physikalischer Grundlagen getroffen werden. Damit ist die Ordnung der Systemspeicher exakt erfasst. Durch das Verfahren der experimentellen Systemidentifikation ergibt sich häufig ein Modell reduzierter Ordnung. |
| Modellvarianten | vollständig | vereinfacht | Je nach Bedeutung eines dynamischen Prozesses wird ein vollständiges oder vereinfachtes Modell der Aufgabenstellung angepasst (Kosten-Nutzen-Bewertung). |
Modellierung eines unbekannten dynamischen Systems
[Bearbeiten]Für die Ermittlung eines guten mathematischen Modells eines realen Systems müssen sowohl die Systemstruktur als auch die Parameter (Systemkonstanten) ermittelt werden. Die Aufgabe der Systemidentifikation kann theoretisch (anhand physikalischer Grundlagen) oder experimentell durch Messung des Ein- Ausgangsverhaltens mittels geeigneter Testsignale erfolgen:
- Vorgehensweise zur Modellierung eines dynamischen Systems mit Differenzialgleichungen
- Systemzerlegung in rückwirkungsfreie einfache Teilsysteme,
- Definition der physikalischen Gesetze der Teilsysteme:
- Mechanische Systeme: Newtonsches Gesetz, Kräfte- und Momenten-Gleichgewicht, Erhaltungssätze von Impuls, Drehimpuls und Energie.
- Elektrische Systeme: Kirchhoffsche Gesetze, Ohmsches Gesetz, Induktionsgesetz, Maxwellsche Gleichungen (bei Feldern, d.h. örtlich verteilten Systemen),
- Thermische Systeme: Wärmeleitungs- und Wärmeübertragungsgesetze, Erhaltungssätze der inneren Energie oder Enthalpie.
- Systeme mit Stofftransport: Gesetz der Gasdynamik, Diffusionsgesetz.
- Kopplungsbeziehungen bei Mehrgrößensystemen beschreiben,
- Zusammenfassung aller Gleichungen zu einer Differenzialgleichung, eines Differenzialgleichungssystems oder einer Übertragungsfunktion.
Systeme mit Energiespeichern wie Spannung an einem Kondensator, Strom in einer Induktivität, bei einem Feder-Massesystem die potentiellen und kinetischen Energieanteile führen trotz der unterschiedlichen physikalischen Systemgrößen zu identischen Strukturen der systembeschreibenden Differenzialgleichungen bzw. im komplexen Frequenzbereich zu identischen Übertragungsfunktionen.
Für lineare bzw. angenäherte lineare dynamische Systeme sind verschiedene Methoden der Modellierung bekannt.
Die Analyse eines bestehenden technischen Übertragungssystems erfolgt bei globalen P- oder I-Verhalten meistens durch die Sprungantwort, Impulsantwort oder durch Einspeisen einer variablen sinusförmigen Frequenz konstanter Amplitude.
Für einfache Ansprüche der schnellen Bestimmung einer Ersatzbeschreibung eines realen Übertragungssystems existieren verschiedene heuristische Verfahren, die auch unter dem Begriff "Faustformelverfahren" in der Regelungstechnik bekannt sind. Sie beziehen sich meist auf die grafisch aufgezeichnete Sprungantwort einer Regelstrecke für nichtschwingende lineare Systeme höherer Ordnung. Häufig werden für diese Verfahren der einfachen Bestimmung der Streckenparameter die für einen Regelkreis erforderlichen Parameter der Standardregler (P-, I-, PI-, PD-, und PID-Regler) zugehörig mitgeliefert.
Modellierung eines linearen dynamischen Systems durch die Aufstellung der Differenzialgleichung
[Bearbeiten]Ein einfaches Beispiel der theoretischen Entwicklung der systembeschreibenden Differenzialgleichung wird in dem Kapitel „Entstehung einer Differenzialgleichung“ mit einem RLC-Netzwerk gezeigt. Bei diesem Beispiel der Berechnung eines Systems aus Kombinationen von Bauelementen aus Widerständen, Kondensatoren und Induktivitäten unter Vernachlässigung von parasitären Eigenschaften der Bauelemente (Kapazität einer Induktivität, Induktivität eines gewickelten Widerstandes, Temperatureinfluss) handelt es sich um ein reales Modell eines linearen Systems mit konzentrierten Energiespeichern und nicht um eine Annäherung.
Modellierung nach der Frequenzganganalyse
[Bearbeiten]Die experimentelle Systemidentifikation eines realen Systems erfolgt durch Messung des Eingangs-Ausgangs-Verhaltens durch Anregung mit einer Wechselspannung variabler Frequenz. Anhand der Asymptoten-Schnittpunkte des Frequenzgangs im Bode-Diagramm kann auf die Übertragungsfunktion des Systems geschlossen werden. Die Prüfung des Phasengangs ist erforderlich, wenn das Gesamtsystem eine Totzeitkomponente enthält.
Modellierung eines linearen Systems mit Totzeit durch ein PT2-Verzögerungsglied und Ersatztotzeit
[Bearbeiten]Sehr gute Modelle erhält man aus der Sprungantwort eines Systems durch Approximation mit einem PT2-Glied und einer Ersatztotzeit. Das PT2-Glied und das Ersatz-Totzeitglied wirken als Reihenschaltung. Details werden in den nachfolgenden Kapiteln behandelt!
Mathematische Werkzeuge
[Bearbeiten]Die Analyse des Verhaltens eines dynamischen Systems zur Erstellung eines Modells und insbesondere für die experimentelle Systemidentifikation erfordert die Kenntnis der mathematischen Werkzeuge zur Beschreibung der synthetischen Zusammenstellung unterschiedlicher Teilsysteme wie zum Beispiel entkoppelte Verzögerungssysteme, Integrationen, Totzeitsysteme, nichtlineare statische Systeme.
Wegen des hohen Bekanntheitsgrades und der übersichtlichen Gleichungsdarstellung werden lineare Modelle häufig im s-Bereich als Übertragungsfunktionen dargestellt. Lineare gewöhnliche Differenzialgleichungen mit konstanten Koeffizienten können durch die Laplace-Transformation beliebig in den s-Bereich und umgekehrt können Übertragungsfunktionen vom s-Bereich in den Zeitbereich transformiert werden. Für die Systemberechnung mit Anfangswerten ist die mathematische Form der Differenzialgleichungen vorteilhaft.
Die transzendente Darstellung der Totzeitsysteme ist nur für die grafische Darstellung im komplexen Frequenzbereich geeignet. Der Systementwurf im Frequenzbereich hat nur eine informative didaktische Bedeutung. Regelkreise mit Totzeitsystemen lassen sich nur numerisch einfach berechnen.
Mit der numerische Behandlung und der diskreten Zeit Δt lässt sich jede Modellanpassung eines Übertragungssystems oder eines Regelkreises berechnen. Es ist gleichgültig, ob die Systembeschreibungen als Übertragungsfunktion oder Differenzialgleichungen vorliegen.
Lösung von Differenzialgleichungen mit Anfangswerten:
[Bearbeiten]Lineare gewöhnliche Differenzialgleichungen mit konstanten Koeffizienten beliebiger Ordnung lassen sich im Gegensatz zur klassischen Lösung sehr einfach mit der numerischen Differenzengleichung der Integration lösen.

Beispiel systembeschreibende DGL 2. Ordnung:
[Bearbeiten]- Es wird die explizite Form nach der höchsten Ableitung verwendet, d.h. alle Terme der Gleichung werden durch den Koeffizienten a2 dividiert und dann nach freigestellt.
- Jede Ableitung von y(t) wird nach dem Signalflussplan der expliziten Darstellung numerisch durch die Differenzengleichung der Integration integriert. Die Differenzengleichung der numerischen Integration mit der Berechnungsfolge k(0, 1, 2 ...kMAX) und T = 1 (Euler-Streckenzugverfahren) lautet:
- Sämtliche Signaloperationen erfolgen algebraisch
- Anfangswerte können einfach für jeden Integrator (Energiespeicher) vorgegeben werden. Die Integrationen finden über Integrierglieder mit den gewünschten Anfangswerten statt. Die Integratoren starten zum Zeitpunkt t = k*Δt = 0 mit der Rekursionsfolge k = 0 und enden bei kMAX. Weil es sich damit um bestimmte Integrale handelt, müssen keine Integrationskonstanten wie bei der klassischen Lösung einer Differenzialgleichung ermittelt werden.
- Siehe Beispiel des Hauptkapitels „Numerische Berechnung dynamischer Systeme“ unter Anwendung numerischer Berechnungen.
→ Siehe "Berechnungsbeispiel gewöhnliche DGL 2. Ordnung mit Anfangswerten" Kapitel: Numerische Berechnung dynamischer Systeme
Kombinierte nichtlineare und lineare Systeme
[Bearbeiten]Die Zusammensetzung unterschiedlicher Teilsysteme mit einer Totzeit und differenzierendem, verzögerndem, begrenzendem und nichtlinearem Verhalten zu Steuerstrecken und Regelkreisen können nur numerisch berechnet werden.
- Lineare Systeme: Für die Beschreibung der linearen Systeme stehen Differenzengleichungen zur Verfügung.
- Nichtlineare Systeme können mit Werteangaben in tabellarischer Form benutzt werden.
- Begrenzungseffekte erfordern logische zeitunabhängige Gleichungen. (WENN-, DANN-, SONST-Anweisungen)
- Totzeitsysteme können durch programmierte Laufzeit-Schleifenbildung beliebiger Rechenprogramme nachgebildet werden bzw. bei Anwendung der Tabellenkalkulation durch die INDEX-Anweisung:
- Die Anweisung „INDEX ( Bezug: Spalte; Bereich)“ verwendet einen Index, um aus einem Bezug einen Wert zu wählen.
- Tabellarische Darstellung der Zwischen- und Endergebnisse. Zum Verständnis des Systemverhaltens und insbesondere des inneren System-Bewegungsablaufs bei Mit- und Rückkopplungen sollten alle Teil- und Endergebnisse numerischer Berechnungen tabellarisch pro Berechnungsfolge k=(0, 1, 2, ...kMAX) pro Zeile abgelegt werden. Die Programmiersprache numerischer Berechnungen ist beliebig. Es empfiehlt sich die Anwendung der Tabellenkalkulation, weil keine Formatierungsaufgaben erforderlich sind und die grafische Darstellung beliebiger Ergebnisse bereits mitgeliefert wird.
Modell-Bestimmung durch Approximation an die Sprungantwort eines Systems höherer Ordnung
[Bearbeiten]Das bekannteste Verfahren der Identifikation eines dynamischen Systems mit globalen P-Verhalten aus der Sprungantwort ist das Wendetangentenverfahren. Es ist kein Modell im Sinne der Systemtheorie, bei dem sich das Modell ähnlich wie das modellierte Originalsystem verhält, sondern es handelt sich um empirisch gefundene Werte, aus denen sich Parameter für die Anwendung von Standardreglern für Regelkreise geringer Ansprüche bilden lassen.

Wendetangentenverfahren:
[Bearbeiten]Industrielle Regelstrecken höherer Ordnung mit globalen P-Verhalten mit oder ohne Totzeit lassen sich nach einer messtechnischen Aufzeichnung der System-Sprungantwort durch eine grafisch an den Gradienten des Signalanstiegs im Wendepunkt angelegte Tangente für eine Auslegung von Standardregelkreisen identifizieren. Die Abszisse mit dem Zeitmaßstab wird durch die Tangente in die Zeitabschnitte der Verzugszeit TU und Anstiegszeit Tg zerlegt.
Die genaue Lage des Wendepunktes der Sprungantwort kann – falls erforderlich – durch einfaches Differenzieren dy / dt oder manuell Δy / Δt ermittelt werden.
Die stationäre P-Verstärkung Kp des Systems ergibt sich nach genügend langer Zeit aus dem Ausgangs-Eingangssignalverhältnis y(t) / u(t).
Das Wendetangentenverfahren liefert Kennwerte einer System-Sprungantwort, anhand derer Einstellwerte für regelungstechnische Anwendungen aus einer Tabelle entnommen werden können.
→ Siehe auch Wikipedia-Artikel: Faustformelverfahren (Automatisierungstechnik)
Synthetische Modell-Bestimmung nach der System-Sprungantwort
[Bearbeiten]Für ein bestehendes dynamisches Übertragungssystem höherer Ordnung handelt es sich in den meisten Fällen um ein System mit globalen P-Verhalten (Regelstrecke mit Ausgleich) oder globalen I-Verhalten mit und ohne Totzeit. Aus der Sprungantwort eines dynamischen Systems mit P-Verhalten kann nicht so einfach die Systemordnung und ein mögliches Totzeitverhalten erkannt werden. Deshalb bietet sich für ein derartiges System ein Modell an, das aus der Reihenschaltung eines Totzeitgliedes und eines Verzögerungsgliedes zu wählender Ordnung besteht.
Je nach Ergebnis des Verhaltens der Sprungantwort eines linearen Systems höherer Ordnung mit und ohne Totzeit folgt die synthetische Zusammensetzung eines Modells aus einfachen Komponenten wie die Reihenschaltung von einem Totzeitglied und Verzögerungsgliedern und gegebenenfalls die eines I-Gliedes, deren mathematische Schreibweisen bekannt sind.
Das Ziel für die Auslegung des Modells ist, das möglichst identische Zeitverhalten bei der Sprungantwort oder der Impulsantwort mit dem Original zu erreichen. Mit der numerischen Berechnung und grafischen Darstellung können die zu optimierenden Parameter des Modells in weiten Grenzen verändert werden, bis die Sprungantworten des Originals mit dem Modell übereinstimmen.
- Vorgehensweise
- Die Sprungantwort des Originals mit globalen P-Verhalten (Regelstrecke mit Ausgleich) ist bekannt.
- Als Modell wird die Reihenschaltung eines Ersatz-Totzeitgliedes (Ersatztotzeit Tte) mit einem Verzögerungsglied n-ter Ordnung (Ersatz-Zeitkonstante Te) wie folgt gewählt:
- Durch die vorzugsweise numerische Berechnung wird der Verlauf des Verzögerungsgliedes mit dem Parameter Te dem Verlauf des Gradienten der Originalfunktion in Übereinstimmung gebracht. Die Ordnung n des Verzögerungsgliedes kann beliebig sein. Es empfiehlt sich die Ordnung 1 oder 2. Die Ordnung 2 erlaubt eine leichtere Anpassung des Modell-Verzögerungsgliedes an das Original.
- Durch zeitliche Verschiebung der Verzögerungsfunktion bis zur Deckung mit der Originalfunktion wird die Ersatztotzeit Tte bestimmt.
Die Übergangsfunktion (Sprungantwort) eines Modells niedriger Ordnung für ein lineares System höherer Ordnung kann natürlich nicht mit dem Original identisch sein. Es stellt sich die Frage, wie exakt die Sprungantwort des Modells mit dem Original übereinstimmen muss, damit der Modellfehler gering bleibt?

Das Modell wird genauer, wenn der Anstiegsgradient des Verzögerungsgliedes grafisch zeitlich über die Lage des Wendepunktes des Anstiegsgradienten des Originals zu größeren Werten verschoben wird und damit drei kleine Flächen mit dem Original einschließt.
PT1-Tte-Modell eines Systems höherer Ordnung aus der Sprungantwort
[Bearbeiten]In dem dargestellten grafischem Beispiel der Sprungantwort eines dynamischen Systems 5. Ordnung gleicher Zeitkonstanten mit dem PT1-Tte-Modell wurde numerisch berechnet und mit dem im nächsten Kapitel angegebenen Verfahren auf gute Annäherung geprüft. Es handelt sich um ein relativ genaues und geprüftes PT1-Tte-Modell, das sich auch in einem Regelkreis – in bestimmten Grenzen – wie das Original verhält.
- Andere PT1-Tte-Modellierungsverfahren
In der Fachliteratur werden auch Methoden für die Bestimmung der Größe der Ersatzzeitkonstanten Te beschrieben, in dem durch die zwei Schnittpunkte des Modells mit dem Original Y1(t1), Y2(t2) geometrisch die Ersatz-Verzögerungszeitkonstante Te berechnet wird. [1]
Die Berechnung setzt voraus, dass eine Annahme getroffen wird, wie der Verlauf des PT1-Gliedes um die Ersatztotzeit Tte versetzt erfolgen muss, damit die Schnittpunkte zwischen Original und Modell entstehen können.
Ersatz-Zeitkonstante Te:
Ersatztotzeit Tte
Andere empirische Verfahren der Bestimmung eines PT1Tte--Modells beziehen sich direkt auf das Zeitverhalten der Sprungantwort eines PT1-Gliedes:
PT1-Modell:
- PT1-Tte-Modell
Für die angegebenen Gleichungen werden für die Parameter Te und Tte so oft unterschiedliche Werte eingesetzt, bis die Sprungantworten des Modells mit der des Originals ungefähr übereinstimmen.
Fazit: Es gibt keine vernünftige Alternative zur genauen Modellbestimmung als die numerische Berechnung.

PT2-Tte-Modell eines Systems höherer Ordnung aus der Sprungantwort
[Bearbeiten]Verzögerungen 1. Ordnung haben keinen Wendepunkt, weil das zeitliche Verhalten der Sprungantwort sich kontinuierlich mit abnehmender Geschwindigkeit der Asymptote nähert. Die Sprungantwort einer PT2-Verzögerung hat im Bereich des Wendepunktes einen annähernd linearen Bereich konstanter Signal-Geschwindigkeit, bei der sich das grafische Anlegen einer Tangente vereinfacht.
Der Verlauf des PT2-Gliedes mit zwei gleichen Zeitkonstanten Te wird dem Verlauf des Originals im Bereich beider Wendepunkte durch die Ersatzzeitkonstante Te und durch die Ersatztotzeit Tte so angeglichen, dass im Bereich der Wendepunkte das PT2-Tte-Modell zeitlich mit dem Original zwei Schnittpunkte und damit drei kleine Flächen bildet, also Tte >> Tu ist.
Das grafische Bild zeigt das optimierte PT2-Tte-Modells zur Sprungantwort eines dynamischen Systems 5. Ordnung mit gleichen Zeitkonstanten und globalen P-Verhalten. Das Modell und das Original zeigen in je einem Regelkreis mit gleichem PI-Regler weitgehend identische Eigenschaften. Selbst bei Einsatz in je einem Regelkreis mit einem PID-Regler bei einer gewählten Dämpfung mit einer Überschwingweite von ca. 5 % verhält sich das Modell sehr ähnlich gegenüber dem Original. Das ist insofern erstaunlich, weil die zwei in der Reihenstruktur zerlegbaren PD-Anteile des PID-Reglers bei Pole-Nullstellen-Kompensation der Regler-Auslegung mit der Original-Regelstrecke bei dem Modell den Einfluss der Pole reduzieren und damit eine Modell-Regelstrecke mit dominanter Totzeit hervorrufen.
PT2-Tte-Tt-Modell eines Systems höherer Ordnung mit Totzeit
[Bearbeiten]Modell für Systeme mit Totzeit Tt:
An dem Modell hat sich gegenüber dem mit echter Totzeit Tt behafteten Original nur die Totzeitsumme Tt+Tte geändert. Alle übrigen Beziehungen gelten wie für das PT2-Tte-Modell.
Weil in einer Sprungantwort eines realen Übertragungssystems höherer Ordnung der Anteil der echten Totzeit Tt nicht erkennbar ist, gilt das bewährte Modell mit einer Verzögerung 2. Ordnung und Ersatztotzeit Tte sowohl für Übertragungssysteme mit und ohne Totzeit Tt:

Prüfung des Modellverfahrens in einem Regelkreis mit einem I-Regler
[Bearbeiten]Das Verfahren der Erstellung eines Modells kann überprüft werden, indem man durch Abschätzung der Sprungantwort des unbekannten Übertragungssystems ein nicht genaues, aufwendiges, bekanntes, virtuelles Original mit Totzeit und Verzögerung höherer Ordnung bestimmt. Werden das virtuelle Original und das Modell des virtuellen Originals in je einen Regelkreis mit einem I-Regler gleicher Regelparameter eingebunden, dann muss bei einem guten Modell eine weitgehende Übereinstimmung in den Sprungantworten der Regelgrößen erzielt werden.
Die Verstärkung Kp des I-Reglers sollte so groß gewählt werden, dass die Kreisdämpfung mit der Regelstrecke des Originals sehr gering ist und die Regelgröße sehr stark überschwingt. Damit machen sich Modellfehler stärker bemerkbar.
Beispiel der Prüfung der Modell-Güte
[Bearbeiten]- Virtuelles Original 5. Ordnung mit bekannten Parametern ohne Totzeit:
- Gewähltes Modell des virtuellen Originals mit einer Verzögerung 2. Ordnung und Ersatztotzeit Tte:
- Anmerkung: Die Approximation eines Modells an das Original höherer Ordnung mit gleichen Zeitkonstanten ist schwieriger als die Anpassung an ein Original mit unterschiedlichen Zeitkonstanten der gleichen Ordnung!

- Vorzugsweise werden die Sprungantworten des virtuellen Originals und des Modells mittels numerischer Berechnungen an einem PC durchgeführt.
- Die Sprungantwort des virtuellen Originals wird für die gewählte Zeitkonstante T grafisch am Bildschirm abgebildet.
- Der Gradient der Sprungantwort des Modells wird durch empirische Wahl der Zeitkonstante Te dem Gradienten des virtuellen Originals in Übereinstimmung gebracht.
- Die Ersatztotzeit Tte des Modells wird im Diagramm wird durch zeitliche Verschiebung der Verzögerungsfunktion zur Deckung mit der Sprungantwort des virtuellen Originals bestimmt. Der Feinabgleich für Te und Tte zur korrekten Deckung der beiden Sprungantworten ist noch jederzeit möglich.
Die bevorzugte vereinfachte Modellstruktur des Modells und das virtuelle Original können durch Einbindung in je einem Regelkreis mit einem I-Regler und einer eingestellten Kreisdämpfung D < 0,1 (d.h. große Überschwingung der Regelgröße) mit gleichen Reglerparametern geprüft werden. Sind für beide Modell-Regelkreise die An- und Ausregelzeiten und die Überschwingweiten der Regelgrößen näherungsweise identisch, handelt es sich um ein gutes Modell.
Modelle für Systeme mit verteilten Energiespeichern
[Bearbeiten]Systemspeicher im dynamischen System
[Bearbeiten]Physikalisch betrachtet ist der Zustand eines dynamischen Systems durch den Energiegehalt der im System vorhandenen Energiespeicher zu einem beliebigen Zeitpunkt bestimmt. Das zeitliche Verhalten der Systemausgangsgröße y(t) eines Übertragungssystems zu einem beliebigen Zeitpunkt t = t0 ist abhängig vom Energiegehalt der Systemspeicher (Anfangswerte), von den Systemparametern und der Systemeingangsgröße
u(t). Die Vorgeschichte des Systems für y(t) zur Zeit t < 0 hat keine Bedeutung für die betrachtete Zeit t > 0.
Lineare zeitinvariante dynamische Systeme mit konzentrierten Speichern (ohne räumliche Ausdehnung!) werden durch gewöhnliche Differenzialgleichungen y =f(t) mit konstanten Koeffizienten beschrieben. Konstante Koeffizienten bedeuten, dass sich das Zeitverhalten des Systems nicht ändert. Diese Systeme können auch in einer speziellen Darstellung der Differenzialgleichung im Zustandsraum y = f(t) oder durch Transformation der Differenzialgleichung zu Übertragungsfunktionen G = f(s) beschrieben werden. Übertragungsfunktionen behandeln keine Anfangswerte, das System mit f(s) ist für den Ruhezustand definiert.
Systeme mit verteilten Energiespeichern
[Bearbeiten]Dynamische Systeme mit räumlicher Verteilung der Systemspeicher enthalten verteilte Systemparameter. Beispiel: Wärmefluss in einem homogenen Medium, Spannungsabfall in elektrischen Übertragungsleitungen. Bei diesen Systemen sind die Variablen nicht nur Funktionen der Zeit, sondern auch von Ortskoordinaten abhängig. Als Beschreibung eines derartigen Systems gilt allgemein die partielle Differenzialgleichung, bei der die gesuchte Funktion von zwei Variablen abhängt, vom Ort und von der Zeit.
Problematisch ist beispielsweise die zeitabhängige Beschreibung des Wärmeflusses in verschiedenen Medien wie bei Gasen, Flüssigkeiten, Feststoffen und Metallen. Bei einer gewöhnlichen Heizungsregelung handelt es sich bei der Regelstrecke um ein System mit verteilten Energiespeichern in Flüssigkeiten oder Feststoffen.
Kompliziert oder beinahe unmöglich ist die geforderte Systemabgrenzung der in der Praxis bei ausgeführten Übertragungssystemen verschiedenster geometrischer Formen von der Umgebung. Trifft eine bekannte Strahlungsenergie auf ein System, bei dem die Masse, Oberfläche, Homogenität, Wärmewiderstand, Wärmeableitungen unbekannt sind, so kann nur ein messtechnischer Versuch das zeitliche Verhalten der Temperatur an einem bestimmten Ort des Systems zu bestimmten Umgebungsbedingungen klären.
Vereinfachtes Ersatzmodell für Systeme mit verteilten Energiespeichern
[Bearbeiten]Betrachtet man den Temperaturverlauf in einem homogenen Medium an verschiedenen weit entfernten Messorten von der Wärmequelle nach einem positiven Wärme-Energiesprung, so erreicht der am weitesten entfernte Messort am spätesten das Temperatur-Maximum. Nach genügend langer Zeit ist der stationäre Zustand am Messort erreicht, wenn der Wärmezufluss gleich dem Wärmeabfluss ist. Im stationären Zustand beliebiger Messorte sind die Temperaturwerte nach einem Temperatursprung mit steigender Entfernung vom Systemeingang immer kleiner. Die Ursache liegt darin, dass das Medium ein mehr oder weniger guter Wärmeleiter ist, von dem je nach äußeren Abmessungen die Wärmeenergie durch Konvektion, Strahlung oder Ableitung mit anderen Materialien abfließt.

Ein elektrisches Modell zum Verständnis dieses Verhaltens ist eine Kombination von gleichen RC-Gliedern (Widerstand-Kondensator-Schaltung T = R * C) mit gleichen Zeitkonstanten T. Die Übergangsfunktion (Sprungantwort) eines derartigen Systems mit einer Kette von z. B. vier RC-Gliedern ohne Abschlussglied in Reihenschaltung lautet:
Durch die Nullstellen-Bestimmung und Umrechnung der Pole in Zeitkonstanten wird ersichtlich, dass die Sprungantwort mit zunehmender Ordnung durch eine kleine Totzeit und eine dominante Zeitkonstante (Verzögerungsglied 1. Ordnung) bestimmt wird. Erst wenn dieses RC-Glieder-Modell einen Widerstands-Abschluss erhält, wird mit der zunehmenden Entfernung von der Einspeisung verständlich, dass im stationären Zustand die Spannungsabfälle ortsabhängig sind und die Spannungen an den Kondensatoren kleiner werden.
Das dargestellte grafische Bild zeigt das Temperaturverhalten einer auf einer Sandsteinplatte aufgestrahlte Wärmeenergie an zwei Messorten. Das Zeitverhalten des Wärmeflusses an beiden Messpunkten entspricht annähernd dem Verhalten eines PT1-Gliedes mit einer dominanten Zeitkonstante und der Reihenschaltung eines sehr kleinen Ersatz-Totzeitgliedes.
Das System weist unterschiedliche Ersatz-Zeitkonstanten TE für den Anstieg und Abfall des Wärmeflusses auf und verhält sich damit auch zeitvariant. Dies erklärt sich durch die Wärmeflussdifferenz der beiden Oberflächen der Platte links und rechts. Beim Ansprung ist das System im Ruhezustand. Beim Rücksprung (Strahlungsquelle = 0 W) hat das System am Messpunkt 1 höhere Anfangswerte. Ein bestimmter Teil der gespeicherten Wärmeenergie um den Messpunkt 1 fließt nach Messpunkt 2, was sich als vergrößerte Zeitkonstante bemerkbar macht.
In der praktischen Anwendung wird ein aufzuheizendes Medium eine festzulegende Wärme-Isolation aufweisen. In diesem Falle wird für das genannte Experiment eine gewählte Endtemperatur als Ausschnitt einer e-Funktion früher erreicht. Beim Energierücksprung ist die Temperatur-Differenz der beiden Messpunkte wegen verminderter Verluste geringer, und die Unterschiede der beiden Zeitkonstanten für Temperatur-Aufbau und -Abbau werden wegen der Isolation größer.
Das mathematische Modell für den Wärmefluss in einem homogenen Medium lässt sich nach der Aufzeichnung der Sprungantwort durch ein einfaches Modell mit einem PT1-Glied und einem Totzeitglied annähern. Die Parameter der Ersatztotzeit TtE und der Ersatzzeitkonstanten TE sind anhand des Messprotokolls zu bestimmen.
Heuristische Methoden der Modellbeschreibungen
[Bearbeiten]Ziegler-Nichols (Veröffentlichung: 1942):
[Bearbeiten]- Ziegler und Nichols haben zwei heuristische Verfahren entwickelt:
- Verfahren 1 bezieht sich auf eine unbekannte Regelstrecke und einen unbekannten Regler mit P-, I-, D-Verhalten. Ohne Kenntnis der Strecken- und Reglerparameter werden manuell zunächst in dieser Reihenfolge die P-Verstärkung und danach auch die I- und D-Anteile bis jeweils an die Stabilitätsgrenze des Regelkreises eingestellt. Alle auf diese Weise ermittelten Parameter der Stabilitätsgrenze werden dann halbiert.
- Verfahren 2: Für die aus dem Wendetangentenverfahren ermittelten Streckenparameter werden tabellarisch Reglerparameter für P-, PI, PD- und PID-Regler angegeben.
- Chien, Hrones und Reswick (1952) haben später überarbeitete empfohlene Parameter-Einstellungen für die Standard-Regler in verschiedenen Varianten festgelegt.
T-Summen-Regel mit einer Ersatz-Summen-Zeitkonstante (nach Udo Kuhn 1995)
[Bearbeiten]- Wenn die Übertragungsfunktion der Strecke vorliegt:
- Summe über alle n Verzögerungszeitkonstanten minus Summe aller m Nullstellenzeitkonstanten plus Totzeit.
- Damit lautet die Übertragungsfunktion des Modells mit Kp als statische Verstärkung:
- Wenn die Sprungantwort vorliegt:
- Bei der T-Summen-Regel zur Identifikation einer PTn-Regelstrecke (ohne Totzeit) eignet sich für lineare Systeme höherer Ordnung ähnlicher Zeitkonstanten. Das Verfahren teilt mit einer senkrechten Linie die Anstiegsfunktion der Sprungantwort in zwei gleiche Flächen. Der Wert der so getroffenen Zeitachse entspricht der Summenzeitkonstante .
Zeit-Prozent-Verfahren für nicht schwingende Übertragungssysteme
[Bearbeiten](Veröffentlichungen: G. Schwarze 1962 und Wolfgang Latzel: Einstellregeln 1993)
- Aus der positiven normierten Sprungantwort (Sprungeingang u(t) = 1) werden aus dem Verlauf der Ausgangsgröße y(t) die Werte y(t) = 10 %, 50 % und 90 % des Maximalwertes yMAX(t) die zugehörigen Zeitwerte T10, T50 und T90 erfasst und daraus eine Modell-Übertragungsfunktion aus n gleichen Verzögerungsgliedern gebildet. Es wird eine Tabelle benötigt, die in jedem guten Fachbuch der Regelungstechnik zu entnehmen ist. Die Tabelle gibt die Systemordnung und benötigten Faktoren nach folgender Gleichung für die Ersatzzeitkonstante TM an:
- Bestimmung der Ersatzzeitkonstanten TM:
- Bestimmung des Modells mit Kp als statische Verstärkung:
- Anmerkung: Dieses Verfahren ergibt eine erstaunlich gute Anpassung des Modells an ein lineares Übertragungssystem ohne Totzeit.
- Die Tabellen dieses Verfahrens sind in jedem guten Fachbuch der Regelungstechnik enthalten, z. B.:
- Gerd Schulz: "Regelungstechnik 1" Verlag Oldenbourg, 3. Auflage 2004
- Manfred Reuter - Serge Zacher: "Regelungstechnik für Ingenieure" Verlag Vieweg, 11. Auflage 2003
→ Siehe auch Wikipedia-Artikel: Faustformelverfahren (Automatisierungstechnik)
Einzelnachweise
[Bearbeiten]- ↑ Jan Lunze: Regelungstechnik 1: Systemtheoretische Grundlagen. 7 Auflage. Springer, 2008, ISBN 3540689079. Kapitel: Kennwertermittlung für PT1Tt-Glieder.
Gewöhnliche Differenzialgleichungen
[Bearbeiten]Gewöhnliche Differenzialgleichungen
[Bearbeiten]Eine Differenzialgleichung (kurz DGL) ist eine Gleichung, die eine oder mehrere Ableitungen einer unbekannten Funktion enthält.[1]
Kommen Ableitungen nur bezüglich einer Variablen vor, spricht man von „gewöhnlichen Differenzialgleichungen“, wobei der Begriff „gewöhnlich“ sich darauf bezieht, dass die betrachtete Funktionen nur von einer Veränderlichen abhängt.
Mit den gewöhnlichen DGL-en lassen sich viele dynamische Systeme aus der Technik, Natur und Gesellschaft beschreiben. Viele auf den ersten Blick sehr verschiedene physikalische Probleme lassen sich mit der DGL jedoch formal identisch darstellen.
Gleichungen, deren Lösungen Funktionen mehrerer Variablen sind und die partielle Ableitungen dieser Funktionen enthalten, sind „partielle Differenzialgleichungen“.
Eine lineare DGL enthält die gesuchte Funktion und deren Ableitungen nur in der ersten Potenz. Es dürfen keine Produkte der gesuchten Funktion und ihren Ableitungen auftreten. Die gesuchte Funktion darf auch nicht in Argumenten von Winkelfunktionen, Logarithmen usw. erscheinen.
Nichtlineare Differenzialgleichungen sind nur in sehr seltenen Ausnahmefällen analytisch lösbar. Sie können mittels der numerischen zeitdiskreten Methoden gelöst werden
Ein dynamisches System kann durch das Aufstellen von Differenzialgleichungen modelliert werden. Dazu werden für sämtliche Energiespeicher des Systems die zugehörigen Bilanzgleichungen benötigt, die durch eine Differenzialgleichung 1. Ordnung beschrieben werden. Für jeden konzentrierten Energiespeicher entsteht eine Differenzialgleichung erster Ordnung. Das Ergebnis ist eine lineare zeitinvariante gewöhnliche DGL mit konstanten Koeffizienten.
Nach der Systemtheorie wird ein lineares dynamisches System g(t) durch einen oder mehrere Eingänge u(t) und einen oder mehrere Ausgänge y(t) beschrieben. Lineare Systeme mit mehreren Ein- und Ausgängen werden durch ein System von Differenzialgleichungen beschrieben.
Grundlagen der Differenzialgleichung
[Bearbeiten]- Notation zur Darstellung der Ableitungen[2]
In der Differenzialrechnung gibt es keine einheitliche Notation für Differenziale!
- Die formal korrekte Darstellung einer Ableitung einer Funktion f(x) lautet:
- oder
- (Leibnizsche Notation)
- Die gleiche Funktion in Kurzform: . (Lagrangesche Notation)
- Die 2. Ableitung dieser Funktion lautet:
- Bei höheren Ableitungen ist diese Kurzform nicht geeignet, stattdessen wird n = Zahl der Ableitungen in Klammern angegeben:
- Bei physikalischen Prozessen wird häufig nach der Zeit abgeleitet und dies bei der Kurzform durch Punkte gekennzeichnet.
- Beispiel: Geschwindigkeit v = Weg Δs / Zeit Δt.
- Bestimmung der Geschwindigkeit:
- Bestimmung der Geschwindigkeit in Kurzform: . (Newton'sche Notation)
- Bestimmung der Beschleunigung a als 2. Ableitung des Weges s:
- Allgemeine Definition
Eine Differenzialgleichung ist eine Gleichung, in der eine Funktion y(x) und deren Ableitungen auftreten. Gesucht ist die Funktion.
Beispiele für Formen gewöhnlicher DGL:
Eine gewöhnliche Differenzialgleichung erster Ordnung ist eine DGL, die nur die Ableitung erster Ordnung der gesuchten Funktion enthält, nicht jedoch höhere Ableitungen. Außerdem kann die DGL erster Ordnung noch die Funktion selbst, einen konstanten Term oder die unabhängige Variable enthalten.
Eine DGL erster Ordnung ist linear, wenn sie in folgender Form darstellbar ist.
Die Funktion g(t) wird als Störfunktion oder Störglied bezeichnet. Fehlt das Störglied, so handelt es sich um eine homogene lineare Differenzialgleichung erster Ordnung. Ist g(t) von Null verschieden, so wird die DGL als inhomogen bezeichnet. Der Zusatzterm g(t) ist die Inhomogenität.
- Mathematische Definition der Differenzialgleichung mit der Systemausgangsgröße y(t) als Variable
Eine gewöhnliche Differenzialgleichung (DGL) ist eine Bestimmungsgleichung für eine Funktion einer Variablen. Die Ordnung der DGL ist bestimmt durch die höchste auftretende Ableitung:
Eine Gleichung, in der gewöhnliche Ableitungen einer unbekannten Funktion y(t) bis zur n-ten Ordnung auftreten, wird als gewöhnliche DGL n-ter Ordnung bezeichnet. Eine gewöhnliche DGL n-ter Ordnung enthält als höchste Ableitung die n-te Ableitung y(n)(t) der unbekannten Funktion y(t). Sie kann auch Ableitungen niedrigerer Ordnung sowie die Funktion y(t) und deren unabhängige Variable t enthalten.
Eine DGL erster Ordnung heißt linear, wenn sie in der Form je nach Art der Variable wie folgt darstellbar ist:
Die DGL können in impliziter oder expliziter Form dargestellt werden.
In der impliziten Form lässt sich eine DGL n-ter Ordnung wie folgt beschreiben:
Ist die implizit dargestellte DGL nach der höchsten Ableitung y(n) auflösbar, so ergibt sich die explizite Form:
- Lösung einer Differenzialgleichung durch Separation der Variablen
Eines der bekanntesten Verfahren zum expliziten Lösen der DGL ist das Lösen durch Trennung der Variablen. Für die homogene DGL erster Ordnung ist das Standardlösungsverfahren die Trennung bzw. Separation der Variablen. Dabei wird die DGL auf eine Form gebracht, bei der die Variablen x und y nur noch in voneinander getrennten Termen auftreten. Die entstehende Gleichung kann dann sofort integriert werden.
Dazu werden alle Terme mit y auf die eine Seite der Gleichung gebracht, alle Terme mit x auf die andere.
- Beispiel der Lösung einer linearen DGL 1. Ordnung
Differenzialgleichung Rechenschritte Aufgabenstellung: Lösung der DGL nach dem Separationsverfahren. Die Gleichung wurde durch y2 dividiert und mit dx multipliziert. Beide Seiten der DGL wurden integriert. Lösung des Integrals. C1 auf beiden Seiten subtrahiert und C = C2 - C1 eingesetzt. Gleichung wurde nach y aufgelöst mit .
(C ist ein Element der reellen Zahlen)
Entstehung einer Differenzialgleichung
[Bearbeiten]Eine DGL ist eine Bestimmungsgleichung für eine unbekannte Funktion. Die Lösung einer DGL ist keine Zahl, sondern eine Funktion!
- Beispiel elektrischer Schwingkreis
Spannungsbilanz: Nach dem 2. Kirchhoffschen Satz ist Summe aller Spannungen einer Masche gleich Null.
Der Spannungsabfall am Widerstand R ergibt sich zu UR = i * R. Nach dem Induktionsgesetz ist die Spannung an der Induktivität UL = L * di / dt. Der Ladestrom am Kondensator ist proportional der Spannungsänderung am Kondensator i(t) = C * dy / dt.

Die Anwendung des Maschensatzes führt zunächst zu einer Differenzialgleichung 1. Ordnung:
Setzt man in die DGL für i(t):
ein, dann ergibt sich die Schwingungsgleichung:
Es können Zeitkonstanten wie T1 = R * C und T2² = L * C eingeführt werden. Ersetzt man auch die in der Systembeschreibung übliche Darstellung der Eingangsgröße u(t) und Ausgangsgröße y(t), dann lautet die bekannte DGL für einen Reihenschwingkreis:
oder in allgemeiner Darstellung:
Aus der Mechanik existiert das bekannte Beispiel einer linearen gewöhnlichen DGL eines schwingfähigen Systems mit der Federkraft c, Masse m und Dämpfung d. Eingangsgröße: Kraft F, Ausgangsgröße: Weg x
Es handelt sich hier in beiden Fällen um eine lineare gewöhnliche DGL 2. Ordnung mit konstanten Koeffizienten. Befinden sich beide Systeme in Ruhe, d. h. die Anfangswerte der Energiespeicher sind Null, dann ist der Verlauf einer Sprungantwort abhängig von der Größe der Koeffizienten a1 und a0, ob der Systemausgang y(t) aperiodisch oder gedämpft schwingend das Niveau des Eingangssprungs u(t) erreicht.
Derartige DGL-en können in eine allgemeine Form beliebiger Ordnung dargestellt werden für die in der Systembeschreibung üblichen Signalbezeichnungen der Ausgangsgröße y(t) und der Eingangsgröße u(t).
- Allgemeine Form einer DGL mit konstanten Koeffizienten ai der System-Ausgangsgröße und mit bi der System-Eingangsgröße
- Anmerkungen zur Form einer DGL aus der Sicht der Systemtheorie
- Die Koeffizienten der Terme der DGL enthalten die Parameter, aus denen die DGL entstanden ist. Es kann für die verschiedenen Lösungswege der DGL sinnvoll sein, den Koeffizienten der höchsten Ableitung an auf 1 zu beziehen, in dem sämtliche Terme durch an dividiert werden.
- Die Koeffizienten ai beziehen sich auf die Ableitungen der Ausgangsgröße y(t), deren Terme üblicherweise links des Gleichheitszeichens stehen.
- Die Koeffizienten bi beziehen sich auf die Ableitungen der Eingangsgröße u(t), deren Terme rechts des Gleichheitszeichens stehen.
- Die Ein- und Ausgangsgrößen y(t) und u(t) sind die Variablen der DGL.
- Der höchste Grad der Ableitung von gibt die Anzahl der Speicherelemente des Übertragungssystems wieder. Das Verhältnis der maximalen Ableitungen der Ausgangsgröße zur Eingangsgröße eines Übertragungssystems bezieht sich auf n ≥ m. In der Praxis sind nur Systeme n > m realisierbar.
Lösung gewöhnlicher linearer Differenzialgleichungen
[Bearbeiten]- Gesamtlösung einer inhomogenen DGL
- Ein lineares dynamisches Übertragungssystem mit dem Eingangssignal u(t) und dem Ausgangssignal y(t) wird durch eine gewöhnliche inhomogene DGL mit konstanten Koeffizienten beschrieben.
- Die Lösung einer inhomogenen DGL besteht aus der allgemeinen Lösung der homogenen DGL und einer speziellen Lösung (partikuläre Lösung) der inhomogenen DGL. Deshalb erfolgt das Lösungsverfahren der inhomogenen DGL unabhängig von der Ordnung in zwei Stufen. Die Gesamtlösung ist die Summe der beiden Lösungen:
- Die homogene Lösung der DGL beschreibt das Systemverhalten mit Anfangswerten der Systemspeicher zum Zeitpunkt t = 0 und dem Eingangssignal u(t) = 0. Die homogene Lösung der DGL ist 0, wenn alle Anfangsbedingungen von y(0) = 0 sind.
- Die partikuläre Lösung der DGL beschreibt das Übertragungsverhalten von y(t) für u(t) ≠ 0 als erzwungene Bewegung. Je nach Systemordnung müssen alle Anfangsbedingungen y(0) = 0 sein.
Ist die Übertragungsfunktion G(s) als Laplace-transformierte DGL gegeben, so ist die Berechnung des System-Ausgangssignals y(t) für ein gegebenes Eingangssignal Y(s) bei Anwendung der inversen Laplace-Transformation immer eine partikuläre Lösung.
Die partikuläre Lösung der DGL ist in der Regelungstechnik meist von hauptsächlichem Interesse.
- Die Gesamtlösung der inhomogenen DGL ist y(t) = yH(t) + yP(t)
- Integrationskonstante
- Die Lösung einer DGL erfolgt durch Integration. Die Integration ist keine eindeutige Rechenoperation, denn man erhält zu jeder Funktion f(x) verschiedene Stammfunktionen F(x) mit dem Begriff des unbestimmten Integrals.
- Bei der Integration wird zwischen dem bestimmten und dem unbestimmten Integral unterschieden. Die Stammfunktion F(x) ist Lösung des unbestimmten Integrals:
- Diese Lösung ist unbestimmt wegen der unbestimmten Integrationskonstante C.
- Jede Integration ergibt Integrationskonstanten, deren Anzahl durch die Ordnung der DGL bestimmt ist. Die Lösung einer DGL n-ter Ordnung enthält n voneinander unabhängige Integrationskonstanten. Diese sind für eine spezielle Lösung der DGL, abhängig von den Eigenwerten und gegebenen Anfangsbedingungen des Übertragungssystems, zu bestimmen.
- Anfangsbedingungen
- Als Übertragungsverhalten eines dynamischen Systems ist die Bewegung des Ausgangssignals y(t) dieses Systems in Abhängigkeit vom Eingangssignal u(t) bei verschwindenden Anfangsbedingungen definiert. Dieses Verhalten kennzeichnet die partikuläre Lösung der systembeschreibenden DGL.
- Die Anfangsbedingungen beschreiben einen speziellen Zustand des Übertragungssystems.
- Liegen Anfangswerte y(0), y'(0), …, y(n)(0) der Energiespeicher des Übertragungssystems vor, so wird der homogene Teil der DGL für das Eingangssignal u(t) = 0 gelöst.
- Die Lösung der homogenen DGL entspricht der freien Bewegung des Systems und ist abhängig von den Anfangswerten y(t = 0) = y(0) zum Zeitpunkt t = 0. Sind keine Anfangswerte gegeben, ist die homogene Lösung der DGL yH = 0.
- Lösungsschema der gewöhnlichen linearen DGL
- Die homogene (charakteristische) DGL beschreibt das Verhalten ohne Eingangsgröße (also für u(t) = 0), das sog. Eigenverhalten, d. h. das System bleibt, ausgehend von den Anfangswerten, sich selbst überlassen:
- Für diese DGL ist die homogene Lösung für yH(t) zu bestimmen.
- Mit Hilfe des Exponentialansatzes und der sich daraus ergebenden charakteristischen Gleichung lassen sich auch DGL höherer Ordnung lösen. Er gilt als universelles Lösungsverfahren für homogene DGL beliebiger Ordnungen mit konstanten Koeffizienten.
- Folgender Exponentialansatz für y(t) liefert Ableitungen der Form:
- Die Ableitungen des Lösungsansatzes ergeben sich zu:
- Werden diese Ableitungen in die oben stehende homogene DGL eingesetzt, entsteht die charakteristische Gleichung als Polynom n-ter Ordnung:
- Die homogene Lösung einer inhomogenen Differenzialgleichung lautet damit allgemein für den Fall reeller ungleicher Nullstellen λi:
- Anmerkung: Das Verfahren der Separation der Variablen auf lineare homogene DGL-gen ist auf DGL-gen 1. Ordnung beschränkt.
- Eigenwerte (Nullstellen)
- Unter der Nullstelle einer Funktion versteht man den Wert, der die Funktion zu Null macht. Zu unterscheiden sind reelle und konjugiert komplexe Nullstellen.
- Die Lösungen der Ableitungen des Exponentialansatzes für ein Beispiel 2. Ordnung lauten:
- Die Lösungen werden in die folgende homogene DGL 2. Ordnung eingesetzt:
- Damit entsteht die allgemeine Bestimmungsgleichung beliebiger Ordnung für die Eigenwerte von λi.
- Polynome mit λ zweiter Ordnung werden mit der Formel der gemischt-quadratische Gleichung gelöst. Für die Berechnung der Nullstellen von Polynomen höherer Ordnung sind gegebenenfalls aufwendige Rechenverfahren anzuwenden. Beispiele mit DGL-gen 2. Ordnung siehe nachfolgende Kapitel!
- Bestimmung der Integrationskonstanten
- Aus der charakteristischen DGL lassen sich bei gegebenen Koeffizienten mittels verschiedener Methoden die Nullstellen λi des Polynoms bestimmen.
- Die Berechnung der Integrationskonstanten Ci erfolgt durch Einsetzen der Anfangswerte von anstelle y(t) durch y(0)(t) und y'(0)(t) in die Gleichung der allgemeinen homogene Lösung mit dem Lösungsansatz
- Für ein Beispiel 2. Ordnung ergeben sich folgende zwei Gleichungen:
- Für yH(t) wird der Anfangswert von y(0)(t) eingesetzt und die Gleichung für t = 0 gerechnet. Damit verschwinden die exponentiellen Funktionen:
- In der zweiten Gleichung wird anstelle von yH(t) der Anfangswert der Ableitung y'(0)(t) eingesetzt. Danach folgen 2 mathematische Operationen:
- Die zwei Terme der Exponentialfunktionen werden einmal differenziert.
- Für die so behandelten zwei Terme wird t = 0 eingegeben, damit die Exponentialfunktionen verschwinden.
- Aus diesen zwei Gleichungen lassen sich die beiden Integrationskonstanten C1 und C2 algebraisch berechnen.
Homogene Lösung einer DGL 1. Ordnung
[Bearbeiten]Die DGL der Beschreibung einer elektrischen Beschaltung mit einem Widerstands R im Eingang und einem Kondensator C mit dem Eingangssignal u(t) und dem Ausgangssignal y(t) am Kondensator lautet: [3]
Diese Gleichung wird so umgeformt, dass der Koeffizient der Ableitung R * C = 1 ist, in dem sämtliche Terme der Gleichung durch R*C dividiert werden und die Koeffizienten neu geordnet werden. Damit verschwindet der Koeffizient der Ableitung und wird zu 1.
Die Normalform der inhomogenen DGL 1. Ordnung lautet:
- Lösung der DGL 1. Ordnung
Die Gesamtlösung der gewöhnlichen DGL ergibt sich aus der Überlagerung der Systemantworten für die Anfangsbedingung und dem Eingangssignal:
Für die homogene Lösung der DGL wird das Eingangssignal u(t) gleich 0 gesetzt. Die Ausgangsgröße y(t) beschreibt das Verhalten des Systems g(t) für einen Anfangswert y(0) des Systemspeichers zum Zeitpunkt t ≥ 0:
Die homogene Lösung der DGL mit einem Anfangswert y(0) z. B. = 1 = 100 % lautet:

Die partikuläre Lösung der DGL geschieht mit Hilfe des Faltungsintegrals. Das Faltungsintegral beschreibt die Beziehung des Eingangssignals zum Ausgangssignal des Übertragungssystems g(t) im Zeitbereich.
- = Faltungsoperator
Das Faltungsintegral der DGL 1. Ordnung lautet:
Die partikuläre Lösung der DGL für einen Einheitssprung 1 für t ≥ 0 als Eingangssignal u(t) lautet:
Es ergeben sich für den normierten Eingangssignal-Sprung 1(t) mit dem Koeffizienten a0 je drei Fälle des Verhaltens des Ausgangssignal y(t) der homogenen und partikulären Lösung der DGL:
Einfluss Koeffizient a0 Signalverlauf des Ausgangssignals Koeffizient a0 > 0 yH(t) klingt exponentiell von der Anfangsbedingung y(0) auf 0 ab
yP(t) nähert sich von 0 exponentiell dem Endwert b0 / a0Koeffizient a0 = 0 yH(t) verbleibt an dem Niveau der Anfangsbedingung y(0)
yP(t) steigt von 0 rampenförmig stetig anKoeffizient a0 < 0 yH(t) wächst exponentiell über die Anfangsbedingung y(0) hinaus über alle Grenzen
yP(t) wächst von 0 exponentiell über alle Grenzen
Homogene Lösung einer DGL 2. Ordnung
[Bearbeiten]Eine Differenzialgleichung zweiter Ordnung ist eine Erweiterung der DGL erster Ordnung, bei der eine zusätzliche 2. Ableitung der gesuchten Funktion auftritt. Die technische Realisierung entspricht, abhängig von den Koeffizienten ai, untereinander einem Übertragungssystem mit zwei in Reihe geschalteten Verzögerungsgliedern 1. Ordnung (2 PT1-Glieder) mit reellen Polen oder einem Schwingungsglied mit konjugiert komplexen Polen und einer Dämpfung 1 > D > 0.
Eine DGL einer elektrischen Schaltung folgender Art ist gegeben:
Diese Gleichung wird so umgeformt, dass der Koeffizient der höchsten Ableitung a2 = 1 ist, indem sämtliche Terme der Gleichung durch a2 dividiert werden und die Koeffizienten neu geordnet werden. Damit verschwindet a2.
Die homogene Lösung der DGL 2. Ordnung lautet:
Die Ableitungen des Exponentialansatz werden in die homogene DGL eingesetzt
Diese charakteristische Gleichung ist für beliebige y erfüllt, wenn das charakteristische Polynom verschwindet.
Die Ermittlung der Eigenwerte (Nullstellen) erfolgt mit der bekannten Lösung der gemischt quadratischen Gleichung:
Anfangswertproblem der Integrationskonstanten Cn
[Bearbeiten]Eine homogene DGL n-ter Ordnung hat mindestens einen Anfangswert bis n Anfangswerte. Für die homogene DGL zweiter Ordnung mit zwei vorzugebenden Anfangswerten y0 > 0 und y'0 > 0 können die Integrationskonstanten C1 und C2 errechnet werden, wenn die Wurzeln der homogen DGL bekannt sind.
Die Integrationskonstanten C1 und C2 errechnen sich durch Vorgabe von Anfangswerten y0 und y'0, die anstelle von yH(t) der Lösungsgleichung der homogenen DGL 2. Ordnung eingesetzt werden. Damit ergeben sich zwei Gleichungen für die zwei Anfangswerte. Für yH = y0 wird die erste Gleichung für t = 0 bestimmt. Für die zweite Gleichung mit yH = y'0 wird erst die Ableitung der Gleichung und dann die Gleichung für t = 0 errechnet.
Beispiel für eine homogene DGL mit zwei reellen Wurzeln λ1 = -0,5 und λ2 = -1 und Anfangswerten der Energiespeicher y'0(t) = 1; y0(t) = 1:
Lösung der homogenen DGL 2. Ordnung:
Berechnung der Integrationskonstanten:
Aus den beiden Gleichungen von y0(t=0) und y'0(t=0) lassen sich die Integrationskonstanten C1 und C2 bestimmen.
Anmerkung: Die Ableitung d / dt von
Tabelle: Durch die verschiedenen Arten der Lösungen der Wurzel, bedingt durch die Größe des Radikanden, ergeben sich drei unterschiedliche Fälle der Eigenwerte λ der DGL wie:
Lösung der homogenen linearen Differenzialgleichung
2. Ordnung mit konstanten KoeffizientenWurzeln (Nullstellen) Anfangswertproblem
Bestimmung C1, C2Der Radikand > 0 hat 2 reelle Wurzeln
Der Radikand = 0 hat 2 gleiche Wurzeln
Der Radikand < 0 führt zu konjugiert komplexen Wurzeln
Berechnungsbeispiel der Lösung einer homogenen DGL 2. Ordnung mit reellen Nullstellen
[Bearbeiten]
- Übertragungsfunktion
- Zugehörige systembeschreibende DGL
- Vorgegeben: Anfangswerte der Energiespeicher (Integratoren): y'0(t) = 1; y0(t) = 1;
- Vorgegeben: Eingangsgröße u(t) ist eine normierte Sprungfunktion 1 für t > 0.
- Für die homogene Lösung wird u(t) = 0 gesetzt.
- Errechnet: Es ergeben sich zwei reelle Wurzeln:
- Errechnet: Die Integrationskonstanten errechnen sich laut Tabelle mit C1 = -1; C2 = 2
- Analytische homogene Lösung laut Tabelle für zwei reelle Wurzeln:
- Mit den eingesetzten Zahlenwerten lautet die analytische Lösung der homogenen DGL wie folgt:
Berechnungsbeispiel der partikulären Lösung einer DGL 2. Ordnung mit der Laplace-Transformationstabelle
[Bearbeiten]- Vorgegeben:
- Eingangssignal: Sprungfunktion U(s) = 1 / s
- Übertragungsfunktion des Systems:
- Gesucht: Partikuläre Lösung yP(t) für die gegebene Übertragungsfunktion:
- Suchbegriff für die Laplace-Transformationstabelle:
- Errechnet:
- Die gefundene analytische Gleichung f(t) der partikulären Lösung laut Transformationstabelle durch Eingabe der Koeffizienten lautet:
Allgemeine Lösung der DGL 2. Ordnung mit Hilfe der Laplace-Transformation
[Bearbeiten]Die partikuläre Lösung beschreibt das Übertragungsverhalten des Systems als Funktion des Eingangssignals u(t) und ist meist von hauptsächlichem Interesse. Die Anfangsbedingungen y(0) und y'(0) haben dabei den Wert 0.[4]
Die bereits durchgeführte partikuläre Lösung der DGL 1. Ordnung erfolgte über das Faltungsintegral. Die Berechnung des Faltungsintegrals ist jedoch aufwendig für Systeme höherer Ordnung. Die Zeitfunktionen g(t) und u(t) können sehr kompliziert werden, und damit ist das Faltungsintegral schwierig zu lösen.
Deshalb gestaltet sich der partikuläre Lösungsweg der DGL über die Laplace-Transformation mit anschließender Rücktransformation einfacher.
Lösung der gegebenen DGL 2. Ordnung:
Die Gleichung wird so umgeformt, dass der Koeffizient der höchsten Ableitung a2 = 1 wird, indem die restlichen Terme der Gleichung durch a2 dividiert wird und die Bezeichnung der übrigen Koeffizienten beibehalten wird.
Die Übertragungsfunktion eines Systems entsteht z.B. durch Austausch der zeitabhängigen Terme einer DGL mit den Laplace-Transformierten. Voraussetzung ist, dass die Anfangsbedingung des Systems Null ist. Je nach Grad der Ableitungen einer Funktion y(t) entstehen nach der Transformation folgende Laplace-Transformierte y(s):
Mit den transformierten Termen kann die Übertragungsfunktion des dynamischen Systems G(s) aufgestellt werden:
Polynome einer Übertragungsfunktion werden durch Nullstellenbestimmungen in Linearfaktoren (Grundpolynome: Monom, Binom und Trinom) zerlegt. Liegen Zahlenwerte der Koeffizienten einer Übertragungsfunktion 2. Ordnung vor, können die Pole (= Nullstellen im Nenner der Übertragungsfunktion) durch die bekannte Formel zur Lösung einer gemischt-quadratischen Gleichung ermittelt werden.
Durch die verschiedenen Arten der Lösungen der Pole bedingt durch die Größe des Radikanden der Wurzel ergeben sich drei unterschiedliche Fälle der Eigenwerte si der Übertragungsfunktion. Nachfolgend ist eine Korrespondenztabelle des s-Bereichs mit y(s) = u(s) * G(s) und des Zeitbereichs für y(t) für einen transformierten Eingangssprung u(t) = 1 → u(s) = 1 / s
Folgende Grundpolynome (Binome und Trinome bei konjugiert komplexen Polen) entstehen in Abhängigkeit von den Nullstellen. Die Lösungen der Übertragungsfunktionen als Sprungantwort im Zeitbereich sind einer Laplace-Transformationstabelle entnommen worden:
Die Laplace-Transformationstabellen können in zwei Formen der Produkt-Darstellung aufgeführt sein, wobei unterschiedliche Faktoren a0 und K berücksichtigt werden müssen. Die Umrechnung der Pole- Nullstellen in Zeitkonstanten ist einfach:
- Pole- Nullstellen-Darstellung (Stabiles System):
- Zeitkonstanten-Darstellung (Stabiles System):
f(s)
Übertragungsfunktion 2. Ordnung
Eingangssprung u(t) = 1 = Multiplikation mit 1/sf(t)
Partikuläre Lösung
Sprungantwort im ZeitbereichBestimmung der Pole s1 und s2
aus der Polynom-DarstellungDer Radikand > 0 hat 2 reelle Wurzeln
Der Radikand = 0 hat 2 gleiche Wurzeln
Der Radikand < 0 hat konjugiert komplexe Wurzeln
ω0 = Kreisfrequenz (ungedämpft) = 1 / T
Dämpfung D
Wird für den Fall der zwei reellen Wurzeln in die Gleichung für f(t) T1 = T2 eingesetzt, entsteht eine Division durch 0 (1 / (T1-T1), was nicht zulässig ist. Als „verschiedene“ Nullstellen gelten bereits Nullstellen, wenn sie sich in einer theoretisch unendlichen Dezimalstelle eines Wertes unterscheiden.
Die Gesamtlösung einer DGL ergibt sich aus der Überlagerung der Systemantworten auf die Anfangsbedingungen und auf das Eingangssignal:
Homogene Lösung einer DGL höherer Ordnung
[Bearbeiten]Bei DGL-en höherer Ordnung wird muss ebenfalls unterschieden werden, ob es sich um gleiche oder verschiedene Nullstellen handelt.
Für die homogene Lösung der DGL höherer Ordnung mit n verschiedenen Nullstellen: Für die homogene Lösung der DGL höherer Ordnung mit n gleichen Nullstellen:
Einzelnachweise
[Bearbeiten]- ↑ Prof. Dr. May-Britt Kallenrode, Universität Osnabrück, Fachbereich Physik: Vorlesungsmanuskript „Mathematik für Physiker“, Kapitel: „Differenzialgleichungen“, 611 Seiten, ausgestellt 2007.
- ↑ Prof. Dr. May-Britt Kallenrode, Universität Osnabrück, Fachbereich Physik: Vorlesungsmanuskript „Mathematik für Physiker“, Kapitel: „Differenzialrechnung“, 611 Seiten, ausgestellt 2007.
- ↑ Prof. Dr.-Ing. Oliver Nelles, Universität Siegen: Vorlesungskonzept Mess- und Regelungstechnik I, Kapitel: „Lösung der DGL 1. Ordnung“, 446 Seiten vom 8. Oktober 2009.
- ↑ Prof. Dr.-Ing. Oliver Nelles, Universität Siegen: Vorlesungskonzept Mess- und Regelungstechnik I, Kapitel: „Laplace-Transformation“, 446 Seiten vom 8. Oktober 2009.
Übertragungsfunktion
[Bearbeiten]
Eine Übertragungsfunktion beschreibt die Abhängigkeit des Ausgangssignals eines linearen, zeitinvarianten Systems (LZI-System) von dessen Eingangssignal im Bildbereich (Frequenzbereich, s-Bereich). Sie wird definiert als Quotient der transformierten Ausgangsgröße zur transformierten Eingangsgröße :
Die Übertragungsfunktion G(s) beschreibt das Eigenverhalten des Übertragungssystems vollständig und unabhängig von den Signalen. Eine Übertragungsfunktion ermöglicht es somit, das Ausgangssignal des Übertragungssystems aus dem Eingangssignal und der Übertragungsfunktion zu berechnen.
Dynamische zeitinvariante Systeme mit konzentrierten Energiespeichern (z. B. Feder-Masse-Dämpfer-Systeme oder elektrische L-, C- und R-Glieder) werden durch gewöhnliche Differenzialgleichungen mit konstanten Koeffizienten beschrieben. Wenn sich das System im Ruhezustand befindet, haben die Energiespeicher den Wert Null. Unter dieser Bedingung, dass die Anfangsbedingungen der systembeschreibenden Differenzialgleichung zu dem betrachteten Zeitpunkt gleich Null sind, ist die Übertragungsfunktion des Systems gleich der laplacetransformierten Differenzialgleichung des Systems. Durch Anwendung des Differenziationssatzes und des Integrationssatzes der Laplace-Transformation kann jeder Term der Differenzialgleichung einzeln transformiert und daraus die Übertragungsfunktion gebildet werden. Es können auch die Differenzialgleichungen einzelner Komponenten des Übertragungssystems transformiert werden und daraus die Übertragungsfunktion berechnet werden.
Die Übertragungsfunktion kann immer als gebrochen-rationale Funktion geschrieben werden. Durch die Nullstellenbestimmung des Polynoms im Zähler und des Polynoms im Nenner (= Pole) lässt sich die Übertragungsfunktion in Linearfaktoren aufteilen. Bestimmte Eigenschaften des Systems lassen sich bereits ohne Rücktransformation in den Zeitbereich direkt aus dieser Darstellung der Übertragungsfunktion ableiten.
Im Zeitbereich betrachtet, haben die Terme im Zähler ein differenzierendes Verhalten, im Nenner haben sie ein global verzögerndes oder integrierendes Verhalten. Dies gilt auch für die Behandlung linearer nicht-phasenminimaler, instabiler Übertragungssysteme mit Polen in der rechten s-Halbebene.
Der Übertragungsfunktion eines Systems kann die transzendente Funktion des Totzeitgliedes multiplikativ angehängt werden zu . Diese Form der Übertragungsfunktion als Gesamtsystem ist nur für Frequenzgang-Analysen geeignet.
Grundlagen Laplace-Transformation
[Bearbeiten]Die Übertragungsfunktion eines linearen dynamischen Systems entsteht z. B. aus der Laplace-Transformation einer systembeschreibenden gewöhnlichen Differenzialgleichung. Sie ist in der Regelungstechnik die häufigste Darstellungsform des Eingangs- und Ausgangsverhaltens von linearen Übertragungssystemen im komplexen Frequenzbereich.
Die Laplace-Transformation dient ähnlich wie die Fourier-Transformation der Zerlegung einer nicht sinusförmigen Funktion in sehr viele sinusförmige Teilfunktionen. Weil nach der Fourier-Transformation die Funktion für große Zeiten gegen Null gehen muss, können instabile Systeme mit wachsender Ausgangsgröße nicht transformiert werden. Auch für die in der Systemtheorie und Regelungstechnik häufig benutzte System-Eingangsgröße der Sprungfunktion (t) existiert keine Fourier-Transformierte. Die Laplace-Transformierte entsteht aus der Fourier-Transformierten indem durch ersetzt wird. [1]
Die Laplace-Transformation ist eine Integraltransformation, mit deren Anwendung sich eine Zeitfunktion in die Bildfunktionen mit der komplexen Frequenz übertragen lässt.
Die folgende Gleichung der einseitigen Laplace-Transformation einer Zeitfunktion ist gültig unter der Voraussetzung, dass alle Signale für verschwinden. Die Integrationsgrenze -0 berücksichtigt auch die Impulsfunktion (Diracimpuls) bei .
Laplace-Transformation einer Zeitfunktion:
Laplace-Rücktransformation einer Funktion F(s) des komplexen Frequenzbereichs:
- t bezeichnet die unabhängige Variable im Originalbereich.
- mit = Realteil und = Imaginärteil ist die unabhängige Variable im Bildbereich.
- ist das Symbol für die inverse Laplace-Transformation des Bildbereichs.
Das Laplace-Integral muss nicht für jede Zeitfunktion mit der Ausgangsgröße und der Eingangserregung neu berechnet werden, die Standardfunktionen sind bekannt. Eine der wichtigsten Anwendungen der Laplace-Transformation ist die Bestimmung der Übertragungsfunktion aus der einem dynamischen System zugehörigen Differenzialgleichung .
Die Transformation
der Differenziale und Integrale einer gewöhnlichen Differenzialgleichung erfolgt nach dem Laplace-Differenziationssatz und Integrationssatz. Die Zahlenwerte der Koeffizienten ai und bi sind identisch mit denen der Differenzialgleichung f(t) und der Übertragungsfunktion G(s) der Polynomdarstellung.
Nach dem Differenziationssatz oder dem Integrationssatz erfolgt die Transformation der Zeitfunktion f(t) zur Variablen s:
- k bedeutet die jeweilige Ordnung der Ableitung.
Ebenso werden zur Bestimmung des Systemverhaltens Laplace-transformierte Eingangssignale als Erregung des Systems verwendet wie Impuls-, Sprung- und Sinusfunktionen, deren Schreibweisen im Bildbereich bekannt sind. Die Funktionen des Bildbereiches und des Originalbereiches können je nach Aufgabenstellung von dem einen in den anderen Zustand transformiert werden.
Allgemeine Darstellungsformen der Übertragungsfunktion
[Bearbeiten]Aus der Laplace-Transformation einer systembeschreibenden Differenzialgleichung entsteht die Grundform der Übertragungsfunktion G(s) in Polynom-Darstellung. Daraus lassen sich weitere bekannte Schreibweisen der Übertragungsfunktionen errechnen, die unterschiedliche Eigenschaften für die Berechnung der Ausgangsgröße y(t) im Zeitbereich des Übertragungssystems G(s) bei gegebenem Eingangssignal U(s) aufweisen. Alle Formen der Übertragungsfunktionen sind mathematisch bei Rückrechnung mit der Polynomdarstellung identisch.
Übertragungsfunktion Darstellungsform im s-Bereich Polynom-Darstellung Pol-Nullstellen-Darstellung
(Darstellung für reelle Pole und Nullstellen)
s = Laplace-Operator, sn = Zahlenwert der Nullstelle, sp = Zahlenwert der PolstelleZeitkonstanten-Darstellung
(Für reelle Pole und Nullstellen mit Absolutglied und negativen Zahlenwerten)Partialbruch-Darstellung
(Für reelle Pole und Nullstellen mit Absolutglied)
Die Zerlegung der Zähler- und Nennerpolynome der Übertragungsfunktion in je eine Produktform (Linearfaktoren) gestattet eine einfache detaillierte Interpretation des Systemverhaltens und der Bestimmung der Koeffizienten des Übertragungssystems. Diese Zerlegung in Linearfaktoren (Faktorisierung von Polynomen) erfolgt durch die Bestimmung der Nullstellen der Polynome.
Ein lineares zeitinvariantes Übertragungssystem ohne Totzeit ist durch Pole, Nullstellen und Proportionalitätsfaktoren der Übertragungsfunktion vollständig bestimmt.
Die Linearfaktoren symbolisieren als kleinste Übertragungseinheit ein typisches System-Zeitverhalten, das sich zusätzlich konträr verhält, ob die Linearfaktoren im Nenner oder Zähler der Übertragungsfunktion stehen.
Die Übertragungsfunktion eines dynamischen Übertragungssystems kann einfache und mehrfache Linearfaktoren im Zähler und Nenner enthalten. Derartige Systeme beschreiben das Frequenzverhalten mit der komplexen Frequenz mit einem Systemeingang und einen Systemausgang . Sie wird erfolgreich eingesetzt für Systemanalyse, Systemsynthese, Systemstabilität und erlaubt die algebraische Behandlung von beliebig geschalteten rückwirkungsfreien Teilsystemen.
Die komplexe Frequenz ist eine unabhängige Variable des Laplace- oder Bildbereichs. Sie tritt mit einem ganzzahligen Exponenten als Potenz im Zähler und Nenner einer Übertragungsfunktion auf, ist aber nur ein Symbol für eine vollzogene Transformation einer Ableitung bestimmter Ordnung der gewöhnlichen Differenzialgleichung. Die Größe s in der Übertragungsfunktion kann beliebig algebraisch behandelt werden, enthält aber keinen Zahlenwert. (Imaginäre Einheit: ; Re = Realteil, Im = Imaginärteil)
Elektrische, mechanische, biologische und andere dynamische Systeme können durch die gleiche Form der Übertragungsfunktion beschrieben werden, wenn die Anzahl und die Struktur der Systemspeicher identisch sind.
Die Übertragungsfunktion eines dynamischen Systems kann algebraisch für die multiplikative (Reihenstruktur), subtraktive, additive und zurückgekoppelte Struktur (Regelkreis) beliebig zusammengestellt werden. Dabei kann es sich um einen industriellen Prozess, um eine Steuerstrecke, eine Regelstrecke, einen Regler oder einen Regelkreis handeln. Zum Beispiel kann die Übertragungsfunktion des sehr bekannten PID-Reglers in der Reihenstruktur oder Parallelstruktur beschrieben werden, die sich äußerlich nicht gleichen, aber bei unterschiedlichen Koeffizienten ein identisches Frequenz- und Zeitverhalten haben. Beide Schreibweisen haben technische Vorteile.
Die folgenden idealen PID-Reglerstrukturen sind mathematisch identisch. Die Koeffizienten T1 und T2 ergeben sich durch Faktorenvergleich mit den Koeffizienten , und :
PID-Reglerstruktur Übertragungsfunktion mit Nullstellenüberschuss Reihenstruktur Parallelstruktur
Polynom-Darstellung
[Bearbeiten]Die Anwendung der Laplace-Transformation einer systembeschreibenden Differenzialgleichung führt zu der Übertragungsfunktion als gebrochen-rationale Funktion in die Polynom-Darstellung. Dabei werden die Koeffizienten der Differenzialgleichung in die Übertragungsfunktion vollständig übernommen. Anstelle der Ableitungen der Differenzialgleichung tritt der Laplace-Operator entsprechend dem Grad der Ableitung als Potenz von auf.
Erst die Aufspaltung der Polynome im Nenner und Zähler der Übertragungsfunktion in Linearfaktoren (Teilsysteme, Produktterme) 1. Ordnung und 2. Ordnung (mit konjugiert komplexen Polen) zeigt anschaulich im nächsten Kapitel jeweils im Zähler und Nenner maximal drei verschiedene Linearfaktoren, mit fundamental unterschiedlichen Eigenschaften im Zeitbereich.
Zeitkontinuierliche lineare Systeme werden im Zeitbereich durch die lineare Differenzialgleichung n-ter Ordnung beschrieben
[Bearbeiten]ist Ausgangs- und Eingangssignal als Funktion der Zeit, die 1. Ableitung nach der Zeit.
Wenn die Koeffizienten und konstant (also zeitunabhängig) sind, ist die Laplace-Transformation ausführbar.
Mit den vorgegebenen Anfangsbedingungen für das Ein- und Ausgangssignal (Werte zum Zeitpunkt )
- für alle
- für alle
lautet die Laplace-Transformierte der Ein- und Ausgangsgrößen
und sind die komplexe Eingangs- bzw. Ausgangsfunktion in Abhängigkeit von der komplexen Variablen im Bildbereich.
Die Laplace-Transformierte der Differenzialgleichung ist
- .
Es handelt sich anstelle der Differenzialgleichung um eine algebraische Gleichung, deren Analyse mit Methoden der Algebra möglich ist.
Die Übertragungsfunktion G(s) in Polynomdarstellung
[Bearbeiten]ist das Verhältnis der Laplace-Transformierten der Wirkung (Ausgang) durch die Laplacetransformierte der Ursache (Eingang):
Die statische Verstärkung des Übertragungssystems ist durch das Verhältnis der Koeffizienten bestimmt.
Alle Koeffizienten der Differenzialgleichung, die das Zeitverhalten bestimmen, sind in der Übertragungsfunktion im Nenner enthalten. Die Koeffizienten des Zählers bestimmen die Größe der Amplitude . Die Übertragungsfunktion beschreibt das Verhalten des Systems vollständig. Damit ist es möglich, Aussagen über das Verhalten des Systems ohne Lösung der Differenzialgleichung zu erhalten.
Die Übertragungsfunktion ist eine analytische Funktion. Da sie Funktion der komplexen Variablen ist, kann sie als
geschrieben werden. Das ist eine Abbildung der von aufgespannten -Ebene in die von aufgespannte -Ebene. Alle Methoden der Funktionentheorie können zur Analyse eingesetzt werden. Das Erstellen einer Grafik ist wegen der vier Dimensionen nur in zwei dreidimensionalen Grafiken möglich, z. B. als
Pol-Nullstellen-Darstellung
[Bearbeiten]Unter dem Begriff Nullstellen versteht man jene Werte, die in eine Funktion eingesetzt, den Funktionswert Null liefern. Nullstellen von Polynomen werden in der Mathematik auch häufig mit Wurzeln oder Nullstellen bezeichnet. In der Regelungstechnik werden die Nullstellen des Zählerpolynoms mit Wurzeln oder Nullstellen, die des Nennerpolynoms mit Polen bezeichnet.
Ein Polynom -ten Grades hat genau Nullstellen bzw. Pole. Diese Nullstellen und Pole können reelle oder komplexe Zahlen sein.
Die Nullstellen eines Polynoms 2. Ordnung lassen sich durch die bekannte Formel der quadratischen Gleichung lösen. Für Polynome bis 4. Ordnung existieren Rechenprogramme, die auch im Internet unter dem Suchbegriff "Nullstellen (Lösungen) von Polynomen" zu finden sind. Polynome noch höherer Ordnung können numerisch mit dem Newton-Verfahren gelöst werden.
Die Nullstellen eines Polynoms sind unabhängig von Polynomfaktoren. Der System-Verstärkungsfaktor der Übertragungsfunktion in der Pol-Nullstellen-Darstellung beträgt .
Nach dem Fundamentalsatz der Algebra gilt für ein Polynom:
mit dessen Nullstellen . Sie können einfach oder mehrfach, reell oder paarweise konjugiert komplex sein.
Die Übertragungsfunktion in Pol-Nullstellen-Darstellung lautet:
In dieser allgemeinen Darstellung ist noch nicht definiert, um welche Art von Linearfaktoren es sich bei der Übertragungsfunktion handelt. Das Systemverhalten wird erst deutlich, wenn Zahlenwerte für die Nullstellen, Pole und Verstärkung vorliegen.
Bei gegebenen Zahlenwerten mit den (Nullstellen) und den (Polen, Nullstellen des Nennerpolynoms) ist die Übertragungsfunktion vollständig bestimmt und mit der Polynom-Darstellung identisch. Diese Darstellung ist für allgemeine Aussagen über das System z. B. für Stabilitätsuntersuchungen wichtig.
Linearfaktoren
[Bearbeiten]Linearfaktoren[2] sind Produktterme eines Polynoms im Zähler und Nenner einer Übertragungsfunktion G(s).
Sind die Nullstellen bzw. die Pole einer Übertragungsfunktion G(s) in der Polynomdarstellung bekannt, kann das Zähler- und Nennerpolynom in Produktterme (Linearfaktoren) zerlegt werden, z. B.:
- im Zähler mit der Nullstelle der Linearfaktor und
- im Nenner mit dem Pol der Linearfaktor gebildet werden.
Weil die Nullstellen aus zu Null gesetzten Polynomen berechnet werden, muss sichergestellt werden, dass keine Faktoren gekürzt worden sind. Es empfiehlt sich eine Prüfung vorzunehmen, ob die Pol- Nullstellendarstellung (= Produktdarstellung) durch Ausmultiplizieren auch mit dem Polynom identisch ist.
Eine Nullstelle des Zählerpolynoms sn oder ein Pol des Nennerpolynoms sp kann folgende drei stabile Formen von Zahlenwerten einnehmen:
- {sn; sp} = 0, (Absolutglied des Polynoms fehlt),
- {sn; sp} = (reeller Wert der Pole und Nullstellen),
- {sn; sp} = (konjugiert komplexer Wert der Pole oder Nullstellen).
Sind die Realteile von Nullstellen und Polen negativ, handelt es sich um ein stabiles System. Negative Realteile der Pole bedeuten asymptotische Stabilität des Teilsystems.
Bei reellen Nullstellen entsteht der Produktterm 1. Ordnung . Ist der Wert der Nullstelle sp negativ, lässt sich dafür auch schreiben, wenn a ein negativer Wert der Nullstelle ist (stabiles System).
Bezeichnet man bei konjugiert komplexen Nullstellen bzw. Polen den Realteil mit und den Imaginärteil mit , dann ergeben sich bei Übertragungsfunktionen in der Produktdarstellung bei reellen und konjugiert komplexen Nullstellen und Polen unterschiedliche Gleichungen, die durch die Größe der Zahlenwerte der Koeffizienten der Polynomdarstellung bestimmt werden. Die angegebenen 3 Formen der Linearfaktoren können einfach und mehrfach auftreten.
In der linearen Regelungstechnik und Systemtheorie ist es eine willkommene Tatsache, dass praktisch alle vorkommenden regulären (stabilen) Übertragungsfunktionen bzw. Frequenzgänge von Regelkreisgliedern auf drei Grundformen geschrieben bzw. zurückgeführt werden können. Die Linearfaktoren haben eine völlig unterschiedliche Bedeutung, je nachdem ob sie im Zähler oder im Nenner einer Übertragungsfunktion stehen.
Stehen die Linearfaktoren im Zähler, haben sie eine differenzierende Wirkung, stehen sie im Nenner, haben sie eine verzögernde (speichernde) Wirkung:
Typ Linearfaktor
Pol-Nullstellen-DarstellungTyp Linearfaktor
Zeitkonstanten-DarstellungBedeutung im Zähler Bedeutung im Nenner
Absolutglied a0 oder b0 fehlt
Nullstelle oder PolDifferenzierer, D-Glied Integrator, I-Glied
Pole und Nullstellen sind reell
Negative Werte = stabile Systeme
T = 1 / sn oder T = 1 / sp
"reelle Zahl"PD1-Glied Verzögerung, PT1-Glied Polynom:
mit undNormalform:
T = 1 / sn oder T = 1 / sp
PD2-Glied:
für -1 < D < 1
mit konjugiert komplexen NullstellenSchwingungsglied PT2-Glied:
für -1 < D < 1
mit konjugiert komplexen Polen
- Dabei ist T die Zeitkonstante, s die komplexe Frequenz, D der Dämpfungsgrad.
Globales Systemverhalten
[Bearbeiten]Die Linearfaktoren in der Pol- Nullstellen-Darstellung mit den Bezeichnungen sn und sp müssen negativen Zahlenwerten entsprechen, wenn es sich um sogenannte phasenminimale (stabile) Systeme handelt. Dies kann zu Missverständnissen führen, deshalb werden anstelle der Bezeichnungen der Pole und Nullstellen Hilfsgrößen eingeführt (wie a, b, c. ...), die negativen Zahlenwerten entsprechen. Daraus folgt, dass die Linearfaktoren in der Pol-Nullstellen-Darstellung z. B. (s + a) mit a einen positiven Zahlenwert darstellen, die zugehörigen Pole sp oder Nullstellen sn des Linearfaktors negativen Zahlenwerten entsprechen.
Beispiel: Bestimmung des Pols eines Linearfaktors G(s) = s + 3 im Nennerpolynom:
Sind Zahlenwerte einer Übertragungsfunktion in der Polynomdarstellung gegeben, können mit verschiedenen Methoden, wie mit der pq-Formel für Systeme zweiter Ordnung, oder fertige im Internet verfügbare Programme bis 4. Ordnung mit dem Aufruf - "Nullstellen (Lösungen) von Polynomen bestimmen" - die Pole und Nullstellen bestimmt werden.
Für Systeme mit Polynomen 2. Ordnung der Form errechnen sich die Nullstellen bzw. die Pole:
Wenn das Polynom 2. Ordnung mit konjugiert komplexen Polen in die Form zur Lösung einer gemischt quadratischen Gleichung gebracht wird, lassen sich die Nullstellen für p und q durch Faktorenvergleich bestimmen. wird positiv, wenn negative Realteile von oder vorliegen.
Die Pol- Nullstellendarstellung der Übertragungsfunktion für ein asymptotisch stabiles System enthält immer positive Zahlenwerte, was voraussetzt, dass die Pole und Nullstellen negative Realteile enthalten.
Wenn in einer systembeschreibenden Differenzialgleichung oder in der zugehörigen Übertragungsfunktion aus der geschlossenen Reihenfolge der Ableitungen bestimmte Koeffizienten fehlen, bzw. zu Null gesetzt sind, ergibt sich für das Gesamtverhalten im Zeitbereich folgendes typische Systemverhalten:
- Beispiel einer Übertragungsfunktion der Polynomdarstellung und der Zerlegung in die Pol-Nullstellen-Darstellung mit reellen Linearfaktoren:
- Sind in der Polynomdarstellung alle Ableitungen und zugehörige Koeffizienten lückenlos mit positivem Vorzeichen vorhanden, stellt die Übertragungsfunktion für die Exponenten n > m ein zeitverzögerndes asymptotisch stabiles System dar. Werden negative Werte der Pole und Nullstellen eingesetzt, entstehen positive Linearfaktoren.
- Das Gesamtsystem wird als "globales proportionales Systemverhalten" bezeichnet.
- Beispiel einer Übertragungsfunktion der Polynomdarstellung ohne Absolutglied im Nennerpolynom und der Zerlegung in die Pol-Nullstellen-Darstellung mit reellen Linearfaktoren:
- Der Term der gewöhnlichen Differenzialgleichung oder eines transformierten Polynoms im Zähler und Nenner der Übertragungsfunktion mit den Koeffizienten und wird allgemein als Absolutglied bezeichnet. Für oder gilt:
- Linearfaktor ohne Absolutglied des Polynoms im Nenner, Pol .
- Fehlt das Absolutglied a0 im Nennerpolynom (a0 = 0), kann die Variable s aus dem Nennerpolynom ausgeklammert werden. Dieses Gesamtverhalten des Systems wird als "globales integrierendes Systemverhalten" bezeichnet. Fehlt das Absolutglied b0 im Zählerpolynom (b0 = 0), kann die Variable s aus dem Zählerpolynom ausgeklammert werden. Dieses Gesamtverhalten des Systems wird als "globales differenzierendes Systemverhalten" bezeichnet.
- Beispiel einer Übertragungsfunktion in der Pol-Nullstellen-Darstellung mit einem konjugiert komplexen Pol im Nennerpolynom:
- Bei dynamischen Systemen 2. Ordnung (z.B. Feder-Masse-Dämpfungssystem) oder bei Systemen 1. Ordnung, die eine positive Rückführung enthalten (Regelkreise), kann ein Energieaustausch stattfinden. Solche Systeme mit konjugiert komplexen Lösungen der Pole und Nullstellenkönnen können in einem Gesamtsystem enthalten sein und treten immer paarweise - meist im Nenner der Übertragungsfunktion - mit einem identischen Realteil auf.
- und , oder zusammengefasst
- Die Polynome mit konjugiert komplexen Nullstellen werden zur einfacheren Berechenbarkeit zu quadratischen Termen zusammengefasst, in denen nur reelle Koeffizienten auftreten. Deshalb lässt sich ein Elementarsystem 2. Ordnung mit konjugiert komplexen Polen und Nullstellen nicht in 2 Linearfaktoren 1. Ordnung mit nur reellen Koeffizienten zerlegen.
- Wird der Klammerausdruck mit den komplexen Größen im Nenner aufgelöst, entsteht:
- und
- Sind in der Polynomdarstellung alle Ableitungen und zugehörige Koeffizienten lückenlos mit positivem Vorzeichen vorhanden, stellt diese Übertragungsfunktion für die Exponenten n > m und einem Polynom mit konjugiert komplexen Polen ein zeitverzögerndes asymptotisch stabiles, gedämpft schwingendes System dar.
Zeitkonstantendarstellung
[Bearbeiten]Es existieren 2 faktorielle Darstellungsformen, die Pol-Nullstellen-Darstellung und die Zeitkonstanten-Darstellung. Die Zeitkonstanten-Darstellung hat einen höheren Anschauungswert und den Vorteil, dass bei Änderung der Zeitkonstante sich die Systemverstärkung nicht ändert.
Die Zeitkonstanten-Darstellung errechnet sich direkt aus der Pol-Nullstellendarstellung, indem der Produktterm so umgeformt wird, dass beide Formen mathematisch identisch sind: mit . Der Produktterm s - sn wird so umgestellt, dass der Reziprokwert 1/sn = T gebildet wird.
Der Produktterm in der Zeitkonstanten-Darstellung mit negativem Wert der Polstelle sP (Term im Nenner asymptotisch stabiles System) lautet damit:
Bei der Zeitkonstantendarstellung des Linearfaktors werden die Terme positiv dargestellt. Dies setzt voraus, dass die Realanteile der zugehörigen Nullstellen und Pole negativ sind.
Dabei bedeutet a eine Hilfsgröße für die negative Nullstelle (-sn) oder Polstelle (-sp).
Übertragungsfunktion in Zeitkonstanten-Darstellung mit dem Linearfaktor 1. Ordnung mit Absolutglied eines phasenminimalen Systems:
Globales Proportionalverhalten für und .
Vorteil der Zeitkonstanten-Darstellung
[Bearbeiten]- Das Zeitverhalten ist direkt ablesbar.
- Die statische Verstärkung ändert sich nicht, wenn eine Zeitkonstante geändert wird.
Zeitliches Verhalten in Abhängigkeit von der Pol-Nullstellen-Anzahl
[Bearbeiten]Je nach Anzahl der Pole und Nullstellen einer Übertragungsfunktion ergibt sich folgendes Systemverhalten für Linearfaktoren 1. Ordnung mit Absolutglied:
- Bei dieser Übertragungsfunktion ist das Systemverhalten im Zeitbereich bei Polüberschuss definiert. Die Sprungantwort nähert sich asymptotisch dem Maximum.
- Bei gleicher Anzahl von Polen und Nullstellen hängt das Systemverhalten von der Größe der Zeitkonstanten ab. Die Sprungantwort kann ein differenzierendes oder verzögerndes Verhalten zeigen.
- Nullstellenüberschuss ist technisch nicht realisierbar.
Tabelle wichtiger regulärer (phasenminimaler) Übertragungsfunktionen in Zeitkonstanten-Darstellung:
| Übertragungsfunktion G(s) |
|||||||
|---|---|---|---|---|---|---|---|
| Übergangsfunktion (Sprungantwort) |
 |
 |
 |
 |
 |
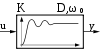 |

|
| Benennung | P-Glied | I-Glied | D-Glied | PD1-Glied | PT1-Glied | PT2-Glied | Totzeitglied |
Die praktische Bedeutung des Linearfaktors 2. Ordnung mit konjugiert komplexen Nullstellen im Zähler der Übertragungsfunktion liegt z. B. in der Anwendung als Vorfilter. Ein PD2KK-Glied im Eingang eines Regelkreises kann das gedämpfte Schwingungsverhalten der Regelgröße (Einschwingvorgang) vollständig kompensieren.
Verstärkungsfaktor K
[Bearbeiten]Erst durch die Kenntnis der Produktform mit Linearfaktoren ist eine Rücktransformation des Systemverhaltens in den Zeitbereich möglich.[3][4]
In den Laplace-Transformationstabellen zur Berechnung des System-Zeitverhaltens werden für die Linearfaktoren in der Pol-Nullstellen-Darstellung die Werte von Polen und Nullstellen meistens die Buchstaben verwendet. In der Zeitkonstanten-Darstellung treten anstelle der Nullstellen und Pole deren Reziprokwerte als Zeitkonstanten. In beiden Darstellungsformen sind Faktoren zu berücksichtigen, die im s-Bereich und Zeitbereich identisch sind, d. h. nicht transformiert werden.
Die Verstärkungsfaktoren der Pol-Nullstellen-Darstellung und der Zeitkonstanten-Darstellung sind unterschiedlich. Da sich die Verstärkungsfaktoren aus der Polynomdarstellung der Übertragungsfunktion errechnen, müssen im Falle der Rückrechnung der beiden Formen in die Polynom-Darstellung identische Polynome ergeben.
- Der Verstärkungsfaktor der Pol-Nullstellen-Darstellung errechnet sich aus den Koeffizienten der Polynom-Darstellung.
- Wenn sich in der Pol-Nullstellen-Darstellung ein Pol oder Nullstelle ändert, dann ändert sich auch die Verstärkung .
- Der statische Verstärkungsfaktor der Zeitkonstanten-Darstellung berechnet sich aus der Polynom-Darstellung oder mit den Polen und Nullstellen aus der Pol-Nullstellen-Darstellung. Siehe Tabelle!
- Wenn sich in der Zeitkonstanten-Darstellung eine Zeitkonstante ändert, bleibt die statische Verstärkung konstant.
Maximal existieren drei unterschiedliche Linearfaktoren für phasenminimale Übertragungssysteme. Bei nichtphasenminimalen Systemen mit Absolutglied (positive Pole und / oder Nullstellen) existieren 2 weitere Linearfaktoren, die sich an dem negativen Vorzeichen erkennen lassen.
Phasenminimumsysteme und Nichtphasenminimumsysteme
[Bearbeiten]Ein Phasenminimumsystem kann aus mehreren Teilsystemen bestehen und hat für einen gegebenen Amplitudengang eine minimale Phasenverschiebung. Bei Phasenminimumsystemen besteht zwischen Amplitudengang und Phasengang ein eindeutiger Zusammenhang.
- Phasenminimumsysteme sind Systeme ohne Totzeit, deren rationale Übertragungsfunktionen G(s) keine Pole und keine Nullstellen in der rechten s-Halbebene haben.
- Nicht alle Phasenminimumsysteme sind stabil. Sie erfüllen alle den Begriff der "Internen Stabilität" aber nicht alle sind "Extern stabil".
- Nichtphasenminimale Systeme haben ein Minuszeichen in der Übertragungsfunktion.
- Nichtphasenminimumsysteme enthalten eine Totzeit oder Pole oder Nullstellen in der rechten s-Halbebene.
- Nichtphasenminimumsysteme mit Polen in der rechten s-Halbebene sind instabile Systeme. Dieses System reagiert auf ein Eingangssignal mit einem unbeschränkten Ausgangssignal.
- Nichtphasenminimumsysteme mit Polen in der rechten s-Halbebene und Phasenminimumsysteme sind relativ leicht zu regeln.
- Nichtphasenminimumsysteme mit Nullstellen in der rechten s-Halbebene (Allpass-Systeme) sind stabile Systeme aber sehr schwierig zu regeln.
- Nullstellen in Phasenminimumsystemen und Nichtphasenminimumsystemen haben Einfluss auf die Amplituden der Ausgangssignale. Pole bestimmen das Zeitverhalten.

Zeitverhalten der Linearfaktoren für ein gegebenes Eingangssignal u(t)
[Bearbeiten]Das Zeitverhalten der drei Formen der Linearfaktoren im Nenner der Übertragungsfunktion ist für gleiche Zahlenwerte der Zeitkonstanten im nebenstehenden Diagramm als Sprungantwort des normierten Eingangssignal dargestellt. Dem Linearfaktor PT2KK-Glied mit den konjugiert-komplexen Polen (Schwingungsglied) wurde ein willkürlich bestimmter Wert der Dämpfung mit vorgegeben. Wenn die Dämpfung beträgt, ergeben sich zwei reelle Pole, und das Nenner-Polynom lässt sich in zwei PT1-Verzögerungsglieder aufspalten.
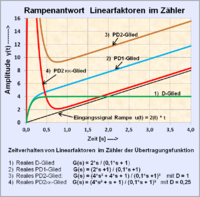
Das Zeitverhalten der drei Formen der Linearfaktoren im Zähler der Übertragungsfunktion mit differenzierender Wirkung ist in dem nächsten Diagramm dargestellt. Differenzierende ideale Systeme ( Nullstellen-Überschuss) kann man nicht als Sprungantwort darstellen, weil die Differenziation eines Sprunges zur Zeit stattfindet.
Die Einheits-Sprungantwort (für ) eines D-Gliedes ( oder ) verläuft nach der Einschwingzeit auf . Die Einheits-Sprungantwort (für ) eines PD-Gliedes oder PD2-Gliedes ( oder ) verläuft nach der Einschwingzeit auf .
Eine Anstiegsfunktion (Rampe) im -Bereich: und im Zeitbereich: (gewählt: ) eignet sich zur Darstellung des Systemverhaltens (Rampenantwort) mit Nullstellen-Überschuss.
Linearfaktoren mit PD-Verhalten verlaufen nach dem Einschwingen parallel zur Anstiegsfunktion mit steigendem Abstand der Ordnung wie dargestellt. PD2KK-Glieder mit konjugiert komplexen Nullstellen verlaufen nach dem Einschwingen parallel zur Rampe und nähern sich mit kleiner werdenden Dämpfung der Rampe an. Begründung: Mit kleiner werdender Dämpfung nähert sich die Übertragungsfunktion an. Der Term ist in dem Polynom bei verschwunden.
Partialbruch-Darstellung zur Rücktransformation in den Zeitbereich
[Bearbeiten]Mit der Partialbruchzerlegung einer Übertragungsfunktion G(s) in der Pol-Nullstellen-Darstellung wird die faktorisierte Darstellung in additive Teilbrüche überführt, die sich relativ einfach ohne Anwendung von Laplace-Transformationstabellen in den Zeitbereich übertragen lassen.
Partialbruchzerlegung der Zähler und Nennerpolynome der Übertragungsfunktion
Eine Übertragungsfunktion G(s) als gebrochen-rationale Funktion lässt sich durch die Partialbruchzerlegung in einfache additive Funktionen zerlegen, die einer Parallelschaltung der Teilsysteme entsprechen:
Die Überführung in den Zeitbereich auf einfache bekannte Grundfunktionen der inversen Laplace-Transformation erfolgt durch:
Dazu muss das Nennerpolynom N(s) einer Übertragungsfunktion G(s) in folgende Form faktorisiert werden. Die Pole der Übertragungsfunktion bestimmen die Partialbrüche:
Ein Produktterm eines einfachen PT1-Verzögerungsgliedes des Nenners einer Übertragungsfunktion mit der Polstelle a kann unmittelbar in den Zeitbereich überführt werden:
Die Nenner der Partialbruchterme im s-Bereich bestimmen das Systemverhalten im Zeitbereich und können auf einfache Laplace-Korrespondenzen zurückgeführt werden. Dabei bedeutet a im s-Bereich einen reellen negativen Wert der Polstelle. Es ergeben sich additive Komponenten der Übertragungsfunktion, deren Signalanteile einer Parallelschaltung von Einzelsystemen entsprechen. Die inverse Transformation der additiven Komponenten f(s) in f(t) ist einfach und hat einen hohen Bekanntheitsgrad.
Ein Systemausgangssignal Y(s) soll in den Zeitbereich y(t) überführt werden:
Die Partialbruchzerlegung dient der einfachen Überführung eines Systemausgangssignals Y(s) in den Zeitbereich y(t) für ein gegebenes Eingangssignal U(s). Deshalb bezieht sich die Partialbruchzerlegung auf das Produkt G(s)*U(s).
Bei der Partialbruchzerlegung sind 3 Fälle zu unterscheiden:[5]
- Die Pole sind reell und verschieden
- Die Pole sind reell und gleich
- Die Pole sind konjugiert komplex
Partialbruchzerlegung von Übertragungsfunktionen mit reellen verschiedenen Polen:
Das Systemausgangssignal y(t) ergibt sich durch die Suchfunktion der Laplace-Transformationstabellen Y(s) = G(s) * U(s).
U(s) kann z. B. ein Testsignal als Impulsfunktion, Sprungfunktion oder Anstiegsfunktion sein.
Die Residuen Ai lauten:
- Lösung im Zeitbereich
- Anwendungsbeispiel der Partialbruchzerlegung einer Übertragungsfunktion G(s) mit 2 PT1-Gliedern
Beispiel: Übertragungsfunktion ohne differenzielle Anteile (Nullstellen).[6]
Das Eingangssignal U(s) = 1/s ist ein normierter Eingangssprung f(t) = 1:
Fall: Die Pole sind reell und verschieden!
Das Produkt U(s) * G(s) wird mittels der Partialbruchzerlegung von der Reihendarstellung
der Einzelkomponenten in eine Paralleldarstellung zerlegt:Die Gleichung der Lösung der Residuen lautet:
Daraus folgt:
Damit erhält man durch die inverse Transformation einfacher Komponenten des s-Bereichs
die Gleichung der Ausgangsgröße y(t) für den Zeitbereich:
Anmerkung: Die unbekannten Parameter A1 bis An lassen sich auch durch Koeffizientenvergleich ermitteln!
Frequenzgang und Übertragungsfunktion
[Bearbeiten]- Übertragungsfunktion
Die Übertragungsfunktion G(s) ist eine abstrakte nicht messbare Form der Systembeschreibung zur mathematischen Behandlung linearer dynamischer Systeme. Sie bestimmt das Eingangs-Ausgangssignal-Verhalten eines Übertragungssystems für beliebige Eingangssignale im komplexen Frequenzbereich. Die Übertragungsfunktion G(s) mit dem Laplace-Operator kann in Realteil und Imaginärteil oder in Betrag und Phase zerlegt werden.
Mit Ausnahme der Anfangsbedingungen enthält die Übertragungsfunktion alle Informationen über ein lineares dynamisches System.
Typische aperiodische Eingangssignale als Testsignale sind Sprungfunktion, Anstiegsfunktion und Impulsfunktion. Für diese aperiodischen Eingangssignale U(s) kann das Systemausgangssignal y(t) im Zeitbereich mit der Suchfunktion G(s) * U(s) über die Laplace-Transformationstabellen bestimmt werden.
- Frequenzgang [7]
Der Frequenzgang G(jω) ist eine frequenzabhängige komplexe Größe und beschreibt ein Übertragungssystem im eingeschwungenen Zustand. Er definiert das Verhältnis der Ausgangs- zur Eingangsamplitude und berücksichtigt den Phasenwinkel. Er ist ein Spezialfall der Übertragungsfunktion als messbare Beschreibungsform, die zur empirischen Systemidentifikation eines unbekannten linearen technischen Übertragungssystems genutzt werden kann.
Der Frequenzgang kennzeichnet das Verhalten eines Systems mit erzwungener Dauerschwingung und der imaginären Frequenz (p = Differenzialoperator).
Wird der Realteil des Laplace-Operators der Übertragungsfunktion G(s) zu Null gesetzt, geht die komplexe Übertragungsfunktion G(s) in den komplexen Frequenzgang
- über.
Beide mathematischen Begriffe der Übertragungsfunktion und des Frequenzgangs unterscheiden sich nur durch die Entstehungsweise. Sie können je nach Aufgabenstellung als Übertragungsfunktion im s-Bereich oder als Frequenzgang mit geschrieben werden.
Der Frequenzgang eines Übertragungssystems beschreibt das Signalverhalten des Systems für eine Erregung des Systemeingangs mit einer sinusförmigen Frequenz.
System-Eingangssignal:
Für ein Eingangssignal u(t) konstanter Amplitude und variabler Kreisfrequenz ω ist die Systemantwort eines zeitabhängigen linearen Systems in Abhängigkeit des Eingangssignals frequenzabhängig und phasenverschoben.
System-Ausgangssignal:
Ist der Einschwingvorgang abgeklungen, ändert sich die Systemausgangsgröße mit der gleichen harmonischen Frequenz der Eingangsgröße aber mit einer anderen Amplitude und einer Phasenverschiebung.
Das Verhältnis der Scheitelwerte der Amplituden und die Phasenverschiebung hängen von der Kreisfrequenz ab.
Herleitung des Frequenzgangs:
Aus dem sinusförmigen Eingangssignal im Zeitbereich wird die komplexe Funktion im Frequenzbereich:
Nach der Eulerschen Formel (= Beziehung der trigonometrischen Funktionen mit den Exponentialfunktionen) wird das Eingangssignal:
Für das Ausgangssignal gilt in gleicher Weise:
Der Frequenzgang G(jω) ergibt sich aus dem Quotient der beiden Gleichungen des Ausgangs- zum Eingangssignal:
Der Frequenzgang G(jω) eines Übertragungssystems gibt das Verhältnis der sinusförmigen Ausgangsschwingung zur sinusförmigen Eingangsschwingung in der komplexen Form für alle Werte der Kreisfrequenzen ω an. Der Betrag |G(jω)| ist ein Maß für die Amplitudenänderung in Abhängigkeit von ω.
Der Frequenzgang wird entweder in Real- und Imaginärteil:
oder in Betrag und Phase angegeben:
- Herleitung des Frequenzgangs aus der Übertragungsfunktion
Der Frequenzgang kann aus der systembeschreibenden Differenzialgleichung, aus der Übertragungsfunktion oder über empirische Messungen eines linearen Hardware-Systems mit sinusförmiger Erregung und der Systemantwort bestimmt werden.
Die Herleitung des Frequenzgangs G(jω) aus der Übertragungsfunktion G(s) ist besonders einfach. Der Frequenzgang geht durch den Grenzübergang mit s → jω aus der Übertragungsfunktion hervor. Es muss nur gegen ausgetauscht werden.
- Übertragungsfunktion G(s) eines linearen Übertragungssystems in der Zeitkonstantendarstellung
- Frequenzgang G(jω) eines linearen Übertragungssystems in der Zeitkonstanten-Darstellung
Grafische Darstellung des Frequenzgangs (Kurzdarstellung)
[Bearbeiten]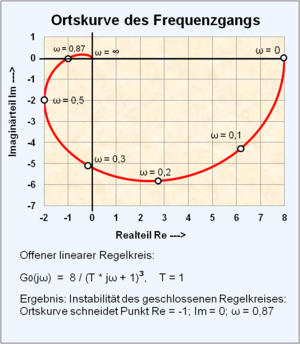
- Ortskurve
Der Wert des Frequenzgangs für (jω) ist eine komplexe Größe mit einem Real- und Imaginärteil.
Für die Ermittlung der Ortskurve wird der Frequenzgang in Realteil und Imaginärteil zerlegt und für verschiedene Frequenzen in der Gaußschen Zahlenebene eingetragen.
- Bodediagramm
Eine häufige Anwendung ist die grafische Beurteilung des Frequenzgangs durch Zerlegung in Betrag und Phase. Dabei werden die Frequenzganggleichungen in Produktform mit „Kompensationsgliedern“ z. B. mit dem konjugiert komplexen Wert eines Produktes im Zähler und Nenner so erweitert, dass der Realteil und Imaginärteil getrennt dargestellt werden können.
Es wird eine Wertetabelle aufgestellt, bei der für den Realteil und für den Imaginärteil der Frequenzganggleichung G(jω) mehrere Werte als Funktion der Kreisfrequenz ω berechnet werden.
Der mit Amplitudengang bezeichnete Betrag G(jω) lautet:
Der Phasengang (jω) lautet:
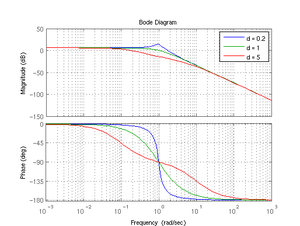
(K = 2, T = 1; Varianten: D = 0,2; D = 1; D = 5).
- Prinzipielle Anwendung des Frequenzgangs für den Reglerentwurf
- Bodediagramm zur Stabilitätsbetrachtung
- Betrag und Phasenwinkel des Frequenzgangs des offenen Kreises werden in 2 getrennten Diagrammen aufgetragen, als Amplitudengang und Phasengang. Ein geschlossener Regelkreis ist stabil, wenn die nacheilende Phasenverschiebung φ vom Ausgangs- zum Eingangssignal des offenen Kreises bei der Kreisverstärkung K = 1 und φ > −180° beträgt.
- Die Ermittlung der Stabilität eines Übertragungssystems mit dem Bodediagramm dient dem mathematischen Systemverständnis, hat aber heutzutage keine Bedeutung mehr. Mit geeigneten Rechenprogrammen kann das Systemverhalten für ein Test-Eingangssignal direkt im Zeitbereich dargestellt werden.
- Bodediagramm zur Systemanalyse
- Das Bodediagramm kann für die Systemanalyse eines linearen unbekannten dynamischen Systems benutzt werden, indem das unbekannte System mit einer elektrischen Spannung mit variabler sinusförmiger Frequenz konstanter Amplitude erregt und die Systemantwort gemessen wird. Mit Hilfe des Bodediagramms können die Eckfrequenzen und damit auch die Übertragungsfunktion G(s) und gegebenenfalls auch eine vorhandene Totzeit über den Phasengang festgestellt werden.
- Ortskurve zur Stabilitätsbetrachtung
- Die Frequenzganggleichung des offenen Kreises wird nach Realteil und Imaginärteil aufgelöst und in ein Koordinatensystem eingetragen. In Richtung steigender Werte von ω darf der kritische Punkt (-1; j0) auf der linken (negativen) Seite der Achse der Realteile nicht umschlungen bzw. berührt werden, dann ist der geschlossene Regelkreis stabil.
- Die Ermittlung der Stabilität eines Übertragungssystems mit der Ortskurve des Frequenzgangs dient dem mathematischen Systemverständnis, hat aber für die Stabilitätsbetrachtung keine Bedeutung mehr.
Grundlagen Mehrgrößensysteme
[Bearbeiten]Industrielle Prozesse können unterschiedliche abgegrenzte dynamische Systeme enthalten, die untereinander vermascht sind und mehrere Ausgangssignale und Eingangssignale haben. Solche Systeme werden im Gegensatz zu Eingrößensystemen als Mehrgrößensysteme bezeichnet. Die zugehörigen Übertragungsfunktionen stellen sich als Grafik symbolisch durch einen Block dar. Die Pfeile an den Ein- und Ausgängen eines Blockes zeigen die Richtung und die Verknüpfung des Signalflusses an. Das Gesamtsystem entspricht einem mathematischen Modell.
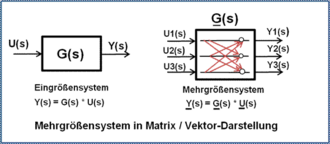
Hat ein Gesamtsystem beispielsweise je 2 Ein- und Ausgänge, deren Teilsysteme miteinander additiv vermascht sind, so kann die Übertragungsfunktion als Übertragungsmatrix geschrieben werden. Es werden P-kanonische und V-kanonische Strukturen unterschieden.
In Matrix-Vektor-Schreibweise ergibt sich folgende Darstellung als Übertragungsmatrix:
Allgemein lässt sich ein Mehrgrößensystem z. B. eine Regelstrecke mit beliebiger Anzahl von Eingängen (Stellgrößen) und Ausgängen (Regelgrößen) durch folgende Matrixgleichung beschreiben:
Die genannten Größen haben folgende Bedeutung:
- = Ausgangsgrößenvektor,
- = Strecken-Übertragungsmatrix,
- = Eingangsgrößenvektor.
Anwendung der Korrespondenztabelle der Laplace-Transformation
[Bearbeiten]Einschwingvorgänge dynamischer Systeme, die sich im Ruhezustand befinden und in einen bewegten Zustand überführt werden, können durch Differenzialgleichungen beschrieben werden. Ein wirksames Mittel, diese Differenzialgleichungen zu lösen, ist die Laplace-Transformation für den Fall leerer Energiespeicher (Anfangswerte = 0). Mit der Durchführung der Laplace-Transformation entsteht die Übertragungsfunktion mit G(s) = Y(s) / U(s) als das Verhältnis der Ausgangsgröße zur Eingangsgröße im sogenannte Bildbereich (s-Bereich). G(s) ist eine algebraische Gleichung in Form einer gebrochen-rationalen Funktion. Die Rücktransformation vom Bildbereich F(s) in den Zeitbereich f(t) wird als inverse Laplace-Transformation bezeichnet.
Die Korrespondenztabellen der Laplace-Transformation geben je nach Ausführlichkeit die Lösung der inversen Transformation vom Bildbereich in den Zeitbereich für zahlreiche Formen der Übertragungsfunktionen wieder. Das Zeitverhalten für die Systemausgangsgröße y(t) eines dynamischen linearen Übertragungssystems kann für ein gegebenes Eingangssignal u(t) aus den Laplace-Korrespondenztabellen für die entsprechende Funktion im Bildbereich F(s) (Produkt ) für den Zeitbereich f(t) bestimmt und berechnet werden.
Diese Korrespondenztabellen können im Fachbuchhandel erworben werden, stehen aber im eingeschränkten Umfang in fast jedem Fachbuch der Mathematik oder der Regelungstechnik zur Verfügung. Die korrespondierenden Gleichungen f(t) höherer Ordnung mit konjugiert komplexen Polen und Nullstellen sind zur leichteren Berechenbarkeit in mehrere Gleichungen aufgeteilt, weshalb in der Fachliteratur leider häufig unterschiedliche Formen und Gleichungssymbole verwendet werden.
Die Funktionen im Bildbereich F(s) der Transformationstafeln sind im Nenner und Zähler der Übertragungsfunktion G(s) als Linearfaktoren in Produktform dargestellt.
- Bei der Produktform der Pol-Nullstellen-Darstellung werden der Einfachheit halber anstelle der Bezeichnungen für Pole und Nullstellen die Anfangsbuchstaben des Alphabetes benutzt und negative Werte als stabile Systeme vorausgesetzt. Diese Buchstaben entsprechen Pole und Nullstellen gleichermaßen und unterscheiden sich als Pole oder Nullstellen dadurch, ob sie im Nenner oder Zähler der Übertragungsfunktion stehen.
- Bei der Produktform als Zeitkonstanten-Darstellung werden die Pole bzw. die Nullstellen mit T = 1 / sp bzw. T = 1 / sn umgerechnet. Die dabei entstehenden Faktoren unterliegen keiner Transformation in den Zeitbereich, müssen aber berücksichtigt werden.
- Die Linearfaktoren mit konjugiert komplexen Nullstellen werden zu einem Polynom so umgerechnet, das keine imaginären Größen entstehen.
Linearfaktoren der Laplace-Transformationstabellen
[Bearbeiten]Die Darstellung der Linearfaktoren ist in den Laplace-Korrespondenztabellen ist nicht einheitlich. Sie unterscheiden sich in der Pol- Nullstellendarstellung und insbesondere bei der Produktform mit konjugiert-komplexen Nullstellen. Es existieren in den Laplace-Transformationstabellen zwei verschiedene Schreibweisen in der Zeitkonstanten-Darstellung mit und der Frequenzdarstellung mit . Häufig werden für den Dämpfungsgrad D und im Zeitbereich zur Reduzierung der großen Gleichungen verschiedene griechische Buchstaben für Teillösungen verwendet.
Die korrespondierenden Gleichungen im Zeitbereich mit reellen Polen und Nullstellen sind sehr einfach zu berechnen. Dagegen führt das Produkt der Linearfaktoren mit konjugiert komplexen Nullstellen und Polen zu umfangreichen Gleichungen des Zeitbereichs.
Das Produkt der Linearfaktoren mit konjugiert komplexen Nullstellen oder Polen ist ein Polynom 2. Ordnung, das keine imaginären Anteile enthält und auch nicht in Linearfaktoren ohne imaginäre Größen zerlegbar ist.
Im Zähler und Nenner einer Übertragungsfunktion existieren folgende drei Formen von Linearfaktoren:
- {sn; sp} = 0, (Absolutglied des Polynoms fehlt),
- {sn; sp} = (reeller Wert der Pole und Nullstellen),
- {sn; sp} = (konjugiert komplexer Wert der Pole oder Nullstellen).
Negative Realteile der Pole bedeuten asymptotische Stabilität des Teilsystems.
Bei reellen Nullstellen oder Polen entsteht der Produktterm 1. Ordnung oder . Ist der Wert der Nullstelle sn oder der Pol sp negativ, lässt sich dafür auch schreiben, wenn a ein negativer Wert der Nullstelle oder Pol ist (stabiles System).
In den Transformationstabellen sind keine negativen Zeichen in den Produktformen der Übertragungsfunktionen enthalten. Die reellen Pole und Nullstellen in den Linearfaktoren werden mit den Anfangsbuchstaben des Alphabetes bezeichnet und entsprechen negativen Realteilen. Negative Zahlenwerte für die Zeichen (a, b, c, ...) würden positive Pole und Nullstellen bedeuten und damit Systeminstabilität.
Die Linearfaktoren in der Pol-Nullstellen-Darstellung der Transformationstabellen für reelle Pole und Nullstellen lauten: s + a.
Die Linearfaktoren in der Pol-Nullstellen-Darstellung der Transformationstabellen für konjugiert komplexe Pole und Nullstellen lauten wie folgt:
Zur Vermeidung imaginärer Größen in den Linearfaktoren werden die konjugiert komplexen Nullstellenpaare bzw. Polepaare multipliziert, damit das imaginäre Symbol verschwindet . Zur Übersichtlichkeit dieser Rechenoperation wird für den negativen Realteil der Nullstelle sn bzw. Pol sp die Hilfsgröße eingeführt. Der Wert des Imaginärteils bei Polen und Nullstellen bleibt .
Damit entstehen keine negative Zeichen in der Pol-Nullstellen-Darstellung des Polynoms.
Tabelle der drei Formen der Linearfaktoren in den Transformationstabellen
[Bearbeiten]Linearfaktoren
Ordnung des PolynomsPol-Nullstellen-Darstellung Zeitkonstanten-Darstellung Linearfaktor
ohne Absolutglied
oder der DGLLinearfaktor
(Reeller Pol
oder Nullstelle)
(a; b; c...) entsprechen negativen
Werten der Pole oder Nullstellen.
Verstärkungsfaktoren K unterliegen nicht der Transformation.Polynom 2. Ordnung
Produkt zweier Linearfaktoren
mit konjugiert komplexen
Polen oder Nullstellen
Normalform im Nenner oder Zähler:
Schreibweise mit
Beispiel Verzögerungsglied PT2KK:
Suchbegriff der Laplace-Korrespondenztabelle
[Bearbeiten]Für die Ermittlung des Zeitverhaltens eines dynamischen Systems wird die Übertragungsfunktion G(s) mit dem transformierten Eingangssignal U(s) multipliziert.
Die direkte Überführung einer Übertragungsfunktion F(s) über die Laplace-Korrespondenztabelle - ohne Multiplikation mit einem transformierten Testsignal - in den Zeitbereich f(t) ist immer die Impulsantwort (Gewichtsfunktion) y(t), weil 1 das transformierte Signal der Impulsfunktion ist.
Allgemein gilt für die inverse Transformation vom s-Bereich in den Zeitbereich der Suchbegriff:
- Transformierte Eingangssignale
Die üblichen Eingangssignale U(s) als Testsignale sind:
Impulsfunktion (Stoß):
Sprungfunktion:
Anstiegsfunktion (Rampe):
Korrespondenzen zur Laplace-Transformation (Auszüge)
[Bearbeiten]Laplace-Transformation-Korrespondenztabelle [8]
| s-Bereich F(s) |
Zeitbereich y(t); t > 0 | s-Bereich F(s) |
Zeitbereich y(t); t > 0 | |
|---|---|---|---|---|
| 1 | Dirac-Impuls | |||
| 1 / s | Sprung σ(t) = 1 | |||
| 1 / s² | Rampe t | |||
| - | - | |||
| | ||||
| |
Anmerkung: Die Systemantwort von Übertragungssystemen höherer Ordnung Ordnung mit konjugiert komplexen Polen und Nullstellen sind durch die analytischen Gleichungen f(t) der Laplace-Korrespondenztabellen wegen der zahlreichen trigonometrischen und exponentiellen Funktionen nur sehr zeitaufwendig zu berechnen. Die Anwendung der numerischen Berechnung mit Differenzengleichungen der Teilsysteme mittels eines Computers ist erheblich einfacher.
Berechnungsbeispiele mit den Laplace-Transformationstabellen
[Bearbeiten]Während das Zeitverhalten von dynamischen Systemen mit einfachen Polstellen sich leicht berechnen lässt, sind Übertragungssysteme mit Schwingungsanteilen wie beim PT2KK-Glied in der Korrespondenztabelle für f(t) manchmal schwierig zu lesen. Manche Korrespondenztabellen für F(s) beziehen sich auf die Pol-Nullstellen-Darstellungen, andere auf die Zeitkonstanten-Darstellungen. Instabile Übertragungsglieder 2. Ordnung mit positiven Nullstellen (d. h. Minuszeichen in der Übertragungsfunktion in Zeitkonstanten-Darstellung) sind in den Korrespondenztabellen der Fachliteratur selten - praktisch nie - angegeben.
Die grafische Darstellung der Sprungantwort (Übergangsfunktion) eines dynamischen Systems ist die häufigste bekannte Darstellung des System-Zeitverhaltens. Wird die korrespondierende Zeitfunktion in den Laplace-Korrespondenztabellen gefunden, kann durch Einsetzen verschiedener Werte für t das Systemverhalten für ein gegebenes Eingangssignal grafisch dargestellt werden.
Die Anwendung der Impulsantwort (Gewichtsfunktion) hat insbesondere Vorteile bei der Systemanalyse einer empirisch aufgenommenen Impulsantwort einer Regelstrecke durch Modellvergleiche.
Beispiel der Anwendung der Laplace-Korrespondenztabelle für ein dynamisches System mit reellen Polen[9]
Es ist darauf zu achten, dass manche Korrespondenztabellen im s-Bereich in der Pol-Nullstellen-
Darstellung oder Zeitkonstanten-Darstellung definiert sind. Verstärkungsfaktoren werden nicht
transformiert und sind im s-Bereich und Zeitbereich identisch.Gegeben: Übertragungsfunktion für zwei PT1-Glieder in Reihenschaltung:
Eingangssignal: Sprungfunktion U(s) = 1/s
Gesucht: Zeitverhalten der Systemausgangsgröße y(t) :
Lösung: Übergangsfunktion (Sprungantwort)
Die nachfolgende Gleichung für y(t) ergibt sich aus der Korrespondenztabelle:
- Anmerkung: Für a ≠ b gelten auch für Zahlenwerte der Pole und Nullstellen, die sich z. B. nur in der 10. Dezimalstelle nach dem Komma unterscheiden, vorausgesetzt es wird genau gerechnet! Diese Anwendung der Korrespondenztabelle ist erheblich einfacher, als die Ermittlung der Residuen (lat.: „das Zurückgebliebene“) über die Partialbruchzerlegung!
- Beispiel der Umrechnung des Zeitverhaltens der Pol-Nullstellen-Darstellung zur Zeitkonstanten-Darstellung eines PT1-Gliedes
Die Übertragungsfunktion eines PT1-Gliedes kann als Pol-Nullstellen-Darstellung
oder als Zeitkonstanten-Darstellung mit gewählt werden.Gegeben: Übertragungsfunktion:
Eingangssignal: Impulsfunktion U(s) = 1
Lösung im Zeitbereich:
Die zugehörigen Zeit-Impulsfunktion laut Transformations-Korrespondenztabelle lautet:Gesucht:
Wie lautet das Zeitverhalten für die Übertragungsfunktion ,
wenn keine Transformationstabelle zur Verfügung steht?Lösung:
Faktoren wie T im Zähler der Übertragungsfunktion unterliegen nicht der Transformation.
Folglich muss die Zeitfunktion in Relation zu um den Faktor 1 / T berücksichtigt werden.
Beispiel des Zeitverhaltens eines PT2KK-Gliedes mit Schwingeigenschaften:
Gegeben: Normalform der Übertragungsfunktion eines -Schwingungsgliedes:
Eingangssignal: Sprungfunktion U(s) = 1 / s
Suchfunktion laut Laplace-Transformationstabellen:
Lösung im Zeitbereich:
Durch Faktorenvergleich mit der Normalform können die erforderlichen Parameter wie D, ω0, ωe und Φ für die
korrespondierende Gleichung des Zeitverhaltens f(t) berechnet werden.Die zugehörigen Sprungantwort y(t) für ein -Schwingungsglied laut Korrespondenztabelle f(t) lautet:
- .
Ein Übertragungssystem 2. Ordnung mit Proportionalverhalten und Schwingeigenschaften setzt voraus,
dass der Dämpfungswert 0 < D < 1 beträgt.
Anmerkung: Die Systemantwort von Übertragungssystemen für Systemen 2. Ordnung und beliebiger höherer Ordnung sind durch die analytischen Gleichungen f(t) der Laplace-Korrespondenztabellen wegen der zahlreichen trigonometrischen und exponentiellen Funktionen nur sehr zeitaufwendig zu berechnen. Die Anwendung der numerischen Berechnung mit Differenzengleichungen der Teilsysteme mittels eines Computers ist erheblich einfacher.
Bedeutung der Pole und Nullstellen der Übertragungsfunktion für das Zeitverhalten
[Bearbeiten]Bedeutung der Lage der Pole und Polpaare bei Verzögerungs-Systemen 1. und 2. Ordnung
[Bearbeiten]Die Nullstellen eines Nennerpolynoms bezeichnet man als Pole. Die Zeitkonstanten-Darstellung einer Übertragungsfunktion errechnet sich aus den Polen und Nullstellen der faktoriellen Darstellung der verschiedenen Linearfaktoren.
Die Pol-Nullstellen-Darstellung und die Zeitkonstanten-Darstellung zeigen einen wesentlichen Unterschied in der Anwendung:
- Die Pole- Nullstellen-Darstellung der Übertragungsfunktion bedeutet für die Änderung von Zahlenwerten der Pole und Nullstellen, dass sich die Verstärkungsfaktoren gleichzeitig ändern.
- Die Zeitkonstanten-Darstellung der Übertragungsfunktion bezieht sich nur auf die Größe der Zeitkonstanten, die Verstärkung K der Übertragungsfunktion ändert sich nicht.
Die Übertragungsfunktion G(s) ist eine Funktion, welche die komplexe Variable auf einen komplexen Wert abbildet. G(s) kann in einen Realteil und einen Imaginärteil zerlegt werden.
Die Lage der reellen und komplexen Pole und Nullstellen lässt sich im s-Diagramm darstellen.
Die Pole eines Nennerpolynoms einer Übertragungsfunktion sind gleichzeitig die Lösung des Systems. Die Pole bzw. die Lage der Pole im s-Diagramm bestimmen unter anderem das Zeitverhalten und die Stabilität des Systems, die Nullstellen im Zähler der Übertragungsfunktion bestimmen die Größe der Amplituden.
Beispiel des Systemverhaltens 2. Ordnung durch Lage der Pole s1/2 und der Dämpfung D [10]
Ein Verzögerungsglied 2. Ordnung hat die Übertragungsfunktion:
Wird an Stelle der Zeitkonstante T die Eigenfrequenz ω0 = 1 / T gesetzt, so entsteht die Übertragungsfunktion:
Realteil und Imaginärteil der Pole
Die Pole bzw. Polpaare des PT2-Gliedes lassen sich durch die nachfolgende Gleichung in Realteile und Imaginärteile zerlegen:
Wie aus der Gleichung sichtbar, sind Realteil und Imaginärteil von ω0 und D abhängig und können nicht beliebig unabhängig voneinander für eine Übertragungsfunktion gewählt werden. Das Systemverhalten mit Schwingungsanteilen ist durch die Lage der Polpaare im s-Diagramm auf der Re(s)-Achse und Im(s)-Achse bestimmt.
Systemverhalten eines Verzögerungsgliedes 2. Ordnung durch die Größe der Dämpfung
Sind Zahlenwerte der Übertragungsfunktionen eines PT2-Gliedes gegeben, lassen sich daraus der Wert der Zeitkonstante T bzw. ω0 = 1 / T und die Größe der Dämpfung D bestimmen, die das zeitliche Systemverhalten festlegen. Bedingt durch die Größe des Wertes der Dämpfung D > 0, D = 0 und D < 0 lässt sich die Übertragungsfunktion des PT2-Gliedes in neue Gleichungsformen aufspalten. Aus den Werten ω0 und D lassen sich die Pole bzw. Polpaare aus der Übertragungsfunktion bestimmen, deren Lage im s-Diagramm eindeutigen Stabilitätskriterien zugeordnet sind.
Folgende Dämpfungswerte bestimmen das Zeitverhalten und die Normalform der Gleichung der Übertragungsfunktion:
- Dämpfung D > 1:
- Die Übertragungsfunktion lässt sich in zwei PT1-Glieder mit zwei unterschiedlichen Zeitkonstanten aufspalten. Sie enthält zwei negative reelle Pole.
- Dämpfung D = 1:
- Grenzwert für einen Doppelpol. Die Übertragungsfunktion lässt sich in zwei PT1-Glieder mit zwei gleichen Zeitkonstanten aufspalten. Sie enthält einen negativen Doppelpol.
- Dämpfung 0 < D < 1:
- Die Übertragungsfunktion enthält ein konjugiert komplexes Polpaar mit negativem Realteil. Das System schwingt gedämpft.
- Dämpfung D = 0:
- Die Übertragungsfunktion hat nur ein Polpaar ohne Realteil. Das System schwingt ungedämpft mit konstanter Amplitude.
- Dämpfung -1 < D < 0:
- Das System ist instabil mit positivem konjugiert komplexem Polpaar. Das System schwingt mit zunehmender Amplitude.
- Dämpfung D = - 1:
- Das System enthält einen instabilen positiven reellen Doppelpol. Die Systemantwort steigt progressiv bis zu einer endlichen Begrenzung.
- Dämpfung D = < -1:
- Das System enthält zwei instabile positive reelle Pole. Die Systemantwort steigt progressiv bis zu einer endlichen Begrenzung.
Systemverhalten bei Änderung der Realteile und Änderung der Imaginärteile
Nachfolgend wird das System-Zeitverhalten von Systemen des PT1- und des PT2kk-Gliedern als Funktion der Polstellen-Lage und der Polpaar-Lage von Zahlenwerten im s-Diagramm für Re(s) < 0, Re(s) = 0 und Re(s) > 0 dargestellt.
Zunehmende Zahlenwerte der Lage der Realteile der Polpaare bei konstanten Imaginärteilen in der negativen s-Halbebene:
- Der Dämpfungswert wird größer und damit die Überschwingung kleiner,
- Die Schwingungsperioden bleiben gleich bei konstanten Imaginäranteilen.
Zunehmende Zahlenwerte der Lage der Imaginärteile der Polpaare bei konstanten Realteilen in der negativen s-Halbebene:
- Der Dämpfungswert wird kleiner und damit die Überschwingung größer,
- Die Periodendauer wird kleiner und damit die Schwingfrequenz größer.
Die bekannten algebraischen Gleichungen der Übertragungsfunktionen des PT1- und PT2kk-Gliedes als Phasenminimum-Systeme ändern ihre Form, wenn positive Pole auftreten und werden zu Nichtphasenminimum-Systemen.
Anmerkung: PT1-, PT2-Verzögerungsglieder mit positiven Polen sind instabil und haben damit kein verzögerndes sondern ein beschleunigendes Zeitverhalten. Ein PT1-Glied - bezeichnet aus den Abkürzungen "Proportional", Zeitkonstante = "T" und "Zahl der Ordnung" - im Zusammenhang mit positiven Polen als instabiles Verzögerungsglied zu bezeichnen, ist trotz der ähnlichen mathematischen Schreibweise nicht korrekt.
Die in der Tabelle dargestellten grafischen Sprungantworten wie auch die nicht dargestellten Impulsantworten sind messbar und berechenbar.
Tabellarische Darstellung der Polstellen- und Polpaar-Lage der Übertragungsfunktionen und des System-Zeitverhaltens für Verzögerungssysteme 1. und 2. Ordnung:
[Bearbeiten]Bedeutung der Lage der Pole und Polpaare von Verzögerungs-Systemen höherer Ordnung
[Bearbeiten]Übertragungsfunktionen höherer Ordnung in Polynomdarstellung lassen sich durch die Nullstellenbestimmung in Linearfaktoren zerlegen. Für die Bestimmung der Pole und Nullstellen von Übertragungsfunktionen kann man sich fertiger Rechenprogramme für Polynome bis 4. Ordnung bedienen. Derartige Programme findet man auch im Internet unter dem Suchbegriff „Nullstellen von Polynomen“.
Die Überführung der faktorisierten Übertragungsfunktion für ein gegebenes Eingangssignal in den Zeitbereich erfolgt über Laplace-Transformationstabellen. Enthalten die Übertragungsfunktionen mehrfache Pole und Nullstellen oder auch konjugiert komplexe Pole, können umfangreiche trigonometrische Berechnungen zur Ermittlung der Systemausgangsgröße erforderlich werden.
Bei Verwendung der Übertragungsfunktion der Partialbruchform ist die Übertragung der Teilbrüche in den Zeitbereich sehr einfach, dafür ist die Durchführung der Partialbruch-Zerlegung bei Systemen höherer Ordnung aufwändig. Dies gilt besonders bei Linearfaktoren 1. und 2. Ordnung im Zähler der Übertragungsfunktion.
Identische phasenminimale Linearfaktoren im Zähler und Nenner einer Übertragungsfunktion können gegeneinander gekürzt werden (Pol-Nullstellen-Kompensation). Damit vereinfacht sich die Übertragungsfunktion. Dies gilt nicht für nichtphasenminimale Linearfaktoren.
Grundsätzlich interessiert für das Zeitverhalten folgende globale Pol-Eigenschaft:
Eine Übertragungsfunktion G(s) höherer Ordnung hat n verschiedene reelle Pole:
- Alle Pole sind negativ, d. h. für alle .
- Die Sprungantwort der Systemausgangsgröße in Abhängigkeit vom Eingangssignal strebt exponentiell gegen einen Maximalwert. → Stabiles globales P-Verhalten!
- Ein Pol ist gleich Null, alle anderen sind negativ.
- Die Sprungantwort der Systemausgangsgröße in Abhängigkeit vom Eingangssignal verläuft erst exponentiell, dann linear gegen unendlich. → Grenzstabiles globales I-Verhalten!
- Mindestens ein Pol ist positiv, alle anderen sind beliebig.
- Die Sprungantwort der Systemausgangsgröße in Abhängigkeit vom Eingangssignal strebt exponentiell gegen unendlich. → Global instabiles Verhalten!
Übertragungsfunktion G(s) höherer Ordnung mit einem konjugiert komplexen Polpaar:
- Alle Pole haben einen negativen Realteil:
- Die Sprungantwort der Systemausgangsgröße in Abhängigkeit vom Eingangssignal strebt als gedämpfte Schwingung gegen einen Maximalwert. → Global stabiles P-Verhalten!
- Konjugiert komplexes Polpaar hat einen Realteil gleich Null:
- Die Sprungantwort der Systemausgangsgröße in Abhängigkeit vom Eingangssignal verläuft als Dauerschwingung mit der Kreisfrequenz ω. → Oszillatorisch grenzstabiles Verhalten!
- Mindestens ein Pol hat einen positiven Realteil für das konjugiert komplexe Polpaar:
- Die Sprungantwort der Systemausgangsgröße in Abhängigkeit vom Eingangssignal verläuft als eine exponentiell aufklingende Dauerschwingung mit der Kreisfrequenz aus. → Oszillatorisch instabiles Verhalten!
Übertragungsfunktion mit dem Deltaimpuls
Mit der Gewichtsfunktion (Impulsantwort) mit sind folgende Schlussfolgerungen für das Zeitverhalten und die Stabilität des Systems ableitbar:
- Bedeutung des Realteils und Imaginärteils der Polstellen:
- Ist mindestens ein , so schwingt das System.
- Sind alle , so ist das System stabil. Der Eingangsimpuls klingt zeitlich ab.
- Mit mindestens einem ist das System instabil. Der Eingangsimpuls wächst zeitlich unbegrenzt an.
- Ist mindestens ein und alle anderen , so ist das System grenzstabil. Es geht asymptotisch in einen konstanten Wert oder eine ungedämpfte Schwingung über.
- Je weiter links in der negativen Halbene von liegt, desto schneller klingt der entsprechende Anteil der Gewichtsfunktion ab.
- Die Lage des Realteils der Polstellen bestimmt die Dynamik, und der Imaginärteil bestimmt die Frequenz der Schwingungen des Systems.
- Bedeutung der Nullstellen:
- Je weiter die Nullstellen von der Polstelle in der -Ebene liegen, desto stärker wird der Anteil an der Gewichtsfunktion.
- Nullstellen mit positivem Realteil (nichtpasenminimales Verhalten) führen zu einem schwer regelbaren Verhalten.
Experimentelle Ermittlung
[Bearbeiten]Die Übertragungsfunktion ist im Gegensatz zum Frequenzgang nicht direkt messbar, kann aber mit Methoden der Systemidentifikation unter anderem aus der Sprungantwort bestimmt werden.
Einzelnachweise
[Bearbeiten]- ↑ Fachbuch: Lunze "Regelungstechnik 1", Systemtheoretische Grundlagen, Analyse und Entwurf einschleifiger Regelungen. Kapitel: „Laplace-Transformation", 7. Auflage, Springer, 2008, ISBN 978-3-540-68907-2.
- ↑ Prof. Manfred Ottens, TFH Berlin: Vorlesungsmanuskript "Grundlagen der Systemtheorie", Kapitel: „Die Übertragungungsfunktion", 227 Seiten, 2008.
- ↑ Prof. Dr.-Ing. Oliver Nelles, Universität Siegen: Vorlesungsmanuskript "Mess- und Regelungstechnik I", Kapitel 5: „Übertragungsfunktion“, 446 Seiten vom 8. Oktober 2009.
- ↑ Prof. Dr.-Ing. W. Schumacher, Technische Universität Braunschweig, Institut für Regelungstechnik, Vorlesungsmanuskript "Grundlagen der Regelungstechnik", Kapitel: „4.3 ¨Ubertragungsfunktion und Differenzialgleichung“, 309 Seiten 24. Oktober 2008.
- ↑ Lutz / Wendt: Taschenbuch der Regelungstechnik, Kapitel: Laplace-Transformation, Unterkapitel "Partialbruchzerlegung".
- ↑ Prof. Dr.-Ing. H. Peter Jörgel, TU Wien: Vorlesungsmanuskript Mess- und Regelungstechnik VT, Kapitel: „Laplace-Transformation“, 164 Seiten, ausgestellt 2006.
- ↑ Fachbuch: Lutz / Wendt: Taschenbuch der Regelungstechnik, 12. Auflage. Verlag Europa-Lehrmittel, 2021, ISBN 978-3-8085-5870-6. Kapitel: "Frequenzgang von Übertragungselementen".
- ↑ Siehe Fachbuch: Lutz / Wendt: Taschenbuch der Regelungstechnik, Kapitel: "Mathematische Methoden zur Berechnung von Regelkreisen", Unterkapitel: "Tabellen für die Laplace-Transformation", Auszüge.
- ↑ Lutz / Wendt: Taschenbuch der Regelungstechnik, Kapitel: Laplace-Transformation.
- ↑ Siehe Fachbuch: Lunze / Regelungstechnik 1: Kapitel: "Eigenschaften wichtiger Übertragungsglieder im Frequenzbereich".
Literatur
[Bearbeiten]- Jan Lunze: Regelungstechnik 1: Systemtheoretische Grundlagen, Analyse und Entwurf einschleifiger Regelungen. 7. Auflage. Springer, 2008, ISBN 978-3-540-68907-2.
- Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink. 12. Auflage. Europa-Lehrmittel, 2021, ISBN 978-3-8085-5870-6.
- Manfred Reuter, Serge Zacher: Regelungstechnik für Ingenieure: Analyse, Simulation und Entwurf von Regelkreisen. 12. Auflage. Vieweg+Teubner, 2008, ISBN 3-8348-0018-X.
- Heinz Unbehauen: Regelungstechnik I. Friedr. Vieweg & Sohn Verlagsgesellschaft mbH, 1997, ISBN 3-528-83332-7.
Numerische Berechnung dynamischer Systeme
[Bearbeiten]Numerische Berechnung dynamischer Systeme
[Bearbeiten]Relativ einfache Übertragungssystem-Strukturen mit nichtlinearen Elementen sind durch konventionelle Rechenmethoden im kontinuierlichen Zeitbereich nicht mehr geschlossen lösbar. Mit handelsüblichen Personal-Computern kann das Verhalten beliebig vermaschter Systemstrukturen mittels numerischer Berechnung relativ einfach ausgeführt werden.
Vorteile der Simulation von Systemen mit Differenzengleichungen
- Einfache mathematische Anforderungen durch algebraische Operationen,
- Behandlung kombinierter LZI-Systeme mit nichtlinearen Systemen,
- Darstellung eines Regelkreises als Blockschaltbild mit Eintrag der Differenzengleichung und logischen Operatoren,
- Behandlung von mehrschleifigen Systemen (MIMO-Systeme),
- Einfache Lösung einer gewöhnlichen Differenzialgleichung höherer Ordnung mit Anfangswerten. Da es sich um bestimmte Integrale handelt, müssen keine Integrationskonstanten wie bei der klassischen Lösung einer homogenen Differenzialgleichung ermittelt werden.
- Bei tabellarischer Darstellung der Berechnung der einzelnen Teilsysteme völlige Durchsicht des inneren System-Bewegungsablaufs zum Beispiel eines Regelkreises. Bei Anwendung der Tabellenkalkulation unmittelbare grafische Darstellung der Systemausgangsgröße y(k) = f(k*∆t) mittels verfügbarer grafischer Werkzeuge.
Methode der numerischen Berechnung
[Bearbeiten]- Simulation dynamischer Systeme
Dynamische zeitinvariante Systeme mit konzentrierten Energiespeichern werden durch gewöhnliche Differenzialgleichungen vollständig beschrieben. Die Lösung der Differenzialgleichung, die Ausgangsgröße y(t), ist für ein gegebenes Eingangssignal u(t) eine Funktion der Zeit.
Werden die Differenziale der Ausgangsgröße y(t) einer Differenzialgleichung durch kleine Zeit-Differenzen (Differenzenquotienten Δy / Δt) als diskretisierte Zeit ersetzt, entsteht eine numerisch lösbare Differenzengleichung in Annäherung an die Differenzialgleichung.
Differenzengleichungen oder eine Kette von Differenzengleichungen, die mehrere hintereinander geschaltete Teilsysteme beschreiben, lassen die Ausgangsgröße algebraisch für einen kleinen Zeitschritt errechnen. Die numerische Gesamtlösung des Systems erfolgt - bei einfachen Differenzengleichungen - rekursiv (sich selbst aufrufend) über viele Berechnungsfolgen in je kleinen konstanten Zeit-Stufen. Die Form der Gesamt-Lösung ist damit tabellarisch. Alle Zeilen enthalten die gleichen Differenzengleichungen, alle Spalten berechnen die Folgen k (0, 1, 2, 3, ...kMAX). Der gesamte betrachtete Zeitraum der numerischen Lösung beträgt . Die Ausgangsgröße y(k, Δt) folgt in Amplituden-Stufen im zeitlichen Abstand Δt einer jeden Berechnungsfolge.
Die tabellarische Form der numerischen Lösung erlaubt auch die Berechnung nichtlinearer statischer Systeme, indem die nichtlineare Beziehung als Wertetabelle der Tabellenspalte der Folge k zugeordnet wird. Ebenso ist die Berechnung der Totzeit eines Systems durch Verschiebung der Zeilen mit geeigneten Programmbefehlen möglich.
Andere Methoden bedienen sich zur besseren Approximation z. B. an Stelle des Rechteck-Verfahrens (Explizites Eulerverfahren) des Trapezflächenverfahrens (Heun-Verfahren), des Mehrschrittverfahrens (Runge-Kutta-Verfahren) und anderer Verfahren.
Grund der aufwendigeren Approximationsverfahren ist die erzielbare höhere Genauigkeit und damit Reduzierung der Rekursionsfolgen, was bei langsamen Rechnern bei Echtzeitberechnungen erforderlich sein kann.
- Digitale Regelung online
Bei Echtzeitberechnungen, beispielsweise mit einem programmierbaren digitalen Regler, der auf eine Hardware-Regelstrecke wirkt, wird die Diskretisierungszeit durch die "Abtastzeit" ersetzt.
Digitale Regler werden durch Mikrocomputer realisiert. Der Computer benötigt für die digitale Signalverarbeitung Ein- und Ausgangsschnittstellen, um das kontinuierliche Eingangssignal – die Regelabweichung – mittels A/D-Wandler zyklisch abzutasten und digital mit speziellen Programmiersprachen berechnen zu können. Der Mikrocomputer verarbeitet die abgetasteten Signalwerte als Eingangsfolgen mit Hilfe von Differenzengleichungen zu Ausgangsfolgen. Die so schrittweise errechneten Stellgrößen-Anteile jeder Komponente der Ausgangsfolge werden über einen D/A-Wandler und ein Halteglied wieder als feingestuftes quasi kontinuierliches Signal an die meist kontinuierlich wirkende Regelstrecke geliefert. Bei schnellen Regelstrecken spielen die Systemgeschwindigkeiten des Rechners, der A/D-D/A-Wandler, die Sample-and-Hold-Schaltung, wie auch die verwendeten Differenzengleichungen beziehungsweise deren Approximations-Algorithmen eine große Rolle.
Zeitdiskretisierung
[Bearbeiten]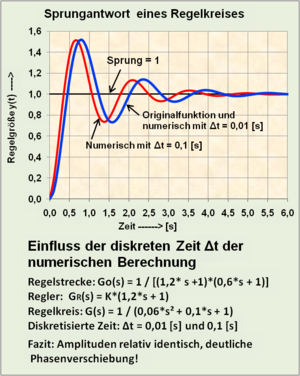
Die Zeitdiskretisierung eines dynamischen zeitinvarianten Übertragungssystems bedeutet der Übergang der Berechnung eines kontinuierlichen Systems f(t) mit unendlicher hoher Auflösung zu einem System f(k; ∆t) mit einer endlichen Auflösung eines fortlaufenden konstanten Zeitintervalls ∆t.
Bei der Simulation von dynamischen Übertragungsmodellen ist das diskrete Zeitintervall ∆t ein konstanter Zahlenwert, der unabhängig von der tatsächlichen Rechengeschwindigkeit des Rechners ist und mit der Berechnungsfolge k = (0, 1, 2, 3, ...kMAX) ständig fortlaufend aufgerufen wird. Die aktuelle Zeit einer bestimmten Folge beträgt:
Das Zeitintervall ∆t muss genügend klein gegenüber der kleinsten Systemzeitkonstante sein, damit die Systembewegungen auch vollständig erfasst werden können, bzw. der Approximationsfehler gegenüber dem Verlauf der analytischen Funktion gering ist. ∆t muss kleiner als die kleinste Systemzeitkonstante T sein, anderenfalls ergeben sich zusätzlichen Berechnungsfehler.
Berechnungsfolge
[Bearbeiten]Die Folge ist bestimmt, wenn die Beziehung der Anwendung (Bildungsgesetz) bekannt ist. Differenzengleichungen des Verfahrens "Euler-Rückwärts" werden rekursiv für ein Zeitintervall von k = 0 bis kMAX fortlaufend berechnet.
In einer Folge k = (0, 1, 2, 3,…kMAX) werden beliebig viele zeitdiskrete Einzelsysteme eines Gesamtsystems hintereinander für ein gleiches, konstantes Zeitintervall ∆t mittels Differenzengleichungen berechnet. Danach erfolgt die gleiche Berechnung der Einzelsysteme des Gesamtsystems mit der nächsthöheren Folge und bezieht sich dabei auf die vorhergehende Folge (k-1).
Für explizite (direkt, eindeutig) Approximationsalgorithmen bezieht sich die Ausgangsgröße eines Einzelsystems y(k) auf die zurückliegende Folge y(k-1).
Für implizite (mit enthalten, mit gemeint) Approximationsalgorithmen wird die unbekannte Ausgangsgröße y(k+1) durch Iterationsverfahren bestimmt und auf y(k) zurückgerechnet.
Jedes Einzelsystem mit dem Ausgangssignal y(k) = f(System, k, ∆t, u(k)) wird einzeln berechnet.
Für eine Systemkette unterschiedlichster Strukturen der gleichen Folge k ist jedes Ausgangssignal y(k) eines Systems für das nachfolgende System das Eingangssignal u(k). Das Eingangssignal u(k) einer Systemkette ist meist ein Testsignal oder die Führungsgröße w(k). Jedes Eingangssignal muss ebenfalls eine Funktion von ∆t und k eine zeitdiskrete Größe sein.
Anmerkung:
- Die mit Folge k bezeichnete Größe wird auch gelegentlich in der Fachliteratur auch mit n und das Zeitintervall ∆t mit T bezeichnet.
- Alle Signalgrößen wie zum Beispiel das System-Eingangssignal U(s) und das System-Ausgangssignal Y(s) im s-Bereich werden in der zeitdiskreten Darstellung als u(k,Δt) und y(k,Δt) dargestellt. Um die Indizierungen in den Differenzengleichungen noch übersichtlicher zu gestalten (wegen der Bezüge auf die Folgen k, k-1, k+1) werden für die Signalbezeichnungen die indizierte Größe der diskreten Zeit Δt fortgelassen. y(k) und u(k) bedeuten immer aktuelle Werte eines Signals einer unbestimmten Folge einer Differenzengleichung. Die Signale y(k-1) und u(k-1) bedeuten eine zurückliegende Folge gegenüber dem aktuellen Wert einer Signalfolge.
Analyse eines linearen zeitinvarianten Übertragungssystems
[Bearbeiten]Beispiel einer Übertragungsfunktion der Polynomdarstellung und der Zerlegung in die Pol-Nullstellen-Darstellung mit reellen Linearfaktoren:
Polynomdarstellungen G(s):
- Sind in der Polynomdarstellung alle Ableitungen und zugehörige Koeffizienten lückenlos mit positivem Vorzeichen vorhanden, stellt die Übertragungsfunktion für die Exponenten n > m ein zeitverzögerndes asymptotisch stabiles System dar.
- Fehlt das Absolutglied im Nennerpolynom (), kann die Variable s aus dem Nennerpolynom ausgeklammert werden. Dieses Gesamtverhalten des Systems wird als "globales integrierendes Systemverhalten" bezeichnet.
- Fehlt das Absolutglied im Zählerpolynom (), kann die Variable s aus dem Zählerpolynom ausgeklammert werden. Dieses Gesamtverhalten des Systems wird als "globales differenzierendes Systemverhalten" bezeichnet.
- Hat ein Teilsystem der Polynomdarstellung im Nenner bei der Polstellenzerlegung ein konjugiert-komplexes Polpaar , so stellt diese Übertragungsfunktion für die Exponenten n > m ein zeitverzögerndes asymptotisch stabiles, gedämpft schwingendes System dar.
Eine Nullstelle des Zählerpolynoms sn oder ein Pol des Nennerpolynoms sp kann bei Stabilität des Teilsystems (negativer Realteil der Pole und Nullstellen) folgende drei Formen von Zahlenwerten einnehmen:
Einfluss der Zahlenwerte von Nullstellen und Polen:
Nullstellen; Pole Linearfaktoren in
Pol- NullstellendarstellungErklärung Absolutglied des Polynoms fehlt Reeller Wert der Pole oder Nullstellen Konjugiert komplexer Wert der Pole oder Nullstellen
Der Realteil einer Nullstelle oder eines Poles wird üblich mit und der Imaginärteil mit bezeichnet. Die angegebenen 3 Formen der Linearfaktoren können einfach und mehrfach auftreten.
Bei der Berechnung der Pole und Nullstellen aus Polynomen beispielsweise aus der gemischt quadratischen Gleichung (pq-Gleichung) können je nach Zahlenwerten reelle und konjugiert komplexe Werte entstehen. Die Polynome mit konjugiert komplexen Nullstellen oder Polen werden zur einfacheren Berechenbarkeit zu quadratischen Termen zusammengefasst, in denen nur reelle Koeffizienten auftreten.
Entstehung der Schwingungsgleichung im Nenner der Polynomdarstellung:
Ein dynamisches System ist intern stabil, wenn alle (Teil-)Übertragungsfunktionen nur Pole in der linken s-Halbebene haben. Negative Zahlenwerte des reellen Anteils der Pole und Nullstellen bedeuten Stabilität des Teilsystems. Werden negative Zahlenwerte der Pole und Nullstellen eingesetzt, entstehen positive Linearfaktoren. Bei stabilen Systemen ist der Wert von negativ.
Die konjugiert komplexe Polstelle mit negativem Realteil lautet:
Damit enthält die Schwingungsgleichung nur positive Terme:
Bei negativen Werten der Pole und Nullstellen kann die Übertragungsfunktion algebraisch mit beziehungsweise in die Zeitkonstanten-Darstellung umgerechnet werden:
Beispiel der allgemeinen Form der Zeitkonstantendarstellung mit reellen Linearfaktoren:
Die Zeitkonstanten-Darstellung errechnet sich direkt aus der Pol-Nullstellendarstellung, indem der Produktterm so umgeformt wird, dass beide Formen mathematisch identisch sind: Der Produktterm s - sn wird so umgestellt, dass der Reziprokwert 1/sn = T gebildet wird. Die Variable a entspricht der Nullstelle oder der Polstelle mit negativem Realteil.
Der Produktterm in der Zeitkonstanten-Darstellung mit negativem Wert der Polstelle sP (Term im Nenner asymptotisch stabiles System) lautet damit:
- .
Bei der Zeitkonstantendarstellung des Linearfaktors werden die Terme positiv dargestellt. Dies setzt voraus, dass die Realanteile der zugehörigen Nullstellen und Pole negativ sind.
Dieses Gesamtsystem wird für n > m (Anzahl der differenzierenden Elemente ist kleiner als die Anzahl der verzögernden Elemente) als "globales proportionales Systemverhalten" bezeichnet.
Es wird aus der Systemtheorie der Analyse der Übertragungsfunktion gezeigt, dass nur drei verschiedene nicht mehr zerlegbare Polynom-Produkte entstehen, die ein unterschiedliches Verhalten haben, ob sie im Nenner oder Zähler der Übertragungsfunktion stehen. Alle Übertragungsfunktionen G(s) höherer Ordnung setzen sich aus diesen drei unterschiedlichen Polynomprodukten zusammen. Bereits aus den zwei Linearfaktoren 1. Ordnung vom Typ und , jeweils im Zähler oder im Nenner stehend, lassen sich sämtliche phasenminimale lineare Übertragungssysteme oder verschachtelte Übertragungsfunktionen oder Regelsysteme mit Rückführungen nachbilden, auch -Schwingungsglieder durch einen Hilfsregelkreis mit -Glied und -Glied.
Linearfaktoren in der Zeitkonstantendarstellung:
Typ Linearfaktor Bedeutung im Zähler Bedeutung im Nenner Differenzierer, D-Glied Integrator, I-Glied Proportionales Differentiales-Glied; PD1-Glied Verzögerung, PT1-Glied
(besteht aus 2 Linearfaktoren)PD2-Glied: für 0 < D < 1
mit konjugiert komplexen NullstellenSchwingungsglied PT2-Glied: für 0 < D < 1
mit konjugiert komplexen Polen
Die Berechnung der Ausgangsgröße y(t) einer gegebenen Übertragungsfunktion G(s) und gegebenen Eingangssignal U(s) erfolgt über die inverse Laplace-Transformation.
Für y(t) lautet der Suchbegriff für die inverse Transformation in der Laplace-Transformationstabelle für den Zeitbereich:
Verstärkungsfaktoren K einzelner Teilsysteme im s-Bereich haben kein Zeitverhalten und können zusammengefasst werden.
Lineare dynamische Systeme können aus folgenden 6 verschiedenen Teilsystemen G(s) bestehen:
I-Glied D-Glied PT1-Glied, PD1-Glied PT2kk-Glied PD2kk-Glied
Die dargestellten Systeme mit differenzierender Wirkung, wie das -Glied, -Glied und -Glied, sind ideale Übertragungsglieder, die technisch so nicht realisierbar sind. Für eine Simulation am Computer lässt sich aber mit den idealen differenzierenden Übertragungssystemen vortrefflich rechnen.
Das Modell eines beliebigen Übertragungssystems wird üblicherweise zum besseren Verständnis in Funktionsblöcken dargestellt. In Reihe geschaltete Teilsysteme in Blockstruktur wirken multiplikativ, parallelgeschaltete Teilsysteme additiv. Wird das Ausgangssignal eines Teilsystems in den Eingang des von links nach rechts angeordneten nächsten Teilsystems gegeben und das Ausgangssignal der Systemkette auf den System-Eingang zurückgeführt, handelt es sich um eine Kreisschaltung mit positiver (nichtphasenminimale) oder negativer (phasenminimale) Rückkopplung.
Für die numerische Berechnung der dargestellten Übertragungsglieder G(s) des s-Bereiches in den Zeitbereich werden Differenzengleichungen verwendet, die aus den Differenzialgleichungen der zugehörigen Übertragungsfunktionen entwickelt werden.
Fazit:
Es existieren nur 3 Formen von Linearfaktoren - jeweils im Zähler und Nenner der Übertragungsfunktion - also 6 Formen von Elementarsystemen oder deren Vielfache in einem linearen dynamischen System. Gleiche Formen von Linearfaktoren mit gleichen Zeitkonstanten im Zähler und Nenner der Übertragungsfunktion G(s) stehend, kompensieren sich vollständig zu 1.
Das gilt auch für die Anwendung diesen Linearfaktoren zugehörigen Differenzengleichungen zur Berechnung der Ausgangsgröße für ein Zeitintervall im diskreten Zeitbereich bei gegebener Eingangsgröße. In diesem Fall existieren je drei Formen von Differenzengleichungen mit verzögerndem oder differenzierendem Systemverhalten. Die Differenzengleichung mit differenzierendem und verzögerndem Verhalten bei gleichen Zeitkonstanten kompensieren sich vollständig.
Einführung Differenzengleichungen
[Bearbeiten]Differenzengleichungen der einfachsten Art beziehen sich auf die Differenzialgleichungen der Linearfaktoren G(s) erster Ordnung, deren Differentialquotienten durch Differenzenquotienten ersetzt wurden. Das Ergebnis der Ausgangsgröße eines Systems für eine gegebene Eingangsgröße wird rekursiv für die Folgen im zeitlichen Abstand berechnet. Die kontinuierlichen mathematischen Operationen der Integration und Differentiation werden zeitdiskret durch Summen- und Differenzenbildung angenähert.
Je nach Anwendung des expliziten oder impliziten Eulerverfahrens erfolgt die Approximation (Annäherung) an die Integrationsfunktion schrittweise durch einen über Differenzengleichungen errechneten Wert zwischen zwei Rekursionsfolgen k-1 zu k oder k+1 zu k.
Meistens wird zur Aufstellung der Differenzengleichungen das explizite Euler-Rückwärtsverfahren verwendet. Nach diesem Verfahren können aus den zugehörigen Differenzialgleichungen der 4 Elementarsysteme G(s) erster Ordnung der Übertragungsfunktionen Differenzengleichungen gebildet werden, indem an Stelle des Differenzialquotienten mit der Differenzenquotient näherungsweise eingeführt wird.
Die Differenzengleichungen beschreiben mit dem Approximationsalgorithmus für ein kleines Zeitintervall ∆t die Signaländerungen nach jedem Zeitintervall als Funktion des betreffenden Teilsystems (Linearfaktoren) und des Eingangssignals. Mit der fortlaufenden Wiederholung der Berechnung mit dem Zeitintervalls ∆t und Addition der Änderungsergebnisse ergibt sich der Signalverlauf eines Systems über die Zeit .
Für eine Berechnung des Ausgangssignals y(t) eines dynamischen Systems mit Differenzengleichungen werden die Linearfaktoren ersten Grades der Übertragungsfunktion G(s) berücksichtigt. Jede Berechnung einer Differenzengleichung ist die Lösung im Zeitbereich für ein Zeitintervall .
Beispiel für ein Verzögerungsglied:
Jede aktuelle Berechnungsfolge bezieht sich auf das vorhergehende Ergebnis und addiert die Änderung des Eingangssignals u(k) unter Berücksichtigung der Zeitkonstante T und des Zeitintervalls .
Verzögerungssysteme zweiter Ordnung mit konjugiert komplexen Poilen (im Nenner der Übertragungsfunktion = PT2KK-Glied, Schwingungsglied) können durch einen einfachen Hilfsregelkreis mit der Reihenschaltung eines I-Gliedes und eines PT1-Gliedes und der negativen Rückführung nachgebildet werden. Für die Nachbildung mit diesen beiden Elementarsystemen sind die zugehörigen Differenzengleichungen erforderlich.
Instabile nicht phasenminimale elementare Übertragungsfunktionen enthalten ein negatives Zeichen in der Übertragungsfunktion und in der zugehörigen Differenzengleichung.
Die Genauigkeit der numerischen Berechnung eines dynamischen Systems mit dem Euler-Verfahren steigt linear mit dem kleiner werdenden Zeitintervall ∆t.
Der numerische Berechnungsalgorithmus nach dem Euler-Rückwärts-Verfahren ist in den nachfolgen Kapiteln mit der Tabelle "Tabellarische Darstellung der Differenzengleichungen" aufgestellt.
Theorie der Rechteckapproximation des Eulerverfahrens
[Bearbeiten]Eulerverfahren
[Bearbeiten]
Die einfachste Methode ist die Rechteckapproximation mit dem Zeitintervall ∆t (Integrationsintervall) an eine analytische Funktion f(t). [1]
Die numerische Integration einer monoton steigenden analytischen Funktion für ein Zeitintervall entspricht der Fläche des berechneten Ausgangssignals y(k) einer beliebigen Folge für die Zeit Δt, also y(k) * Δt. Je nach verwendetem Verfahren der numerischen Annäherung an die rechte oder linke Intervallgrenze der Folge k-1, k, k+1 spricht man von der Annäherung als Obersumme oder Untersumme der Integration.
Die Funktion einer einfachen Integration wird durch die Summe der Folgen des Produktes u(k) * ∆t nachgebildet:
Bei der numerischen Berechnung der Sprungantwort der Integrations-Funktion zur Annäherung an die analytische Funktion f(t) wird als Treppenkurve dargestellt. Es wird unterschieden, ob die Rechteck-Annäherung mit der rechten oder linken Intervallgrenze erfolgt und sich als Obersumme oder Untersumme zeigt.
Explizites Eulerverfahren
[Bearbeiten]Das einfachste numerische Verfahren der Berechnung des Ausgangssignals eines linearen Übertragungssystems als Funktion des Eingangssignals ist das sogenannte explizite Eulerverfahren (auch Euler-Vorwärtsverfahren, Streckenzugverfahren, Rechteckverfahren, Tangentenverfahren genannt), bei dem durch wiederholte Berechnungen für eine kleines Zeitintervall eine Annäherung an die analytische Funktion des Systems durchgeführt wird.
Diese Annäherung bezieht sich auf die linke Seite des Streckenzuges der (Rechteckapproximation) und liegt unterhalb einer ansteigenden Originalfunktion. Deshalb wird diese Annäherung auch mit Untersumme bezeichnet.
Implizites Eulerverfahren
[Bearbeiten]Alternativ kann das Eulerverfahren (Euler-Rückwärts) auch an der rechten Seite des Streckenzuges am Ende des Integrationsintervalls definiert werden.
Diese Anwendung führt zu dem implizierten Euler-Verfahren, weil der nicht bekannte Wert y(k+1) auch in der rechten Seite der Gleichung steht. Nur in sehr einfachen Fällen kann diese Gleichung in eine explizite Gleichung überführt werden. Die Anwendung des Verfahrens führt zu einer Annäherung oberhalb der Originalfunktion und wird deshalb mit Obersumme bezeichnet.
Das implizite Euler-Verfahren gilt als das genauere, rechenintensivere aber auch als numerisch stabilere Verfahren.
Modifiziertes explizites Euler-Rückwärtsverfahren
[Bearbeiten]Ein modifiziertes explizites Euler-Rückwärts-Verfahren als Integrationsalgorithmus bezieht sich auf die Zurücksetzung der Integrationsgrenzen des implizierten Euler-Verfahrens des Streckenzuges k und k+1 um (-1). Die Annäherung an die Originalfunktion wirkt als Obersumme.
Damit lautet die Annäherung des Differenzen-Quotienten an den Differential-Quotient:
Der Wert für wird in der Praxis wie folgt gewählt:
- << als die dominante Zeitkonstante des dynamischen Systems, zum Beispiel 1 % oder noch kleiner.
- < als die kleinste System-Zeitkonstante, anderenfalls entstehen Fehler.
Beispielsweise lautet der Integrationsalgorithmus:
Die nachfolgenden Definitionen der Differenzengleichungen beziehen sich auf diese Form. Der Vorteil:
- leichteres Verständnis der numerischen Integration. Sie bezieht sich auf eine Folge der Addition einer zurückliegenden Berechnung und einem aktuellen additiven Anteil als Funktion:
- .
- Teilsysteme mit gleichen Polen und Nullstellen kompensieren sich.
- Zum Zeitpunkt t = 0 = k(0) * Δt hat eine Funktion 1. Ordnung beispielsweise ein Verzögerungsglied einen Anfangswert proportional u(k), der differenzierbar ist. Damit kann in einer Reihenschaltung von Teilsystemen 1. Ordnung mit verzögerndem und differenzierendem Verhalten bei gleichen Polen und Nullstellen innerhalb der Berechnung jeder Folge k eine vollständige Systemkompensation stattfinden. So kompensieren sich die Ergebnisse der Differenzengleichungen eines PT1-Gliedes mit dem eines PD1-Gliedes bei gleichen Zeitkonstanten vollständig.
Ableitung der Differenzengleichungen erster Ordnung nach dem modifizierten Euler-Rückwärtsverfahren
[Bearbeiten]Differenzengleichung der Integration (I-Glied)
[Bearbeiten]Die Übertragungsfunktion lautet:
Die zugehörige Differenzialgleichung lautet:
Der Differenzenquotient wird an Stelle des Differenzialquotienten eingesetzt:
Damit lautet die nach umgestellte Differenzengleichung des I-Gliedes:
Differenzengleichung des Differenzierers (ideales D-Glied)
[Bearbeiten]Mit der Zeitdiskretisierung wird der Übergang einer Differenzialgleichung in eine Differenzengleichung von einer zeitkontinuierlichen Systembeschreibung in eine Systembeschreibung mit kleinen Zeitintervallen Δt der diskreten Zeit geschaffen. Der Differentialquotient wird durch einen Differenzenquotient ersetzt.
Die Übertragungsfunktion des idealen Differenzierers lautet:
Differenzialgleichung des idealen Differenzierers:
Der Differenzialquotient wird durch einen Differenzenquotient mit der Anpassung an die linke Intervallgrenze ersetzt. Für eine Anpassung an die rechte Intervallgrenze steht der Wert u(k+1) nicht zur Verfügung.
- Differenzengleichung der Differentiation (Ideales D-Glied)
Differenzengleichung der Verzögerung (PT1-Glied)
[Bearbeiten]
- Übertragungsfunktion des PT1-Gliedes
- Zugehörige Differenzialgleichung
Der Differenzialquotient der Differenzialgleichung wird durch den Differenzenquotient ersetzt mit folgendem Ansatz:
Diese Gleichung wird nach y(k) aufgelöst.
Die Differenzengleichung des PT1-Gliedes lautet:
Differenzengleichung des PT1-Gliedes in vereinfachter Schreibweise mit identischer mathematischer Funktion:
Differenzengleichung der Proportional-Differenzialfunktion (Ideales PD1-Glied)
[Bearbeiten]Übertragungsfunktion PD1-Glied:
Die zugehörige Differenzialgleichung lautet:
Der Differenzialquotient der Differenzialgleichung wird ersetzt durch den Differenzialalgorithmus mit folgendem Ansatz:
Die Differenzengleichung des idealen PD1-Gliedes lautet:
Anmerkung: Differenzierende Systeme ohne sogenannte parasitäre Zeitkonstanten von PT1-Gliedern lassen sich als Hardware technisch nicht herstellen. Die parasitäre Zeitkonstante ist wesentlich kleiner als die Zeitkonstante des Differenzierers. Dennoch kann man numerisch mit idealen Differenzierern rechnen, dabei ist die Größe des Impulses der Sprungantwort umgekehrt proportional der Größe von Δt. Erst bei der energetischen Bereitstellung der Stellgröße des Reglers aus Zahlenwerten ergibt sich durch die nachgeschaltete Hardware eine unvermeidbare Zeitverzögerung.
Differenzengleichungen höherer Ordnung
[Bearbeiten]Differenzengleichungen können auch aus gewöhnlichen Differenzialgleichungen höherer Ordnung entwickelt werden, wenn ab dem Zeitpunkt die letzten vergangenen Ausgangs-Wertefolgen mit und die Eingangs-Wertefolgen mit bekannt sind.
Zeitkontinuierliche lineare Systeme werden im Zeitbereich durch die gewöhnlichen Differenzialgleichungen n-ter Ordnung mit konstanten Koeffizienten für beschrieben. Dabei sind n und m die höchsten Ableitungen der Ausgangssignale und Eingangssignale .
Eine gegebene gewöhnliche Differentialgleichung wird durch den Koeffizienten dividiert, um freistellen zu können. Diese Form der Differentialgleichung wird entsprechend der dargestellten Koeffizienten wie folgt neu geordnet.
- .
Diese Differentialgleichung kann in eine Differenzengleichung überführt werden:
- Es wird als Abtastzeit gesetzt, wie in der digitalen Regelung üblich.
- wird vereinfacht als geschrieben und entspricht einem aktuellen Folgeglied.
- Die kontinuierlichen Systemgrößen und werden zeitdiskret dargestellt.
- Die Ableitungen im Zeitbereich werden entsprechend der Ordnung durch Differenzenquotienten der zugehörigen Ordnung ersetzt.
- Jede Ableitung der Systemgrößen wird im zeitdiskreten Bereich entsprechend der Ordnung als zurückliegende Folgeglieder der Eingangs- und Ausgangsfolgen k-1 bis k-n oder k-m berücksichtigt.
Daraus folgt die Differenzengleichung:
- .
Damit kann die allgemeine Form der Differenzengleichung nach aufgelöst werden:
- .
Für die numerische Berechnung eines dynamischen Systems wird die Übertragungsfunktion oder die zugehörige Differentialgleichung benötigt. Die Umsetzung einer systembeschreibenden Differentialgleichung in eine angenäherte Differenzengleichung zur Beschreibung von Eingangsfolgen und Ausgangsfolgen eines dynamischen Systems wird ermöglicht, wenn die Differentiale der Differentialgleichung durch Rückwärts-Differenzenquotienten über die Abtastperiode ersetzt werden. [2]
Die folgenden Ableitungen der Differentialquotienten in Differenzenquotienten der 1. 2. und 3. Ordnung sind gegeben:
Differenzenquotient 1. Ordnung:
Der Differenzenquotient 2. Ordnung entsteht aus Differenzen der Differenz:
Der Differenzenquotient 3. Ordnung lautet:
Nach erfolgtem Einsetzen der Differenzenquotienten in die Differenzengleichung eines dynamischen Systems lassen sich die neuen Koeffizienten aus den Koeffizienten der Differentialgleichung berechnen.
Beispiel der Entwicklung einer Differenzengleichung zur Berechnung der Sprungantwort eines -Gliedes mit konjugiert komplexen Polen:

Gegeben: Übertragungsfunktion im s-Bereich:
Gesucht: Differenzengleichung zur numerischen Bestimmung des System-Zeitverhaltens. Zugehörige Differentialgleichung nach dem Differentiationssatz der Laplace-Transformation: Die Differenzenquotienten für und werden in die nachfolgende Differenzengleichung eingesetzt: Die Brüche werden in einzelne additive Terme aufgelöst, um freistellen zu können:
Berechnungsbeispiel für einige Werte der Ausgangsfolge mit :
|
Diese Differenzengleichung entspricht einem Rekursionsalgorithmus eines dynamischen Systems, der schrittweise mit einem digitalen Rechner gelöst werden kann. Aus der Eingangsfolge berechnet der Rechner synchron zur Abtastung die Ausgangsfolge .
Die rekursive Berechnung der Differenzengleichung 2. Ordnung bezieht sich für die aktuelle Ausgangsfolge durch Einsetzen der zurückliegenden Werte der Ausgangsfolge und in die Gleichung. Für das 1. Folgeglied der Berechnungsfolge k=0 sind die zurückliegenden Werte der Ausgangsfolge noch nicht verfügbar und damit Null. Die Anzahl der Glieder der Ausgangsfolge wird durch die diskrete Zeit und durch die gewünschte zu beobachtende Gesamtzeit des Einschwingvorgangs bestimmt.
Als Offline-Berechnung mit [s] und einer Beobachtungszeit von 24 [s] wird die diese Gleichung 2400-mal berechnet und ergibt damit 2400 Folgewerte, die zur grafischen Darstellung gespeichert werden. Gegenüber der analytischen Funktion ist mit einem Approximationsfehler um ca. 1 % zu rechnen.
Zusammenfassung der Berechnung mit Differenzengleichungen
[Bearbeiten]- Euler-Rechteck-Verfahren
- Durch unterschiedliche Verfahren der Approximation (Annäherung) an eine zeitabhängige Funktion wie zum Beispiel für ein Verzögerungsglied 1. Ordnung existieren unterschiedliche Differenzengleichungen.
- Das einfachste Verfahren ist das Euler-Rechteck-Verfahren. Für die genannten vier linearen Teilsysteme wurden aus den zugehörigen DGL Differenzengleichungen abgeleitet.
- Berechnungsfolge
- Eine Berechnungsfolge bezieht sich auf das gesamte Übertragungssystem für das Zeitintervall ∆t.
- In einer Folge k = (0, 1, 2, 3, … kMAX) werden beliebig viele Einzelsysteme eines Gesamtsystems hintereinander für ein konstantes Zeitintervall ∆t mittels Differenzengleichungen berechnet.
- Reihendarstellung
- Jeder Signalausgang eines Teilsystems ist in der Reihendarstellung der Signaleingang des nächsten Teilsystems (multiplikative Funktion).
- Maximale Folge kMAX
- Der Endwert der Folge kMAX ergibt sich für den gewünschten Betrachtungszeitraum tMAX:
- .
- Nichtlineare Systeme
- Nichtlineare statische Systeme in Verbindung mit linearen dynamischen Systemen benötigen analytische Gleichungen oder Wertetabellen.
- Tabellarische Anordnung der Differenzengleichungen
- Für die Anwendung der Differenzengleichungen empfiehlt sich eine tabellarische Anordnung der Gleichungen, indem entsprechend einem Blockdiagramm der Signalflüsse beginnend von einer Spalte von links nach rechts die multiplikativen Zusammenhänge der Teilsysteme in den Zellen einer Zeile stehen.
- Damit steht in der ersten Spalte der absolute Zeitmaßstab , in der 2. Spalte die Eingangsgröße (das zeitdiskrete Testsignal) und für alle weiteren Zellen der Spalten der gleichen Zeile die Differenzengleichungen, für die jeweils jede Berechnungsfolge mit durchgeführt wird.
- Es können auch unstetige sprungartige Eingangssignale als Wertetabelle in die 2. Spalte eingetragen werden.
- PT2-Glieder mit konjugiert komplexen Polen können durch Differenzengleichungen mit Differenzenquotienten 2. Ordnung oder durch einen unterlagerten Regelkreis mit einem PT1-Glied und einem I-Glied nachgebildet werden.
- PD2-Glieder mit konjugiert komplexen Nullstellen
- Sie entstehen durch Produktbildung zweier PD1-Glieder und Subtraktion mit einem D-Glied.
- Anwendung: Als Vorfilter an einem Regelkreis zur Reduzierung von Schwinganteilen der Ausgangsgröße y(k).
- Die Differenzengleichung eines nichtregulären (instabilen) PT1-Gliedes GPT1(s) = 1 / (T*s-1) entsteht durch Vorzeichenumkehr der betreffenden Differenzengleichung.
- Nichtlineares Verhalten einer Signalbegrenzung
- Die Signalbegrenzung kann mit einem logischen Operator als WENN-DANN-SONST-Anweisung realisiert werden. Zum Beispiel mit Zelleneintrag einer Spalte: Wenn u(k) > Bezugswert, dann u(k) = Bezugswert (positive Begrenzung)
- Nichtlineares Verhalten einer Geräte-Kennlinie erfordert eine Wertetabelle als Tabellenspalte, die der Folge k zugeordnet werden muss. Dies gilt für den Fall, dass eine analytische Gleichung das nichtlinearem Systemverhalten nicht beschreiben kann.
- Totzeitsysteme
- Totzeitsysteme lassen sich mit einer Programmschleife beschreiben.
- Bei Anwendung der Tabellenkalkulation gilt die Rechenanweisung:
- INDEX(F20; F200; 180 - Tt / Δt) und bedeutet: Diese Gleichung steht in der obersten Spalte G200 für k = 0 und k * Δt = 0 und bezieht sich auf die Spalte F20 bis F200. Es dürfen keine Zeichen innerhalb der Zellen 20 bis 200 dieses Spaltenbereichs stehen.
- Numerische Stabilität
- Zur Vermeidung der numerischen Instabilität kann die Verstärkung nicht unbegrenzt hoch gewählt werden, wenn es auch theoretisch bei stetig wirkenden Regelkreisen bis zu zwei Verzögerungsgliedern möglich wäre.
- Bedingung: Bei sehr großer Kreisverstärkung K einer Regelkreisnachbildung muss kleiner als sein. ist das Produkt aller Einzelverstärkungen, ist die dominante Systemzeitkonstante.
- Genauigkeit der numerischen Simulation
- Die Genauigkeit steigt mit kleiner werdendem Zeitintervall gegenüber der dominanten Systemzeitkonstante . Der Approximationsfehler im Vergleich zur analytische Funktion beträgt .
- Das Zeitintervall muss kleiner als die kleinste zu berechnende Systemzeitkonstante betragen. Anderenfalls treten zusätzliche Fehler auf.
- Eingangssignale / Testsignale:
- Das Eingangstestsignal u(k) eines Übertragungssystems ist eine Funktion von ∆t und bezieht sich meistens auf die Testsignale: Impulsfunktion, Sprungfunktion und Anstiegsfunktion.
- Normierte Sprungfunktion: u(k) = 1
- Normierter δ-Impuls: u(k=0) = 1 / Δt ; u(k > 0) = 0
- Anstiegsfunktion: u(k) = u(k-1) + c * Δt ; c = Δu / Δt
- Kommerzielle Programme
- Kommerzielle Programme zu numerischen Berechnungen wie MatLab unterscheiden sich von selbst entwickelten numerischen Berechnungen in drei wesentlichen Punkten:
- Es kann eine gewünschte Berechnungsgenauigkeit durch ausgewählte Verfahren bestimmt werden.
- Die gewählten Verfahren sind adaptiv, d.h. es muss keine diskrete Zeit und maximale Folge vorgegeben werden. Die Größe des Zeitintervalls ist auch nicht über alle Folgen konstant.
- Die gewählten Verfahren kontrollieren die Stabilität der Lösung.
Tabellarische Darstellung der Differenzengleichungen 1. Ordnung
[Bearbeiten]In der folgenden Tabelle sind die Differenzengleichungen der vier elementaren Übertragungssysteme und einige nichtlineare Funktionen und Signale als f(∆t) dargestellt.
Die numerischen Berechnungen mit den Differenzengleichungen können mit jeder Programmiersprache durchgeführt werden. Es empfiehlt sich aber der Einfachheit halber die Anwendung der Tabellenkalkulation, mit der auch die grafische Darstellung des Systemverhaltens für ein beliebiges Testsignal hergestellt werden kann. Programmierfehler anderer Programmiersprachen werden vermieden.
- Tabelle der Differenzengleichungen und logischen Operationen für die Simulation von Übertragungssystemen
Typ Übertragungsfunktionen
Definition der Testsignale und OperatorenDifferenzengleichungen,
Operatoren als Funktion von k*ΔtHinweise
1 P-Glied:
Die Einzelfaktoren K1, K2 ... der Übertragungsglieder werden sinnvollerweise zu einem Faktor K multipliziert.
2 I-Glied:
k = Nummer der Folge
Δt = konstante diskretisierte Zeit
k * Δt = t = aktuelle Zeity(k) = aktueller Ausgangswert
u(k) = aktueller Eingangswert
y(k-1) = Ausgangswert einer zurückliegenden Folge
k = 0: Rechenfolge aller Anfangswerte
Normale Anfangswerte sind meist Null3 PT1-Glied:
4 Instabiles PT1-Glied:
Pole-Nullstellenkompensation bei instabilen PT1-Gliedern ist nicht erlaubt! 5 D-Glied:
6 PD1-Glied (Regler):
7 Totzeitglied:
Schleife im Rechenprogramm oder:
Anwendung Tabellenkalkulation:
INDEX(F20; F200; 180 - Tt / Δt)
Maximale Totzeit:
Für KTt ist eine eigene Spalte erforderlichTabellenkalkulation:
F20;F200 bedeutet Bezug der Spalte F für Zellen F20 bis F200.Sämtliche Gleichungen für INDEX stehen z. B. in der Spalte G ab G200 bis z. B. G1200. In F200 bis F1200 stehen die Eingangswerte bzw. Gleichungen.
Spalte F20 bis F200 darf keine Zeichen enthalten, sonst entsteht eine fehlerhafte Zuweisung.8 Regelabweichung:
Regelabweichung = Sollwert – Istwert 9 Symmetrische Signalbegrenzung:
WENN-, DANN-; SONST-Anweisung:
WENN(X > A; DANN A; WENN(X < -A; DANN -A; SONST X))X = Zahlenwert einer Zelle
A = Parameter der Begrenzung10 Nichtlineare Kennlinie:
als Funktion der Eingangsgröße, Kontinuierliche Funktion:
Nichtkontinuierliche Funktion:
zum Beispiel Sprung und Rücksprung als Funktion der Zeit (k*Δt)Anwendung der Tabellenkalkulation:
Zelleneintrag einer Gleichung y(k) = f(k; u(k))
Zelleneintrag einer Tabelle:
Allen Zellen einer Spalte muss ein Wert zugewiesen werden: y(k) = f(k*Δt)Für alle Gleichungen gilt:
Gleichungen werden pro Zelle z. B. in Zeile 201 einmal geschrieben und beliebig oft entsprechend der gewünschten Signalauflösung z. B. 1000 mal in der Spalte kopiert.11 Testsignale: Impulsfunktion
U(s) = 1Amplitude:
Amplitude:Normierter Impuls! 12 Testsignal Sprungfunktion:
U(s) = 1 / sSprungfunktion: Normierter Sprung!
13 Testsignal Anstiegsfunktion:
U(s) = 1 / s²Anstieg: Anstiegskonstante c = Δ u / Δ t
Anwendung numerischer Berechnungen
[Bearbeiten]Dynamische Systeme, deren Zeitverhalten in Form einer gewöhnlichen Differenzialgleichung g(t) oder durch die Laplace-transformierte Übertragungsfunktion G(s) beschrieben werden, lassen sich sehr vorteilhaft numerisch mit Differenzengleichungen berechnen. Ein dynamisches System besteht häufig aus einer in Funktionsblöcken dargestellten Reihenschaltung, Parallelschaltung oder Zurückkopplung von Teilsystemen, die durch zugehörige Differenzengleichungen beschrieben werden können. Zur besseren Übersicht werden die Rechenergebnisse der einzelnen Differenzengleichungen tabellarisch dargestellt. Mit jeder neuen Berechnungsfolge k des Gesamtsystems einer Tabellenzeile mit beliebig vielen Teilsystemen wird mit den zugehörigen Differenzengleichungen ein neues Gesamtergebnis y(k) für ein Zeitintervall Δt berechnet.
Dabei wird die These vertreten, die Differenzengleichungen nur für Linearfaktoren der Übertragungsfunktion ersten Grades zu verwenden, weil nur 4 solcher Formen (2 im Nenner und 2 im Zähler der Übertragungsfunktion) existieren. Eine 5. und 6. Form von Übertragungssystemen zweiter Ordnung mit konjugiert komplexen Polen können mit den Linearfaktoren erster Ordnung simuliert werden. Es macht wenig Sinn, z.B. einen PID-Regler mit einer mittels z-Transformation gefundenen Differenzengleichung als eine einzige spezielle Gleichung zu benutzen, während es bei Verwendung mit Differenzengleichungen 1. Ordnung 3 einfache Differenzengleichungen für den P-I- D-Anteil eine völlige tabellarische Systemübersicht auf überprüfbare Richtigkeit gegeben ist.
Die numerische Berechnung allgemein erlaubt die Berechnung verschiedenster Problemstellungen, die mit konventionellen Methoden sehr schwierig oder analytisch gar nicht zu lösen sind, wie:
- Dynamischer Systeme, die sich linear und nichtlinear verhalten.
- Verhalten dynamischer Systeme als Folge logischer Befehle oder Wertetabellen.
- Lösen von Differenzialgleichungen ohne und mit Anfangswerten der Systemspeicher.
- Systeme ohne Zeitverhalten, bei denen z.B. die kleinste Einheit Δu eine Funktion der dimensionslosen Eingangsgröße u ist (Beispiel: Mehrpunktregler, oder kombinierte Mehrpunktregler mit zeitabhängigen Rückführungen).
Die Hauptanwendung der numerischen Berechnung mit Differenzengleichungen bezieht sich auf die Berechnung des Ausgangs- Eingangsverhalten von dynamischen Systemen, die gesteuert oder geregelt werden. Da bestimmte Übertragungssysteme sich nichtlinear verhalten, können mittels der numerischen Behandlung logische Operationen (Z.B. WENN - DANN - SONST- Anweisung) mit den Differenzengleichungen kombiniert werden.
Das Eingangs- Ausgangsverhalten eines Dreipunktreglers mit Schaltkriterien als Funktion der Hysterese und der Totzone lässt sich mit logischen Befehlen numerisch beschreiben und grafisch darstellen.
Sehr nützlich ist die Anwendung der numerischen Behandlung in der Regelungstechnik. Durch die Simulation eines Regelkreises - bestehend aus den hintereinander geschalteten Einzelkomponenten des Reglers und der Regelstrecke mit der Schließbedingung zu einem Kreis - können die Systemparameter des Reglers für eine gegebene Regelstrecke optimiert und das Verhalten der Regelgröße grafisch dargestellt werden.
- Gesamtsystem als gewöhnliche Differenzialgleichung
- Das Modell eines linearen Systems mit n Systemspeichern, dass durch eine gewöhnliche Differenzialgleichung mit konstanten Koeffizienten beschrieben ist, kann durch n-fache numerische Integration berechnet werden.
- Von der höchsten Ableitung der Ausgangsgröße y(t) werden über Integratoren erzeugte n Zustandsvariablen x(t) subtrahiert. Die numerische Berechnung bezieht sich fortlaufend auf ein kleines Zeitintervall.
- Dieses numerische Verfahren ist erheblich einfacher als die Lösung einer DGL mit konventionellen Methoden, weil es sich um die Lösung einfacher algebraischer Gleichungen handelt.
- Die numerische Berechnung der Differenzialgleichung erlaubt die homogene Lösung mit Vorgabe der Anfangswerte mit y(k) = 0 , die partikuläre Lösung ohne Anfangswerte mit y(k) ≠ 0 und die Gesamtlösung mit Anfangswerten und y(k) ≠ 0.
- Es sind keine Integrationskonstanten zu berechnen.
Numerische Berechnung von Übertragungssystemen mit linearen und nichtlinearen Teilsystemen
[Bearbeiten]Lineare zeitinvariante Übertragungssysteme werden durch DGL-en und Übertragungsfunktionen beschrieben. Durch Zerlegung der Polynome der Übertragungsfunktion in Linearfaktoren 1. Ordnung mit und ohne Grundglied ergeben sich 4 elementare Übertragungsfunktionen mit den Funktionseigenschaften I-Glied, PT1-Glied, D-Glied und PD1-Glied, mit denen in beliebiger Reihen-, Parallel- und Kreisstruktur sich alle phasenminimale Übertragungsfunktionen nachbilden lassen. Für diese elementaren Teilsysteme lassen sich aus den zugehörigen DGL-en je eine Differenzengleichung bilden. Der Approximationsalgorithmus dieser 4 Differenzengleichungen ist aus den zugehörigen DGL abgeleitet. Von den verschiedenen Verfahren ist die Euler-Rechteckannäherung die einfachste.

Für nichtlineare speicherlose Übertragungssysteme wie Signalbegrenzer, nichtlineare oder gebrochene Kennlinien, Totzeitsysteme und diskontinuierliche Eingangssignale lassen sich analytische Gleichungen oder Wertetabellen finden.
Die numerische Berechnung eines Übertragungssystems von linearen und nichtlinearen Einzelsystemen erfolgt sinnvollerweise in Form einer Tabelle mit den Zeilen der Rekursion der Folge k = 0 bis k = kMAX untereinander für je einen kleinen Berechnungszeitschritt Δt mit den Spaltenzellen der numerischen Gleichungen.
Da statische Gleichungen wie auch Differenzengleichungen nur einmal in die Zelle einer Spalte eingetragen und dann zum Beispiel für kMAX = 1000 die Gleichungen 1000-mal kopiert werden, muss eine Wertetabelle je nach gewünschter Auflösung von Hand in die Spalte einer Tabelle eingetragen werden.
Sämtliche Systemgleichungen können mit jeder Programmiersprache berechnet werden. Es wird die Anwendung der Tabellenkalkulation wegen der Einfachheit der Anwendung und der einfachen Möglichkeit der grafischen Darstellung der Berechnungsergebnisse empfohlen.
- Berechnungsbeispiel eines Modells aus verschiedenen Teilsystemen bestehenden Übertragungssystems
- Tabellarische Darstellung der numerischen Gesamtlösung y(k*Δt) ≈ y(t) eines Regelkreises mit PI-Regler mit Stellgrößenbegrenzung und PT2-Regelstrecke
Spalte A Spalte B Spalte C Spalte D Spalte E Spalte F Spalte G Spalte H Spalte I Spalte J Folge k Diskr.Zeit
ΔtEing.-Signal
u(k)Soll-Istw.
Gl. 1I-Glied
Gl. 2PD-Glied
Gl. 3Begrenz.
Gl. 4PT1-Glied
Gl. 5PT1-Glied
Gl. 6Bemerkungen Zeile 1 - - - - - - - - - Kein Eintrag Zeile 2 0 0*Δt 1 Gl. 1 Gl. 2 Gl. 3 Gl. 4 Gl. 5 Gl. 6 Gleichungen Zeile 3 1 1*Δt 1 Gl. 1 Gl. 2 Gl. 3 Gl. 4 Gl. 5 Gl. 6 Kopie Zeile 2 Zeile 4 2 2*Δt 1 Gl. 1 Gl. 2 Gl. 3 Gl. 4 Gl. 5 Gl. 6 Kopie Zeile 2 Endzeile kMAX kMAX*Δt 1 Gl. 1 Gl. 2 Gl. 3 Gl. 4 Gl. 5 Gl. 6 Kopie Zeile 2
- Die Lösung des Systemverhaltens liefert die Spalte I mit der Ausgangsgröße y(k*Δt).
Nachbildung eines PT2KK-Schwingungsgliedes
[Bearbeiten]Ein PT2KK-Schwingungsglied hat konjugiert komplexe Pole und kann deshalb nicht in Linearfaktoren ersten Grades ohne komplexe Anteile von Zahlenwerten zerlegt werden. Für die Bildung der Differenzengleichung eines Übertragungssystems zweiter Ordnung mit konjugiert komplexen Polen kann mit Hilfe eines einfachen Hilfsregelkreises und Anwendung von zwei Differenzengleichungen erster Ordnung erreicht werden.
- Berechnung der Koeffizienten eines Hilfsregelkreises aus der Übertragungsfunktion
Die einfachste Form der Nachbildung des Hilfsregelkreis erfolgt durch die offene Hilfsregelstrecke G0(s) (Indizierung mit H) als Reihenschaltung mit einem I-Glied (KH / s) mit einem PT1-Glied (1 / (TH s + 1)). Damit lassen sich zwei Differenzengleichungen für Linearfaktoren erster Ordnung verwenden.
Wird der Ausgang Y(s) von G0(s) in Blocksymbol-Darstellung negativ auf den Systemeingang W(s) zurückgeführt, entsteht der Hilfsregelkreis G(s).
Die Übertragungsfunktion des Hilfsregelkreises G(s) = G0 / (1+G0) lautet in der allgemeinen Form für ein PT2KK-Schwingungsglied:
Es gilt nun aus der Normalform des Schwingungsgliedes mit gegebenen Zahlenwerten über einen Koeffizientenvergleich die Hilfsgrößen TH und KH zu bestimmen, damit die Differenzengleichungen angewendet werden können.
Für eine gegebene Übertragungsfunktion eines Schwingungsgliedes mit den Zahlenwerten der Koeffizienten und müssen die Parameter der Verstärkung KH und der Zeitkonstante TH des offenen Regelkreises G0(s) aus dem geschlossenen Hilfsregelkreis GPT1KK(s) errechnet werden.
Durch Koeffizientenvergleich lassen sich die gewünschten Parameter und des offenen Hilfsregelkreises bestimmen:
Mit diesen Parametern kann die numerische Berechnung mit den nachstehend aufgeführten Differenzengleichungen durchgeführt werden.

G(s) = 1 / (0,25 s² + 0,125 s +1)
Dämpfung D = 0,125.
Berechnungsbeispiel:
Gegeben: Übertragungsfunktion eines Schwingungsgliedes :
Gesucht: Parameter KH und TH eines offenen Hilfsregelkreises zur Simulation der Übertragungsfunktion
des geschlossenen Kreises als ein PT2KK-Schwingungsglied mit konjugiert komplexen Polen.Mit diesen Angaben können die nachstehend aufgeführten Differenzengleichungen berechnet werden.
- Numerische Nachbildung des Hilfsregelkreises für ein Schwingungsglied im zeitdiskreten Bereich f(k*Δt)
Der offene Hilfsregelkreis G0(s) besteht aus der Reihenschaltung eines I-Gliedes mit einem PT1-Glied. Die Hilfsgrößen wie die Zeitkonstante TH des PT1-Gliedes und die Verstärkung KH des I-Gliedes werden in die zugehörigen Differenzengleichungen eingebracht.
Wird die Regelabweichung w(k) - y(k-1) in die Reihenschaltung G0(k) geleitet, ist der Hilfsregelkreis geschlossen. Es müssen folgende drei Differenzengleichungen berechnet werden. w(k) ist ein Testsignal oder das Ausgangssignal y(k) eines in der Reihenfolge links liegenden Übertragungsgliedes vor dem Hilfsregelkreis.

Systembezeichnung Differenzengleichung Schwingungsglied
Regelabweichung e(k)
I-Glied u(k) PT1-Glied y(k)
Sollte das zu berechnende Zeitverhalten des Schwingungsgliedes G(s) einen Verstärkungsfaktor K im Zähler der Übertragungsfunktion enthalten, so wird dieser Faktor separat vor oder nach dem Hilfsregelkreis algebraisch berücksichtigt.
Numerische Lösung einer systembeschreibenden Differenzialgleichung
[Bearbeiten]Die partikuläre Lösung (Eingangs- Ausgangsverhalten) einer gewöhnlichen DGL mit konstanten Koeffizienten ist abhängig von der Zahl n der Ableitungen der Ausgangsgröße y(t), der Ableitungen der Eingangsgröße u(t), der Größe der Koeffizienten und der Funktion des Eingangssignals u(t). Sie geht von Anfangswerten gleich Null aus. Dabei wird die Differenzialgleichung in die explizite Form nach der höchsten Ableitung umgestellt und grafisch in der Regelungsnormalform der Zustandsraumdarstellung dargestellt.
Sind Anfangswerte der Differenzialgleichung gegeben, werden die Integratoren der Regelungsnormalform auf diese Anfangswerte gesetzt.
Die Differenzialgleichung eines Übertragungssystems in der allgemeinen Form ohne Ableitungen der Eingangsgröße lautet:
- Beispiel
- Erstellung des Signalflussplanes zur Lösung der DGL 2. Ordnung:

- Systembeschreibende DGL
Für die numerische Lösung einer gewöhnlichen DGL wird die explizite Form nach der höchsten Ableitung verwendet, d.h. in dem alle Terme der Gleichung durch den Koeffizienten a2 dividiert werden und dann freigestellt wird. [3]
Der in dem Strukturbild dargestellte Signalflussplan zeigt anschaulich die Umsetzung der DGL in ein Modell mit Zustandsvariablen xi zur Lösung der DGL.
Dieses Modell entspricht auch der Lösung einer DGL mit Hilfe der Analogrechentechnik und ist seit langem bekannt. Das Interesse galt weniger den dargestellten Zustandsvariablen, sondern nur dem Verhalten der Ausgangsgröße y(t).
Hat die Übertragungsfunktion oder die zugehörige DGL auch differentielle Anteile, d. h. Ableitungen der Eingangsgröße u(t), eignet sich als Signalflussdiagramm der DGL besser die Regelungsnormalform der Zustandsraumdarstellung.
Die numerische Lösung dieser DGL mit n-fachen Ableitungen erfolgt durch n-fache numerische Integrationen, die sich auf ein diskretes Zeitintervall Δt und rekursive Berechnung der Folgen k = (0, 1, 2, 3, ...kMAX) bezieht.
Die Differenzengleichung zur numerischen Lösung einer Integration lautet (hier T = 1):
- Partikuläre Lösung yP(k):
- Für ein gegebenes Eingangssignal u(Δt) zur Zeit k * Δt = 0 und den Anfangswerten der Integratoren y'0 = 0 und y0 = 0 ergibt sich eine geschlossene Lösung für y(k) für k = 0 bis kMAX.
- Homogene Lösung yH(k):
- Für ein gegebenes Eingangssignal u(Δt) = 0 zur Zeit k * Δt = 0 werden Anfangswerte der Integratoren für y'0 und y0 eingesetzt. Es müssen dabei keine Integrationskonstanten Ci ermittelt werden, weil die Integratoren als bestimmte Integrale mit den Integralgrenzen der Anfangswerte bis zum Ende des Betrachtungszeitraumes k * Δt wirken.
- Gesamtlösung y(k):
- Sie ergibt sich automatisch, wenn ein Eingangssignal u(k) ≠ 0 und gleichzeitig Anfangswerte der Integratoren y'0 ≠ 0 und y0 ≠ 0 vorliegen.
Berechnungsbeispiel einer gewöhnlichen Differenzialgleichung 2. Ordnung mit Anfangswerten
[Bearbeiten]
Übertragungsfunktion gegeben:
Zugehörige systembeschreibende DGL in expliziter Darstellung:
- Anfangswerte der Energiespeicher (Integratoren): y'0(t) = 1; y0(t) = 1;
- Eingangsgröße u(k) ist eine normierte Sprungfunktion 1 für t > 0. Die zu berechnenden Gleichungen ergeben sich aus dem dargestellten Signalflussplan.
- In der Tabellendarstellung erfolgt die Berechnung der Zellen einer Zeile von links nach rechts und danach von einer oberen Zeile zu den unteren Zeilen. Benötigte Werte, die an einer bestimmten Stelle einer Zeile noch nicht bekannt sind, werden aus einer vorhergehenden Zeile der gleichen Spalte entnommen.
- Gleichung 1 bildet die Differenzen der noch zu berechnenden Ableitungen von y(k) in Spalte E der Tabelle laut Signalflussplan:
- Gleichung 2 ist eine Differenzengleichung der Integration in Spalte F (mit T = 1):
- Gleichung 3 ist eine Differenzengleichung der Integration in Spalte H (mit T = 1):
- Die Spalte B der diskreten Zeit (k * Δt) berechnet sich ab Zeile B3: B3 = B2 + Δt und kann beliebig oft kopiert werden!
- Die Lösung der DGL liefert die Spalte H mit der Ausgangsgröße y(k*Δt)!
- Tabellarische Darstellung der numerischen Gesamtlösung y(k*Δt) ≈ y(t) einer Differenzialgleichung 2. Ordnung.
Spalte A Spalte B Spalte C Spalte D Spalte E Spalte F Spalte G Spalte H Spalte I Spalte J Folge k Zeit
ΔtEingangs
SignalKoeffiz.
b0Differenz
Gl. 1I-Glied
Gl. 2Koeffiz.
a1I-Glied
Gl. 3Koeffiz.
a0Bemerkungen Zeile 1 - - - - - 1 - 1 - Anfangswerte Zeile 2 0 0*Δt 1 0,5 Gl. 1 Gl. 2 1,5 Gl. 3 0,5 Gleichungen Zeile 3 1 1*Δt 1 0,5 Gl. 1 Gl. 2 1,5 Gl. 3 0,5 Kopie Zeile 2 Zeile 4 2 2*Δt 1 0,5 Gl. 1 Gl. 2 1,5 Gl. 3 0,5 Kopie Zeile 2 Endzeile kMAX kMAX*Δt 1 0,5 Gl. 1 Gl.2 1,5 Gl. 3 0,5 Kopie Zeile 2
Anmerkung:
- Bei der homogenen Lösung sind in Spalte C sämtliche Werte auf 0 gesetzt mit Anfangswerten in Zeile 1.
- Bei der partikulären Lösung sind in Spalte C sämtliche Werte auf 1 gesetzt ohne Anfangswerte in Zeile 1.
- Der Approximationsfehler der Annäherung an die analytische Lösung beträgt ungefähr Δt / T = 0,003 / 2 = 0,0015 = 0,15 %.
Einzelnachweise
[Bearbeiten]- ↑ Lutz / Wendt: Taschenbuch der Regelungstechnik, Kapitel: Basisalgorithmen Digitale Regelungen.
- ↑ Prof. Dr. W. Schuhmacher: Technische Universität Braunschweig, Vorlesungsskript Grundlagen der Regelungstechnik, 309 Seiten, erstellt 6.10.2011, Kapitel: Diskrete Signalverarbeitung durch Digitalrechner.
- ↑ Zustandsgleichungen von Eingrößensystemen. In: Gerd Schulz: Regelungstechnik 2.
























































![{\displaystyle G_{3}(s)={\frac {Y(s)}{U(s)}}={\frac {b_{m}s^{m}+\ldots +b_{2}s^{2}+b_{1}s+b_{0}}{a_{n}s^{n}+\ldots +a_{2}s^{2}+a_{1}s+a_{0}}}:=k\cdot {\frac {(s-s_{n1})(s-s_{n2})\dotsm (s-s_{nm})}{[s-(\delta +j\omega )]\cdot [s-(\delta -j\omega )]\dotsm (s-s_{pn})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64fe83541f064e2584d768e4ea5a4752fe750270)
![{\displaystyle G(s)=[s-(\delta +j\omega )]\cdot [s-(\delta -j\omega )]=s^{2}-2\cdot \delta \cdot s+\delta ^{2}+\omega ^{2}\ :=s^{2}-p\cdot s+q\ {\bigg |}\qquad p=2\cdot \delta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1999f57a0ea3765c0b792402458551a59c65fb1)



























































































![{\displaystyle F_{A}\approx {\frac {\Delta t\cdot 100}{T_{D}}}\ [\%]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32357be7e691ba4c328f939110f3c6d2b864ea02)

![{\displaystyle y_{(k)}=y_{(k-1)}+\Delta t\cdot f[u_{(k)}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2c6413631fe92a869dcfa20d2843a33b5b90cdc)


























![{\displaystyle y(t)=F[u(t)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/598ade1a11743d2dd810a3255b50cbef031dada9)




![{\displaystyle F[K\cdot u(t)]=K\cdot F[u(t)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a058f866ccc00c2b1bc5f91ca313eebbefcc2a6)







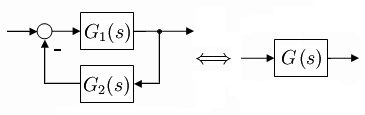


































![{\displaystyle \mathrm {PT_{1}} -{\text{Glied:}}\quad y1_{(k)}=y_{(k-1)}+[u_{(k)}-y_{(k-1)}]\cdot {\frac {6\cdot \Delta t}{T_{t}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c6dc6bd519db17bdeeb293e8fd0ebb7d109e35f)
![{\displaystyle {\text{D-Glied:}}\ \ \ \qquad y2_{(k)}=[u_{(k)}-u_{(k-1)}]\cdot {\frac {T_{t}}{6\cdot \Delta t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4a803396a6fa395f98a6463abe684d419c9255d)
![{\displaystyle {\text{Subtraktion:}}\ \quad y_{(k)}=K\cdot [y1_{(k)}-y2_{(k)}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a2f6fe5b095177a548ea6880c80860398f9315c)

























































![{\displaystyle [f'(e^{-\lambda \cdot t})=-\lambda \cdot e^{-\lambda \cdot t}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cc3f6a2e4d883ad9e3ca4b110a865ef4e475928)

























![{\displaystyle y_{H}(t)=e^{\alpha \cdot t}\cdot [C_{1}\cdot \cos(\beta \cdot t)+C_{2}\cdot \sin(\beta \cdot t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8d273239169e2c81a77e36eaae8bc4a5686fd35)











![{\displaystyle {\underline {\underline {y_{p}(t)=1-{\frac {1}{T_{1}-T_{2}}}\cdot [T_{1}\cdot e^{-{\frac {t}{T_{1}}}}-T_{2}\cdot e^{-{\frac {t}{T_{2}}}}]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bad5bbe99491877f6b1c9a4cfccd4fd1dddf4b74)































































































![{\displaystyle G_{3}(s)=[s-(\delta +j\omega )]\cdot [s-(\delta -j\omega )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea9f558b8c8c0d0d62a10da7eb5978445ce680bc)











































![{\displaystyle A_{i}=\left.[G(s)\cdot (s-s_{pi})]\right|_{s=s_{pi}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d707c5508296da391f390f50f98cacd162dcd5e)







![{\displaystyle G(s)=\operatorname {Re} [G(s)]+j\cdot \operatorname {Im} [G(s)]=|G(s)|\cdot e^{j\cdot \varphi }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c25f1ae4310f7cdc6ad4ec5f575388df5662dc1)




![{\displaystyle y(t)={\hat {y}}(\omega )\cdot \sin[\omega \cdot t+\varphi (\omega )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83257a7a2ed61d7ea775719221a018531a67047f)


![{\displaystyle U(j\omega )={\hat {U}}\cdot [\cos(\omega t)+j\cdot \sin(\omega t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f28d3274581c460fd535c92f51e044454c43bc14)



![{\displaystyle G(j\omega )=\operatorname {Re} [G(j\omega )]+j\cdot \operatorname {Im} [G(j\omega )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fde7170de323af825c97e02e741c7b925799e665)




![{\displaystyle G(j\omega )=\operatorname {Re} [G(j\omega )]+j\cdot \operatorname {Im} [G(j\omega )]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af087e3352eddda3720f4e735c0018a49c5d7519)
![{\displaystyle |G(j\omega )|={\sqrt {(\operatorname {Re} {[G(j\omega )])}^{2}+{(\operatorname {Im} {[G(j\omega )}])}^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35aedbc63d435761b668ebe5784fd288e59c872f)
![{\displaystyle \varphi (j\omega )=\arctan {\frac {\operatorname {Im} [G(j\omega )]}{\operatorname {Re} [G(j\omega )]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b18433f03079d806f36d925de4f608987a7b989)













![{\displaystyle [s-(-\delta +j\omega )]\cdot [s-(-\delta -j\omega )]\ :=[s-(\alpha +j\omega )]\cdot [s-(\alpha -j\omega )]\ =s^{2}+2\cdot \alpha \cdot s+\alpha ^{2}+\beta ^{2}\ :=s^{2}+p\cdot s+q\ {\bigg |}\qquad mit\ p=2\cdot \alpha ;\ q=\alpha ^{2}+\omega ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8658699909c67a02e5515b4f68556aa0121f507)



![{\displaystyle [s-(\alpha +j\omega )]\cdot [s-(\alpha -j\omega )]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6186d10955815d2d098c86d1ec26c2126e2b54b)












































![{\displaystyle y(t)={\frac {1}{a\cdot b}}\cdot [1-{\frac {b}{b-a}}\cdot e^{-a\cdot t}+{\frac {a}{b-a}}\cdot e^{-b\cdot t}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c925f86308f51bef1dbbd49e06896db7a700180b)












![{\displaystyle G(s)=\operatorname {Re} [G(s)]\ +\ j\cdot \operatorname {Im} [G(s)]\quad \Vert \qquad {\text{mit}}\quad \operatorname {Re} (s)=\delta ;\quad {\text{und}}\quad \operatorname {Im} (s)=\omega .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00ec05f1adc64f0b085b1d90d54660dcea89c8aa)

























































![{\displaystyle G(s)={\frac {1}{[s-(\delta +j\omega )]\cdot [s-(\delta -j\omega )]}}={\frac {1}{s^{2}-2\cdot \delta \cdot s+\delta ^{2}+\omega ^{2}}}\ {\mathrel {\hat {=}}}\ {\frac {1}{s^{2}-p\cdot s+q}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b6453ce325f8d601635255bc836561e7a28ab9a)
![{\displaystyle G(s)=\left.{\frac {1}{[s+(\delta -j\omega )]\cdot [s+(\delta +j\omega )]}}={\frac {1}{s^{2}+2\cdot \delta \cdot s+\delta ^{2}+\omega ^{2}}}\ {\mathrel {\hat {=}}}\ {\frac {1}{s^{2}+p\cdot s+q}}\qquad \right|\ p=2\cdot \delta ;\quad q=\delta ^{2}+\omega ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a465bda3eb00a8a28f31abb13f6b1b3d27c044b)





















![{\displaystyle y_{(k+1)}=y_{(k)}+\Delta t\cdot f[y_{(k)},u_{(k)}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e46a2b117647bf34010fdf3274f8da3d85452531)
![{\displaystyle y_{(k+1)}=y_{(k)}+\Delta t\cdot f[y_{(k+1)},u_{(k+1)}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ec99e5c3c485ed5e3edd3746bcf6b1d22987804)

![{\displaystyle f[{\text{Übertragungsglied}};u_{(k)};\Delta t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea82c04c98c8372c67a6969468bc8ecee4dc4469)













![{\displaystyle y_{(k)}=K_{PD}\cdot [u_{(k)}+(u_{(k)}-u_{(k-1)})\cdot {\frac {T_{V}}{\Delta t}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7507a8de434e24028690613f0930b721e5e834c9)

![{\displaystyle k=[-1\to -n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a01d3fff736891fdc4822b7d11fdb875a9b31237)
![{\displaystyle k=[-1\to -m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f7cd54355a41d43102cd7bc489c62994f90d30d)





































![{\displaystyle y_{(k-1)}+[K_{PT1}\cdot u_{(k)}-y_{(k-1)}]\cdot {\frac {\Delta t}{T+\Delta t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9b2775ab1319b5552521c2fd7d20904f1b683de)

![{\displaystyle u_{(k-1)}+[K_{PT1}\cdot u_{(k)}+y_{(k-1)}]\cdot {\frac {\Delta t}{T+\Delta t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2449e80f6fc4f01934cc16c63854b851bd3fa3ea)

![{\displaystyle y_{(k)}=[u_{(k)}-u_{(k-1)}]\cdot {\frac {T}{\Delta t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce6e53f3d979ff1b6f2b440cfe0b46ac00c14c2e)

![{\displaystyle y_{(k)}=K_{PD1}\cdot [u_{(k)}+[u_{(k)}-u_{(k-1)}]\cdot {\frac {T}{\Delta t}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b799553479c07c109cdf0c8026497476a9849a9)










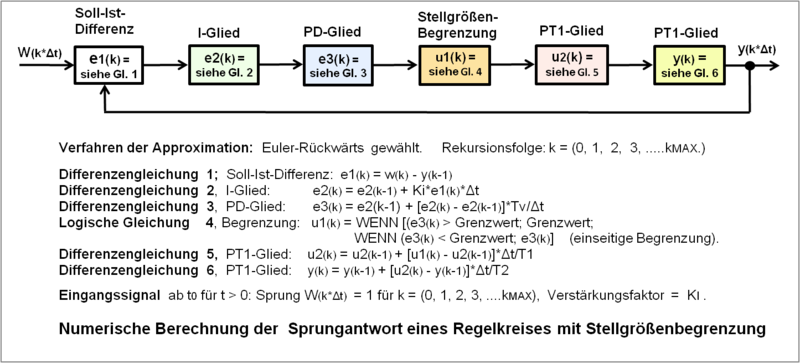












![{\displaystyle y_{(k)}=y_{(k-1)}+[u_{(k)}-y_{(k-1)}]\cdot {\frac {\Delta t}{T_{H}+\Delta t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/939da97299dacbdce0fb3aa3b13980637a37e01d)


![{\displaystyle {\ddot {y}}(t)={\frac {1}{a_{2}}}\cdot [-a_{0}\cdot y(t)-a_{1}\cdot {\dot {y}}(t)+b_{0}\cdot u(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ed6fa147ee4c4f56cc341229de5501f27be92c7)



