Go/ Einführung/ Notation
Notation von Partien
[Bearbeiten]Eine festgelegte Norm gibt es nicht. Es finden sich zwar in verschiedenen Büchern Versuche, eine Kürzelsprache zu etablieren, aber durchgesetzt hat sich noch keine. Hier folgen deshalb nur Hinweise, welche Art der Notation möglichst fehlerfrei und eindeutig ist.
Kifu
[Bearbeiten]
Der Spielbericht oder Spielbogen (jap. Kifu 棋譜) besteht aus einem Gitterpapier, auf dem die Zugnummern mit zwei unterschiedlichen Farben eingetragen werden.
Der rote Kreis markiert den Siegelzug (jap. Fujite 封じ手), der bei Partien, die über mehrere Tage dauern, gespielt wird.
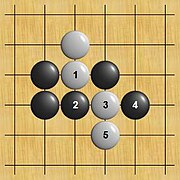
Wird ein Stein geschlagen, verbleibt seine Zugnummer auf dem Spielbogen, was für Anfänger die größte Schwierigkeit beim Lesen ist. Wenn dann ein Stein auf den im Spiel freien Schnittpunkt gesetzt wird, notiert man diesen Zug am Rand (z.B. 63 auf 12). Folglich ist auf dem Gitterpapier keine durchgehende Zahlenreihe vorhanden, was im ersten Moment verwirrend ist.
Alternative Notationen
[Bearbeiten]- algebraische Notation: Durchnummerierung von A1 bis T19 (das "i" bleibt unbenutzt). Komischerweise ist A1 der Eckpunkt links unten, z.B.
- 1. A17 D16
- 2. Q17 D17
- ....
- 25. xD17 (wenn ein Stein geschlagen wird)
- "Pierre Audouard-Notation": Die Ecken heißen a, b, c, d und die Schnittpunkte werden relativ zu den Ecken angegeben. B3 entspricht hier a2-3 und R17 ist c3-3.
Notation von Problemstellungen
[Bearbeiten]Die Notation von Problemstellungen folgt dem Prinzip des Kifu mit dem Unterschied, dass nur der relevante Brettteil gezeigt wird. Bei Problemen, die eine Eck- oder Seitenstellung beinhalten, sollte die Randlinie hervorgehoben werden.
Bei der ausführlichen Diskussion eines Problems empfiehlt es sich ein Referenzdiagramm vorwegzuschicken, auf das sich die folgenden Diagramme beziehen (siehe Beispiel). Bei der Verwendung von SGF-Editoren hat man den Vorteil, dass Steine und Schnittpunkte zusätzlich markiert oder benannt werden können.
Beispiel:
-
Dia 1
-
Dia 2
-
Dia 3
Bei der Diskussion von Ganzbrettsituationen kann es Vorteil sein, eine algebraische Notation zu verwenden, wenn es z.B. um die Kennzeichnung von mehreren Alternativzügen geht.