Imaginäre und komplexe Zahlen

Dieses Buch steht im Regal Mathematik.

Diese Seite überschneidet sich thematisch mit [[Komplexe Zahlen]]. Hilf mit, die Seite unter einem Lemma zu vereinigen oder inhaltlich besser voneinander abzugrenzen. Mehr Informationen stehen auf Wikibooks:Seiten zum gleichen Thema, dort sollte der Grund stehen, warum dieser Baustein gesetzt wurde. Bitte äußere dich dort auch, bevor du diesen Baustein ohne Änderungen entfernst. Shogun (Dis.)

  Hier gibt es eine PDF-Version [1].  

Grundlagen und Voraussetzungen: Reelle Zahlen

Die Menge der reellen Zahlen besteht aus den rationalen und den irrationalen Zahlen.

Die Menge der rationalen Zahlen umfasst alle Zahlen, die sich als gemeine Brüche m / n (m und n ganzzahlig) darstellen lassen. Dies sind: Die ganzen Zahlen, die endlichen Dezimalbrüche und die unendlichen periodischen Dezimalbrüche.

Die Menge der irrationalen Zahlen umfasst alle unendlichen nicht periodischen Dezimalbrüche. Zu den irrationalen Zahlen gehören z. B. die Wurzeln aus positiven Zahlen, die keine Quadratzahlen sind, die Eulersche Zahl e, die Zahl π, fast alle Logarithmen und fast alle Werte der trigonometrischen Funktionen.

Die reellen Zahlen sind eineindeutig (= umkehrbar eindeutig) auf die Zahlengerade abbildbar. Das heißt: Jeder reellen Zahl entspricht genau ein Punkt der Zahlengeraden und jedem Punkt der Zahlengeraden entspricht genau eine reelle Zahl.

Das System der reellen Zahlen kann insofern als vollständig und nicht weiter ergänzbar bezeichnet werden, als jedem Punkt der Zahlengeraden eine reelle Zahl zugeordnet ist. Innerhalb der Menge der reellen Zahlen sind alle vier Grundrechenarten unbeschränkt ausführbar (außer Division durch 0) und es gibt eine Kleiner-als-Relation (die sich mit Addition und Multiplikation gemäß der bekannten Gesetze verträgt). Die Menge der reellen Zahlen ist daher ein "geordneter Zahlenkörper".

 

Imaginäre Zahlen

Andererseits kann man das System der reellen Zahlen aber auch als unvollständig betrachten, weil es in ihm z. B. keine Lösung der rein quadratischen Gleichung

$x^2 = - 1 \$

gibt, denn es gibt keine reelle Zahl, deren Quadrat gleich -1 ist.

Eine lediglich formale Lösung der Gleichung lautet

$x = \pm \sqrt { - 1} \;,$

wobei aber dem Symbol $\sqrt {-1}\$ keine reelle Zahl entspricht, und es überhaupt undeutlich ist, was man hier unter "Wurzel" verstehen sollte.

Der Ausweg ist nun, eine neuartige Zahl i zu betrachten, deren Quadrat gleich -1 ist, und zu untersuchen, ob wir brauchbare, widerspruchsfreie Ergebnisse erhalten, wenn wir auf diese "Zahl" die bekannten Rechengesetze für reelle Zahlen anwenden. Wir nennen die Zahl i (historisch bedingt) die "imaginäre Einheit".

Für diese Zahl i gilt also:

$i^2 = -1\,$

Beim Rechnen mit dieser Zahl wird überall das Quadrat dieser Zahl durch -1 ersetzt.

Jetzt kann man die vorgelegte Gleichung lösen. Die Lösungen sind:

$x_{1,2} = \pm i\,.$

Fügt man die Zahl i den reellen Zahlen zu, dann entsteht beim Rechnen eine ganze Mengen neuer Zahlen, z. B.;

$2i, 3i, -i, 1+i, 2+i, 1+2i, -23 + 78i, 0{,}45 - 0{,}93i\,$ usw.

Die allgemeine Form dieser Zahlen ist:

$a+bi\,,$

worin a und b beliebige reelle Zahlen sind. Es sind diese Zahlen, die man komplexe Zahlen nennt. Man rechnet mit ihnen wie mit reellen Zahlen und ersetzt immer i² durch -1. Zum Beispiel:

$(1+2i)+(3+4i)=(1+3)+(2+4)i=4+6i\,$ $(1+2i)-(3+4i)=(1-3)+(2-4)i=-2-2i\,$ $(1+2i)\cdot(3+4i)=1\times 3 + 1\times 4i + 2\times 3i + 2\times 4i^2=3+4i+6i-8=-5+10i\,$

Allgemein:

$(a+bi)+(c+di)=(a+c)+(b+d)i\,$ $(a+bi)-(c+di)=(a-c)+(b-d)i\,$ $(a+bi)\cdot(c+di)=ac + adi + bci + bdi^2=(ac-bd)+(ad+bc)i\,$

Zur Division siehe nächster Abschnitt.

Soweit steht das ganze nicht auf einer soliden Grundlage; wir haben nur so getan, als ob dieses i existieren würde. Um zu zeigen, dass diese Annahme widerspruchsfrei ist, kann man - ausgehend von der Existenz der reellen Zahlen - wie folgt vorgehen: Man führt die komplexen Zahlen als Paare reeller Zahlen ein, definiert Addition und Multiplikation entsprechend obiger Formeln - z. B. ist das Produkt des Zahlenpaars (a, b) mit (c, d) das Zahlenpaar (ac-bd, ad+bc) - und rechnet dann (ziemlich langwierig und langweilig) nach, dass die üblichen Rechengesetze gelten: Jeweils für Addition und Multiplikation Kommutativgesetz, Assoziativgesetz, Existenz von neutralen und inversen Elementen; sowie das Distributivgesetz. (Wenn man Polynomringe oder Matrizenringe kennt, kann man die komplexen Zahlen auch anders einführen und sich so das Nachprüfen der Rechenregeln größtenteils ersparen.)

Es gibt keine mit Addition und Multiplikation verträgliche Kleiner-als-Relation auf den komplexen Zahlen. (Andernfalls müsste ja wie bei den reellen Zahlen jedes Quadrat nicht-negativ sein.)

Es gibt jedoch wie bei den reellen Zahlen eine Topologie, d.h. es lassen sich Grenzwerte definieren. Zusammengefasst: Die komplexen Zahlen bilden einen bewerteten Körper.

Konjugiert-komplexe Zahl und Division

Für eine beliebige komplexe Zahl $z = a+bi$ heißt $\operatorname{Re}(z) := a$ der Realteil und $\operatorname{Im}(z) := b$ der Imaginärteil von $z$. Weiter heißt $\bar{z}:=a-bi$ die zu z konjugiert-komplexe Zahl.

Das Produkt $z\cdot \bar{z}=a^2+b^2$ ist reell und positiv, falls $z\not\neq 0$. Man kann durch eine komplexe Zahl dividieren, indem man mit der konjugiert-komplexen Zahl erweitert:

$\frac{a+bi}{c+di}=\frac{(a+bi)(c-di)}{(c+di)(c-di)}=\frac{(ac+bd)+(bc-ad)i}{c^2+d^2} =\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i$

Imaginäre Zahlen

Mit i beginnend erhalten wir durch fortwährende Addition bzw. Subtraktion von i die "Zahlen"

$\dots, - 3i, - 2i, - i, 0, i, 2i, 3i, \dots$

die gleichsam die imaginären Gegenstücke zu den reellen ganzen Zahlen sind. Allgemeiner erhalten wir die (rein-)imaginären Zahlen als Produkte der reellen Zahlen mit i. Als nächstes können wir die imaginären Zahlen auf eine eigene, die "imaginäre Zahlengerade" abbilden. Dabei ist es zweckmäßig, die "imaginäre Einheitsstrecke" gleich der reellen Einheitsstrecke zu machen.

Da die beiden Zahlengeraden die Null gemeinsam haben, müssen wir sie so anordnen, dass sie einander in 0 schneiden. Schon aus Symmetriegründen erscheint es zweckmäßig, die beiden Zahlengeraden senkrecht zueinander anzubringen.

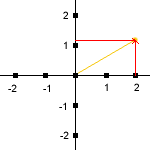
Mit den imaginären Zahlen können nun auch die Lösungen der rein quadratischen Gleichungen

$x^2 = -a^2 \$

(a reell) angegeben werden. Sie lauten

$x_{1,2} = \pm a\,i\;.$

Die Regeln zur Addition und Subtraktion imaginärer Zahlen ergeben sich durch Anwendung der einschlägigen Regeln der Algebra:

$a\;i \pm b\;i = \left( {a \pm b} \right)\;i\;.$

Die "graphische Addition bzw. Subtraktion" auf der imaginären Zahlengeraden führt zum gleichen Ergebnis.

Für die Multiplikation und Division zweier imaginärer Zahlen berechnen wir zunächst das Produkt und den Quotienten zweier imaginärer Einheiten i. Es ist (siehe oben)

$i \cdot i = i^2 = - 1\;,$

und

$\frac{i} {i} = 1\;.$

Damit ergeben sich

$pi \cdot qi = - pq$

und

$\frac{{pi}} {{qi}} = \frac{p} {q}\;,$

wobei p und q reelle Zahlen sind.

Ergebnis: Produkt und Quotient zweier imaginärer Zahlen sind reelle Zahlen

Durch wiederholte Multiplikation findet man die positiven ganzzahligen Potenzen von i:

$i^2 = - 1\,,\quad i^3 = i^2 \cdot i = - i\,,\quad i^4 = i^3 \cdot i = 1\,,\quad i^5 = i^4 \cdot i = i\,, \ldots$

Wenn wir verabreden, dass für positive ganzzahlige n

$i^{ - n} \equiv \frac{1} {{i^n }}$

sein soll, ergeben sich die negativen ganzzahligen Potenzen von i wie folgt:

$i^{ - 1} = \frac{1} {i} = \frac{i} {{i^2 }} = - i\,,\quad i^{ - 2} = \frac{1} {{i^2 }} = \frac{1} {{ - 1}} = - 1\,,\quad i^{ - 3} = \frac{1} {{i^3 }} = - \frac{1} {i} = i\,,\quad i^{ - 4} = \frac{1} {{i^4 }} = 1\,,\, \ldots$

Die Berechnung der Wurzeln aus i ist erst später möglich.

 

Lösung quadratischer Gleichungen

Betrachten wir nun eine gemischt quadratische Gleichung

$x^2 - 4x + 13 = 0\,.$

Auf die bekannte Weise (durch quadratische Ergänzung) findet man die Lösungen

$x_{1,2} = 2 \pm \sqrt { - 9} = 2 \pm 3\,i\;.$

Die Lösungen sind weder reelle, noch imaginäre Zahlen, sondern die Summe aus einer reellen und einer imaginären Zahl. Wir nennen solche Zahlen komplexe Zahlen.

Setzt man eine der beiden Zahlen in die Gleichung ein und führt die mathematischen Operationen nach den obigen Regeln aus, so findet man die Gleichung erfüllt.

Die allgemeine Form einer komplexen Zahl ist

$z = a + b\,i,$

wobei a und b reelle Zahlen sind.

Mit Hilfe komplexer Zahlen können uneingeschränkt die Lösungen gemischt quadratischer Gleichung angeben werden. Aus:

$x^2 + p \cdot x + q = 0$

folgt

$x_{1,2} = - \frac{p} {2} \pm \sqrt {\frac{{p^2 }} {4} - q} \,.$

Für

$\frac{{p^2 }} {4} - q \ge 0$

ergeben sich zwei bzw. eine reelle Lösung.

Für

$\frac{{p^2 }} {4} - q < 0$

schreibt man die Lösungen in der Form

$x_{1,2} = - \frac{p} {2} \pm i\sqrt {q - \frac{{p^2 }} {4}} \;.$

Die Lösungen sind "konjugiert komplex", d. h. sie unterscheiden sich nur durch das Vorzeichen ihres imaginären Teils.

Bemerkung: Das Ausgangsproblem, die Lösung quadratischer Gleichungen, ist nun also gelöst, wenn die Gleichung reelle Koeffizienten hat. Tatsächlich gilt jedoch viel mehr (Fundamentalsatz der Algebra): Jedes Polynom über den komplexen Zahlen zerfällt in Linearfaktoren. Der Körper der komplexen Zahlen ist damit algebraisch-abgeschlossen. Die Vorgehensweise, die uns von den reellen Zahlen zu den komplexen Zahlen geführt hat, lässt sich also nicht erneut anwenden, um einen noch größeren Zahlkörper zu bekommen.

Darstellung komplexer Zahlen in der Zahlenebene

Für die graphische Darstellung komplexer Zahlen bietet sich die "komplexe Zahlenebene" an, die von der reellen und der imaginären Zahlengeraden aufgespannt wird.

Die komplexe Zahl z = a + b i kann dabei wahlweise (abwechselnd oder gleichzeitig) durch einen Punkt P mit den "Koordinaten" a und b, wo die Koordinate b dem Punkt bi auf der imaginären Zahlengerade entspricht, oder durch den "Zeiger" 0P dargestellt werden. Dieser wird dann beschrieben durch seine Länge $r \$ und den Winkel $\varphi$;, den er mit der reellen Achse bildet. (Das ist natürlich nichts anderes als die Darstellung des Punktes P in Polarkoordinaten.)

r heißt Betrag der komplexen Zahl, φ heißt ihr Argument oder ihre Phase.

Für die beiden Darstellungsformen gelten folgende Transformationsgleichungen::

$r = \sqrt {a^2 + b^2 } \,,\quad \tan \varphi = \frac{b} {a}\,,\quad \quad a \ne 0$

$a = r\cos \varphi \,,\quad b = r\sin \varphi \,.$

Aus

$\tan \varphi = \frac{b} {a}$

folgt

$\varphi = \arctan \frac{b} {a} + k \cdot \pi ,\quad {\mbox{wobei}}\quad - \frac{\pi } {{\mbox{2}}} < \arctan \frac{b} {a} < \frac{\pi } {2}\quad {\mbox{und }}k{\mbox{ ganzzahlig ist}}.$

Der Wert

$\varphi _0 = \arctan \frac{b} {a}$

heißt Hauptwert von $\varphi$; Aus ihm ergeben sich alle übrigen Werte durch Addition von k 2π.

Damit kann die komplexe Zahl z auch so beschrieben werden:

$z = a + bi = r\left( {\cos \varphi + i\sin \varphi } \right)\,.$

Später ergibt sich daraus mit Hilfe der "Eulerschen Formel"

$e^{i\varphi } = \cos \varphi + i\sin \varphi$

eine dritte Darstellungsweise:

$z = a + bi = r\left( {\cos \varphi + i\sin \varphi } \right) = r\,e^{i\varphi } \,.$

Die drei Darstellungsformen einer komplexen Zahl heißen in der angegebenen Reihenfolge arithmetische Form, goniometrische (oder trigonometrische) Form und Exponentialform.

Da die Eulersche Formel erst später bewiesen werden kann, soll die Exponentialform hier zwar genannt, aber nicht für Beweise benutzt werden.

 

Rechnen mit komplexen Zahlen

Gegeben zwei komplexe Zahlen

$z_1 = a_1 + b_1 i\,,\quad z_2 = a_2 + b_2 i\,.$

Summe und Differenz komplexer Zahlen

Für die Summe bzw. Differenz der beiden Zahlen findet man, wenn man i wie irgendeine Buchstabengröße behandelt, nach den Regeln der Algebra

$z_1 + z_2 = a_1 + b_1 i + a_2 + b_2 i = \left( {a_1 + a_2 } \right) + \left( {b_1 + b_2 } \right)i\,$

$z_1 - z_2 = a_1 + b_1 i - \left( {a_2 + b_2 i} \right) = \left( {a_1 - a_2 } \right) + \left( {b_1 - b_2 } \right)i$

Die Zeiger komplexer Zahlen werden wie Vektoren addiert und subtrahiert.

 

Das Produkt komplexer Zahlen

Es ist

$z_1 z_2 = \left( {a_1 + b_1 i} \right)\left( {a_2 + b_2 i} \right) = \left( {a_1 a_2 - b_1 b_2 } \right) + \left( {a_1 b_2 + a_2 b_1 } \right)i.$

Dieser Wert des Produkts hat keine unmittelbar erkennbare anschauliche Bedeutung. Führt man dagegen die "Polarkoordinaten" ein, so erhält man

$a_1 a_2 - b_1 b_2 = r_1 r_2 \left( {\cos \varphi _1 \cos \varphi _2 - \sin \varphi _1 \sin \varphi _2 } \right) = r_1 r_2 \cos \left( {\varphi _1 + \varphi _2 } \right)$

$a_1 b_2 + a_2 b_1 = r_1 r_2 \left( {\cos \varphi _1 \sin \varphi _2 + \sin \varphi _1 \cos \varphi _2 } \right) = r_1 r_2 \sin \left( {\varphi _1 + \varphi _2 } \right).$

und damit

$z_1 z_2 = r_1 r_2 \left[ {\cos \left( {\varphi _1 + \varphi _2 } \right) + i\sin \left( {\varphi _1 + \varphi _2 } \right)} \right].$

Also ist

$\left| {z_1 z_2 } \right| = \left| {z_1 } \right|\left| {z_2 } \right|\qquad \text{und} \qquad \varphi \left( {z_1 z_2 } \right) = \varphi _1 + \varphi _2 .$

Der Betrag des Produkts ist also gleich dem Produkt der Beträge, das Argument ist gleich der Summe der Argumente.

Man erkennt (durch wiederholte Anwendung) sofort, dass dieser Satz auch für mehr als zwei Faktoren gilt:

$\left| {z_1 \cdot z_2 \cdot \ldots \cdot z_n } \right| = \left| {z_1 } \right| \cdot \left| {z_2 } \right| \cdot \ldots \cdot \left| {z_n } \right| \quad {\text{und}} \quad \varphi = \varphi _1 + \varphi _2 + \ldots + \varphi _n .$

 

Division komplexer Zahlen

Analog findet man für z₂ ungleich 0:

$\left|\frac{z_1}{z_2}\right| = \frac{|z_1|}{|z_2|} \quad \text{und} \quad \varphi = \varphi _1 - \varphi _2 .$

Setzt man darin z₁ = 1 und z₂ = z, so erhält man für den Kehrwert einer komplexen Zahl:

$\frac{1} {z} = \frac{1}{|z|}\left[\cos (0 - \varphi ) + i\sin(0 - \varphi ) \right] = \frac{1} {r}( \cos \varphi - i\sin \varphi ),$

und spezielle für z = i

$\frac{1} {i} = - i.$

 

Ganzzahlige Potenzen einer komplexen Zahl

Wir verabreden zunächst für positive ganzzahlige Werte von n:

1. Unter der n-ten Potenz zⁿ einer komplexen Zahl verstehen wir das Produkt aus n gleichen Faktoren z.

2. Es sei

$z^{ - n} \equiv \frac{1} {{z^n }}.$

Aus (siehe Multiplikation komplexer Zahlen)

$\left| {z_1 \cdot z_2 \cdot \ldots \cdot z_n } \right| = \left| {z_1 } \right| \cdot \left| {z_2 } \right| \cdot \ldots \cdot \left| {z_n } \right|\quad \text{und} \quad \varphi = \varphi _1 + \varphi _2 + \ldots + \varphi _n .$

folgt dann für lauter gleiche Faktoren z:

$z^n = \left| z \right|^n \left( {\cos n\varphi + i\sin n\varphi } \right).$

Wie man leicht erkennt, gilt diese Beziehung auch für negative ganzzahlige Werte von n.

Ferner folgt daraus

$z^p \cdot z^q = z^{p + q} ,\quad \left( {z^p } \right)^q = z^{p \cdot q} ,\quad z_1^p \cdot z_2^p = \left( {z_1 \cdot z_2 } \right)^p ,\quad \frac{{z^p }} {{z^q }} = z^{p - q} ,\quad \frac{{z_1^p }} {{z_2^p }} = \left( {\frac{{z_1 }} {{z_2 }}} \right)^p .$

 

Der binomische Lehrsatz

Aus den Rechenregeln für Potenzen und den Multiplikationsregeln für zwei Klammern folgt sofort, dass der binomische Lehrsatz für positive ganzzahlige Exponenten auch für komplexe Zahlen gilt:

$\left( {z_1 + z_2 } \right)^n = {n \choose 0} z_1^n + {n \choose 1} z_1^{n-1} z_2 + \ldots + {n \choose k} z_1^{n - k} z_2^k + \ldots + {n \choose n} z_2^n .$

 

 

Die Moivreschen Formeln

Aus der Gleichung (siehe oben)

$z^n = \left| z \right|^n \left( {\cos n\varphi + i\sin n\varphi } \right)$

folgt für

$\left| z \right| = 1:\qquad \left( {\cos \varphi + i\sin \varphi } \right)^n = \cos n\varphi + i\sin n\varphi .$

Andererseits liefert der binomische Lehrsatz für positive ganzzahlige Exponenten:

$\left( {\cos \varphi + i\sin \varphi } \right)^n = \cos ^n \varphi + i {n \choose 1} \cos ^{n - 1} \varphi \cdot \sin \varphi - {n \choose 2} \cos ^{n - 2} \varphi \cdot \sin ^2 \varphi$

$\quad \quad - i {n \choose 3} \cos ^{n - 3} \varphi \cdot \sin ^3 \varphi + {n \choose 4} \cos ^{n - 4} \varphi \cdot \sin ^4 \varphi + \ldots + i^n {n \choose n} \sin ^n \varphi .$

Wenn man die rechten Seiten der beiden Gleichungen gleich setzt und dann berücksichtigt, dass die Realteile und die Imaginärteile jeweils gleich sein müssen, erhält man die Moivreschen Formeln:

$\cos n\varphi = \cos ^n \varphi - {n \choose 2} \cos ^{n - 2} \varphi \cdot \sin ^2 \varphi + {n \choose 4} \cos ^{n - 4} \varphi \cdot \sin ^4 \varphi - + \ldots ,$

und

$\sin n\varphi = n\cos ^{n - 1} \varphi \cdot \sin \varphi - {n \choose 3} \cos ^{n - 3} \varphi \cdot \sin ^3 \varphi + {n \choose 5} \cos ^{n - 5} \varphi \cdot \sin ^5 \varphi - + \ldots ,$

wobei die rechten Seiten so weit zu ergänzen sind, bis die Binomialkoeffizienten null werden.

 

Wurzeln aus komplexen Zahlen

Die Lösungen der Gleichung

$x^n = z\qquad n \text{ positiv ganzzahlig}$

heißen die n-ten Wurzel aus der komplexen Zahl z:

$x = \sqrt[n]{z}.$

Setzen wir

$z = r\left( {\cos \varphi + i\sin \varphi } \right)$

und

$x = \rho\left( {\cos \psi + i\sin \psi } \right),$

so muss wegen xⁿ = z

$\rho ^n = r\quad \text{und} \quad n\psi = \varphi$

und folglich

$\rho = \sqrt[n]{r}\quad \text{und} \quad \psi = \frac{\varphi } {n}$

sein.

Bei der Division durch n ist jedoch zu beachten, dass das Argument φ periodisch ist mit der Periode 2π, also

$\varphi = \varphi _0 + k \cdot 2\pi \quad \quad k = 0,\;1,\;2,\; \ldots$

Folglich findet man für ψ genau n verschiedene Werte, nämlich

$\psi = \frac{\varphi } {n},\quad \frac{{\varphi + 2\pi }} {n},\quad \frac{{\varphi + 2 \cdot 2\pi }} {n},\; \ldots \;\frac{{\varphi + \left( {n - 1} \right) \cdot 2\pi }} {n}.$

Von k = n an werden lediglich die vorderen Werte (vom zweiten an) wiederholt.

Also gilt:

$\sqrt[n]{z} = \sqrt[n]{r}\left( {\cos \frac{{\varphi + k \cdot 2\pi }} {n} + i\sin \frac{{\varphi + k \cdot 2\pi }} {n}} \right)\quad \quad k = 0,\;1,\;2,\; \ldots \;\left( {n - 1} \right)$

Jeder dieser Werte wird eine n-te Wurzel der komplexen Zahl z genannt und mit

$\sqrt[n]{z}\quad {\mbox{oder}}\quad z^{\frac{1} {n}}$

bezeichnet.

Die diesen n Werten entsprechenden Punkte der Zahlenebene liegen alle auf einem Kreis um 0 und sind die Ecken eines regulären n-Ecks.

Für die Quadratwurzeln aus

$i = i\sin \frac{\pi } {2}$

ergeben sich die Werte

$\cos \frac{\pi } {4} + i\sin \frac{\pi } {4}\quad {\mbox{und}}\quad \cos \frac{{5\pi }} {4} + i\sin \frac{{5\pi }} {4},$

und für die Quadratwurzel aus

$- i = i\sin \frac{{3\pi }} {2}$

findet man

$\cos \frac{{3\pi }} {4} + i\sin \frac{{3\pi }} {4}\quad {\mbox{und}}\quad \cos \frac{{7\pi }} {4} + i\sin \frac{{7\pi }} {4}.$

Wenn wir nun noch verabreden, dass wie bei reellen Zahlen

$z^{\frac{m} {n}} = \left( {z^{\frac{1} {n}} } \right)^m = \left( {\sqrt[n]{z}} \right)^m$

sein soll, wobei n eine natürliche und m eine beliebige ganze Zahl ist, dann sind damit die Potenzen komplexer Zahlen mit rationalen Exponenten definiert. Es bleibt als vorläufig letzter Schritt die Zulassung und Erklärung irrationaler Exponenten.

 

Potenzen mit beliebigen reellen Exponenten

Ist z eine beliebige, von 0 verschiedene komplexe Zahl.

$z = r\left( {\cos \varphi + i\sin \varphi } \right) = r\left[ {\cos \left( {\varphi_0 + k \cdot 2\pi } \right) + i\sin \left( {\varphi_0 + k \cdot 2\pi } \right)} \right],$

wobei

$k = 0,\; \ 1,\; \ 2,\; \ldots$

ist, so soll unter z^ν (ν reell) jede der folgenden komplexen Zahlen verstanden werden:

$r^\nu \left[ {\cos \nu \left( {\varphi + k \cdot 2\pi } \right) + i\sin \nu \left( {\varphi + k \cdot 2\pi } \right)} \right].$

Hinweis: Für die so allgemein definierten Potenzen komplexer Zahlen gelten die Grundregeln für das Rechnen mit Potenzen, nämlich

$z^\mu \cdot z^\nu = z^{\mu + \nu } ,\quad z_1^\mu \cdot z_2^\mu = \left( {z_1 \cdot z_2 } \right)^\mu ,\quad \left( {z^\mu } \right)^\nu = z^{\mu \cdot \nu }$

nicht mehr.