Ing Mathematik: Vektoren

Aus Wikibooks

Wechseln zu: Navigation, Suche

Zurück zu Permutationen, ... |

Hoch zu Gesamtinhaltsverzeichnis |

Vor zu Matrizen

Inhaltsverzeichnis

1 Vektorraum
2 Addition von Vektoren
3 Multiplikation eines Vektors mit einem Skalar
4 Skalarprodukt
5 Orthogonalität
6 Linearkombinationen
7 Projektionen
8 Vektorprodukt
9 Spatprodukt
- 9.1 Regeln
10 Geraden
- 10.1 Gerade durch Punkt und Richtung
- 10.2 Gerade durch zwei Punkte
11 Ebenen
12 Anwendungen: Punkte, Geraden und Ebenen
13 Übungen

[Bearbeiten] Vektorraum

Ein Vektorraum $\mathbb{R}^n$ sei die Menge aller geordneter n-Tupel von reellen Zahlen. Ein Element eines Vektorraumes heißt Vektor

$\mathbf{a}=(a_1, \ldots, a_n)\ = \begin{pmatrix} a_1 \\ \vdots \\ a_n \end{pmatrix} ; \quad \mathbf{a}\in \mathbb{R}^n$

mit den Koordinaten des Vektors

$a_1, \ldots, a_n \ ; \quad a_i \in \mathbb{R}$

Vektoren weisen einen Zahlenwert (Betrag) und eine Richtung auf. Skalare haben nur einen Zahlenwert.

Freie Vektoren können beliebig im Raum verschoben werden. Ortsvektoren (gebundene Vektoren) sind ortsgebunden.

[Bearbeiten] Addition von Vektoren

$\mathbf{a}=(a_1,\ldots,a_n) \in \mathbb{R}^n$

$\mathbf{b}=(b_1,\ldots,b_n) \in \mathbb{R}^n$

$\mathbf{a}+\mathbf{b} = \left(a_1+b_1, \ldots , a_n+b_n\right) = \begin{pmatrix} a_1+b_1 \\ \vdots \\ a_n+b_n \end{pmatrix}$

[Bearbeiten] Assoziativgesetz

$(\mathbf{a}+\mathbf{b})+\mathbf{c} = \mathbf{a} + (\mathbf{b}+\mathbf{c})$

[Bearbeiten] Kommutativgestz

$\mathbf{a}+\mathbf{b} = \mathbf{b} + \mathbf{a}$

[Bearbeiten] Nullvektor

Der Nullvektor ist das neutrale Element der Vektoraddition.

$\mathbf{o}=(0,\ldots,0) \in \mathbb{R}^n$

$\mathbf{o}+\mathbf{a} = \mathbf{a}+\mathbf{o} = \mathbf{a}$

[Bearbeiten] Differenzvektor

$\mathbf{a}+\mathbf{c}=\mathbf{b}$ läßt sich stets umformen zu $\mathbf{c} = \mathbf{b}-\mathbf{a}$ . $\mathbf{c}$ sei in diesem Fall der Differenzvektor.

[Bearbeiten] Beispiel

Gegeben seien die Vektoren $\mathbf{a}=(1,-1,5)$ und $\mathbf{b}=(2,0,1)$ . Gesucht sind $\mathbf{a}+\mathbf{b}$ und $\mathbf{a}-\mathbf{b}$ .

$\mathbf{a}+\mathbf{b} = \begin{pmatrix} 1 \\ -1 \\ 5 \end{pmatrix} + \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 3 \\ -1 \\ 6 \end{pmatrix}$

$\mathbf{a}-\mathbf{b} = \begin{pmatrix} 1 \\ -1 \\ 5 \end{pmatrix} - \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} -1 \\ -1 \\ 4 \end{pmatrix}$

[Bearbeiten] Multiplikation eines Vektors mit einem Skalar

Geometrisch entspricht die Multiplikation eines Vektors mit einem Skalar der Streckung eines Vektors.

$\alpha , \; \beta \ \in \mathbb{R}$

$\alpha \mathbf{a} = \left( \alpha a_1, \ldots , \alpha a_n\right)= \begin{pmatrix} \alpha a_1 \\ \vdots \\ \alpha a_n \end{pmatrix}$

$1\mathbf{a} = \mathbf{a}$

[Bearbeiten] Assoziativgesetz

$(\alpha\beta) \mathbf{a} = \alpha (\beta \mathbf{a})$

[Bearbeiten] Distributivgesetze

$(\alpha + \beta) \mathbf{a} = \alpha \mathbf{a} + \beta \mathbf{a}$

$\alpha (\mathbf{a} + \mathbf{b}) = \alpha \mathbf{a} + \alpha \mathbf{b}$

[Bearbeiten] Gegenvektor

$-\mathbf{a} = \left( -a_1, \ldots, -a_n\right) = \begin{pmatrix} -a_1 \\ \vdots \\ -a_n \end{pmatrix}$

$\mathbf{a} + (-\mathbf{a}) = \mathbf{o}$

[Bearbeiten] Parallelität

Die zwei Vektoren a und b sind dann parallel, wenn gilt

$\mathbf{a} = \lambda \mathbf{b}\ ; \quad \lambda \in \mathbb{R} \wedge \lambda\neq 0$

$λ > 0$ : gleichsinnig parallel

$λ < 0$ : gegensinnig parallel

[Bearbeiten] Beispiel

Sind die Vektoren $\mathbf{a}=(5,1,-1)$ und $\mathbf{b}=12(4,1,-1)-(63,15,-15)$ zueinander parallel?

$\mathbf{b} = 12 \begin{pmatrix} 4 \\ 1 \\ -1 \end{pmatrix} - \begin{pmatrix} 63 \\ 15 \\ -15 \end{pmatrix} = \begin{pmatrix} -15 \\ -3 \\ 3 \end{pmatrix} =-3 \begin{pmatrix} 5 \\ 1 \\ -1 \end{pmatrix}$

$\Rightarrow \; \mathbf{b} = -3\mathbf{a}\; \Rightarrow \;\mathbf{a} || \mathbf{b}$ .

[Bearbeiten] Skalarprodukt

Gegeben sind zwei Vektoren

$\mathbf{a}=(a_1,\ldots,a_n) \in \mathbb{R}^n$

$\mathbf{b}=(b_1,\ldots,b_n) \in \mathbb{R}^n$

Das Skalarprodukt ergibt sich zu

$\mathbf{a}\cdot \mathbf{b}=\sum_{i=1}^n a_ib_i$

Das Skalarprodukt ordnet einem Paar von Vektoren eine reelle Zahl zu.
Das Skalarprodukt unterscheidet sich grundlegend von der Multiplikation reeller Zahlen oder der Multiplikation eines Vektors mit einem Skalar.

Mittels Skalarprodukt lassen sich lineare Funktionen einfach anschreiben

$f(x)=a_1x_1 + a_2x_2 + \ldots + a_nx_n = \mathbf{a}\cdot\mathbf{x}$

[Bearbeiten] Norm eines Vektors

Die Norm (Länge) eines Vektors a ist gegeben durch

$\|\mathbf{a}\| = \sqrt{\mathbf{a}\cdot \mathbf{a}} = \sqrt{a_1^2+\cdots + a_n^2}$

$\|\alpha \mathbf{a}\| = |\alpha| \| \mathbf{a}\|$

Vektoren mit der Länge Eins heißen Einheitsvektoren. Normiert man einen Vektor a, so bringt man ihn auf die Länge Eins

$\mathbf{a}_0 = \frac{\mathbf{a}}{\|\mathbf{a}\|}$

Das Skalarprodukt ist auch definiert durch

$\mathbf{a}\cdot \mathbf{b}= \|\mathbf{a}\| \|\mathbf{b}\|\cos(\angle)$

wobei $\angle$ den Winkel zwischen den Vektoren a und b bezeichnet.

[Bearbeiten] Kommutativgesetz

$\mathbf{a}\cdot \mathbf{b} = \mathbf{b}\cdot \mathbf{a}$

[Bearbeiten] Assoziativgesetz gilt nicht

$\mathbf{a}\cdot(\mathbf{b} \cdot \mathbf{c}) \neq (\mathbf{a}\cdot\mathbf{b}) \cdot \mathbf{c}$

[Bearbeiten] Distributivgesetz

$\mathbf{a}\cdot(\mathbf{b} + \mathbf{c}) = \mathbf{a}\cdot\mathbf{b} + \mathbf{a} \cdot \mathbf{c}$

[Bearbeiten] Chauchy-Schwarzsche Ungleichung

$(\mathbf{a}\cdot \mathbf{b})^2 \le \|\mathbf{a}\|^2\|\mathbf{b}\|^2$

[Bearbeiten] Dreiecksungleichung

$\|\mathbf{a}+ \mathbf{b}\| \le \|\mathbf{a}\| + \|\mathbf{b}\|$

[Bearbeiten] Beispiel: Parallelogrammgleichung

Es ist folgende Gleichung herzuleiten

$\|\mathbf{a}+\mathbf{b}\|^2 + \|\mathbf{a}-\mathbf{b}\|^2= 2\left( \|\mathbf{a}\|^2 + \|\mathbf{b}\|^2\right)$

Lösung:

$\|\mathbf{a}+\mathbf{b}\|^2 = (\mathbf{a}+\mathbf{b})\cdot(\mathbf{a}+\mathbf{b})$

$\|\mathbf{a}-\mathbf{b}\|^2 = (\mathbf{a}-\mathbf{b})\cdot(\mathbf{a}-\mathbf{b})$

$\|\mathbf{a}+\mathbf{b}\|^2 + \|\mathbf{a}-\mathbf{b}\|^2= \mathbf{a}\mathbf{a} + \mathbf{a}\mathbf{b} +\mathbf{a}\mathbf{b} + \mathbf{b}\mathbf{b} + \mathbf{a}\mathbf{a} - \mathbf{a}\mathbf{b} - \mathbf{a}\mathbf{b} + \mathbf{b}\mathbf{b} = 2\mathbf{a}\mathbf{a} + 2\mathbf{b}\mathbf{b}$

und somit, wie zu zeigen war

$\|\mathbf{a}+\mathbf{b}\|^2 + \|\mathbf{a}-\mathbf{b}\|^2= 2\left( \|\mathbf{a}\|^2 + \|\mathbf{b}\|^2\right)$

[Bearbeiten] Orthogonalität

Zwei Vektoren a, b heißen orthogonal (= senkrecht), wenn $\mathbf{a}\cdot \mathbf{b} = 0$ gilt.

Man schreibt dies auch als $\mathbf{a}\bot \mathbf{b}$ .

Es gilt dann der Satz von Pythagoras

$\|\mathbf{a}+ \mathbf{b}\|^2 = \|\mathbf{a}\|^2 + \|\mathbf{b}\|^2$

[Bearbeiten] Orthogonalsystem

Die Vektoren $\mathbf{a}_i\in \mathbb{R}^n$ bilden ein Orthogonalsystem, wenn

$\forall i \quad \mathbf{a}_i\ne \mathbf{o}$
$\forall (i\ne j) \quad \mathbf{a}_i\cdot \mathbf{a}_j=0$

Gilt zusätzlich noch

$\forall i: \; \|\mathbf{a}_i\| = 1$

dann bilden die Vektoren ein Orthonormalsystem.

[Bearbeiten] Gram-Schmidtsches Orthogonalisierungsverfahren

Wikipedia: Gram-Schmidtsches Orthogonalisierungsverfahren

[Bearbeiten] Beispiel: Satz von Thales

Es ist der Satz von Thales "Jeder Peripheriewinkel über dem Durchmesser eines Kreises beträgt 90°" zu überprüfen.

Lösung:

$\mathbf{a} = \mathbf{r} + \mathbf{c}$

$\mathbf{b} = \mathbf{r} - \mathbf{c}$

$\|\mathbf{r}\| = \|\mathbf{c}\|$

$\mathbf{a}\cdot\mathbf{b} = (\mathbf{r} + \mathbf{c})\cdot(\mathbf{r} - \mathbf{c}) = \mathbf{r}\mathbf{r} + \mathbf{r}\mathbf{c} - \mathbf{r}\mathbf{c} - \mathbf{c}\mathbf{c} = \|\mathbf{r}\|^2 - \|\mathbf{c}\|^2 = 0$

$\Rightarrow\; \mathbf{a} \bot \mathbf{b}$

[Bearbeiten] Linearkombinationen

Den Vektor

$\mathbf{b} = \alpha_1 \mathbf{a}_1 + \ldots + \alpha_n \mathbf{a}_n$

nennt man Linearkombination aus den Vektoren $\mathbf{a}_1, \ldots, \mathbf{a}_n \; \in \mathbb{R}^n$ .

Ist $\mathbf{b}=0$ , so nennt man die Vektoren $\mathbf{a}_1, \ldots, \mathbf{a}_n$

linear abhängig, wenn $\exists i: \; \alpha_i\ne 0$
linear unabhängig, wenn $\forall i: \; \alpha_i = 0$

[Bearbeiten] Natürliche Basis

Die Einheitsvektoren (Basisvektoren)

$\mathbf{e}_1= \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix} , \; \cdots \; , \mathbf{e}_n= \begin{pmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{pmatrix}$

nennt man natürliche Basis des $\mathbb{R}^n$ .

Für diese Basisvektoren gilt das sogenannte Kronecker-Delta

$\delta_{ij} = \mathbf{e}_i \cdot \mathbf{e}_j = \begin{cases} 1, & \mbox{wenn}\ i=k \\ 0, & \mbox{wenn}\ i\ne k \end{cases}$

Für einen beliebigen Vektor $\mathbf{x} = \left( x_1,\ldots ,x_n\right) \in \mathbb{R}^n$ gilt

$\mathbf{x} = x_1 \mathbf{e}_1 + \ldots + x_n \mathbf{e}_n$

$x_1 \mathbf{e}_1, \ldots, x_n \mathbf{e}_n$ nennt man die Komponenten des Vektors bezüglich der natürlichen Basis des $\mathbb{R}^n$ .

[Bearbeiten] Richtungskosinus

$\mathbf{x}\cdot \mathbf{e}_i = \|\mathbf{x}\| \cos\alpha_i$

daraus folgt

$\cos\alpha_i = \frac{\mathbf{x}\cdot \mathbf{e}_i}{\|\mathbf{x}\|} = \frac{x_i}{\|\mathbf{x}\|}$

[Bearbeiten] Beispiel

Gesucht ist der Winkel, den der Vektor $\mathbf{a}=(3,-1,-5)$ mit dem Basisvektor $\mathbf{e}_1$ einschließt.

Lösung:

$\mathbf{a}\cdot\mathbf{e}_1 = \|\mathbf{a}\|\cos\angle$

$\cos\angle = \frac{\mathbf{a}\cdot\mathbf{e}_1}{\|\mathbf{a}\|} = \frac{3}{\sqrt{35}}$

$\angle = 1,04\ {\rm rad}$

[Bearbeiten] Projektionen

Unter Projektion ist hier die Orthogonalprojektion gemeint.

[Bearbeiten] Skalare Projektion

$\mathbf{a}\cdot \mathbf{b} = \|\mathbf{b}\| \underbrace{\|\mathbf{a}\| \cos \angle}_{\|\mathbf{a}_{\mathbf{b}}\|}$

Daraus folgt die Gleichung für die skalare Projektion des Vektors a auf b

$\|\mathbf{a}_{\mathbf{b}}\| = \frac{\mathbf{a}\cdot \mathbf{b}}{\|\mathbf{b}\|}$

[Bearbeiten] Vektorprojektion

$\mathbf{a}_{\mathbf{b}} = \|\mathbf{a}_{\mathbf{b}}\|\ \mathbf{b}_0$

$\mathbf{b}_0 = \frac{\mathbf{b}}{\|\mathbf{b}\|}$

Daraus folgt

$\mathbf{a}_{\mathbf{b}} = \frac{\mathbf{a}\cdot \mathbf{b}}{\|\mathbf{b}\|^2} \mathbf{b}$

[Bearbeiten] Beispiel

Gegeben ist ein Vektor $\mathbf{a}=(3,-1,-5)$ . Gesucht ist der Winkel, den die Orthogonalprojektion des Vektors a auf die $\mathbf{e}_1\mathbf{e}_2$ -Ebene mit dem $\mathbf{e}_1$ -Basisvektor einschließt.

Lösung:

$\mathbf{a}_1 = \frac{\mathbf{a}\cdot\mathbf{e}_1}{\|\mathbf{e}_1\|}\mathbf{e}_1 = a_1\mathbf{e}_1 = (3,0,0)$

$\mathbf{a}_2 = \frac{\mathbf{a}\cdot\mathbf{e}_2}{\|\mathbf{e}_2\|}\mathbf{e}_2 = a_2\mathbf{e}_2 = (0,-1,0)$

$\mathbf{a}_{12} = \mathbf{a}_1 + \mathbf{a}_2 = (3,-1,0)$

Dieses Zwischenergebnis hätte man natürlich auch direkt aus der Skizze ermitteln können, dann wäre aber der Witz dieses Beispiels verloren gegangen.

$\cos\angle = \frac{\mathbf{a}_{12}\mathbf{e}_{1}}{\|\mathbf{a}_{12}\|} = \frac{3}{\sqrt{10}}$

$\angle = 0,32\ {\rm rad}$

[Bearbeiten] Vektorprodukt

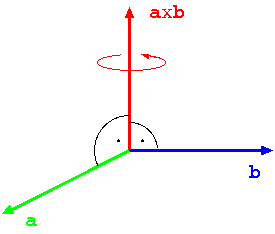
Das Vektorprodukt zweier linear unabhängiger Vektoren ist nur für den euklidischen Raum $\mathbb{R}^3$ definiert.

$\mathbf{a}\times \mathbf{b} = \left( a_2b_3-a_3b_2,\ a_3b_1-a_1b_3,\ a_1b_2-a_2b_1\right)$

Die Vektoren $\mathbf{a}, \mathbf{b}, \mathbf{a}\times \mathbf{b}$ bilden ein Rechtssystem.

[Bearbeiten] Regeln

Das Vektorprodukt ist nicht kommutativ: $\mathbf{a}\times \mathbf{b} = -(\mathbf{a}\times \mathbf{b})$
Orthogonalität: $(\mathbf{a}\; \bot \; \mathbf{a}\times \mathbf{b}) \wedge (\mathbf{b}\; \bot \; \mathbf{a}\times \mathbf{b})$
Parallelität: $\mathbf{a} \times \mathbf{b}=\mathbf{o} \Leftrightarrow \begin{cases} \mathbf{a}=\mathbf{o}\; \vee \; \mathbf{b}=\mathbf{o} \\ \mathbf{a} \| \mathbf{b} \end{cases}$
Lagrangesche Identität: $\|\mathbf{a}\times \mathbf{b}\|^2 = \| \mathbf{a}\|^2 \| \mathbf{b}\|^2 - (\mathbf{a}\cdot \mathbf{b})^2$
Parallelogramm: $F_\Diamond = \|\mathbf{a}\|\|\mathbf{b}\| \sin \angle = \|\mathbf{a}\times \mathbf{b}\|$ ist der Flächeninhalt des von den Vektoren $\mathbf{a}, \mathbf{b}$ aufgespannten Parallelogrammes. $\angle$ ist der von a und b eingeschlossene Winkel.
Distributivgesetz: $(\mathbf{a} + \mathbf{b})\times \mathbf{c} = (\mathbf{a} \times \mathbf{b}) + (\mathbf{b} \times \mathbf{c})$
$\mathbf{a} \times (\mathbf{b}\times \mathbf{c}) = (\mathbf{a} \cdot \mathbf{c})\mathbf{b} + (\mathbf{a} \cdot \mathbf{b})\mathbf{c}$

[Bearbeiten] Rechnungen

$\mathbf{A} \times \mathbf{B} =\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \times\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}= \begin{pmatrix} a_2 b_3 - a_3 b_2 \\ a_3 b_1 - a_1 b_3 \\ a_1 b_2 - a_2 b_1 \end{pmatrix}$

$\mathbf{A} \times \mathbf{A} = \begin{pmatrix} a_2 a_3 - a_3 a_2 \\ a_3 a_1 - a_1 a_3 \\ a_1 a_2 - a_2 a_1 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}$

$\mathbf{B} \times \mathbf{A} = \begin{pmatrix} b_2 a_3 - b_3 a_2 \\ b_3 a_1 - b_1 a_3 \\ b_1 a_2 - b_2 a_1 \end{pmatrix} =- \begin{pmatrix} a_2 b_3 - a_3 b_2 \\ a_3 b_1 - a_1 b_3 \\ a_1 b_2 - a_2 b_1 \end{pmatrix} =-\mathbf{A} \times \mathbf{B}$

$\begin{matrix} \mathbf{B}(\mathbf{A} \cdot \mathbf{C})- \mathbf{C}(\mathbf{A}\cdot \mathbf{B}) &=&\begin{pmatrix} a_1 b_1 c_1 + a_2 b_1 c_2 + a_3 b_1 c_3 \\ a_1 b_2 c_1 + a_2 b_2 c_2 + a_3 b_2 c_3 \\ a_1 b_3 c_1 + a_2 b_3 c_2 + a_3 b_3 c_3 \\ \end{pmatrix} - \begin{pmatrix} a_1 b_1 c_1 + a_2 b_2 c_1 + a_3 b_3 c_1 \\ a_1 b_1 c_2 + a_2 b_2 c_2 + a_3 b_3 c_2 \\ a_1 b_1 c_3 + a_2 b_2 c_3 + a_3 b_3 c_3 \end{pmatrix} \\ &=& \begin{pmatrix} a_2 b_1 c_2 + a_3 b_1 c_3 - a_2 b_2 c_1 - a_3 b_3 c_1 \\ a_1 b_2 c_1 + a_3 b_2 c_3 - a_1 b_1 c_2 - a_3 b_3 c_2 \\ a_1 b_3 c_1 + a_2 b_3 c_2 - a_1 b_1 c_3 - a_2 b_2 c_3 \end{pmatrix} \end{matrix}$ $\begin{matrix} \mathbf{A} \times (\mathbf{B} \times \mathbf{C}) &=& \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \times \begin{pmatrix} b_2 c_3 - b_3 c_2 \\ b_3 c_1 - b_1 c_3 \\ b_1 c_2 - b_2 c_1 \end{pmatrix} &=& \begin{pmatrix} a_2 b_1 c_2 - a_2 b_2 c_1 - a_3 b_3 c_1 + a_3 b_1 c_3 \\ a_3 b_2 c_3 - a_3 b_3 c_2 - a_1 b_1 c_2 + a_1 b_2 c_1 \\ a_1 b_3 c_1 - a_1 b_1 c_3 - a_2 b_2 c_3 + a_2 b_3 c_2 \end{pmatrix} \\ &=& \mathbf{B}(\mathbf{A} \cdot \mathbf{C})- \mathbf{C}(\mathbf{A}\cdot \mathbf{B}) & & \end{matrix}$

$ε i j k$

$\left(\mathbf{A} \times \mathbf{B}\right)_i=\epsilon_{ijk} \mathbf{A}_j \mathbf{B}_k$

[Bearbeiten] Beispiel

Gesucht ist ein normierter Normalenvektor auf die beiden Vektoren $\mathbf{a}=(1,1,0),\ \mathbf{b}=(5,4,1)$ .

Lösung:

$\mathbf{n} = \mathbf{a} \times \mathbf{b} = \left( a_2b_3-a_3b_2,\ a_3b_1-a_1b_3,\ a_1b_2-a_2b_1\right) = (1, -1, -1)$

$\|\mathbf{n}\| = \sqrt{3}$

$\mathbf{n}_0=\frac{1}{\sqrt{3}}(1,-1,-1)$

[Bearbeiten] Spatprodukt

Das Spatprodukt der Vektoren $\mathbf{a},\mathbf{b},\mathbf{c}\in \mathbb{R}^3$ ist definiert als

$\mathcal{h}\mathbf{a},\mathbf{b},\mathbf{c}\mathcal{i} = (\mathbf{a}\times \mathbf{b})\cdot \mathbf{c}$

[Bearbeiten] Regeln

Unabhängigkeit: Die Vektoren a, b, c sind linear unabhängig,wenn $\mathcal{h}\mathbf{a},\mathbf{b},\mathbf{c}\mathcal{i} \ne 0$
Rechtssystem: $\mathcal{h}\mathbf{a},\mathbf{b},\mathbf{c}\mathcal{i} > 0$
Linkssystem: $\mathcal{h}\mathbf{a},\mathbf{b},\mathbf{c}\mathcal{i} < 0$
Spatvolumen: $V_{spat} = |\mathcal{h}\mathbf{a},\mathbf{b},\mathbf{c}\mathcal{i}|$
Vertauschungssatz: $\mathcal{h}\mathbf{a},\mathbf{b},\mathbf{c}\mathcal{i} = \mathcal{h}\mathbf{b},\mathbf{c},\mathbf{a}\mathcal{i} = \mathcal{h}\mathbf{c},\mathbf{a},\mathbf{b}\mathcal{i} = -\mathcal{h}\mathbf{b},\mathbf{a},\mathbf{c}\mathcal{i} = -\mathcal{h}\mathbf{a},\mathbf{c},\mathbf{b}\mathcal{i} = -\mathcal{h}\mathbf{c},\mathbf{b},\mathbf{a}\mathcal{i}$

[Bearbeiten] Geraden

[Bearbeiten] Gerade durch Punkt und Richtung

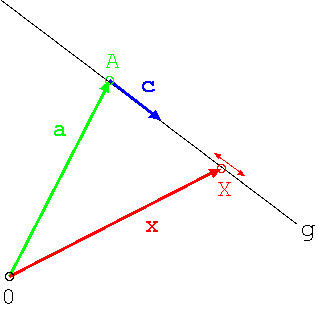
Gegeben sei ein Punkt A (Ortsvektor a) und ein Richtungsvektor c. Der Punkt X liegt auf der Geraden g ( $X\in g$ ) wenn,

$g: \; \mathbf{x} = \mathbf{a} + \lambda \mathbf{c}, \quad \lambda \in \mathbb{R}\; \wedge\; \mathbf{a},\mathbf{c} \in \mathbb{R}^n$

Obige Gleichung nennt man auch eine Parameterdarstellung (Parameter $λ$ ).

[Bearbeiten] Gerade durch zwei Punkte

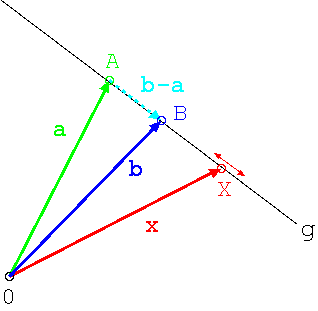
Die Gerade sei durch die Punkte A und B gegeben (Ortsvektoren a,b). Der Punkt X liegt auf der Geraden g ( $X\in g$ ) wenn,

$g: \; \mathbf{x} = \mathbf{a} + \lambda (\mathbf{b}-\mathbf{a}), \quad \lambda \in \mathbb{R}\; \wedge\; \mathbf{a},\mathbf{b} \in \mathbb{R}^n$

Die Punkte A, B und X heißen kollinear, d.h. diese drei Punkte liegen auf der gleichen Geraden.

[Bearbeiten] Ebenen

[Bearbeiten] Ebene durch einen Punkt und zwei Richtungen

Gegeben sei ein Punkt A (Ortsvektor a) und zwei Richtungsvektoren c,d. Der Punkt X liegt in der Ebene E ( $X\in E$ ) wenn,

$E: \; \mathbf{x} = \mathbf{a} + \lambda \mathbf{c} + \mu \mathbf{d}, \quad \lambda,\mu \in \mathbb{R}\; \wedge\; \mathbf{a},\mathbf{c},\mathbf{d} \in \mathbb{R}^n$

Die Ebene E wird also durch die zwei Geraden g und h aufgespannt.

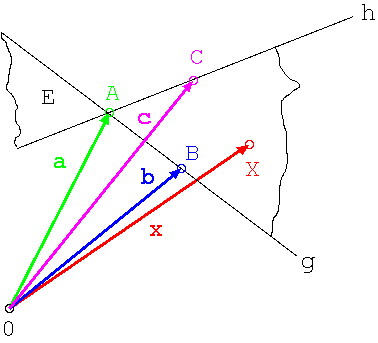
[Bearbeiten] Ebene durch drei Punkte

Gegeben seinen drei Punkte A, B und C (Ortsvektoren a,b,c). Der Punkt X liegt in der der Ebene E ( $X\in E$ ) wenn,

$E: \; \mathbf{x} = \mathbf{a} + \lambda (\mathbf{b}-\mathbf{a}) + \mu (\mathbf{c}-\mathbf{a}), \quad \lambda,\mu \in \mathbb{R}\; \wedge\; \mathbf{a},\mathbf{b},\mathbf{c} \in \mathbb{R}^n$

Die Ebene kann in diesem Fall auch über das Spatprodukt definiert werden:

$V_{Spat} = |\mathcal{h}\mathbf{x}-\mathbf{a},\; \mathbf{b}-\mathbf{a},\; \mathbf{c}-\mathbf{a} \mathcal{i}|$

Da die Punkte B, C und X in einer Ebene liegen, ist $V S p a t = 0$ und

$E:\; \mathcal{h}\mathbf{x}-\mathbf{a},\; \mathbf{b}-\mathbf{a},\; \mathbf{c}-\mathbf{a} \mathcal{i} = 0$

[Bearbeiten] Hessesche Normalform

n sei ein Normalenvektor zur Ebene E. Es gilt $\mathbf{n}\; \bot \; (\mathbf{x}-\mathbf{a})$ , und somit

$\mathbf{n} \cdot (\mathbf{x}-\mathbf{a}) = 0$

Dividiert man diese Gleichung durch die Norm des Normalenvektors $\|\mathbf{n}\|$ , so erhält man die Ebenengleichung in der Hesseschen Normalform

$E: \mathbf{n}_0 \cdot (\mathbf{x}-\mathbf{a}) = 0$

[Bearbeiten] In Koordinatenschreibweise

Aus der Parameterdarstellung

$E: \mathbf{x} = \mathbf{a} + \lambda\mathbf{b} + \mu\mathbf{c}\ ; \quad \mathbf{a},\mathbf{b},\mathbf{c},\mathbf{x}\in\mathbb{R}^3$

erhält man in Koordinaten angeschrieben

$\begin{matrix} x_1 = a_1 + \lambda b_1 + \mu c_1 \\ x_2 = a_2 + \lambda b_2 + \mu c_2 \\ x_3 = a_3 + \lambda b_3 + \mu c_3 \\ \end{matrix}$

Eliminiert man $\lambda,\ \mu$ aus diesen Gleichungen, so erhält man die sogenannte Abschnittsform der Ebenengleichung

$E:\; ax + by +cz = d$

[Bearbeiten] Anwendungen: Punkte, Geraden und Ebenen

[Bearbeiten]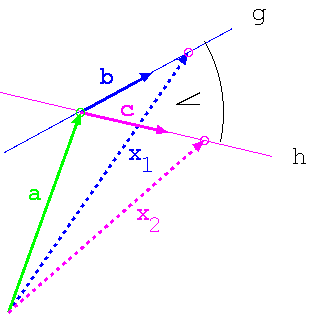 Winkel zwischen Geraden

Gegeben sind zwei Geraden im $\mathbb{R}^3$

$g: \mathbf{x}_1 = \mathbf{a} + \lambda \mathbf{b}$

$h: \mathbf{x}_2 = \mathbf{a} + \mu \mathbf{c}$

Den Winkel zwischen den beiden Geraden g und h kann man über das Skalarprodukt gewinnen

$\cos\angle = \frac{\mathbf{x}_1\cdot\mathbf{x}_2}{\|\mathbf{x}_1\|\|\mathbf{x}_2\|}$

[Bearbeiten] Normale: Abstand Punkt - Ebene

Gegeben sei ein Punkt P und eine Ebene E. D sei der Durchstoßpunkt von n durch die Ebene E.

Der Abstand von Punkt P zu Ebene E ist $\delta = \overline{PD} = \|\mathbf{p} - \mathbf{d}\|$

Direkt aus der Abbildung oder auch mittels der Hesseschen Ebenengleichung ergibt sich

$(\mathbf{d}-\mathbf{a})\cdot \mathbf{n} = 0$

Weiters ist

$\mathbf{d} = \mathbf{p} + \lambda\mathbf{n}$

Aus den beiden vorigen Gleichungen kann man nun $λ$ ermitteln

$(\mathbf{p}+\lambda\mathbf{n}-\mathbf{a}) \mathbf{n}=0$

$(\mathbf{p}-\mathbf{a})\mathbf{n} + \lambda\mathbf{n}\mathbf{n}=0$

$\lambda = -\frac{(\mathbf{p}-\mathbf{a})\mathbf{n}}{\mathbf{n}\cdot\mathbf{n}} = -\frac{(\mathbf{p}-\mathbf{a})\mathbf{n}}{\|\mathbf{n}\|^2}$

Und somit ist

$\delta = \|\mathbf{p} - \mathbf{p} + \frac{(\mathbf{p}-\mathbf{a})\mathbf{n}}{\|\mathbf{n}\|^2}\mathbf {n}\| = \|\underbrace{(\mathbf{p}-\mathbf{a})\mathbf{n}_0}_k \mathbf {n_0}\| = |k|\|\mathbf{n}_0\| = |k| = |(\mathbf{p}-\mathbf{a})\mathbf{n}_0|$

[Bearbeiten] Gerade als Schnitt zweier Ebenen

Eine Gerade im Raum $\mathbb{R}^3$ kann man auch in der Form

$g = \begin{cases} E_1:\ a_1x_1 + a_2x_2 + a_3x_3 = c \\ E_2:\ b_1x_1 + b_2x_2 + b_3x_3 = d \end{cases}$

darstellen. Natürlich dürfen die Ebenen hierbei nicht parallel liegen.

Beispiel: Gegeben sei eine Gerade $\mathbf{x} = \mathbf{a}+\lambda \mathbf{b}$ mit $\mathbf{a}=(1,1,0),\ \mathbf{b}=(3,4,-2),\ \lambda\in\mathbb{R}$ . Gesucht sind die beiden Ebenen, welche g als Schnittgerade besitzen.

$x_1 =\ 1 + 3\lambda$

$x_2 =\ 1 + 4\lambda$

$x_3 =\ -2\lambda$

Daraus folgt

$\lambda = -\frac{x_3}{2}$

und schließlich ist

$E_1:\ x_1 + \frac{3}{2}x_3 = 1$

$E_2:\ x_2 + 2x_3 = 1$

Beispiel: Gegeben seinen zwei Ebenen $E_1:\; x_1+x_2+x_3=1;\;E_2:\; x_1+x_3 = -3$ . Gesucht ist die Schnittgerade in Parameterdarstellung.

Wir wählen z.B.: $x_1 =\ \lambda$

und berechnen sukzessive

$x_3 =\ -3 - \lambda$

$x_2 =\ 4$

Somit ist die Darstellung der Geraden in Parameterform

$g:\;\mathbf{x} = \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} = \begin{pmatrix} 0\\ 4\\ -3 \end{pmatrix} + \lambda \begin{pmatrix} 1\\ 0\\ -1 \end{pmatrix}$

[Bearbeiten] Durchstoßpunkt einer Geraden durch eine Ebene

Es gibt drei Möglichkeiten:

Die Gerade g schneidet die Ebene E in einem Punkt
Die Gerade liegt parallel zur Ebene, aber nicht in der Ebene
Die Gerade liegt in der Ebene

Beispiel: Gegeben sei eine Gerade $g:\; \mathbf{b}= \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix} + \lambda \begin{pmatrix} -1\\ 5\\ 0 \end{pmatrix} \ ;\; \alpha=\mathbb{R}$ und eine Ebene $E:\; x_1+x_2+x_3=0$ . Der Durchstosspunkt der Gerade durch die Ebene soll berechnet werden.

Gerade g:

$x_2=\ 5\left(1-x_1\right)$

$x_3=\ 0$

Ebene E:

$x_1+x_2+x_3=\ 0$

Das sind drei Gleichungen für drei Unbekannte, aufgelöst

Durchstosspunkt $D= \begin{pmatrix} \frac{5}{4}\\ -\frac{5}{4}\\ 0 \end{pmatrix}$

[Bearbeiten] Winkel zwischen einer Geraden und einer Ebene

$\mathbf{a}\cdot\mathbf{n} = \|\mathbf{a}\|\|\mathbf{n}\| \cos\left( \frac{\pi}{2}-\alpha\right)$

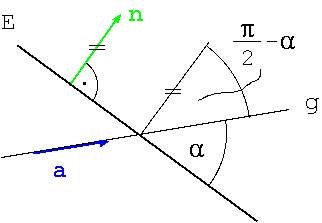
Daraus kann man leicht den Winkel $α$ ausrechnen.

Ähnlich funktioniert die Bestimmung eines Winkels zwischen zwei Ebenen. Dort verwendet man eben die Normalenvektoren der beiden Ebenen zur Winkelberechnung.

[Bearbeiten] Übungen

Zurück zu Permutationen, ... |

Hoch zu Gesamtinhaltsverzeichnis |

Vor zu Matrizen

Ing Mathematik: Vektoren

Aus Wikibooks

Inhaltsverzeichnis

[Bearbeiten] Vektorraum

[Bearbeiten] Addition von Vektoren

[Bearbeiten] Assoziativgesetz

[Bearbeiten] Kommutativgestz

[Bearbeiten] Nullvektor

[Bearbeiten] Differenzvektor

[Bearbeiten] Beispiel

[Bearbeiten] Multiplikation eines Vektors mit einem Skalar

[Bearbeiten] Assoziativgesetz

[Bearbeiten] Distributivgesetze

[Bearbeiten] Gegenvektor

[Bearbeiten] Parallelität

[Bearbeiten] Beispiel

[Bearbeiten] Skalarprodukt

[Bearbeiten] Norm eines Vektors

[Bearbeiten] Kommutativgesetz

[Bearbeiten] Assoziativgesetz gilt nicht

[Bearbeiten] Distributivgesetz

[Bearbeiten] Chauchy-Schwarzsche Ungleichung

[Bearbeiten] Dreiecksungleichung

[Bearbeiten] Beispiel: Parallelogrammgleichung

[Bearbeiten] Orthogonalität

[Bearbeiten] Orthogonalsystem

[Bearbeiten] Gram-Schmidtsches Orthogonalisierungsverfahren

[Bearbeiten] Beispiel: Satz von Thales

[Bearbeiten] Linearkombinationen

[Bearbeiten] Natürliche Basis

[Bearbeiten] Richtungskosinus

[Bearbeiten] Beispiel

[Bearbeiten] Projektionen

[Bearbeiten] Skalare Projektion

[Bearbeiten] Vektorprojektion

[Bearbeiten] Beispiel

[Bearbeiten] Vektorprodukt

[Bearbeiten] Regeln

[Bearbeiten] Rechnungen

[Bearbeiten] Beispiel

[Bearbeiten] Spatprodukt

[Bearbeiten] Regeln

[Bearbeiten] Geraden

[Bearbeiten] Gerade durch Punkt und Richtung

[Bearbeiten] Gerade durch zwei Punkte

[Bearbeiten] Ebenen

[Bearbeiten] Ebene durch einen Punkt und zwei Richtungen

[Bearbeiten] Ebene durch drei Punkte

[Bearbeiten] Hessesche Normalform

[Bearbeiten] In Koordinatenschreibweise

[Bearbeiten] Anwendungen: Punkte, Geraden und Ebenen

[Bearbeiten] Winkel zwischen Geraden

[Bearbeiten] Normale: Abstand Punkt - Ebene

[Bearbeiten] Gerade als Schnitt zweier Ebenen

[Bearbeiten] Durchstoßpunkt einer Geraden durch eine Ebene

[Bearbeiten] Winkel zwischen einer Geraden und einer Ebene

[Bearbeiten] Übungen

Ansichten

Persönliche Werkzeuge

Navigation

Suche

Mitmachen

Werkzeuge

Drucken/exportieren