Ing Mathematik: Wichtige Funktionen

Zurück zu Grenzwerte und Stetigkeit |

Hoch zu Gesamtinhaltsverzeichnis |

Vor zu Differentialrechnung

Exponentialfunktionen

Es sei $a\ >\ 0$ , sowie $n\in \mathbb {N}$ . Dann ist

$a^{n}=\underbrace {a\cdot a\cdot \ldots \cdot a} _{n\;mal}$

a nennt man Basis und n den Exponenten der Potenz $a^{n}$ (Exponentialfunktion zur Basis a). Es gilt auch, daß $a^{n}$ für jedes $0<a<\infty$ und $n\in \mathbb {R}$ definiert ist.

Eine Exponentialfunktion ist stetig und für $a>1$ monoton steigend, für $0<a<1$ monoton fallend.

Rechenregeln

$a^{0}\ =1$
$a^{1}\ =a$
$a^{-n}={\frac {1}{a^{n}}}$
$r={\frac {p}{q}}:\;a^{r}={\sqrt[{q}]{a^{p}}}$
$a^{n+m}=a^{n}\cdot a^{m}$
$a^{n-m}={\frac {a^{n}}{a^{m}}}$
$a^{n\cdot m}=(a^{n})^{m}$
$a^{n}\cdot b^{n}=(a\cdot b)^{n}$

Natürliche Exponentialfunktion

Die Exponentialfunktion zur Basis e (e = 2,718..., Eulersche Zahl) kann für alle $z\in \mathbb {C}$ folgendermaßen definiert werden

$e^{z}=\sum _{i=0}^{\infty }{\frac {z^{i}}{i!}}$

oder

$e^{z}=\lim _{n\to \infty }\left(1+{\frac {z}{n}}\right)^{n}$

Beispiele aus der Physik und Technik

Radioaktiver Zerfallsprozess
Barometrische Höhenformel: $p(h_{1})=p(h_{0})\mathrm {e} ^{-{\frac {Mg}{RT}}\Delta h}$
Lade-/Entladevorgang beim Kondensator: $u_{\text{C}}(t)=U_{0}+\left(U_{{\text{C}},t_{0}}-U_{0}\right)\cdot e^{-{\frac {t}{\tau }}}$

Logarithmen

Den Logarithmus zur Basis a schreibt man $\,\log _{a}x$ . Manchmal ist das auch in dieser Schreibweise $\,_{a}\log x$ zu sehen.

Logarithmen sind Umkehrfunktionen zu den Exponentialfunktionen.

$y=a^{x}$

$x=\log _{a}y$

Rechenregeln

$a^{\log _{a}x}=x$
$\log _{a}\left(a^{x}\right)=x$
$\log _{a}\left(1\right)=0$
$\log _{a}\left(a\right)=1$
$\log _{a}\left(xy\right)=\log _{a}x+\log _{a}y$
$\log _{a}\left({\frac {x}{y}}\right)=\log _{a}x-\log _{a}y$
$\log _{a}\left({\frac {1}{x}}\right)=-\log _{a}x$
$\log _{a}\left(x^{y}\right)=y\log _{a}x$
${\frac {\log _{a}x}{\log _{a}y}}={\frac {\log _{b}x}{\log _{b}y}}$

Wichtige Basen

Basis 2

Zweierlogarithmus, Duallogarithmus oder binärer Logarithmus

$\log _{2}x\ =\ {\mbox{lb}}\ x$

oder

$\log _{2}x\ =\ {\mbox{ld}}\ x$

Basis 10

Zehnerlogarithmus, dekadischer Logarithmus oder Briggscher Logarithmus

$\log _{10}x\ =\ \lg x$

Basis e

natürlicher Logarithmus, Logarithmus naturalis

$\log _{e}x\ =\ \ln x$

oder

$\log _{e}x\ =\ \log x$

Umrechnung zwischen verschiedenen Basen

$x=a^{\log _{a}x}=b^{\log _{b}x}$

$b=a^{\log _{a}b}$

eingesetzt

$a^{\log _{a}x}=a^{\log _{a}b^{\log _{b}x}}=a^{\log _{b}x\cdot \log _{a}b}$

daraus folgt, dass

$\log _{a}x=\log _{b}x\cdot \log _{a}b$

sein muss.

Alternativ kann man diese Beziehung auch aus der Rechenregel

${\frac {\log _{a}x}{\log _{a}y}}={\frac {\log _{b}x}{\log _{b}y}}$

ableiten.

${\frac {\log _{a}x}{\log _{a}b}}={\frac {\log _{b}x}{\log _{b}b}}$

$\log _{a}x=\log _{b}x\cdot \log _{a}b$

Beispiele

Funktionen auf doppeltlogarithmischem Papier
Prinzip des Rechenschiebers, $2\cdot 3=6$
Schalldruckpegel-Messgerät, $L_{\mathrm {p} }=20\,\lg \left({\frac {\tilde {p}}{p_{0}}}\right)\,\mathrm {dB}$

Trigonometrische Funktionen (Winkel-, Kreisfunktionen)

Das Bogenmaß

Das Bogenmaß ist definiert als dimensionslose Größe

$\phi \ ={\frac {s}{r}}$

Bekannt ist der Umfang eines Kreises

$U=2\pi r=\phi _{V}\cdot r$ .

Somit gilt für den Vollkreis

$\phi _{V}\ =\ 2\pi$

Genauso wird das Bogenmaß definiert. 360° entsprechen $2\ \pi$ im Bogenmaß. Das Bogenmaß ist eigentlich dimensionslos, wird aber oft mit der Einheit Radiant [rad] versehen.

Winkel in [°]	Bogenmaß in [1] oder in [rad]
1	${\frac {2\pi }{360}}={\frac {\pi }{180}}$
45	${\frac {\pi }{4}}$
~57,3	1
90	${\frac {\pi }{2}}$
180	$\pi \$
360	$2\pi \$

Umrechnung von Graden in das Bogenmaß:

$\phi ={\frac {\pi }{180}}\varphi$

mit $\phi \$ in [rad] und $\varphi$ in [°].

Sind Kreisbogenlänge und Radius gleich lang, dann wird $\phi \ =\ 1$ . Am Einheitskreis entspricht das Bogenmaß der Kreisbogenlänge.

Die trigonometrischen Funktionen am Einheitskreis

Sinus und Cosinus

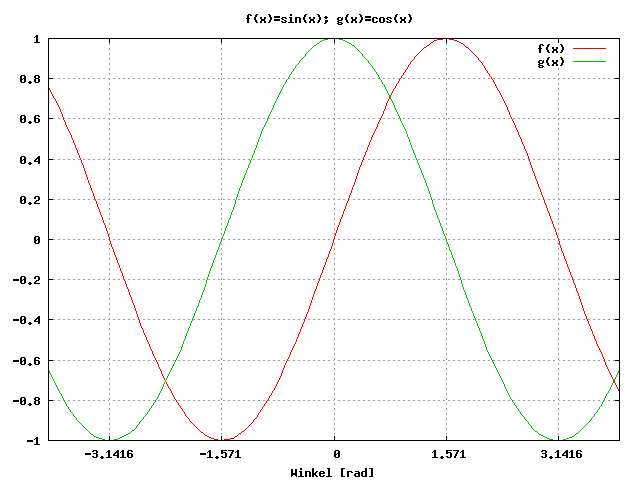
sin x ist eine schiefsymmetrische Funktion, während cos x eine symmetrische Funktion repräsentiert, d.h.

$\sin(-x)\ =\ -\sin x$
$\cos(-x)\ =\ \cos x$

Sinus und Kosinus (statt Cosinus wird häufig auch Kosinus geschrieben) sind periodische Funktionen, es gilt:

$\sin(x+2k\pi )\ =\ \sin x$
$\cos(x+2k\pi )\ =\ \cos x$

Des Weiteren gilt:

$\cos(x)\ =\ \sin(x-{\frac {\pi }{2}})$

Definition:

$\sin x=\Im \left(e^{ix}\right)={\frac {e^{ix}-e^{-ix}}{2i}}$
$\cos x=\Re \left(e^{ix}\right)={\frac {e^{ix}+e^{-ix}}{2}}$

Daraus folgt unmittelbar die Eulerformel:

$e^{ix}=\Re \left(e^{ix}\right)+\Im \left(e^{ix}\right)=\cos x+i\sin x$

Direkt aus den Verhältnissen am Einheitskreis läßt sich mittels des Satzes von Pythagoras die Beziehung

$\sin ^{2}x+\cos ^{2}x\ =\ 1$

ableiten.

Alternativ muss sich natürlich auch aus der obigen Definition selbiges Ergebnis ableiten lassen:

$e^{ix}e^{-ix}\ =\ e^{ix-ix}\ =\ 1$

$e^{ix}\ =\ \cos x+i\sin x$ $e^{-ix}\ =\ \cos x-i\sin x$

$e^{ix}e^{-ix}\ =\ \sin ^{2}x+\cos ^{2}x\ =\ 1$

Am Einheitskreis läßt sich auch leicht erkennen, dass

$|\sin x|\ \leq 1$
$|\cos x|\ \leq 1$

sein muss.

Additionstheoreme

$\sin \left(x\pm y\right)=\sin x\cos y\pm \cos x\sin y$
$\cos \left(x\pm y\right)=\cos x\cos y\mp \sin x\sin y$
$\sin x+\sin y=2\sin {\frac {x+y}{2}}\cos {\frac {x-y}{2}}$
$\cos x+\cos y=2\cos {\frac {x+y}{2}}\cos {\frac {x-y}{2}}$
$\sin x-\sin y=2\cos {\frac {x+y}{2}}\sin {\frac {x-y}{2}}$
$\cos x-\cos y=-2\sin {\frac {x+y}{2}}\sin {\frac {x-y}{2}}$

Übung: Leiten Sie die Additionstheoreme her.

Ein Beispiel aus der Technik (Schwingungen):

Tangens und Cotangens

Tangens
Cotangens

$\tan x={\frac {\sin x}{\cos x}}={\frac {1}{\cot x}}$

$\cot x={\frac {\cos x}{\sin x}}={\frac {1}{\tan x}}$

Beispiel für den Tangens (Steigung):

Umkehrfunktionen zu den trigonometrischen Funktionen

Hauptwerte der Arkusfunktionen:

Arkussinus und Arkuskosinus
Arkustangens und Arkuskotangens

Hyperbel- und Areafunktionen

Sinus hyperbolicus (oder Hyperbelsinus), Kosinus hyperbolicus (oder Hyperbelkosinus), Tangens hyperbolicus (oder Hyperbeltangens):

$\sinh(x):={\frac {\mathrm {e} ^{x}-\mathrm {e} ^{-x}}{2}}$

$\cosh(x):={\frac {\mathrm {e} ^{x}+\mathrm {e} ^{-x}}{2}}$

$\tanh(x)={\frac {\sinh(x)}{\cosh(x)}}={\frac {\mathrm {e} ^{x}-\mathrm {e} ^{y}}{\mathrm {e} ^{x}+\mathrm {e} ^{y}}}$

Übungen: Leiten Sie

$\sinh x+\cosh x=e^{x}$
$\cosh ^{2}x-\sinh ^{2}x=1$
$\cosh(x+y)=\cosh x\cosh y+\sinh x\sinh y$
$\sinh(x+y)=\cosh x\sinh y+\sinh x\cosh y$

her.

Die Areafunktionen sind die Umkehrfunktionen zu den Hyperbelfunktionen.

Areasinus hyperbolicus
Areakosinus hyperbolicus
Areatangens hyperbolicus

$\operatorname {arsinh} (x)=\ln(x+{\sqrt {x^{2}+1}})$

$\operatorname {arcosh} (x)=\pm \ln(x+{\sqrt {x^{2}-1}}),\quad x\geq 1$

$\operatorname {artanh} (x)={\frac {1}{2}}\ln {\frac {1+x}{1-x}},\quad |x|<1$

Übung: Leiten Sie die obigen Formeln (Area... hyperbolicus) her.

Polynome

Polynom n-ten Grades:

$P(x)=a_{0}+a_{1}x+a_{2}x^{2}+\dotsb +a_{n}x^{n},\quad n\in \mathbb {N} _{0},\quad a_{n}\neq 0$

Polynome 1. Grades (Geraden $y=kx+d$ )
Polynome 2. Grades (Normalparabeln $y=ax^{2}$ )
Polynom 5. Grades

Rationale Funktionen

$f(x)={\frac {a_{m}x^{m}+a_{m-1}x^{m-1}+\dotsb +a_{1}x+a_{0}}{b_{n}x^{n}+b_{n-1}x^{n-1}+\dotsb +b_{1}x+b_{0}}}={\frac {P_{m}(x)}{Q_{n}(x)}}$

Parameterdarstellung

Ein Kreis lässt sich als $x^{2}+y^{2}=r^{2}$ darstellen. Eine andere Darstellungsweise geht vom Parameter $\phi$ (Winkel) aus (der Radius r sei konstant):