Karnaugh-Veitch-Diagramm: Beispiele (Teil 3)

Beispiel: Don’t-Care-Zustände

Don’t-Care-Zustände (ungebräuchliche deutsche Übersetzung: Egal-Zustände) sind Ergebnisse, die egal sind. Beispielsweise handelt es sich um Zeilen in der Wahrheitstabelle, für die keine Eingaben vorgesehen sind und folglich auch keine Ausgaben berücksichtigt werden wollen. Sie werden als „X“ in das KV-Diagramm eingetragen und dürfen für den Zweck der Gruppenbildung als „1“ oder „0“ betrachtet werden. Die Wahl erfolgt so, dass sich besonders günstig Gruppen bilden lassen (wenig Gruppen, große Gruppen).

Bild 7-1 zeigt zwei Don’t-Care-Zustände (blau umrahmt, aber keine Gruppe). Bild 7-2 zeigt eine fast optimale Gruppenbildung mit diesen Don’t-Care-Zuständen. Zu diesem Zweck wurde das rechte „X“ wie eine „1“ behandelt und das linke „X“ wie eine „0“. Werden beide „X“ auch noch in den roten Block einbezogen, und dieser zum 4er-Block erweitert, ist die Blockbildung optimal (Bild 7-2a).

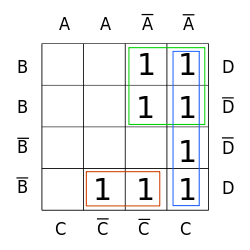
Ohne diese Don’t-Care-Zustände wäre die Gruppenbildung ungünstiger (Bild 7-3).

Die Variante in Bild 7-4 ist nicht optimal, da die blaue Gruppe größer sein könnte.
Die Variante in Bild 7-5 ist nicht optimal, da die Don’t-Care-Zustände nicht genutzt werden und die blaue Gruppe größer sein könnte.
Die Variante in Bild 7-6 ist nicht optimal, da die Don’t-Care-Zustände nicht genutzt werden.

Für das Problem in Bild 7-7 erweist sich die Gruppenbildung in Bild 7-8 als optimal. Die rote Gruppe reduziert sich zu CD und die blaue Gruppe zu ¬B¬C¬D.
Das Endergebnis lautet:CD ∨ ¬B¬C¬D.

Für das Minimierungsproblem in Bild 7-9 erweisen sich die in Bild 7-10 dargestellten Gruppen als optimal.
Die rote Gruppe reduziert sich zu C¬D. Die blaue Gruppe reduziert sich zu B¬C. Die grüne Gruppe reduziert sich zu ¬CD.
Das Endergebnis lautet:C¬D ∨ B¬C ∨ ¬CD.

Weitere Beispiele für Gruppenbildungen mit vorgegebenen Don’t-Care-Zuständen zeigen Bild 7-11 und 7-12. Hier wurden die Don’t-Care-Zustände mit einem Bindestrich statt mit einem „X“ gekennzeichnet. Beide KV-Diagramm sind identisch, nur die Gruppenbildung unterscheidet sich.

Ein weiteres Beispiel zeigt Bild 7-13. Die Gruppenbildung in Bild 7-14 ist nicht optimal, da die Gruppen kleiner als möglich sind. Besser ist die Wahl der Gruppe in Bild 7-15.

Beispiel: Race hazards

A	B	C	Z
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	0

Race hazards (Glitch) in kombinatorischen Schaltungen führen nicht unbedingt zu Fehlfunktionen. Kritisch kann ihr Auftreten aber bei synchronen sequentiellen Schaltungen sein, z. B. bei Flipflops und Zustandsmaschinen. Im KV-Diagramm lassen sich Race hazards sehr leicht erkennen. Sie treten beim Übergang von einer Gruppe zur anderen Gruppe auf. Wegen Race hazards nimmt man in digitalen Schaltungen manchmal nicht die mit dem KV-diagramm gefundene minimale Form des logischen Ausdrucks.

Bild 8-1 zeigt das zur Wahrheitstabelle (rechts) gehörende KV-Diagramm. Beim Übergang vom Feld mit der blauen Eins zum Feld mit der grünen Eins kann ein Race hazard auftreten (Bild 8-1). Zur Vermeidung des Race hazards wird ein weiterer Minterm hinzugefügt (rote Gruppe), der die beiden isolierten Minterme (grüne und blaue Gruppe) verbindet (Bild 8-2). Diese rote Gruppe fügt zwar redundante Logik hinzu, verhindert aber Race hazards. Bei der redundanten Gruppe handelt es sich um eine redundante Primkonjunktion. Aus der Minimallösung A¬B ∨ ¬A¬C wird durch Hinzufügen der Gruppe zur Verhinderung des Race hazards der nicht mehr minimale Term A¬B ∨ ¬A¬C ∨ ¬B¬C

Etwas schwieriger sind Race hazards zu erkennen, wenn sie am Rand des KV-Diagramms auftreten. Beim Übergang von der blauen zur grünen Eins (Bild 8-3), natürlich auch in umgekehrter Richtung, kann ein Race hazard auftreten, der auch hier durch eine zusätzliche Gruppe (rot) verhindert werden kann (Bild 8-4). Aus der Minimallösung AB ∨ ¬AC wird dann AB ∨ ¬AC ∨ BC.

Die zu Bild 8-3 bzw. 8-4 dazugehörigen Logikschaltungen sind in Bild 8-5 bzw. 8-6 zu sehen.

A	B	C	Z
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

Der in Bild 8-5 drohende Race hazard ist in den Bildern 8-7 bis 8-9 illustriert. In Bild 8-7 liegt an A, B und C der logische Wert Eins an – durch rote Leitungen illustriert (schwarze Leitungen für den Wert Null) – letzte Zeile der Wahrheitstabelle (blaue Eins). Es ergibt sich der Ausgangswert Z = 1. In Bild 8-8 tritt der Race hazard auf, beim Umschalten von A = 1 auf A =0, beim Umschalten von Zeile 8 (blaue Eins) auf Zeile 4 (grüne Eins). Das Ergebnis sollte laut Tabelle und KV-Diagramm Eins sein, ist aber kurzzeitig Null, ein Glitch – eine kurzzeitige Falschaussage – ein Race hazard. Das falsche Ergebnis (Bild 8-8) dauert nur einen Sekundenbrauchteil an. Das richtige logische Ergebnis (Bild 8-9) folgt erst nach diesem Sekundenbruchteil. Die dazugehörige Tabelle steht rechts. Ursache für den Glitch ist die notwendige Schaltzeit für die Negation – im Inverter.

Ein weiteres Beispiel für Race hazards sind die drei Gruppen in Bild 8-10. Hier kann ein Race hazard sowohl beim Übergang von der roten zur blauen Eins auftreten (mit grüner Brücke hervorgehoben), als auch beim Übergang von der roten zur grünen Eins (mit roten Punkten hervorgehoben). Verhindert werden diese Race hazards durch Hinzufügen der gelben Gruppe (Bild 8-11), die alle drei Gruppen überlappt.

Beispiel: XNOR und XOR

Die XNOR-Verknüpfung und die XOR-Verknüpfung sind im KV-Diagramm durch diagonale Einzelfelder gekennzeichnet und können nicht weiter vereinfacht werden.

Weitere Wikibücher zu KV-Diagrammen:

Digitale Schaltungstechnik/ Schaltalgebra/ KV-Diagramm - mit zahlreichen Beispielen zu KV-Diagrammen
Digitale Schaltungstechnik/ Zähler/ Synchron/ JK Flipflop/ beliebige Zählfolge#KV-Diagramme - KV-Diagramme für JK-Flipflops

Zur Titelseite: Karnaugh-Veitch-Diagramm - zum vorherigen Kapitel: Beispiele (Teil 2) - zum nächsten Kapitel: Mengendiagramm und Hyper-Einheitswürfel