Karnaugh-Veitch-Diagramm: Mengendiagramm und Hyper-Einheitswürfel
Mengendiagramm
[Bearbeiten]Das Karnaugh-Veitch-Diagramm ist eine abgewandelte, abstrakte Form des Mengendiagramms (Venn-Diagramm).
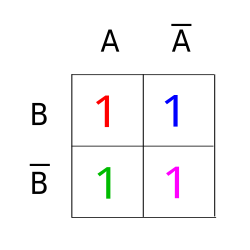
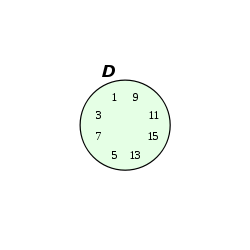
Die Bilder 1 bis 4 zeigen ein Venn-Diagramm und das äquivalente KV-Diagramm.
- 2 Variablen
-
Bild 1: KV-Diagramm
-
Bild 2: Venn-Diagramm
- 4 Variablen
-
Bild 3: KV-Diagramm
-
Bild 4: Venn-Diagramm
Die Bilder 5 bis 8 zeigen noch einmal die einzelnen Teilmengen, aus denen sich das Venn-Diagramm in Bild 4 zusammensetzt.
- 4 Variablen
-
Bild 5: Venn-Diagramm
-
Bild 6: Venn-Diagramm
-
Bild 7: Venn-Diagramm
-
Bild 8: Venn-Diagramm
Veranschaulichung durch Hyper-Einheitswürfel
[Bearbeiten]
Boolesche Funktionen mit n Variablen lassen sich grafisch mittels Einheitswürfeln der Dimension n veranschaulichen. Würfel beliebiger Dimension bezeichnet man auch als Hyperwürfel. Da Karnaugh-Diagramme selbst eine spezielle Darstellungsform für Boolesche Funktionen sind, überrascht es nicht, dass sich zwischen Hyper-Einheitswürfeln und Karnaugh-Diagrammen ein anschaulicher Zusammenhang herstellen lässt. Und zwar entsprechen Karnaugh-Diagramme für n Variablen umkehrbar eindeutig den Hyper-Einheitswürfeln der Dimension n. Die Ecken-Koordinaten des Hyperwürfels entsprechen dabei den dualen Nummern der Felder im Karnaugh-Diagramm.
Bild 3-2 zeigt den Einheitswürfel für 3 Variablen. Das entspricht einem 2x4 KV-Diagramm. Das KV-Diagramm in Bild 3-3 ist in Bild 3-4 entsprechend markiert (grüne Ebene). Die Knoten (Eckpunkt oder Kreise) am Hyper-Einheitswürfel entsprechen jeweils einem Feld im KV-Diagramm. Die Übergänge (Nachbarschaft der Felder) sind durch die Kanten des Würfels symbolisiert. Beim Wandern auf der Kante entsteht ein Gray-Code. Auf jeder Kante ändert sich genau 1 Bit. Eine wesentliche Eigenschaft ist, dass sich die Gray-Codes für zwei benachbarte Zahlen nur um 1 Ziffer, bei Binärcode also 1 Bit, unterscheiden (Hamming-Distanz).
Das KV-Diagramm hat so viel Nachbarschaften, wie der Würfel Kanten hat. Bild 3-5 zeigt eine ebene Darstellung des Hyper-Einheitswürfels. Ohne seine innere Struktur der Übergänge zu ändern lässt sich der Würfel in beliebige Richtungen „umstülpen“, wie in der Animation in Bild 3-9 dargestellt ist. So ist zu erklären, warum es KV-Diagramm mit verschiedenen Anordnungen der Variablen gibt (Randbeschriftung). Sie wurden praktisch wie ein Würfel „umgestülpt“.
 |
 |
 |
 |
Für das KV-Diagramm mit 2 Variablen (2x2 Feld) ergibt sich ein einfacherer Hyper-Einheitswürfel (Bild 3-6). Bei 1 Variable ist der „Würfel“ trivial (Bild 3-7). Mit zunehmenden Variablen steigt die Anzahl der Kanten allerdings exponentiell an. So gibt es bei 4 Variablen (Bild 3-8) bereits 32 Kanten.
 |
 |
 |
Siehe auch
[Bearbeiten]- Verfahren nach Quine und McCluskey – bei mehr als 5 Eingangsvariablen besser geeignet, als das KV-Diagramm
- Pseudotetraden
- Schaltalgebra
- Karnaugh-Diagramme (oben), wegen der gleichen Aussprache der Personennamen, nicht zu verwechseln mit den Diagrammen des Carnot-Kreisprozesses
Literatur
[Bearbeiten]- Maurice Karnaugh: The Map Method for Synthesis of Combinational Logic Circuits, Transactions of the AIEE, Vol. 72, No. 9 (1953), 593–599.
- Edward W. Veitch: A chart method for simplifying truth functions, Mai 1952, Proc. Assoc. for Computing Machinery, Pittsburgh, 127–133.
- Klaus Beuth: Digitaltechnik (Kapitel 5), 2001, Vogel Buchverlag, ISBN 3-8023-1755-6
- Günter Wellenreuther, Dieter Zastrow: Steuerungstechnik mit SPS: Von der Steuerungsaufgabe zum Steuerprogramm (Kapitel 4.5.2), 1998, Vieweg+Teubner Verlag, ISBN 3-5284-4580-7
Weblinks
[Bearbeiten]- Java-Applet zum KV-Diagramm von der Universität Karlsruhe
- Java-Applet zum KV-Diagramm von der Universität Erlangen-Nürnberg
- Kostenloses Lernprogramm. Lernziele: Aufstellen von Wahrheitstabellen und der disjunktiven Normalform (DNF), Vereinfachen von Schaltnetzen mit KV-Tafeln für 2 bis 5 Variable.
- Java-Applet zum KV-Diagramm mit Wertetabelle von der Technischen Universität Ilmenau
- Herleitung einer Formel mittels KV-Diagramm zur Bestimmung, ob Rechtecke mit partiell gleichem Flächeninhalt überlappend angeordnet werden können, ein Artikel von Herbert Glarner [en]
- Applet zum bearbeiten von KV-Diagrammen der Universität Hamburg
Zur Titelseite: Karnaugh-Veitch-Diagramm - zum vorherigen Kapitel: Beispiele (Teil 3) - Ende des Buches