Mathematik für Wirtschaftswissenschaftler: Relation und Abbildung

Wir wollen für die Erläuterung der Relation noch einmal auf das kartesische Produkt A × B = {(a; b)| a ∈ A und b ∈ B} zurückgreifen. Es wird hier jedes Element einer Menge A paarweise mit jedem Element einer Menge B verknüpft.

Ein spezielles kartesisches Produkt ist A × A, das Produkt von A mit sich selber. Man schreibt hier auch A × A = A², A × A × A = A³, ... A₁ × A₂ × A₃ × … × A_n = Aⁿ, wenn alle A_i gleich sind.

Ein Beispiel ist etwa R × R = R², das kartesische Produkt der reellen Zahlen, was grafisch die gesamte (unendlich große) Fläche des kartesischen Koordinatensystems bedeckt.

Relation

Die Relation ist eine Teilmenge des kartesischen Produkts, wobei die Teilmenge beliebig sein kann.

Beispiel 1 aus dem Kapitel Mengen:

A = {0, 1, 8}, B = {0, x} mit dem kartesischen Produkt A × B = {(0,0), (0,x), (1,0), (1,x), (8,0), (8,x)}.

Eine Relation wäre nun beispielsweise R = {(0,0), (1,x), (8,0), (8,x)}. Man sieht, dass R ⊂ A × B ist.

Beispiel 2:

Gegeben sind die Mengen A={1, 2, 3, 4} und B=A.

Das kartesische Produkt ist A × B =

{(1,1), (1,2), (1,3), (1,4)
 (2,1), (2,2), (2,3), (2,4)
 (3,1), (3,2), (3,3), (3,4)
 (4,1), (4,2), (4,3), (4,4)}

Die Relation mit der Beschreibung R={(a,b)| (a,b) ∈ A × B und a=b} ergibt R={(a,b)| (1,1), (2,2), (3,3), (4,4)}.

Abbildung

Ein Spezialfall der Relation R ⊂ A × B ist die Abbildung oder auch Funktion. Sie ist folgendermaßen charakterisiert:

Eine Abbildung oder Funktion von der Menge A in die Menge B ist eine Relation f, welche folgende Eigenschaften hat:

• f ist eine Teilmenge von A × B.
• f ordnet jedem Element von A genau ein Element von B zu. f ist die Zuordnungsvorschrift.

Für f ⊂ A × B schreibt man f: A → B. Statt (a,b) ∈ f schreibt man f: a ↦ f(a) = b.

Wir nennen A Definitionsbereich von f und B zunächst allgemein die Zielmenge. Ein Element b=f(a) wird Bild genannt, das dazuhörige a Urbild von b. Die Menge aller Bilder ist der Wertebereich von f.

Der Begriff Abbildung und Funktion ist synonym. Häufig liest man, dass der Begriff Funktion speziell für die Abbildung f: R → R verwendet wird. Das ist streng genommen unzutreffend.

Abbildungsarten

Eine Abbildung ist

• injektiv, wenn jedes Element des Zielbereichs höchstens ein Urbild hat.

Abbildung ist injektiv

• surjektiv, wenn jedes Element der Zielmenge mindestens ein Urbild hat.

Abbildung ist surjektiv

• bijektiv, wenn sie injektiv und surjektiv ist, also wenn jedes Element der Zielmenge genau ein Urbild hat.

Abbildung ist bijektiv

Zusammengesetzte Abbildungen

auch Komposition oder verkettete Abbildungen genannt.

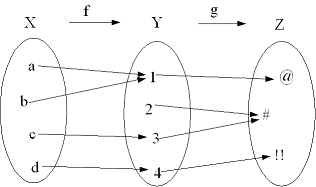
Die Abbildungen f: A → B und g: B → C, jeweils mit Elementen a, b und c, können miteinander verkettet werden. Man erhält dann die Abbildung g(f(a)), die auch als (g o f)(a) bezeichnet und als "g nach f" ausgesprochen wird.

In der Notation der Relation erhält man

$g\circ f=\{(a,c)\in A\rightarrow C|{\mbox{es gibt mindestens ein }}b\in B:(a,b)\in f\land (b,c)\in g\}$.

Komposition mit den Mengen X, Y, Z

Beispiel

Gegeben sind die Funktionen f: R → R; x ↦ x+1 und g: R → R⁺₀; x ↦ x².

Die Komposition von f und g ergibt die Funktion h mit

$h(x):=\left(g\circ f\right)(x)=\left(x+1\right)^{2}$.

Bei der Komposition muss überprüft werden, ob die jeweiligen Mengen zusammenstimmen, d.h. ob das obengenannte b existiert. Eine Verkettung ist möglich, wenn der Wertebereich von f eine Teilmenge des des Definitionsbereichs von g ist:

$\mathbb {W} _{f}\subset \mathbb {D} _{g}$.

Man beachte: Die Komposition ist nicht kommutativ, es ist also im allgemeinen g o f ≠ f o g.

Umkehrabbildung

auch inverse Funktion, Umkehrfunktion genannt.

Gehen wir von einer Abbildung f: A → B aus, wird bei der Umkehrabbildung die Richtung des Abbildungspfeils umgedreht. Man erhält dann

$f^{-1}:B\rightarrow A$.

Eine Umkehrabbildung existiert nur, wenn die Abbildung bijektiv ist.

Navigation

↓  Funktionstypen

↑  Logarithmen

↑↑ Inhaltsverzeichnis