Physik Oberstufe/ Schwingungen und Wellen/ Elektromagnetische Wellen

Vom elektrischen Schwingkreis zum Hertzschen Dipol

Elektrischer Schwingkreis. Die Schwingung kann z.B. über induktive Kopplung angeregt werden.

Elektrisches und magnetisches Feld um einen Dipol.

Schwingungsphasen eines oszillierenden Dipols.

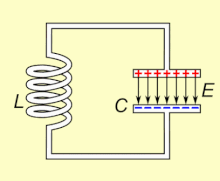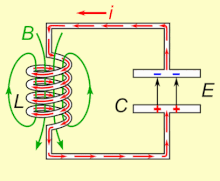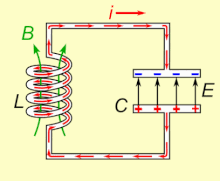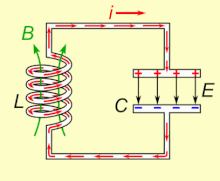
Wir modifizieren in Gedanken einen Schwingkreis, bestehend aus einer Spule und einem Kondensator: Zuerst ziehen wir die Kondensatorplatten auseinander. Dadurch sinkt die Kapazität des Kondensators: Die Schwingungsfrequenz des Schwingkreises wird gemäß der Thomsonschen Formel größer. Anschließend verringern wir die Plattengröße: Die Kapazität des Kondensators wird noch kleiner, die Schwingungsfrequenz entsprechend noch größer. Wir ziehen die Spule auseinander bzw. verringern die Anzahl der Windungen. Dadurch sinkt die Induktivität der Spule. Wieder zeigt die Thomsonsche Formel, dass die Schwingungsfrequenz des Schwingkreises weiter ansteigt. Letzten Endes können wir die Spule auch ganz auseinander ziehen. Übrig bleibt ein Draht/Leiter, um den sich bei Stromfluss ein Magnetfeld bildet. Ergebnis: Der Hertzsche Dipol ist ein elektromagnetischer Schwingkreis sehr hoher Frequenz.

Abstrahlung einer elektromagnetischen Welle

Experiment: Ein Hertzscher Dipol wird zum Schwingen angeregt. Nachweis der Schwingung: Elektrische Feldsonde: Die Sonde leuchtet an den Enden des Dipols auf und erlischt in der Mitte. Elektrisch gekoppelter Schwingkreis mit Glühlampe: Eine in die Mitte eines identischen Dipols eingebaute Glühlampe leuchtet auf, wenn die Dipole parallel und nah zueinander gebracht werden. Elektrisch gekoppelter Schwingkreis mit Ampèremeter. Beobachtung: Das elektrische Wechselfeld des Dipols ist in großer Entfernung noch nachweisbar. Es breitet sich im Raum aus.

Betrag der elektrischen Feldstärke$E=|{\vec {E}}|$ (farbig) und der Poynting-Vektor (schwarze Pfeile) im Nahfeld des vertikal in der Bildebene liegenden Dipols. Blaue/rote Farben bedeuten ein nach unten/oben orientiertes elektrisches Feld.

Elektrische Feld eines schwingenden Dipols.

Experiment: Wir messen das Feld mit dem Mess-Dipol vor einer leitenden Metallplatte (Blech). Beobachtung: Zwischen Dipol und Metallplatte messen wir eine periodisch Modulation der Feldstärke, wir finden Schwingungsknoten und -Bäuche. Erklärung: Vor der Metallplatte bildet sich eine stehende Welle aus.

Aus dem Abstand $d=34\,{\rm {cm}}$ der Knoten und der Anregungsfrequenz $f=440\,{\rm {MHz}}$ des Dipols berechnen wir die Ausbreitungsgeschwindigkeit der Welle zu:

$c=\lambda \cdot f=2\cdot d\cdot f=34\,{\rm {cm}}\cdot 440\,{\rm {MHz}}\approx 3\times 10^{8}{\rm {\frac {m}{s}}}$

Die elektromagnetische Welle breitet sich mit Lichtgeschwindigkeit aus.

Eigenschaften des Dipol-Fernfeldes

Animation der Zeit- und Orts­abhängigkeit von E- und H-Feld in der xy-Ebene

Elektronenverteilung in einem Dipol

• ${\vec {E}}$ und ${\vec {B}}$ stehen senkrecht aufeinander.
• ${\vec {E}}$ und ${\vec {B}}$ schwingen in Phase.
• ${\vec {E}}$ und ${\vec {B}}$ bilden eine Sinuswelle.
• Die Amplituden nehmen mit wachsender Entfernung ab.
• Keine Abstrahlung in Längsrichtung des Dipols.
• Die Länge $l$ des Dipols bestimmt seine Eigenfrequenz.
  Es gilt:

$l={\frac {\lambda }{2}}={\frac {c}{2f}}$

Wechselwirkung veränderlicher EM-Felder

Induktionsgesetz

Ändert sich der magnetische Fluss, so wird er von einem elektrischen Wirbelfeld E umgeben.

Eine Änderung des magnetischen Flusses in der linken Spule induziert einen Strom in der rechten Spule . Erinnerung: Ändert sich der magnetische Flusses durch eine kurzgeschlossene Spule, so wird ein Strom induziert (M. Faraday). Was passiert, wenn wir die Spule nicht kurzschließen? → Wir messen eine Spannung zwischen den Spulenanschlüssen. Was passiert, wenn wir die Spule entfernen? → Um das sich ändernde Magnetfeld bildet sich ein elektrisches Wirbelfeld.

Jedes sich ändernde Magnetfeld ist von einem ringförmigen, geschlossenen elektrischen Feld umgeben.

Maxwellscher Verschiebungsstrom

Elektrisches und magnetisches Feld einer ebenen elektromagnetischen Welle.

Ein Kondensator wird entladen. Um den stromdurchflossenen Leiter bildet sich ein Magnetfeld. Gedankenexperiment: Ein Kondensator wird über einen Widerstand entladen, es fließt der Strom $I$. Maxwell: Das ringförmige Magnetfeld des stromdurchflossenen Leiters umgibt auch das sich ändernde elektrische Feld des Kondenstors.

Jedes sich ändernde elektrische Feld ist von einem ringförmigen, geschlossenen Magnetfeld umgeben.

Maxwell formulierte diese beiden Zusammenhänge mathematisch und leitete um 1860 die Existenz elektromagnetischer Wellen ab. Als Ausbreitungsgeschwindigkeit der Welle erhält er:

$c={\frac {1}{\sqrt {\varepsilon _{0}\cdot \mu _{0}}}}$

Der experimentelle Nachweis erfolgte erst über zwei Jahrzehnte später, um 1886, durch H. Hertz.

---

Aufgabe: Lichtgeschwindigkeit aus $\varepsilon _{0}$ und $\mu _{0}$ berechnen.

---

Das Spektrum elektromagnetischer Wellen

EM Spectrum Properties

Eigenschaften elektromagnetischer Wellen

Am Beispiel von cm-Wellen $\lambda \approx 3\;{\rm {cm}}$ untersuchen wir die Eigenschaften von elektromagnetischen Wellen. Man beachte dabei, dass viele Eigenschaften von der Wellenlänge abhängen.

Experiment: Sender und Empfänger werden einander gegenüber aufgestellt und die Intensität der empfangenen Welle beobachtet. Wie beeinflussen verschiedene Materialien zwischen Sender und Empfänger die Intensität? Beobachtung: Holz: leichte Abschwächung Metall: Signal verschwindet … Erklärung: In leitenden Materialien verhindern bewegliche Ladungen die Propagation der Welle. Experiment: Zwischen Sender und Empfänger wird ein Gitter aus Metallstäben eingebaut (Abstand der Gitterstäbe < Wellenlänge). Das Gitter wird um die Achse der Ausbreitungsrichtung der Welle gedreht, abhängig vom Drehwinkel die Signalstärke beobachtet. Beobachtung: Die Signalstärke ändert sich abhängig vom Drehwinkel. Die Drehwinkel maximaler und minimaler Intensität sind 90° gegeneinander verdreht. Erklärung: Elektomagnetische Wellen sind transversale Wellen, d.h. elektrisches und magnetisches Feld stehen senkrecht auf der Ausbreitungsrichtung. Steht das elektrische Feld parallel zu den Gitterstäben, so können Elektronen in den Gitterstäben schwingen, wie bei der Metallplatte wird die Welle reflektiert (→ kein Signal im Empfänger). Steht das elektrische Feld senkrecht auf den Gitterstäben, so kann kein Strom in Richtung des E-Felds fließen und die Welle propagiert ungehindert (→ Signal im Empfänger). Analogon: Seilwelle und „Schlitzblende“ zwischen Stangen. Diese Eigenschaft nennt man Polarisation. Sie tritt nur bei transversalen Wellen auf, longitudinale Wellen sind nicht polarisierbar. Bei elektromagnetischen Wellen gibt die Richtung des elektrischen Feldvektors ${\vec {E}}$ die Polarisationsrichtung an. Aufgabe: Wie ist zu verfahren, wenn die Gitterstäbe weder senkrecht noch parallel zum elektrischen Feld stehen? Experiment: Bestimmung der Wellenlänge: Eine Metallplatte reflektiert die Welle, ein- und auslaufende Welle überlagern sich zu einer stehenden Welle. Durch Vermessung der Knoten-/Bauch-Struktur der stehende Welle kann die Wellenlänge $\lambda$ bestimmt werden. Experiment: Reflexionsgesetz: Es gilt: „Einfallswinkel gleich Ausfallswinkel“. Experiment: Ein Gitter (Polarisationsfilter) wird senkrecht zur Polarisationsrichtung in die Welle gestellt, das Signal verschwindet. Nun wir vor das Gitter ein weiteres Gitter um 45° verdreht eingefügt: Das Signal erscheint wieder. Erklärung: Durch die Anordnung der Gitter kommt es zu einer Drehung der Polarisation.

---

Absorptionsspektrum flüssigen Wassers.

Aufgabe: Polarisation und Gitter

---