Physik Oberstufe/ Schwingungen und Wellen/ Interferenzphänomene
Das Huygenssche Prinzip
[Bearbeiten]
Erinnerung:
- Kreiswelle, Wellenfronten bilden Kreise. In 3-D: Kugelwelle, Wellenfronten bilden Kugelschalen. Kreis- und Kugelwellen werden auch als Elementarwellen bezeichnet.
- Ebene Wellen: Wellen sind Geraden bzw. Ebenen. Ein kleiner Ausschnitt einer Kreiswelle kann häufig als ebene Welle betrachtet werden.

|
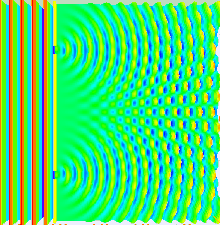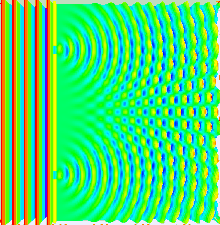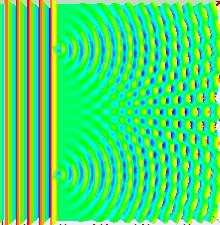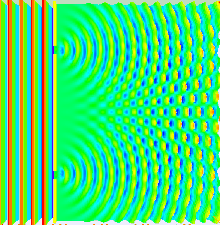
Experiment: Eine ebene Wasserwelle wird in der Wellenwanne auf einen Spalt geschickt. |
Huygenssches Prinzip: Jeder Punkt einer Welle kann als Ausgangspunkt einer Elementarwelle betrachtet werden.
 Die Elementarwellen, die von einer Wellenfront der ebenen Welle ausgehen, überlagern sich wieder zu einer ebenen Welle. Jede Wellenfront kann als Einhüllende von Elementarwellen aufgefasst werden. |
|
Experiment: Eine Mikrowelle strahlt am Empfänger vorbei. Platziert man einen Spalt vor den Sender, so misst man an der selben Stelle ein Signal. |
Interferenzexperimente
[Bearbeiten]Der Doppelspalt
[Bearbeiten]Bestimmung der Richtungswinkel
[Bearbeiten]
Die Kreiswellen der Spalte verstärken sich in einem Punkt (konstruktive Interferenz), wenn Wellenberg auf Wellenberg und Wellental auf Wellental trifft. Auslöschung tritt auf, wenn Wellenberg auf Wellental und umgekehrt trifft. Die Wegdifferenz zu den beiden Spalten kann für einen weit entfernten Schirm leicht bestimmt werden. In diesem Fall sind die Winkel nahezu gleich und wir finden mit dem Wegunterschied :
mit dem Spaltabstand .

Maxima
[Bearbeiten]Die Wegdifferenz zu den beiden Spalten muss ganzzahlige Vielfache von betragen, die Phasendifferenz ganzzahlige Vielfache von :
| Bedingung für die Richtungswinkel der Maxima des Doppelspalts:
|
Minima
[Bearbeiten]Die Wegdifferenz zu den beiden Spalten muss eine ungerade Anzahl von betragen, die Phasendifferenz eine ungerade Anzahl von :
| Bedingung für die Richtungswinkel der Minima des Doppelspalts:
|
Aufgabe: Mikrowellen treffen auf einen Doppelspalt.
Beugung von Licht am Doppelspalt
[Bearbeiten]

Wir wollen untersuchen, ob Licht Welleneigenschaften besitzt.
|
Experiment: Wir richten einen Laserpointer (monochromatisches Licht) auf einen Doppelspalt. |
Man bezeichnet das Muster auf dem Schirm als Beugungs- oder Interferenzmuster.
- Licht breitet sich wie eine Welle aus!
Aufgabe: Licht trifft auf einen Doppelspalt.
Der Einzelspalt
[Bearbeiten]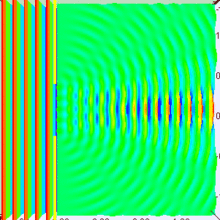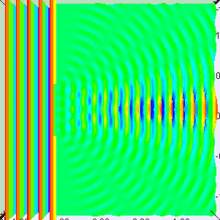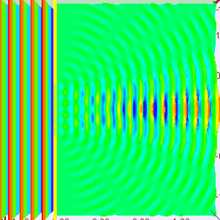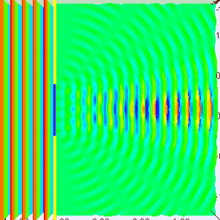
Frage: Entsteht hinter dem Spalt wirklich eine Elementarwelle?
Bestimmung der Richtungswinkel für die Minima
[Bearbeiten]


Beim Einzelspalt kann man mit unseren Methoden nur die Position der Minima berechnen. Jeder Punkt des Einzelspalts kann als Ausgangspunkt einer Elementarwelle gesehen werden. Ein Minimum entsteht, wenn zu jedem Strahl ein anderer mit Phasendifferenz bzw. Wegdifferenz existiert.
Wir teilen den Spalt in zwei Zonen und und betrachten die bei und startenden Strahlen:
- Sie löschen sich aus, wenn zwischen ihnen eine Wegdifferenz besteht.
- Nun löschen sich aber paarweise alle Strahlen aus. Zu jedem Strahl aus existiert genau ein Strahl aus mit .
In diesem Fall gilt (siehe Bild): .
- Das zweite Minimum tritt auf, wenn sich schon im Bereich alle Stahlen auslöschen. Das ist der Fall wenn die bei und startenden Strahlen eine Wegdifferenz von aufweisen.
In diesem Fall gilt: .
Allgemein findet man:
| Bedingung für die Richtungswinkel der Minima des Einzelspalts:
|
Interpretation für
[Bearbeiten]Für existiert nur ein Minimum :
- .
Wird die Spaltbreite weiter verringert, breitet sich nach dem Spalt tatsächlich mehr und mehr eine in alle Richtungen mit gleicher Amplitude verlaufende Elementarwelle aus.
Aufgabe: Einzelspaltbreite aus Beugungsbild.
Das optische Gitter
[Bearbeiten]
Bestimmung der Richtungswinkel für die Maxima
[Bearbeiten]
Wir gehen davon aus, dass von jeder Gitterlinie eine Elementarwelle ausgeht. Ein Maximum entsteht, wenn sich alle Elementarwellen konstruktiv überlagern. In diesem Fall haben nebeneinander liegende Strahlen einen Wegunterschied von Vielfachen von und es gilt:
| Bedingung für die Richtungswinkel der Maxima des Gitters:
|
Warum löschen sich in allen anderen Fällen alle Strahlen aus? Nehmen wir an, der Wegunterschied benachbarter Strahlen beträgt . Dann ist der Wegunterschied zwischen den nächsten Strahlen:
Strahlen 1 und 2 1 und 3 1 und 4 1 und 5 1 und 6 2 und 7 3 und 8 Wegdifferenz
Strahl 1 und Strahl 6 löschen sich wegen aus, ebenso Strahl 2 und Strahl 7, Strahl 3 und Strahl 8 … usw., d.h. am Ende haben sich alle Strahlen paarweise ausgelöscht. Dies gilt allgemein nicht für alle möglichen Wegdifferenzen benachbarter Strahlen, die kein Vielfaches von betragen. Man kann aber immer Kombinationen mehrerer Strahlen finden, die sich auslöschen und damit löschen sich dann alle Strahlen aus.
Aufgabe: Wellenlängenbestimmung mit einer CD als Reflexionsgitter.
Aufgabe: Beugungsmaxima eines gekippten Gitters.
Beschreibung von Mehrfachspalt und Gitter mit Zeigern
[Bearbeiten]
Eine harmonische Welle kann mit einem rotierenden Zeiger beschrieben werden. Bei Mehrfachspalt und Gitter überlagern sich die Wellen der verschiedenen Spalte. Die Wellen benachbarter Spalte haben jeweils eine vom Beobachtungswinkel abhängige Phasenverschiebung zueinander. Mit jedem weiteren Spalt kommt eine wiederum um phasenverschobene Welle hinzu.
Wir können die Zeiger aller dieser Wellen addieren und erhalten damit den resultierenden Zeiger. Die Länge dieses Zeigers gibt die resultierende Amplitude an. Die Amplitude wird Maximal, wenn alle Zeiger in dieselbe Richtung zeigen, also in Phase sind. Ein Minimum entsteht, wenn alle Zeiger aneinandergereiht einen geschlossenen Linienzug bilden, der resultierende Zeiger also verschwindet.
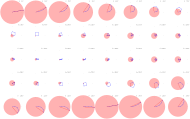
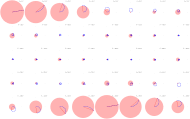
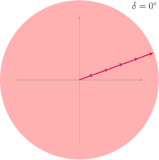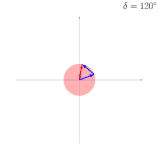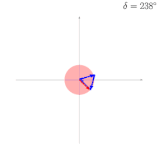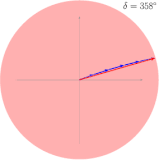
- Beispiele für Mehrfachspalt-Interferenzen und die Analyse mittels Zeigern
-
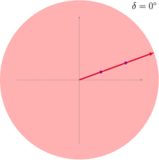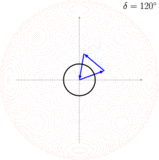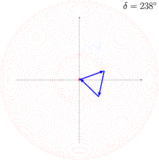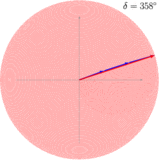
Addition dreier Wellen: Jede Welle weist zur vorhergehenden eine Phasenverschiebung von auf.
-
Doppelspalt
-
Dreifachspalt
-
Vierfachspalt
-
Fünffachspalt
-
Sechsfachspalt
-
Siebenfachspalt
-
Achtfachspalt

- Zeiger-Animationen zur Erläuterung von Mehrfachspalt-Interferenzen
-
Doppelspalt
-
Dreifachspalt
-
Fünffachspalt
-
Zehnfachspalt
-
Gitter, 20 Linien
-
Gitter, 30 Linien
-
Gitter, 40 Linien
Man erkennt folgende Gesetzmäßigkeiten:
- Zwischen den Haupmaxima eines Gitters mit Spalten befinden sich immer Minima, dazwischen sind Nebenmaxima.
- Die Haupmaxima werden umso schärfer, je mehr Gitterlinien vorhanden bzw. beleuchtet sind.
- Die Intensität der Nebenmaxima wird mit mehr Gitterlinien immer geringer.
Einzelspalteffekte bei Mehrfachspalt-Experimenten
[Bearbeiten]

In vielen Fällen werden Mehrfachspalt-Experiemente mit Spaltbreiten durchgeführt, die größer sind als die Wellenlänge . Dies hat zur Folge, dass von jedem einzelnen Spalt statt idealer Elementarwellen bereits Wellen mit dem entsprechenden winkelabhängigen Einzelspalt-Intensitätsprofil ausgehen. In Folge ist das Beugungsbild der Gesamtstruktur von dem des einzelnen Spalts überlagert: In Richtung der Minima des Einzelspalts bleiben Maxima der Gesamtstruktur, beispielsweise eines Gitters oder Doppelspalts, unsichtbar.
Aufgabe: Einzelspalteffekte und Doppelspalt.
Aufgabe: Sichtbare Beugungsordnungen eines Liniengitters.
Spektralanalyse mit Liniengittern
[Bearbeiten]

Beleuchtet man ein Gitter mit Licht unterschiedlicher Wellenlängen, so liegen die Maxima jeder Wellenlänge unter einem anderen Richtungswinkel. Man erhält also ein Spektrum der Strahlung, d.h. eine Zerlegung in alle in der Strahlung vorhandenen Wellenlängen. Die Analyse von Licht (Spektroskopie) erlaubt mannigfaltige Anwendungen in Physik, Chemie, Astronomie, …
Grundsätzlich unterscheidet man drei Arten von Spektren:
- Kontinuierliche Spektren: Man kann keine einzelnen Linien erkennen, alle Wellenlängen (und damit Farben) kommen vor, möglicherweise mit unterschiedlicher Intensität.
- Diskrete Spektren:
- Emissionsspektren: Die Strahlung enthält nur einzelne, diskrete Wellenlängen. Ihre Analyse ermöglicht Eigenschaften der Strahlungsquelle herauszufinden.
- Absorptionsspektren: In einem kontinuierlichen Spektrum fehlen einzelne, diskrete Wellenlängen. Sie ermöglichen Eigenschaften eines zwischen der Quelle und dem Spektrometer befindlichen Transportmediums zu untersuchen.
Aufgabe: ToDo: Überlappende Ordnungen bei der Gitterspektroskopie.
Kohärenz
[Bearbeiten]

Lichtquellen senden keine unendlich langen Wellenzüge aus. Abhängig von der Art der Erzeugung der Welle besteht das emmitierte Licht aus sehr kurzen (~µm, z.B. Glühlicht) oder bei z.B. LASERN sehr langen Wellenzügen (viele ~km).
Besteht zwischen zwei Wellen eine feste Phasenbeziehung, so bezeichnet man diese Wellen als kohärent. Überlagert man kohärente Wellenzüge, kann man Interferenzerscheinungen beobachten.
Zwischen inkohärenten Wellen besteht keine feste Phasenbeziehung, bei einer Überlagerung beobachtet man keine Interferenz.
Bei Interferenzexperimenten vergleicht man Wellenzüge, die meist unterschiedliche Strecken zurückgelegt haben. Beträgt die Wegdifferenz mehr als die Kohärenzlänge, so sind keine Interferenzen mehr sichtbar. Statistisch verteilte Phasen verschiedener Wellenpakete überlagern sich inkohärent.