Physik Oberstufe/ Schwingungen und Wellen/ Mechanische Schwingungen

Grundwissen mechanische Schwingungen

• Beispiele für mechanische Oszillatoren
• 
  Fadenpendel
• 
  Federpendel
• 
  Federpendel animiert
• Torsionspendel
• 
  Schwingende Wassersäule
• 
  Animation einer harmonischen Schwingung
• 
  $t$-$s$-Diagramm einer Schwingung
• 
  Federpendel: Ruhelage,Koordinatensystem und Rückstellkraft

Merkmale eines Oszillators

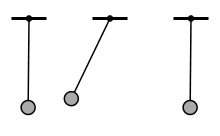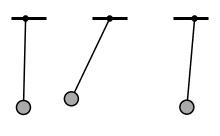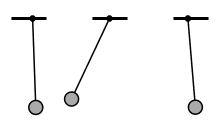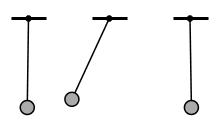
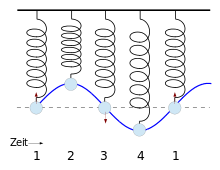
1. Der Oszillator besitzt eine Ruhe-/Gleichgewichtslage.
2. Lenkt man den Oszillator aus der Ruhelage aus, so wirkt eine rücktreibende Kraft/Rückstellkraft.
3. Aufgrund der Trägheit bewegt sich der Oszillator nach dem Loslassen unter Einfluss der Rückstellkraft durch die Ruhelage hindurch.

Begriffe

• Auslenkung, Elongation $s(t)$
• Amplitude (maximale Auslenkung) ${\hat {s}}$
• Geschwindigkeit $v={\frac {\Delta s}{\Delta t}}\quad \Rightarrow \quad v(t)={\dot {s}}(t)$
• Beschleunigung $a={\frac {\Delta v}{\Delta t}}\quad \Rightarrow \quad a(t)={\dot {v}}(t)={\ddot {s}}(t)$
• Periodendauer $T$, verstreicht zwischen zwei aufeinander folgenden, gleichsinnigen Durchgängen des Oszillators an beliebigem Ort $s$.
• Frequenz $f={\frac {1}{T}},\quad [f]={\frac {1}{\rm {s}}}={\rm {Hz}}$
• Kreisfrequenz $\omega =2\pi f,\quad [\omega ]={\frac {1}{\rm {s}}}={\rm {Hz}}$

Das Federpendel

Bestimmung der Rückstellkraft

Ein Federpendel in Ruhelage und ausgelenkt. → Animation

Wir wollen die Rückstellkraft abhängig von der Auslenkung $s$ bestimmen. In der Ruhelage ist die Feder um $s_{0}$ ausgelenkt. Die Kraft der Feder $F_{F}=D\cdot s_{0}$ kompensiert die Gewichtskraft $G=mg$, es gilt also:

$F_{F}=D\cdot s_{0}=G=mg\quad \Rightarrow D\cdot s_{0}=mg\,.\quad (1)$

Für die Rückstellkraft $F_{R}$ gilt:

$F_{R}=F_{F}-G=D\cdot (s_{0}-s)-mg$

und mit (1) folgt:

$F_{R}=-D\cdot s$.

Bestimmung der Funktion $s(t)$

Die Rückstellkraft $F_{R}$ wirkt auf die Masse $m$ und beschleunigt diese in Richtung der Ruhelage, entgegengesetzt zur Auslenkung $s$.
Mit Newtons Gesetz:

$F=m\cdot a$

ergibt sich:

$F_{R}=-D\cdot s(t)=m\cdot a(t)$.

Setzen wir für die Beschleunigung $a(t)$ den Zusammenhang $a(t)={\ddot {s}}(t)$ ein, erhalten wir:

$-D\cdot s(t)=m\cdot {\ddot {s}}(t)$

Umgestellt ergibt sich die

Differentialgleichung (DGL) des harmonischen Oszillators: ${\ddot {s}}(t)+{\frac {D}{m}}\cdot s(t)=0$

Gesucht ist eine Funktion $s(t)$, die zwei mal abgeleitet bis auf den Faktor $-{\frac {D}{m}}$ sich selbst ergibt.
Wir machen einen Ansatz:

$s(t)={\hat {s}}\cdot \sin(\omega t-\varphi )$

$\Rightarrow \,{\dot {s}}(t)={\hat {s}}\omega \cdot \cos(\omega t-\varphi )$

$\Rightarrow \,{\ddot {s}}(t)=-{\hat {s}}\omega ^{2}\cdot \sin(\omega t-\varphi )$

Eingesetzt in Die DGL ergibt sich:

$-{\hat {s}}\omega ^{2}\cdot \sin(\omega t-\varphi )+{\frac {D}{m}}\cdot {\hat {s}}\cdot \sin(\omega t-\varphi )=\left(-\omega ^{2}+{\frac {D}{m}}\right)\cdot {\hat {s}}\cdot \sin(\omega t-\varphi )=0$

Diese Gleichung ist für alle Zeiten $t$ nur erfüllt, wenn die Klammer verschwindet, d.h.:

$\left(-\omega ^{2}+{\frac {D}{m}}\right)=0\quad \Rightarrow \quad \omega ^{2}={\frac {D}{m}}$

Schwingendes Federpendel.

Damit ist die allgemeine Lösung der Differentialgleichung des harmonischen Oszillators:

$s(t)={\hat {s}}\cdot \sin \left({\sqrt {\frac {D}{m}}}\cdot t-\varphi \right)$

Die Amplitude ${\hat {s}}$ und die Phase $\varphi$ sind Integrationskonstanten, die durch die Anfangsbedingungen definiert werden.

Für die Schwingungsdauer $T$ des das Federpendels gilt: $T=2\pi {\sqrt {\frac {m}{D}}}$

Merke:

Ein Oszillator ist genau dann harmonisch, wenn die Rückstellkraft $F_{R}$ proportional zur Auslenkung $s$ ist: $F_{R}\propto s,\qquad F_{R}=-D\cdot s.$ Die Schwingungsdauer $T$ des harmonischen Oszillators ist unabhängig von seiner Schwingungsamplitude ${\hat {s}}$.

Weitere Oszillatoren

Um Oszillatoren beschreiben zu können, benötigen wir immer die Rückstellkraft in Abhängigkeit der Auslenkung.

Fadenpendel

Rückstellkraft am Fadenpendel: ${\vec {F}}_{\mathrm {R} }={\vec {F}}_{\mathrm {tan} }$

Fadenpendel und Rückstellkraft.

Bestimmung der Rückstellkraft

Für das Fadenpendel können wir die Rückstellkraf durch Kräftezerlegung herleiten. Aus der Zerlegung (siehe Bild) findet man:

$F_{\mathrm {R} }=-|{\vec {F}}_{\mathrm {tan} }|=-F_{g}\cdot \sin(\alpha )$.

Wenn wir den Winkel $\alpha$ im Bogenmaß verwenden, gilt die Beziehung $\alpha ={\frac {x}{l}}$. Dabei ist $x$ die Bogenlänge, d.h. die Auslenkung entlang der Kreisbahn. Eingesetzt und mit $F_{g}=mg$ ergibt sich:

$F_{\mathrm {R} }(x)=-mg\cdot \sin \left({\frac {x}{l}}\right)$.

Offensichtlich ist die Rückstellkraft $F_{\mathrm {R} }$ nicht proportional zur Auslenkung. Im allgemeinen Fall ist das Fadenpendel also kein harmonischer Oszillator.

Näherung für kleine Auslenkungen $\alpha ={\frac {x}{l}}$

Für hinreichend kleine Auslenkungen gilt:
$\sin(x)\approx x,\quad \tan(x)\approx x$.

Trigonometrie an einem sehr spitzen, rechtwinkligen Dreieck:
$\sin(\Theta )={\frac {O}{H}}\approx {\frac {s}{A}}=\Theta$.

Für kleine Winkel $\alpha$ gilt im Bogenmaß:

$\sin(\alpha )\approx \alpha \quad \Rightarrow \quad \sin \left({\frac {x}{l}}\right)\approx {\frac {x}{l}}$.

Eingesetzt in die Formel für die Rückstellkraft ergibt sich:

$F_{\mathrm {R} }(x)=-mg\cdot \sin \left({\frac {x}{l}}\right)\approx -mg\cdot {\frac {x}{l}}=-{\frac {mg}{l}}\cdot x$.

Für hinreichend kleine Auslenkungen ist $F_{\mathrm {R} }$ also proportional zur Auslenkung, das Pendel führt in diesem Fall eine harmonische Schwingung aus.

Differentialgleichung der Schwingung für kleine Auslenkungen und Lösung

Als Bewegungsgleichung erhält man:

$F=m\cdot a=F_{\mathrm {R} }=-{\frac {mg}{l}}\cdot x$.

Setzen wir für die Beschleunigung $a(t)$ den Zusammenhang $a(t)={\ddot {x}}(t)$ ein und kürzen $m$ weg, so erhalten wir:

${\ddot {x}}(t)=-{\frac {g}{l}}x(t)$

und es ergibt sich die

Differentialgleichung (DGL) des Fadenpendels für kleine Auslenkungen: ${\ddot {x}}(t)+{\frac {g}{l}}\cdot x(t)=0$

Vergleich mit der Differentialgleichung des harmonischen Oszillators zeigt, dass wir die selben Lösungen erhalten, wenn wir statt $\omega ^{2}={\frac {D}{m}}$ einfach $\omega ^{2}={\frac {g}{l}}$ setzen, also:

Allgemeine Lösung der Differentialgleichung des Fadenpendels für kleine Auslenkungen: $x(t)={\hat {x}}\cdot \sin \left({\sqrt {\frac {g}{l}}}\cdot t-\phi \right)$

Die Amplitude ${\hat {x}}$ und die Phase $\phi$ sind wieder Integrationskonstanten, die durch die Anfangsbedingungen definiert werden.

Für die Schwingungsdauer $T$ des Fadenpendels gilt: $T=2\pi {\sqrt {\frac {l}{g}}}$

Es fällt auf, dass die Schwingungsdauer $T$ nicht von der Masse $m$, sondern allein von der Erdbeschleunigung $g$ und der Pendellänge $l$ abhängt.

---

Aufgabe: Verkürzen eines Fadenpendels.

---

Schwingende Wassersäule

Ausgelenkte Wassersäule. → Animation

Wir starten wieder mit der Bestimmung der Rückstellkraft.

Bestimmung der Rückstellkraft

Wird die Wassersäule ausgelenkt, so führt das Ungleichgewicht der Wassersäulen zu einer Rückstellkraft. Wird die Wassersäule um $s$ ausgelenkt drückt die Masse eines Zylinders der Höhe $2s$ gegen die Auslenkung (siehe Bild). Die Rückstellkraft ist damit:

$F_{R}=-g\cdot \varrho \cdot A\cdot 2s$,

wobei $\varrho$ die Dichte der Flüssigkeit und $A$ den Rohrquerschnitt angibt. Die Rückstellkraft ist proportional zur Auslenkung und damit handelt es sich beim Wassersäulenpendel für Auslenkungen im geraden Rohrbereich um einen harmonischen Oszillator.

Differentialgleichung der Schwingung und Lösung

Setzen wir die Rückstellkraft $F_{R}$ in die Newtonsche Bewegungsgleichung $F=m\cdot a$ ein, ergibt sich:

$m\cdot a=-g\cdot \varrho \cdot A\cdot 2s$.

Die Masse $m$ ist die insgesamt beschleunigte Masse, also die Masse der gesamten Wassersäule. Mit der Länge $L$ der Wassersäule erhält man:

$m=\varrho \cdot L\cdot A$.

Eingesetzt in die Bewegungsgleichung und mit $a={\ddot {s}}(t)$ ergibt sich:

$\varrho \cdot L\cdot A\cdot {\ddot {s}}=-g\cdot \varrho \cdot A\cdot 2s\quad \Rightarrow$

Differentialgleichung einer schwingenden Wassersäule der Länge $L$: ${\ddot {s}}(t)+{\frac {2g}{L}}\cdot s(t)=0$

Die Lösungen sind wieder harmonische Schwingungen, hier mit der Kreisfrequenz:

$\omega ^{2}={\frac {2g}{L}}\quad \Rightarrow \quad \omega ={\sqrt {\frac {2g}{L}}},\qquad T=2\pi {\sqrt {\frac {L}{2g}}}$.

---

Aufgabe: Ein Wassersäulenpendel wird weit ausgelenkt.

---

Die Energie harmonischer Oszillatoren

Potentielle Energie des Federpendels

Wir bestimmen die potentielle Energie $W_{\text{pot}}$ des Federpendels in Abhängigkeit der Zeit.

Lösungsweg 1: Es gilt mit der Spannenergie $W_{\text{Sp}}$ und er Lageenergie $W_{\text{L}}$ im Gravitationsfeld:

$W_{\text{pot}}=W_{\text{Sp}}+W_{\text{L}}$.

Die Spannenergie $W_{\text{Sp}}$ ist gegeben durch:

$W_{\text{Sp}}={\frac {1}{2}}D\cdot \left(s_{0}-s(t)\right)^{2}\,;$

die Lageenergie $W_{\text{L}}$ durch:

$W_{\text{L}}=mg\cdot \left(x+s(t)\right)\,,$

wobei $x$ ein beliebig festzulegendes Nullniveau definiert. Wir wählen $x$ so, dass in der Ruhelage $W_{\text{pot}}=0$ gilt:

$W_{\text{pot}}=0=W_{\text{Sp}}+W_{\text{L}}={\frac {1}{2}}D\cdot \left(s_{0}-0\right)^{2}+mg\cdot \left(x+0\right)={\frac {1}{2}}D\cdot s_{0}^{2}+mg\cdot x$

$\Rightarrow \quad x=-{\frac {D}{2mg}}\cdot s_{0}^{2}$.

Für die potentielle Energie $W_{\text{pot}}$ des Federpendels in Abhängigkeit der Zeit erhalten wir damit:

$W_{\text{pot}}=W_{\text{Sp}}+W_{\text{L}}={\frac {1}{2}}D\cdot \left(s_{0}-s(t)\right)^{2}+mg\cdot \left(-{\frac {D}{2mg}}\cdot s_{0}^{2}+s(t)\right)$

$W_{\text{pot}}={\frac {1}{2}}D\cdot \left(s_{0}^{2}-2s_{0}s(t)+s(t)^{2}\right)-{\frac {D}{2}}\cdot s_{0}^{2}+mg\cdot s(t)$

$W_{\text{pot}}={\frac {1}{2}}D\cdot \left(-2s_{0}s(t)+s(t)^{2}\right)+mg\cdot s(t)$

$W_{\text{pot}}={\frac {1}{2}}Ds(t)^{2}+(-Ds_{0}+mg)\cdot s(t)$

Da $Ds_{0}=mg$ gilt, erhalten wir:

Potentielle Energie des Federpendels: $W_{\text{pot}}={\frac {1}{2}}Ds^{2}$

Lösungsweg 2: Wir integrieren die Rückstellkraft $F_{R}$ aus der Ruhelage bis zur Position $s$:

$W_{\text{pot}}=-\int _{0}^{s}F_{R}(s)\,{\rm {d}}s=\int _{0}^{s}D\cdot s\,{\rm {d}}s={\frac {1}{2}}Ds^{2}$

Kinetische Energie des Federpendels

Einheitskreis und Satz des Pythagoras verdeutlichen:
$\sin ^{2}(\alpha )+\cos ^{2}(\alpha )=1$

Die kinetische Energie des Federpendels ist gegeben durch:

$E_{\text{kin}}={\frac {1}{2}}mv^{2}={\frac {1}{2}}m{\dot {s}}^{2}$

Aufgabe: Zeige, dass die Summe aus potentieller und kinetischer Energie zeitlich konstant ist. Verwende die Beziehung: $\sin ^{2}(\alpha )+\cos ^{2}(\alpha )=1$.

Der Oszillator wandelt periodisch potentielle Energie $W_{\text{pot}}={\frac {1}{2}}Ds^{2}$ in kinetische Energie $E_{\text{kin}}={\frac {1}{2}}mv^{2}$ und umgekehrt um. Die Summe der Energien ist stets konstant.

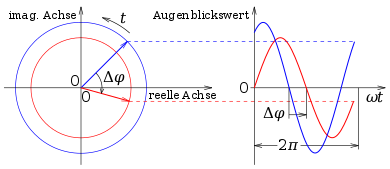
Phasendifferenz zwischen zwei Oszillatoren

Rechts: Zwei Schwingungen, die sich im Phasenwinkel um Δφ unterscheiden. Die blaue Schwingung eilt der roten um 60° voraus. Links: Zwei rotierende Zeiger mit demselben Unterschied im Phasenwinkel.

Zueinander phasenverschoben schwingende Oszillatoren.

Gegeben sind zwei Oszillatoren gleicher Frequenz. Die Schwingungen werden beschrieben durch:
Oszillator 1:

$s_{1}(t)={\hat {s_{1}}}\sin(\omega t)$

Oszillator 2:

$s_{2}(t)={\hat {s_{2}}}\sin(\omega t-\varphi )$

Man bezeichnet $\varphi$ als Phasendifferenz zwischen den Oszillatoren.

Spezialfälle:

• $\varphi =0$  → Die Oszillatoren schwingen „gleichphasig“/„in Phase“.
• $\varphi =\pi$ → Die Oszillatoren schwingen „gegenphasig“.
• $\varphi ={\frac {\pi }{2}}$ → Oszillator 2 hinkt Oszillator 1 um ${\frac {\pi }{2}}$ hinterher oder Oszillator 1 eilt Oszillator 2 um ${\frac {\pi }{2}}$ voraus.

Erzwungene Schwingung und Resonanz

Amplitudengang des harmonischen Oszillators für verschieden starke Dämpfung D aufgetragen gegen das Frequenzverhältnis $\omega /\omega _{0}$.

Identische Pendel bei verschiedenen Anregungsfrequenzen. Experiment: Ein Oszillator der Eigen(kreis)frequenz $\omega _{0}$ wird periodisch mit der Kreisfrequenz $\omega$ angeregt. Beobachtung: Nach einer Einschwingphase macht der Oszillator eine erzwungene Schwingung mit der Anregungsfrequenz $\omega$ des Erregers. Für $\omega \ll \omega _{0}$ sind Erreger und Oszillator in Phase, für $\omega \gg \omega _{0}$ sind Erreger und Oszillator gegenphasig. Im Resonanzfall $\omega =\omega _{0}$ beträgt die Phasendifferenz ${\frac {\pi }{2}}$, die Anregung eilt dem Oszillator um eine Viertelperiode voraus. Die Schwingungsamplitude hängt von der Erregerfrequenz $\omega$ ab. Im Resonanzfall $\omega =\omega _{0}$ treten sehr große Amplituden auf.