Intermediate value theorem – Serlo
The intermediate value theorem says that every continuous function attains every value between and at least once. Continuous functions reach every intermediate value between and (if there are no holes in the domain between and ). So the intermediate value theorem can be used to determine the existence of functional values.
Motivation
[Bearbeiten]Let be an arbitrary continuous function. At the point , it has the functional value and at the point it has the functional value . Let us assume that . Furthermore, let be an arbitrary value between and , meaning :

By our current perception, continuous functions don't have any jumps in their domain. Since is defined on the entire interval and its domain is connected, the graph binds the points and without jumps. If we bind and without "taking our pencil off the paper," at some point we must cross the line . So there is at least one point of intersection between the line and the graph of :

For the -values of the points of intersection it holds . The intermediate value is therefore attained once by the function . We have intuitively seen that continuous functions attain all values between any two functional values at least once, provided the domain doesn't contain any gaps between the two arguments.
The Intermediate Value Theorem
[Bearbeiten]Theorem (Intermediate Value Theorem)
Let be a continuous function with and . Let be some value between the two functional values and . This means it holds or . Then there exists at least one real number with . The intermediate value is attained at least once by the function .
Bolzano's Root Theorem
[Bearbeiten]For the proof of the intermediate value theorem, it suffices to prove this for the special case . This special case is also called "Bolzano's Root Theorem."
Theorem (Bolzano's Root Theorem)
Let be a continuous function with and . Furthermore let zero be an intermediate value of and , meaning or . Then has at least one root. This means, there exists at least one argument such that .
Why is it sufficient to only consider this special case? Let's take a function and a value between the functional values and . By the intermediate value theorem, we have to find a with . Now it holds:
Therefore if and only if . Now we will define the helping function with . As we've already determined, the equation is satisfied precisely in the case . So if we find a root of , then the function also attains the value .
Now the function fulfills all of the requirements to use Bolzano's Root Theorem. It's a function of the form with the closed interval as its domain. As a concatenation of continuous functions, the function is continuous. In the case it holds:
Using we can deduce the chain of inequalities . Now if we consider the case :
Altogether we can concude that zero is an intermediate value of and . Therefore satisfies the requirements for Bolzano's Root Theorem. By this root theorem there exists a with . For this it holds . This shows that the general intermediate value theorem can be easily deduced from Bolzano's root theorem. So now we must only prove Bolzano's theorem.
Proof of Bolzano's Root Theorem
[Bearbeiten]Proof (Bolzano's Root Theorem)
Let be a continuous function with or . In the following we will consider the case . The other case can be proved similarly. We have to find a root of . This can be shown by finding a fitting sequence of nested intervals (this means that any interval in the sequence is a subset of the preceding interval in the sequence). As a starting interval we choose , so and . Namely, we know that the desired root must lie in the interval .
For or we already have found a root at or , respectively. In this case, we are already finished. In the case and , we reduced the size of our interval. For this purpose we consider the midpoint of the starting interval. If the value of at this point is equal to zero, then we've found a root and we are finished.
If , then we choose another interval which must contain a root. Let us assume that . Then we get the following image:

We can see that the graph must cross the -axis from to . Since is a continuous function and can't have any jumps, and since this interval doesn't contain any gaps, there must be a root of in this interval. Since both functional values and are positive, we can't say whether this root lies in to . For this reason we choose a second interval .
If is less than zero, the graph of has to undergo a change in sign in the second interval from to . Correspondingly, a zero should lie in this interval and in this case we choose as the second interval :
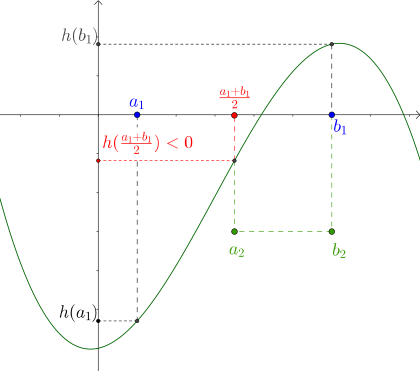
Altogether we determine in the following way:
We keep repeating this process: in the -th step we calculate the midpoint of the interval . If attains the value here, we are finished and can return as a root. Otherwise we choose a new interval using the following definition:
By this procedure we obtain either the desired root after a certain iteration or we get a sequence of intervals . By this method of choosing the sequence elements, the sequence is monotone increasing and the sequence is monotone falling. Since every sequential element lies in the interval , the sequences are both bounded. Then we can use Monotoniekriterium für Folgen to conclude that both sequences converge. Note that the length of each interval is cut in half at each iteration, meaning:
From here it follows . For this reason, the sequences of lower and upper interval limits converge to the same value . Furthermore, by our construction, it holds that and for all . For this reason it holds for the limits: and . Because is continuous, it holds
From the above line we can conclude and , and therefore must hold. In this case we've also found a root of the function .
Corollaries of the Intermediate Value Theorem
[Bearbeiten]Continuous functions map intervals to intervals
[Bearbeiten]With the help of the intermediate value theorem we can prove that continuous functions map intervals to intervals.
Theorem (Corollary of the Intermediate Value Theorem)
Let be an interval and a continuous function. Then is also an interval.
Proof (Corollary of the Intermediate Value Theorem)
We set and . We also allow (if is bounded from below) and (if is bounded from above). We now take some real number with . From the definition of the infimum and the fact that we get that there exists some with . Similarly there exists some with . Altogether we have .
So is an intermediate value of two functional values of . Since is continuous, the intermediate value theorem guarantees us the existence of some with . Since was arbitrary, it holds . Now or could be elements of . Therefore must be one of the following four intervals:
We see that is an interval.
Range of Power Functions
[Bearbeiten]Example (Range of power functions )
The power functions with for are continuous. Furthermore it holds
Damit ist . Außerdem ist
For odd it holds . For even it holds , since for all it holds and zero is attained as a value because . The by the intermediate value theorem we have
Range of the Exponential Function
[Bearbeiten]Example (Range of the exponential function)
The exponential function is continuous. Also it holds for all . It holds and . Then and . Since neither nor are attained by the exponential function, the intermediate value theorem says
Exercise (Domain of the Generalized Exponential Function)
For ,
defines the generalized exponential function. Show: .
Tip: Differentiate between the cases and .
Solution (Domain of the Generalized Exponential Function)
Since and are continuous on , it holds that is also continuous (as the concatenation of continuous functions) on all of . Further, , since .
Fall 1:
Here it holds , and therefore holds. From here it follows . On the other hand, , and therefore . Altogether this case yields .
Fall 2:
Here it holds , and therefore . We then can conclude . On the other hand it holds , and therefore . So it also holds in this case .
Exercise: Fixed-point theorem
[Bearbeiten]Proof of a Fixed-point Theorem
[Bearbeiten]In the following exercise we will prove a fixed-point theorem. Fixed points are arguments of a function that satisfy the equation . In a sentence: fixed points are those points not changed by a function transformation. Fixed point theorems are therefore theorems, that prove the existence of fixed points in certain situations. For mathematics, such theorems are important because sometimes we can reduce the problem of proving the existence of a certain object to proving the existence of a fixed point. For example, the argument is a root of the function , if and only if the function with the ordering has a fixed point. Using the existence of a fixed point of the function , we can prove the existence of a root for . In the following exercise we are going to prove a kind of intermediate value theorem:
Exercise (Fixed point theorem)
Let be a continuous function. Show that has at least one fixed point. Fixed points are points with .
How to get to the proof? (Fixed point theorem)
By rearranging the equation we obtain . Therefore is a fixed point of if and only if is a root of the function . So let us define a helping function with . As you might have guessed, we can use Bolzano's Root Theorem here to prove the existence of a root. For that we have to prove that satisfies all the assumptions of the theorem:
- is continuous
- Zero is an intermediate value of and .
is continuous as the concatenation of continuous functions and we can also prove that holds. The root theorem guarantees us the existence of the limit.
Proof (Fixed point theorem)
Let be a continuous function. We define the helping function . For this function it holds:
- is continuous on as the difference of the continuous functions and .
- It holds because:
- .
Therefore fulfills the assumptions of the root theorem. Then there exists some with . This means . In other words, has a fixed point.
Assumptions of the Fixed Point Theorem
[Bearbeiten]In the fixed point theorem above, the continuity is a necessary condition of the proven theorem. If we leave this condition out, we can find a function for which this theorem is no longer true. This will be shown in the following exercise:
Exercise (Fixed Point Theorem)
Find a function with for all .
Proof (Fixed Point Theorem)
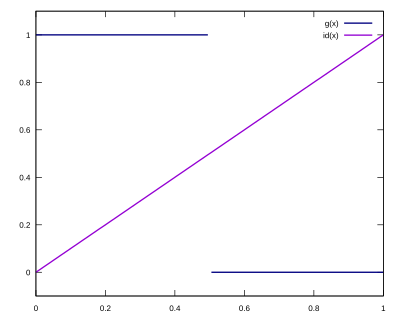
For example, the function
doesn't have a fixed point. This is shown in the following graph of the function . Namely, there is not point of intersection of the graph of with the graph of the identity function :
Exercise: Roots and Range of Polynomials
[Bearbeiten]Roots of Polynomials
[Bearbeiten]The following exercise exemplifies a special case of the fundamental theorem of algebra. This theorem says that a non-constant polynomial
with complex coefficients has at least one complex root. In the real case this claim does not hold in general. A polynomial with real coefficients need not necessarily have real roots. A polyomial function without real roots could be, for example, . For certain polynomials, we can still prove the existence of a root:
Exercise (Roots of Polynomials)
Let
be a polynomial function with and . If , meaning if the degree of is odd, then has at least one (real) root.
Summary of proof (Roots of Polynomials)
We will prove the exercise with the help of the root theorem. For that, we need to find two real numbers with or . This is a consequence of and , which we can show by using a clever rewriting of for the case . We will now thoroughly investigate the case . The case can be handles similarly.
Solution (Roots of Polynomials)
We will demonstrate the proof for . The case is similar. For we can factor out to obtain:
The expression in the parentheses converges for to . This holds since the terms converge for to . Since is odd, it holds:
und
However, there must exist with . Further, for , the polynomial is continuous as the composition of continuous functions . Using Bolzano's root theorem, we can conclude the existence of some with . Then the polynomial function as at least one root.
Range of Polynomials
[Bearbeiten]Exercise (Range of Polynomials)
Let
be a polynomial function with and , and odd. Show .
Solution (Range of Polynomials)
Fall 1:
For it holds:
and
Since is continuous, it follows .
Fall 2:
Similar to the first case.
Exercise: The existence of n-th order Roots
[Bearbeiten]The intermediate value theorem also offers a possibility to check the existence of -th order roots. In the chapter "Wurzel reeller Zahlen“ we have already proven this using the concept of nested intervals. Now we will see an alternative proof that uses the intermediate value theorem. Just a reminder: the -th order root for some positive number is a real number with .
Exercise (Existence of n-th order Root)
Let . Show that for all there exists a positive number with .
Solution (Existence of n-th order Root)
It is the case that if and only if . The desired number must therefore be e a positive zero of the polynomial with . First we observe that , be a polynomial, is continuous on all. . Therefore is also continuous on the interval . Furthermore it holds
as well as
Therefore . By the intermediate value theorem, has at least one zero in the interval . Because all numbers in are positive, the zero must also be positive. Furthermore, the zero satisfies the equality .
Exercise: Solving an Equation
[Bearbeiten]Both the intermediate value and root theorems can be used to justify the existence of a solution of a given equation. The equation is used to build a continuous function, on which we can apply either the root theorem or the intermediate value theorem.
Exercise (Solution to an Equation)
Show there exists only one with .
Solution (Solution to an Equation)

Proof step: Show the equation has a solution
We will use the helping function
It is continuous since it is the difference of the two continuous functions and . Furthermore it holds
as well as
By the root theorem, there exists some with . For this it then holds . This solves our equation.
Proof step: Show there exists exactly one solution
We will examine four cases:
Fall 1:
We have . Therefore there exists no with .
Fall 2:
We have . So there can be no satisfying .
Fall 3:
We've already proven above that there exists some with . Since is strictly monotone increasing and is strictly monotone falling on , there can not exist some further such that .
Fall 4:
We have . So there can not exist any such that .
From both steps in the proof we can conclude that there exists exactly one with .


![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)








![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)









![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)


![{\displaystyle h:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1833b6178fc06e33367b794d4c27d8f9e1a9f36e)





![{\displaystyle {\tilde {x}}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7a70e57f199d3304bbe0964d741eeafd3ee2e32)





![{\displaystyle [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/641f4ab7608607e1e61bd1958d0b9da424be1752)
![{\displaystyle {\begin{aligned}f(a)\leq s\iff f(a)-s\leq 0\iff h(a)\leq 0\\[0.3em]f(b)\geq s\iff f(b)-s\geq 0\iff h(b)\geq 0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbaa2c8f353583041cc79a845c2fce48304cd40f)

![{\displaystyle {\begin{aligned}f(a)\geq s\iff f(a)-s\geq 0\iff h(a)\geq 0\\[0.3em]f(b)\leq s\iff f(b)-s\leq 0\iff h(b)\leq 0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/633ae0786835624a0891771c2885ee58ad0c68ab)
![{\displaystyle [a_{1},b_{1}]=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad3ba71c5021f6b79dc6acd9fdb655f20a633ba5)















![{\displaystyle [a_{2},b_{2}]=\left[a_{1},{\tfrac {a_{1}+b_{1}}{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e514878526ae4dc87f68106e20b7d8cdc453a2e)
![{\displaystyle \left[{\tfrac {a_{1}+b_{1}}{2}},b_{1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8c24ad014b725551415179361689d06261c22ea)
![{\displaystyle [a_{2},b_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2cae95a31bf77847185496288d80966494407a6)
![{\displaystyle [a_{2},b_{2}]={\begin{cases}\left[a_{1},{\frac {a_{1}+b_{1}}{2}}\right]&;h\left({\frac {a_{1}+b_{1}}{2}}\right)>0\\\left[{\frac {a_{1}+b_{1}}{2}},b_{1}\right]&;h\left({\frac {a_{1}+b_{1}}{2}}\right)<0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34e9af43757190a432b206673de3a2ca51e89629)


![{\displaystyle [a_{n},b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e30ce1f218c7164247ad32fbbcde76c02c817bd1)

![{\displaystyle [a_{n+1},b_{n+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4218a0524695e40f6c164b3aa6f0ceeda8e0f4c2)
![{\displaystyle [a_{n+1},b_{n+1}]={\begin{cases}\left[a_{n},{\frac {a_{n}+b_{n}}{2}}\right]&;h\left({\frac {a_{n}+b_{n}}{2}}\right)>0\\\left[{\frac {a_{n}+b_{n}}{2}},b_{n}\right]&;h\left({\frac {a_{n}+b_{n}}{2}}\right)<0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a492f4ed071893d6d0f36cd21d63c6ae16546956)

![{\displaystyle ([a_{n},b_{n}])_{n\in \mathbb {N} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46a01f7a0639bafdbc58ce4b0f3f4975a6e60949)


![{\displaystyle {\begin{aligned}\lim _{n\rightarrow \infty }{(b_{n}-a_{n})}&=\lim _{n\rightarrow \infty }{{\frac {1}{2}}\cdot (b_{n-1}-a_{n-1})}\\[0.3em]&=\lim _{n\rightarrow \infty }{{\frac {1}{2}}\cdot {\frac {1}{2}}\cdot (b_{n-2}-a_{n-2})}\\[0.3em]&\vdots \\[0.3em]&=\lim _{n\rightarrow \infty }{{\frac {1}{2^{n}}}\cdot (b_{1}-a_{1})}=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b956430d61cacbc7c3997e375c83ae25f0af297)

![{\displaystyle c\in [a;b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02b8df5ba00bbc02820be401c0dbc93d73392da8)






























![{\displaystyle {\begin{aligned}f(I)={\begin{cases}[A,B]&A{\text{ and }}B{\text{ are attained by }}f\\[0.5em][A,B)&A{\text{ is attained by }}f{\text{ , but not }}B\\[0.5em](A,B]&B{\text{ is attained by }}f{\text{ , but not }}A\\[0.5em](A,B)&A{\text{ and }}B{\text{ are not attained by }}f\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81d2e9d8797bc18a43af3df10dba9d4a3cde13b1)















































![{\displaystyle f:[a,b]\to [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f359e29e1446d9bfea5759414f0f320db9f7796e)



![{\displaystyle h:[a,b]\to \mathbb {R} :x\mapsto h(x)=f(x)-x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/809932a2003de787ae164661a63528f3664cd8c2)
![{\displaystyle {\text{id}}:[a,b]\to [a,b]:x\mapsto x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71edd132aab83df0a40f98d7285f56893c940915)
![{\displaystyle h(a)=\underbrace {f(a)} _{\in [a,b]}-a\geq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c338aad1556500ef398c4e96618bf4b66628845)
![{\displaystyle h(b)=\underbrace {f(b)} _{\in [a,b]}-b\leq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/923d3af35c516619ab49d871857439aa64169a8b)


![{\displaystyle g:[a,b]\to [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d99b57dcedc3a03efd7b9652a9eec76fefc853f)
![{\displaystyle g:[0,1]\to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0329691aecddec5158ad537f5df2e83578a302e2)

![{\displaystyle x\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64a15936df283add394ab909aa7a5e24e7fb6bb2)
![{\displaystyle g:[0,1]\to [0,1]:x\mapsto g(x)={\begin{cases}1&{\text{ für }}0\leq x\leq {\tfrac {1}{2}},\\0&{\text{ für }}{\tfrac {1}{2}}<x\leq 1\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0188a3c26bc42b9c0739a7bbd7ef3907b32ff96b)
![{\displaystyle {\text{id}}:[0,1]\to [0,1],\ x\mapsto x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5011821f7da6ec444e105635caac19e7c80534d1)



























![{\displaystyle {\sqrt[{n}]{\alpha }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/531fb33f9c467602294387d194015ce0e0e23e6d)






![{\displaystyle [0,\alpha +1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86505e10814a30d1a0fd85d6dd90b97771172234)

![{\displaystyle {\begin{aligned}p(1+\alpha )&=(1+\alpha )^{n}-\alpha \\[0.3em]&\quad {\color {Gray}\left\downarrow \ {\text{Bernoulli Inequality}}\right.}\\[0.3em]&\geq 1+n\alpha -\alpha \\&=1+\underbrace {(n-1)} _{\geq 0}\alpha \\&\geq 1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf3e8aea552f414aec50689e08ec349130b85f33)




















