Lim sup and lim inf – Serlo

By limes superior and limes inferior, mathematicians denote the largest and the smallest accumulation point of a sequence. They are useful, if there are multiple limits and intuitively say what the "greatest limit" (limes superior) and the "smallest limit" (limes inferior) of that sequence are.

Motivation

We already learned about limits of a sequence. A limit is that unique number, to which a sequence tends. In every neighbourhood of the sequence, there are almost all elements, meaning only a finite number is allowed to be on the outside:

There are only finitely many elements outside the neighbourhood.

Sometimes, it seems like a sequence tends towards multiple numbers (like "multiple limits"). We also discussed that case: these numbers are then called "accumulation points" instead of "limits", since a limit must always be unique.

The set of accumulation points may be bounded or unbounded. In case it is bounded, there is a best upper and a best lower limit for the accumulation points, which we will call limes superior and limes inferior. Both are real numbers. Mathematically, for a sequence $(a_{n})_{n\in \mathbb {N} }$ we will denote the limes superior as $\limsup _{n\to \infty }a_{n}$ and the limes inferior as $\liminf _{n\to \infty }a_{n}$.

The closed interval $\left[\liminf _{n\to \infty }a_{n},\limsup _{n\to \infty }a_{n}\right]$ then includes all accumulation points. We can even show that in any neighbourhood of this interval (i.e. a slightly bigger interval), there are almost all elements inside this neighbourhood. The following figure illustrates this situation for some $\epsilon$-neighbourhood $\left[\liminf _{n\to \infty }a_{n}-\epsilon ,\limsup _{n\to \infty }a_{n}+\epsilon \right]$ around the original interval:

Any interval that is slightly bigger than the grey one (both above and below) contains almost all sequence elements

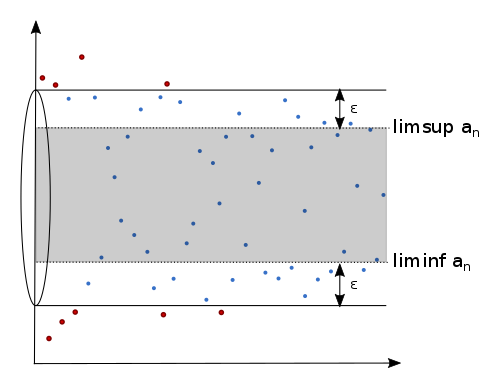
Definition

Now, let us turn to a mathematical description of "greatest and smallest accumulation point". We can directly define:

Definition (limes superior)

For a sequence $(a_{n})_{n\in \mathbb {N} }$ bounded from above, the limes superior denotes the greatest accumulation point and is denoted by $\limsup a_{n}$ . If the sequence is unbounded from above or there are no accumulation points, we write $\limsup _{n\to \infty }a_{n}=\infty$.

Definition (limes inferior)

For a sequence $(a_{n})_{n\in \mathbb {N} }$ bounded from below, the limes inferior denotes the smallest accumulation point and is denoted by $\liminf a_{n}$ . If the sequence is unbounded from below or there are no accumulation points, we write $\liminf _{n\to \infty }a_{n}=-\infty$.

But: Does this definition even make sense? The accumulation points form a set. Those sets need not to have a maximum (greatest value) or minimum (smallest value), but might instead just have a supremum or infimum. Mathematicians wondered, when this is the case and soon found a surprising answer: The "awkward case" that there is no greatest/smallest limit does never occur! This statement ca actually be proven

Theorem (greatest and smallest accumulation point exist)

If the accumulation points of a sequence $(a_{n})_{n\in \mathbb {N} }$ are bounded from above, then it has a greatest accumulation point. If the accumulation points of a sequence $(a_{n})_{n\in \mathbb {N} }$ are bounded from below, then it has a smallest accumulation point.

Proof (greatest and smallest accumulation point exist)

Suppose first that the accumulation points of $(a_{n})_{n\in \mathbb {N} }$ are bounded from above. Then, there must be a supremum $S$ (smallest upper bound) for the accumulation points. If $S$ is an accumulation point, it is also the greatest one and we get no contradiction to the above statement.

So let us assume that $S$ is not an accumulation itself. In that case, each interval $(S-\epsilon ,S]$ for $\epsilon$ must contain an accumulation point $S_{\epsilon }$. Otherwise, $S-\epsilon$ would be an upper bound for the accumulation points which is smaller than $S$ (which cannot be). But since each $S_{\epsilon }$ subsequence element $a_{n_{\epsilon }}$ with $|a_{n_{\epsilon }}-S_{\epsilon }|<\epsilon$. By the triangle inequality, $|a_{n_{\epsilon }}-S|\leq |a_{n_{\epsilon }}-S_{\epsilon }|+|S_{\epsilon }-S|<2\epsilon$. This holds true for any $2\epsilon >0$, so $S$ is an accumulation point of $(a_{n})_{n\in \mathbb {N} }$ itself and we get a contradiction to $S$ not being an accumulation point.

This theorem establishes that the two definitions above actually make sense, so limes superior and limes inferior are well-defined.

Examples

Example

Consider the sequence $(a_{n})_{n\in \mathbb {N} }=(-1)^{n}\;n$ . we can decompose it into the products $(b_{n})_{n\in \mathbb {N} }=(-1)^{n}$ and $(c_{n})_{n\in \mathbb {N} }=n$.

The sequence $b_{n}$ diverges, but has two accumulation points $\lim \limits _{k\to \infty }b_{2k-1}=-1$ and $\lim \limits _{k\to \infty }b_{2k}=1$.

The sequence $c_{n}$ is improperly convergent (which is a special kind of divergence): it goes to infinity $\lim \limits _{n\to \infty }c_{n}=\infty$.

We multiply the limits/accumulation points of $b_{n}=(-1)^{n}$ and $c_{n}=n$. Since there is $\lim \limits _{k\to \infty }b_{2k-1}=-1$ , we obtain a subsequence of $(a_{n})_{n\in \mathbb {N} }$, unbounded from below: $\lim _{k\to \infty }a_{2k-1}=\lim _{k\to \infty }-2k+1=-\infty$. And since $\lim \limits _{k\to \infty }b_{2k}=1$ there is also a subsequence unbounded from above: $\lim _{k\to \infty }a_{2k}=\lim _{k\to \infty }2k=\infty$.

So $(a_{n})_{n\in \mathbb {N} }$ dies not converge improperly to $\infty$ or $-\infty$, but we can say that $\limsup _{n\to \infty }a_{n}=\infty$ and $\liminf _{n\to \infty }a_{n}=-\infty$.

Example

In case $(a_{n})_{n\in \mathbb {N} }={\tfrac {(-1)^{n}}{n}}$, there is $\lim _{n\to \infty }a_{n}=0$. Since $(a_{n})$ converges, it has the unique accumulation point $0$. This must be the greatest and smallest accumulation point at the same time and we have

$\limsup _{n\to \infty }a_{n}=\liminf _{n\to \infty }a_{n}=0$

Example

For $(a_{n})_{n\in \mathbb {N} }=n$, there is $\lim _{n\to \infty }a_{n}=\infty$. So $(a_{n})$ is unbounded from above and $\limsup _{n\to \infty }a_{n}=\infty$. Further, $(a_{n})$ is bounded from below by $1$. But is has no accumulation points, as $\forall S\in \mathbb {R}$ there is $a_{n}\geq S$ . So we also have $\liminf _{n\to \infty }a_{n}=\infty$.

limsup, liminf and limit

If limes superior and limes inferior of a sequence $(a_{n})_{n\in \mathbb {N} }$ exist and coincide, then the greatest and smallest accumulation point are identical, so there can only be one accumulation point. And the sequence cannot be unbounded, so it should converge to this one accumulation point. But does it actually do that? And does the converse hold true? I.e., if the sequence $(a_{n})_{n\in \mathbb {N} }$ converges, are limes superior and inferior identical? The answer turns out to be yes:

Theorem (limes superior/inferior and convergence)

A sequence $(a_{n})_{n\in \mathbb {N} }$ converges if and only if

$-\infty <\limsup _{n\to \infty }a_{n}=\liminf _{n\to \infty }a_{n}<\infty$

How to get to the proof? (limes superior/inferior and convergence)

We need to prove equivalence

$\lim _{n\to \infty }a_{n}=a\in \mathbb {R} \iff -\infty <\limsup _{n\to \infty }a_{n}=a=\liminf _{n\to \infty }a_{n}<\infty$

which are two directions:

"$\Rightarrow$" is easy: if a sequence $(a_{n})_{n\in \mathbb {N} }$ converges, then there is exactly one accumulation point (namely the limit $a$). This must be the greatest and smallest accumulation point at the same time, so $\limsup =\liminf =a$.

"$\Leftarrow$" needs some technical work, where we will use the definition of a limit and accumulation point via neighbourhoods. We recall:

• A point $a\in \mathbb {R}$ is the limit of $(a_{n})$ , if and only if $\forall \epsilon >0$ there are almost all $a_{n}\in (a-\epsilon ,a+\epsilon )$
• A point $a\in \mathbb {R}$ is an accumulation point of $(a_{n})$ , if and only if $\forall \epsilon >0$ there are infinitely many $a_{n}\in (a-\epsilon ,a+\epsilon )$.

Proof (limes superior/inferior and convergence)

Step 1: "$\Rightarrow$"

If $\lim _{n\to \infty }a_{n}=a$ , then the sequence $(a_{n})_{n\in \mathbb {N} }$ is bounded and $a$ is its only accumulation point. By definition of limsup and liminf:

$\limsup \limits _{n\to \infty }a_{n}={\text{greatest accumulation point of }}(a_{n})=a={\text{smallest accumulation point of }}(a_{n})=\liminf \limits _{n\to \infty }a_{n}$

Step 2: "$\Leftarrow$"

Let $\limsup \limits _{n\to \infty }a_{n}=a=\liminf \limits _{n\to \infty }a_{n}$.

Since $a=\limsup \limits _{n\to \infty }a_{n}$ is the greatest accumulation point of $(a_{n})_{n\in \mathbb {N} }$ , we know that for all $\epsilon >0$ , there are infinitely many sequence elements in $(a-\epsilon ,a+\epsilon )$ and almost all in $(-\infty ,a+\epsilon )$ (i.e. only finitely many on the outside).

Since $a=\liminf \limits _{n\to \infty }a_{n}$ is the smallest accumulation point of $(a_{n})_{n\in \mathbb {N} }$ , for any $\epsilon >0$ , there are infinitely many sequence elements in $(a-\epsilon ,a+\epsilon )$and almost all of them in $(a-\epsilon ,\infty )$ (i.e. only finitely many on the outside).

So if we fix $\epsilon >0$ , then only "finite + finite = finite"-ly many sequence elements can be outside $(a-\epsilon ,a+\epsilon )$. So almost all are on the inside which is equivalent to saying that $(a_{n})_{n\in \mathbb {N} }$ converges to $a$.

Hint

This theorem can be extended to improperly converging sequences:

$\lim _{n\to \infty }a_{n}=\pm \infty \iff \liminf _{n\to \infty }a_{n}=\limsup _{n\to \infty }a_{n}=\pm \infty$

Exercise (limes superior/inferior and improper convergence)

Prove that the statement in the above hint holds for $+\infty$. (The case $-\infty$ is proven analogously)

How to get to the proof? (limes superior/inferior and improper convergence)

Again, we need to show two directions: $\Rightarrow$" is by definition of limsup and liminf and $\Leftarrow$" needs some technical work.

Proof (limes superior/inferior and improper convergence)

Step 1: $\Rightarrow$. Let $\lim _{n\to \infty }a_{n}=\infty$. Then, $(a_{n})_{n\in \mathbb {N} }$ is unbounded from above, but bounded from below. So by definition, $\limsup _{n\to \infty }a_{n}=\infty$ (and $\liminf _{n\to \infty }a_{n}\neq -\infty$). Further, $(a_{n})$ has no accumulation point (otherwise it would not converge improperly to infinity), which implies by definition that $\liminf _{n\to \infty }a_{n}=\infty$.

Step 2: $\Leftarrow$. Let $\liminf _{n\to \infty }a_{n}=\limsup _{n\to \infty }a_{n}=\infty$. Then, $(a_{n})_{n\in \mathbb {N} }$ is unbounded from above, but bounded from below. Since $\liminf _{n\to \infty }a_{n}\neq a\in \mathbb {R}$ we know that $(a_{n})_{n\in \mathbb {N} }$ has no accumulation points. We will show that this implies $\lim _{n\to \infty }a_{n}=\infty$:

Let $(a_{n})_{n\in \mathbb {N} }$ be any real sequence bounded from below, without an accumulation point in $\mathbb {R}$ . Then, $(a_{n})_{n\in \mathbb {N} }$ converges improperly to $\infty$.

This is shown by contradiction: Assume that $(a_{n})_{n\in \mathbb {N} }$ is bounded from below, but it does not converge improperly to $\infty$, which means

${\begin{aligned}\Rightarrow &\neg (\forall S>0\ \exists N\in \mathbb {N} \ \forall n\geq N:a_{n}\geq S)\\\Rightarrow &\exists S>0\ \forall N\in \mathbb {N} \ \neg (\forall n\geq N:a_{n}\geq S)\\\Rightarrow &\exists S>0\ \forall N\in \mathbb {N} \ \exists n'\geq N:a_{n'}<S\end{aligned}}$

This means, there are infinitely many $n'\in \mathbb {N}$ with $a_{n'}<S$. By means of the Bolzano-Weierstrass theorem, one can find a subsequence $(a_{{n'}_{k}})_{k\in \mathbb {N} }$ of $(a_{n'})_{n'\in \mathbb {N} }$ which converges to some $a\in \mathbb {R}$. This means, $a$ is an accumulation point of $(a_{n})_{n\in \mathbb {N} }$, which contradicts $(a_{n})_{n\in \mathbb {N} }$ not having any accumulation points. So any $(a_{n})_{n\in \mathbb {N} }$ bounded from below without accumulation points must diverge improperly to $\infty$. This also holds true for our $(a_{n})_{n\in \mathbb {N} }$ above and by definition, $\lim _{n\to \infty }a_{n}=\infty$, which is what we wanted to show.

Alternative characterization

In the literature, $\limsup _{n\to \infty }a_{n}$ and $\liminf _{n\to \infty }a_{n}$ are often defined in a different but equivalent way: Suppose, $(a_{n})_{n\in \mathbb {N} }$ is bounded. Then we have:

Theorem (alternative definition of limsup and liminf)

If $(a_{n})_{n\in \mathbb {N} }$ is a bounded sequence, then

${\begin{aligned}\limsup _{n\to \infty }a_{n}=\lim _{k\to \infty }\sup\{a_{n}:n\geq k\}=\inf _{k\in \mathbb {N} }\sup\{a_{n}:n\geq k\}\\\liminf _{n\to \infty }a_{n}=\lim _{k\to \infty }\inf\{a_{n}:n\geq k\}=\sup _{k\in \mathbb {N} }\inf\{a_{n}:n\geq k\}\end{aligned}}$

Intuitively, the limes superior is the "smallest upper" and the limes inferior the "greatest lower bound" of $(a_{n})_{n\in \mathbb {N} }$, as $n\to \infty$. Or in other words: The bound is allowed to be violated by finitely many elements.

Examples

Example

Let $(a_{n})_{n\in \mathbb {N} }=((-1)^{n})_{n\in \mathbb {N} }=(-1,1,-1,1,-1,1,\ldots )$. This sequence has two accumulation points: $1$ and $-1$. So by the original definition, $\limsup _{n\to \infty }a_{n}=1$ and $\liminf _{n\to \infty }a_{n}=-1$. In order to apply the alternative definition above, we have to determine $(b_{k})_{k\in \mathbb {N} }=(\sup\{a_{n}:n\geq k\})_{k\in \mathbb {N} }$ and $({\tilde {b}}_{k})_{k\in \mathbb {N} }=(\inf\{a_{n}:n\geq k\})_{k\in \mathbb {N} }$ , as well as their limits. This is an easy task here: since $(a_{n})_{n\in \mathbb {N} }$ only attains the values $\pm 1$ and both infinitely many, there is just $b_{k}=\sup\{a_{n}:n\geq k\}=1$ and ${\tilde {b}}_{k}=\inf\{a_{n}:n\geq k\}=-1$ for all $k\in \mathbb {N}$. So we have two constant sequences with limits

$\limsup _{n\to \infty }a_{n}=\lim _{k\to \infty }b_{k}=\lim _{k\to \infty }1=1$

and

$\liminf _{n\to \infty }a_{n}=\lim _{k\to \infty }{\tilde {b}}_{k}=\lim _{k\to \infty }-1=-1$

and both definitions coincide.

Example

Consider $(a_{n})_{n\in \mathbb {N} }=({\tfrac {(-1)^{n}}{n}})_{n\in \mathbb {N} }=(-1,{\tfrac {1}{2}},-{\tfrac {1}{3}},{\tfrac {1}{4}},-{\tfrac {1}{5}},{\tfrac {1}{6}},\ldots )$. this is a null sequence, so by the original definition,

$\limsup _{n\to \infty }=\liminf _{n\to \infty }=0$

For the new definition of limsup, we determine

$(b_{k})_{k\in \mathbb {N} }=(\sup\{a_{n}:n\geq k\})_{k\in \mathbb {N} }=({\tfrac {1}{2}},{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{4}},{\tfrac {1}{6}},{\tfrac {1}{6}},\ldots )$

which implies

$\limsup _{n\to \infty }a_{n}=\lim _{k\to \infty }b_{k}=0$

and both definitions of the limsup coincide.

Question: Analogously, determine $\liminf _{n\to \infty }a_{n}$ by the new definition.

There is

$({\tilde {b}}_{k})_{k\in \mathbb {N} }=(\inf\{a_{n}:n\geq k\})_{k\in \mathbb {N} }=(-1,-{\tfrac {1}{3}},-{\tfrac {1}{3}},-{\tfrac {1}{5}},-{\tfrac {1}{5}},-{\tfrac {1}{7}},-{\tfrac {1}{7}},\ldots )$

so

$\liminf _{n\to \infty }a_{n}=\lim _{k\to \infty }{\tilde {b}}_{k}=0$

which also coincides with the original definition.

Proof of the theorem

How to get to the proof? (alternative definition of limsup and liminf)

At first, we focus on the "limsup-case" and prove that $(b_{k})_{k\in \mathbb {N} }=(\sup\{a_{n}:n\geq k\})_{k\in \mathbb {N} }$ indeed converges. Since $(b_{k})_{k\in \mathbb {N} }$ This sequence is monotonously decreasing and bounded, so it converges by the monotony criterion. Then, we need to show that $(b_{k})$ indeed converges to $\limsup _{n\to \infty }a_{n}$, i.e. the greatest accumulation point of $(a_{n})_{n\in \mathbb {N} }$. This is done by establishing the two inequalities $\lim _{k\to \infty }b_{k}\geq \limsup _{n\to \infty }a_{n}$ and $\lim _{k\to \infty }b_{k}\leq \limsup _{n\to \infty }a_{n}$.

The "liminf-case" works analogously. We use that $({\tilde {b}}_{k})_{k\in \mathbb {N} }=(\inf\{a_{n}:n\geq k\})_{k\in \mathbb {N} }$ in monotonously increasing an d bounded, so it converges. And we show that the limit is indeed $\liminf _{n\to \infty }a_{n}$, meaning the smallest accumulation point of $(a_{n})$.

Proof (alternative definition of limsup and liminf)

Since $(a_{n})$ is bounded (by assumption), so is $(b_{k})=(\sup\{a_{n}:n\geq k\})$ . In addition,

$\{a_{n}:n\geq k+1\}\subseteq \{a_{n}:n\geq k\}\Rightarrow b_{k+1}=\sup\{a_{n}:n\geq k+1\}\leq \sup\{a_{n}:n\geq k\}=b_{k}$

So $(b_{k})$ is monotonously decreasing. By the monotony criterion, $(b_{k})$ converges to some limit which we call $b^{*}$.

Let us denote the greatest accumulation point of $(a_{n})$ by $\limsup _{n\to \infty }a_{n}=h^{*}$ . Our aim is to show $b^{*}=h^{*}$. This is done by proving $b^{*}\geq h^{*}$ and $b^{*}\leq h^{*}$:

Since $h^{*}$ is an accumulation point of $(a_{n})$ , we know that for each $N\in \mathbb {N}$ there is some $n\in \mathbb {N}$ with $n\geq N$ and $a_{n}\geq h^{*}-\epsilon$ for any $\epsilon >0$ . This especially implies $b_{k}=\sup\{a_{n}:n\geq k\}\geq h^{*}$ for all $k\in \mathbb {N}$. Taking the limit, we obtain $b^{*}=\lim _{k\to \infty }b_{k}\geq h^{*}$.

On the other hand, as $(b_{k})$ is monotonously decreasing, there is also $b^{*}\leq b_{k}<h^{*}+\epsilon$. This holds for all $\epsilon >0$. Taking the limit $\epsilon \to 0$ , we get $b^{*}\leq h^{*}$, which finishes the proof.

Rules for computing with limsup and liminf

Theorem (monotony rule)

Let $(a_{n})_{n\in \mathbb {N} }$ and $(b_{n})_{n\in \mathbb {N} }$ be bounded real sequences with $a_{n}\leq b_{n}$ for all $n\in \mathbb {N}$. Then

$\liminf _{n\to \infty }a_{n}\leq \liminf _{n\to \infty }b_{n}$

and

$\limsup _{n\to \infty }a_{n}\leq \limsup _{n\to \infty }b_{n}$

Proof (monotony rule)

Let $\limsup _{n\to \infty }a_{n}=h_{a}^{*}$ be the greatest accumulation point of $(a_{n})$ and $\limsup _{n\to \infty }b_{n}=h_{b}^{*}$ the greatest accumulation point of $(b_{n})$. Those accumulation points exist by the Bolzano-Weierstrass theorem and by boundedness of the sequences. Let $\epsilon >0$ be given. since $h_{b}^{*}$ is the greatest accumulation point of $(b_{n})$ , there must be an $N\in \mathbb {N}$, such that for all $n\geq N$: $h_{b}^{*}+\epsilon >b_{n}$. But since $a_{n}\leq b_{n}$ , there is also $h_{a}^{*}+\epsilon >a_{n}$. Therefore $h_{a}^{*}\leq h_{b}^{*}+\epsilon$ holds. Taking the limit $\epsilon \to 0$ , we obtain $h_{a}^{*}\leq h_{b}^{*}$.

Exercise (v)

Analogously, prove that $\liminf _{n\to \infty }a_{n}\leq \liminf _{n\to \infty }b_{n}$.

Theorem (Relation between limsup and liminf - mirroring along the x-axis)

Let $(a_{n})_{n\in \mathbb {N} }$ be a bounded real sequence. Then,

$-\limsup _{n\to \infty }a_{n}=\liminf _{n\to \infty }(-a_{n})$

Proof (Relation between limsup and liminf - mirroring along the x-axis)

Let $h^{*}=\limsup _{n\to \infty }a_{n}$ be the greatest accumulation point of $(a_{n})$. We need to show that $-h^{*}=\liminf _{n\to \infty }(-a_{n})$ , i.e. $-h^{*}$ is tha smallest accumulation point of $(-a_{n})$ . This is done in two steps:

1. We prove that $-h^{*}$ is an accumulation point of $(-a_{n})$
2. We prove that $-h^{*}$ is the smallest accumulation point of $(-a_{n})$

Step 1: Since $h^{*}=\limsup _{n\to \infty }a_{n}$ , there is a subsequence $(a_{n_{k}})_{k\in \mathbb {N} }$ of $(a_{n})_{n\in \mathbb {N} }$ with $\lim _{k\to \infty }a_{n_{k}}=h^{*}$. By the limit theorems, we have $\lim _{k\to \infty }-a_{n_{k}}=-\lim _{k\to \infty }a_{n_{k}}=-h^{*}$. So the subsequence $(-a_{n_{k}})$ of $(-a_{n})$ converges to $-h^{*}$, i.e. $-h^{*}$ is an accumulation point of $(-a_{n})$.

Step 2: Let $h$ be any accumulation point of $(-a_{n})$. Then, there is a subsequence $(-a_{n_{k}})$ of $(-a_{n})$ with $\lim _{k\to \infty }-a_{n_{k}}=h$. By the limit theorems, $\lim _{k\to \infty }a_{n_{k}}=\lim _{k\to \infty }-(-a_{n_{k}})=-\lim _{k\to \infty }(-a_{n_{k}})=-h$. hence, $-h$ is an accumulation point of $(a_{n})$. Since $h^{*}$ was the greatest accumulation point of $(a_{n})$ , we know that $-h\leq h^{*}$, or equivalently $h\geq -h^{*}$.

As $h$ was any accumulation point of $(-a_{n})$ , we know that any accumulation point is greater or equal $-h^{*}$ . So $-h^{*}$ is the smallest one and $-h^{*}=\liminf _{n\to \infty }(-a_{n})$.

Theorem (Sum rule)

Let $(a_{n})_{n\in \mathbb {N} }$ and $(b_{n})_{n\in \mathbb {N} }$ be real sequences. Then,

$\limsup _{n\to \infty }a_{n}+\liminf _{n\to \infty }b_{n}\leq \limsup _{n\to \infty }(a_{n}+b_{n})\leq \limsup _{n\to \infty }a_{n}+\limsup _{n\to \infty }b_{n}$

Proof (Sum rule)

Step 1: We start with the second inequality $\limsup _{n\to \infty }(a_{n}+b_{n})\leq \limsup _{n\to \infty }a_{n}+\limsup _{n\to \infty }b_{n}$:

Let $h_{a}^{*}=\limsup _{n\to \infty }a_{n}$, $h_{b}^{*}=\limsup _{n\to \infty }b_{n}$ and let $h_{a+b}$ be an accumulation point of $(a_{n}+b_{n})$. Then, there is a subsequence $(a_{n_{k}}+b_{n_{k}})$ of $(a_{n}+b_{n})$ with $\lim _{k\to \infty }a_{n_{k}}+b_{n_{k}}=h_{a+b}$.

Let further $\epsilon >0$ be arbitrary. Since $h_{a}^{*}$ is the greatest accumulation point of $(a_{n})$ and $h_{b}^{*}$ is the greatest accumulation point of $(b_{n})$ , there must be a $K\in \mathbb {N}$, such that for all $k\geq K$ there is: $a_{n_{k}}<h_{a}^{*}+{\tfrac {\epsilon }{2}}$ and $b_{n_{k}}<h_{b}^{*}+{\tfrac {\epsilon }{2}}$. So, for $k\geq K$ we also have $a_{n_{k}}+b_{n_{k}}<h_{a}^{*}+h_{b}^{*}+\epsilon$. By monotony of the limits, we know that $h_{a+b}=\lim _{k\to \infty }a_{n_{k}}+b_{n_{k}}\leq h_{a}^{*}+h_{b}^{*}+\epsilon$, so the $h_{a+b}$ can be at most $\epsilon$ above our desired threshold $h_{a}^{*}+h_{b}^{*}$. But now, $\epsilon >0$ can be chosen arbitrarily close to 0, so we get $h_{a+b}\leq h_{a}^{*}+h_{b}^{*}$. Since this inequality holds for all accumulation points $h_{a+b}$ of $(a_{n}+b_{n})$ , it also holds for the greatest one and

$h_{a+b}^{*}=\limsup _{n\to \infty }(a_{n}+b_{n})\leq h_{a}^{*}+h_{b}^{*}=\limsup _{n\to \infty }a_{n}+\limsup _{n\to \infty }b_{n}$

Step 2: Now, we prove $\limsup _{n\to \infty }a_{n}+\liminf _{n\to \infty }b_{n}\leq \limsup _{n\to \infty }(a_{n}+b_{n})$. This can be done by usind the second inequality which we just have proven and the rule$-\limsup _{n\to \infty }a_{n}=\liminf _{n\to \infty }(-a_{n})$ above. there is

${\begin{aligned}\limsup _{n\to \infty }a_{n}=&\limsup _{n\to \infty }(a_{n}+b_{n})+(-b_{n})\\&{\underset {2^{nd}{\text{ inequality}}}{\leq }}\limsup _{n\to \infty }(a_{n}+b_{n})+\limsup _{n\to \infty }(-b_{n})\\&{\underset {\text{rule}}{\overset {\text{limsup/liminf-}}{=}}}\limsup _{n\to \infty }(a_{n}+b_{n})-\liminf _{n\to \infty }(-(-b_{n}))\\&=\limsup _{n\to \infty }(a_{n}+b_{n})-\liminf _{n\to \infty }b_{n}\end{aligned}}$

This is exactly equivalent to $\limsup _{n\to \infty }a_{n}+\liminf _{n\to \infty }b_{n}\leq \limsup _{n\to \infty }(a_{n}+b_{n})$.

Exercise (Example for the sum rule)

Find explicit sequences $(a_{n})$ and $(b_{n})$ with strict bounds

$\limsup _{n\to \infty }a_{n}+\liminf _{n\to \infty }b_{n}<\limsup _{n\to \infty }(a_{n}+b_{n})<\limsup _{n\to \infty }a_{n}+\limsup _{n\to \infty }b_{n}$

Solution (Example for the sum rule)

The trick is to let sequence elements cancel against each other. One needs to play a bit around with alternating sequences to get to a solution. One example is

$a_{n}={\begin{cases}(-1)^{k}&{\text{ if }}n=2k\\{\frac {1}{2}}&{\text{if }}n=2k+1\end{cases}}$

and

$b_{n}={\begin{cases}(-1)^{k+1}&{\text{ if }}n=2k\\{\frac {1}{2}}&{\text{if }}n=2k+1\end{cases}}$

The first sequence elements are

$(a_{n})=({\tfrac {1}{2}},-1,{\tfrac {1}{2}},1,{\tfrac {1}{2}},-1,{\tfrac {1}{2}},1,\ldots )$

and

$(b_{n})=({\tfrac {1}{2}},1,{\tfrac {1}{2}},-1,{\tfrac {1}{2}},1,{\tfrac {1}{2}},-1,\ldots )$

So both $(a_{n})$ and $(b_{n})$ have the three accumulation points $-1,{\tfrac {1}{2}}$ and $1$. The sum of both sequences is

$a_{n}+b_{n}={\begin{cases}0&{\text{ falls }}n=2k\\1&{\text{falls }}n=2k+1\end{cases}}$

And has the accumulation points $0$ and $1$. Therefore,

$\underbrace {\limsup _{n\to \infty }a_{n}+\liminf _{n\to \infty }b_{n}} _{=1+(-1)=0}<\underbrace {\limsup _{n\to \infty }(a_{n}+b_{n})} _{=1}<\underbrace {\limsup _{n\to \infty }a_{n}+\limsup _{n\to \infty }b_{n}} _{=1+1=2}$