Limit: Convergence and divergence – Serlo
In this chapter we will introduce the central concept of a limit (also called the Limes) in the context of sequences. We will discuss what the term convergence is and what it means for a sequence to be convergent. All of the important concepts of Analysis like continuity, derivatives and integrals can only be defined if we have a notion of limits and convergence. Thus the concepts introduced in this chapter will serve as the backbone of our entire discussion about Analysis.
Intuition behind the idea of convergence
[Bearbeiten]Before one goes about to find a precise mathematical definition of a new concept, it is always a good idea to first develop an intuition. Let us therefore consider the harmonic sequence . The first few elements of the sequence are:
You can already tell that elements become smaller and go towards zero as we increase the index . We can make the following intuitive assertions:
- The sequence will get arbitrary close to .
- The bigger the index , the more the member gets close to .
- The sequence tends to .
- The sequence will reach at infinity .
- …
All this intuitive statements, already give us an idea of what the limit of a sequence is. To give a first intuitive definition we would say: The limit is the thing (or in this case the value) that the sequence approaches as we go further and further, i.e as the index goes to infinity. In our case is the limit of the harmonic sequence . We say that the harmonic sequence is convergent. Of course not all sequences are convergent and thus have a finite limit: Think about the natural numbers as a sequence. They grow bigger and bigger and never get closer to any particular value. We say that the sequence of the natural numbers is divergent.
Finding a definition for the limit
[Bearbeiten]First steps
[Bearbeiten]In mathematics we need an exact definition of what we mean by a "limit" to be able to talk and reason precisely. We can find such a definition if we start with an intuitive idea and gradually concretize it until we have a rigorous mathematical definition. The process of concretion will go on until we have a definition that employs only previously defined terms. Let's start with the following intuitive description of a limit:
„A sequence has a limit , if the members of the sequence get arbitrary close to .”
But what does „arbitrary close" mean in the above sentence? We could translate as follows: Imagine the members of the sequence in a coordinate system, where the -axis are the indices and the -axis has the members/values of the sequence . So every member of the sequence corresponds to a point in this coordinate system. The limit is marked by a dotted line.

If the members get "arbitrary close" to then the distance to the limit will keep getting smaller. Try to visualize a really narrow "hose" (maybe think about a garden hose) that has a radius of . Imagine taking this hose and "threading" it over the limit from the right. As long as the distance of the members from the limit is smaller than the thickness of the hose, we can keep pushing the hose to the left. All points are still inside the hose. But as soon as a point has a bigger distance from the limit, this point will not be inside the hose. At this point we stop threading the hose.
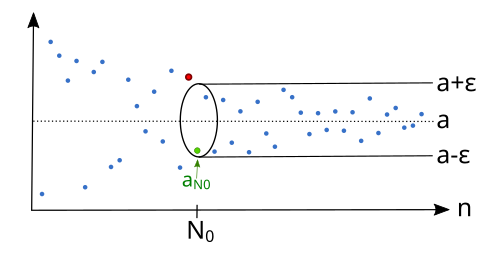
The point is the member of the sequence, from which on all members (so those with index greater than or equal ) will be inside the hose. Directly before there is a point that is outside of the hose (even by just a tiny amount). If we make the hose smaller, maybe some of the points that were inside the bigger one, now will be outside, and thus if your goal is to capture all points inside you can't "push" the hose as far as the bigger one. But even with this smaller hose it's still possible to capture almost all points:

The points that don't fit into the smaller hose are now more to the right than in the previous image. Let's call the first new member in the hose . All members with an index greater or equal to will be inside the smaller hose.
Of course this "garden hose" has no mathematical meaning. We used it as a mental tool to show that the members of the sequence are closer to the dotted line the bigger the index . They keep approaching and will indeed not start drifting away from the dotted line, because we have seen that all members starting from a certain index will be inside the hose, no matter how small we choose to make it. If we understood that, we don't need the "hose" anymore. We will replace our arbitrary small "hoses" with radius with a mathematical object we call a -neighbourhood (it sounds more scary than it really is).
Every neighbourhood around the limit contains almost all members
[Bearbeiten]
We have found indices or , from which on all later members of the sequence will be contained in the respective -hose. If we make the hose smaller then we can find another , from which on all members will be inside the hose and so on. No matter how small we choose our hose, we will always find a point so that all subsequent points are captured inside that "hose".
Since all this starting indices are natural numbers, there are only a finite amount of members that are outside of the hose ( to be precise). All other points are inside the hose. Since a sequence has infinitely many members, we can "ignore" the finite amount of members that are outside and say that "almost all" members are inside the hose. This is still true, even if we choose to be really big. Compared to infinity a finite amount – no matter how big you choose - is still little. Understanding this is important to understand the idea of limits.
Let's repeat this one more time: No matter how small you choose your hose to be, almost all members will be captured inside it. That means that the members will approach . And this is the central idea about the limit. The members will get arbitrary close to , if we choose a sufficiently large index .
What is a neighbourhood of a number?
[Bearbeiten]We can construct the neighbourhood of a number geometrically with a circle. Let be the center of a circle with radius . Then we have only marked the point on the number line. If we increase the radius of the circle, we see that the diameter expands from .
On an intuitive level a neighbourhood is set of numbers that encloses .
In one dimension this circle is just an open interval. A neighbourhood of a number can be mathematically described by such an interval. The radius of the circle is the distance to the left and right boundary of the interval . The radius is a arbitrary (small) positive number .
An interval of this sort is characterized as the set of all numbers that are less than apart from . Thus this intervals will have the form .
We call this interval -neighbourhood of , and it looks like this:

The -neighbourhood of will more generally define a neighbourhood of . A set is a neighbourhood of , if and only if there exists an -neighbourhood , such that . Let's see how this works by considering the following set :

First we need to find an -neighbourhood of . Choose an adequate and draw a circle with radius around . So that will mark an interval . The set is also an interval. It encloses the interval . Thus is a superset of the -neighbourhood of . So our definition says that is a neighbourhood of .

Definition (Neighbourhood)
A set is a neighbourhood of a number , if there exists an , such that (i.e. -neighbourhood is contained in ).
What does „almost all" mean?
[Bearbeiten]To better understand this idea imagine a coordinate system in which we have infinitely many members of a convergent sequence with limit . We thread a small -hose from the right over the limit. Then there are only a finite amount of members which are outside the hose, because their distance to is not small enough. But infinitely many members are inside the interval and thus in the -hose.
The amount of members that are inside the interval is overwhelmingly larger than the ones outside. Therefore is reasonable to say that almost all members are inside .
Another way of expressing this idea would be to say that all but finitely many members are contained in the -hose.
A mathematical definition for the limit
[Bearbeiten]Now that we have an idea about what we are trying to define, we will try to find a rigorous mathematical definition. We start by observing that:
„A sequence has a limit , if for every -neighbourhood of , i.e. , there exists a member, that starting from it all following members are inside the neighbourhood.“
We could already work with this definition. But for practical purposes it's useful to further formalise this definition.
Note that a member is an element of , if and only if . Thus:
„A sequence has a limit , if for every , there exists a member , starting from which all following members are less than away from , that means that they satisfy .
The part with „there exists a member, starting from which…“ can be equivalently formulated as „there exists a natural number , so that for all with follows that …“. Thus:
„A sequence has a limit , if for every there exists a natural number , so that for all .
This is the mathematical definition of the limit.
Definition of limit
[Bearbeiten]Definition (Limit)
A sequence has a limit , if for every there exists an index , so that for every member with the inequality is true. So is a limit of if and only if:
This is what the individual parts of the above formula mean:
There are a few other important definitions when studying limits:
- Convergence
- A sequence is convergent, if the sequence has a limit. We say that the sequence converges towards , if there is a limit .
- Divergence
- If there is no limit a sequence is called divergent. Thus a sequence is divergent if it is not convergent.
- Null Sequence
- A sequence that has a limit of is called a Null Sequence.
If a sequence converges to , we also write it like or „ für “. We say „Limes of for goes to infinity, is “.
Question: What is the formula in predicate logic to express that is convergent?
As we discussed above the forumla to express that a sequence has a limit is the following:
If we only want to express convergence, we do it like this:
Question: What is the formula in predicate logic to express that diverges?
We need to negate the previous formula. We need to invert the all- and existence-quantifiers. The negated statement is:
In words: For every there is a real number , so that for all there is a with .
Hint
For the absolute value we have: . Thus also:
We could use either or in our definition of limit.
Hint
From the definition of convergence it follows immediately that converges towards , if and only if is a Null Sequence. If converges to , then from the definition we see:
But this is exactly the definition for what it means for to converge towards . If conversely converges to , we use the definition to conclude:
But this implies that and the quantifiers and the variables in the formula don't change, so that converges to and thus is a Null Sequence.
Warning
A common misconception is that "A sequence is divergent if and only if it is unbounded". This statement is false!
The intuitive mistake that often happens is to assume that: „The opposite of is , thus must become arbitrary large.“ But as we have seen this is not the definition of divergence!
What is true, is that every unbounded sequence is divergent (more on this in„Unbounded sequences are divergent“), but not every divergent sequence must necessarily be unbounded. Take for example the following alternating sequence , which is in fact divergent but bounded.
Explanation of convergence
[Bearbeiten]Besides the above derivation of limits there is another intuition for the limit: The quantity is the distance between the n-th member and . It is a measure of the error between and . The inequality means, that the error between and is guaranteed to be smaller than . Therefore we can interpret the definition of limit as follows: No matter how small we choose our maximum error to be, almost all members are less than away from the limit . The error between the members and the limit becomes arbitrary small.
There are also historical reasons for this interpretation. Augustin-Louis Cauchy, who first proposed this definition[1], maybe wanted to remind of the french word „erreur“ which means „error".[2].
Example: Convergence of the harmonic progression
[Bearbeiten]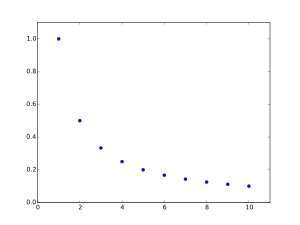
Let's see this concepts in action by studying the harmonic progression with the generic member . It should be intuitive that this sequences converges towards . If this is correct, then this sequences should satisfy the definition for convergence towads .
Take for example . Starting from the third member the distance between and is smaller than . All later members of this sequence are contained inside the -neighbourhood of . For this is true starting from and for starting from .
But the definition of limit requires that this is true for all . Therefore, let us assume we are given an . From the archimedean axiom it follows that there exists an , so so that for all (See Archimedean Axiom whit the choices of and .) From this onwards all members are contained inside the -neighbourhood . The definition tells us that is the limit of the harmonic progression.
The limit is unique
[Bearbeiten]Theorem (Uniqueness of the limit)
The limit of a convergent sequence is unique.
This theorem allows us to write things such as . Imagine that there is a sequence with more than one limit. Then it is not clear what the expression should stand for (there are two possibilities). But because we know that has a unique limit, it is clear that can only mean one thing, i.e. the (unique) limit of that sequence (if it is convergent). The above theorem allows us to talk about the limit and not a limit.
How to get to the proof? (Uniqueness of the limit)
We can prove this by contradiction. We assume that there is a sequence with two distinct limits. Now we need to show that this assumption will result in a contradiction, and that it therefore cannot be true.
We label the two distinct limits and . To find a contradiction, we can use the following method: We try to prove the opposite of what we really want to show. Of course we set ourself up for failure. Why do we even try then? Because by understanding why it fails we get a lot of clues that will help us prove the right thing. So for the sake of gathering insight, let us (try) to prove that there is a sequence with two distinct limits.
Take a piece of paper and draw a Number line. Mark two distinct numbers and that will represent our two limits. Now try to find a real sequence that converges to both this limits (Remember that starting from a certain index you sequence has to be in an arbitrary small -neighbourhood around and ). But for arbitary small -neighbourhoods of and , that do not intersect, it is impossible that almost all members are contained in both. The following drawing will highlight this problem:

Thus if we choose so small, that and do not overlap, the we know that there must be a contradiction hiding somewhere (the one we need to prove our original proposition!). We choose . We now that there must be a that must be contained both in and . But such an can't exists, since those two neighbourhoods can't intersect for A contradiction emerges from the triangle inequality:
We cancel both sides with and find the contradiction .
Proof (Uniqueness of the limit)
Proof by contradiction: Let be a sequence with two distinct limits and . Distinct means that and therefore . Per definition there exists and with
and
This follows from the definition of limit if we set . Thus for all members with index , both and is true. In this case we have:
Because of we have and we can cancel both sides in the inequality with . This results in the contradiction:
It is essential for this prove that and thus . Else we could not have divided by (division by zero!) and we could not have chosen .

































![{\displaystyle {\begin{array}{l}\underbrace {{\underset {}{}}\forall \epsilon >0:} _{{\text{ For every }}\epsilon >0}\ \underbrace {{\underset {}{}}\exists N\in \mathbb {N} :} _{{\text{ there exists an index }}N}\ \underbrace {{\underset {}{}}\forall n\geq N:} _{{\text{ so that for all indices }}n\geq N}\\[1em]\quad \quad \underbrace {{\underset {}{}}|a_{n}-a|<\epsilon } _{{\text{ the distance between }}a_{n}{\text{ and }}a{\text{ is smaller than }}\epsilon }\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f94261f351f3142084b0e8d6dd02a260acc3615)




















![{\displaystyle ]-{\tfrac {1}{2}},{\tfrac {1}{2}}[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b06dfb798f50c27ed60d7f55d09ce66c96eca17)







![{\displaystyle ]-\epsilon ,\epsilon [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db49874c62a6ff2a4b766845f77b8b96897f9a47)






![{\displaystyle {\begin{aligned}|a-b|&=|a+\overbrace {(-a_{n}+a_{n})} ^{=0}-b|\\[1ex]&=|(a-a_{n})+(a_{n}-b)|\\[1ex]&\quad {\color {OliveGreen}\left\downarrow \ {\text{Triangle inequality}}\right.}\\[1ex]&\leq |a-a_{n}|+|a_{n}-b|\\[1ex]&<{\frac {|a-b|}{3}}+{\frac {|a-b|}{3}}\\[1ex]&={\frac {2\cdot |a-b|}{3}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4c323eff1876224861af2c3a98b4942534f0407)









![{\displaystyle {\begin{aligned}|a-b|&=|a+(-a_{n}+a_{n})-b|\\[1ex]&=|(a-a_{n})+(a_{n}-b)|\\[1ex]&\quad {\color {OliveGreen}\left\downarrow \ {\text{Triangle inequality}}\right.}\\[1ex]&\leq |a-a_{n}|+|a_{n}-b|\\[1ex]&<{\frac {|a-b|}{3}}+{\frac {|a-b|}{3}}\\[1ex]&={\frac {2\cdot |a-b|}{3}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8bd30a63a46c6418ac2286f25c7c85f8a4e5885)


