Mean value theorem – Serlo
The mean value theorem is one of the central theorems of differential calculus. It states (roughly speaking) that the slope of the secant between two different points of a differentiable function somewhere between these two points is assumed to be a derivative. Thus, the mean value theorem links the secant slope with the derivative of a function. Global properties, which can be expressed using the secant slope, can thus be traced back to properties of the derivative using the mean value theorem. In the section „Schrankensatz“ we will examine a useful application. Others then follow in the chapters constant functions, derivative and local extrema and L'Hospital's rule. The main theorem of differential and integral calculus is also based on the mean value theorem.
Motivation
[Bearbeiten]We've already viewed at Rolle's theorem. To repeat: Rolle's theorem states that for each continuous function , which is differentiable in and for which must give an argument , which satisfies :

How can we generalize this theorem for the case ? Does the derivative for a also have to have a certain value? First of all, it is noticeable that does not necessarily have to be :

Let's reconsider what the situation was with the situation with Rolle's theorem. On the one hand, the slope of the tangent at the graph is in equal to . On the other hand, the slope of the secant through the two boundary points and from equal to , since and thus . The secant between the points and and the tangent in the point are thus parallel:

Be more general . Consider the secant slope between the points and . This is unequal to zero and corresponds to the mean slope of in the interval . For example, if we consider the function as a position function of a car as a function of time, the average slope corresponds to the average speed of the car in the time from to .
If the car at the moment drives faster than (meaning: The derivation is greater than the secant slope ) so it is has to exist a moment at which it has driven more slowly than , otherwise it cannot reach the average speed . During an acceleration or braking process, the car takes on all speeds between the starting and final speeds and does not simply jump from the starting to the final speed (here we assume that the speed function is continuous). As the car was sometimes faster and sometimes slower than , there must exists a moment at which it has exactly the speed . Analogously we can argue, if the car at the moment drives more slowly than . For our function this means that there must actually be a with . This is the message of the mean value theorem.

So there seems to be a with . In the following we want to form this intuition into a theorem and prove it formally correctly. In our argumentation we have used, for example, that the derivation is continuous. Now the studied function does not have to be constantly differentiable. However, we will show in the proof that the mean value theorem is also fulfilled in this case.
Mean value theorem
[Bearbeiten]The mean value theorem of differential calculus is a generalization of Rolle's theorem and reads as follows:
Theorem (Mittelwertsatz)
Be a continuous function with and differentiable on the open interval . Then there is a with .
Hint
The prerequisites for applying the mean value theorem correspond to those of the Rolle's theorem, only that need not apply. The prerequisites required must apply for the same reasons as for the set of roles. Similarly, the mean value theorem only provides a statement of existence. The with this property exists, but often cannot be determined explicitly in practice. Also, the has not to be unique. The following graphics show a function which assumes the secant slope at two points and :
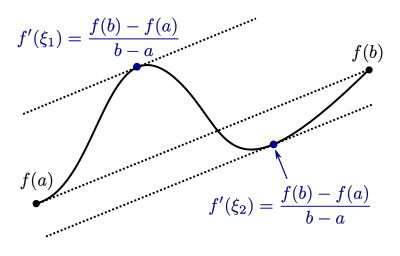
A special case are linear functions for with . In this case for all . In other words: the secant slope is assumed to be the tangent slope everywhere:

Proof
[Bearbeiten]How to get to the proof? (Mean value theorem)
As already mentioned above, we want to prove the mean value theorem with the help of Rolle's theorem. To do this, we have to take the given function an auxiliary function so that we can apply Rolle's theorem to it. For this we need a function that is continuous at and differentiable at . In addition, it should apply that . Then for . If we can also choose the auxiliary function so that , the equation results from . This is equivalent to , the formula of the mean value theorem. The function
has the desired properties. In particular
The following graphics illustrate the relationship between the function and the auxiliary function :
-
The function from mean value theorem.
-
The auxiliary function for Rolle's theorem.
Proof (Mean value theorem)
Be a continuous function with and can be differentiated. A suitable auxiliary function is given by
is differentiable at and is continuous at , as firstly fulfils these conditions by our assumption at the beginning and secondly is a composition of and the first degree polynomial . Furthermore
According to Rolle's theorem there is a with . A was found, which fulfils . Thus follows the claim of the mean value theorem.
Equivalence of mean value theorem and Rolle's theorem
[Bearbeiten]The mean value theorem and Rolle's theorem are actually equivalent. To show this, we have to deduce Rolle's theorem from the mean value theorem and prove the mean value theorem from Rolle's theorem. But we have already done the latter in the proof of this chapter, so that we only have to deduce Rolle's theorem from the mean value theorem.
Be a continuous function with and is differentiable. is therefore a function to which the mean value theorem can be applied. Furthermore, applies, so that all prerequisites of the set of role are given. According to the mean value theorem there is now a with , because with is . So there is actually a with , which is exactly the statement of Rolle's theorem. Thus, the mean value theorem and Rolle's theorem are equivalent.
Exercise
[Bearbeiten]Exercise (Exercise)
Let be any continuous function which can be differentiated on with . Which value must the derivative function take in any case?
Solution (Exercise)
Since all conditions of the mean value theorem are satisfied, it is applicable here. Therefore a exists with . The derivation function must therefore always attain the value .
Application: Proof of inequalities
[Bearbeiten]The mean value theorem can often be used to prove useful inequalities. The trick is to first apply the mean value theorem to an auxiliary function (often on one side of the inequation). Then we estimate the bounds to the expression appropriately.
Exercise: Proof of an inequality
[Bearbeiten]Exercise (Proof of an inequality, using the mean value theorem)
Prove that the following inequality holds for all :
Proof (Proof of an inequality, using the mean value theorem)
We choose as an auxiliary function
Let be arbitrary. The function is as a composition of continuous functions on , so it is continuous and it is differentiable on . By the mean value theorem there is hence a with
Now we can estimate :
Hence, we have the inequality:
This is equivalent to the claim
Logarithm inequalities
[Bearbeiten]
Exercise (Logarithm inequations)
Show that the following inequation is fulfilled for all , using the mean value theorem :
How to get to the proof? (Logarithm inequations)
For the inequation follows
The expression corresponds to the difference quotient in the mean value theorem applied to the function . So there is a with . If we can estimate , then we have reached our goal. Now and with for we can prove the inequality . Let us now look at the missing inequality :
Again the difference quotient appears, which according to the mean value theorem, is equal to a derivative for some . Now and thus we can prove the missing inequality .
Proof (Logarithm inequations)
Let be arbitrary. We define by . Then is continuous on the complete domain of definition and can be differentiated on . Thus the mean value theorem is applicable. According to this, there exists a with
Proof step:
Since there is
Proof step:
Since there is
Hint
The inequiality can be extended to all . For there is
If now , there is a with . So we have
as well as
We have used the two inequalities above to make our estimates. So for all :
Application: Lipschitz continuity of differentiable functions
[Bearbeiten]Theorem (Lipschitz continuity of differentiable functions)
Let be continuous and differentiable on . Further the derivative function is assumed to be bounded. Then with we have a Lipschitz constant so that holds for all . That means, is Lipschitz continuous. In particular, the statement holds if can is continuously differentiable on .
Proof (Lipschitz continuity of differentiable functions)
Let be arbitrary with . If we now restrict the domain of definition from to , continuity and differentiability are preserved. The mean value theorem is applicable. So there is a with .
Since is bounded, we have an . For this , applies to all . Thus . This is equivalent to the assertion.
If is continuously differentiable on , the continuous derivative function has a maximum and a minimum. It is thus bounded and the theorem can then also be applied to this function.

Example (Lipschitz continuity of sine and cosine)
and are continuous and differentiable on . Furthermore, their derivatives are bounded, since for all :
Thus, the two functions are Lipschitz continuous with Lipschitz constant . In particular, for all we have the estimates
and
Question: The inversion of the above theorem is: "Let be continuous and differentiable on . Further, let be Lipschitz continuous. Then the derivative function is bounded". Is this statement correct?
Yes, this statement is also true. Since can be differentiated, the following limit value exists for each :
Since Lipschitz is continuous, there is an for all with
With the continuity of the absolute function and the limit value theorems, we have
So is bounded.
Practical example: Speed control with light
[Bearbeiten]
Some people who got caught speeding have come into contact with the mean value theorem. At least if it was by a Photoelectric sensor. Imagine driving a car on a country road. The maximum permitted speed is or 60 mph. The distance covered by your car is given by the differentiable position function , which depends on the time . The derivative of the position function at the time corresponds to the current speed, i.e. . When measuring speed with light barriers, one passes through two light barriers which are placed at two fixed points and . If you pass the two light barriers at the times and , the average speed between these two measuring points is
Since the position function fulfils the conditions of the mean value theorem, there is a time with
The average speed measured between the two barriers must therefore have been reached at least at one point of time. If now , where is a certain tolerance limit (usually 3%), you will get a speeding ticket! To avoid wrong measurements, in practice more than two light barriers are used and more than one measurement is carried out. But the principle remains the same. Another more recent technique for measuring speed is based on the Doppler effect and uses a Radar to determine speed.
Second mean value theorem
[Bearbeiten]There is another version of the mean value theorem, which is called the second or also generalized mean value theorem. Therefore the "usual" mean value theorem is also called the "first mean value theorem". We will see that also the second mean value theorem follows from the Rolle's theorem. For the second version we need, besides our function , another function , which also fulfils the requirements of the mean value theorem. The second mean value theorem will be useful for deriving L'Hospital's rule.
Theorem and proof
[Bearbeiten]Theorem (Second mean value theorem)
Let be two continuous functions which can be differentiated on . Further let for all . Then and there exists a with
Proof (Second mean value theorem)
If we have , then there is a with by Rolle's theorem. This contradicts the condition of the theorem that for all the inequality applies and consequently must hold. In analogy to the auxiliary function from the proof of the mean value theorem, we choose here the auxiliary function
This function is continuous on and differentiable on as a composition of continuous or differentiable functions. Furthermore, applies. Thus, Rolle's theorem is applicable, and there is a with
This is equivalent to .
Counter-example: Second mean value theorem
[Bearbeiten]Exercise (Counter-example: Second mean value theorem)
Consider the polynomial functions
Show that no exists with
How is this result compatible with the second version of the mean value theorem?
Solution (Counter-example: Second mean value theorem)
There is
On the other hand, for all :
Thus must hold for all . Now the condition for all must be fulfilled for the second mean value theorem. The derivative is continuous on and the following inequalities hold:
and
By the Intermediate value theorem there is an with . So the conditions of the second mean value theorem are not fulfilled and therefore it can not be applied here.
Remarks
[Bearbeiten]Remark 1: Obviously we get for the first mean value theorem from the second. But we have concluded the second one from Rolle's theorem. Since the first mean value theorem and Rolle's theorem are equivalent, the second mean value theorem also follows from the first. The two mean value theorems are therefore equivalent.
Remark 2: If we omit the precondition for all , the second mean value theorem still applies in the form
Question: Why does the second mean value theorem also apply in this more general form?
Assuming there is (at least) one with . If, in addition, applies, there is a with by Rolle's theorem, and we get zero on both sides of the equation. If holds, the proof works in the same way as the one above with the auxiliary function .
Overview. Implications of mean value theorems
[Bearbeiten]In the introduction, we already mentioned that several important results can be deduced from the mean value theorem.
- We have proved Lipschitz continuity of differentiable functions with limited derivation. This allows to show Lipschitz continuity of numerous functions.
- Another practical conclusion is the constant function theorem. This states that a function is constant if (the derivative is constantly zero). Thus we can derive the identity theorem of differential calculus. It says that two functions with identical derivative differ only by one constant. It is an essential part of the fundamental theorem of calculus . A further consequence of the criterion for constance is the characterisation of the exponential function via the differential equation .
- Likewise, the mean value theorem serves for proving the monotony criterion for differentiable functions. This establishes a connection between the monotonicity of the function and the sign of the derivative function. More precisely, is monotonically increasing (or decreasing) exactly when (or ). From this, one can derive a sufficient criterion for the existence of an extremum of a function at a point.
- From the second mean value theorem, L'Hospital's rule can be concluded. With their help, numerous limit values of quotients of two functions can be calculated, computing certain derivatives.
The points listed are summarised in the following overview diagram:



![{\displaystyle f:a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5674fb2127019780e5541997d5d8919f1d6b6f8)














![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)







![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)







![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)



![{\displaystyle H:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e8df43c0e303136cb915539221cc9ff141727b5)





![{\displaystyle H:[a,b]\to \mathbb {R} ,\ H(x)=f(x)-{\tfrac {f(b)-f(a)}{b-a}}(x-a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93175c5a90eaad13904db32ce8dc945043727007)
![{\displaystyle {\begin{aligned}H(a)&=f(a)-{\frac {f(b)-f(a)}{b-a}}(a-a)\\[0.5em]&=f(a)\\[0.5em]&=f(b)-(f(b)-f(a))\\[0.5em]&=f(b)-{\frac {f(b)-f(a)}{b-a}}(b-a)=H(b)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/171d10772a21b61f6e646c471d7ebf7df37ad7c6)







![{\displaystyle f:[0,1]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2de6d0d4c98d4ca7ad937c772dc3e3e914b062f5)


![{\displaystyle f':[0,1]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d30b7ed7936385475d9d8173c519fd9b7937b3a7)







![{\displaystyle [0,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/725684c883c7ef386e8a0fe4d111e72c565747ed)









![{\displaystyle {\begin{aligned}&&\ln(x)&<x-1\\[0.3em]&\iff {}&{\frac {\ln(x)}{x-1}}&<1\\[0.3em]&\iff {}&{\frac {\ln(x)-\ln(1)}{x-1}}&<1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c8f57dc021e05c29b46571f163315655f37e77e)


![{\displaystyle \ln :[1,x]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c59d5dca9f8ac103b841870fc529b38449155993)








![{\displaystyle {\begin{aligned}&&1-{\frac {1}{x}}&<\ln(x)\\[0.3em]&\iff {}&{\frac {x-1}{x}}&<\ln(x)\\[0.3em]&\iff {}&{\frac {1}{x}}&<{\frac {\ln(x)}{x-1}}\\[0.3em]&\iff {}&{\frac {1}{x}}&<{\frac {\ln(x)-\ln(1)}{x-1}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8098ee1cf385d5edccd5eb34c56011c4bc554dbe)



![{\displaystyle f:[1,x]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae5a5dec32656c8990c6f05e3f809f5cf6f4036f)

![{\displaystyle [1,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63470e8fe9faf7ae30b257d12486bf1730330e5f)

![{\displaystyle {\begin{aligned}&&f'(\xi )&={\frac {f(x)-f(1)}{x-1}}\\[0.3em]&\iff {}&\ln '(\xi )&={\frac {\ln(x)-\ln(1)}{x-1}}\\[0.3em]&\iff {}&{\frac {1}{\xi }}&={\frac {\ln(x)}{x-1}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41b93e44c00194c78125aef7879c19a0ee07ae6f)
![{\displaystyle {\begin{aligned}&&{\frac {\ln(x)}{x-1}}={\frac {1}{\xi }}&{\overset {\xi >1}{<}}{\frac {1}{1}}=1\\[0.3em]&\iff {}&\ln(x)&<x-1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bafecc04a3a51865c64d28d1d83b0dbc0f31b72)

![{\displaystyle {\begin{aligned}&&{\frac {\ln(x)}{x-1}}&={\frac {1}{\xi }}{\overset {\xi <x}{>}}{\frac {1}{x}}\\[0.3em]&\iff {}&\ln(x)&>{\frac {x-1}{x}}=1-{\frac {1}{x}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ba92153fe95794a5e32d0b36538c904c64b9db8)











![{\displaystyle x,y\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e14f38807bc231b9e43d45c8e909d463afb17b5)

![{\displaystyle [x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7bd6292c6023626c6358bfd3943a031b27d663)









![{\displaystyle {\begin{aligned}|(\sin )'(x)|&=|\cos(x)|\leq 1\\[0.3em]|(\cos )'(x)|&=|\sin(x)|\leq 1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01a9da11a276c61246d359dd92c9fd2e9a4e6076)







![{\displaystyle x,{\tilde {x}}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73eb4a9707daa29cfced5f7ec72abbdad44b149c)











![{\displaystyle s:[t_{0},t_{1}]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f8eab7f810b860ef99b58cb9d813f0471a88404)





![{\displaystyle f,g:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e569de0fc730b7a75b46b6fd57598e0c94712f91)





![{\displaystyle F:[a,b]\to \mathbb {R} ,\ F(x)=f(x)-{\tfrac {f(b)-f(a)}{g(b)-g(a)}}(g(x)-g(a))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d038fe996fbc6b232d47850228e8b8db09b689a6)



![{\displaystyle {\begin{aligned}f:[0,1]\to \mathbb {R} ,\ f(x)=3x^{4}-2x^{3}-x^{2}+1\\g:[0,1]\to \mathbb {R} ,\ g(x)=4x^{3}-3x^{2}-2x\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87f633b17bc7f1e9c6467f0524c5b20e2fde56f5)







![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)














