Proving discontinuity – Serlo
Overview
[Bearbeiten]Recall that whenever we want to prove the negation of a statement about some elements of a set, we need to show that there as at least one element in that set for which the statement is not true. So, in order the prove the discontinuity of a function, all you have to show is that the function has (at least) one point of discontinuity. There are several methods available for proving the existence of a point of discontinuity:
- Sequence criterion: Show that the function doesn't fulfill the sequence criterion at one particular point
- Considering the left- and right-sided limits: Calculate the left-sided and right-sided limits of the function at a particular point. If either one of these limits doesn't exist, or if the limits are different, then the function is discontinuous at that point.
- Epsilon-Delta Criterion: Show that the function doesn't fulfill the epsilon-delta criterion at a particular point.
Sequence Criterion
[Bearbeiten]→ Main article: Sequential definition of continuity
Review: Sequence Criterion
[Bearbeiten]Definition (Sequence criterion of continuity for a single argument)
A function with is continuous at an argument , if for all squences with and there is:
Sketch of the proof
[Bearbeiten]In order to show that a function is discontinuous at using the sequence criterion, we need to find one specific sequence of arguments with for all which is converging to , such that the sequence of function values does not converge to . So there shall be but . In order for to hold, there are two cases to be distinguished:
- The sequence of function values diverges.
- The sequence of function values converges, but its limit is not .
Therefore, a proof of discontinuity using the sequence criterion could take the following form:
Let be a function defined by . This function is discontinuous at for the following reason: We take the sequence with and all these elements are inside the domain of definition for . This sequence converges to
However, there is . And instead, there is ...Proof that diverges or that the limit of exists and is different from ...
Example exercises
[Bearbeiten]Exercise (Discontinuity of the topological sine function)
Prove discontinuity of the following function:
How to get to the proof? (Discontinuity of the topological sine function)
Discontinuity of means that this function has at least one argument where is discontinuous. For each , is equal to the functionn in a sufficiently small neighbourhood of . Since is just a composition of continuous functions, it is continuous itself and therefore, must be continuous for all , as well. So we know that the discontinuity may only be situated at .
In order to prove that is discontinuous at , we need to fincd a sequence of arguments converging to but with . To find such a function, let us take a look at the graph of the function :
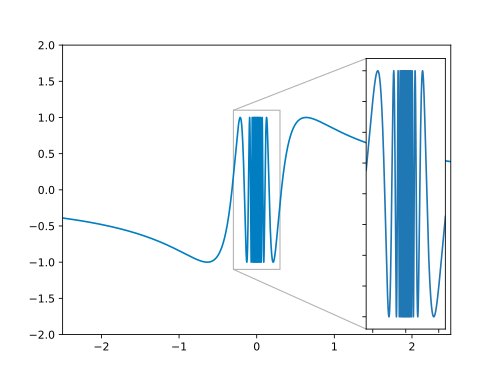
In this figure, we recognize that takes any value between and infinitely often in the vicinity of . So, for instance, we may just choose such that is always . This guarantees that - and actually any other real number between and in place of would do the job. But we need to make a specific choice for , and is a very simple one. In addition, we will choose to converges to zero from above.
The following figure also contains the sequence elements beside our function . We may clearly see that for the sequence of function values converges to , which is different from the function value :
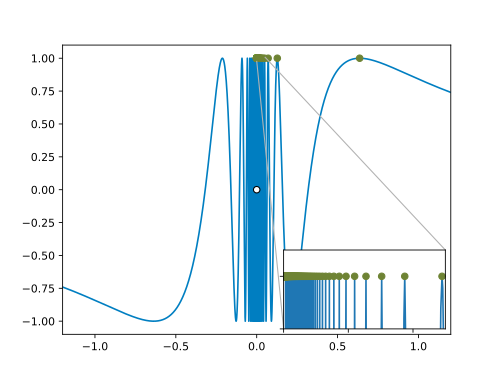
But what are the exact values of these for which we would like to have To answer this question, let us resolve the equation for :
So for each with , we have . In order to get positive converging to zero from above, we may for instance choose . In that case:
And we have seen that . So we found just a sequence of arguments , which proves discontinuity of at .
Proof (Discontinuity of the topological sine function)
Let with for and . We consider the sequence defined by . For this sequence:
And there is:
Hence, although . This proves that is discontinuous at and therefore it is a discontinuous function.
Epsilon-Delta Criterion
[Bearbeiten]→ Main article: Epsilon-delta definition of continuity
Review: Epsilon-Delta Criterion
[Bearbeiten]Definition (Epsilon-Delta definition of discontinuity)
A function with is discontinuous at , if and only if there is an , such that for all a with and exists. Mathematically written, is discontinuous at iff
General proof structure
[Bearbeiten]The Epsilon-Delta criterion of discontinuity can be formulated in predicate logic as follows:
From here we get a schematic that allows us the prove the discontinuity of a function using the delta-epsilon criterion:
Example exercise
[Bearbeiten]Exercise (Discontinuity of the topological sine fucntion)
Prove the discontinuity at for the topological sine function:
How to get to the proof? (Discontinuity of the topological sine fucntion)
In this exercise, discontinuity has to be shown for a given function. This is done by the negation of the epsilon-delta criterion. Our objective is to find both an and an , such that and . Here, may be chosen depending on , while has to be the same for all . For a solution, we may proceed as follows
Step 1: Simplify the target inequality
First, we may simplify the two inequalities which have to be fulfilled by plugging in and . We therefore get: and .
Step 2: Choose a suitable
We consider the graph of the function . It will help us finding the building bricks for our proof:

We need to find an , such that there are arguments in each arbitrarily narrow interval whose function values have a distance larger than from . Visually, no matter how small the width of the --rectangle is chosen, there will always be some points below or above it.
Taking a look at the graph, we see that our function oscillates between and . Hence, may be useful. In that case, there will be function values with in every arbitrarily small neighborhood around . We choose . This is visualized in the following figure:
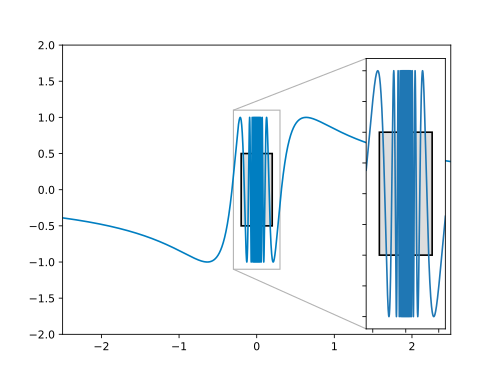
After has been chosen, an arbitrary will be assumed, for which we need to find a suitable . This is what we will do next.
Step 3: Choice of a suitable
We just set . Therefore, has to hold. So it would be nice to choose an with . Now, is obtained for any with . The condition for such that the function gets 1 is therefore:
So we found several , where . Now we only need to select one among them, which satisfies for the given . Our depend on . So we have to select a suitable , where . To do so, let us plug into this inequality and solve it for :
So the condition on is . If we choose just any natural number above this threshold , then will be fulfilled. Such a has to exist by Archimedes' axiom (for instance by flooring up the right-hand expression). So let us choose such a and define via . This gives us both and . So we got all building bricks together, which we will now assemble to a final proof:
Proof (Discontinuity of the topological sine fucntion)
Choose and let be arbitrary. Choose a natural number with . Such a natural number has to exist by Archimedes' axiom. Further, let . Then:
In addition:
Hence, the function is discontinuous at .
Exercises
[Bearbeiten]Epsilon-delta criterion: Signum function
[Bearbeiten]Exercise (Discontinuity of the signum function)
Prove that the signum function is is discontinuous:
How to get to the proof? (Discontinuity of the signum function)
In order to prove discontinuity of the entire function, we just have to find one single argument where it is discontinuous. Considering the graph of , we can already guess, which argument this may be:

The function has a jump at . So we expect it to be discontinuous, there. It remains to choose an that makes it impossible to find a , that makes the function fit into the --rectangle. This is done by setting smaller than the jump height - for instance . For that , no matter how is given, there will be function values above or below the --rectangle.
So let be arbitrary. We need to show that there is an with but . Let us take a look at the inequality :
This inequality classifies all that can be used for the proof. The particular we choose has to fulfill :
So our needs to fulfill both and . The second inequality may be achieved quite easily: For any , the value is either or . So does always fulfill .
Now we need to fulfill the first inequality . From the second inequality, we have just concluded . This is particularly true for all with . Therefore, we choos to be somewhere between and , for instance .
The following figure shows that this is a sensible choice. The --rectangle with and is drawn here. All points above or below that rectangle are marked red. These are exactly all inside the interval excluding . Our chosen (red dot) is situated directly in the middle of the red part of the graph above the rectangle:
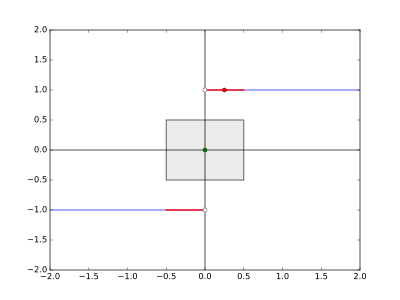
So choosing is enough to complete the proof:
Proof (Discontinuity of the signum function)
We set (this is where is discontinuous). In addition, we choose . Let be arbitrary. For that given , we choose . Now, on one hand there is:
But on the other hand:
So indeed, is discontinuous at . Hence, the function is discontinuous itself.






































![{\displaystyle {\begin{aligned}{\begin{array}{rrrl}&&f(x)&=1\\[0.5em]{\overset {f(0)\neq 0}{\iff {}}}&&\sin \left({\frac {1}{x}}\right)&=1\\[0.5em]\iff {}&\exists k\in \mathbb {Z} :&{\frac {1}{x}}&={\frac {\pi }{2}}+2k\pi \\[0.5em]\iff {}&\exists k\in \mathbb {Z} :&x&={\frac {1}{{\frac {\pi }{2}}+2k\pi }}\end{array}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ee2a00a2f43e5e9d665e22fb3757d1c17b30b5e)






![{\displaystyle {\begin{aligned}\lim _{n\to \infty }f(x_{n})&=\lim _{n\to \infty }f\left({\frac {1}{{\frac {\pi }{2}}+2n\pi }}\right)\\[0.5em]&=\lim _{n\to \infty }\sin \left({\frac {1}{\frac {1}{{\frac {\pi }{2}}+2n\pi }}}\right)\\[0.5em]&=\lim _{n\to \infty }\sin \left({\frac {\pi }{2}}+2n\pi \right)\\[0.5em]&=\lim _{n\to \infty }1=1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a891cfa8167534da2fbdc7f3ff20d74e618118ce)







![{\displaystyle {\begin{array}{l}{\color {Red}\underbrace {{\underset {}{}}{\text{Choose }}\epsilon =\ldots } _{\exists \epsilon >0}}\ {\color {RedOrange}\underbrace {{\underset {}{}}{\text{Let }}\delta >0{\text{ beliebig.}}} _{\forall \delta >0}}\\{\color {OliveGreen}\underbrace {{\underset {}{}}{\text{Choose }}x=\ldots {\text{ Es ist }}x\in D{\text{, weil}}\ldots } _{\exists x\in D}}\\{\color {Black}{\text{We have:}}}\\[0.5em]\quad \quad {\color {DarkOrchid}{\text{Proof for }}|x-x_{0}|<\delta }\\[0.5em]\quad \quad {\color {Blue}{\text{Proof for }}|f(x)-f(x_{0})|\geq \epsilon }\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7213487a0d03d33b17caa29a0e3425762584ae9a)





















![{\displaystyle {\begin{aligned}\left|x\right|<\delta &\iff \left|{\frac {1}{{\frac {\pi }{2}}+2k\pi }}\right|<\delta \\[0.5em]&\iff {\frac {1}{{\frac {\pi }{2}}+2k\pi }}<\delta \\[0.5em]&\iff 2k\pi +{\frac {\pi }{2}}>{\frac {1}{\delta }}\\[0.5em]&\iff 2k\pi >{\frac {1}{\delta }}-{\frac {\pi }{2}}\\[0.5em]&\iff k>{\frac {1}{2\pi }}\left({\frac {1}{\delta }}-{\frac {\pi }{2}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25af20f89560c07b3820129dd8d10ce2b902d7e9)


![{\displaystyle {\begin{aligned}k>{\frac {1}{2\pi }}\left({\frac {1}{\delta }}-{\frac {\pi }{2}}\right)&\implies 2k\pi >{\frac {1}{\delta }}-{\frac {\pi }{2}}\\[0.5em]&\implies 2k\pi +{\frac {\pi }{2}}>{\frac {1}{\delta }}\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ {\frac {1}{a}}>{\frac {1}{b}}>0\iff 0<a<b\right.}\\[0.5em]&\implies {\frac {1}{{\frac {\pi }{2}}+2k\pi }}<\delta \\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ {\frac {1}{{\frac {\pi }{2}}+2k\pi }}>0\right.}\\[0.5em]&\implies \left|{\frac {1}{{\frac {\pi }{2}}+2k\pi }}\right|<\delta \\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ x={\frac {1}{{\frac {\pi }{2}}+2k\pi }}\right.}\\[0.5em]&\implies \left|x\right|<\delta \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad7985a4bd1699ae43466813ef6cb9d56079acd3)
![{\displaystyle {\begin{aligned}\left|f(x)-f(0)\right|&=\left|\sin \left({\frac {1}{x}}\right)-0\right|\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ x={\frac {1}{{\frac {\pi }{2}}+2k\pi }}\right.}\\[0.5em]&=\left|\sin \left({\frac {\pi }{2}}+2k\pi \right)\right|\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sin \left({\frac {\pi }{2}}+2k\pi \right)=1\right.}\\[0.5em]&=\left|1\right|\geq {\frac {1}{2}}=\epsilon \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3fa308896735c40f86148e2d6dfd09fa66590f03)




![{\displaystyle {\begin{aligned}{\begin{array}{rrl}&|f(x)-f(x_{0})|&\geq \epsilon \\[0.5em]\iff &|\operatorname {sgn}(x)-\operatorname {sgn}(x_{0})|&\geq {\frac {1}{2}}\\[0.5em]\iff &|\operatorname {sgn}(x)-\operatorname {sgn}(0)|&\geq {\frac {1}{2}}\\[0.5em]\iff &|\operatorname {sgn}(x)|&\geq {\frac {1}{2}}\end{array}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcc44b40d90ac63c780e7d0dc1f8f767d68457c2)









![{\displaystyle {\begin{aligned}{\begin{array}{rrl}&{\frac {1}{2}}&<1\\[0.5em]\implies &{\frac {1}{2}}\delta &<\delta \\[0.5em]\implies &\left|{\frac {1}{2}}\delta \right|&<\delta \\[0.5em]\implies &\left|{\frac {1}{2}}\delta -0\right|&<\delta \\[0.5em]\implies &|x-x_{0}|&<\delta \end{array}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57e7f87669f9fd77335e50cfd861641e94a2002b)
![{\displaystyle {\begin{aligned}|f(x)-f(x_{0})|&=|\operatorname {sgn}(x)-\operatorname {sgn}(x_{0})|\\[0.5em]&=\left|\operatorname {sgn} \left({\frac {\delta }{2}}\right)-\operatorname {sgn}(0)\right|\\[0.5em]&=\left|1-0\right|\\[0.5em]&=1\\[0.5em]&\geq {\frac {1}{2}}=\epsilon \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3167c8c11ff695bed71173f7068a3da353af4e5)
