Sine and cosine – Serlo
In this chapter we introduce the two trigonometric functions sine and cosine. They are the most important trigonometric functions and are used in geometry for triangle calculations and trigonometry. Waves such as electromagnetic waves and harmonic oscillations can be described by sine and cosine functions, so they are also omnipresent in physics.
Definition via unit circle
[Bearbeiten]There are several ways to define the sine and cosine. The visually most accessible one is that on the unit circle. Here, a point is considered that is located on a circle around the origin with radius . The axis includes the angle with the distance from the origin to :

The angle uniquely determines where the point is located. Thus the -coordinate and the -coordinate can be described by a function depending on . We call these functions and the sine function and cosine function respectively:

In the following we take as the angle and write instead of and instead of . This results in the following definition:
Definition (Definition of sine and cosine on the unit circle)
Let be the point on the unit circle whose position vector with the horizontal coordinate axis encloses the angle . The coordinates of are then defined as . Here is called the cosine of and the sine of .
Graph of the sine and cosine function
[Bearbeiten]The following animation shows how the graphs of the sine and cosine functions are constructed step by step:

This gives the following graph for the sine function:
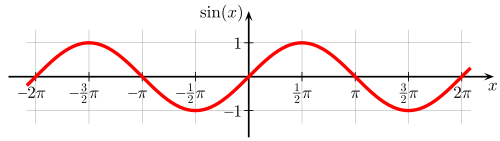
For the cosine function we get:

Definition via exponential function
[Bearbeiten]Representation by the complex exponential function
[Bearbeiten]The sine and cosine function can also be defined as the sum of certain complex exponential functions. With this representation, properties of the sine and cosine can be demonstrated in a particularly elegant way.
Definition (Sine and cosine via complex exponential function)
We define the functions (sine) and (cosine) by
These functions are well-defined: For every real number the complex number is the complex conjugate of . Thus is a real number and there is . In an analogous way, one can show that .
Deriving the exponential definition
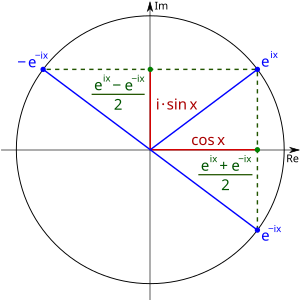
[Bearbeiten]One can show that is the point on the unit circle whose position vector with the axis encloses the angle :

The real part of the complex number is , and the imaginary part is . There is hence . At we consider the angle . The point is mirrored on the real axis on the other side:

Thus the real part of is the same as for , i.e. . However, the imaginary part is multiplied by the number and thus equal to . We get . So we have:
By adding both equations we get:
And by subtracting the two equations we get:
Thus we have derived the two definitions and . This derivation is illustrated again in the following figure:
Series expansion of sine and cosine
[Bearbeiten]Definition as a series
[Bearbeiten]
.
Another mathematically precise definition that does not require geometrical notions is the so-called series representation, in which the sine and cosine are defined as a series. The series representation is less visual than the definition over the unit circle, but with it some properties of the sine and cosine can be proved more easily. It can also be used to extend the sine and cosine to complex numbers.
Definition (sine and cosine)
We define the functions (sine) and (cosine) by
Well-definedness
[Bearbeiten]We have to prove that our series representation of the sine and cosine function is well-defined. That is, we have to show that for all the series and converge to a real number.
Theorem
For all real numbers the series and converge.
Proof
We prove the theorem explicitly for the series of the sine function. The proof for the series of the cosine function can be done analogously. For we first find:
For the series therefore converges. For we apply the ratio test. For this, let for all , so that we have . There is:
Since the series converges according to the ratio test.
Equivalence of exponential and series definition
[Bearbeiten]We have learned several definitions of the sine and cosine function. We have already established a connection between the exponential representation and the definition on the unit circle. Now we need to show that the exponential and series definitions are equivalent to each other.
Theorem
There is for all :
Thus it does not matter whether the sine or cosine function is defined via its series representation or via its exponential representation.
Proof
We already know from the chapter on the exponential function (missing) that the exponential function has the series representation . If we now substitute for in the series representation, we get:
Now we plug into the series representation of the exponential function:
If we write and then we have shown that
For the difference, we get
So:
And analogously:
Hence:

















![{\displaystyle {\begin{aligned}&\sin :\mathbb {R} \to \mathbb {R} :x\mapsto {\frac {1}{2\mathrm {i} }}\left(\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}\right)\\[0.3em]&\cos :\mathbb {R} \to \mathbb {R} :x\mapsto {\frac {1}{2}}\left(\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18fea4d6273aa2215edb762bc859c1a7cb1a071f)












![{\displaystyle {\begin{aligned}e^{\mathrm {i} \theta }&=\cos(\theta )+\sin(\theta )\mathrm {i} \\[0.3em]e^{-\mathrm {i} \theta }&=\cos(\theta )-\sin(\theta )\mathrm {i} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aff8b06ff43c4b3ef1375f75e521471f69091aa8)







![{\displaystyle {\begin{aligned}&\sin :\mathbb {R} \to \mathbb {R} ,x\mapsto \sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k+1)!}}x^{2k+1}\\[0.3em]&\cos :\mathbb {R} \to \mathbb {R} ,x\mapsto \sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k)!}}x^{2k}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe8c17ff3511f1dab32e72316bb4b1f31f754f32)




![{\displaystyle {\begin{aligned}&\sum _{k=0}^{\infty }{{\frac {(-1)^{k}}{(2k+1)!}}x^{2k+1}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ x=0\right.}\\[0.3em]=\ &\sum _{k=0}^{\infty }{{\frac {(-1)^{k}}{(2k+1)!}}0^{2k+1}}\\[0.3em]=\ &\sum _{k=0}^{\infty }{0}=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/372ae50417058d96933aab61faa49ed58b3b05c5)




![{\displaystyle {\begin{aligned}&\lim _{k\to \infty }{\left|{\frac {a_{k+1}}{a_{k}}}\right|}\\[0.3em]=\ &\lim _{k\to \infty }{\left|-{\frac {x^{2(k+1)+1}\cdot (2k+1)!}{x^{2k+1}\cdot (2(k+1)+1)!}}\right|}\\[0.3em]=\ &\lim _{k\to \infty }{\left|-{\frac {x^{2k+3}\cdot (2k+1)!}{x^{2k+1}\cdot (2k+3)!}}\right|}\\[0.3em]=\ &\lim _{k\to \infty }{\left|{\frac {x^{2}}{(2k+2)(2k+3)}}\right|}=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d1d4cf3d12509d03e5e2a4abe8227bbf48e17e9)

![{\displaystyle {\begin{aligned}\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k+1)!}}x^{2k+1}&={\frac {1}{2\mathrm {i} }}\left(\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}\right)\\[0.5em]\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k)!}}x^{2k}&={\frac {1}{2}}\left(\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a78644e97a0c9226c1a8999da18e8db69fd455)


![{\displaystyle {\begin{aligned}\mathrm {e} ^{\mathrm {i} {\tilde {x}}}&=\sum _{k=0}^{\infty }{\frac {(\mathrm {i} {\tilde {x}})^{k}}{k!}}\\[0.5em]&\ {\color {OliveGreen}\left\downarrow \ {\text{absolute convergence}}\implies {\text{split the series}}\right.}\\[0.5em]&=\sum _{l=0}^{\infty }{\frac {(\mathrm {i} {\tilde {x}})^{2l}}{(2l)!}}+\sum _{l=0}^{\infty }{\frac {(\mathrm {i} {\tilde {x}})^{2l+1}}{(2l+1)!}}\\[0.5em]&\ {\color {OliveGreen}\left\downarrow \ \mathrm {i} ^{2l}=(-1)^{l}{\text{and }}\mathrm {i} ^{2l+1}=\mathrm {i} \cdot (-1)^{l}\right.}\\[0.5em]&=\sum _{l=0}^{\infty }{\frac {(-1)^{l}}{(2l)!}}{\tilde {x}}^{2l}+\mathrm {i} \sum _{l=0}^{\infty }{\frac {(-1)^{l}}{(2l+1)!}}{\tilde {x}}^{2l+1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/616491e86b7a50e65c07f2052d08e49e66d0e203)

![{\displaystyle {\begin{aligned}\mathrm {e} ^{-\mathrm {i} {\tilde {x}}}&=\sum _{k=0}^{\infty }{\frac {(-\mathrm {i} {\tilde {x}})^{k}}{k!}}\\[0.5em]&\ {\color {OliveGreen}\left\downarrow \ {\text{absolute convergence}}\implies {\text{split the series}}\right.}\\[0.5em]&=\sum _{l=0}^{\infty }{\frac {(-\mathrm {i} {\tilde {x}})^{2l}}{(2l)!}}+\sum _{l=0}^{\infty }{\frac {(-\mathrm {i} {\tilde {x}})^{2l+1}}{(2l+1)!}}\\[0.5em]&\ {\color {OliveGreen}\left\downarrow \ (-\mathrm {i} )^{2l}=(-1)^{l}{\text{and }}(-\mathrm {i} )^{2l+1}=-\mathrm {i} \cdot (-1)^{l}\right.}\\[0.5em]&=\sum _{l=0}^{\infty }{\frac {(-1)^{l}}{(2l)!}}{\tilde {x}}^{2l}-\mathrm {i} \sum _{l=0}^{\infty }{\frac {(-1)^{l}}{(2l+1)!}}{\tilde {x}}^{2l+1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d14a33819af50a7df07ed32397153591b166850d)







