Continuity of functions – Serlo
Introduction
[Bearbeiten]Naive intuition behind continuity
[Bearbeiten]The term continuity is occasionally used to describe a property of certain processes. We refer to a process as continuous that proceeds without sudden interruptions or unexpected behaviour. A similar notion can be applied to functions and their respective graphs as well. In the following examples we will notice that some graphs have sudden “jumps”:
-
The graph of the function can be drawn with a single stroke of the pencil.
-
Similarly the graphs of Sine and Cosine can be drawn without lifting the pencil as well.
-
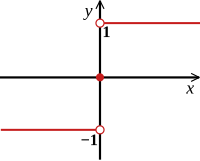
The sign function has a sudden "jump" at .
-
The graph of the ceiling function that maps a number to the least integer that is greater than or equal to has sudden "jumps".
Based on the above examples, we assume that functions can be classified into two groups: those that can be (continuously) drawn with a single stroke of a pencil and those which show sudden "jumps". This criterion seems very intuitive. However, we will quickly stumble upon certain functions which are continuous in a formal mathematical sense although our naive intuition may tell us something different. Nonetheless our intuition will be certainly helpful in understanding the notion of continuity.
Problems with our naïve intuition behind continuity
[Bearbeiten]Let us have a look at the function and an adapted version of the sign function
Both functions are continuous in a formal mathematical sense although their graphs have "jumps" at :
-
The function is continuous although the graph cannot be drawn with a single stroke of the pencil.
-
The sign function that is not defined for is continuous as well.
Our current naïve intuition is misleading in both cases since it doesn't take into account that both functions aren't defined for . In fact, it never makes sense to investigate continuity at points at which a function is not defined. Nonetheless, we just call those points discontinuities. Although a function may have discontinuities when being undefined at certain points we will not take those exact points into consideration when talking about overall continuity.
Unfortunately our intuition, even with the remark about undefined points, is not sufficient to decide for all possible functions, whether they are continuous or not. Examples for when we are not able to come to a satisfactory conclusion are the following:
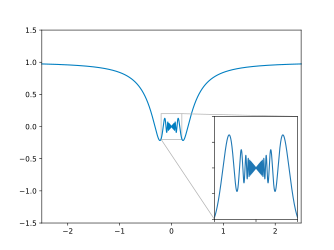
Both functions are oscillating around which can be seen here:
-
The function oscillates around .
-
The function oscillates in a way similar to .
Are those functions continuous or not? Our intuition does not yield a conclusive result since it is unclear whether those graphs can be drawn with a single stroke of the pencil. The corresponding pencil line would just be infinitely long! At this point it seems that we have to come up with a concise definition for continuity of functions.
What is the purpose of continuity?
[Bearbeiten]We have seen that our intuition has some shortcomings and thus we are in need of a concise definition for continuity. But why are we even interested in continuity in the first place?
- Continuous functions are very lovely since they have a lot of useful properties. Those properties can be used (and to some extent even exploited) in order to simplify some proofs.
- Approximating values of a function inherently requires to be continuous even though we sometimes aren't aware of that. Instead of computing we can consider the approximation as long as is sufficiently close to . This is only reasonable if is continuous at .
- Many processes and relations between physical quantities are continuous. Of course, there are discontinuous processes as well like fluctuations at the stock exchange or the behaviour of chaotic systems like the weather.
- Continuous functions between topological spaces preserve neighbourhoods, i.e. any point will have at least the same neighbours after a transformation and no two points are pulled apart.
- The techniques used in proofs concerning continuity will be useful in other topics of calculus as well.
Formal definition of continuity
[Bearbeiten]How can we deduce a formal definition?
[Bearbeiten]So far we have stumbled upon functions that are continuous although they cannot be drawn with a single stroke of the pencil. Since this observation conflicts with our initially described intuition we are in need of a concise and formal definition of continuity. In order to infer such a definition we will make a list of certain properties that should hold true for every continuous function. Afterwards we will decide on just one property that we consider to be the most characteristic for continuity. Such a property has to be both succinct and generalizable. Some of the properties, which we would like continuous functions to have, include:
- Small causes only have small impacts: minor changes to an argument of a continuous function will yield minor changes to the value of the function.
- The limit will commute with the composition for continuous functions. For a sequence with and a continuous function it holds true that as long as .
- Continuous functions preserve neighbourhoods, i.e. any point will have at least the same neighbours after a transformation and no two points are pulled apart (the graph has no sudden "jumps").
- Intermediate value property: For a given interval a continuous function will take all values between and at least once.
During the course of this chapter and the other chapters as well we will notice that these properties do make sense. Over the years, formal definitions were established based upon the first two properties from our list. We will formalize them into the "Epsilon-Delta-Criterion" and an alternative definition in terms of limits of sequences.
Epsilon-Delta-criterion
[Bearbeiten]→ Main article: Epsilon-delta definition of continuity
The Epsilon-Delta-criterion formalizes the intuition that minor changes to an argument of a continuous function yield minor changes to the value of the function as well as preserving neighbourhoods. The definition of continuity at a certain point is the following:
Definition (Epsilon-Delta-definition of continuity)
A function with is continuous at , if and only if for any there is a , such that holds for all with . Written in mathematical symbols, that means is continuous at if and only if
Definition in terms of limits of sequences
[Bearbeiten]→ Main article: Sequential definition of continuity
There exists an equivalent definition in terms of limits of sequences. Continuous functions commute with the limit. The definition of continuity at a certain point is the following:
Definition (Sequence criterion of continuity for a single argument)
A function with is continuous at an argument , if for all squences with and there is:
Both definitions are used to show continuity at a specific point. A function is considered continuous if it is continuous at every point.
Why don't we use the intermediate value property as a definition?
[Bearbeiten]The intermediate value property states that for a given interval a continuous function will take all values between and at least once. Until the 19th century it was believed that the intermediate value property is equivalent to continuity[1]. It is hard to believe that there exists a function that is not continuous at any point but still satisfies the intermediate value property.
In this case, our intuition is misleading. The intermediate value property is too weak to serve as a criterion for continuity. A counterexample is the Conway base 13 function. This function takes all real values for a given interval no matter how small that interval is. Every minor change to an argument will yield arbitrarily big changes to the value of the function. The Conway base 13 function fulfills the intermediate value property although being continuous nowhere.
Overview on the properties of continuous functions
[Bearbeiten]Now that we got to know the definition of continuous functions we are able to take a look at some of their useful properties.
Small causes have small impacts
[Bearbeiten]→ Main article: Epsilon-delta definition of continuity
Our naive intuition claims that continuous functions can be drawn with a single stroke since they have no sudden "jumps". Take a function into consideration that takes the value at the position . Changing the argument to yields the new function value which can be depicted by the following sketch:

For a continuous function the distance between and can be arbitrarily small for arbitrarily small which is possible since minor changes to an argument of a continuous function yield minor changes to the value of the function itself. Therefore the approximation implies . This property has been characterized by the Epsilon-Delta-criterion.
The limit will commute with the composition for continuous functions
[Bearbeiten]→ Main article: Sequential definition of continuity
Let be a continuous function and a convergent sequence with . In order to deduce the value of we can rely on the definition in terms of sequences which yields the following:
This property will simplify the computation of limits since is arbitrarily close to as long as is sufficiently close to which is possible since minor changes to an argument of a continuous function yield minor changes to the value of the function itself.
An example which shows the usefulness of this property is the composition of the exponential function with the sequence . It follows that
The following sketch illustrates that example:

Continuous functions between topological spaces preserve neighbourhoods
[Bearbeiten]The intuition that small causes have small impacts can be described in terms of neighbourhoods: Continuous functions preserve neighbourhoods, i.e. any point will have at least the same neighbours after a transformation and no two points are pulled apart (the graph has no sudden "jumps"). This phenomenon is analyzed in the field of topology.
Intermediate value theorem
[Bearbeiten]→ Main article: Intermediate value theorem
Let be an arbitrary value and a function that takes at and the values and respectively (assuming ):

If is continuous and defined on the entire interval , then it is possible to draw the corresponding graph from to with a single stroke. Thus the graph must intersect the line at least once and there exists at least one position for which :

Intuitively it is clear that this is not only true for but for all values between and as well. Therefore takes all values between and at least once.
Using the intermediate value theorem we can show that has at least one solution. First, we observe that . Since the sine is continuous it follows from the intermediate value theorem that there exists at least one between and with . This method can be applied to many other equations in order to show the existence of a solution.
Compositions of continuous functions are continuous
[Bearbeiten]→ Main article: Composition of continuous functions
Compositions, sums and products of continuous functions are continuous as well. Since both the identity function and the constant function are continuous, their composition is as well.
Intuition of continuity
[Bearbeiten]As we have seen, our initial intuition of continuity was not entirely correct. In order to prevent wrong conclusions we should rephrase our intuition according to the formal definition:
Minor changes to the argument of a continuous function yield arbitrarily small changes to the value of the function.
An alternative intuition may be obtained by the definition in terms of limits of sequences:
All functions that commute with the limit are continuous, i.e. .
Hint
Be careful: the improved intuitions crucially differ from our first attempt describing continuous functions as functions without sudden jumps. For continuous functions you should usually work with one of the two explanations above, i.e. "small causes have small impact", or "function commutes with limit".
Important properties of continuity
[Bearbeiten]So far we have became acquainted with the general notion of continuity but we haven't discussed the important properties of the concept yet.
Continuity is a local property
[Bearbeiten]Our intuition makes us believe that continuity is a global property, however the formal definition implies otherwise. To make use of the definition, we only have to take an arbitrarily small neighbourhood of a point in order to figure out whether the function is continuous at that point. Two functions that are equal in an arbitrarily small neighbourhood of a point must be either both continuous or discontinuous.
With that in mind we can prove the continuity of the specific sign function that is not defined for :
This function is locally constant, i.e. for each point there exists a neighbourhood such that restricted to that neighbourhood is constant:

Such a restriction exists for every single point of the specific sign function. Hence it behaves like a constant function in terms of continuity. Since constant functions are continuous that property transfers to the specific sign function as well. Therefore the specific sign function is continuous at every point. This can be shown alternatively by using the definition in terms of sequence limits or using the Epsilon-Delta-criterion.
Why is continuity a local property?
[Bearbeiten]In order to understand why continuity is a local property we may also go back to our first intuition of continuity. This intuition tells us that a function is discontinuous at a point if the respective graph has a sudden jump there. Continuity is equivalent to the absence of a sudden jump at a point. Since having a sudden jump at a specific point is a local property, its converse, the absence of a sudden jump, is as well.
Meaning of the domain of definition for continuity
[Bearbeiten]

The specific sign function shows how important the domain of definition is for continuity. While the (non-specific) sign function
defined on all real numbers is not continuous, we may obtain a continuous specific sign function by just "kicking" the out of the domain of definition:
Even though both functions use the same rule for assigning values to arguments , one is continuous and the other one not! This example shows how important it is to consider the domain of definition when analyzing whether a function is continuous or not.
Continuity is only defined on the domain of definition
[Bearbeiten]
Continuity s only define for arguments of a function. Therefore, statements about continuity at a point only make sense, if the function is well-defined at the respective argument . Both the Epsilon-Delta-criterion and the sequence criterion use the value of the function at this point. Hence, the function must be defined at in order to apply those definitions.
Now, consider the function . This function is not defined at . Asking the question, whether is continuous at therefore makes about as much sense as asking whether it is continuous at the summit of the Mount Everest or at some place on the moon. Those are all points, where is not defined, so the question makes no sense! By contrast, it indeed makes sense to say: „We cannot extend to in a way that it stays continuous.“ So we carefully need to distinguish between continuity of a function and being able to find a continuous extension.
Remember: continuity is only defined for in the domain of definition. Outside this domain, statements about continuity do not make sense.
Outlook on the next chapters
[Bearbeiten]In the next chapters, we will talk about different definitions for continuity. We will learn, how to show continuity of a function and we will prove some important properties of continuous functions (such as the intermediate value property).
Quellen
[Bearbeiten]- Thread How can I motivate the formal definition of continuity? der Q&A Seite matheducators.stackexchange.com mit verwendeten Beiträgen von Amir Asghari, user52817 und Carl Mummert. Alle Inhalte des Threads stehen unter einer CC-BY-SA 3.0 Lizenz. Abgerufen am 17.07.2016.
- Thread Why should we study continuity? der Q&A Seite matheducators.stackexchange.com mit verwendeten Beiträgen von Daniel R. Collins, Rory Daulton, fmlin, Joel, Benoît Kloeckner und Wrzlprmft. Alle Inhalte des Threads stehen unter einer CC-BY-SA 3.0 Lizenz. Abgerufen am 16.07.2016.
- Antwort auf die Frage „Why is continuity defined as a local property?“ von Jessica B der Q&A Seite matheducators.stackexchange.com, lizenziert unter CC-BY-SA 3.0, abgerufen am 17.07.2016.
- Antwort auf die Frage „Why is continuity only defined on its domain?“ von quid der Q&A Seite matheducators.stackexchange.com, lizenziert unter CC-BY-SA 3.0, abgerufen am 17.07.2016.













![{\displaystyle {\begin{aligned}h&:\mathbb {R} \to \mathbb {R} :x\mapsto h(x)={\begin{cases}\sin \left({\tfrac {1}{x}}\right)&;x\neq 0\\0&;x=0\end{cases}}\\[0.5em]g&:\mathbb {R} \to \mathbb {R} :x\mapsto g(x)={\begin{cases}x\sin \left({\tfrac {1}{x}}\right)&;x\neq 0\\0&;x=0\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f9d3a3bea768248f4c8c9d4669d39afa07b73a6)












![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

















































