The Bolzano-Weierstrass theorem – Serlo
This article concerns about a theorem that can be useful for many proofs in real analysis (and also in deeper maths topics): the Bolzano-Weierstrass theorem. It is named after Bernard Bolzano and Karl Weierstraß.
This theorem guarantees that there are accumulation points whenever a sequence is bounded. It is crucial for proving existence of limits (or at least accumulation points) for such sequences. One may also carry through these proofs using nested intervals, but it is often shorter to just use the Bolzano-Weierstrass theorem - which already makes use of nested intervals.
Some textbooks use the Bolzano-Weierstrass theorem to prove validity of the monotony criterion for sequences and series. One may also go the other way round and prove the Bolzano-Weierstrass theorem if the monotony criterion is known to hold. Another implication of the Bolzano-Weierstrass theorem is that continuous functions on a compact interval with are bounded and take a minimum and a maximum value.
The Bolzano-Weierstrass theorem
[Bearbeiten]The Bolzano-Weierstrass theorem reads as follows:
Theorem (Bolzano-Weierstrass theorem)
Every bounded sequence of real numbers has at least one accumulation point. That means, there is a real number , such that at least one subsequence of converges to .
You can intuitively justify this theorem as follows: A sequence is bounded if and only if all of its infinitely many elements fit inside the finite interval . Putting infinitely many points in a finite interval will necessarily make it crowded. So there should be some regions with a lot of points, crowding very closely together. The Bolzano-Weierstrass theorem now states that around one point , there are infinitely many points in each -neighbourhood. No matter how small is. This is an accumulation point. Note that does not need to be part of the sequence and there may be multiple (even overcountably infinitely many) of those .
Hint
Often, the Bolzano-Weierstrass theorem is formulated in the literature as follows: "Every real and bounded sequence has a convergent subsequence". This formulation is equivalent to the above one.
Why the completeness axiom is necessary
[Bearbeiten]Completeness of the real numbers means that each Cauchy sequence within converges to an element in . Roughly speaking, a Cauchy sequence is a sequence which "looks as if it would converge" and it will be precisely defined elsewhere. For now, you need to know that in and , a Cauchy sequence is any sequence with a limit in . Some of these sequences in converges to an element in , e.g. . The limit would be the only possible accumulation point of . But . So has no limit in , which means the Bolzano-Weierstrass theorem cannot hold for .
The above example shows that the domain of the sequence elements is crucial for the Bolzano-Weierstrass theorem to hold. The complete does work, whereas the incomplete does not. Mathematicians often go one step further and give a name to any domain of a sequence, where the Bolzano-Weierstrass theorem works (i.e. Cauchy sequences have a convergent subsequence). Those sets are called compact. For instance, any bounded and closed interval is compact. Finite unions of these intervals are compact, too. The real numbers are not compact, since the Bolzano-Weierstrass theorem only guarantees for an accumulation point if the sequence is bounded within some . Generally, unbounded sets are not compact.
Proof (by nested intervals)
[Bearbeiten]Proof (Bolzano-Weierstrass theorem)
Let be a bounded sequence. We know that there is a lower bound and an upper bound , such that all sequence elements lie in :

Now, we need to find an accumulation point of the sequence. Certainly, the completeness of will be necessary, which we introduced via nested intervals. Recall: Nested intervals are a way to approximate any real number . Here, is a lower bound and an upper bound for . So is included in each of the nested interval . Nested means that for all , so the intervals are included in each other and get narrower and narrower.
If the width of the intervals converges to , then is indeed the only elements included in all intervals for all .
So if we can construct a sequence of nested intervals which are all including infinitely many points of the sequence , then there must be a point included in all intervals . This is a good candidate for an accumulation point of , as there are infinitely many sequence elements around it.
How do find we find such a sequence of nested intervals containing infinitely many sequence elements? The interval certainly contains infinitely many sequence elements (namely, all of them).

Now, we need to make smaller. So let us divide into two equally large sub-intervals:

Since the sequence contains infinitely many elements, at least one of the two sub-intervals also has to contain infinitely many elements of . Otherwise, there would be only finitely many sequence elements, which is not the case. We define this interval with infinitely many elements as .

We can repeat the step and split into two equal parts:
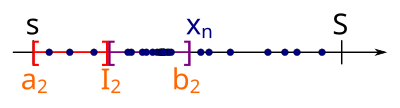
The next interval is chosen as exactly that part of , which in turn contains infinitely many sequence elements. One of the two parts of has to contain infinitely many elements, since there are infinitely many elements in and otherwise, we would only have finitely many elements available. So we can indeed find a suitable with half the width of :
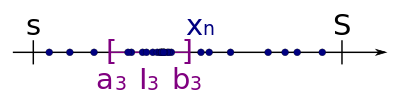
We iterate this procedure arbitrarily many times and get a sequence of nested intervals , where each has half the width of .
Mathematically, we can describe this inductive procedure as follows: We set . In each step, for we define the middle of the interval as and choose
Indeed, the width of is cut into half in each step:
Here, is the width of interval number . Hence,
The interval width tends to . So there must be a unique point , which is included in all intervals . This is the desired accumulation point candidate.
Let us finish the proof by verifying that is indeed an accumulation point. For any , we consider the -neighbourhood of . Since , there must be an with . And since there is (visualize this on a piece of paper or in your head). But now, we constructed the intervals such that they all contain infinitely many elements . So also and contain infinitely many elements.
Since this works for any , we verified that is an accumulation point of , which was to be shown.
Proof (alternatively via monotony criterion)
[Bearbeiten]A further way to prove the Bolzano-Weierstrass theorem goes by the monotony criterion. This criterion says that every monotone and bounded sequence of real numbers converges.
Boundedness is one of the assumptions of the Bolzano Weierstrass. So if we can establish that there is a monotonous subsequence, we know that it must converge, which is what we want to show. Can we select such a subsequence? The answer is yes, as the following theorem will prove:
Theorem (Bolzano Weierstrass selection criterion)
Every real sequence has a monotone subsequence.
How to get to the proof? (Bolzano Weierstrass selection criterion)
How can we select a monotone subsequence? Let's try to find a monotonously decreasing subsequence, first. It is good to select an element with as many of the following elements smaller than it, i.e. for , as possible. If there is no such elements, we can definitely not proceed in selecting more elements for a monotonously decreasing sequence. If there are only finitely many elements like this, we will sooner or later run out of elements to select, so this should also be avoided. By contrast, the best case is if for all . We will call a "peak element" in that case.
As an example, we may consider the sequence with , i.e. the sequence .
All odd numbers are "peak elements", since for all , for all and so on. So there are infinitely many peak elements for . If we proceed selecting one peak element after the other, we will certainly end up with a monotonously decreasing sequence:
If denotes the index of the (peak) element , then this element must be smaller than all of the previous elements , since they were peak elements, too. So . That means, whenever the sequence has infinitely many "peak elements", we can select a monotonously decreasing subsequence .
And what if we cannot find infinitely many "peak points"? Consider the following example:
Let be the sequence with , i.e. .
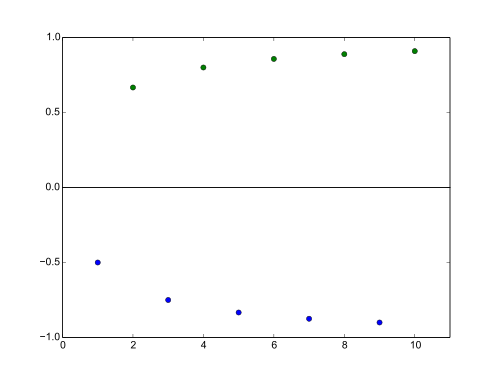
This sequence has no peak points at all: The off indices have negative elements, which are situated below the even elements , i.e. . However, the even indices can also not contain peak points, since the subsequence of even-indexed elements is monotonously increasing: . So there is always an with . But the even-indexed subsequence is already a monotone subsequence! It is only monotonously increasing, instead of decreasing.
Is there always such a monotonously increasing subsequence, if we cannot find any peak elements? The answer is yes: If we selected , which is not a peak point and there is also no peak point after it, then there is some with , with . Otherwise, would be a peak point. So we can select as the next element of the subsequence, which is again not a peak point. Now the same assumptions hold for , as for (not a peak point and no peak points after it) and we can choose a further subsequence element bigger than . This step is repeated literately and renders an infinite subsequence of .
The argument even runs through, if there are finitely many peak points: If are peak element indices, then is not a peak point and has no peak points after it. So it can be used as a starting point for a construction.
We recap: if there are finitely many peak points, we are able to construct a monotonously increasing subsequence. If there are infinitely many peak points, we just choose them as a monotonously decreasing subsequence. In any case, there is a monotonous subsequence.
Proof (Bolzano Weierstrass selection criterion)
Case 1: has infinitely many peak points . Then, the subsequence is by definition (strictly) monotonously decreasing.
Case 2: has finitely many peak points . Set . Then choose with , and iteratively for all : with . This is possible, since is not a peak point. The subsequence is then monotonously increasing.
The above Bolzano-Weierstrass selection principle makes it very easy to prove the Bolzano-Weierstrass theorem:
Proof (alternative proof for the Bolzano-Weierstrass theorem)
Let be a bounded real subsequence. The Bolzano-Weierstrass selection principle shows that there is a monotonous subsequence . Since is bounded, so is . The monotony criterion then implies convergence of . Therefore, has a convergent subsequence and hence an accumulation point.


![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)






![{\displaystyle [s,S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa89eaacbc711abc21f726338470978db420e117)










![{\displaystyle I_{n}=[a_{n},b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c37f3e46f5c868cfdd53ab13ff0c30b69aa8c293)


![{\displaystyle [a_{n},b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e30ce1f218c7164247ad32fbbcde76c02c817bd1)
![{\displaystyle [a_{n+1},b_{n+1}]\subseteq [a_{n},b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ce3eafb6d60faff4b75caadaedc8a535bbda3fa)


![{\displaystyle x\in [a_{n},b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39d10949d96060511349bc11900f5b507ef4a575)
![{\displaystyle I_{1}:=[s,S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb76c71c91060cd113663464919b8a5575dfe7db)







![{\displaystyle I_{k}=[a_{k},b_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/242d0e8ba6e5da6f32782b09ef11aa02bdd82eb6)

![{\displaystyle I_{k+1}=[a_{k+1},b_{k+1}]={\begin{cases}\;[a_{k},M]&{\text{in }}[a_{k},M]{\text{ contains infinitely many }}x_{n}\\\;[M,b_{k}]&{\text{else}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7c16e99c3c69497066f71a18de025f5b226c99d)






















































