Divergence to infinity – Serlo
Until to now, we investigated when and how a sequence diverges. In this chapter, we will investigate divergent series. Not every divergent series behaves the same: some can be seen to diverge to or (so we can assign a formal limit to them) and some don't.
Motivation
[Bearbeiten]Some sequences do not converge, but they unambiguously tend to or . For instance consider the sequences , and :
-
The sequence tends towards .
-
The sequence tends towards even faster.
-
The sequence tends towards .
We will give a mathematical definition which classifies these sequences as diverging towards or . Some other sequences may not diverge this way. For instance, consider or .
The sequence is bounded and can therefore neither tend to , not to .
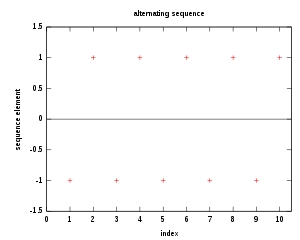
The sequence is unbounded, but contains parts (subsequences) tending towards and parts tending towards :
-
The alternating sequence is bounded, so it cannot tend towards infinity.
-
The sequence is unbounded, but neither tends to nor to .
Definition
[Bearbeiten]We have observed some sequences, which tend towards or . How can we give a mathematically precise classification for this observation?
Let us start with divergence to : "A sequence diverges to " means that it grows larger than any number , no matter how large (since is greater than any ). Even further, almost all sequence elements must be greater than . Or equivalently, we need a sequence element number , such that any element coming after it is bigger than . Indeed, this is already sufficient as condition for divergence to :
Definition (Divergence to )
A sequence diverges to , if for any almost all sequence elements are greater or equal to . That means, for all , there is an index , such that for all . In quantifier notation:
We can translate this quantifier notation piece by piece:
Divergence to is just defined analogously:
Definition (Divergence to )
A sequence diverges to , if for any almost all sequence elements are lower or equal to . That means, for all , there is an index , such that for all . In quantifier notation:
Notation
[Bearbeiten]For diverging to , we write
Analogously, for diverging to , we write
Examples
[Bearbeiten]Example
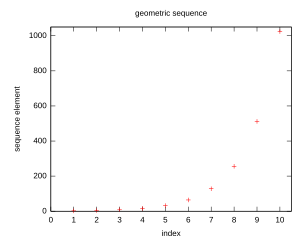
Example (geometric sequence)
We have seen in the article "unbounded sequences diverge" that the geometric sequence diverges for . The reason is that for any and any real number , the inequality holds for almost all . Therefore, for . However, if , there is neither a divergence to nor to : For even , the sequence element is positive and for , it is negative. Hence, the geometric sequence cannot diverge for . For and , it is convergent.
Improper convergence
[Bearbeiten]The notation suggests that kind of "converges" to infinity. This is no convergence in the usual sense, since the symbolic expression is not a number. However, the divergence to has a lot in common with convergence to a number (except for boundedness):
| Convergence | Divergence to |
|---|---|
| In each -neighbourhood (interval), we can find almost all sequence elements. | In each interval , we can find almost all sequence elements. |
| All subsequences converge to the same limit. | All subsequences also diverge to . |
| Every convergent sequence is bounded. | Every sequence diverging to is unbounded. |
Especially, some of the limit theorems hold true for and in some cases, one may threat a sequence diverging to , similar as a convergent sequence. Sometimes, the divergence to is even called "improper convergence". However, always keep in mind that an an improper convergence is still a divergence.
Warning
Some sequences are called "improperly convergent". Despite their name, they are actually divergent sequences. Some limit theorems still hold for improperly divergent sequences, for instance the product rule in case both sequences diverge. If one sequence converges and a second one diverges, some rules may also turn out wrong. For instance,
Applying the product rule to a product of a convergent and divergent sequence leads to the wrong result . Always be careful, when using limit theorems for improperly convergent sequences!



















![{\displaystyle {\begin{array}{l}\underbrace {{\underset {}{}}\forall S\in \mathbb {R} } _{{\text{For any real }}S}\ \underbrace {{\underset {}{}}\exists N\in \mathbb {N} } _{{\text{ there is a minimal index }}N,}\ \underbrace {{\underset {}{}}\forall n\geq N:} _{{\text{such that for all indices }}n\geq N}\\[0.5em]\quad \quad \underbrace {{\underset {}{}}a_{n}\geq S} _{{\text{ the element }}a_{n}{\text{ is bigger or equal }}S}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95f579dbd81acc61cd656e53887a918ce0f7f619)






![{\displaystyle {\begin{aligned}\lim _{n\to \infty }n&=+\infty \\[0.5em]\lim _{n\to \infty }n^{2}&=+\infty \\[0.5em]\lim _{n\to \infty }-n&=-\infty \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2436811277a75f6bc9f9458093cb79a8be1241d9)

















