Teilchenphysik: Klassifizierung
Einteilungen und Klassifizierung der Teilchen
[Bearbeiten]Eine der Aufgaben der Teilchenphysik ist es auch, die Teilchen zu klassifizieren und in Gruppen einzuteilen. Im bisherigen Verlauf des Buches haben wir bereits einige Gruppen genannt (Zum Beispiel den Begriff "Leptonen"), nun wollen wir sie in einen Gesamtzusammenhang bringen und ihre allgemeinen Eigenschaften erklären. Im Laufe der Geschichte wurden hier immer wieder neue Ansätze entwickelt - und nach Entdeckung von neuen Teilchen wieder verworfen. Im Folgenden wollen wir die verschiedenen Klassifizierungen erläutern.
Historisch (I): Einteilung aufgrund der Massen
[Bearbeiten]Die Einteilung der Teilchen nach ihrer Masse ist heute nicht mehr aktuell. Wir wollen jedoch trotzdem darauf hinweisen, da von ihr einige der Namen von Teilchenfamilien übriggeblieben sind.
In den 1930er Jahren geprägt, als die Erkenntnisse in der Teilchenphysik noch nicht sehr umfangreich waren, klassifizierte man die damals bekannten Teilchen in drei Kategorien:
- Leptonen vom griechischen leptos = leicht, für Teilchen besonders geringer Masse
- Mesonen vom griechischen mesos = mittleres, für Teilchen mittlerer Masse
- Baryonen vom griechischen barys = schwer, für Teilchen mit großer Masse
Als man ein weiteres Teilchen mittlerer Masse fand, nannte man es µ-Meson und gliederte es als Meson ein, siehe Myon. Jedoch stellte man nach einiger Zeit fest, dass eine Einteilung auf Grund der Massen ungeeignet ist und wählte stattdessen eine Einteilung nach den Wechselwirkungen, denen die Teilchen unterliegen. Also benannte man das µ-Meson in Myon um und stufte es als Lepton ein.
Die Klassifizierung auf Grund der Masse wurde verworfen; die Namen Lepton, Meson und Baryon blieben jedoch bis heute erhalten.
Einteilung auf Grund der Wechselwirkung
[Bearbeiten]Die aktuelle Einteilung basiert auf der Wechselwirkung, welcher die Teilchen unterliegen. Eine Auswahl:
- Hadronen unterliegen der starken, der elektromagnetischen und der schwachen Wechselwirkung;
- Leptonen unterliegen der schwachen und (sofern elektrisch geladen) der elektromagnetischen Wechselwirkung;
- Photonen unterliegen nur der elektromagnetischen Wechselwirkung.
Alle Teilchen unterliegen außerdem der Gravitation, sofern ihre Masse nicht Null ist.
Damit ergibt sich etwa folgende Übersicht (eine viel vollständigere Teilchenliste findet man in der graphischen Übersicht weiter unten):
| Familie | Teilchen | Symbol | Ruhemasse × c² in MeV | Mittlere Lebensdauer (s) |
| Photon | photon | 0 | stabil | |
| Leptonen | Elektron | , | 0,511 | stabil |
| Myon | , | 105,7 | ||
| Tauon | , | 1777 | ||
| Elektronneutrino | ~0 | stabil | ||
| Myonneutrino | ~0 | stabil | ||
| Tauonneutrino | ~0 | stabil | ||
| Hadronen | Pion | , | 139,6 | |
| Pion | 135,0 | |||
| Kaon | , | 493,7 | ||
| Kaon | 497,6 | |||
| Kaon | 497,6 | |||
| Etameson | 547,5 | |||
| Proton | 938,3 | stabil | ||
| Neutron | 939,6 | 886 | ||
| Lambda | 1116 | |||
| Sigma | 1189 | |||
| Sigma | 1193 | |||
| Sigma | 1197 | |||
| Xi | 1315 | |||
| Xi | 1322 | |||
| Omega | 1672 |
Zu den Hadronen gehören Mesonen, Baryonen und Pentaquarks:
- Mesonen (Pion, Kaon...) bestehen aus zwei Quarks, sind daher Bosonen;
- Baryonen (Proton, Neutron,...) bestehen aus drei Quarks, sind daher Fermionen;
- Pentaquarks bestehen (wie der Name sagt) aus fünf Quarks, sind daher Fermionen; ihre Existenz ist erst seit wenigen Jahren bekannt (sie sind in der Liste oben nicht enthalten).
Die Hadronen sind daher keine Elementarteilchen im Sinne der in der Einleitung genannten Definition, da sie aus kleineren Bestandteilen aufgebaut sind. Man kann allerdings Hadronen nicht in ihre Bestandteile zerlegen, da freie Quarks nicht vorkommen.
Die Rolle des Spins und der Ladung
[Bearbeiten]Wir haben bereits gehört, dass alle Teilchen einen Spin haben - sie scheinen sich zu drehen. Dieser Spin wird als rationale Zahl angegeben. Diese Zahl kann entweder ganzzahlig (1, 2, 3) oder halbzahlig sein (1/2, 3/2, 5/2). Die Aussage: "Das Teilchen hat Spin ½" bedeutet: in Bezug auf jede beliebige Achse im Raum kann der Eigendrehimpuls des Teilchens nur den Wert +½ oder -½ annehmen, wobei ist, und das plancksche Wirkungsquantum.
Dieses elementare Unterscheidungsmerkmal nutzt man, um die Teilchen in zwei Gruppen einzuteilen:
- Fermionen sind Teilchen mit halbzahligen Spin
- Bosonen sind Teilchen mit ganzzahligen Spin
Zu den Fermionen gehören die Quarks und die Leptonen. Von den Bosonen haben wir bereits die Eichbosonen kennen gelernt. Hadronen können zu beiden Gruppen von Teilchen gehören. Genauer gesagt, gehören alle Baryonen zu den Fermionen - die Mesonen hingegen zu den Bosonen.
Jedoch kann man nicht nur bei diesen Teilchen den Spin messen, grundsätzlich haben auch alle Atomkerne einen Spin, mit welchem man sie in eine dieser beiden Gruppen einteilen kann. Wenn wir in diesem Buch (und generell in der Teilchenphysik) von Bosonen und Fermionen sprechen, so sind damit - soweit nicht anders vermerkt - subatomare Teilchen gemeint.

Ob der Spin halb- oder ganzzahlig ist, wirkt sich entscheidend auf das Verhalten der Teilchen aus. Bosonen gehorchen der Bose-Einstein-Statistik, Fermionen hingegen gehorchen der Fermi-Dirac-Statistik. Der Begriff "Statistik" bezieht sich in diesem Zusammenhang auf das Verhalten mehrerer Teilchen mit identischen Eigenschaften. Die Fermi-Dirac-Statistik schreibt vor, dass sich in einem räumlichen Bereich niemals zwei oder mehrere Fermionen befinden dürfen, welche in ihren Quantenzahlen übereinstimmen - man spricht bei diesem Quantenmechanischen Phänomen von dem paulischen Ausschließungsprinzip. Die Fermionen können sich also nicht beliebig nahe kommen. Eine Folge davon ist, dass normale Materie nicht beliebig komprimierbar ist. Die Bosonen können sich jedoch, nach der Bose-Einstein-Statistik, auf einem beliebig kleinen Volumen aufhalten. Ein Beispiel dazu ist ein starker Laserstrahl. Dort kommen sehr viele Photonen in einem kleinen Raum - dem Lichtstrahl - vor.
Die Fermionen lassen sich wiederum nach ihrer Ladung aufteilen. Die Quarks haben alle drittelzahlige - die Leptonen hingegen immer ganzzahlige Ladungen.
Das Generationenmodell
[Bearbeiten]| Familie 1 | Familie 2 | Familie 3 |
|---|---|---|
| Quarks | ||
| up (u) | charm (c) | top (t) |
| down (d) | strange (s) | bottom (b) |
| Leptonen | ||
| Elektron (e-) | Myon () | Tauon () |
| Elektron-Neutrino () | Myon-Neutrino () | Tauon-Neutrino () |
Wie wir bereits weiter oben festgestellt haben, sind zum Aufbau unserer Welt und zur Erklärung aller physikalischen Phänomene nur die folgenden elementaren Fermionen nötig:
- Das Up-Quark
- Das Down-Quark
- Das Elektron
- Das Elektron-Neutrino
Nun haben wir jedoch gesehen, dass jedoch noch 8 andere elementare Fermionen existieren. Dem aufmerksamen Leser wird - wie einst den Physikern - aufgefallen sein, dass die Fermionen sich immer in Dreiergruppen einteilen lassen: Zwei Dreiergruppen mit Quarks; eine Dreiergruppe mit geladenen Leptonen und eine Dreiergruppe mit Neutrinos. Die oben gelisteten, in der Natur vorkommenden Teilchen, sind jeweils das leichteste Teilchen aus jeder dieser Gruppen.
Man ist also auf die Idee gekommen, die Fermionen in drei "Familien" oder "Generationen" einzuteilen. Die erste Familie enthält die Teilchen aus denen wir bestehen; die beiden anderen Familien enthalten Teilchen, welche zwar ähnliche Eigenschaften wie die der ersten Familie haben - jedoch deutlich schwerer sind. Ebenso, wie die Teilchen der zweiten Familie deutlich schwerer sind, als die der ersten, so sind auch die der dritten Familie deutlich schwerer als die der zweiten. Eine Ausnahme des hier gesagten stellen die Neutrinos dar, da diese laut Standardmodell keine Massen haben.
Ladungs-Multipletts
[Bearbeiten]Beim Isospin haben wir es schon einmal angesprochen - die starke Ähnlichkeit zwischen Teilchen, wie dem Neutron und dem Proton. In der obigen Grafik können sie weitere solche Teilchen erkennen. So gibt es je drei Pionen, Kaonen, D-Mesonen und Sigma-Baryonen sowie zwei Xi- und vier Delta-Baryonen. Die Teilchen dieser Teilchengruppen haben alle die gleichen Eigenschaften wie ihre Gruppenmitglieder - mit einer Ausnahme: Der elektrischen Ladung. Aus diesem Grund nennt man solche Teilchengruppen Ladungsmultipletts. Ladungsmultipletts, die nur aus zwei Teilchen bestehen, werden oft Ladungsdupletts genannt. Neben den bereits genannten, gibt es noch eine Vielzahl anderer Ladungsmultipletts, auf welche wir jedoch nicht weiter einzugehen brauchen. Der winzige Massenunterschied zwischen den Teilchen eines Ladungsmultipletts folgt aus ihrer elektrischen Ladung, welche sie "abbremst" und dadurch träge macht. So ist es auch nicht verwunderlich, dass das Verhältnis der Massendifferenz zur Gesamtmasse des leichtesten Teilchens, gleich dem Verhältnis zwischen der elektromagnetischen und der starken Kraft ist.
Wenn wir uns zunächst auf die Seltsamkeit (Strangeness) beschränken, so haben alle Teilchen eines solchen Ladungs-Multipletts dieselbe Strangeness. Damit lässt diese sich wie folgt berechnen: S = 2Q - B, wobei Q (auch QØ ) die durchschnittliche Ladung aller Teilchen des Multipletts und B die Baryonenzahl ist.
Allgemein benutzt man die Hyperladung Y = B + S + C + B' + T. Alle Teilchen eines Ladungs-Multipletts stimmen nicht nur in der Stangeness S, sondern auch in den anderen Flavour-Quantenzahlen Charm C, Bottomness B' und Topness T, und damit in ihrer Hyperladung überein. Wegen der Gell-Mann-Nishijima-Relation Y = 2(Q-Iz), wobei Iz die z-Komponente des Isospins bezeichnet, sind daher Ladungs-Multipletts auch Isospin-Multipletts. Für ein solches Ladungs- oder Isospin-Multiplett von Baryonen bzw. Mesonen gilt daher verallgemeinert: Y = 2Q, bzw. S + C + B' + T = 2Q - B, wobei Q wieder die mittlere Ladung der Teilchen des Multipletts bezeichnet.
Historisch (II): Das Sakata-Modell
[Bearbeiten]Wie schon öfters angesprochen gibt es eine Vielzahl an Hadronen, das war der Grund, warum bereits in den 40er Jahren die Teilchenphysiker versuchten diese Teilchen zu ordnen. Einen ersten Ansatz dazu schlug der japanische Physiker S. Sakata im Jahre 1956 vor. Er vermutete, dass alle 17 bis dahin bekannten Hadronen sich aus Kombinationen von zwei aus sechs andern Teilchen zusammensetzen. Diese sechs nach Sakata elementaren Teilchen wären das Proton, das Neutron das neutrale Lambda und deren Antiteilchen. Alle anderen Hadronen sind demnach Teilchen-Antiteilchen-Paare dieser sechs Teilchen. Das π- wäre demnach aus einem Neutron und einem Antiproton zusammengesetzt; das K+ wäre hingegen eine Kombination aus Proton und dem neutralem Anti-Lambda.
Ein scheinbares Problem des Sakata-Modells war, dass die Masse eines zusammengesetzten Teilchens viel kleiner ist, als die Summe aller Teilchen, aus denen es besteht. So addieren sich die Massen von Proton und Antiproton zu 1877 MeV, während das neutrale Pion - welches laut Sakata aus diesen beiden Teilchen zusammengesetzt ist - eine Masse von lediglich 135 MeV. Dies sollte jedoch nicht unbedingt als ein Fehler im Modell angesehen werden, denn laut der Speziellen Relativitätstheorie sind Masse und Energie ineinander umwandelbar. So ist auch ein Atomkern leichter als seine Bestandteile, die Differenz liegt als Bindungsenergie vor. Das Sakata-Modell wurde von den Physikern sehr unterschiedlich aufgenommen, schließlich aber verworfen, da weitere Hadronen gefunden wurden.
Supermultipletts
[Bearbeiten]Es gibt eine einfache, aber faszinierende Methode um die Hadronen in Gruppen einzuteilen und - sortiert nach ihren Eigenschaften - in ein "Koordinatensystem" einzuzeichnen.
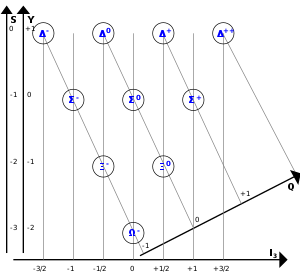
Zunächst lassen sich die drei Spins der Quarks zu einem Gesamtspin von 1/2 oder einem Gesamtspin von 3/2 koppeln. Aus dem Pauli-Prinzip folgt, wie viele mögliche Kombinationen von Baryonen es in dieser Gruppe gibt: So gibt es acht Baryonen mit einem Gesamtspin von 1/2 und 10 Baryonen mit einem Spin von 3/2. Die Baryonen mit dem Spin 1/2 ergeben also ein Baryonoktett - während die anderen ein Baryondekuplett ergeben. Wir zeichnen also zwei getrennte Koordinatensysteme. Bei beiden wählen wir die dritte Komponente des Isospins als waagerechte x-Achse und die Strangeness des Teilchens als senkrechte y-Achse.
Zeichnen wir nun die Baryonen nach ihrem Spin getrennt in die beiden Koordinatensysteme, so ordnen sich die Teilchen in den beiden Koordinatensystemen nach je einem symmetrischen, geometrischen Muster. Und in diesen Mustern, erkennt man noch weitere Regelmäßigkeiten. So steigt die elektrische Ladung von unten links nach oben rechts. Und die Hyperladung steigt parallel zur Strangeness - jedoch um eins verschoben. Die Masse hingegen steigt von oben nach unten und sehr schwach auch von rechts nach links. Wenn sie sich die Teilchen, welche auf demselben waagerechten Niveau liegen, betrachten, so fällt ihnen vielleicht auf, dass es sich hier um die oben vorgestellten Ladungs-Multipletts handelt. Wenn wir uns den Quark-Aufbau der Teilchen anschauen, erkennen wir noch eine weitere Auffälligkeit: Die Teilchen sind nach ihren Quarks geordnet. In den Ecken befinden sich jeweils Teilchen, welche nur aus eine Sorte von Quarks aufgebaut sind. In den Mitte hingegen befinden sich die Teilchen, welche alle drei Arten von Quarks enthalten. Die Tatsache, dass in der Mitte des Baryonoktetts zwei Teilchen eingezeichnet sind (Sigma-null und Lambda-null) heißt nicht, dass dies nur zwei unterschiedliche Namen für dasselbe Teilchen sind. Die Teilchen unterscheiden sehr wohl. So hat das neutrale Sigma eine Masse von 1,192.5 GeV, das neutrale Lambda hat hingegen nur 1,115.6 GeV. Sehr deutlich unterscheiden sie sich in ihrer Lebensdauer: Das Lambda-null-Meson lebt 5 Milliarden mal länger (allerdings ist das immer noch weniger als ein Milliardstel einer Sekunde).
-
Das Baryondekuplett
-
Dieselbe Grafik wie links, jedoch sind hier die Quarks eingezeichnet
-
Das Baryonoktett
-
Dieselbe Grafik wie links, jedoch sind hier die Quarks eingezeichnet
Zum Zeitpunkt der Entdeckung dieser Symmetrie, war beispielsweise das Omega-Teilchen noch nicht bekannt. Mit Hilfe der gerade genannten Symmetrien, konnte man jedoch seine Eigenschaften problemlos vorhersehen.
Auch Mesonen bilden solche Multipletts wenn man sie in ein Koordinatensystem einzeichnet. Auch die Mesonen teilt man dafür in zwei Gruppen ein. Mesonen bestehen aus zwei Quarks, deren Spinausrichtungen entweder parallel oder antiparallel sein können. Der Spin ist dementsprechend entweder null oder eins. Die ersteren nennt man pseudoskalare Mesonen, die Mesonen mit Spin 1 hingegen Vektormesonen.
Sowohl die pseudoskalaren Mesonen, als auch die Vektormesonen bilden ein Nontet - also ein Gebilde aus neun Teilchen. In der Mitte dieser Nontets - welche in der Form dem Baryondekuplett ähneln - sitzen jeweils drei Teilchen. Des Weiteren findet man in den Mesonen-Nontets das Antiteilchen eines bestimmten Teilchens immer genau gegenüber. Den Quarkaufbau der Teilchen einzuzeichnen sparen wir uns hier, da dies bei Mesonen etwas komplizierter ist. So ist der exakte Quarkaufbau des ρ0-Mesons .
-
Das Mesonennonet für pseudoskalare Mesonen
-
Das Mesonennonet für Vektormesonen
Dreidimensionale Supermultipletts
[Bearbeiten]
Vielleicht ist ihnen schon aufgefallen, dass wir in diesen Grafiken nur Teilchen betrachten, welche aus den drei leichtesten Quarks - nämlich den Up-, Down- und Strange-Quark - aufgebaut sind. Das liegt daran, dass man damals nur diese Teilchen kannte. Heute ist jedoch bekannt, dass es außer diesen drei leichten Quarks noch drei weitere sog. schwere Quarks (charm, bottom und top) gibt. Mit diesen schweren Quarks können weitere Hadronen erzeugt werden. Indem man beispielsweise beim Lambda-Baryon (uds) das Strange-Quark durch ein Charm-Quark ersetzt, erhält man das mit einer etwa 1200 MeV größeren Masse. Auch die Hadronen, welche ein oder mehrere Charm-Quarks enthalten, lassen sich gut in Supermultipletts wie die obigen einzeichnen, indem am eine dritte räumliche Achse verwendet. Auch hier ergeben sich wieder verblüffend symmetrische Objekte. So ergeben die Baryonen mit Spin 3/2 eine dreikantige Pyramide, deren Grundfläche das Baryondekuplett von oben ist.
Aus diesen Supermultipletts kann man acht Quantenzahlen ablesen: Baryonenzahl, Ladung, Hyperladung, Strangeness, Spin, Isospin, dritte Komponente des Isospins und Multiplizität. In Anlehnung an den Edlen Achtfachen Pfad - welcher im Buddhismus den Weg zur Aufhebung des Leidens darstellt - nannte man diese gruppentheoretischen Überlegungen den Achtfachen Weg (engl.: Eightfold Way). Dieser Weg wurde in den 1960er Jahren von Murray Gell-Mann und Yuav Ne'eman entwickelt. Die mathematische Grundlage greift auf ein Konzept zurück, welches Sophus Lie schon im 19. Jahrhundert entwickelte: Die Lie-Gruppen. Die Lie-Grupe in diesem Fall bezeichnet man als SU(3). Dies ist die Schreibform für eine spezielle unitäre Gruppe der 3x3 Matrizen. Was dies wiederum konkret ist, können wir aufgrund der Komplexität in diesem Buch nicht erläutern. Wichtig ist nur, dass Sie den Ausdruck SU(N) kennen. Der Achtfache Weg führte unmittelbar zur Quark-Hypothese.
Referenzen
[Bearbeiten]