Werkstoffkunde Metall/ Innerer Aufbau/ Struktur

Um den Inneren Aufbau eines Metalls zu verstehen, müssen wir uns mit seinem strukturellem Aufbau befassen. Die Theorie hierzu liefert die Festkörperphysik. Ebenso wichtig, wenn es um die Vorgänge im Inneren geht, ist die Thermodynamik, auch bekannt als Wärmelehre. Die Ursache für die mikroskopischen Eigenschaften finden wir dagegen bei den kleinsten Teilchen: – bei den Atomen, ihren Bausteinen und deren Wechselwirkung.	Zwischen den Bausteinen der einzelnen Atome wirken sowohl anziehende, als auch abstoßende elektromagnetische Kräfte, die ungerichtet wirken. Die anziehenden Kräfte resultiert aus der gemeinsamen Anziehung der Atomrümpfe zu den freien Elektronen. Die abstoßenden Kräfte resultieren aus der gegenseitigen Abstoßung der Atomrümpfe untereinander.
Bei ro besteht ein Gleichgewicht zwischen diesen Kräften – oder anders ausgedrückt: ohne den Einfluss äußerer Kräfte wird sich ein Atomradius, und damit der halbe Abstand zwischen zwei gleichen Atomen von ro einstellen. Dieses Maß ist aber nicht unbedingt bindend: eine andere Atomart des Nachbarn sowie verschiedene Bindungsarten können ro um Größenordnungen verändern. Und sobald äußere Kräfte wirken, muss der Abstand zwischen den Atomen von der Ruhelage abweichen – womit die Grundlage für die Elastizität eines Körpers gegeben wäre.
Eine wichtige Einflussgrößen auf ro ist die Temperatur eines Körpers. Der Verlauf der Resultierenden zeigt, dass es gegen die Verschiebung aus der Ruhelage in Druckrichtung einen größeren Widerstand gibt als in Zugrichtung. Eine stärke Amplitude der Atomschwingungen durch höhere Temperaturen führt also zu einer Verschiebung der Mittellage dieser Amplitude – anders ausgedrückt: wäre der Widerstand gegen Zug- und Druckkräfte gleich, bliebe die Lage von ro bei einer Änderung der Temperatur konstant – so aber gibt es für jeden Stoff einen spezifischen Längenausdehnungskoeffizienten (α). Interessant wird es, wenn man Schmelztemperatur und α einiger Metalle miteinander vergleicht. Multipliziert man die Werte von α mit der jeweiligen Schmelztemperatur (in Kelvin) erhält man durchweg das Ergebnis: 0,020 ± 0,004 Auf dem Weg vom absoluten Nullpunkt (0 K) bis zum Schmelzpunkt weisen also alle Metall eine Längendehnung zwischen 1,6% und 2,4% auf, bevor sie schmelzen. Interessant ist in diesem Zusammenhang auch die Abhängigkeit zwischen Schmelztemperatur und E-Modul. Beide Kennwerte sind in gleicher Weise von der oben dargestellten Kraft-Abstands-Kurve der Atome abhängig.	Hier sind Schmelztemperatur und der Kehrwert von α der wichtigsten Metalle zueinander aufgetragen. Auffällig ist der geradezu lineare Verlauf.

---

Bis hier hin reicht das Model der „frei Elektronen“ des Elektronengases noch. Damit können die Effekte des Magnetismus, sowie die Anordnung der Atome in Kristallstrukturen aber nicht erklärt werden. In der Einleitung wurde bereits das Bändermodel des Atoms erwähnt. Hier gibt es verbotene und erlaubte Bänder für die Energieniveaus der Elektronen. Die Lage dieser Bänder ist aber nicht in jede Richtung des Atoms gleicht – abhängig von Wechselwirkungen mit anderen Atomen und den thermisch bedingten Energieniveaus ihrer Elektronen gibt es richtungsabhängige Unterschiede in der Lage dieser Bänder. Somit ist die Aussage aus dem Model der freien Elektronen, die Bindungskräfte seien ungerichtet, nicht richtig. In dem Streben nach der energetisch günstigsten Position, werden sich die Elektronen an bestimmten Plätzen aufhalten.

In letzter Konsequenz wirkt sich dies auf die benachbarten Atome aus, und sie werden in die energetisch günstigste Position gezwungen – wodurch die Elementarzelle festgelegt wäre. Dadurch wird auch die Koordinationszahl bestimmt – die Anzahl der nächsten Nachbarn eines Atoms. Beim Kohlenstoff zum Beispiel entscheidet die Koordinationszahl zwischen Graphit (3) und Diamant(4).

• Wer dieses Thema vertiefen möchte, dem sei das Stichwort  Fermi-Fläche genannt.

Grundlagen der Kristallgeometrie

Kristallgitter und Elementarzelle

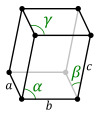
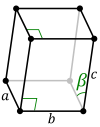
Das Kristallgitter wird durch ein räumliches Koordinatensystem beschrieben. Seine Regelmäßigkeit entsteht durch wiederholte Translation – oder Verschiebung – der Elementarzelle entlang der Gitterachsen. Die Verschiebung erfolgt auf der x-, y- und z-Achse jeweils über die Translationsabstände a, b bzw. c. Die Gitterachsen kreuzen sich unter den Winkeln α, β und γ. Diese Faktoren werden Gitterparameter genannt. Die Achsen müssen sich nicht zwangläufig unter 90° schneiden, und die Abstände a, b und c können voneinander abweichen – auf diese Weise lassen sich sieben Grundtypen bilden.

Die Elementarzelle ist die kleinste Einheit von Atomen im Kristallgitter. Sie enthält sämtliche Symmetrieelemente, gegenüberliegende Flächen sind parallel angeordnet. Das Gittersystem kann durch reine Translation – ohne Rotation – der Elementarzelle gebildet werden. Der Grund-Gittertyp wird durch die zusätzliche Platzierung von Atomen um raumzentrierte oder flächen- bzw. basiszentrierte Typen erweitert.

Gitterarten

Das mit Abstand wichtigste Kristallsystem ist das kubische mit seinen Varianten raumzentriert und flächenzentriert

Kubisch-raumzentriert	Kubisch-flächenzentriert
Zusätzlich zu den acht Eckatomen befindet sich im Volumenzentrum ein weiteres Atom α-/ δ-Fe; β-Ti, β-Zr, Cr, V, Mg, Mo, W, Ta, Li, Na, K	Zusätzlich zu den acht Eckatomen befinden sich im Zentrum der Seitenflächen sechs weitere Atome γ-Fe, β-Co, Cu, Pt, Al, Au, Ag, Pb

Darüber hinaus gibt es einige Metalle mit folgenden Kristallsystemen.

Hexagonal	Tetragonal	Rhomboedrisch
Der Winkel zur z-Achse beträgt 90°	α = β = γ = 90° und a = b ≠ c	a = b = c
Cd, Graphit, Os, Zn	In, Sn, Zr	Bismut

Der Vollständigkeit halber sollen diese drei Kristallsysteme erwähnt werden, obwohl diese nur bei mineralischen Verbindungen vorkommen.

Triklin	Orthorhomisch	Monoklin
a ≠ b ≠ c	α = β = γ = 90° und a ≠ b ≠ c	a ≠ b ≠ c

 Chemische Stoffe sortiert nach ihrem Kristallsystem

Millersche Indizes

(Millersche Indizes)

Packungsdichte / Gitterlücken

Für ein beliebiges Kristallgitter kann dessen Packungsdichte bestimmt werden. Gemeint ist damit das Verhältnis zwischen dem Volumen der Elementarzelle und dem Volumen der daran beteiligten Atome. Diese Atome werden dabei als harte Kugeln gleicher Größe angenommen.

Das dichteste Packungsverhältnis erreichen das KFZ-Gitter sowie das hexagonale Gitter dichtester Kugelpackung (h.d.P.) mit:	${1 \over 6}\pi {\sqrt {2}}\approx 74\%$
Das kubisch-raumzentrierte Gitter erreicht nur	${1 \over 8}\pi {\sqrt {3}}\approx 68\%$
Das kubische-primitive Gitter erreicht sogar nur eine Packungsdichte von	${1 \over 6}\pi \ \quad \approx 52{,}4\%$

Ein Kristallgitter kann noch so dicht gepackt sein, in den Gitterlücken zwischen den Atomen findet sich immer noch Platz für kleinere Atome.

Die Tetraederlücke ist von vier Atomen umgeben. Sie ist im KFZ- und im hexagonalen Gitter zu finden. Ein Tetraeder ist eine Pyramide, deren Grund- und Seitenflächen aus identischen Dreiecken bestehen. Mit dem Radius der Außenatom kann der Radius des größten Atoms berechnet werden, dass noch in diese Lücke passt:

$r_{kfz}=R\cdot {\frac {1}{2}}\left({\sqrt {6}}-2\right)\approx R\cdot 0{,}225$

Die Oktaederlücke ist von sechs Atomen umgeben. Der Name kommt daher, dass die Atome zusammen einen Oktaeder bilden, in dessen Mitte die Lücke sitzt. Bei kubisch flächenzentrierter Packung sind die beteiligten Atome alle flächenzentrierten der Elementarzelle. Sie ist sowohl im KFZ- als auch im KRZ-Gitter zu finden. Der Oktaeder ist eine Pyramide mit quadratischer Grundfläche und dreieckigen Seitenflächen. Der Radius der Innenkugel wird hierbei wie folgt berechnet:

$r_{kfz}=R\cdot \left(\quad {\sqrt {2}}-1\right)\approx R\cdot 0{,}414$

$r_{krz}=R\cdot \left({\frac {2}{3}}{\sqrt {3}}-1\right)\approx R\cdot 0{,}155$

Die Größe der Gitterlücken trägt entscheidend zum Lösungsvermögen von Legierungselementen mit kleinen Atomradien in Metallen bei. So kann Austenit, die Kfz-Modifikation des Eisens, bei 1147°C max. 2,06% Kohlenstoff lösen. Ferrit ist kubisch-raumzentriertes Eisen und kann bei 723°C max. 0,02% C lösen – ein hundertstel des Lösungsvermögens von Austenit.

Theorien der Thermodynamik

Kurz gesagt, beschäftigt sich die Thermodynamik mit dem Energiehaushalt eines Systems, wobei die Temperatur nur eine von vielen Größen ist. Ohne auf dieses Gebiet der theoretischen Physik weiter einzugehen, sollen hier ein paar wichtige Erkenntnisse aus der Thermodynamik angesprochen werden, die wir in diesem Kapitel im Hinterkopf behalten sollten:

Thermodynamische Größen

Energie kann nicht aus dem Nichts erzeugt werden,

und sie kann nicht verloren gehen.
(Energieerhaltungssatz - 1. Hauptsatz der Thermodynamik; sinngemäß)

Energie fließt immer von einem höheren zu einem niedrigeren Niveau.

Aber: ein Körper kann Energie aus seiner Umgebung aufnehmen oder diese an sie abgeben – in jedem Fall ist die Umgebung dann als Teil des Systems zu sehen. An diesem Energietransfer ist Wärme sehr stark beteiligt, aber auch mechanische Kräfte, die immer zu Verformungen (ob nun elastisch oder plastisch) führen, spielen eine wichtige Rolle.

Ein wichtiger Aspekt ist die innere Energie U eines Systems. Sie setzt sich aus der kinetischen oder der Wärmeenergie und der potenziellen Energie zusammen. Die potenzielle Energie wiederum ist in den Spannungen der Gitterbaufehler (siehe nächstes Kapitel) und als Bindungsenergie in dem Stoff gespeichert.

Thermodynamische Größen
freie Energie	F = U – TS	gilt bei gleichem Volumen
Enthalpie	H = U + pV
freie Enthalpie	G = U – TS + pV	gilt bei gleichem Druck
hierbei ist:	U – innere Energie T – Temperatur S – Entropie	p – Druck V – Volumen

So wie sich unterschiedliche Energieniveaus ausgleichen, verhält es sich auch bei unterschiedlicher Verteilung von Stoffmengen. Genauer gesagt, versuchen sich Konzentrationsunterschiede in einer Lösung (also auch in einer Legierung) gegenseitig auszugleichen. Die Thermodynamik verwendet hier den Begriff Entropie S – die als „Grad der Unordnung“ zu sehen ist. Jedoch ist die Verwendung des Begriffs „Unordnung“ etwas problematisch. Wir betrachten nicht die exakte Anordnung der Atome – teilweise hier treffen wir hier auf eine hohe strukturelle Ordnung – sondern die Vielzahl, mit der diese Strukturen entstehen können.

Das obere Diagramm zeigt die Möglichkeiten einer Vier-Bit-Wahrscheinlichkeit. Die maximale Entropie eines Systems ist gegeben, wenn jede der 16 Mikrozustände in einem makroskopischen Systeme mit gleicher Häufigkeit erreicht ist. Außerdem zeigt das Diagramm die Wahrscheinlichkeit, mit der eine bestimmte Gruppen dieser Zustände auftritt (4:0 – 6,25%; 3:1 – 25%; 2:2 - 37,5%; usw.) Systeme wie Legierungen streben nach maximaler „Entropie“ durch möglichst gleichmäßige Verteilung ihrer Komponenten. Jedoch muss die Durchmischung kinetisch möglich sein.

In Gasen kann diese Durchmischung fast ungehindert stattfinden, und in Flüssigkeiten stellt eine hohe Viskosität schon ein beachtliches Hindernis dar. In Festkörper ist die Durchmischung dagegen sehr stark eingeschränkt. Sie hängt hier von der Dichte der Kristallstruktur und der Leerstellenkonzentration ab. Denn größten Einfluss hat aber die Temperatur: kurz unter dem Schmelzpunkt eines Körpers sind seine Atome durch ihre hohe kinetische Energie und die weiten Gitterabstände noch recht beweglich. Bei Raumtemperatur beträgt die Reichweit der atomaren Bewegungen in Metallen nur noch Bruchteile eines Millimeters. (Siehe Diffusion im Kapitel „Legierungen“)

Stabilität

Die Physik ist geprägt von den Wechselwirkungen zwischen den unterschiedlichsten Kräften. In diesem hin und her ist nimmer nur derjenige Zustand stabil, bei dem alle physikalischen Größen im Gleichgewicht sind. Um dieses Gleichgewicht zu erreichen, streben alle Systeme nach

• maximaler Entropie und dem
• minimalem energetischem Potenzial, geprägt durch Druck, Temperatur und der inneren Energie

Alle Systeme besitzen theoretisch eine gewisse Stabilität. Sie sind in einem Gleichgewicht, das gegenüber äußeren Störungen (in Form von Energie, besonders Wärme) immun ist.	In der Thermodynamik (und in der Realität) sind die meisten Systeme jedoch in einem meta-stabilen Gleichgewicht.	In vielen Grenzbereichen ist das System in einem instabilen Zustand.
Eine Störung bringt das System aus der Ruhlage – jedoch nicht aus dem Gleichgewicht. Nachdem die Störung abgeklungen ist, kehrt das System in seine Ruhelage zurück	Das System (1) ist nur gegenüber geringen Störungen immun. Sind die Störungen groß genug, kommt das System in einen instabilen Zustand (2), um schließlich irreversibel in den Zustand (3) zu fallen, der energetisch niedriger liegt als die Ausgangslage.	Das System (2) geht schon bei geringsten Störungen in eine energetisch günstigere Lage über (1 oder 3)

Aus der Chemie kennen wir diese „Störung“ als Aktivierungsenergie einer chemischen Reaktion. In der Werkstoffkunde sind darunter sowohl chemische Vorgänge, als auch strukturelle Vorgänge im Kristallsystem zu sehen.

Der Begriff: „Phase“

Materie kann in unterschiedlichen Zuständen in Erscheinung treten. Am offensichtlichsten sind die Aggregatzustände:

• fest, flüssig und gasförmig

Neben diesen klassischen Aggregatzuständen, ist auch der Zustand Plasma von Bedeutung. Dabei sind die Elektronen vollständig von ihren Atomkernen losgelöst. In der Festkörperphysik kommt unter anderem noch die Struktur des Kristallsystem oder die Bildung amorpher Strukturen dazu. All diese Eigenschaften sind abhängig von:

• Temperatur, Zusammensetzung und Druck

Zum Beispiel ist der Diamant „nur“ eine spezielle Form des Kohlenstoffs, die sich bei extrem hohem Druck bildet.
Er weist ein besonderes Kristallsystem auf, das sich von dem des Graphits unterscheidet. Chemisch sind sie aber identisch.

Als Phase wird eine physikalisch und chemisch einheitliche Substanz (oder ein Teil von ihr) bezeichnet. Anders ausgedrückt: eine Phase ist ein homogener Bereich eines Werkstoffs. Wobei mit homogen gemeint ist, dass in jedem Teil der Phase der gleiche Aggregatzustand, das gleiche Kristallsystem und die gleiche Zusammensetzung besteht – in einem gewissen Toleranzbereich. Konzentrationsunterschiede und Gitterstörungen sind unvermeidlich.

Zum Beispiel ist Salzwasser EINE Phase: bestehend aus den Komponenten Wasser und dem darin gelösten Salz.
Aber: ab einem bestimmten Punkt kann das Wasser kein Salz mehr lösen. Das überschüssige Salz bleibt fest und sammelt sich am Boden.
Salzwasser und Salzkristalle bilden ein Phasengemisch.

Praktisches Beispiel: Abkühlungskurven

Betrachten wir verschiedene Materialien bei der Abkühlung.

(1) - Typische Abkühlungskurve eines amorphen Materials ohne kristalline Ordnung (z.B. Glas).

(2) Reinstoffe (Elemente, Verbindungen) halten beim Übergang gasförmig ⇒ flüssig und flüssig ⇒ fest ihre Temperatur bis der Übergang abgeschlossen ist. Die Bindungskräfte beginnen wieder zu wirken und die Energie, die beim Schmelzen bzw. beim Verdampfen nötig war, um sie aufzubrechen, wird wieder freigesetzt. Diese Punkt wird Haltepunkt genannt. Nicht nur beim Wechsel des Aggregatzustands gibt es einen Haltepunkt – an bestimmten (Temperatur-) Punkten kommt es zu spontanen Änderungen des Kristallaufbaus, oder z.B. Eisen, das oberhalb von 768°C nicht magnetisch ist, erhält seinen Magnetismus zurück. Allgemein werden diese Punkte Phasenübergang genannt.

(3/4) - Typische Abkühlungskurve einer Legierung: Hier gibt es keinen Haltpunkt, sondern einen Haltebereich – die Abkühlung findet allmählich statt.

Kristallisation

Was passiert eigentlich, wenn ein Stoff erstmals seine feste Form erhält – wenn ein Festkörper entsteht?

• Abhängig von Zusammensetzung und ihrer Entstehung können Festkörper, unabhängig davon ob es Metalle sind oder nicht, auf mikroskopischer Ebene verschiedene Ordnungsgrade erreichen.
• Kristalline Festkörper bestehen meistens aus einer Vielzahl mikroskopisch kleiner Kristalle, sie weisen eine polykristalline Struktur auf.
• Es ist möglich durch besondere Verfahren Einkristalle zu züchten, das Material besteht dann aus einem einzigen makroskopischen Kristall ohne die typischen Korngrenzen.

Amorph	Kristall	Quasi-Kristall
Den Atomen fehlt jede strukturelle Ordnung, sie sind völlig regellos angeordnet. Das ist bei Gläsern der Fall, und auch Metalle können bei extrem schneller Abkühlung den „Glas-Zustand“ erreichen.	Die Atome sind in einem regelmäßigen Gitter angeordnet. Die Analyse dieser Strukturen ist Aufgabe der Kristallographie.	Aus der Nähe betrachtet folgen die einzelnen Atome keiner regelmäßigen Anordnung. Betrachtet man aber ein Paar hundert Atome, werden komplexe, wiederkehrende Muster deutlich. Komplexe Legierungen und Mineralien besitzen meist einen quasikristallinen Aufbau.

Die Frage ist, wie man dahin gelangt – aber betrachten wir zunächst die möglichen Ausgangszustände, aus denen ein Festkörper bzw. ein Kristall entstehen kann: Der Stoff mag zunächst vollständig als Schmelze, als Gas oder Plasma vorliegen – oder ist Teil einer Lösung, z.B. als gelöstes Salz. Aber auch Festkörperreaktionen spielen eine Rolle, dabei wird aus einer Kristallart ein oder zwei neue Kristallarten gebildet. Der Übergang zum festen Zustand ist durch eine Änderung der physikalischen Rahmenbedingungen geprägt:

• So wird z.B. eine Schmelze immer weiter abgekühlt, bis ihre Temperatur den Schmelzpunkt unterschreitet.
• Auch durch eine Erhöhung des Drucks kann dieser Punkt überschritten werden.
• Durch angelegte Spannungen werden bei der Elektrolyse Metalle aus Salzlösungen abgeschieden.

Die Erstarrung setzt dann aber nicht augenblicklich ein und ist eher ein langwieriger Prozess als eine spontane Reaktion. Was noch fehlt sind Kristallisationskeime und eine treibende Kraft, um diese wachsen zu lassen. Denn, wie wir im nächsten Kapitel sehen werden, muss ein Kristall zu seinem Wachstum erhebliche Widerstände überwinden. Gehen wir von konstantem Druck bei gegebener Temperatur aus, ist die freie Enthalpie G von besonderer Bedeutung dafür, welcher Aggregatzustand gerade stabil ist. Dieses Diagramm zeigt die unterschiedlich steilen Verläufe der freien Enthalpien eines beliebigen Systems in Abhängigkeit von Temperatur und Aggregatzustand. Von ganz besonderer Bedeutung sind die Schnittpunkte dieser Linien – dies sind die Übergangpunkte Schmelzpunkt bzw. Siedepunkt. Stabil ist immer der Aggregatzustand mit der geringsten freien Enthalpie.

Keimbildung

Die Grundvoraussetzung dafür, dass Kristalle wachsen können ist, dass genügend stabile Keime vorhanden sind - die Betonung liegt auf stabil. Aufgrund thermischer Fluktuationen bilden sich ständig Gruppen von Atomen, die als Keimzelle eines Kristalls dienen können – auch oberhalb der Schmelztemperatur (T_S). Jedoch sind diese noch nicht stabil. Was noch fehlt ist eine treibende Kraft (ΔG) um diese wachsen zu lassen. Oberhalb von T_S ist ΔG stets positiv. Die Keime lösen sich schneller wieder auf, als sie wachsen können, weil die freie Enthalpie des Keims höher ist als die der Schmelze – der Keim löst sich unter Energiegewinn auf. Erst unterhalb von T_S wird ΔG negativ, und der feste Zustand wird der energetisch günstigere, sodass die Kristalle wachsen können.

An dieser Stelle sollten wir auf ein Phänomen eingehen, das  Unterkühlung genannt wird. Durch diesen Effekt kann eine Flüssigkeit (teilweise weit) unter ihren Schmelzpunkt abgekühlt werden, ohne zu erstarren. Die Ursache hierfür sind die Widerstände beim Kristallwachstum – gleichzeitig liefert die Unterkühlung die treibende Kraft, diese zu überwinden. Dieser Widerstand resultiert aus der Oberflächenspannung zwischen Schmelze und Kristall. Soll der Kristall wachsen, muss auch seine Oberfläche größer werden – und dazu muss die spezifische Oberflächenenergie (γ) aufgebracht werden. Nun ist jeder Körper bestrebt, seine (Oberflächen-) Energie und damit seine Fläche so gering wie möglich zu halten. γ liefert also immer einen positiven Beitrag zu ΔG.

Metall Schmelztemperatur TS in K Max. Unterkühlung ΔT in K ΔT / TS in % Au 1336 190 14,2 Co 1768 310 17,5 Cu 1356 180 13,3 Fe 1809 280 15,5 Ge 1210 200 16,5 Ni 1726 290 16,8 Pd 1825 310 17,0

Es ist allgemein bekannt, dass der Schmelzpunkt von Wasser bei 0°C liegt. Durch das Phänomen der Unterkühlung lässt sich reinstes Wasser auf –40°C abkühlen und es ist trotzdem noch flüssig.

• Bei −5 °C müssen sich Cluster von etwa 50.000 Wassermoleküle zusammenfinden.
• Bei −20°C sind es immer noch einige hundert.
• Bei −40°C reichen bereits 70 Moleküle aus.

Bei der Unterkühlung handelt es sich um einen meta-stabilen Zustand – oftmals reichen kleine Erschütterungen aus, um die Kristallisation auszulösen.

Für die Änderung der freien Enthalpie beim Übergang flüssig ⇒ fest gilt:

$\Delta G=-\Delta G_{V}+\Delta G_{O}$

Beim Wachstum des Kristalls wird unterhalb von TS Umwandlungsenergie gewonnen:	$\Delta G_{V}$ ist proportional zum Volumen.
Dagegen muss zur Vergrößerung der Oberfläche Energie aufgewendet werden:	$\Delta G_{O}$ ist proportional zur Oberfläche.

Nehmen wir in erster Näherung an, dass der Keim eine ideale Kugelform hat, mit einer scharfen Grenzfläche zur flüssigen Phase, deren Energie wir unter Vernachlässigung der Abhängigkeit von Temperatur und Gitterausrichtung des Kristalls bestimmen können. Dann ist:

$\Delta G=-{\tfrac {4}{3}}\pi r^{3}\Delta g+4\pi r^{2}\gamma$
Δg ist die Umwandlungsenergie pro Volumen

T > TS	T < TS	T1 < T2 < T3 < TS< T
Keime, die sich oberhalb der Schmelztemperatur durch thermische Fluktuationen bilden, haben in jedem Fall eine höhere Enthalpie als die Schmelze und sind instabil – sie lösen sich schneller auf, als sie wachsen können. Sowohl Oberflächenspannung als auch Bildungsenthalpie leisten einen positiven Beitrag zur Energie des Keims.	Unterhalb von TS reduziert ΔGV die Energie eines Kristalls mit wachsendem Volumen – wenn eine gewisse Größe überschritten wird: der kritische Keimradius. Bei diesem Radius hat der Keim die maximale Enthalpie erreicht und befindet sich in einem labilen Zustand. Sowohl die Reduzierung, als auch die Vergrößerung des Keims, senken die Energie des Keims.	Jeder Keim muss diese Barriere überwinden, wenn er weiter wachsen soll. Dabei muss Keimbildungsarbeit durch thermische Fluktuationen geleistet werden. Mit zunehmender Unterkühlung wird Δg immer größer und die kritische Keimgröße immer kleiner. Oberhalb TS ist rc = ∞.

Die bis hier beschriebene Art der Erstarrung wird homogene Kristallisation genannt. Homogen deshalb, weil der Übergang fest ⇒ flüssig ohne Beteiligung einer dritten Phase erfolgt. Das ist nur möglich bei besonders reinen Metallen ohne bereits vorhandene feste Kristallisationskeime. Die zur Keimbildung notwendige Oberflächenenergie muss dabei vollständig von der Umwandlungsenergie aufgebracht werden. In diesem Fall kann eine recht große Unterkühlung erreicht werden.

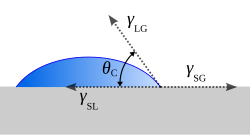
Andernfalls können bei der heterogenen Keimbildung feste Fremdteilchen in der Schmelz als Kristallisationskeime dienen. Diese werden von der festen Phase benetzt wie von Wassertropfen. Die zur Keimbildung notwendige (Oberflächen-) Energie kann erheblich reduziert werden. (A) – Bei einem sehr großem Benetzungswinkel (θ) findet kaum eine Benetzung satt. Die homogene Keimbildung hat noch einen relativ großen Anteil an der Keimbildung. (B) – Bei θ = 90° ist die Oberfläche und damit die Oberflächenenergie der festen Phase nur halb so groß, wie bei der ideale Kugel. (C) – Bei einem sehr kleinem Benetzungswinkel kann die homogene Keimbildung vollständig unterdrückt werden und die heterogene Keimbildung dominiert.

Durch das Impfen der Schmelze mit Keimkristallen kann der Erstarrungsprozess beeinflusst werden. Dabei werden beim Gießen Fremdteilchen in die unterkühlten Schmelze gestreut. Die Keimzahl und damit die Korngröße kann so in weiten Grenzen gesteuert werden.

Auch bei der Herstellung von Einkristallen kommt ein Impfkristall zur Anwendung. Beim Czochralski-Verfahren wird die Schmelze kurz unter dem Schmelzpunkt gehalten und ein winziger Einkristall wird in die Schmelze getaucht. Dieser kühlt die Schmelze ab und die Kristallisation beginnt. Dabei wird der Impfkristall zusammen mit der erstarrten Masse aus der Schmelze gezogen. Das Ergebnis ist ein hochreiner monokristalliner Werkstoff. Auf diese Weise werde die Silizium-Wafer für die Halbleitertechnik und Turbinenschaufeln für Strahltriebwerke hergestellt.

Kristallwachstum

Sobald der Keim den kritischen Radius überschritten hat, kann er unter Energiegewinn weiter wachsen. Um die Vorgänge bei diesem Prozess zu beschreiben, müssen wir uns von den Vereinfachungen des vorherigen Kapitels lösen. Vor allem sind die Keimzellen und die daraus wachsenden Kristalle NICHT Kugelförmig.

Grundsätzlich folgen Atome bei ihrer Anordnung dem Prinzip der sog. dichtesten Kugelpackung. Die Struktur wird dabei von ihrer Koordinationszahl bestimmt – der Anzahl der nächsten Nachbaratome. Metallische Elemente weisen durchweg Koordinationszahlen von 8 oder 12 auf. Ein Koordinationszahl von 8 hat ein kubisch-raumzentriertes Gitter zur Folge – oder ähnliche Gitter mit veränderten Abständen und/oder Winkeln der Translationsachsen. Ein Koordinationszahl von 12 hat ein kubisch-flächenzentriertes Gitter oder ein hexagonales Gitter dichtester Kugelpackung (h.d.P.) zur Folge.

Beim Kristallwachstum ist der Energiegewinn nicht nur von dessen Volumen abhängig, es spielt auch eine Rolle, an welchem Platz das Atom eingelagert wird. Der Energiegewinn ist umso höher, je mehr Nachbarplätze bereits besetzt sind.

• Demnach ist der Gewinn am geringsten, wenn ein einzelnes Atom auf einer flachen Ebene andockt.
• Günstiger ist der Einbau eines Atoms an der Stufe zweier Ebenen
• Am höchsten ist der Energiegewinn, wenn dieses Atom ein Loch in einer Ebene schließen kann.

Als Ergebnis entsteht ein Kristallgitter, gebildet durch vielfache Translation der Elementarzelle. Idealerweise sind seine Grenzen atomar glatte Flächen, was streng genommen nur bei einer Temperatur von T = 0 K möglich ist. Darüber hinaus sorgen Gitterschwingungen für eine Aufrauung dieser Flächen – und nicht zuletzt führen sie zu den vielen strukturellen Fehlordnungen, die den Realkristall ausmachen.

Wie der Einbau eines einzelnen Bausteins erfolgt, sollen folgende Schritte zeigen:

• Durch Konvektion oder Diffusion erfolgt der Transport des Bausteins an die Phasengrenze
• Adsorption des Bausteins an der festen Phase auf einer flachen Ebene
• Durch Oberflächendiffusion wandert der Baustein an energetisch günstigere Plätze, etwa Stufen oder Löcher in der Ebene

Vielfach sind Komponenten im flüssigen Zustand beliebig Mischbar, im festen Zustand jedoch nicht. Eventuell mit dem Baustein verbundene Fremdatome können bei jedem Schritt von diesem abgetrennt werden, wenn es energetisch günstiger ist. So werden tiefschmelzende Komponenten vor der Kristallisationsfront hergeschoben, während der Schmelze die hochschmelzenden Komponenten entzogen werden.

Es kann auch zur Bildung von Mischkristallen kommen – homogene Kristalle aus mehreren Komponenten. Kleine Atome wie Kohlenstoff oder Stickstoff finden in den Gitterlücken Platz und bilden Einlagerungs-Mischkristalle. Gleichartige Atome mit ähnlichen Atomradien bilden Austausch-Mischkristalle. So bilden ähnliche Atome wie Kupfer und Nickel bei jeder Zusammensetzung Mischkristalle.

Stabile oder instabile Kristallisationsfront

Bei der Erstarrung wird Kristallisationswärme frei. Diese heizt den Kristall wieder auf, unter Umständen bis zum Schmelzpunkt (er wird aber nicht wieder aufschmelzen). Die Erstarrungswärme muss also abgeführte werden, sonst kommt die Kristallisation zum Stillstand. Prinzipiell gibt es zwei Wege für die Wärmeabfuhr, mit entscheidendem Einfluss auf die Gefügeausbildung:

• Zu Beginn wird die Erstarrung an der Formwand (Tiegel oder Kokille) beginnen, weil diese die Wärmeenergie schnell aufnehmen und abführen kann. Die feste Phase wird eine niedrigere Temperatur haben als die Schmelze. Jeglicher Vorsprung an der Erstarrungsfront wird im Vergleich zum Rest der Front in ein Gebiet mit höherer Temperatur führen. Das Wachstum dieses Vorsprungs wird verlangsamt oder ganz gestoppt – diese stabile Erstarrungsfront bleibt glatt und eben bis sie auf konkurrierende Kristalle trifft.

• Mit fortschreitender Erstarrung wird die Temperatur im Kristall steigen und sogar höher liegen als die in der Schmelz, sodass die Wärme über die Schmelze abgeführt wird. Jede noch so kleine Erhebung in der Erstarrungsfront kommt in ein Gebiet größerer Unterkühlung. Aus dieser instabilen Kristallisationsfront sprießen stängelförmige Kristallarme, die ihrerseits fraktale Verzweigungen bilden. Auf diese Weise wachsen Dendriten bis weit in die Schmelze hinein.