Das Mehrkörperproblem in der Astronomie/ Allgemeine Lösungsmethoden/ Zwischenschritt-Verfahren: Leapfrog und Runge-Kutta
Ein entscheidender Schwachpunkt des Euler-Verfahrens besteht darin, dass man die Momentanbeschleunigungen und -geschwindigkeiten zu einem Zeitpunkt benutzt, um den Zustand des Systems zu einer Zeit zu bestimmen. Es ist naheliegend, dass man den tatsächlichen Verlauf der Geschwindigkeiten und Beschleunigungen während der Zeitspanne genauer wiedergeben kann, wenn man zusätzlich dabei auftretende Zwischenwerte berücksichtigt.
Im Folgenden werden zwei Methoden zur Konstruktion solcher Zwischenwerte vorgestellt. Das Leapfrog-Verfahren kommt mit einem einzigen Zwischenschritt aus, vermag die Genauigkeit einer Mehrkörpersimulation im Vergleich zur Euler-Methode dennoch um etliche Größenordnungen zu steigern. Das Runge-Kutta-Verfahren erfordert mehrere Zwischenstufen, liefert dafür aber noch präzisere Ergebnisse.
Leapfrog-Verfahren
[Bearbeiten]Herangehensweise
[Bearbeiten]Der einfachste Weg hin zu Zwischenwerten besteht darin, die Momentangeschwindigkeiten zur Zeit nicht für einen ganzen, sondern nur einen halben Zeitschritt gelten zu lassen. Damit gewinnt man Positionen zum Zeitpunkt . Aus solchen Zwischenpositionen folgen unmittelbar Zwischenwerte für die Momentanbeschleunigungen. Diese lassen genauer auf die Momentangeschwindigkeiten zum Zeitpunkt schließen als die im Rahmen des Euler-Verfahrens herangezogenen Werte zu Beginn eines Zeitschritts. Die neuen Momentangeschwindigkeiten gestatten es schließlich, aus den Zwischenpositionen zum Zeitpunkt die für gültigen Endpositionen zu berechnen. Das Schema sieht also jetzt folgendermaßen aus:

Um von einer alten zu einer neuen Position zu gelangen, arbeitet man nun mit dem Mittel der alten und neuen Momentangeschwindigkeiten. Dieses stellt eine viel bessere Näherung der für die Zeitspanne zwischen und geltenden Durchschnittsgeschwindigkeit dar als die von dem Euler-Verfahren ausschließlich benutzte alte Momentangeschwindigkeit zu Beginn des Zeitintervalls.
Die Verwendung des Mittels der Momentangeschwindigkeiten zu Anfang und Ende eines Zeitschritts bedeutet, dass man die wahre Fläche unter der Geschwindigkeitskurve nicht mehr durch Rechtecke, sondern Trapeze ersetzt. Es leuchtet sofort ein, dass dieses Vorgehen wesentlich zuverlässiger ist.

Als kritischer Aspekt bleibt bestehen, dass man die Momentangeschwindigkeit zum Zeitpunkt bereits kennen muss, bevor man die entsprechende Position berechnet hat. Dies ist nur nach dem Schema des Euler-Verfahrens möglich, d.h. erneut wird die Fläche unter der Beschleunigungskurve durch Rechtecke angenähert. Die Höhe eines solchen wird nun aber jeweils durch die Beschleunigung in der Mitte eines Zeitintervalls festgelegt und nicht durch den Wert zu Beginn. Somit wird auch für die Beschleunigung die Fläche unter der Kurve genauer wiedergegeben.

Genauigkeit
[Bearbeiten]Wieder sei die Güte der Lösung am Beispiel der Kreisbahn demonstriert. Nach dem ersten Halbschritt scheint keine signifikante Verbesserung eingetreten zu sein, da dieser genau dem Schema des Euler-Verfahrens folgt. Die Beschleunigung an der Zwischenposition wirkt jedoch derart auf die kleine Masse , dass mit der für den zweiten Halbschritt geltenden neuen Geschwindigkeit der Fehler des ersten Halbschritts fast vollständig kompensiert wird.

Eine genaue Analyse der Erdbahn liefert für einen Zeitschritt von 1 Tag (zwei Halbschritten von je 1/2 Tag) einen erstaunlich kleinen Fehler von nur etwa 5 Milliardstel des wahren Bahnradius. Nimmt man wieder den ungünstigsten Fall an, dass die Fehler der einzelnen Schritte sich aufaddieren (die später skizzierten Tests zeigen, dass dies für die Leapfrog-Methode nicht zutrifft), erhält man auf 1 Jahr hochgerechnet einen relativen Fehler von etwa 2 Millionstel! Die auf dem Leapfrog-Verfahren beruhende Lösung ist um mehrere Größenordnungen genauer als diejenige nach Euler. Ein Fehler von 2 Millionstel des Radius pro Jahr ist allerdings immer noch viel zu hoch, um beispielsweise die Stabilität der Erdbahn (welche ja nicht isoliert ist, sondern von den übrigen Planeten des Sonnensystems gestört wird) auf geologischer Zeitskala zu prüfen.
Das im Vergleich zur Euler-Methode gute Resultat ist kein Zufall, denn für den prozentualen Fehler pro Schritt gilt:
Dieser ist jetzt der 4. Potenz des Zeitschritts proportional, d.h. eine Halbierung der Zeitintervalle erbringt pro Schritt das 16-fache an Genauigkeit. Verringert man allgemein um einen Faktor , steigert man die Präzision eines Einzelschritts um bzw. der gesamten Simulation um . Kleinere Zeitschritte erhöhen nun sehr effizient die Genauigkeit der Lösung. Umgekehrt muss man aber sehr darauf achten, zwecks kürzerer Rechenzeit die Schrittweite nicht allzu sehr zu vergröbern, da dann die Qualität des Verfahrens sehr rasch abnimmt.
Die Effizienz des Leapfrog-Verfahrens darf keineswegs zu dem Schluss verleiten, man könne mit genügend kleiner Schrittweite eine im Prinzip beliebige Genauigkeit erzielen. Die bei Computersimulationen verwendeten Gleitkommazahlen weisen selbstverständlich eine endlich Anzahl von Nachkommastellen auf, so dass jeder Zeitschritt zwangsläufig mit Rundungsfehlern behaftet ist. Kleinere Schritte bedeuten mehr Einzelberechnungen und damit Rundungsfehler, wodurch die höhere nominelle Genauigkeit der Näherung zunehmend unterlaufen wird. Auch hier handelt es sich um eine prinzipielle, jedem nominell noch so guten Verfahren anhaftende Einschränkung.
Dem beachtlichen Abschneiden der Leapfrog-Methode bezüglich der zeitlichen Schrittweite steht leider eine enorme Instabilität hinsichtlich des Abstandes der beiden Massen gegenüber. Es schält sich nämlich folgende Beziehung heraus:
Der prozentuale Fehler steigt sage und schreibe mit der 6. Potenz des Kehrwertes von an – bei der Hälfte des ursprünglichen Abstands schon auf das 64-fache, bei einem Drittel desselben gar bereits auf das 729-fache! Man könnte daher vermuten, dass sehr enge Vorübergänge zweier Punktmassen mit dem Euler-Verfahren zuverlässiger behandelt würden. In der Tat gibt es einen kritischen Abstand, bei dem letzteres einen kleineren prozentualen Fehler pro Zeitschritt liefert. Allerdings ist der Fehler selbst eines einzigen Schrittes an dieser Stelle schon so hoch, dass keine der beiden Näherungen mehr auch nur ansatzweise tauglich ist. Beide Verfahren brechen zusammen, lange bevor sich zwei Massenpunkte bis auf den relevanten Abstand genähert haben. Damit aber ist dieser in der Praxis völlig belanglos.
Um ein Mehrkörpersystem auch unter den Bedingungen von Beinahezusammenstößen korrekt behandeln zu können, sind spezielle Techniken notwendig, denen das ganze nächste Kapitel gewidmet ist. Dazu gehört unter anderem eine dynamische zeitliche Schrittweite. Dort wo die Körper eng zusammenstehen, werden die Berechnungen mit kleineren durchgeführt als in Gebieten geringer Dichte.
Analog zum Euler-Verfahren kann man auch für die Leapfrog-Methode das 3. eplersche Gesetz auf den relativen Fehler anwenden. Abermals erweist sich das Verhältnis zeitliche Schrittweite / Umlaufdauer als entscheidend, denn man erhält:
Einschub für Fortgeschrittene: Wiedergabe einer Kreisbahn durch das Leapfrog-Verfahren
Die kleine Masse startet erneut von der Position aus. Die Anfangsgeschwindigkeit soll jetzt aber nur für einen halben Zeitschritt gelten. Für die Zwischenposition und ihren Abstand von der großen Masse gilt somit:
Daraus folgt mittels des Gravitationsgesetzes die entsprechende Zwischenbeschleunigung , wobei der immer wieder im Nenner auftauchende etwas unhandliche Ausdruck durch abgekürzt wird.
Um auf die Geschwindigkeit nach dem ganzen Schritt zu schließen, wird obige Beschleunigung für das volle Zeitintervall festgehalten. Das Ergebnis lautet:
Mit der ebenfalls nur für eine Zeit angewandten Endgeschwindigkeit gelangt man von der Zwischen- zur Schlussposition. Für diese gilt:
Nun stehen alle für die Bestimmung der relativen Fehler erforderlichen Ergebnisse bereit. Da wieder angenommen wird, muss man bei der Berechnung des Endabstandes und des Betrags der Endgeschwindigkeit nur die niedrigsten Potenzen von berücksichtigen. Dabei ist zu beachten, dass auch der Term solche Potenzen enthält, denn wegen gilt die Näherung:
Unter Verwendung aller Terme lautet zunächst:
Bei dem quadratischen Glied fällt nach dem Einsetzen des genäherten Wertes von die 1 weg, so dass sich dieses effektiv als ein Term der 4. Potenz mit dem Beitrag erweist. Bei dem nächsten Glied genügt es, mit zu rechnen, da alle weiteren Terme nur höhere Potenzen von liefern. Es lautet so . Das letzte Glied kann einfach gestrichen werden. All diese Überlegungen führen zu:
Die Wurzel kann auf die gleiche Art und Weise genähert werden wie bereits unter dem Euler-Verfahren besprochen, womit sich folgender relativer Fehler ergibt:
Die abermalige Anwendung der Sonnenmasse und des Bahnradius der Erde bestätigt die bereits diskutierte Genauigkeit des Leapfrog-Verfahrens. Setzt man wiederum das 3. Keplersche Gesetz ein, so gewinnt man den einprägsamen Ausdruck:
Setzt man die Fehler von Leapfrog- und Euler-Methode gleich, so erhält man einen kritischen Abstand , unterhalb dessen das Euler-Verfahren anscheinend besser abschneidet.
Setzt man jedoch wiederum in den relativen Fehler ein, so gilt einfach:
Für ist der relative Fehler größer als der Abstand zwischen den beiden Massen selbst! Damit ist der Zusammenbruch beider Verfahren schon lange vor Erreichen des kritischen Abstands gezeigt.
Zuletzt sei auch der relative Fehler der Geschwindigkeit erörtert. Der Betrag der Endgeschwindigkeit lautet unter Mitnahme aller Terme:
Beim quadratischen Glied fällt analog zum Abstand die 1 weg, so dass sich dieses erneut als Term der 4. Potenz entpuppt. Damit ist für den Vorfaktor erlaubt, alle anderen Terme würden nur höhere Potenzen von darstellen. Es ergibt sich so der Beitrag . Für das Glied 4. Potenz gilt wiederum , so dass es den Wert beisteuert. Somit lautet das Endergebnis:
Wie bei dem Euler-Verfahrens weist der Geschwindigkeitsbetrag absolut betrachtet den gleichen relativen Fehler auf wie der Abstand. Doch nun wird die Geschwindigkeit leicht unter- anstatt überschätzt, was angesichts des leicht überschätzten Abstandes eine zusätzliche Stabilisierung der Simulation bedeutet. Die Euler-Methode überschätzt sowohl als auch , was eine Unterschätzung der Gravitation, aber eine Überschätzung der Zentripetalkraft nach sich zieht. Dementsprechend driftet die kleine Masse mit jedem Zeitschritt rasch nach „außen“. Nun aber werden beide Kräfte unterschätzt, so dass sie weiterhin in guter Näherung im Gleichgewicht bleiben. Die Fehler der Einzelschritte weisen im Vergleich zum Euler-Verfahren so eine viel schwächere Tendenz auf, sich aufzusummieren.
C-Code: Mehrkörpersimulation mit dem Leapfrog-Verfahren
Für eine effiziente Programmierung ist es hilfreich, wenn man gemäß dem zu Beginn dieses Abschnitts gezeigten Schemas einige Schritte hintereinander aufschreibt. Man erkennt dann, dass das Leapfrog-Verfahren folgendem Algorithmus folgt:
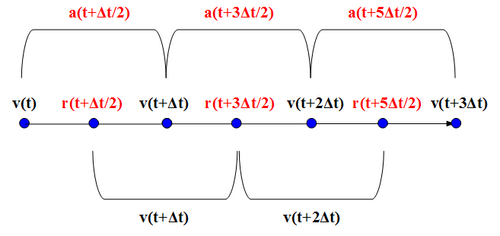
Zu Beginn der Simulation zum Zeitpunkt muss man sich mit der Geschwindigkeit um einen halben Zeitschritt zur Position bewegen. Mit der dort herrschenden Beschleunigung gewinnt man die Geschwindigkeit , d.h. die Geschwindigkeit zum Zeitpunkt kann man überspringen. Mit gelangt man nicht nur bis zur Positionen , sondern bis nach , kann also überspringen. Die Beschleunigung liefert wiederum die Geschwindigkeit und jene die Position usw. Dieses permanente wechselseitige Überspringen von Positionen und Geschwindigkeiten gibt dem Verfahren seinen Namen, welches im Englischen Bockspringen bedeutet. Für den nachfolgenden Code werden im Vergleich zum Euler-Verfahren keine neuen Variablen und Prozeduren benötigt.
Ein Vergleich der Codes für die beiden Methoden zeigt, dass für das Leapfrog-Verfahren kein höherer Rechenaufwand erforderlich ist. Seine im Vergleich zum Euler-Verfahren viel bessere Genauigkeit verdankt es allein der geschickten Wahl der Zeitpunkte, für welche Positionen, Geschwindigkeiten und Beschleunigungen berechnet werden.
/* Globale Variablen */
unsigned int N;
double *m;
double **r;
double **v;
double **a;
unsigned int i,k;
double t,dt;
double T;
for (t = 0;t < T;t += dt)
{
/* Initialer Halbschritt zur Position r(dt/2) */
if (t == 0)
{
for (i = 0;i < N;i ++)
{
for (k = 0;k < 3;k ++)
r[i][k] += v[i][k] * dt / 2;
}
}
/* Beschleunigungen a(dt/2), a(3dt/2) usw. */
for (i = 0;i < N;i ++)
beschleunigung (i,N,m,r,a[i]);
/* Geschwindigkeiten v(t+dt), v(t+2dt) usw. */
/* Positionen r(t+3dt/2), r(t+5dt/2) usw. */
for (i = 0;i < N;i ++)
{
for (k = 0;k < 3;k ++)
{
v[i][k] += a[i][k] * dt;
r[i][k] += v[i][k] * dt;
}
}
}
Aufgrund des vergleichsweise geringen Rechenaufwandes wird das Leapfrog-Verfahren häufig in der Praxis eingesetzt. Mit der hier geschilderten Darstellung als Ziwschenschritt-Methode ist es aber nicht möglich, dynamische zeitliche Schrittweiten anzuwenden. Jedoch lassen sich die Beziehungen zwischen Positionen, Geschwindigeiten und Beschleunigungen zu diesem Zweck relativ leicht umformulieren, wie das nächste Unterkapitel zeigt.
Klassisches Runge-Kutta-Verfahren
[Bearbeiten]Heun-Verfahren als Vorstufe
[Bearbeiten]Von allen Methoden, mehrere Zwischenschritte von alten nach neuen Positionen zu bilden, ist das Runge-Kutta-Verfahren bei weitem am gebräuchlichsten. Es leitet sich jedoch nicht von dem Leapfrog-Algorithmus ab, sondern dem folgenden, auf den Mathematiker Heun zurückgehenden Schema. Auf den ersten Blick ist dieses dem Leapfrog-Verfahren unterlegen, weil für die Berechnung der Geschwindigkeit am Ende des Zeitintervalls die Beschleunigung zu dessen Beginn verwendet wird und nicht der Zwischenwert in dessen Mitte.

Als Folge dessen zeigt der relative Fehler eines Zeitschritts lediglich eine Proportionalität . Die Genauigkeit eines solchen Schritts steigt so nur mit und diejenige einer kompletten Simulation nur mit , wenn man um den Faktor verringert. Das Verfahren lässt sich jedoch, wie die Mathematiker Runge und Kutta erkannten, stringenter zu mehreren Zwischenschritten ausbauen als die Leapfrog-Methode.
Erweiterung zum klassischen Verfahren
[Bearbeiten]Um eine solche Verbesserung zu erreichen, startet man zunächst wie bei dem Leapfrog-Verfahren mit der Geschwindigkeit und Beschleunigung an der Position zu Beginn eines Zeitintervalls und geht damit einen halben Schritt zur Position , wo neue Werte für Geschwindigkeit und Beschleunigung gelten. Mit diesen startet man nun abermals von der Ausgangsposition aus und gelangt so wiederum mit einem Halbschritt an die Position , wo die Geschwindigkeit und Beschleunigung herrschen. Man durchläuft das Zeitintervall einmal unter den Bedingungen zu seinem Beginn (Werte 1) und im Gegensatz zur Leapfrog-Methode ein zweites Mal unter den ungefähren Verhältnissen zu dessen Ende (Werte 2). Dementsprechend stellt das Resultat (Werte 3) im Vergleich zum Leapfrog-Verfahren einen genaueren Zwischenwert für den Zeitpunkt bereit.
Hiermit gelangt man wiederum von der Startposition ausgehend nach einen ganzen Zeitschritt zur Position , welche eine Geschwindigkeit und Beschleunigung liefert. Diese Werte 4 stellen jedoch noch nicht das Endergebnis der Prozedur dar. Vielmehr bildet man aus den Anfangswerten 1, den Zwischenwerten 2 und 3 sowie den ungefähren Endwerten 4 Mittelwerte für Geschwindigkeit und Beschleunigung während des ganzen Zeitintervalls, wobei die Zwischenwerte doppelt gewichtet werden. Diese Mittelwerte führen nun tatsächlich von der Ausgangs- zur Endposition.

Das Runge-Kutta-Verfahren ist zu aufwendig, um dessen Güte anhand einer expliziten algebraischen Rechnung für die Kreisbahn darzulegen. Man kann jedoch allgemein zeigen, dass es die Leapfrog-Methode noch um eine Potenz übertrifft:
Der prozentuale Fehler eines Zeitschritts ist der 5. Potenz, derjenige einer gesamten Simulation der 4. Potenz von proportional. Es gilt jedoch zu beachten, dass dies mit wesentlich mehr Einzelberechnungen erkauft ist und damit die Problematik der Rundungsfehler umso stärker ins Gewicht fällt. Wieder gibt eine optimale Schrittweite, unterhalb derer aufgrund der endlichen Genauigkeit der Gleitkommazahlen die Qualität des Verfahrens sich nicht weiter verbessert, im Gegenteil bei zugleich längerer Rechenzeit sogar abnimmt.
Einschub für Fortgeschrittene: Runge-Kutta-Verfahren und Simpsonregel
Die nochmalige (nominelle) Steigerung der Genauigkeit kann man sich folgendermaßen klarmachen. Das Leapfrog-Verfahren verwendet pro Zeitschritt nur zwei Geschwindigkeitswerte (nämlich zu dessen Beginn und Ende), so dass die Fläche unter der Geschwindigkeitskurve durch Trapeze ersetzt wird. Jetzt stehen drei Werte zur Verfügung, nämlich zu Beginn, am Ende und zusätzlich die Zwischenwerte und , welche durch Mittelung zusammengefasst werden (da beide aus dem ersten Halbschritt hervorgehen).

Die Fläche unter der Geschwindigkeitskurve wird jetzt durch Parabel-Stücke angenähert, welche jeweils durch die drei pro Simulationsschritt gegebenen Werte gelegt werden. Der Flächeninhalt und damit die während eines Schritts zurückgelegte Strecke kann mit Hilfe der Simpsonregel. berechnet werden. Diese Formel erklärt die doppelte Gewichtung der Werte 2 und 3 im letzten Schritt des Runge-Kutta-Verfahrens, denn es gilt:
Auch für die Beschleunigung kann man mit Parabel-Flächen arbeiten, wohingegen man sich bei der Leapfrog-Methode mit Rechtecken als Ersatz für die tatsächliche Fläche unter der Beschleunigungskurve begnügen muss. Für die Änderung der Geschwindigkeit gilt:
Die Simpson-Regel begründet auch die Abhängigkeit der Genauigkeit des Runge-Kutta-Verfahrens von . Die Abweichung zwischen der Fläche unter einer Ersatzparabel und derjenigen unter der tatsächlichen Kurve ist direkt proportional zur 5. Potenz des Abstands zwischen zwei Stützstellen.
C-Code: Mehrkörpersimulation mit dem Runge-Kutta-Verfahren
Bedingt durch die zahlreichen Zwischenschritte ist der Code komplexer als für die bisher diskutierten Methoden. Für Position, Geschwindigkeit und Beschleunigung müssen nun jeweils 4 Datensätze vorgehalten werden - ein Datensatz pro Zwischenschritt. Diese Größen werden daher jetzt als dreidimensionale Arrays bzw. als zweidimensionale Arrays von Zeigern deklariert. Nicht nur für jeden Massenpunkt, sondern auch für jeden Zwischenschritt existiert damit ein Zeiger, der wie bisher auf jede der drei Vektorkoordinaten deuten kann. Der erste Index eines jeden Zeigerarrays bezieht sich auf den gerade abgearbeiteten Zwischenschritt (läuft aber von 0 bis 3 anstatt von 1 bis 4, da die Indizes für ein Array gemäß der Syntax von C mit 0 und nicht mit 1 beginnen), der zweite jeweils auf einen bestimmten Körper. Beim Aufruf der Beschleunigungsprozedur muss für r und a nun jeweils der Index des aktuellen Zwischenschrittes angegeben werden.
/* Globale Variablen */
unsigned int N;
double *m;
double ***r;
double ***v;
double ***a;
unsigned int i,k;
double t,dt;
double T;
for (t = 0;t < T;t += dt)
{
/* Beschleunigungen a1 an den Positionen r1 */
for (i = 0;i < N;i ++)
beschleunigung (i,N,m,r[0],a[0][i]);
/* Positionen r2 = r1 + v1 * dt/2 */
/* Geschwindigkeiten v2 = v1 + a1 * dt/2 an den Positionen r2 */
/* Beschleunigungen a2 an den Positionen r2 */
for (i = 0;i < N;i ++)
{
for (k = 0;k < 3;k ++)
{
r[1][i][k] = r[0][i][k] + v[0][i][k] * dt / 2;
v[1][i][k] = v[0][i][k] + a[0][i][k] * dt / 2;
}
}
for (i = 0;i < N;i ++)
beschleunigung (i,N,m,r[1],a[1][i]);
/* Positionen r3 = r1 + v2 * dt/2 */
/* Geschwindigkeiten v3 = v1 + a2 * dt/2 an den Positionen r3 */
/* Beschleunigungen a3 an den Positionen r3 */
for (i = 0;i < N;i ++)
{
for (k = 0;k < 3;k ++)
{
r[2][i][k] = r[0][i][k] + v[1][i][k] * dt / 2;
v[2][i][k] = v[0][i][k] + a[1][i][k] * dt / 2;
}
}
for (i = 0;i < N;i ++)
beschleunigung (i,N,m,r[2],a[2][i]);
/* Positionen r4 = r1 + v3 * dt */
/* Geschwindigkeiten v4 = v1 + a3 * dt an den Positionen r4 */
/* Beschleunigungen a4 an den Positionen r4 */
for (i = 0;i < N;i ++)
{
for (k = 0;k < 3;k ++)
{
r[3][i][k] = r[0][i][k] + v[2][i][k] * dt;
v[3][i][k] = v[0][i][k] + a[2][i][k] * dt;
}
}
for (i = 0;i < N;i ++)
beschleunigung (i,N,m,r[3],a[3][i]);
/* Endpositionen = Startpositionen + mittlere Geschwimndigkeiten * dt */
/* Endgeschwindigkeiten = Startgeschwindigkeiten + mittlere Beschleunigungen * dt */
for (i = 0;i < N;i ++)
{
for (k = 0;k < 3;k ++)
{
r[0][i][k] += (v[0][i][k] + 2 * v[1][i][k] + 2 * v[2][i][k] + v[3][i][k]) * dt / 6;
v[0][i][k] += (a[0][i][k] + 2 * a[1][i][k] + 2 * a[2][i][k] + a[3][i][k]) * dt / 6;
}
}
}
Im Prinzip könnte man die pro Zwischenschritt immer gleiche Abfolge von neuer Position, Geschwindigkeit und Beschleunigung durch eine weitere Prozedur zusammenfassen, doch wird zugunsten einer klareren Darstellung der Zusammenhänge darauf verzichtet.
Da in den nachfolgenden Buchkapiteln immer wieder dreidimensionale Arrays (wie hier für die Position) benutzt werden, soll auch für solche die Speicherverwaltung kurz skizziert werden. Die Speicheradressierung geschieht nun in drei Stufen. Im ersten Schritt wird für jedes erforderliche Zeigerarray (Vektorarray-Objekt) Speicher zur Verfügung gestellt, daher die Anweisung sizeof (double **). Um alle Zwischenschritte des Runge-Kutta-Verfahrens abzudecken, werden insgesamt 4 Zeigerarrays benötigt. Im zweiten Schritt wird innerhalb jeden Zeigerarrays für jedes Vektorobjekt Platz geschaffen (was dem ersten Schritt der Speicheradressierung für ein zweidimensionales Array entspricht). Zuletzt wird für jedes Vektorobjekt Speicher für dessen Komponenten reserviert (wie im Falle zweidimensionaler Arrays).
r = malloc (4 * sizeof (double **));
for (j = 0;j < 4;j ++)
{
r[j] = malloc (N * sizeof (double *));
for (i = 0;i < N;i ++)
r[j][i] = malloc (3 * sizeof (double));
}
Die Speicherfreigabe durchläuft jetzt ebenfalls drei Stufen, wobei wie für zweidimensionale Arrays im Vergleich zur Speicheradressierung die Abfolge sich umkehrt. Abermals wird zuerst der Speicher für die Vektorkomponenten geleert, dann für die Vektorobjekte, zuletzt für die Vektorarray-Objekte.
for (j = 0;j < 4;j ++)
{
for (i = 0;i < N;i ++)
free (r[j][i]);
free (r[j]);
}
free (r);
Trotz seiner großen allgemeinen Bedeutung und Genauigkeit wird das Runge-Kutta-Verfahren nur relativ selten auf astronomische Mehrkörpersysteme angewandt, da es sich aufgrund seines komplexen Vorgehens bei der Bildung von Zwischenschritten kaum mit dynamischen Zeitintervallen vereinbaren lässt. Es kann bei Aufgabenstellungen eingesetzt werden, bei denen konstant gehalten werden darf. Als Beispiel sei eine Diplomarbeit von Geisler (2006) [1] genannt, welcher untersuchte, wie die ausgedehnten Gashüllen sehr leuchtkräftiger Sterne durch die von einem Begleitstern ausgehende Schwerkraft gestört werden. Die Gashülle wird durch Massenpunkte jeweils gleicher Masse dargestellt. Da im Vergleich zu den Sternmassen sehr gering ist, üben diese Modellkörper untereinander nur sehr kleine Beschleunigungen aufeinander aus. Die Sterne werden nicht als punktförmig behandelt, sondern deren endlicher Radius wird berücksichtigt, so dass ein verschwindender Abstand zwischen einem Mitglied der Gashülle und einem Stern ausgeschlossen ist. Die Simulation bleibt somit auch ohne dynamische Zeitschritte ausreichend stabil, was man anhand der Energieerhaltung überprüfen kann.
Einzelnachweise
- ↑ Geisler R., Gravitativer Einfluss eines Begleitsterns auf LBV-Nebel, Diplomarbeit, Ruprecht-Karls-Universität Heidelberg, 2006






































































![{\displaystyle [t,t+\Delta t/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82732b388172c9c9b37824e254dc79bca5d42dbf)








