Digitale bildgebende Verfahren/ Druckversion

Vorwort
[Bearbeiten]Einführung
[Bearbeiten]Dieses Buch möchte dem Leser einen ersten Überblick über die vielfältigen Möglichkeiten geben, wie digitale Bilder erzeugt werden können, welche Eigenschaften diese gespeichert haben und wie sie für einen Betrachter wiedergegeben werden können. Die Bedeutung von bildgebenden Verfahren ist ungebrochen. 2015 wurde von der Generalversammlung der Vereinten Nationen als Internationales Jahr des Lichts und der lichtbasierten Technologien ausgerufen. Dies soll auch an die zentrale wissenschaftliche Bedeutung des Lichts erinnern, da durch Licht unser Kosmos besser verstanden, kranke Menschen besser behandelt und neue Kommunikationsmittel erfunden werden können.
Lichtteilchen haben keine Ruhemasse und bewegen sich daher immer mit Lichtgeschwindigkeit. Daraus erwächst das Prinzip vom Welle-Teilchen-Dualismus, da Licht sowohl als elektromagnetische Welle (Lichtwelle) als auch als Korpuskel (Photonen) interpretiert werden kann oder sogar muss. Insofern spielen sowohl Strahlungsaspekte eine Rolle, wie zum Beispiel bei Lichtstrahlen in der geometrischen Optik oder bei klassisch erklärbaren Wellenphänomenen, wie Brechung und quantenmechanische Wellenphänomene, allen voran die Beugung.

Die Photographie wurde in der ersten Hälfte des 19. Jahrhunderts entwickelt und stellte eine revolutionäre Technik dar, weil optische Abbildungen damit dauerhaft gespeichert werden konnten. Der aus den altgriechischen Wörtern "φωτός" ("photós": zu Deutsch "des Lichtes") und γράφειν ("gráphein": zu Deutsch "schreiben" oder "zeichnen") zusammengesetzte Begriff geht auf den Astronomen Johann Heinrich Mädler (1794–1874) zurück, der ihn als Alternative zu "Lichtzeichnenkunst" erstmals in seinem Beitrag mit dem Titel "Photographie" in der Beilage der überregional erschienene Tageszeitung "Königlich privilegierten Berlinischen Zeitung von Staats- und gelehrten Sachen" vom 25. Februar 1839 erwähnte. Mädler beschrieb dort die beiden damals erfundenen photochemischen Verfahren mit Silbersalzen:[1]
- Die direkt im Auflicht als Unikat registrierte photopositive Daguerreotypie von Louis Daguerre (1787–1851). Das Bild auf einer mit Silber beschichteten und mit Jod bedampften, spiegelglatt polierten Metallplatte ist stets spiegelverkehrt zum aufgenommenen Objekt.
- Das photonegative Verfahren (fotogenische Zeichnung) von William Henry Fox Talbot (1800–1877). Hier kann das gewonnene Negativbild anschließend beliebig oft mit Hilfe von Sonnenlicht durch Schattenwurf im Durchlicht auf lichtempfindliches Papier übertragen (Kontaktkopie) danach photochemisch fixiert werden (Schutzverfahren).
In heutiger Zeit ist es zunehmend üblich, dass Information, die in Form von Licht vorliegt, nicht mehr mit photochemischen Filmmaterial, sondern mit elektronischen Sensoren registriert wird. Dadurch wird die Digitalisierung der Daten und deren informationstechnische Weiterverarbeitung vereinfacht. Gleichermaßen gilt dies für die computergestützte Generierung, die Speicherung, die Nachbearbeitung und die Wiedergabe digitaler Steh- und Bewegtbilder. Digitale Bilder können Information in Form von verschiedenen Helligkeiten, in Form verschiedener Farben oder in einer Kombination von beidem beinhalten, und sie können zwei- oder dreidimensional gestaltet sein.

Darüber hinaus ist es möglich, dieses Prinzip auf die elektromagnetischen Wellenlängenbereiche zu übertragen, die für Menschen unsichtbar sind. So können beispielsweise Mikrowellen oder Infrarotstrahlung zur Bildgebung herangezogen werden, aber genauso ist es möglich, hochenergetische Photonen im Ultraviolett-, im Röntgen- oder sogar im Gammastrahlenbereich dafür zu verwenden. Dies beschränkt sich keineswegs auf medizinische Verfahren, für die sich der Begriff bildgebende Verfahren in besonderem Maße etabliert hat.
Der Vollständigkeit halber sei noch erwähnt, dass auch mit Materiewellen, also zum Beispiel mit Elektronen- oder Ionenstrahlen, teilchenoptische Abbildungen gemacht werden können, die heute in der Regel ebenfalls digital registriert werden. Teilchen mit Ruhemasse können sich zwar nicht mit Lichtgeschwindigkeit bewegen, ihnen kann aber dennoch die De-Broglie-Wellenlänge zugeordnet werden.
Eine weitere Klasse von bildgebenden Apparaturen rastern Oberflächen oder Körper, wie zum Beispiel bei der Rastersondenmikroskopie und -spektroskopie (Rasterelektronen-, Rastertunnel-, Rasterkraft- oder Rasternahfeldmikroskope) oder beim Einsatz von Scannern. Hierbei werden die Bilder nicht unmittelbar gewonnen, sondern aus zeitlich und örtlich versetzt gewonnenen Signalen synthetisiert.
Erwartungen an den Leser
[Bearbeiten]Dem Leser wird es nützlich sein, wenn ihm die folgenden Begriffe und Zusammenhänge aus der Optik geläufig sind.
Es gibt mehrere, ganz verschiedenartige Möglichkeiten, elektromagnetische Wellen und somit auch Lichtteilchen zu beeinflussen:
- Emission (spontane (also zufällige) oder stimulierte (also angeregte oder erzwungene) Erzeugung)
- Remission durch Reflexion (Spiegelung, Reflexionsgesetz: Einfallswinkel gleich Ausfallswinkel) oder Transmission (Hindurchschickung)
- Absorption (Vernichtung von Photonen durch Dissipation oder Extinktion)
- Refraktion (Brechung, Snelliussches Brechungsgesetz) inklusive Dispersion (Verteilung verschiedener Wellenlängen)
- Diffraktion (Beugung an Kanten)
- Diffusion (Streuung an Elementarteilchen, Atomen, Molekülen oder Feinstaub mit und ohne Änderung der Energie)
- Polarisation (lineare, zirkulare oder elliptische Auslenkung)
- Gravitation (Massenanziehung)
Der letzte Punkt stellt einen Sonderfall dar, da die Photonen bei nicht-euklidischer Geometrie des Raumes durch Massen gar nicht unmittelbar beeinflusst werden, sondern sich ebenfalls geradlinig ausbreiten. Trotz der Tatsache, dass es im Universum Gravitationslinseneffekte gibt, ist dieser Effekt für diese Veröffentlichung nicht relevant.
Alle anderen der genannten Effekte werden uns hier jedoch immer wieder begegnen, so dass es sehr hilfreich ist, die Eigenschaften und Ausprägungen dieser grundlegenden Prinzipien verstanden zu haben. Darüberhinaus werden einfache Gleichungen, wie die trigonometrischen Funktionen, die Abbildungsgleichung (respektive Linsenformel) oder der Strahlensatz als bekannt vorausgesetzt.
Das Verhalten der elektromagnetischen Strahlung kann oft rein geometrisch behandelt werden. In manchen Fällen ist es daher nützlich, die elektromagnetische Strahlung als Teilchen zu betrachten, die sich geradlinig durch Raumabschnitte bewegen. In anderen Fällen ist es unerlässlich, auch die wellenförmige Ausbreitung des Lichts in geometrische Schattenräume zu berücksichtigen. Die bewusste Wahl der jeweils besser geeigneten Betrachtungsweise kann die Überlegungen und Schlussfolgerungen oft deutlich vereinfachen, in vielen Fällen ist es jedoch notwendig, beide Ausprägungen der elektromagnetischen Strahlung zu berücksichtigen, um vollständige und korrekte Aussagen machen zu können. Weitere als bekannt vorausgesetzte Begriffe aus der Wellentheorie sind daher:
- Elementarwellen / Huygenssches Prinzip
- Kohärenz / Interferenz
Mit diesem Rüstzeug gewappnet, sollte es jedem Leser möglich sein, den Inhalten der verschiedenen Kapitel zu folgen und gegebenenfalls Anhaltspunkte für weitergehende Recherchen zu finden.
Einzelnachweise
[Bearbeiten]- ↑ Johann Heinrich Mädler: Königlich privilegierte Berlinischen Zeitung von Staats- und gelehrten Sachen, Nummer 47, Beilage. Im Verlage der Vossischen Erben (Redakteur E. F. Lessing), Vossische Zeitungs-Expedition in der breiten Straße No. 8. Montag, den 25sten Februar 1839.
Grundlagen
[Bearbeiten]Dieses Kapitel beschäftigt sich mit prinzipiellen Eigenschaften von optischen Abbildungen. In den folgenden Abschnitten sind einige grundlegende Aspekte aufgeführt, die bei der Aufnahme und Registrierung von Bildern eine Rolle spielen.
Optik
[Bearbeiten]Die Optik (von altgriechisch ὀπτική τέχνη (optikḗ téchnē), zu Deutsch: „Lehre vom Sehen“) beschäftigt sich mit der Ausbreitung von Licht unter Berücksichtigung der Wechselwirkung zwischen Licht und Materie. Im engeren Sinne werden in der Optik optische Systeme behandelt, mit denen Objekte abgebildet werden können. Reelle Bilder können beispielsweise mit Bildwänden, photographischen Filmen oder elektronischen Bildsensoren aufgefangen werden, wohingegen virtuelle Bilder direkt durch das menschliche Auge gesehen werden können.
Lichtquellen haben immer eine endliche Ausdehnung. Wenn die leuchtende Fläche im Vergleich zu einem ausgedehnten optischen System klein ist, wird die entsprechende Lichtquelle als punktförmig bezeichnet. In der Praxis kann ein Fixstern als eine solche punktförmige Lichtquelle betrachtet werden. Im Labor kann eine punktförmige Lichtquelle durch die Beleuchtung einer kleinen Kreislochblende aus einer hinreichend großen Entfernung erzeugt werden. Das aus der Blende austretende Licht bildet ein Lichtbündel. Ein Lichtstrahl kann durch ein paralleles Lichtbündel mit kleinem Durchmesser angenähert werden. Lichtstrahlen werden in der geometrischen Optik verwendet, um die Richtung des Flusses der Lichtenergie anzugeben.
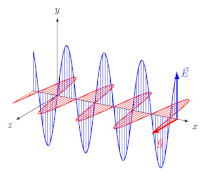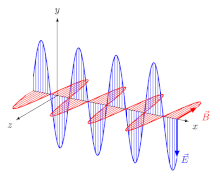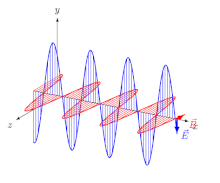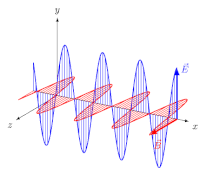
Beugungseffekte sind durch die Welleneigenschaften des Lichtes bedingt und treten immer auf, wenn es auf Kanten trifft. Die Beugung wird in der Wellenoptik behandelt und wird in der geometrischen Optik nicht berücksichtigt.
Die Lichtgeschwindigkeit im Vakuum ist eine festgelegte Größe, die für alle Arten elektromagnetischer Strahlung gilt:
Die Wellenlänge der mit der Frequenz transversal schwingenden, elektromagnetischen Welle beträgt hierbei:
Die Vektoren der elektrischen und der magnetischen Feldstärke stehen bei elektromagnetischen Wellen stets senkrecht zueinander und außerdem beide senkrecht zur Ausbreitungsrichtung.
Brechung
[Bearbeiten]
In allen anderen optischen Medien bleibt die Schwingungsfrequenz elektromagnetischer Wellen im Vergleich zu derjenigen im Vakuum erhalten, aber die Lichtgeschwindigkeit und die Wellenlänge sind kleiner. Dies kann durch den maßeinheitenlosen Brechungsindex (auch Brechzahl genannt) des optischen Mediums beschrieben werden:
Der Brechungsindex des Vakuums ist demzufolge gleich Eins, und bei allen anderen optischen Medien ist der Brechungsindex größer als Eins. Bei Gasen ist der Brechungsindex bei normalem Luftdruck nur geringfügig größer als Eins. Die meisten optischen Medien aus flüssigem oder festem Material haben typische Brechungsindices zwischen 1,3 und 2,0. Wasser hat bei Zimmertemperatur einen Brechungsindex von 1,333. Besondere Materialien haben Brechungsindices, die größer als Zwei sind, wie zum Beispiel Dimant (Kohlenstoffkristall) mit rund 2,4 oder Rutil (Titandioxid) mit rund 3,1.
Beim Übergang von Lichtstrahlen von einem optischen Medium mit der Brechzahl in ein optisches Medium mit der Brechzahl wird ein einfallender Lichtstrahl (in der Abbildung rechts weiß) zu einem Teil in das Einfallsmedium zurück gespiegelt (Reflexion, in der Abbildung rechts dunkelgrau) und zu einem anderen Teil in das Ausfallsmedium gebrochen (Refraktion, in der Abbildung rechts hellgrau). Die Richtungen der Reflexion und der Refraktion werden über die Winkel zur Flächennormalen (Lot) an der Stelle des Übergangs der beiden optischen Medien bestimmt.
Für die Reflexion gilt das Reflexionsgesetz:
- Einfallswinkel gleich Ausfallswinkel .
Für die Refraktion gilt das Snelliussche Brechungsgesetz:
Ist größer als , wird der Lichtstrahl zum Lot hingebrochen, und ist größer als , wird der Lichtstrahl vom Lot weggebrochen.
Am Einheitskreis (Radius gleich Eins) gilt:
und:
Das Snelliussche Brechungsgesetz geht damit in die folgende Form über:
Es gilt entsprechend:
Zur Herleitung des Brechungsgesetzes unter Berücksichtigung der Ausbreitung mit Huygensschen Elementarwellen mit der jeweiligen Lichtgeschwindigkeit auf dem schnellsten Weg entsprechend dem Fermatschen Prinzip siehe auch:
→ Kapitel "Bildaufnahme" / Abschnitt "Ablenkung von Lichtstrahlen"
Optische Achse
[Bearbeiten]
Die optische Achse beschreibt in der geometrischen Optik die Rotationsachse aller rotationssymmetrischen Bestandteile einer optischen Abbildung oder eines optischen Systems.
Schnittebene von zweidimensionalen Skizzen werden üblicherweise durch die optische Achse gelegt, so dass die Schnitte der rotationssymmetrischen optischen Elemente an dieser Achse gespiegelt dargestellt werden. Die optische Achse wird in solchen Skizzen immer als Strichpunktlinie dargestellt.
Hauptebenen
[Bearbeiten]
Hauptebenen stehen in der Regel senkrecht zur optischen Achse. Sie beschreiben vereinfacht betrachtet Flächen, an denen alle Strahlen in einem optischen Strahlengang gebrochen oder gespiegelt werden, und sie teilen den Objektraum links der Hauptebene vom Bildraum rechts der Hauptebene. In der Praxis gilt dies mit hinreichender Genauigkeit häufig nur für achsnahe Strahlen (paraxialer Strahlengang mit Gaußschen Strahlen).
Bei konvergenten Systemen werden die Strahlen zur optischen Achse abgelenkt, und bei divergenten Systemen werden die Strahlen von der optischen Achse weggelenkt.
Von den Hauptebenen werden in Richtung der optischen Achse Schnittweiten, Brennweiten, Objektweiten und Bildweiten gemessen. Die Schnittpunkte der Hauptebenen mit der optischen Achse werden als Hauptpunkte bezeichnet. Lichtstrahlen, die durch einen Hauptpunkt gehen, heißen Hauptstrahlen und werden nicht abgelenkt.
Linsen haben zwei Hauptebenen, deren Hauptpunkte mit den Scheitelpunkten der Linsenoberflächen auf der optischen Achse übereinstimmen können. Meist liegen sie jedoch zwischen der Mitte und den Scheitelpunkten der Linse. Bei hinreichend dünnen Linsen fallen die beiden Hauptebenen annähernd zu einer einzigen Hauptebene in der Mitte der Linse zusammen, so dass sich Berechnungen und graphische Darstellungen mit nur einer Hauptebene deutlich vereinfachen lassen. Von dünnen Linsen wird gesprochen, wenn der Radius der Oberflächen und somit auch die Brennweite deutlich größer sind als die Dicke der Linse entlang der optischen Achse.
Optische Systeme, wie zum Beispiel ein Objektiv, können sehr viele Hauptebenen haben, die nicht notwendigerweise alle im optischen System liegen müssen, wie zum Beispiel bei Retrofokusobjektiven oder teleskopischen Objektiven.
Messtechnisch können von außen unmittelbar nur die Lagen der beiden äußersten Hauptebenen eines optischen Systems bestimmt werden. Bei Zoomobjektiven, also bei Objektiven mit variabler Brennweite, variiert die Lage der Hauptebenen mit der Einstellung der Brennweite. Auch bei Objektiven mit innenliegender Fokussierung verändert sich beim Scharfstellen die Lage der Hauptebenen zueinander.
Bildwinkel
[Bearbeiten]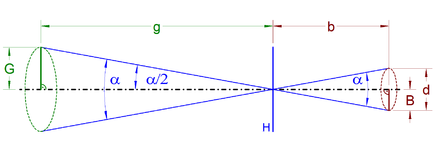
Der Bildwinkel ist der ebene Winkel, innerhalb dessen das reelle Bild des Objektes in der Bildebene vom bildseitigen Hauptpunkt eines optischen Systems aus gesehen werden kann. Er wird durch die äußeren zur Abbildung beitragenden Hauptstrahlen gebildet, die durch den Hauptpunkt gehen.
Mathematisch ist der Bildwinkel wie folgt definiert, wenn die Bildgröße (sie wird manchmal auch als Bildhöhe bezeichnet) beziehungsweise der Radius des Bildkreises von der optischen Achse aus gemessen ist und die Bildweite zwischen Hauptebene und Bildebene darstellt:
- ,
wobei der Radius des Bildkreises gleich dem halben Bildkreisdurchmesser ist:
Die Bildweite ergibt sich daraus folgendermaßen:
Der Objektwinkel ist der ebene Winkel, innerhalb dessen ein abgebildetes Objekt in der Objektebene (respektive in der Schärfeebene) vom objektseitigen Hauptpunkt eines optischen Systems aus gesehen werden kann, und er ist mit dem Bildwinkel identisch. Daher können unter Berücksichtigung des Abbildungsmaßstabs auch die Objektgröße (sie wird auch als Gegenstandshöhe oder Gegenstandsgröße bezeichnet) beziehungsweise der Radius des Objektkreises von der optischen Achse aus gemessen und die Objektweite (sie wird auch als Gegenstandsweite bezeichnet) zwischen Hauptebene und Objektebene zur Berechnung des Bildwinkels herangezogen werden:
Wegen der ähnlichen rechtwinkligen Dreiecke gilt, dass die Verhältnisse der Katheten gleich sind:
Daraus folgt:
Brennweite
[Bearbeiten]

Die Brennweite ist bei einer optischen Abbildung mit lichtsammelnden Elementen definiert als die von der letzten Hauptebene gemessene Schnittweite paraxialer Lichtstrahlen bei unendlicher Objektweite . In diesem Fall schneiden sich die Strahlen im bildseitigen Brennpunkt und die Bildweite ist identisch mit der Brennweite :
Die Brennweite kann also als Bildweite gemessen werden, wenn die Objektweite unendlich ist.
Der Kehrwert der Brennweite wird Brechkraft genannt:
Liegt das Objekt außerhalb der optischen Achse, wird es nicht in den Brennpunkt abgebildet, sondern in die Brennebene, die durch den Brennpunkt geht und senkrecht auf der optischen Achse steht. Für ein Objekt mit unendlicher Objektweite, das zur optischen Achse unter dem Winkel erscheint, ergibt sich bei gegebener bildseitiger Brennweite die von der optischen Achse gemessene Bildhöhe wie folgt:
Oder nach Umstellung aufgelöst nach dem Winkel in Abhängigkeit der beiden Längen:
Wenn die Bilddiagonale eines Rechteckes beziehungsweise der Bildkreisdurchmesser bekannt sind, ergibt sich die Brennweite als Funktion des (diagonalen) Bildwinkels zu:
Beziehungsweise umgekehrt, der Bildwinkel als Funktion der Brennweite :
Ein Objekt, das in der Brennebene liegt, wird ins Unendliche abgebildet, und der objektseitige Brennpunkt wird bildseitig daher auf der optischen Achse ins Unendliche abgebildet.
Wegen der Dispersion kann die Brennweite bei der Verwendung von brechenden Materialien von der Wellenlänge der abbildenden Strahlen abhängen. Die Dispersion eines bestimmten optischen Mediums kann durch dessen Abbe-Zahl beschrieben werden:
→ siehe hierzu auch Kapitel "Bildaufnahme" / Abschnitt "Chromatische Aberration"
Normalbrennweite
[Bearbeiten]Die Brennweite ist bei einer optischen Abbildung nicht ausreichend, um die Größe einer Aufnahme zu kennzeichnen. In einigen Fällen ist die Bildgröße standardisiert, wie zum Beispiel beim rechteckigen Format des Kleinbildfilms, so dass aus der Angabe einer beliebigen Brennweite auch auf den maximal möglichen Bildwinkel der Bilddiagonale beziehungsweise des Bildkreisdurchmessers geschlossen werden kann.
Es kann eine empirisch zu bestimmende Normalbrennweite definiert werden, bei der ein Bild mit dem Bildwinkel aufgenommen wird, mit dem das abgebildete Objekt mit bloßem Auge bei hinreichender Auflösung gesehen werden kann. Dies ist der Fall, wenn der Bildwinkel des Auges wegen der physiologischen Schwankungsbreite ungefähr zwischen 40° und 55° liegt.
Brennweiten, die kürzer als die Normalbrennweite sind, erzeugen weitwinklige Aufnahmen mit größeren Bildwinkeln, und Brennweiten, die länger als die Normalbrennweite sind, erzeugen teleskopische Aufnahmen mit kleineren Bildwinkeln. Die Größenverhältnisse der in unterschiedlichen Entfernungen aufgenommenen Gegenstände innerhalb einer Aufnahme ändern sich deutlich mit der Brennweite.
Beim durch den 35-Millimeter-Film (Kleinbildfilm) im 20. Jahrhundert sehr weit verbreiteten Kleinbildformat mit einer Bildbreite von 36 Millimetern und einer Bildhöhe von 24 Millimetern hat sich eine Normalbrennweite von
etabliert. Bei diesem Format ergibt sich rechnerisch eine Bilddiagonale beziehungsweise ein Bildkreisdurchmesser von:

Da alle Hersteller von Kleinbildkameras dieselbe, fest vorgegebene Bildgröße verwenden, ist dem Photographen bei diesem Bildformat bekannt, dass ein Objektiv mit Normalbrennweite eine Brennweite von 50 Millimetern hat. Bei anderen Bildformaten und -größen, wie sie zum Beispiel in der digitalen Photographie verwendet werden, ergeben sich zwangsläufig andere Normalbrennweiten, so dass aus der Angabe der Brennweite allein noch nicht folgt, welche Bildgröße oder welcher Bildwinkel bei der optischen Abbildung berücksichtigt wurde.
Abgesehen von einigen digitalen Systemkameras mit Bildsensoren im Kleinbildformat gibt es viele verschiedene Bildsensorgrößen und damit Normalbrennweiten (siehe auch Abschnitt Bildsensoren). Zur Bestimmung von Normalbrennweiten kann das Verhältnis zwischen Normalbrennweite und Bildkreisdurchmesser verwendet werden, das sich beim Kleinbildfilm ergibt:
Anhand der effektiven Bilddiagonalen kann somit die Normalbrennweite berechnet werden:
Beim Sonderfall unendlicher Objektweite sind Bildweite und Brennweite identisch, und der Bildwinkel bei der Normalbrennweite kann leicht aus der Brennweite und dem Radius des Bildkreises berechnet werden:
Am Beispiel des Kleinbildformates ergibt sich der Bildwinkel bei der Normalbrennweite also wie folgt:
Dieser Bildwinkel kann auch bei alle anderen Bildformaten eingesetzt werden.
Die Normalbrennweite kann mithilfe des Bildwinkels bei der Normalbrennweite bei unendlicher Objektweite auch aus der Brennweite und dem dazugehörigen Bildwinkel bestimmt werden:
Ferner lässt sich auch die Bilddiagonale berechnen, wenn die Brennweite bekannt ist und der Bildwinkel gemessen werden kann:
Für einige gängige Bildsensorformate resultieren die folgenden Bilddiagonalen und Normalbrennweiten, sowie die entsprechenden Schärfentiefebereiche (siehe auch Abschnitt Schärfentiefe) für menschliche Betrachter beispielsweise bei einer Blendenzahl von 2,0 (siehe auch Abschnitt Blendenzahl) und einer Objektweite von einem Meter. Ferner die Bildpunktgröße bei 16 Millionen quadratischen Bildpunkten (siehe auch Abschnitt Punktabstand), der dazugehörige tolerierbare Fokussierungsfehler in der Bildebene bei der Blendenzahl 2,0 (siehe auch Abschnitt Fokussierungsfehler) und der Durchmesser des entsprechenden Beugungsscheibchens für grünes Licht mit der Wellenlänge 550 Nanometer (siehe auch Abschnitt Beugungsbegrenzung):
| Bildsensorgröße Bezeichnung |
Bilddiagonale in Millimetern |
Normalbrennweite in Millimetern |
Schärfentiefe in mm bei Blendenzahl 2,0 und Objektweite 1 m |
Bildpunktgröße auf dem Bildsensor in µm bei 16 Millionen Bildpunkten |
Maximal zulässiger Fokussierungsfehler auf dem Bildsensor in µm bei Blendenzahl 2,0 |
Maximale Blendenzahl ohne Beugungsbegrenzung auf dem Bildsensor |
|---|---|---|---|---|---|---|
| 1/3,2″ | 5,6 | 6,5 | 360 | 0,99 | 2,0 | 0,74 |
| 1/2,7″ | 6,0 | 7,0 | 330 | 1,06 | 2,1 | 0,79 |
| 1/2,5″ | 6,4 | 7,5 | 310 | 1,13 | 2,3 | 0,84 |
| 1/2,3″ | 7,7 | 8,9 | 260 | 1,4 | 2,7 | 1,0 |
| 1/1,8″ | 8,9 | 10 | 240 | 1,57 | 3,1 | 1,2 |
| 2/3″ | 11,0 | 13 | 170 | 1,94 | 3,9 | 1,4 |
| 1" | 15,9 | 18 | 130 | 2,8 | 5,6 | 2,0 |
| 4/3″ | 21,6 | 25 | 90 | 3,8 | 7,6 | 2,8 |
| APS-C | 26,8 bis 28,4 | 31 bis 33 | 70 | 5 | 10 | 3,5 |
| Kleinbildformat | 43,3 | 50 | 44 | 8 | 15 | 5,6 |
| Mittelformat | 50 bis 70 | 60 bis 80 | 30 | 11 | 20 | 8,0 |
Wesentliche Unterschiede von Bildsensoren ergeben sich indirekt durch eine unterschiedliche Schärfentiefe bei gleichem Bildwinkel und gleicher Blendenzahl. Dabei gilt näherungsweise bei gleicher Anzahl der Bildpunkte (siehe auch Abschnitt Bildauflösung):
Es ergibt sich bei der Verdopplung der Bilddiagonale also in etwa eine Halbierung der Schärfetiefe. Bei großen Bildsensorformaten ist die Schärfentiefe bei offener Blende möglicherweise so stark eingeschränkt, dass abgeblendet werden muss. Ferner kann es bei der Verwendung von zusätzlichen Einstellhilfen für die Bildschärfe wie zum Beispiel Einstellscheiben oder Autofokussystemen bei kleinen Bildsensoren leicht zu Fokussierungsfehlern kommen, so dass das Bild auf dem Sensor nicht hinreichend scharf aufgenommen werden kann.
Abbildungsmaßstab
[Bearbeiten]

Bei photographischen Aufnahmen mit gegebener Brennweite gilt die Abbildungsgleichung (umgangssprachlich auch "Linsenformel"), die den Zusammenhang zwischen Objektweite und Bildweite herstellt:
oder anders ausgedrückt:
Aus diesen Längen lässt sich der Abbildungsmaßstab berechnen. Dieser kann bei sowohl aus dem Verhältnis von Bildweite zu Objektweite (auch Gegenstandsweite genannt), als auch aus dem Verhältnis von Bildgröße zu Objektgröße (auch Gegenstandsgröße genannt) berechnet werden:
beziehungsweise:
Umgeformt nach der Bildweite lautet der Formelzusammenhang:
Und umgeformt nach der Objektweite lautet der Formelzusammenhang:
Desgleichen können die Objektröße und die Bildgröße ausgerechnet werden:
Bei der gleichzeitigen Aufnahme von Objekten mit verschiedener Objektweite (innerhalb des hinreichend scharf abgebildeten Schärfentiefebereiches) ergeben sich also zwangsläufig unterschiedliche Abbildungsmaßstäbe. Dieser Effekt kann bei Aufnahmen, bei denen es auf Maßhaltigkeit ankommt (zum Beispiel bei einer Industrieanlagenüberwachung, in der Photogrammetrie oder bei der Portraitphotographie), dadurch reduziert werden, dass eine größere Brennweite und entsprechend größere Objektweiten gewählt werden. Alternativ ist der Einsatz von beidseitig telezentrischen Objektiven möglich, bei denen der Abbildungsmaßstab weder von der Objektweite noch von der Bildweite abhängt (siehe auch Abschnitt Telezentrie).
Für zwei Gegenstände mit einem Abstand von zehn Einheiten ergeben sich bei drei verschiedenen Brennweiten beispielsweise die folgenden Abbildungsmaßstäbe:
| Brennweite |
Objektweite |
Abbildungsmaßstab |
Abweichung der Abbildungsmaßstäbe |
|---|---|---|---|
| 10 | 100 | 0,1111 | 11,1% |
| 110 | 0,1000 | ||
| 100 | 1090 | 0,1010 | 1,0% |
| 1100 | 0,1000 | ||
| 1000 | 10990 | 0,1001 | 0,1% |
| 11000 | 0,1000 |
Relativer Abbildungsmaßstab
[Bearbeiten]Um ein von der Brennweite und der Bildgröße unabhängiges Maß zu gewinnen, kann das Verhältnis des tatsächlichen Abbildungsmaßstabes zum entsprechenden Abbildungsmaßstab bei der Normalbrennweite gebildet werden, der sogenannte relative Abbildungsmaßstab :
Bei der Normalbrennweite ist der relative Abbildungsmaßstab eins, bei weitwinkligen Aufnahmen ist er kleiner als eins und bei teleskopischen Aufnahmen ist er größer als eins.
Zoomfaktor
[Bearbeiten]
Der Zoomfaktor von Objektiven, die in der Brennweite variabel sind, wird traditionell als Verhältnis der Extrembrennweiten angegeben:
Dieser Wert ist bei unendlicher Objektweite identisch mit dem Verhältnis der entsprechenden Abbildungsmaßstäbe beziehungsweise relativen Abbildungsmaßstäbe:
Dies ist zwar ein einfacher Ansatz, da die Brennweiten als Kenndaten des Zoomobjektivs in der Regel angegeben werden, dieser lässt jedoch unbeachtet, dass die perspektivische Wirkung einer optischen Abbildung nicht von der Brennweite, sondern vom Bildwinkel bestimmt wird und bei Vergrößerungen der Abbildungsmaßstab einen viel entscheidenderen Einfluss hat. Bei einer Verdopplung der Brennweite ist es bei hinreichend geringer Objektweite ohne weiteres möglich, einen zehn Mal größeren Abbildungsmaßstab respektive einen zehn Mal kleineren Bildwinkel zu erreichen. Der Zoomfaktor ist also nur eine Kenngröße, die die Verhältnisse der Abbildungsmaßstäbe bei unendlicher Objektweite angeben. Für Objektweiten in der Größenordnung der Brennweite ist das Verhältnis der Abbildungsmaßstäbe beziehungsweise der Bildwinkel erheblich aussagekräftiger als der Zoomfaktor.
Die folgenden Tabelle gibt für eine Objektweite von Längeneinheiten die Verhältnisse der Brennweiten, Abbildungsmaßstäbe und Bildwinkel bei verschiedenen Brennweiten bezogen auf die Bezugsbrennweite (dies entspricht einem Abbildungsmaßstab von , einer Bildweite von , einer Bilddiagonale von , wenn die Normalbrennweite des Systems ist, und einem Bildwinkel von ) an:
Brennweite |
Bildweite |
Abbildungs- maßstab |
Bildwinkel in ° |
Verhältnis der Brennweiten |
Verhältnis der Abbildungsmaßstäbe |
Verhältnis der Bildwinkel |
|---|---|---|---|---|---|---|
| 0,999 | 1,000 | 1/1000 | 154 | 0,100 | 0,099 | 0,303 |
| 1,996 | 2,000 | 1/500 | 131 | 0,200 | 0,198 | 0,358 |
| 4,975 | 5,000 | 1/200 | 82,3 | 0,498 | 0,495 | 0,568 |
| 9,901 | 10,00 | 1/100 | 47,2 | 0,990 | 0,990 | 0,991 |
| 10,00 | 10,10 | 1/99 | 46,8 | 1,00 | 1,00 | 1,00 |
| 19,61 | 20,00 | 1/50 | 24,7 | 1,96 | 1,98 | 1,90 |
| 38,46 | 40,00 | 1/25 | 12,5 | 3,85 | 3,96 | 3,75 |
| 100 | 111,1 | 1/9 | 4,51 | 10 | 11 | 10,4 |
| 200 | 250,0 | 1/4 | 2,00 | 20 | 24,75 | 23,4 |
| 250 | 333,3 | 1/3 | 1,50 | 25 | 33 | 31,1 |
| 333 | 500,0 | 1/2 | 1,00 | 33,3 | 49,5 | 46,7 |
| 400 | 666,7 | 2/3 | 0,751 | 40 | 66 | 62,3 |
| 500 | 1000 | 1 | 0,501 | 50 | 99 | 93,4 |
| 667 | 2000 | 2 | 0,250 | 66,7 | 198 | 187 |
| 750 | 3000 | 3 | 0,167 | 75 | 297 | 280 |
| 833 | 5000 | 5 | 0,100 | 83,3 | 495 | 467 |
| 1000 | ∞ | ∞ | 0,000 | 100 | ∞ | ∞ |
Hier ist klar zu sehen, dass bei zunehmenden Bildweiten die Verhältnisse der Brennweiten von denen der Abbildungsmaßstäbe und Bildwinkel deutlich auseinanderlaufen; die Unterschiede der Abbildungsmaßstäbe und der Bildwinkel werden im Vergleich zu den Unterschieden der Brennweiten immer größer und gehen gegen Unendlich.
Anders bei kurzen Bildweiten: hier stimmen die Verhältnisse der Brennweiten gut mit denen der Abbildungsmaßstäbe überein, jedoch ist die Zunahme der Bildwinkel hierbei begrenzt, weil der maximale Bildwinkel auf 180° begrenzt ist. Das minimale Verhältnis der Bildwinkel ergibt sich folglich zu:
Ferner ist unbedingt zu beachten, dass sich insbesondere bei kompakten Objektiven mit innenliegender Fokussierung der Abbildungsmaßstab bei der Scharfstellung ändern kann, auch ohne dass die Brennweite gegebenenfalls variiert wird.
Öffnung
[Bearbeiten]
Die Öffnung (oder auch Apertur) eines rotationssymmetrisch konstruierten Objektivs wird durch den freien Durchmesser beschrieben, der nicht durch die mechanische Vorrichtungen wie beispielsweise Kanten, Linsenfassungen oder Blenden begrenzt ist und welcher auch als Öffnungsweite bezeichnet wird. Die virtuelle Öffnung von Objektiven kann durch das objektseitige und das bildseitige virtuelle Bild der Aperturblende beschrieben werden, die auch wirksame Eintrittspupille beziehungsweise wirksame Austrittspupille genannt wird.
Liegt die Aperturblende vor der ersten Hauptebene der Abbildung (objektseitig) ist die wirksame Eintrittspupille identisch mit der reallen Öffnung. Liegt die Aperturblende hinter der letzten Hauptebene der Abbildung (bildseitig) ist die wirksame Austrittspupille identisch mit der reallen Öffnung.
Idealerweise werden Aperturblenden in die Hauptebenen des Strahlengangs gelegt, damit sie den Bildausschnitt respektive den Bildwinkel der optischen Abbildung nicht beeinflussen. Mit einer solchen Aperturblende kann der Lichtstrom durch ein optisches System begrenzt werden. Mit variablen Aperturblenden (beispielsweise Irisblenden) kann der Lichtstrom in einem optischen System verändert werden.
Befindet sich eine Blende in der Nähe der Objektebene oder der Bildebene, handelt es sich nicht um eine Aperturblende, sondern um eine Feldblende, die den Bildausschnitt beziehungsweise den erfassten Bildwinkel unmittelbar auf die sogenannte Eintrittsluke (objektseitig) beziehungsweise Austrittsluke (bildseitig) begrenzt. Befinden sich solche Feldblenden nicht in der Nähe der Objekt- oder Bildebene, werden die entsprechenden Bilder dieser Feldblenden in der jeweiligen Ebene zur Bestimmung der effektiven Lukendurchmesser herangezogen.
Blendenzahl
[Bearbeiten]Die dimensionslose Blendenzahl eines Objektivs mit der Brennweite und der Öffnungsweite ist wie folgt definiert:
Der Kehrwert der Blendenzahl wird als das Öffnungsverhältnis bezeichnet:
- Objektiv mit Irisblende zur Einstellung der Apertur (Brennweite 42,5 Millimeter)
-
Maximale Apertur (Blendenzahl 1,2)
-
Minimale Apertur (Blendenzahl 16)
Die Änderung der Blendenzahl um eine Blendenstufe kann sowohl durch Auf- als auch durch Abblenden erreicht werden, wobei sich die Blendenzahl um den Faktor Wurzel von zwei und der Lichtstrom im Objektiv um den Faktor zwei ändert. Je kleiner die Blendenzahl, desto mehr Licht trägt zur Abbildung bei und umgekehrt. Nach der Halbierung der Blendenzahl kommt vier Mal soviel Licht durch das Objektiv, bei der Verdopplung der Blendenzahl nur ein Viertel des Lichtes. Zwei Blendenzahlen und unterscheiden sich um die folgende Anzahl von Blendenstufen :
Blendenzahlen werden häufig mit den folgenden elf Vorzugswerten angegeben, die sich jeweils um zirka eine Blendenstufe unterscheiden und demzufolge insgesamt zehn Blendenstufen umfassen:
- 1,0 - 1,4 - 2,0 - 2,8 - 4,0 - 5,6 - 8,0 - 11 - 16 - 22 - 32

Hierbei ist zu beachten, dass die Blendenzahl ohne die Angabe der gewählten Bildgröße wenig Aussagekraft hat. Bei konstantem Bildwinkel und konstanter Öffnungsweite ist nicht nur die zur optischen Abbildung beitragenden Lichtmenge, sondern ist auch das Verhältnis zwischen Bildgröße und Bildweite konstant, obwohl die Abbildungen mit unterschiedlichem Abbildungsmaßstab beziehungsweise unterschiedlicher Brennweite und somit auch mit unterschiedlicher Blendenzahl gemacht werden.
Für die Gegebenheiten in der Abbildung rechts gilt:
Aber:
Öffnungswinkel
[Bearbeiten]
Der Öffnungswinkel ist der Winkel unter dem die wirksame Öffnung mit der Öffnungsweite eines Objektivs erscheint.
Von einem Objektpunkt auf der optischen Achse aus betrachtet handelt es sich um den objektseitigen Öffnungswinkel :
Der halbe objektseitige Öffnungswinkel wird auch Aperturwinkel genannt.
Von einem Bildpunkt auf der optischen Achse aus betrachtet handelt es sich um den bildseitigen Öffnungswinkel :
Der halbe bildseitige Öffnungswinkel wird auch Feldwinkel genannt.
Die Öffnungswinkel dürfen nicht mit dem Bildwinkel verwechselt werden (siehe dazu auch Bildwinkel) !
Bei unendlicher Objektweite ist die Bildweite identisch mit der Brennweite, so dass die Blendenzahl folgendermaßen ausgedrückt werden kann:
Sinusbedingungen
[Bearbeiten]

Die beiden Öffnungswinkel stehen für Abbildungen, bei denen Öffnungsfehler (siehe auch sphärische Aberration) keine Rolle spielen, über Sinusbedingungen in Beziehung. Im folgenden wird etwas vereinfachend davon ausgegangen, dass die optische Abbildung eines Gegenstands mit der Objektgröße in ein reelles Bild mit der Bildgröße außerhalb des optischen Systems, das durch die Hauptebene repräsentiert wird, vom gleichen optischen Medium (zum Beispiel Vakuum, Luft oder Flüssigkeit) mit konstanter Brechkraft umgeben ist.
Ein kleiner flächenhafter Gegenstand mit der Objektgröße , der senkrecht zur optischen Achse steht, kann nur dann hinreichend scharf mit der Bildgröße senkrecht zur optischen Achse abgebildet werden, wenn alle Punkte des Gegenstands beim halben objektseitigen Öffnungswinkel innerhalb einer Wellenlänge einer ebenen Welle erfasst und alle Bildpunkte beim halben bildseitigen Öffnungswinkel ebenfalls innerhalb einer Wellenlänge einer ebenen Welle zu einem Bild zusammengesetzt werden können. Durch diese Voraussetzung kann vermieden werden, dass es im Bild Interferenzen gibt, die Kontraste erzeugen, die nicht dem Aussehen des abgebildeten Gegenstands entsprechen.
Die daraus resultierende Abbesche Sinusbedingung gilt für eine in Bezug auf den Öffnungsfehler korrigierte Abbildung mit dem Abbildungsmaßstab sowie für eine bestimmte Wellenlänge (monochromatisches Licht). Sie lautet wie folgt:
Diese Sinusbedingung kann auch in der Form der Helmholtz-Lagrange-Invariante geschrieben werden:
Paraxiale Strahlengänge
[Bearbeiten]Für paraxiale Strahlengänge können sehr kleine Öffnungswinkel angenommen werden, so dass dann die Sinūs durch die Argumente (im Bogenmaß) ersetzt werden können:
Daraus folgt:
Die paraxiale Optik, die auch gaußsche Optik genannt wird, verwendet in der geometrischen Optik diese Näherung, bei der für eine optische Abbildung nur paraxiale Strahlen berücksichtigt werden.
Schnittweite
[Bearbeiten]
Die auf der optischen Achse gemessenen Schnittweiten und beim Übergang an einer sphärischen Fläche mit dem Radius zwischen zwei optischen Medien mit den Brechungsindices und kann für paraxiale Strahlen leicht abgeschätzt werden. Hierbei gelten für den Grenzwert der Pfeilhöhe (siehe nebenstehende Abbildung) die folgenden Näherungsgleichungen:
Aus dem Snelliusschen Brechungsgesetz folgt für achsnahe Strahlen die Näherung:
Sowie:
Durch Kürzen der Höhe ergibt sich schließlich die Näherungsgleichung:
Dies ist die Schnittweitengleichung einer sphärischen Fläche für paraxiale Strahlen.
Sie kann auch in Form der Abbeschen Invariante geschrieben werden:
Für Objekte auf der optischen Achse mit unendlicher objektseitiger Schnittweite gilt:
In diesem Fall ergibt sich für die bildseitige Schnittweite :
Für Objekte auf der optischen Achse mit unendlicher bildseitiger Schnittweite gilt:
In diesem Fall ergibt sich für die objektseitige Schnittweite :
Dünne Linsen
[Bearbeiten]
Bei einer dünnen Linse ist die Dicke zwischen den Scheitelpunkten ihrer brechenden sphärischen Oberflächen auf der optischen Achse im Vergleich zu den beiden Radien dieser Oberflächen klein. Für eine dünne bikonvexe sphärische Sammellinse mit den beiden Radien und und dem Brechungsindex in einem die Linse umgebenden Medium mit dem Brechungsindex ergibt sich die folgende entsprechende Beziehung für die Schnittweiten:
Für Objekte auf der optischen Achse mit unendlicher objektseitiger Schnittweite gilt damit für die bildseitige Schnittweite :
Für Objekte auf der optischen Achse mit unendlicher bildseitiger Schnittweite gilt entsprechend für die objektseitige Schnittweite :
Bei dünnen plankonvexen sphärischen Sammellinsen mit dem Brechungsindex kann einer der beiden Radien auf Unendlich gesetzt werden. Damit ergibt sich für den verbleibenden Radius :
Die Schnittweiten entsprechen bei paraxialen Strahlen dann den Brennweiten (bildseitig bei der Abbildung aus dem Unendlichen mit ) beziehungsweise (objektseitig bei der Abbildung ins Unendliche mit ):
Befindet sich eine solche Linse in einem optisch sehr dünnen Medium wie Luft () oder im Vakuum (), vereinfacht sich diese Näherungsformel weiter zu:
Große Objektweiten
[Bearbeiten]Bei großer Objektweite ist die Bildweite annhähernd gleich der Brennweite , und der Sinus des halben objektseitigen Öffnungswinkels kann in guter Näherung durch das Verhältnis der Hälfte der Öffnungsweite und Objektweite ausgedrückt werden:
Daraus folgt:
Aus der Beziehung
folgt:
Diese Ungleichung kann auch wieder unter Verwendung der Blendenzahl ausgedrückt werden:
In Worten ausgedrückt:
Die Blendenzahl kann bei der öffnungsfehlerfreien Abbildung von Flächen aus dem Unendlichen minimal den Wert 0,5 annehmen.
Die Strecke vom Schnittpunkt der Randstrahlen mit der Hauptebene zum Bildpunkt auf der optischen Achse beträgt bei der Abbildung aus dem Unendlichen mit der Brennweite :
Mit den geometrischen Ähnlichkeiten der Dreiecke bei der Sinusbedingung ergibt sich das folgenden Verhältnis:
Da die Blendenzahl k nicht kleiner als 0,5 werden kann, gilt als Abschätzung demzufolge:
Numerische Apertur
[Bearbeiten]Die numerische Apertur dient zur Einschätzung des Auflösungsvermögens von optischen Geräten, bei denen die Objektweite dicht bei der objektseitigen Brennweite beziehungsweise bei denen die Bildweite dicht bei der bildseitigen Brennweite liegt. Ein Anwendungsbeispiel sind Immersionsobjektive (insbesondere bei Mikroskopen), die bei der optischen Abbildung in eine hochbrechende Flüssigkeit (zum Beispiel Immersionsöl) eingetaucht werden.
Die numerische Apertur bezieht sich auf den halben Öffnungswinkel und die Brechzahl des optischen Mediums außerhalb des Objektivs. Je höher die dimensionslose Zahl der numerischen Apertur sich dem Brechungsindex des umgebenden Mediums von unten nähert, desto lichtstärker ist das verwendete Objektiv und desto höher wird bei optisch korrigierten Objektiven das optische Auflösungsvermögen.

Für die objektseitige numerische Apertur ergibt sich:
Für die bildseitige numerische Apertur ergibt sich entsprechend:
Die numerische Apertur kann also nicht größer werden als der Brechungsindex des umgebenden Mediums.
Die Sinūs der halben Öffnungswinkel können hierbei mit Hilfe der rechtwinkligen Dreiecke (siehe Skizze rechts) und des Satzes des Pythagoras sowohl objektseitig als auch bildseitig wie folgt aus dem Verhältnis von Gegenkatheten zur Hypotenusen bestimmt werden:
Bei einer Abbildung ins Unendliche () oder wird die Abbildung aus dem Unendlichen gemacht (), kann jeweils die Blendenzahl eingesetzt werden, und dann vereinfachen sich beide Gleichungen wie folgt:
Für große Blendenzahlen () gilt dann näherungsweise:
Für hinreichend große Objektweiten () beziehungsweise hinreichend große Bildweiten () gelten die folgende Näherungen:
Ist zudem auch noch die Brennweite hinreichend nah an der Objektweite () oder an der Bildweite (), dann gilt und wiederum die Näherung (siehe auch oben):
Bei einem Abbildungsmaßstab von eins (siehe unten) sind Objektweite und Bildweite identisch und genau doppelt so groß wie die verwendete Brennweite . In diesem Fall sind auch die objektseitige und die bildseitige numerische Apertur sowie der objektseitige und der bildseitige Öffnungswinkel identisch:
Modulationsübertragung
[Bearbeiten]Modulation
[Bearbeiten]
Die Modulation (auch Michelson-Kontrast genannt) ist ein Maß (lateinisch: modulatio) für relative Helligkeitsschwankungen zwischen zwei Bildpunkten mit den vom Menschen als Helligkeiten empfundenen Leuchtdichten und (siehe auch Kapitel Leuchtdichte), das unter den Voraussetzungen und wie folgt berechnet werden kann:
Die Modulation gibt also keineswegs den Helligkeitsunterschied
zwischen zwei Bildpunkten an, sondern setzt diesen in Bezug auf die Summe dieser beiden Helligkeiten, die auch als der doppelte Mittelwert, also
- ,
der beiden Helligkeiten interpretiert werden kann:
Dies bedeutet, dass die maximale Modulation den Wert eins hat, die genau dann erreicht wird, wenn ist und der dunklere Punkt also keine Helligkeit (die Leuchtdichte null) hat. Die absolute Helligkeit des helleren Bildpunktes hat in diesem Fall keinen Einfluss auf die Modulation. Die Helligkeitsdifferenz zwischen diesen beiden Bildpunkten ist in Bezug auf die Helligkeit des helleren Punktes dann maximal und exakt genauso groß wie diese.
Wenn beide Bildpunkte die gleiche Helligkeit größer als null haben , so ergibt sich immer eine Modulation von null (wenn beide Punkte keine Helligkeit haben, ist die Modulation nicht definiert).
Werden beide Helligkeiten um denselben Faktor verändert, bleibt die Modulation erhalten:
Da innerhalb eines Bildes üblicherweise mehr als zwei Bildpunkte vorhanden sind, ist es meist von Interesse, in welchem Verhältnis der hellste Bildpunkt (Weißwert) und der dunkelste Bildpunkt (Schwarzwert) zueinander stehen, was durch die maximale Modulation bestimmt werden kann:
Es gilt zu beachten, dass bei einem Schwarzwert von einem Drittel des Weißwertes die Modulation nur noch 50 Prozent und bei einem Schwarzwert von der Hälfte des Weißwertes nur noch 33 Prozent beträgt.
Die Modulation kann in farbigen Bildern für jede einzelne Farbe unabhängig bestimmt werden. Bei den drei Primärfarben rot, grün und blau (R, G, B) eines Bildpunktes ergeben sich dann also entsprechend:
Ortsfrequenz
[Bearbeiten]Die Ortsauflösung entspricht der maximalen Anzahl von räumlichen Informationseinheiten, die entlang einer Strecke, meist der Bildhöhe beziehungsweise der Bildbreite, erfasst werden können. Zur Darstellung einer räumlichen Information, also eines Helligkeitswechsels, ist mindestens ein Bildpunktpaar erforderlich, damit eine Modulation vorhanden sein kann.
Die Bezugslänge kann eine absolute Länge sein, bei der die Bildpunktpaare zum Beispiel pro Millimeter ermittelt werden. Bei Filmmaterial wurde diese Informationsdichte meist richtungsunabhängig in Linienpaaren pro Millimeter ermittelt und angegeben.
Auf der anderen Seite kann statt einer metrischen Bezugslänge auch eine relative Bezugslänge gewählt werden, wie zum Beispiel die Bilddiagonale, die Bildbreite oder die Bildhöhe. Dieses Vorgehen hat den Vorteil, dass unabhängig von der Gesamtzahl der Bildpunkte, der Größe der Reproduktion des Bildes und dem Bildseitenverhältnis ein einheitliches und somit leicht vergleichbares Maß für die Ortsauflösung zur Verfügung steht. Dieses Maß ist insbesondere unabhängig von der Größe und vom Bildseitenverhältnis des verwendeten Bildsensors. Bei digitalen Bildern hat es sich daher durchgesetzt, Linienpaare pro Bildhöhe (horizontale Linien) als Bezugsgröße zu verwenden. Diese Bezugsgröße wird dann ebenfalls für die Informationseinheiten in horizontaler Richtung (vertikale Linienpaare) oder für jeden beliebigen anderen Azimut (also schräg liegende Linienpaare) verwendet, obwohl bei rechteckigen Bildformaten in horizontaler Richtung mehr oder weniger Informationseinheiten zur Verfügung stehen können. Rechnerisch ergibt sich die maximal darstellbare Linienauflösung durch die Halbierung der Anzahl der Punkte in der Bildhöhe :
Für die maximale Anzahl vertikaler Linienpaare in horizontaler Richtung ergibt sich mit dem Bildseitenverhältnis dann entsprechend:
Siehe hierzu auch: Bildseitenverhältnis
Dieser Wert entspricht genau der Grenze nach dem Nyquist-Shannon-Abtasttheorem (auch Whittaker-Kotelnikow-Shannon-Abtasttheorem) für die maximal darstellbaren Ortsfrequenzen , wonach diese innerhalb einer Periode mindestens zwei abgetastete Stützstellen haben müssen:
Aus einer beliebigen kleineren Ortsfrequenz ergibt sich die maximal mögliche Häufigkeit von Helligkeitsunterschieden auf einer bestimmten Bezugslänge im Bild (also in der Regel auf der Bildhöhe).
Eine Ortsfrequenz von null entspricht einer konstanten Helligkeit über das gesamte Bild, die selbst nicht notwendigerweise den Wert null haben muss.
Modulation in Abhängigkeit von der Ortsfrequenz
[Bearbeiten]
Eine Modulation mit geringer Ortsfrequenz entspricht also groben Strukturen im Bild, und eine Modulation mit großer Ortsfrequenz entspricht feinen Strukturen im Bild. Jeder Struktur mit einer bestimmten Größe kann in jeder azimutalen Richtung (nicht nur horizontal oder vertikal, sondern auch in beliebiger schräg liegender Richtung) eine Ortsfrequenz mit einer bestimmten Modulation zugeordnet werden.
Beim Siemensstern wird beispielsweise die Ortsfrequenz entlang der um den Mittelpunkt liegenden konzentrischen Kreise linear mit deren Radius größer. Die Modulation beträgt für jede Ortsfrequenz eins, wenn idealisiert davon ausgegangen wird, dass die dunklen Streifen keine Helligkeit aufweisen.
Wird eine photographische Aufnahme von einem solchen Siemensstern als Objekt auf einer Testtafel gemacht, reduzieren sich im Bild die Modulationen für alle Ortsfrequenzen größer als null auf Werte kleiner als eins. Dies beruht auf einer Verminderung der Modulationen im Bild gegenüber der optimalen Modulation im Objektraum, die durch Abbildungsfehler bedingt ist. Neben der immer wirkenden Beugungsbegrenzung ergeben sich in optischen Abbildungen vor allem durch die sphärische Aberration, aber zum Beispiel auch durch Falschlicht Einbußen bei der Modulation im Bildraum.
In der Regel führt dies dazu, dass die Modulation von rein optischen Abbildungen mit zunehmender Ortsfrequenz streng monoton und stetig abnimmt. Das Verhältnis der Modulation im Bildraum zur Modulation im Objektraum in Abhängigkeit von der Ortsfrequenz wird Modulationsübertragungsfunktion (englisch: modulation transfer function = MTF) oder auch Kontrastübertragungsfunktion genannt:
Das Maximum der Modulationsübertragungsfunktion liegt bei optischen Systemen bei der kleinsten Ortsfrequenz, also null, und hat dort den Wert eins. Die Modulationsübertragung ist dabei immer der Betrag der komplexwertigen optischen Übertragungsfunktion, die nicht nur die Amplitude, sondern auch die Phase der übertragenen Lichtwellen berücksichtigt.
Ist die Modulation im Objektraum für alle untersuchten Ortsfrequenzen gleich eins, wie zum Beispiel bei hochwertig hergestellten Testtafeln, sind die Modulationsübertragungsfunktion und die Modulation im Bildraum identisch:
- , wenn
Der Betrag der komplexwertigen, zweidimensionalen Fourier-Transformation der Bilddaten im Bildraum kann zur Ermittlung der spektralen Dichte der Modulationsübertragungsfunktion im Ortsfrequenzraum herangezogen werden. In der digitalen Signalverarbeitung wird hierfür häufig die sehr effiziente Fast-Fourier-Transformation (FFT) eingesetzt. Das Leistungsdichtespektrum der Fourier-Transformierten entspricht hierbei dem Beugungsbild der Bilddaten, das mit einer Bildwand aufgefangen werden kann.
- Auflösungskeile mit 3 bis 72 Linienpaaren pro Bildhöhe mit verschiedenen Kontrastübertragungen, die Bildhöhe wird zwischen den beiden dünnen horizontalen Linien ober- und unterhalb des Auflösungskeils gemessen.
-
Maximaler Kontrast (852 Linienpaare pro Bildhöhe).
-
Kontrast bis 72 Linienpaare pro Bildhöhe.
-
Kontrast bis 36 Linienpaare pro Bildhöhe.
-
Kontrast bis 18 Linienpaare pro Bildhöhe.
-
Kontrast bis 9 Linienpaare pro Bildhöhe.
Weitere Beispiele siehe auch Fourier-Transformation.
Kontrastempfindlichkeitsfunktion
[Bearbeiten]
Zu den Kontrastverhältnissen beim durch den Erdschein beleuchteten aschgrauen Mondlicht siehe auch hier: Kontrastverhältnisse bei aschgrauem Mondlicht

Oben:fünffache Vergrößerung (500 Prozent)
Unten: einfache Vergrößerung (100 Prozent)

Für die Betrachtung der optischen Abbildungen durch Menschen ist nur der Bereich der Ortsfrequenzen interessant, der entsprechend der Contrast Sensitivity Function (CSF, zu Deutsch: Kontrastempfindlichkeitsfunktion) überhaupt wahrgenommen werden kann. Oft wird jedoch die Modulation an der Nyquist-Frequenz als Maß für die wahrnehmbare Qualität einer optischen Abbildung herangezogen. Dieses Vorgehen trägt jedoch nicht dem Umstand Rechnung, dass die vom Betrachter empfundene Qualität einer optischen Abbildung im Sinne der Modulationen bei verschieden feinen Strukturen im allgemeinen gar nicht von der Modulation bei der Nyquist-Frequenz bestimmt ist, insbesondere wenn die feinsten Strukturen mit bloßem Auge gar nicht aufgelöst werden können. Vielmehr kommt es meist auf eine möglichst große Modulation bei Ortsfrequenzen im mittleren Bereich an. Dies kann zu der zunächst paradox scheinenden Situation führen, dass die optische Abbildung mit einem Objektiv, dass bei der Nyquist-Frequenz die gleiche oder gar eine höhere Modulation aufweist als ein anderes Objektiv, subjektiv dennoch als schlechter beurteilt wird (vergleiche Abbildung rechts).
Daher ist es empfehlenswert, die integrale Summe der Modulationen aller Ortsfrequenzen bis zu einer sinnvollen maximalen Ortsfrequenz zu bilden. Dieser Wert wird auch Heynacher-Zahl genannt, die seit den 1970er Jahren nach dem Optiker Erich Heynacher benannt ist. Gegebenenfalls kann diese integrale Summe auch noch bei verschiedenen Ortsfrequenzen mit einer geeigneten Empfindlichkeitsfunktion gewichtet werden (mathematisch also eine Faltung). Je größer das Integral der Modulationsübertragungsfunktion, desto besser die Bildqualität.
Der Betrag der komplexwertigen Spektralfunktion der zweidimensionalen Fourier-Transformation der Bilddaten im Bildraum kann zur Ermittlung der Modulationsübertragungsfunktion im Ortfrequenzraum herangezogen werden.
Die einheitenlose Kontrastempfindlichkeitsfunktion kann nach Kresimir Matkovic (1997) in Abhängigkeit von der Ortsfrequenz in Linienpaaren pro Grad mit einer analytischen Funktion angegeben werden:
Der vertikale Bildwinkel beträgt bei Normalbrennweite und einem Bildseitenverhältnis von 3 zu 2 (wie zum Beispiel beim Kleinbildfilm) 27 Grad. Die Ortsfrequenz in Linienpaaren pro Bildhöhe ergibt sich dann aus dem vertikalen Bildwinkel und der Ortsfrequenz in Linienpaaren pro Grad wie folgt:
- Kontrastempfindlichkeitsfunktion (englisch: Contrast Sensitivity Function) CSF des menschlichen Auges über der Ortsfrequenz
-
Über der Ortsfrequenz in Linienpaaren pro Grad
-
Über der Ortsfrequenz in Linienpaaren pro Bildhöhe bei Normalbrennweite (vertikaler Bildwinkel = 27° bei einem Bildseitenverhältnis von 3 zu 2)

- Zur Kontrastempfindlichkeitsfunktion des menschlichen Auges mit den Ortsfrequenzen von 2 sinusmodulierten Linienpaaren pro Bildbreite (linke Bildhälfte) bis hin zu 1024 Linienpaaren pro Bildbreite (rechts am Bildrand), Bildgröße 3860 mal 2160 Bildpunkte (16:9)
-
Mit maximalem Kontrast unten, ohne Kontrast oben
-
Mit reduziertem Kontrast unten, ohne Kontrast oben
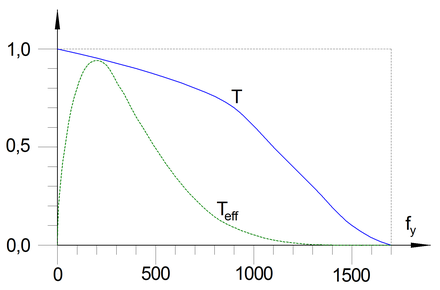
Hierbei ist festzuhalten, dass bei einer Ortsfrequenz von 1000 Linienpaaren pro Bildhöhe der wahrgenommene Kontrast deutlich unter zehn Prozent liegt und somit praktisch kaum noch relevant ist. Die maximale Kontrastempfindlichkeit liegt beim menschlichen Auge bei zirka 200 Linienpaaren pro Bildhöhe und zwischen 50 und 550 Linienpaaren pro Bildhöhe beträgt die Kontrastempfindlichkeit mindestens 50 Prozent. Für Aufnahmen mit guter Kontrastübertragung ist daher genau dieser Bereich von besonderer Wichtigkeit. Zur Auswertung der effektiven Kontrastübertragungsfunktion bei Betrachtung mit dem menschlichen Auge können die Kontrastübertragungsfunktion und die Kontrastempfindlichkeitsfunktion miteinander multipliziert werden:
Wird dieses Produkt über alle Ortsfrequenzen integriert, ergibt sich - ähnlich wie bei und als Verallgemeinerung der Heynacher-Zahl - eine Größe für die totale effektive Kontrastübertragung :
Siehe auch Kontrastverhältnisse bei aschgrauem Mondlicht.
Digitalzoom
[Bearbeiten]Beim Digitalzoom, das heißt also bei der softwaretechnischen Vergrößerung von digitalen Bildern zum Beispiel durch Zeilen- und Spaltenverdopplung, wird die Bildinformation im Sinne der Kontrastübertragung nicht vermehrt, da es sich lediglich um das Kopieren bereits vorhandener Bildinformation handelt. Es gibt also keinen Informationsgewinn. Wenn das digitale Bild zu klein dargestellt wird, so dass ein menschlicher Betrachter das Bild nicht voll auflösen kann, kann durch den Digitalzoom das Bild insgesamt vergrößert werden, oder ein beliebiger Ausschnitt des originalen Bildes kann auf die maximal darstellbare Größe gebracht werden, die beispielsweise durch ein Anzeigegerät oder ein Druckformat vorgegeben ist. Dadurch wird zwar nicht die Bildinformation vergrößert, aber der Betrachter kann mehr von der existierenden Bildinformation erkennen.
Die Frage, welcher Digitalzoomfaktor noch sinnvoll und angebracht ist, hängt bei menschlichen Betrachtern allein von der möglichst guten Ausschöpfung der erkennbaren Modulationen ab, die durch die Kontrastempfindlichkeitsfunktion repräsentiert wird. Bei digitaler maschineller Auswertung besteht diese Problematik nicht, da ein digitaler Algorithmus in der Regel immer die gesamte Bildinformation auswerten kann.
In Unterkapitel MTF-Simulation wird der Effekt des Digitalzooms simuliert und bildlich verdeutlicht.
Siehe auch Kapitel Digitale Bilder: Digitalzoom - Softwarelupe.
Kantenüberhöhung
[Bearbeiten]
Bei digitalen Bildern, die nicht im Rohdatenformat, also ohne rechnerische Eingriffe in die Bilddaten, aufgezeichnet werden, wird die Modulation unmittelbar nach der Aufnahme und vor dem Speichern der Bilddaten oft durch die Firmware der Kamera insgesamt oder insbesondere bei bestimmten Ortsfrequenzen erhöht. In Maßen angewendet führt dies bei digitalen Bildern in der Regel zu einem verbesserten visuellen Bildeindruck. Dies trifft dann zu, wenn die maximale Modulation auf eins erhöht wird und die Modulation entsprechend der Kontrastempfindlichkeitsfunktion des menschlichen Auges bei den wichtigsten Ortsfrequenzen angehoben wird.
In der Modulationsübertragungsfunktion spiegelt sich dies durch die Tatsache wider, dass die maximale Modulation nicht mehr bei der Ortsfrequenz null, sondern bei positiven Ortsfrequenzen auftritt (siehe Abbildung rechts). Dies kann auch so interpretiert werden, dass die Modulation an Kanten in einem günstigen Ortsfrequenzbereich künstlich überhöht wird. Aus einem in der unbearbeiteten optischen Abbildung kontinuierlichen Anstieg der Helligkeit an einer im Original beliebig scharfen Objektkante ergibt sich nach der Optimierung bei einer bestimmten Ortsfrequenz eine deutlich stärkere Modulation.
Wird dieses Prinzip so stark angewendet, dass die Modulation bei mittleren Ortsfrequenzen dominiert, führt dies unter Umständen zu künstlich wirkenden Bildern, bei denen ein Überschwingen des Helligkeitsverlaufs an Kanten mit der entsprechenden Ortsfrequenz erkannt werden kann:
- Vergleich mit unterschiedlichen gerechneten Kontrastübertragungsfunktionen
-
Unbearbeitetes Originalbild
-
Bild mit rechnerisch angepasster Modulation bei mittleren Ortsfrequenzen
-
Bild mit übertrieben verstärkter Modulation bei mittleren Ortsfrequenzen
-
Zentraler Ausschnitt vom unbearbeiteten Originalbild
-
Zentraler Ausschnitt vom Bild mit rechnerisch angepasster Modulation bei mittleren Ortsfrequenzen - der Buchstabe hat außen einen kleinen hellen und innen einen kleinen dunklen Saum
-
Zentraler Ausschnitt vom Bild mit übertrieben verstärkter Modulation bei mittleren Ortsfrequenzen - der Buchstabe hat einen großen hellen Saum, und der innere Rand des Buchstabens ist stark abgedunkelt
-
Spektrale Leistungsdichte der Modulation des zentralen Ausschnittes vom unbearbeiteten Originalbild (die Ortsfrequenz null befindet sich in der Bildmitte, und sie nimmt radial in alle Richtungen zu)
-
Spektrale Leistungsdichte der Modulation des zentralen Ausschnittes vom Bild mit rechnerisch angepasster Modulation bei mittleren Ortsfrequenzen
-
Spektrale Leistungsdichte der Modulation des zentralen Ausschnittes vom Bild mit übertrieben verstärkter Modulation bei mittleren Ortsfrequenzen
Farbauflösung
[Bearbeiten]Durch die im Vergleich zur Dichte der für die Helligkeitsrezeption zuständigen Stäbchen geringere Dichte von Farbzäpfchen auf der menschlichen Netzhaut ist die Farbauflösung, die für das Betrachten von farbigen Bildern erforderlich ist, geringer als die Auflösung, die durch die Kontrastübertragungsfunktion beschrieben wird. In einem digitalen Bild kann ein Mensch bei Betrachtung des gesamten Bildes zwar maximal vier Millionen Bildpunkte in der Helligkeit unterscheiden, jedoch nur etwa eine Million verschiedener Farbpunkte. Bei technischen Anwendungen mit digitaler Auswertung der Bilder, kann die Anforderung an die Farbauflösung je nach Aufgabenstellung jedoch erheblich höher sein.

|

|

|

|
Eine Möglichkeit, die Farbauflösung eines Kamerasensors zu messen, ohne dass es durch das für die optische Abbildung verwendete Objektiv zu einer Verringerung derselben kommt, ist die Verwendung eines direkt auf den Bildsensor projizierten Weißlichtinterferogramms. Dieses Verfahren wurde 2006 von Karsten Zoellner vom Institut für angewandte Optik an der Universität Jena entwickelt. Der Linienabstand des Beugungsbilds eines Spaltes hängt von der Wellenlänge des verwendeten Lichtes sowie vom bildseitigen Öffnungswinkel des verwendeten Interferometers ab:
Wenn für die Primärfarben Rot, Grün und Blau (RGB) die mit abnehmender Wellenlänge kleiner werdenden Linienabstände , und bestimmt werden, kann daraus eine für die Farbauflösung repräsentative Größe , die Farbstrukturtreue (englisch: coloured structure fidelity), bestimmt werden:
Beleuchtung
[Bearbeiten]Dieses Kapitel beschäftigt sich mit Themen, die im Zusammenhang mit der Beleuchtung von Objekten (synonym für "von Gegenständen"), die betrachtet oder photographisch abgebildet werden sollen, von Bedeutung sind.
Photonen
[Bearbeiten]Photonen sind die Ausprägung von elektromagnetischer Strahlung als Teilchen. Sie breiten sich in allen optischen Medien wellenartig aus. Das Produkt aus der Schwingungsfrequenz der elektromagnetischen Welle und deren Wellenlänge ist die Lichtgeschwindigkeit :
Die Vakuumlichtgeschwindigkeit hat eine festgelegte Größe:
In allen anderen optischen Medien ist die Lichtgeschwindigkeit um den Zahlenfaktor kleiner als im Vakuum:
- beziehungsweise
Der einheitenlose Zahlenfaktor wird Brechzahl oder Brechungsindex genannt. Er beträgt für das Vakuum Eins.
Bei elektromagnetischer Strahlung mit der Wellenlänge respektive der Frequenz ergibt sich die Photonenenergie (Maßeinheit Joule, abgekürzt: J) aus der Beziehung:
- ,
wobei für das Plancksche Wirkungsquantum steht.
Der mechanische Impuls eines Photons ist umgekehrt proportional zu dessen Wellenlänge beziehungsweise proportional zu dessen Energie :
Photometrische Grundbegriffe
[Bearbeiten]Photonenstrom
[Bearbeiten]Die Photonenmenge respektive Strahlungsmenge (für Quantität) ist ein einheitenloses Maß für die Anzahl der Photonen mit einer bestimmten Energie (respektive mit einer bestimmten Wellenlänge oder mit einer bestimmten Frequenz). Der Photonenstrom (Maßeinheit 1/s) ergibt sich aus der in einer bestimmten Zeit untersuchten Photonenmenge:
Strahlungsleistung
[Bearbeiten]Die Strahlungsleistung (auch Strahlungsfluss genannt, Maßeinheit Watt, abgekürzt: W, Index e für "elektromagnetisch") ergibt sich bei monochromatischer elektromagnetischer Strahlung wiederum aus dem Produkt von Photonenstrom und der Energie eines einzelnen Photons mit der Wellenlänge .
Entsprechend ergibt sich für die Strahlungsenergie :
Sowie für die Strahlungsstromdichte (auch Bestrahlungsstärke, siehe unten) senkrecht durch eine Fläche :
Photonen, die mit dem Photonenstrom im Winkel zum Oberflächenlot auf eine Fläche treffen, erzeugen dort den mechanischen Strahlungsdruck :
Für monochromatisches Licht mit den Photonenstrom aus Photonen mit dem mechanischen Impuls gilt demnach:
Lichtstrom
[Bearbeiten]Der Lichtstrom (Index v für "visuell", also elektromagnetische Strahlung im sichtbaren Wellenlängenbereich zwischen etwa 380 und 780 Nanometer) ergibt sich aus der Multiplikation der elektromagnetischen Strahlungsleistung mit dem entsprechenden wellenlängenabhängigen photometrischen Strahlungsäquivalent :
Das spektrale photometrische Strahlungsäquivalent hat die Maßeinheit Lumen pro Watt, so dass für den Lichtstrom die Maßeinheit Lumen (abgekürzt: lm, lateinisch: Leuchte) resultiert.
Bezogen auf die spektrale Empfindlichkeit der menschlichen Netzhaut müssen das farbige Tagesehen (photopisches Sehen) mit den Zapfen und das monochrome Nachtsehen (skotopisches Sehen) mit den Stäbchen unterschieden werden. Die entsprechenden photometrischen Strahlungsäquivalente sind in der DIN 5031 festgelegt: das maximale photometrische Strahlungsäquivalent für das Tagsehen beträgt 683,002 Lumen pro Watt, und das maximale photometrische Strahlungsäquivalent für das Nachtsehen beträgt 1700,13 Lumen pro Watt (vergleiche CIE 191:2010 Recommended System for Mesopic Photometry based on Visual Performance, International Commission on Illumination (CIE), Wien).
Mit der physiologischen, wellenlängenabhängigen und einheitenlosen Bewertungsfunktion des menschlichen Auges (auch Hellempfindlichkeitskurve oder relativer spektraler Hellempfindlichkeitsgrad) sowie für das spektrale photometrische Strahlungsäquivalent in Lumen pro Watt ergibt sich für das Tagsehen:
Und für das Nachtsehen mit der entsprechenden Bewertungsfunktion beziehungsweise mit dem spektralen photometrischen Strahlungsäquivalent in Lumen pro Watt:
Die Lichtmenge beim Tagsehen und beim Nachtsehen kann für monochromatisches Licht der Wellenlänge also als Funktion des Lichtstroms ausgedrückt werden:
Bei grünem Licht ( = 550 Nanometer) mit einem Lichtstrom von einem Lumen sind in jeder Nanosekunde beim Tagsehen demzufolge rund vier Millionen Photonen beteiligt.
Der Wirkungsgrad einer Lichtquelle kann durch das Verhältnis des Lichtstroms mit der für die Lichterzeugung aufgewendeten Leistung beschrieben werden, das auch Lichtausbeute genannt wird (Maßeinheit Lumen pro Watt):
- Wahrnehmung von elektromagnetischer Strahlung durch Menschen
-
Relative Hellempfindlichkeitskurven für das Tagsehen V(λ) (rot) und für das Nachtsehen V'(λ) (blau).
-
Spektrale Empfindlichkeit der drei Zapfentypen in der menschlichen Netzhaut (S, M, L) über der Lichtwellenlänge. Der Unterschied zwischen L und M liegt vor allem bei den roten und grünen Wellenlängen, und S reagiert vor allem auf die Wellenlängen im blauen Bereich.
-
Spektrale Empfindlichkeit der drei Zapfentypen und der Stäbchen in der menschlichen Netzhaut über der Lichtwellenlänge in Nanometern (nm). Die maximale Empfindlichkeit der drei Zapfentypen liegt bei den Farben ⬤ (420 nm, violett), ⬤ (534 nm, grün) und ⬤ (564 nm, gelbgrün).
-
Spektrales photometrisches Strahlungsäquivalent für Tagsehen K(λ) und für Nachtsehen K′(λ).
Beleuchtungsstärke
[Bearbeiten]

Wird ein Lichtstrom auf eine entsprechende definierte geometrische Fläche projiziert, kann die Beleuchtungsstärke der Projektion innerhalb dieser Fläche ermittelt werden:
Für eine kreisförmige Projektionsfläche mit dem Durchmesser gilt demzufolge:
Emittiert die definierte geometrische Fläche einer Lichtquelle einen Lichtstrom, wird von der spezifischen Lichtausstrahlung (also eigentlich eine Leuchtstärke) dieser Fläche gesprochen, die sich entsprechend berechnet:
Für einen kreisförmigen Emitter mit dem Durchmesser gilt demzufolge:
Die Beleuchtungsstärke und die spezifische Lichtausstrahlung stellen also eine Lichtstromdichte dar und haben die Maßeinheit Lumen pro Quadratmeter, was meist mit der Maßeinheit Lux (lateinisch: Licht, abgekürzt: lx) abgekürzt wird.
Die Beleuchtungsstärke kann unmittelbar mit einem Messgerät mit definierter Messfläche, einem sogenannten Luxmeter, ermittelt werden.
Bestrahlungsstärke
[Bearbeiten]Die Bestrahlungsstärke ist das photometrische Äquivalent der visuellen Beleuchtungsstärke für das gesamte elektromagnetische Spektrum. Im Gegensatz zur Beleuchtungsstärke als eine Lichtstromdichte mit der Maßeinheit Lumen pro Quadratmeter hat die Bestrahlungsstärke als eine Strahlungsstromdichte die Maßeinheit Watt pro Quadratmeter. Sie ist wie folgt definiert:
Die Bestrahlungsleistung innerhalb einer definierten Messfläche kann mit unmittelbar einem sogenannten Powermeter (Leistungsmessgerät) ermittelt werden. Aus dem Verhältnis von gemessener Leistung und Messfläche ergibt sich dann rechnerisch die Bestrahlungsstärke.
Entsprechend ergibt sich für die spezifische Ausstrahlung einer Strahlungsquelle mit der Strahlungsleistung und der emittierenden Fläche die folgende Beziehung:
Raumwinkel
[Bearbeiten]Der Raumwinkel (Maßeinheit Steradiant, abgekürzt: sr, Kunstwort aus griechisch στερεό für Körper und lateinisch radiant für sie strahlen) ist ein Maß für die Ausdehnung eines flächenhaften Objektes in Winkelkoordinaten.
In der Astronomie wird der Raumwinkel häufig in der Maßeinheit Quadratgrad (abgekürzt: deg²) angegeben:
Raumwinkel eines Kreiskegels
[Bearbeiten]
Der kanonische Raumwinkel eines geraden Kreiskegels kann leicht aus dem Öffnungswinkel oder aus dem Verhältnis der bestrahlten oder strahlenden, kreisrunden Mantelfläche eines Kugelsegments zu ihrem Quadratradius berechnet werden:
Siehe hierzu auch: Öffnungswinkel
Emittiert eine Lichtquelle in den gesamten Raumwinkel oder wird ein Punkt aus dem gesamten Raumwinkel beleuchtet (der Öffnungswinkel beträgt dann 360° beziehungsweise ), dann ist der Wert des Raumwinkels maximal, nämlich:
Die Radien der Kugelsegmente und können hierbei wie folgt aus dem Durchmesser der emittierenden Fläche beziehungsweise aus dem Durchmesser der projizierten Fläche und dem Abstand zwischen der ebenen Grundfläche und Scheitelpunkt des Kugelsegments bestimmt werden:
beziehungsweise
Die Mantelflächen der dazugehörigen Kugelsegmente und ergeben sich dann zu:
beziehungsweise
Raumwinkel einer rechteckigen Pyramide
[Bearbeiten]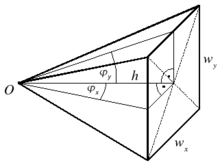
Falls der Raumwinkel senkrecht zur optischen Achse nicht kreisrund, sondern rechteckig begrenzt ist, kann er mit den Pyramidengrundseiten und sowie der Pyramidenhöhe berechnet werden:
Alternativ können auch die beiden senkrecht aufeinander stehenden Öffnungswinkel und verwendet werden, um den Raumwinkel zu berechnen:
Lichtstärke
[Bearbeiten]Soll die Emission von einer punktförmigen Lichtquelle oder die Beleuchtung eines Punktes beschrieben werden, wird in der Photometrie der Lichtstrom auf den Raumwinkel des Punktes der Lichtemission beziehungsweise des Punktes des Lichteinfalls bezogen, so dass die Lichtstärke mit der Maßeinheit Lumen pro Steradiant resultiert, die in der Regel durch die Maßeinheit Candela (lateinisch: Kerze, abgekürzt: cd) ausgedrückt wird:
Eine herkömmliche Haushaltskerze emittiert praktisch fast in den gesamten Raumwinkel und hat eine Lichtstärke von zirka einem Candela. Der Lichtstrom einer solchen Kerze beträgt somit:
Leuchtdichte
[Bearbeiten]Soll die Emission von einer flächenhaften Lichtquelle mit der Fläche in den Raumwinkel oder die Beleuchtung einer Fläche aus dem Raumwinkel beschrieben werden, wird in der Photometrie die Leuchtdichte verwendet, die gemeinhin als Helligkeit interpretiert wird. Bei senkrechter Beobachtung der zu untersuchenden Fläche ergibt sich die Leuchtdichte mit der Maßeinheit Candela pro Quadratmeter beziehungsweise Lux pro Steradiant oder im englischsprachigen Raum auch abgekürzt mit Nit (vom lateinischen Verb "nitere", zu Deutsch "leuchten").
Für emittierende Flächen gilt:
Und für beleuchtete Flächen entsprechend:
Bei konstantem Lichtstrom innerhalb einer optischen Abbildung nimmt die Lichtstärke mit steigendem Abbildungsmaßstab zu, wohingegen die Beleuchtungsstärke mit steigendem Abbildungsmaßstab abnimmt. Siehe auch Abbildungsmaßstab.
Die Leuchtdichte ändert sich durch eine geometrischen Abbildung jedoch nicht, sie wird in der Regel jedoch durch die Absorption oder Zerstreuung in den dafür erforderlichen optischen Komponenten etwas vermindert. Die Invarianz der Leuchtdichte bei optischen Abbildungen wird mit Hilfe der folgenden Skizze deutlich:

Die Flächen von Emitter (links) und Projektion P (rechts) ergeben sich aus ihren quadratischen Flächen, die durch die Objektgröße und die Bildgröße bestimmt sind:
Die kreisförmige Querschnittsfläche in der Hauptebene der optischen Abbildung (blau) ergibt sich aus deren Durchmesser :
Damit können unter Berücksichtigung der Objektweite und der Bildweite die beiden entsprechenden Raumwinkel bestimmt werden:
Die Leuchtdichten des Emitters und in der Projektion lauten:
Der Lichtstrom bleibt erhalten, wenn bei der optischen Abbildung kein Licht absorbiert wird.
Sowohl die Bildweite als auch die Bildgröße können durch den Abbildungsmaßstab ausgedrückt werden, wenn dieser auf die Objektweite und die Objektgröße angewendet wird:
Eingesetzt für die Leuchtdichte in der Projektionsebene ergibt sich schließlich:
Die Leuchtdichte in der Projektionsebene ist also mit der Leuchtdichte des abgebildeten Objekts identisch, und insbesondere ist die Leuchtdichte in der Projektionsebene unabhängig vom Abbildungsmaßstab .
Aus der Beziehung zwischen zwei verschiedenen Leuchtdichten kann ein Kontrastwert bestimmt werden. Siehe auch Modulation.
Geometrischer Fluss
[Bearbeiten]Das Verhältnis aus Lichtstrom und Leuchtdichte wird manchmal auch als geometrischer Fluss oder als Lichtleitwert bezeichnet:
Abstandsgesetz
[Bearbeiten]Das Verhältnis einer zusammenhängenden Teilfläche der Kugeloberfläche zum Quadrat des Kugelradius entspricht dem Raumwinkel dieser Teilfläche, der von Mittelpunkt dieser Kugel umfasst wird, in der Maßeinheit Streradiant:
- beziehungsweise
Die Oberfläche einer Kugel ergibt sich aus:
Daraus folgt unmittelbar, dass die gesamte Kugel von ihrem Mittelpunkt aus gesehen den vollen Raumwinkel von Steradiant umfasst.
- Zum Abstandsgesetz
-
Zwei Kugeln mit dem Verhältnis der Radien .
-
Zwei Kugelausschnitte unter dem Raumwinkel mit dem Verhältnis der Radien und dem Verhältnis der Oberflächen .
Wird eine beliebige Teilfläche auf einer Kugel mit dem Radius mit radialen Strahlen auf eine konzentrische Kugel mit doppeltem Radius projiziert, ergibt sich, dass der Raumwinkel erhalten bleibt, die projizierte Teilfläche auf der Kugel mit dem doppelten Radius jedoch vier Mal so groß ist wie die Teilfläche auf der Kugel mit dem einfachen Radius .
Photometrische Größen, die sich geometrisch ausschließlich auf den Raumwinkel beziehen, sind für solche Teilflächen invariant, wie zum Beispiel die Lichtstärke :
Diejenigen photometrischen Größen, die sich bei konstantem Raumwinkel jedoch auf eine vom Radius abhängige Fläche
beziehen, wie zum Beispiel die Beleuchtungsstärke , verhalten sich bei verändertem Abstand von der Lichtquelle (und bei somit verändertem Radius) umgekehrt proportional zu den Teilflächen auf den jeweiligen Kugeloberflächen und gleichzeitig umgekehrt proportional zu den Quadraten der dazugehörigen Kugelradien. Dieser Sachverhalt wird durch das Abstandsgesetz beschrieben:
Belichtung
[Bearbeiten]Die Belichtung ist ein Maß für die Beleuchtungsstärke während der Belichtungszeit . Im allgemeinen Fall mit zwischen den Zeitpunkten und variierender Beleuchtungsstärke ergibt sich das folgende Integral:
Die Maßeinheit der Belichtung ist demzufolge die Luxsekunde (abgekürzt: lx s).
Wenn die Beleuchtungsstärke zeitlich konstant ist, also
- ,
dann vereinfacht sich die Berechnung der Belichtung wie folgt:
Die Anzahl der Photonen mit einer bestimmten Wellenlänge , die während der Belichtung auf die Fläche fallen, ergibt sich dann wie folgt:
Beim Tagsehen kann bei einer Wellenlänge von 555 Nanometern zum Beispiel gewählt werden, so dass sich ergibt:
Beim Nachtsehen liegt das Empfindlichkeitsmaximum des menschlichen Auges bei einer Wellenlänge von 507 Nanometern, so dass sich ergibt:
Belichtungswert
[Bearbeiten]Im Zusammenhang mit der Photographie wird die Leuchtdichte oft in einen einheitenlosen Belichtungswert (nach DIN 19017) oder (englisch: exposure value) umgerechnet. Mit dem Belichtungswert als Exponent der Basis 2 kann die Leuchtdichte auf eine Referenzleuchtdichte bezogen werden:
Die Referenzleuchtdichte ergibt sich aus einer empirisch zu ermittelnden Konstante , die je nach Messverfahren beziehungsweise Vorzugswerten zwischen 10,6 und 16,9 (oft 12,5 oder 14,0, nach DIN 19017 13,3 bis 16,9) Candelasekunden pro Quadratmeter liegt:
Sie bezieht sich heute auf eine Belichtungszeit von einhundert Sekunden (früher eine Sekunde):
- mit
Somit beträgt die entsprechende Referenzleuchtdichte je nach Messverfahren:
Die Leuchtdichte kann auch mit der am Objektiv einer Kamera gegebenen beziehungsweise eingestellten Blendenzahl (siehe auch Abschnitt Blendenzahl) und der Belichtungszeit bestimmt werden:
steht hierbei für den maßeinheitenlosen Belichtungsindex (englisch: exposure index, E.I.), der typischerweise mit den ISO-Hauptwerten …, 50, 100, 200, 400, … oder auch Zwischenwerten angegeben wird und der auf eine verwendete Filmempfindlichkeit beziehungsweise eine äquivalente Bildsensorempfindlichkeit abgestimmt werden kann. Der Belichtungsindex ist umgekehrt proportional zur Belichtung und ist unabhängig von den Eigenschaften des verwendeten Films oder Bildsensors. Als Bezugswert für die Belichtung wird nach ISO 2721 ein Wert von 10 Luxsekunden angenommen:
Die Leuchtdichte kann daher auch wie folgt zeitunabhängig über die oben definierte Beleuchtungsstärke (trotz des ähnlichen Formelzeichens nicht zu verwechseln mit dem einheitenlosen Lichtwert des APEX-Systems oder dem einheitenlosen Belichtungswert ) berechnet werden:
Ferner können natürlich auch die erforderliche Belichtungszeit t oder die erforderliche Blendenzahl k ermittelt werden, wenn alle anderen Parameter bekannt sind:
Der Belichtungswert kann wie folgt aus der ermittelten Leuchtdichte oder bei maximal ausgenutzter Leuchtdichte aus den Aufnahmeparametern berechnet werden:
Und entsprechend:
- Extreme Belichtungswerte
-
Aufnahme der Sonnenscheibe mit einigen kleinen Sonnenflecken mit einem Neutraldichtefilter mit einem Promille Transmission bei einer Blendenzahl 8, einem Belichtungsindex von ISO 200 und einer Belichtungszeit von 1/32000 Sekunde (der Belichtungswert der Sonnenscheibe betrug 30 EV).
-
Aufnahme der Milchstraße mit einem Fischaugenobjektiv bei einer Blendenzahl 2,8, einem Belichtungsindex von ISO 6400 und einer Belichtungszeit von 40 Sekunden (der Belichtungswert der Himmelssphäre betrug unter -8 EV).
APEX-System
[Bearbeiten]Die einheitenlosen Leitwerte des APEX-Systems sind wie folgt definiert (vergleiche hierzu auch die ehemalige Norm DIN 19017, die ISO 2720 sowie das APEX-System (Additive System of Photographic Exposure)):
Der Blendenleitwert (englisch: aperture value):
Der Zeitleitwert (englisch: time value) wird auf eine Sekunde bezogen:
Der Lichtwert (englisch: exposure value, nicht zu verwechseln mit Beleuchtungsstärke oder dem Belichtungswert ):
Der Empfindlichkeitsleitwert (englisch: sensitivity value):
Der Helligkeitsleitwert (englisch: brightness value, umgangssprachlich auch "Helligkeitswert"):
Und entsprechend:
Beziehungsweise:
Astronomie
[Bearbeiten]Wenn ein Stern den Lichtstrom erzeugt, wird dessen Licht in der Regel in den gesamten Raum emittiert. Die Lichtstärke des Sterns ergibt sich somit zu:
Wird der Stern mit einem Teleskop der Öffnungsweite beobachtet, dann tritt nur ein winziger Bruchteil der Strahlung in das Teleskop mit der Querschnittsfläche :
Der sehr kleine objektseitige Raumwinkel , den ein solches Teleskop vom Stern erfasst, der sich in der Entfernung befindet, ergibt sich zu:
Der Anteil des Lichtstroms , der vom als punktförmig angenommenen Stern in das Teleskop eintritt, ergibt sich dann folgendermaßen:
Der bildseitig erfasste Raumwinkel ergibt sich aus der Brennweite des Teleskops , da ein Stern wegen seiner sehr großen Entfernung in die Brennebene abgebildet wird:
Somit ist die Lichtstärke im Brennpunkt des Teleskops:
Aus dem Lichtstrom im Teleskop kann dann mit dem bildseitig erfassten Raumwinkel die Leuchtdichte des Sterns in einem Flächenelement der Bildebene des Teleskops berechnet werden:
In der Bildebene verteilt sich das Licht des Sterns fast vollständig auf das Beugungsscheibchen mit dem Durchmesser und der Fläche :
Somit ergibt sich für die durch den Stern verursachte Leuchtdichte des Sterns:
Die Leuchtdichte hängt also nur vom im Teleskop erfassten Lichtstrom der beobachteten Sterne ab, welcher proportional zur Fläche der Apertur des Objektivs ist.
Für die visuelle Beleuchtungsstärke in der Bildebene gilt entsprechend:
Je kürzer die Brennweite und je größer die Öffnungsweite sind, desto größer ist also die Beleuchtungsstärke im Beugungsscheibchen des Brennpunkts:
Scheinbare Helligkeit
[Bearbeiten]In der Astronomie wird die Beleuchtungsstärke in der Regel als die scheinbare (visuelle) Helligkeit mit der Maßeinheit "Magnitude" (Größenklasse, abgekürzt mit "mag" oder mit einem hochgestellten "m") angegeben.
Ein astronomisches Objekt in Richtung der optischen Achse mit der scheinbaren visuellen Helligkeit bewirkt in der senkrecht dazu stehenden Bildebene in der Bildmitte die Beleuchtungsstärke:
Anhand der Basis wird deutlich, dass sie die Beleuchtungsstärke verhundertfacht, wenn die scheinbare Helligkeit um fünf Magnituden abnimmt:
Damit glit dann:
Kleine scheinbare Helligkeiten verursachen also eine größere Beleuchtungsstärke als große scheinbare Helligkeiten. Besonders helle Objekte wie die Sonne, der Mond, der Planet Venus oder der hellste Stern des Nachthimmels, Sirius, erreichen sogar negative scheinbare Helligkeiten.
Umgekehrt kann auch die scheinbare visuelle Helligkeit aus der Beleuchtungsstärke berechnet werden:
Beleuchtungsstrahlengänge
[Bearbeiten]Ein Objekt (Gegenstand) muss beleuchtet werden, damit er mit einem Objektiv abgebildet werden kann. Der entsprechende Strahlengang mit einem Leuchtmittel (gegebenenfalls einem Reflektor zur Ausnutzung des rückwärtig abgestrahlten Lichts) und meist auch einem Kondensor zur Bündelung der beleuchtenden Strahlen heißt Beleuchtungsstrahlengang. Im Gegensatz dazu wird bei der Abbildung des Objekts mit einem Objektiv vom Abbildungsstrahlengang gesprochen. Die beiden Strahlengänge können, wie zum Beispiel bei Projektoren üblich, verkettet werden (siehe auch Kapitel Projektoren).
Kondensor
[Bearbeiten]
In Beleuchtungsstrahlengängen können einfache Kollektoren eingesetzt werden, um wie mit einem optisch korrigierten Kollimator eine punktförmige Lichtquelle ins Unendliche abzubilden. Ein nachfolgender lichtsammelnder Kondensor kann im sich anschließenden konvergenten Strahlengang ein Objekt beleuchten und in der Hauptebene des Abbildungsstrahlengangs ein Bild der Lichtquelle erzeugen. Das zu beleuchtenden Objekt wird in der Regel dicht hinter die Kondensorlinse gebracht.
Die optische Güte solcher Kollektoren und Kondensoren muss in der Regel nicht übermäßig groß sein, so dass diese relativ kostengünstig hergestellt werden können, wie zum Beispiel mit plankonvexen Linsen. Oft werden zwei solche plankonvexe Linsen verwendet, deren ebene Flächen nach außen gewandt sind, also mit den Scheitelpunkten der konvexen Flächen in der Mitte einander zugewandt. Zur Optimierung des Kondensors wird für den Kollektor häufig eine asphärische Linse verwendet.
Zwischen der Kollektor- und der Kondensorlinse befindet sich bei Lichtquellen, die auch im infraroten Wellenlängenbereich emittieren, zur Vermeidung von Wärme im nachfolgenden Abbildungsstrahlengang und im zu beleuchtenden Objekt häufig noch eine planparallele Platte mit wärmestrahlungsabsorbierenden Eigenschaften, die durch einen quer zur optischen Achse verlaufenden Luftstrom gekühlt werden kann, oder eine Küvette mit einer entsprechenden Flüssigkeit, die zum Beispiel in einem Kühlkreislauf kontinuierlich ausgetauscht wird.
- Kondensor
-
Schematische Darstellung des Beleuchtungssystems eines Diaprojektors (von links nach rechts):
Sphärischer Hohlspiegel, Leuchtmittel, sphärische Kollektorlinse, Wärmefilter, Kondensorlinse. -
Doppelkondensor eines Diaprojektors mit asphärischer Kollektorlinse und sphärischer Kondensorlinse (von links nach rechts):
Sphärischer Hohlspiegel, Leuchtmittel (Halogenlampe mit Glühwendel), asphärische Kollektorlinse, Wärmefilter, Kondensorlinse, Aufnahme für Diapositiv.
Durchlicht
[Bearbeiten]
Der verkettete Strahlengang kann zur Beleuchtung und Bildaufnahme von durchsichtigen Objekten in Transmission eingesetzt werden, wie zum Beispiel bei der Hellfeldmikroskopie.
Auflicht
[Bearbeiten]

Das Licht des Beleuchtungsstrahlengangs wird mit dem Transmissionsgrad des teildurchlässigen Spiegels hindurchgelassen und mit dem komplementären Wert auf das Objekt reflektiert. Das Licht des Objektstrahlengangs wird ebenfalls mit dem Transmissionsgrad des teildurchlässigen Spiegels hindurchgelassen, so dass für den verketteten Strahlengang insgesamt der folgende Transmissionsgrad resultiert:
Die maximale Helligkeit ergibt sich dann aus der folgenden Bedingung:
Daraus folgt das Maximum bei , und für die maximale Transmission im verketteten Strahlengang gilt dann:
Bei der Auflichtmikroskopie wird das Objekt meist von mehreren Seiten außerhalb des Bildwinkels oder bei verketteten Strahlengängen mit Hilfe von teildurchlässigen Spiegeln beleuchtet, und die am aufzunehmenden Objekt reflektierten Strahlen tragen in diesem Fall zur Bildgebung bei. In der Photographie werden zur Beleuchtung häufig Scheinwerfer oder Blitzlichter eingesetzt. Für Nahaufnahmen gibt es Klammer- oder Ringblitzgeräte, die außerhalb des Bildfeldes aber dennoch nahe am aufnehmenden Objektiv angebracht werden können.
Streuung
[Bearbeiten]
Anders verhält es sich bei seitlicher Beleuchtung, wenn keine hindurchgelassenen oder reflektierten Strahlen zur Abbildung beitragen, sondern das Streulicht des aufzunehmenden Objekts verwendet wird, wie zum Beispiel in der Dunkelfeldmikroskopie oder bei optischen Computermäusen, die die Arbeitsfläche beleuchten und das Bild des Streulichts der Arbeitsfläche auswerten. Je nachdem wie groß die Streuzentren im Verhältnis zur Wellenlänge des verwendeten Lichtes sind, ergeben sich verschiedene Möglichkeiten der Streuung, von denen die wichtigsten in der folgende Tabelle dargestellt sind:
| Art der Streuung | Anwendungsfall | Beschreibung |
|---|---|---|
| Raman-Streuung | Wellenlänge deutlich größer als das Streuobjekt | Streuung an Molekülen oder Atomen durch Wechselwirkung mit den Elektronenhüllen |
| Mie-Streuung | Wellenlänge in der Größenordnung des Streuobjektes | Komplexe Verteilung des gestreuten Lichtes |
| Lichtbrechung in Kugel | Wellenlänge deutlich kleiner als das Streuobjekt | Vorwärtsstreuung in der Regel stärker als Rückwärtsstreuung |
| Thomson-Streuung | Streuung an freien Elektronen | Elastische Stöße zwischen Photonen und Elektronen mit Verlängerung der Photonenwellenlänge |
Bei der Raman-Streuung können drei Fälle unterschieden werden:
| Art der Streuung | Beschreibung |
|---|---|
| Rayleigh-Streuung | Wellenlänge, Kohärenz und Photonenenergie bleiben erhalten; Vorwärtsstreuung bei langwelligem Licht, Rückwärtsstreuung bei kurzwelligem Licht |
| Stokes-Streuung | Wellenlänge wird größer (Verschiebung nach rot); ein Teil der Photonenenergie wird an das Streuobjekt abgegeben |
| Anti-Stokes-Streuung | Wellenlänge wird kleiner (Verschiebung nach blau); die zusätzliche Photonenenergie wird vom Streuobjekt aufgenommen |
Spektroskopie
[Bearbeiten]Mit Spektroskopen kann Strahlung nach den Wellenlängen ihre spektralen Bestandteile zerlegt und betrachtet werden. Die dabei auftretenden Intensitätsverteilungen werden Spektren genannt. Mit Spektrometern können die Wellenlängen der Spektren quantitativ bestimmt und gemessen werden.
Optische Prismen zeigen eine wellenlängenabhängige Brechung (Diffraktion) des einfallenden Lichtes. Die verwendeten optischen Gläser haben in der Regel keine lineare Dispersion, so dass der Zusammengang zwischen Brechungswinkeln und Wellenlängen komplex ist. Dies erschwert die Quantifizierung der Ablenkwinkel bei vorgegebenen Wellenlängen. Prismen werden deswegen oft nur in Spektroskopen zur qualitativen Analyse eingesetzt.
Optische Gitter nutzen die wellenlängenabhängige Beugung (Diffraktion) des einfallenden Lichtes an den Gitterlinien aus und können sowohl in Transmission als auch in Reflexion eingesetzt werden.
- Beugung an einem Liniengitter
-
Bild eines Liniengitters.
-
Beugung am optischen Liniengitter bei einer einfallenden ebenen Welle mit der Intensität . Die Gitterkonstante gibt den regelmäßigen Abstand zwischen den Gitterelementen an, der Ablenkwinkel gilt für abgelenkten Strahlen mit der Intensität , der Gangunterschied in Richtung einer Beugungsordnung ist ein ganzzahliges Vielfaches der Wellenlänge .
Für die Intensität der gebeugten Strahlen in Abhängigkeit vom Ablenkwinkel ergeben sich Extremwerte, wenn sich die Intensität mit dem Winkel nicht ändert:
Dies ist genau dann der Fall, wenn die gebeugten Wellen in der Richtung des Ablenkwinkels im Unendlichen destruktiv oder konstruktiv interferieren.
Bei den Maxima mit konstruktiver Interferenz muss die Phasenlage der an allen Gitterlinien gebeugten Strahlen muss dann ein ganzzahliges Vielfaches der Wellenlänge sein:
- Maxima im Beugungsbild: mit
Das n-te Maximum entspricht hierbei der n-ten Beugungsordnung im Beugungsbild der Gitters.
Bei den Minima mit destruktiver Interferenz muss die Phasenlage der an allen Gitterlinien gebeugten Strahlen muss dann ein um eine halbe Wellenlänge verschobenes ganzzahliges Vielfaches der Wellenlänge sein:
- Minima im Beugungsbild: mit
Bei Spektrometern mit optischen Gittern, die senkrecht zur Oberflächennormalen mit einer ebenen Welle bestrahlt werden, ist der Zusammenhang zwischen Beugungswinkel der ersten Beugungsordnung und Wellenlänge allein von der Gitterkonstante des Gitters, also vom Abstand der benachbarten Gitterlinien abhängig:
Für eine beliebige Beugungsordnung gilt entsprechend:
Bei der nullten Beugungsordnung ist der Ablenkwinkel für alle Wellenlängen gleich Null, und demzufolge tritt hier keine Dispersion auf.
Je mehr Linien des Gitters zur Beugung beitragen, desto ausgeprägter erscheinen die Maxima im Beugungsbild:
Ausführungsbeispiele
[Bearbeiten]- Historische Geräte zur Vermessung von Lichtspektren
-
Das Spektrometer von Joseph Fraunhofer (1787–1826) von 1814 zur Bestimmung des Brechungs- und Farbzerstreuungsvermögens verschiedener Glasarten stand auf einem Goniometer und verwendete ein optisches Prisma. Oben von links nach rechts: 60°-Dreiecksprisma, Objektiv, Okular.
-
Das Spektrometer von Anders Jonas Ångström (1814–1874) von 1868 stand auf einem Goniometer und verwendete ein Transmissionsgitter. Oben von links nach rechts: Spalt, Kollimator, Beugungsgitter, Objektiv, Okular.



Lichtquellen
[Bearbeiten]
Als Lichtquellen werden im Allgemeinen sehr helle Leuchtmittel verwendet, wie zum Beispiel Kohlebogenlampen, Halogenmetalldampflampen oder Hochleistungs-Leuchtdioden. Da die Projektionen meist von Menschen betrachtet werden, die weißes Licht von thermischen Strahlern gewohnt sind, ist es hierbei wichtig, dass das weiße Lichtspektrum ungefähr dem kontinuierlichen Sonnenlichtspektrum entspricht.
Sichtbare Spektrallinien, wie sie bei Leuchtdioden oder Niederdruck-Gasentladungslampen auftreten, können hierbei als sehr störend empfunden werden und werden daher mit Leuchtstoffen verändert und verbreitert. Diese Leuchtstoffe verändern dabei gegebenenfalls auch die Wellenlänge des einfallenden Lichtes, um ein mehr oder weniger kontinuierliches Spektrum zu erzeugen. Bei getakteten Lichtquellen, bei denen zu einem Zeitpunkt immer nur innerhalb eines begrenzten Längenwellenbereichs beleuchtet wird (Drehscheiben mit Farbsegmenten oder nacheinander ein- und ausgeschaltete Leuchtdioden oder Laser) können nicht nur fluoreszierende (kurzes Nachleuchten), sondern auch phosphoreszierende Leuchtstoffe (langes Nachleuchten) eingesetzt werden, um für menschlichen Betrachter eine bessere Farbmischung hervorzurufen.
Manche Menschen können selbst bei mehreren Dutzend Farbwechseln pro Sekunde in bestimmten Situationen (zum Beispiel an kontrastreichen Kanten oder sich schnell bewegenden Bildern) die verschiedenen Einzelfarben unterscheiden, so dass es bei der Wahrnehmung zum sogenannten Regenbogeneffekt kommt.
Lichtspektren
[Bearbeiten]Je nach Erzeugungsart des Lichtes gibt es eine Reihe von typischen Merkmalen der dazugehörigen Lichtspektren. Diese Spektren enthalten häufig unsichtbare Anteile im Ultravioletten (unterhalb von 380 Nanometern) oder im Infraroten (oberhalb von 780 Nanometern). Im folgenden werden einige häufig auftretende Lichtspektren qualitativ erläutert.
- Spektren verschiedener Lichtquellen
-
Grüner Laser
-
Blaue Leuchtdiode
-
Gelblicher Leuchtstoff
-
Blaue Leuchtdiode mit einem gelblich leuchtenden Leuchtstoff
-
Gasentladung mit Quecksilberdampf
-
Mit einem gelblich leuchtenden Leuchtstoff beschichtete Gasentladungslampe mit Quecksilberdampf
Schwarze Körper
[Bearbeiten]Schwarze Körper reflektieren kein Licht, sondern emittieren nur aufgrund ihrer Körpertemperatur Photonen. Das Licht hat eine kontinuierliche Verteilung, und sehr große Teile des kontinuierlichen Spektrums liegen im Infraroten. Der Wirkungsgrad für sichtbares Licht von glühenden Leuchtmitteln aus Festkörpern (in der Regel werden in einem evakuierten Glaskolben wegen des hohen Schmelzpunktes Drähte aus Wolfram verwendet) ist daher sehr gering und liegt typischerweise im Bereich von 5 bis 10 Prozent. Auch die Sonne ist näherungsweise ein Schwarzer Körper mit einem kontinuierlichem Spektrum, dessen maximale Intensität bei 555 Nanometern liegt (die Oberflächentemperatur und die entsprechende Farbtemperatur betragen knapp 5800 Kelvin). Das gleiche gilt für die Anoden von Kohlebogenlampen, die sich durch den Beschuss mit Elektronen aus dem Lichtbogen stark aufheizen und dadurch zum Leuchten angeregt werden.
Durch Hinzufügung eines Halogens, wie zum Beispiel Iod oder Brom, kann das Metallgas in einer Glühlampe stabilisiert werden. Bei dem im Betrieb einsetzenden Wolfram-Halogen-Kreisprozess schlägt sich das unvermeidlich verdampfende Wolfram des Glühdrahtes dann nicht auf der Innenseite des Glaskolbens nieder, sondern auf dem heißen Wolframdraht. Die entsprechenden Leuchtmittel werden als Halogenlampen bezeichnet und haben eine größere Lebensdauer und einen höheren Wirkungsgrad als herkömmliche Wolframdrahtlampen.
- Spektren Schwarzer Körper
-
Spektrum eines Schwarzen Körpers mit einer Oberflächentemperatur beziehungsweise Farbtemperatur von 3500 Kelvin
-
Spektren und Farbeindruck von Schwarzen Körpern mit verschiedenen Farbtemperaturen in Kelvin beziehungsweise Mired (Microreciprocal degrees)
Gasentladungen
[Bearbeiten]
Niederdruck-Kaltkathoden-Gasentladungsröhren konnten seit 1857 von Heinrich Geißler (1814–1879) gebaut werden und werden Geißler-Röhren genannt. Er fand ein Verfahren, um metallische Drähte in Glaskolben einzuschmelzen, die unter niedrigem Druck mit Gasen gefüllt sind.
Gasentladungen erzeugen diskrete Lichtspektren mit mehreren Spektrallinien, die den Energieniveaudifferenzen der Gasatome oder Gasmoleküle entsprechen. Je heißer das leuchtende Gas ist, desto breiter werden die Spektrallinien.
Solche Gasentladungslampen können verwendet werden, um farbiges Licht zu erzeugen. Hierbei werden oft Edelgase, wie Neon oder Krypton, oder Metalldämpfe verwendet, wie zum Beispiel Quecksilber oder Natrium.
Findet die Gasentladung in einem durchsichtigen Gefäß statt, das mit einem Leuchtstoff beschichtet ist, können die kurzwelligen Lichtteilchen der Gasentladung eingesetzt werden, um im Leuchtstoff längerwellige Photonen zu generieren (Fluoreszenz). Je nach Abstimmung zwischen dem Gasentladungsspektrum und dem Emissionsspektrum des Farbstoffes können die spektralen Lichtverteilungen in einen sehr großen Bereich variiert und angepasst werden. Dieses Prinzip wird bei herkömmlichen Leuchtstofflampen angewendet.
Bei Hochdruckgasentladungslampen befindet sich der Metalldampf (meist Quecksilber oder Natrium) während des Betriebs unter hohem Druck in einem Glaskolben, wobei während der Gasentladung hohe Temperaturen herrschen. Die Spektrallinien der Atome sind daher stark verbreitert, und hierdurch entsteht ein quasi-kontinuierliches Spektrum, so dass zur Erzeugung von weißlichem Licht auf den Einsatz von zusätzlichen Leuchtstoffen verzichtet werden kann.
Bei Höchstdruckgasentladungslampen befindet sich das Gas (meist Argon oder Xenon) bereits bei Zimmertemperatur unter einem hohen Druck in einem dickwandigen Glaskolben. Wird die Gasentladung gezündet, steigt dieser Druck während des Betriebs noch weiter an und erreicht unter Umständen mehrere hundert Bar. Die Spektrallinien sind in diesem Fall so stark verbreitert, dass das resultierende Lichtspektrum dem kontinuierlichen Spektrum der Sonne recht ähnlich kommt. Ferner haben Höchstdruckgasentladungslampen in der Regel nur eine lichtemittierende Fläche von wenigen Quadratmillimetern, so dass sie als gute Annäherung an eine Punktlichtquelle verwendet werden können, was beispielsweise in Beleuchtungsstrahlengängen mit einem Kollimator wünschenswert ist. Höchstdruckgasentladungslampen werden daher sehr häufig in Projektoren mit hohem Lichtstrom eingesetzt.
Leuchtstoffe
[Bearbeiten]Leuchtstoffe, die eine Lumineszenz zeigen, erzeugen je nach chemischer Zusammensetzung der beteiligten Farbstoffe verschiedene Lichtspektren, die meist einen größeren Wellenlängenbereich umfassen. Die Farbstoffmoleküle des Leuchtstoffes werden durch Licht bestimmter Wellenlänge angeregt und emittieren bedingt durch inelastische Verluste innerhalb der Moleküle Photonen größerer Wellenlänge (Stokes-Lumineszenz).
Besteht die Anregung der Farbstoffmoleküle nur für kurze Zeit, wird von Fluoreszenz gesprochen. Hier finden sowohl die Anregung als auch die Emission meist innerhalb von Mikrosekunden über erlaubte Übergänge in den Elektronenniveaus statt. Die Bezeichnung leitet sich vom chemischen Stoff Calciumfluorit (CaF2) ab, das im Mineral Fluorit (auch Flussspat)) enthalten ist, bei welchem dieser Effekt häufig durch blaues Leuchten beobachtet werden kann, wenn es mit ultraviolettem Licht bestrahlt wird.
Geben die Elektronen ihre Anregungsenergie indirekt ab, dauert der Vorgang deutlich länger und kann stundenlang anhalten. In diesem Fall wird von Phosphoreszenz gesprochen. Der Name leitet sich vom chemischen Element Phosphor ab, bei dem ein solcher Effekt beobachtet werden kann, der allerdings auf der Aktivierung chemischer Reaktionen beruht. Dennoch hat sich der Begriff Phosphoreszenz allgemein für den Effekt des langen Nachleuchtens von Stoffen etabliert.
Leuchtstoffe können also auch durch ultraviolettes Licht zum Leuchten im sichtbaren Bereich angeregt werden. Solche Farbstoffe werden beispielsweise eingesetzt, um weißes Papier oder weiße Textilien im Sonnenlicht heller erscheinen zu lassen. Der ultraviolette Anteil im Sonnenspektrum wird durch geeignete Farbstoffe (Aufheller) in sichtbare Anteile umgewandelt. Im Extremfall kann der von einer solchen Oberfläche reflektierte sichtbare Lichtstrom sichtbaren Lichts sogar stärker sein, als der sichtbare Lichtstrom der zur Beleuchtung verwendeten Lichtquelle, da die elektromagnetischen Strahlungsleistung unsichtbare Anteile enthält, die in sichtbare Anteile umgewandelt werden.
Wird eine Lichtquelle, die im Blauen oder Ultravioletten kurzwellig emittiert, mit einem geeigneten Leuchtstoff kombiniert, der bei einer längeren Wellenlänge luminesziert, so entsteht ein Lichtspektrum dass auch längere sichtbare Wellenlängen enthält und einem menschlichen Beobachter dann je nach Leuchtstoff mehr oder weniger weißlich erscheinen kann. Dieses Prinzip wird bei zahlreichen Leuchtmitteln für die Beleuchtung von Räumen oder auch für Projektoren und Taschenlampen angewendet. Als Lichtquelle werden hierfür sehr häufig leistungsstarke, im Blauen emittierende Leuchtdioden verwendet.
Für sehr lichtstarke Leuchtmittel werden zunehmend auch im Blauen emittierende Laser verwendet. Die Leistungsdichte im Leuchtmittel kann dann allerdings so groß sein, dass es nach einer gewissen Benutzungsdauer zu einer Beeinträchtigung oder gar der Zerstörung des Leuchtstoffes oder seines Trägermaterials kommen kann. Falls die Energiedichte so groß werden kann, dass eine thermische Beeinträchtigung des Leuchtstoffes droht, besteht die Möglichkeit, die im Leuchtstoff deponierte Energie räumlich zu verteilen, indem der Leuchtstoff auf einen beweglichen Träger aufgebracht und dieser während der Lichterzeugung bewegt wird, wie zum Beispiel mit einer rotierenden Trägerscheibe.
Wenn das Lichtspektrum des Leuchtmittels zeitlich nicht konstant sein muss oder soll, können trotz konstanter Beleuchtung durch die Lichtquelle bei beweglichen Leuchtstoffträgern mehrere nebeneinanderliegende Leuchtstoffe mit verschiedenen Eigenschaften kombiniert werden.
Leuchtdioden
[Bearbeiten]
Leuchtdioden erzeugen monochromatisches Licht, dessen Verteilung sich durch eine geringe Bandbreite von typischerweise 20 bis 40 Nanometern auszeichnet. Je heißer die Leuchtdiode im Betrieb ist, desto breiter wird die Spektrallinie. Je nach Kühlung der Leuchtdiode kann diese Bandbreite begrenzt oder sogar herabgesetzt werden.
Die Farbe von Leuchtdioden hängt vom verwendeten Halbleiter ab, und die verfügbaren Wellenlängen liegen im Bereich zwischen 200 und 1000 Nanometern. Bei der Wellenlänge um 555 Nanometer, im Grünen, bei der die Sonne ihre maximale Emissionsintensität erreicht, ist der Wirkungsgrad der im Markt angebotenen Leuchtdioden nur relativ gering ("green gap"). Daher ist es schwierig, helle Lichtquellen mit den drei Primärfarben rot, grün und blau mit Leuchtdioden zu kombinieren. Aus diesem Grund ist es üblich, die grünen Anteile in einem Lichtspektrum, das ausschließlich mit Leuchtdioden erzeugt werden soll, durch die Kombination einer hellen blauen Leuchtdiode mit einem orange oder gelb leuchtenden Leuchtstoff zu generieren.
Laser
[Bearbeiten]Laser erzeugen monochromatisches Licht, dessen Verteilung sich durch eine sehr geringe Bandbreite auszeichnet.
Divergenz
[Bearbeiten]Geometrische Divergenz
[Bearbeiten]
Ohne Berücksichtigung von Beugungseffekten breiten sich die Randstrahlen eines Strahlenbündels vom Ursprung (, ) entlang der optischen z-Achse geradlinig aus (siehe Abbildung). In diesem Fall kann die geometrische Divergenz des Strahlenbündels mit HIlfe eines an der Stelle gemessenen Strahlradius wie folgt angegeben werden (die Näherung gilt für kleine Divergenzwinkel im Bogenmaß):
Gaußsche Divergenz
[Bearbeiten]
Bei kleinen Strahldurchmessern muss die Beugung berücksichtigt werden. Das Strahlprofil ist hierbei nicht mehr scharf begrenzt, sondern bildet ein Gaußsches Profil (Glockenkurve) mit dem Maximum der Lichtintensität auf der optischen Achse. Dies bedeutet jedoch, dass der Strahl senkrecht zur Ausbreitungsrichtung unendlich ausgedehnt ist. Für mathematische Berechnungen wird üblicherweise der Randstrahl verwendet, bei dem die Amplitude der Lichtwelle mit der Wellenlänge um den Faktor beziehungsweise bei dem die Intensität um den Faktor abgenommen hat.
Befindet sich die engste Stelle eines Strahlenbündels, die sogenannte Strahltaille mit dem Durchmesser , im Ursprung eines Zylinderkoordinatensystems () und breitet sich das Licht in Richtung der optischen z-Achse durch ein Medium mit der Brechzahl aus (siehe Abbildung), heißt die Länge entlang der optischen Achse, bei der der Lichtstrahl die doppelte Querschnittsfläche beziehungsweise das Wurzel-2-fache des Durchmessers der Strahltaille erreicht hat, Rayleigh-Länge :
Daraus ergibt sich die Gaußsche Divergenz für paraxiale Strahlen:
Im Fernfeld (also für ) vereinfacht sich diese Beziehung zu:
Falls die Wellenlänge hinreichend klein gegenüber dem Durchmesser der Strahltaille ist (also für ) und im Bogenmaß bestimmt ist, vereinfacht sich diese Gleichung noch weiter zur folgenden Näherung:
Strahldivergenz
[Bearbeiten]Die Strahldivergenz ist definitionsgemäß doppelt so groß wie die Divergenz und beschreibt den Winkel zwischen gegenüberliegenden Randstrahlen:
Projektionen
[Bearbeiten]Kontrastverhältnis
[Bearbeiten]Bei Projektoren wird häufig das einfache Verhältnis zwischen der größten Leuchtdichte und der kleinsten Leuchtdichte angegeben (siehe auch Kapitel Leuchtdichte), die in der Projektionsebene erreicht werden können:
Dieses Kontrastverhältnis steht folgendermaßen in Bezug zu Modulation :
- beziehungsweise
Siehe hierzu auch: Modulation
Es ist zu beachten, ob die minimale und maximale Helligkeit gleichzeitig an verschiedenen Stellen einer Projektion oder mit verschiedenen Helligkeitseinstellungen des Gerätes in zwei verschiedenen Projektionen gemessen wurden.
Manche Geräte haben im Objektiv eine gesteuerte Blende, mit denen die Gesamthelligkeiten der jeweils zu projizierenden Bilder entsprechend ihrer Bildinhalte in Echtzeit angepasst werden können, um den Kontrast aufeinanderfolgender Bilder zu erhöhen.
Lichtstrom
[Bearbeiten]Zur Ermittlung des Lichtstroms eines Projektors werden in angrenzenden Feldern die Beleuchtungsstärken an der Stelle des Projektionsschirms bestimmt, auf die dazugehörigen Flächeninhalte bezogen und über die gesamte Projektionsfläche summiert.
Siehe hierzu auch: Lichtstrom

Werden wie in der Norm DIN EN 61947 - Teil 1 gleich große, angrenzende Teilflächen mit der Gesamtfläche
- beziehungsweise
betrachtet, vereinfacht sich die Formel für den Lichtstrom zu:
Siehe hierzu auch: Beleuchtungsstärke

Nicht nur bei rechteckigen Projektionen, sondern auch bei kreisförmigen Projektionen kann die Kreisfläche zur Lichtrommessung entsprechend in neun gleich große Teilflächen aufgeteilt werden. Die Teilflächen sind in diesem Fall gleich, wenn die Radien im Verhältnis stehen. Die Messungen finden dann in den Schwerpunkten der Teilflächen statt, die auf Kreisradien im Verhältnis liegen.
Erforderlicher Lichtstrom
[Bearbeiten]Wenn eine Projektionsfläche mit dem Flächeninhalt durch eine vorgegebene Hintergrundbeleuchtung mit der Beleuchtungsstärke erhellt ist, kann der erforderliche Lichtstrom eines Projektors aus dem gewünschten Kontrastverhältnis beziehungsweise aus der gewünschten Modulation berechnet werden:
Bildaufnahme
[Bearbeiten]Dieses Kapitel beschäftigt sich damit, wie durch Berücksichtigung der Parameter Ort und Zeit mit Hilfe von Licht orts- und zeitaufgelöste Bildinformation gewonnen werden kann und welche Komponenten, Verfahren und optischen Geräte dafür häufig zum Einsatz kommen.
Die Lichtwandlung mit Bildsensoren wird im eigenen Kapitel Lichtwandlung behandelt.
Objektive
[Bearbeiten]
Objektive sind lichtsammelnde Geräte, die eine reelle optische Abbildung von Objekten erzeugen.
Grundsätzlich können Objektive als dioptrische, als kataoptrische oder als katadioptrische Systeme gestaltet werden. Dioptrische Systeme (von griechisch "διοπτρον", "Visier") verwenden durchsichtige Elemente und kataoptrische Systeme (von griechisch "κάτοπτρον", "Spiegel") verwenden reflektierende Elemente, um eine optische Abbildung zu erzeugen. Bei katadioptrischen Systemen werden durchsichtige und reflektierende Elemente kombiniert, was zum Beispiel zweckmäßig sein kann, wenn Teleskope, Ultrakurzdistanzprojektoren oder 360-Grad-Panoramakameras in kompakter Form gebaut werden sollen.
Durchsichtige Elemente mit gewölbten Oberflächen, wie zum Beispiel Glaslinsen, lenken das Licht durch Brechung ab. Eine Alternative stellen lichtbeugende Elemente dar. Für die Ablenkung des Lichtes können auch durchsichtige oder reflektierende Zonenplatten eingesetzt werden. Die Stärke der Brechung und der Beugung von Licht sind von dessen Wellenlänge abhängig, so dass hierbei im Gegensatz zu reflektierenden Elementen Dispersion auftritt.
Bei der Aufnahme spielen die Eigenschaften der verwendeten Objektive eine entscheidende Rolle. Moderne Objektive haben konstruktionsbedingte Abbildungsfehler sogar in Abhängigkeit von eingestellter Brennweite, Objektweite und Blendenzahl digital im Objektiv gespeichert und können sie dank eines eigenen Prozessors an die kamerainterne Bildverarbeitung übermitteln, so dass sie in den digitalen Rasterbildern zusammen mit den aufgenommenen Bilddaten als Metadaten (zum Beispiel im Exchangeable Image File Format (EXIF)) gespeichert oder von der Kamera unmittelbar ausgewertet werden können. Somit ist es beispielsweise möglich, den Randlichtabfall, den Farbquerfehler oder die Verzeichnung der optischen Abbildung rechnerisch zu kompensieren.
Durch die stetige digitale Kommunikation zwischen der Objektiv- und der Kamera-Firmware ist es darüberhinaus auch möglich, in verschiedenen Aufnahmesituationen automatisch optimale Abbildungsparameter zu wählen. Sogar während der Aufnahme können beispielsweise die optomechanischen Bildstabilisierungen in einem Kameragehäuse und in einem Objektiv kombiniert und synchronisiert werden. Ferner kann die Objektentfernung kontinuierlich verändert werden, um zum Beispiel Fokus Stacking zu ermöglichen, oder die Aperturblende kann unmittelbar und stufenlos sich ändernden Lichtbedingungen angepasst werden.
Objektivarten
[Bearbeiten]
Links: Bei einer gegenstandsseitig entozentrischen Abbildung wird die hintere Rohröffnung kleiner abgebildet als die vordere Rohröffnung und ist somit sichtbar.
Mitte: Bei einer gegenstandsseitig telezentrischen Abbildung wird die hintere Rohröffnung genauso groß abgebildet wie die vordere Rohröffnung und ist somit deckungsgleich.
Rechts: Bei einer gegenstandsseitig perizentrischen Abbildung wird die hintere Rohröffnung größer abgebildet als die vordere Rohröffnung und ist in der Projektion somit als äußerer Rand der Mantelfläche des Rohres zu sehen.

Es kann zwischen herkömmlichen (oder auch entozentrischen), telezentrischen und perizentrischen (oder auch hyperzentrischen) Objektiven unterschieden werden:
- Bei einer gegenstandsseitig entozentrischen (das perspektivische Zentrum liegt im Inneren) Abbildung wird der Abbildungsmaßstab mit zunehmender Objektweite immer kleiner. Objekte gleicher Größe werden bei größerer Entfernung vom Aufnahmegerät kleiner abgebildet als bei kleiner Entfernung vom Aufnahmegerät. Bei einer herkömmlichen optischen Abbildung ist die Schärfentiefe bei einem Objekt im Brennpunkt vor der ersten Hauptebene, der nach unendlich abgebildet wird, gleich null, beziehungsweise der Abbildungsmaßstab ist unendlich.
- Bei einer gegenstandsseitig telezentrischen (das perspektivische Zentrum liegt in der Ferne) Abbildung ist der Abbildungsmaßstab unabhängig von der Objektweite. Objekte gleicher Größe haben unabhängig von ihrer Entfernung vom Aufnahmegerät immer mit die gleiche Bildgröße.
- Bei einer gegenstandsseitig perizentrischen (das perspektivische Zentrum liegt im Äußeren) Abbildung wird der Abbildungsmaßstab mit zunehmender Objektweite immer größer. Objekte gleicher Größe werden bei größerer Entfernung vom Aufnahmegerät größer abgebildet als bei kleiner Entfernung vom Aufnahmegerät. Dies erfordert besonders große und aufwendig konstruierte Objektive, die ein Objekt aus mehreren Richtungen gleichzeitig erfassen können. Die perspektivischen Projektionen solcher Objektive wirken unnatürlich, können aber zum Beispiel zur einfachen Begutachtung von voluminösen Objekten unter Umständen sinnvoll eingesetzt werden.
Telezentrie
[Bearbeiten]Bei digitalen Bildsensoren ist es nützlich, bildseitig telezentrische Objektive einzusetzen, da diese wegen des weitgehend parallelen Strahlenganges geringere Aberrationen durch die optisch wirksamen Elemente auf dem Bildsensor (wie etwa Mikrolinsen, Sperrfilter oder Farbfilter) verursachen und damit Bilder mit größerer Auflösung ermöglichen.
Mit beidseitig telezentrischen Objektiven ist der Abbildungsmaßstab in großen Bereichen unabhängig von der Objektweite und der Lage des Bildsensors auf der optischen Achse. Dieses Verhalten kann zur Überprüfung von Objektmaßen bei variabler, oder sogar unbekannter Objektweite ausgenutzt werden.
Ferner weist ein beidseitig telezentrischer Strahlengang eine hohe Schärfentiefe auf. Bei einem beidseitig telezentrischen Strahlengang mit zwei gespiegelten, konfokal angeordneten Objektiven ist die Schärfentiefe genauso groß wie die Brennweite, beziehungsweise kann der Bildsensor um eine Brennweite entlang der optischen Achse verschoben werden, ohne dass die durch die Defokussierung verursachten Zerstreuungskreise mehr als halb so groß werden, wie die Aperturblende zwischen den beiden Objektiven. Für eine hohe Messgenauigkeit ist eine entsprechend kleine Aperturblende erforderlich, wobei diese gegebenenfalls durch Beugung auflösungsbegrenzend wirkt.
- Beidseitig telezentrische Abbildungen
-
Beidseitig telezentrische Abbildung mit konstantem Abbildungsmaßstab für verschiedene Objektweiten mit zwei, konfokal zum Punkt F angeordneten Objektiven der gleichen Brennweite f. In der gemeinsamen Brennebene befindet sich eine Aperturblende. Ein Objekt bei doppelter Brennweite wird in die zweite Hauptebene H' abgebildet (blau). Alle Objekte die sich näher an der ersten Hauptebene H befinden, werden reell hinter die zweite Hauptebene H' abgebildet, wobei die Bildgröße und somit der Abbildungsmaßstab nicht variieren. Ein Objekt, das sich genau im Brennpunkt vor der ersten Hauptebene befindet, wird genau in den Brennpunkt hinter der zweiten Hauptebene abgebildet (rot).
-
Zur Schärfentiefe bei einer beidseitig telezentrischen Abbildung mit zwei, konfokal zum Punkt F angeordneten Objektiven der gleichen Brennweite f: Der rote Punkt wird geometrisch scharf in die Brennebene B hinter der zweiten Hauptebene H' abgebildet. Alle Objekte, die sich zwischen der eineinhalbfachen und der halben Brennweite vor der ersten Hauptebene H befinden werden noch hinreichend scharf mit einem Zerstreuungskreis abgebildet. Der akzeptable Durchmesser des Zerstreuungskreises ist in diesem Fall halb so groß wie die Öffnungsweite D, und sowohl die objektseitige als auch die bildseitige die Schärfentiefe betragen f.
-
Beispiel für eine beidseitige telezentrische Abbildung mit zwei konfokal angeordneten Objektiven, die im gemeinsamen Brennpunkt (für Objekte und Bilder in unendlicher Weite) mit einer Blende versehen sind.
-
Beispiel für eine beidseitige telezentrische Abbildung mit zwei konfokal angeordneten Spiegelteleskopen, die im gemeinsamen Brennpunkt (für Objekte und Bilder in unendlicher Weite) mit einer Blende versehen sind.
Retrofokusobjektiv
[Bearbeiten]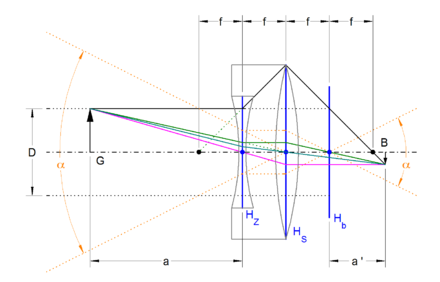
Retrofokusobjektive können eingesetzt werden, wenn die Brennweite kürzer sein soll, als es der minimale Abstand zwischen Objektiv und Bildebene zulässt, zum Beispiel weil an dieser Stelle erforderliche optische Elemente, wie Prismen oder Umlenkspiegel in den Strahlengang gebracht werden sollen.
Ein Retrofokusobjektiv kann beispielsweise durch das Hinzufügen einer Zerstreuungslinse vor dem lichtsammelnden System realisiert werden. In diesem Fall wird die effektive Öffnungsweite des Systems kleiner als der größte Strahlquerschnitt und die größte Sammellinse im Strahlengang. Die scheinbare Hauptebene des Systems liegt bildseitig hinter der letzten Linse.
Wenn der Brennpunkt der Sammellinse mit dem Hauptpunkt der Zerstreuungslinse übereinstimmt und beide Linsen die gleiche Brennweite haben, ist die Brennweite des Gesamtsystems gemessen von der scheinbare Hauptebene Hb ebenfalls .
Telefokusobjektiv
[Bearbeiten]
Bei Telefokusobjektiven liegt die scheinbare Hauptebene objektseitig vor der ersten Linse im Strahlengang. Auf diese Weise können Objektive gebaut werden, deren Baulänge kürzer ist als deren wirksame Brennweite. Ferner können bei unzugänglichen aufzunehmenden Objekten mit Telefokusobjektiven auch bei kleineren Objektweiten lange Brennweiten eingesetzt werden.
Ein Telefokusobjektiv kann beispielsweise durch das Hinzufügen einer Zerstreuungslinse hinter dem lichtsammelnden System realisiert werden. In diesem Fall ist die wirksame Öffnungsweite des Systems kleiner als die Frontlinse des Objektivs.
Wenn der Brennpunkt der Sammellinse mit dem Hauptpunkt der Zerstreuungslinse übereinstimmt und beide Linsen die gleiche Brennweite haben, beträgt die wirksame Brennweite des Gesamtsystems gemessen von der scheinbaren Hauptebene Hb . In diesem Fall ist allerdings keine Bildaufnahme bei unendlicher Objektweite möglich, da das Bild dann innerhalb der Zerstreuungslinse entsteht.
Makroobjektiv
[Bearbeiten]
Mit einem Makroobjektiv können Nahaufnahmen mit großem Abbildungsmaßstab gemacht werden. Der Betrag des Abbildungsmaßstabs ist in der Regel größer als ein Viertel, kann aber auch ohne weiteres größer als eins sein. Beim Abbildungsmaßstab eins ist die Objektweite identisch mit der Bildweite, und beide Werte sind vom Betrag doppelt so groß wie die Brennweite des konvergenten Abbildungsystems.
Ein fokussierbares Objektiv hat in der Regel einen minimale Objektweite , in der noch ein hinreichend scharfes Bild erzeugt werden kann. Bei Kamerasystemen ist es allerdings möglich, durch die Verwendung von geeigneten und gegen Streulicht abgeschirmten und geschützten Zwischenringen oder Balgengeräten zwischen dem Objektivanschluss und dem Kameraanschluss die Bildweite zu vergrößern, so dass auch kleinere Objektweiten scharfgestellt werden können.
Bei vorgegebener Brennweite und bei minimaler Objektweite können die Bildweite , die Objektweite und der Abbildungsmaßstab in Abhängigkeit und der Länge des Zwischenrings wie folgt bestimmt werden:
Für den Sonderfall, dass das Objektiv auf unendliche Objektweite () eingestellt ist (hier entspräche also die Bildweite der Brennweite ), jedoch bildseitig mit einem Zwischenring der Länge versehen wird, ergibt sich:
In diesem Fall gilt für den Aufnahmeabstand d zwischen Objekt und Bildebene:
Hierbei ist gegebenenfalls zu beachten, dass viele Objektive über mehrere Hauptebenen verfügen, so dass der Abstand zwischen den beiden äußersten Hauptebenen unter Umständen noch zu dem solchermaßen berechneten Aufnahmeabstand hinzugerechnet werden muss.
Wenn der Abbildungsmaßstab größer als eins werden soll, kann es sinnvoll sein, das verwendete Objektiv umzudrehen (Retrostellung), um Einschränkungen bei der Bildqualität zu verringern.
- Bildebenensymbol
-
Der Strich in diesem nach DIN 4522-11 standardisierten Symbol kennzeichnet an einem Kameragehäuse die Lage der Bildebene.
-
Relief des Bildebenensymbols auf der Oberseite eines Kameragehäuses aus dunklem Kunststoff.
Lichtausbeute
[Bearbeiten]Es ist insbesondere bei Nahaufnahmen mit geringer Objektweite und beim Einsatz von Zwischenringen zu beachten, dass bei konstanter Bildfläche mit entsprechend großen Bildweiten und Abbildungsmaßstäben die genutzten Bildwinkel und somit auch die im Bild genutzten Lichtströme geringer werden. Bei einem Abbildungsmaßstab von 1/2 ist die Lichtausbeute im Verhältnis zu einer Abbildung aus dem Unendlichen (also beim Abbildungsmaßstab 0) bereits nur noch 4/9, bei einem Abbildungsmaßstab von 1 nur noch 1/4 und bei einem Abbildungsmaßstab von 2 sogar nur noch 1/9.
Die relative Lichtausbeute ergibt sich zu:
Dies ist gleichbedeutend mit einer scheinbaren Vergrößerung der Blendenzahl auf den Wert der effektiven Blendenzahl :
Dieser Wert kann auch in einen Wert für die Anzahl der Blendenstufen umgerechtet werden, bei der die gleiche Lichteinbuße durch das Abblenden der Aperturblende erreicht wird. Die zwei Blendenzahlen und unterscheiden sich durch die folgende Anzahl von Blendenstufen :
In der folgenden Tabelle sind für verschiedene auf die Brennweite normierte Objektweiten jeweils die entsprechende Bildweite , der dazugehörige Abbildungsmaßstab , die relative Lichtausbeute und der Wert des Lichtverlusts in Blendenstufen angegeben:
| Objekt- weite |
Bild- weite |
Abbildungs- maßstab |
Relative Lichtausbeute |
Blenden- stufen |
|---|---|---|---|---|
| 1000 | 1,001 | 0,001 | 1,00 | 0,003 |
| 100 | 1,01 | 0,010 | 0,98 | 0,029 |
| 10 | 1,11 | 0,111 | 0,81 | 0,30 |
| 3,0 | 1,50 | 0,500 | 0,44 | 1,17 |
| 2,0 | 2,00 | 1,00 | 0,25 | 2,0 |
| 1,5 | 3,00 | 2,00 | 0,11 | 3,2 |
Kollimator
[Bearbeiten]
Ein Kollimator dient zur Erzeugung paralleler Strahlenbündel. Der Vorteil dieser parallelen Strahlenbündel besteht darin, dass sich diese in beliebigem Abstand hinter dem Kollimator nicht verändern und bildseitige optische Geräte nicht auf den Abstand zum Kollimator eingestellt werden müssen. Da ein Kollimator ins Unendliche abbildet, müssen nachfolgende optische Geräte, wie zum Beispiel ein Beobachtungsfernrohr, objektseitig stets auf unendliche Objektweite eingestellt sein, damit sie eine scharfe optische Abbildung im Endlichen erzeugen können.
Wenn es nicht auf eine hohe optische Auflösung ankommt, wie zum Beispiel in einem Beleuchtungsstrahlengang, sind die Anforderungen an die Kollimation nicht besonders hoch, so dass ein einfacher optischer Kollektor in Form einer plan-konvexen Linse eingesetzt werden kann.
Siehe hierzu auch Kondensor.
Zonenplatten
[Bearbeiten]
Statt Glaslinsen oder in Ergänzung zu Glaslinsen können auch Fresnelsche Zonenplatten eingesetzt werden, um Licht abzulenken und eine optische Abbildung zu erzeugen.
Optische Medien haben eine Brechzahl größer als eins und eine entsprechende Dispersion, so dass kurzwelliges Licht stärker gebrochen wird als langwelliges. Im Gegensatz dazu beruhen Zonenplatten auf Beugungseffekten, bei denen Licht mit kurzer Wellenlänge schwächer gebeugt wird als Licht mit langer Wellenlänge. Bei geschickter Kombination von Linsen und Zonenplatten in einem Objektiv können deren Farbfehler kompensiert werden.
Fabry-Linse
[Bearbeiten]
Soll ein Objektpunkt geometrisch nicht als Bildpunkt abgebildet werden, weil zum Beispiel in einem hochempfindlichen Photometer ein flächenhafter Detektor für die Messung eines Lichtstroms eingesetzt werden soll, kann an der Stelle des Bildes eines Objektivs eine Feldblende als Austrittsluke in den Strahlengang gebracht werden. Hinter dieser Blende wird dann eine zusätzliche sammelnde Fabry-Linse angeordnet, die den Strahlengang aufweitet und das Licht auf die Detektorfläche projiziert.
Die Abbildungsparameter dieses Strahlengangs können mit Hilfe der Brennweite des Objektivs , der Brennweite der Fabry-Linse , der Öffnungsweite des Objektivs , der Öffnungsweite der Fabry-Linse , der Detektorweite sowie den geometrischen Längenparametern (Abstand zwischen Feldblende und Hauptebene der Fabry-Linse) und (Abstand zwischen Fabry-Linse und Messebene) in Beziehung gesetzt werden. Bei unendlicher Objektweite () ist die Bildweite gleich der Brennweite (), und es gilt:
Befindet sich die Feldblende genau im objektseitigen Brennpunkt der Fabry-Linse und werden die Blendenzahlen und eingeführt
- ,
vereinfachen sich diese Beziehungen zu:
- für
- für
Die Blendenzahlen von Objektiv und Fabry-Linse sind in diesem Fall also gleich, und die Detektorsweite ist identisch mit der Öffnungsweite der Fabry-Linse .
Beugungsbegrenzung
[Bearbeiten]Alle optischen Abbildungen mit Objektiven sind in der Auflösung beugungsbegrenzt, da das Auflösungsvermögen immer durch Beugung an Kanten eingeschränkt wird. Ein Objektpunkt wird also nie als Punkt abgebildet, sondern immer als Beugungsfigur, die für jeden Punkt der Abbildung, wo Beugung auftritt, mit einer Gaußschen Glockenfunktion (also einer Normalverteilung) beschrieben werden kann. Im Allgemeinen müssen alle Punkte berücksichtigt werden, an denen Beugung auftritt, und die Beugungsverteilungen aller einzelnen Punkte müssen unter Berücksichtigung der Amplituden und Phasen der komplexwertigen Wellenfunktionen überlagert werden, um das gesamte aus der Interferenz resultierende Verteilungsmuster zu erhalten.
- Beugungsscheibchen
-
Durch die Wellenoptik (Fourier-Optik) bedingte Gaußsche Normalverteilung einer endlichen Anzahl von in der Bildebene eintreffender Photonen, die von einem Objektpunkt ausgehend rein geometrisch-optisch betrachtet alle exakt in die Bildmitte abgebildet würden.
-
Berechnetes Beugungsbild einer idealen Kreislochblende. Der Durchmesser des zentralen Beugungsscheibchens ergibt sich aus der nullten Beugungsordnung, die weiteren konzentrischen Beugungsringe entstehen durch die Berücksichtigung der höheren Beugungsordnungen.
-
Photographisch aufgenommenes Beugungsbild einer 0,09 Millimeter großen, mit rotem Laserlicht beleuchteten Lochblende in 65 Millimetern Entfernung, in dem die 0. (Beugungsscheibchen in der Mitte mit dem Durchmesser von gut einem Millimeter) bis 27. Beugungsordnung (links oben) zu sehen sind.

Der Durchmesser beziehungsweise der Winkeldurchmesser eines Beugungsscheibchens, das von einer kreisförmigen Blende mit dem Durchmesser in einer Bildebene im Abstand hervorgerufen wird, die im Verhältnis zur Wellenlänge des untersuchten Lichtes weit von der Blende entfernt ist (), ergeben sich wie folgt:
Erzeugt ein Objektiv mit der Öffnungsweite eine optische Abbildung in einer Bildebene mit der Bildweite kann der Quotient dieser beiden Größen durch die Blendenzahl des Objektivs ersetzt werden:
Der Durchmesser und die Fläche des kreisförmigen Beugungsscheibchens ergeben sich dann also wie folgt:
Das Intensitätsprofil eines Beugungsscheibchens kann mit Hilfe der Bessel-Funktion erster Gattung als bestimmtes Integral über das abgeschlossene Intervall [0, π] beschrieben werden:
Die Lichtintensität senkrecht zur optischen Achse, die durch den Punkt bei x=0 geht, ergibt sich dann wie folgt, wobei lediglich eine Proportionalitätskonstante ist:
Die Beugungsscheibchen von zwei punktförmigen Objekten überlagern sich und können in der Bildebene bei zu geringem seitlichen Versatz nicht unterschieden werden. Erst ab einem Abstand vom Radius des Beugungsscheibchens (Rayleigh-Kriterium mit ) ist es es in der Praxis möglich, die beiden Bilder der beiden Objektpunkte zu unterscheiden. Je weiter die beiden Objekte auseinanderliegen, desto besser können sie im Bild unterschieden werden.
Bei einem Abstand, der dem Durchmesser des Beugungsscheibchens entspricht (), sind die beiden Objekte sehr gut zu unterscheiden, wenn sie geometrisch einwandfrei - also ohne Abbildungsfehler - abgebildet werden:
Wenn bildseitig ein maximaler Durchmesser für das Beugungsscheibchen definiert werden kann, folgt daraus unmittelbar die maximale Blendenzahl beziehungsweise bei gegebener Brennweite die minimale Öffnungsweite für das optische System der optischen Abbildung:
Durch die Beugungsbegrenzung können auch zwei dunkle Objekte vor hellem Hintergrund nicht beliebig genau aufgelöst werden. Dieser Effekt wurde zum Beispiel nach der Erfindung des Fernrohrs bei Merkur- und Venusdurchgängen vor der Sonnenscheibe beobachtet. Bei der sogenannten Tröpfchenbildung verschmilzt das Schattenbild der Planeten mit der dunklen Umgebung der Sonnenscheibe, während sich der Planet noch vollständig innerhalb der Sonnenscheibe befindet. Dass dieser Effekt umso stärker ist, je kleiner die Öffnungsweite der optischen Instrumente ist (beziehungsweise je mehr diese optischen Instrumente beugungsbegrenzt sind), war beim Merkurtransit im Mai 1832 durch die beiden deutschen Astronomen Friedrich Wilhelm Bessel und Wilhelm August Argelander nachgewiesen geworden.
- Zwei schwarze Objekte vor weißem Hintergrund
-
Streng geometrische Abbildung bei punktförmiger Berührung zweier schwarzer Kreise.
-
Tropfenphänomen im Bereich des Kontakts bei beugungsbegrenzter optischer Abbildung dieser beiden Kreise.
-
Bereich des Scheitels eines schwarzen Kreises an einer nicht berührten, senkrechten schwarzen Kante bei geometrischer Abbildung.
-
Tropfenphänomen im Bereich des Scheitels eines schwarzen Kreises an einer einer nicht berührten schwarzen Kante bei beugungsbegrenzter optischer Abbildung. Bei der scheinbaren Wölbung des oberen und des unteren Endes der senkrechten Kante nach links hin handelt es sich um eine optische Täuschung.
Wenn bei einer Kamera gefordert ist, dass der Durchmesser des Beugungsscheibchens die Größe der Bildelemente (Pixel) nicht überschreiten soll, ergibt sich beispielsweise bei einer Größe der Bildelemente von zwei Mikrometern und einer Lichtwellenlänge von 550 Nanometern eine maximale Blendenzahl von 1,5. Bei einer Brennweite von 75 Millimetern entspräche diese Blendenzahl einer Öffnungsweite von 50 Millimetern. Bei größeren Blendenzahlen als respektive kleineren Öffnungsweiten als arbeitet die Kamera beugungsbegrenzt.


In der folgenden Tabelle sind die maximalen Blendenzahlen angegeben, bei den bei verschiedenen Bilddiagonalen (respektive Bildkreisdurchmessern) und Bildauflösungen gearbeitet werden kann, wenn die quadratischen Aufnahmen bei einer Wellenlänge von 550 Nanometern nicht beugungsbegrenzt sein sollen. Werden größere Blendenzahlen als diese verwendet, sind die aufgenommenen Bilder in Bezug auf das Auflösungsvermögen des optischen Systems beugungsbegrenzt. Bei größeren Wellenlängen sind die maximalen Blendenzahlen noch kleiner, bei kurzen Wellenlängen kann auch mit etwas größeren maximalen Blendenzahlen ohne Beugungsbegrenzung gearbeitet werden. Bei Bildsensoren ohne Farbfilter oder bei unbunten Objekten beziehungsweise Abbildungen verdoppelt sich in der Bildebene die maximal erreichbare Auflösung gegenüber den in der folgenden Tabelle angegebenen Werten, da unter diesen Bedingungen in jedem Bildpunkt die vollständige gewünschte Bildinformation vorhanden ist.
| Maximale Blendenzahlen bei Bayer-Sensoren ohne Beugungsbegrenzung | ||||
| Bildauflösung in Millionen Bildpunkten | ||||
| 1,0 | 4,2 | 16,8 | 67,1 | |
| Bilddiagonale in Millimetern (Bildsensorklasse) |
||||
| 5,6 (Miniatur) | 2,9 | 1,4 | 0,72 | (0,36) |
| 11 (Kompakt) | 5,7 | 2,8 | 1,4 | 0,71 |
| 16 (1-Zoll) | 8,2 | 4,1 | 2,0 | 1,0 |
| 22 (MFT) | 11 | 5,6 | 2,8 | 1,4 |
| 27 (APS-C) | 14 | 6,9 | 3,4 | 1,7 |
| 43 (Vollformat) | 22 | 11 | 5,6 | 2,8 |
| 54 (Mittelformat) | 28 | 14 | 6,9 | 3,4 |
Auch wenn Objektive mit der Lichtstärke 0,5 gebaut werden können, werden diese nicht für photographische Zwecke eingesetzt. Objektive mit einer kleineren Blendenzahl als 0,7 haben in der Regel sehr große Abbildungsfehler (Aberration), die sich viel stärker auswirken als die Beugungsbegrenzung. Der Arbeitsbereich der Blende, bei dem sich Beugungsbegrenzung und sphärische Aberration bei der Abbildung auf der optischen Achse in der Waage halten, wird auch kritische Blende genannt (siehe unten). Hier ergibt sich das optimale Auflösungsvermögen für die entsprechende Abbildung. Im Übrigen sollte immer berücksichtigt werden, dass selbst wenn alle Abbildungsfehler auf der Achse optisch weitgehend korrigiert sind, wie zum Beispiel bei der Verwendung apochromatischer Objektive, dass immer eine Reihe von weiteren Abbildungsfehlern vorhanden ist, die das optische Auflösungsvermögen zu den Bildrändern und -ecken hin erniedrigen.
Im allgemeinen kann festgestellt werden, dass die Blendenzahl der jeweiligen kritische Blende umso kleiner ist, je kleiner die Bilddiagonale ist. Bei sehr kleinen Bilddiagonalen mit optisch gut korrigierten Objektiven, wie zum Beispiel bei hochwertigen Smartphone-Kameras, ergibt sich oft eine kritische Blendenzahl um 2,0, bei größeren Bilddiagonalen, wie zum Beispiel 43 Millimeter beim Kleinbildformat, liegt die kritische Blendenzahl oft im Bereich von 5,6.
Abhängigkeit des beugungsbegrenzten Auflösungsvermögens von der Objektweite
[Bearbeiten]
Zum Zusammenhang zwischen diesem Beugungsscheibchen in der Bildebene mit der Bildweite bei der optischen Abbildung eines Objekts mit der Objektweite über die Hauptebene und der entsprechenden minimalen geometrischen Größe in der Objektebene (synonym für "Gegenstandsebene") möge die die Abschätzung dienen, dass die Größe des Beugungsscheibchens mit Hilfe des Strahlensatzes einer Scheibe mit dem Durchmesser in der Objektebene rein geometrisch ins Verhältnis gesetzt werden kann (siehe Abbildung rechts):
- ,
wobei der Abbildungsmaßstab ist.
Den Durchmesser des Beugungsscheibchens erhält man aus der bekannten Abhängigkeit von der Wellenlänge und der Blendenzahl (siehe oben):
Bei einer Abbildung, bei der die Objektweite deutlich größer als die Brennweite ist (), ist die Bildweite nur sehr geringfügig größer als die Brennweite (daraus folgt ), so dass sich in der Objektebene G der folgende minimale Kreisdurchmesser ergibt:
Kleinere Strukturen können aufgrund der Beugungsbegrenzung nicht vollständig aufgelöst werden.
Bei einer Öffnungsweite von 100 Millimetern und bei grünem Licht mit einer Wellenlänge von 550 Nanometern ergeben sich in Abhängigkeit von der Objektweite also diese maximalen optischen Auflösungen :
| Objektweite |
Maximal auflösbare Struktur im Objektraum |
|---|---|
| 100 mm | 1,3 µm |
| 1 m | 13 µm |
| 10 m | 130 µm |
| 100 m | 1,3 mm |
| 1 km | 13 mm |
| 10 km | 130 mm |
| 100 km | 1,3 m |
| 1000 km | 13 m |
| 10000 km | 130 m |
| 100000 km | 1,3 km |
Beugungsbegrenztes Auflösungsvermögen bei Teleskopen
[Bearbeiten]Sterne können wegen ihrer großen Entfernung gar nicht aufgelöst werden und erscheinen in optischen Abbildungen daher immer als Beugungsscheibchen. Vom 300000 Kilometer entfernten Mond aus gesehen, kann die Erdoberfläche hierbei also nur in zirka vier Kilometer große Scheibchen aufgelöst werden. Geostationäre Satelliten, die einen Abstand von rund 36000 Kilometern über der Erdoberfläche haben, könnten mit einer entsprechenden Kamera nur Strukturen auflösen, die knapp fünfhundert Meter groß sind. Kameras in Satelliten in erdnäheren Umlaufbahnen von einigen 100 Kilometern Höhe haben eine Auflösung von einigen Metern. Flugzeuge in der Atmosphäre können hingegen bei ausreichend niedriger Flughöhe und hinreichend geringen atmosphärischen Störungen mit ihren Luftbildkameras durchaus optische Auflösungen im Zentimeterbereich erreichen, wie sie zum Beispiel bei modernem Navigationskartenmaterial üblich ist.
Bei Teleskopen ist die Objektweite im Verhältnis zur Brennweite in der Regel sehr groß und der kleinste Winkel zwischen zwei kontrastreichen Objekten (zum Beispiel ein Doppelstern) ergibt sich als Maß des Auflösungsvermögens aus dem halben Durchmesser des Beugungsscheibchens (siehe oben):
Für sehr kleine Winkel gilt im Bogenmaß die Näherung:
Damit ergibt sich:
Durch Substitution von folgt daraus:
Setzt man den Bildwinkel mit diesem Auflösungsvermögen ins Verhältnis, ergibt sich für die maximale Anzahl in einer Bildrichtung auflösbaren Bildpunkte :
Für die kleinen Bildwinkel, die bei Teleskopen üblicherweise erreicht werden, ergibt sich mit dem Bildkreisdurchmesser im Bogenmaß gleichermaßen die Näherung:
Damit gilt:
Für die Informationsübertragung sind zwei benachbarte Punkte unterschiedlichen Kontrast erforderlich (siehe auch Grundlagen / Modulationsübertragung), so dass die Anzahl der Linienpaare pro Bildkreisdurchmesser nur halb so groß ist:
Bei dieser Ortsfrequenz (siehe auch Ortsfrequenz) wird nur ein sehr schwacher Kontrast übertragen. Bei der doppelten Ortsfrequenz ist der Kontrastverlust durch die Beugungsbegrenzung bereits fast vernachlässigbar (siehe oben).
Bildschärfeverluste durch Abblenden
[Bearbeiten]
Anhand eines kleinen Ausschnitts einer photographischen, nicht beugungsbegrenzten Aufnahme mit einem hochwertigen und korrigierten Objektiv kann demonstriert werden, wie sich die Beugungsbegrenzung beim Abblenden auswirkt, wenn die Aufnahme mit einer größeren Blendenzahl und somit einer geringeren Öffnungsweite gemacht worden wäre. Die Aufnahme mit einer Gesamtzahl von 3456 mal 4608 Bildpunkten (16 Megapixel) ist bei einer Blendenzahl von 2,2 aufgenommen worden, wo der Durchmesser des Beugungsscheibchen mit 3 Mikrometern kleiner war als der Punktabstand auf dem Bildsensor von 3,76 Mikrometern.
Die folgende Tabelle gibt für eine mittlere Wellenlänge von 550 Nanometern die Durchmesser der Beugungsscheibchen an (sowohl auf dem Bildsensor in Mikrometern als auch im digitalen Bild in Bildpunkten), die bei verschiedenen Blendenzahlen resultieren, und in den beigefügten Bildern wurde die Auswirkung der Beugungsbegrenzung durch Gaußsche Weichzeichnung simuliert. In der rechten Spalte sind die Leistungsdichtespektren der Bilder zur Verdeutlichung der Modulationen in Abhängigkeit von den Ortsfrequenzen dargestellt. In der Mitte der Modulationsübertragungsdiagramme liegt jeweils die Ortsfrequenz null, und in den Mitten der vier Diagrammkanten beträgt die Ortsfrequenz jeweils 128 Linienpaare pro Bildausschnittshöhe. Der Bildausschnitt auf dem Bildsensor war geringfügig kleiner als ein Quadratmillimeter, und dies entspricht daher einer Ortsfrequenz von 133 Linienpaaren pro Millimeter (Lp/mm) auf dem Bildsensor beziehungsweise von 2304 Linienpaaren pro Bildhöhe (Lp/Bh) in der Originalaufnahme.
Der Strukturanteil gibt den prozentualen Anteil der in den Leistungsdichtespektren der Modulationsübertragungsdiagramme effektiv auftretenden Ortsfrequenzen an. Die maximalen effektiv auftretenden Ortsfrequenzen liegen weit unterhalb der durch die Bildauflösung vorgegebenen maximal möglichen Ortsfrequenz von 133 Lp/mm beziehungsweise von 2304 Lp/Bh (siehe auch Abschnitt Ortsfrequenz).
Das Originalbild mit einer maximal effektiv auftretenden Ortsfrequenz von 82 Lp/mm beziehungsweise von 1420 Lp/Bh kann folglich bei sehr geringem Informationsverlust auch in einem digitalen Bild mit einer Bildauflösung von nur sechs Megapixel gespeichert werden, bei einer entsprechenden Aufnahme bei der Blendenzahl 32 mit einer maximal effektiv auftretenden Ortsfrequenz von 23 Lp/mm respektive von 400 Lp/Bh wäre die für die Informationsübertragung maximal erforderliche Bildauflösung sogar nur ein halbes Megapixel:
Da im optischen Bild keine Strukturen auftreten, die kleiner sind als die Beugungsscheibchen, kann die Kenntnis der Durchmesser der Beugungsscheibchen ausgenutzt werden. So können zum Beispiel ohne weiteres Annahmen über die maximal auftretende Ortsfrequenz des Bildrauschens oder über die maximale Steilheit von Kanten gemacht werden, die zur rechnerischen Verbesserung von digitalen Bilddaten eingesetzt werden können.
Beugungseffekte bei hellen Lichtquellen
[Bearbeiten]
Wenn eine helle nahezu punktförmige Lichtquelle abgebildet wird, kommt es an allen Blenden im Strahlengang zu einer in der Abbildung mehr oder weniger stark wahrnehmbaren Beugung. Kreisförmige Blenden erzeugen hierbei kreisförmige Beugungsscheibchen.
Viele Objektive sind mit verstellbaren Irisblenden ausgestattet, die aus mehreren gleichartigen Lamellen bestehen. Je weiter solche Objektive abgeblendet werden, desto stärker nähert sich die Blendenform einem Polygon an, das genauso viele Kanten beziehungsweise Ecken hat, wie es Blendenlamellen gibt. Die dann zunehmend geradlinig werdenden Kanten der Irisblende erzeugen senkrecht zu den jeweiligen Kanten rechts und links kleine Beugungsstriche, die sich in der Abbildung zu einem Strahlenkranz überlagern. Wenn die Anzahl der Blendenlamellen wie üblich ungerade ist, entstehen doppelt so viele Strahlen wie es Blendenlamellen gibt, ansonsten sind es genauso viele, da die Beugungsstriche der gegenüberliegenden Blendenkanten dann deckungsgleich sind.
Im folgenden Bild ist die optische Abbildung des Planeten Venus am Nachthimmel mit einem auf die Blendenzahl 4 abgeblendeten Objektiv mit 9 Blendenlamellen und somit 18 radial von der Venus weggehenden Strahlen zu sehen:

Güte der optischen Abbildung
[Bearbeiten]
kissenförmige Verzeichnung, Vignettierung und Farbquerfehler. Die beiden konzentrischen weißen Rechtecke symbolisieren zwei verschieden große, zentrale Bildausschnitte innerhalb des Bildkreises des Objektivs, bei denen diese Abbildungsfehler unterschiedlich stark ausgeprägt sind. Alle Abbildungsfehler sind üblicherweise am Bildkreisrand größer als in der Bildmitte. Die optische Auflösung ist bei der Verwendung desselben Objektivs beim kleinen Bildausschnitt im Vergleich zum großen Bildausschnitt in Bezug auf die genutzte Bildgröße ebenfalls entsprechend geringer.
Die Kontrastübertragung einer optischen Abbildung wird stets, mit zunehmenden Ortsfrequenzen zunehmend stark durch Beugung an Kanten begrenzt (siehe oben). Da alle optischen System über Kanten verfügen, wie zum Beispiel Blendenöffnungen oder Einfassungen, kann diese Beschränkung durch geeignete Maßnahmen zwar verringert, aber nie vollständig ausgeschaltet werden.
Ferner können auch gerichtete oder diffuse Reflexionen innerhalb des abbildenden Systems die Kontrastübertragung vermindern, da sie in dunklen Bildbereichen Falschlicht hervorrufen.
Siehe hierzu auch: Modulationsübertragung
Häufig kommen andere Abbildungsfehler deutlich stärker zum Tragen, von denen einige im Folgenden erläutert werden. Sie betreffen nicht unmittelbar die Kontrastübertragung einer optischen Abbildung, sondern werden durch Abschattungen oder durch geometrische Verzerrungen verursacht.
In der Regel ist die optische Güte in der Bildmitte (also auf der optischen Achse bei der Bildhöhe null) am größten und nimmt zum Bildrand (also mit wachsender Bildhöhe) immer mehr ab.
Randlichtabfall
[Bearbeiten]
Ebenso unvermeidlich ist der natürliche Randlichtabfall, der in optischen Systemen durch die geometrische Projektion in verschiedene Winkel zustande kommt. Der Lichtstrom von einer lichtemittierenden Fläche durch eine begrenzende kreisrunde Referenzfläche auf einer Projektionsfläche reduziert sich hierbei in Bezug auf den Lichtstrom entlang der optischen Achse in Abhängigkeit vom betrachteten Winkel zur optischen Achse wie folgt:
Für die effektive Beleuchtungsstärke in einer optischen Projektion unter verschiedenen Winkeln zur optischen Achse in Bezug auf die Beleuchtungsstärke in der Projektion auf der optischen Achse ergibt sich analog:
Die korrigierte Helligkeit in einem Bildpunkt beim Ortsvektor ergibt sich dann aus der dazugehörigen gemessenen Helligkeit zu:
Siehe auch Bildkoordinaten.
Die Kompensation des Randlichtabfalls kann direkt nach der Aufnahme und vor dem Speichern der Bilddaten von der Firmware einer Kamera durchgeführt werden. Wenn die Information in den Metadaten eines digitalen Bildes gespeichert wurde oder aus anderen Quellen beschafft werden kann, kann die Kompensation auch nachträglich mit Hilfe einer geeigneten Bildbearbeitungssoftware berechnet werden.
Vignettierung
[Bearbeiten]
Kommen im Strahlengang mehrere abschattende Blenden oder Einfassungen zum Tragen, verstärkt sich der Helligkeitsabfall in den Bildecken über das Maß des Randlichtabfalls hinaus. Dies wird Vignettierung genannt und kann dazu führen, dass in den Bildecken praktisch kaum noch ein Bildsignal ausgewertet werden kann.
Wird die tatsächlich genutzte Bildkreis einer optischen Abbildung auf einen hinreichend kleinen Bildsensor reduziert, wird der Helligkeitsverlust am Bildrand geringer.
Siehe hierzu auch: Zweidimensionale Bildsensoren
Auch die Vignettierung kann rechnerisch korrigiert werden, wenn die entsprechenden Bildparameter während der Aufnahme und die Objektiveigenschaften bekannt sind.
Sphärische Aberration
[Bearbeiten]
Der Öffnungsfehler (sphärische Aberration) hängt von der maximalen Einfallshöhe der Strahlen ab, die zu einer optischen Abbildung beitragen. Von einem Objektipukt ausgehende Strahlen mit großer Einfallshöhe erzeugen aufgrund des Öffnungsfehlers in der Bildebene keinen geometrischen Bildpunkt, sondern einen Zerstreuungskreis und begrenzen somit die erzielbare optische Auflösung.
Die Einfallshöhe kann hierbei maximal halb so groß werden, wie die Öffnungsweite des verwendeten Objektivs. Der Öffnungsfehler kann mit einer Aperturblende durch Abblenden auf paraxiale Strahlen - also Strahlen mit geringer Einfallshöhe - reduziert, oder durch den Einsatz von asphärischen Linsen korrigiert werden, so dass auch Strahlen mit großer Einfallshöhe bei der Ablenkung keine Schnittweitenverkürzung erfahren.

Mit zunehmender Einfallshöhe H nimmt bei sphärischen Linsen die von der Hauptebene gemessene Schnittweite immer weiter ab, einfallende Strahlen mit großen Einfallshöhen können innerhalb der Linse sogar totalreflektiert werden und tragen dann gar nicht mehr zur optischen Abbildung bei. Nur parallel zur optischen Achse einfallende, achsnahe Strahlen schneiden die optische Achse in die Nähe des Brennpunktes. Bei asphärischen Linsen ergibt sich im Idealfall für alle Einfallshöhen dieselbe von der Hauptebene gemessene Schnittweite, und alle gebrochenen Strahlen schneiden die optische Achse im Brennpunkt F.
Berechnung an plankonvexer Linse
[Bearbeiten]

Anhand einer plankonvexen Linse kann die Form der entsprechenden asphärischen Oberfläche verhältnismäßig leicht veranschaulicht werden. Betrachtet man eine optische Abbildung aus dem Unendlichen mit parallelem, monochromatischem Licht durch eine solche Linse mit dem Krümmungsradius bei der Einfallshöhe , ergibt sich die in nebenstehender Abbildung dargestellte Situation.
Zur Berechnung der asphärischen Oberfläche können Lichtstrahlen betrachtet werden, die mit der Einfallshöhe parallel zur optischen Achse auf die objektseitige, plane Linsenfläche fallen. Diese werden beim Eintritt in das optisch dichtere Medium des Linsenmaterials mit dem Brechungsindex nicht gebrochen, da sie senkrecht auftreffen. Bildseitig bilden diese Strahlen zum Oberflächenlot der Linse in der Linse den Winkel und außerhalb der Linse den Winkel . Diese Winkel verhalten sich wie durch das Snelliussche Brechungsgesetz beschrieben. Dabei gelten die folgenden Beziehungen:
Die optische Achse schneiden diese Strahlen dann unter dem Winkel
Für paraxiale Strahlen (also für ) ergibt sich eine bildseitige Schnittweite respektive Brennweite von:
- ,
wobei der Radius im Scheitel der Linse auf der optischen Achse ist.
Die Pfeilhöhe , gemessen von der Hauptebene der Linse, kann dann in Abhängigkeit von der Einfallshöhe mit Hilfe einiger Hilfsgrößen ausgehend von und in Schritten von iterativ ermittelt werden:
Für die Schnittweite vom Scheitelpunkt der Kugel mit dem Radius auf der optischen Achse gilt:
Schließlich ergibt sich der Scheitelabstand von der Hauptebene aus der Differenz dieser Schnittweite mit der Schnittweite bei paraxialen Strahlen :
Beispiel

In der folgenden Tabelle sind einige auf diese Weise berechnete Beispielwerte für , und den einheitenlosen Längenmaßen und angegeben. Mit zunehmender Einfallshöhe werden die Krümmungsradien immer größer und sowohl die Mittelpunkte als auch Scheitelpunkte der entsprechenden Kreise entfernen sich objektseitig immer weiter von der Hauptebene.
| Einfallshöhe |
Pfeilhöhe |
Radius |
Scheitel- abstand |
Winkel in ° |
Winkel in ° |
Winkel in ° |
|---|---|---|---|---|---|---|
| 0 | 0,0 | 100,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| 10 | 0,5 | 101,1 | 0,0 | 5,7 | 8,5 | 2,9 |
| 20 | 2,0 | 104,4 | 0,1 | 11,0 | 16,7 | 5,7 |
| 30 | 4,5 | 109,7 | 0,3 | 15,9 | 24,2 | 8,3 |
| 40 | 7,8 | 116,7 | 0,8 | 20,0 | 30,9 | 10,9 |
| 50 | 12,0 | 125,2 | 1,6 | 23,5 | 36,8 | 13,3 |
| 60 | 16,9 | 134,8 | 2,8 | 26,4 | 41,9 | 15,5 |
| 70 | 22,4 | 145,3 | 4,5 | 28,8 | 46,3 | 17,5 |
| 80 | 28,5 | 156,6 | 6,5 | 30,7 | 50,0 | 19,3 |
| 90 | 34,9 | 168,5 | 8,9 | 32,3 | 53,2 | 21,0 |
| 100 | 41,8 | 180,8 | 11,6 | 33,6 | 56,0 | 22,5 |
| 110 | 48,9 | 193,6 | 14,6 | 34,6 | 58,5 | 23,8 |
| 120 | 56,3 | 206,6 | 17,9 | 35,5 | 60,6 | 25,1 |
| 130 | 63,9 | 219,9 | 21,4 | 36,2 | 62,5 | 26,2 |
| 140 | 71,7 | 233,4 | 25,0 | 36,9 | 64,1 | 27,3 |
| 150 | 79,6 | 247,1 | 28,9 | 37,4 | 65,6 | 28,2 |
| 160 | 87,7 | 260,9 | 32,9 | 37,8 | 66,9 | 29,1 |
| 170 | 95,8 | 274,9 | 37,0 | 38,2 | 68,1 | 29,9 |
| 180 | 104,1 | 288,9 | 41,2 | 38,5 | 69,2 | 30,6 |
| 190 | 112,4 | 303,0 | 45,5 | 38,8 | 70,1 | 31,3 |
| 200 | 120,9 | 317,3 | 49,9 | 39,1 | 71,0 | 31,9 |
Bis zu einer Einfallshöhe von 140 entspricht die konvexe Oberfläche dieser Linse nach DIN ISO 10110-12 ohne weitere asphärische Parameter in den höheren Gliedern relativ genau der Beziehung für einen Hyperboloiden mit der konischen Konstante :
Verzeichnung
[Bearbeiten]Verzeichnung kommt zustande, wenn sich der Abbildungsmaßstab für verschiedene Bildhöhen (also für verschiedene Abstände der Bildpunkte von der optischen Achse) ändert. Mit korrigierten Objektiven oder mit telezentrischen Objektiven lassen sich solche Abweichungen vermeiden, und wenn der Abbildungsmaßstab über das gesamte Bildfeld konstant ist, wird eine solche Abbildung verzeichnungsfrei genannt.
Siehe hierzu auch: Abbildungsmaßstab und Telezentrie
Bei einfachen Objektivkonstruktionen nimmt der Betrag der Verzeichnung mit zunehmender Bildhöhe typischerweise monoton und stetig zu:
- Verzeichnung von quadratischen Objekten bei optischen Abbildungen
-
Kissenförmig verzeichnete Abbildung mit nach außen hin zunehmendem Abbildungsmaßstab
-
Verzeichnungsfreie Abbildung mit konstantem Abbildungsmaßstab
-
Tonnenförmig verzeichnete Abbildung mit nach außen hin abnehmendem Abbildungsmaßstab
Nimmt der Abbildungsmaßstab mit zunehmender Bildhöhe kontinuierlich zu, wird von einer kissenförmigen Verzeichnung oder Kissenverzeichnung gesprochen, nimmt er kontinuierlich ab, wird von einer tonnenförmigen Verzeichnung oder Tonnenverzeichnung gesprochen.
Verzeichnung tritt bei Linsen und unkorrigierten Objektiven mit sphärischer Aberration auf, wenn die abbildenden Strahlenbündel vor oder hinter den Hauptebenen durch Blenden eingeengt werden. Dabei ist es nicht wesentlich, wie groß oder wie klein diese Blende ist. Liegt die das Strahlenbündel einengende Blende vor der Hauptebene, kommt es zu einer Tonnenverzeichnung, liegt eine solche Blende hinter der Hauptebene, kommt es zu einer Kissenverzeichnung:
- Zur Verzeichnung bei optischen Abbildungen in der Bildebene B
-
Kissenförmig verzeichnete Abbildung mit nach außen hin zunehmendem Abbildungsmaßstab (dunkelblau), da die Hauptstrahlen mit konstantem Abbildungsmaßstab (blau) von der Blende hinter der Hauptebene H ausgeblendet werden.
-
Tonnenförmig verzeichnete Abbildung mit nach außen hin abnehmendem Abbildungsmaßstab (dunkelblau), da die Hauptstrahlen mit konstantem Abbildungsmaßstab (blau) von der Blende vor der Hauptebene H ausgeblendet werden.
Die optische Achse markiert in einer Abbildung das Verzeichnungszentrum. Rechnerisch kann die Verzeichnung mit der Aufnahme von zwei parallelen Geraden bestimmt werden. Die eine Gerade liegt hierbei in der Regel senkrecht zur optischen Achse und hat in diesem Punkt die Objekthöhe null. Diese Gerade erscheint im Bild ebenfalls als Gerade mit der Bildhöhe null. Der Abstand zur zweiten Geraden entspricht der Bildhöhe, bei der die Verzeichnung bestimmt wird. Diese Gerade wird bei vorhandener Verzeichnung jedoch nicht als Gerade abgebildet sondern gebogen.
Traditionell wird die Verzeichnung häufig in Prozent angegeben. Hierzu wird häufig ein einfacher Standard der Europäischen Rundfunkunion (European Broadcasting Union (EBU)) verwendet, der sie als das Verhältnis der Differenz zweier Höhen im Bild (in der Skizze gilt hierfür ) zu der von der optischen Achse gemessenen Höhe bestimmt:
Dieses Vorgehen erfordert jedoch eine große Sorgfalt mit Blick auf die Symmetrie der Abbildung, da bei nicht hinreichend genauer Zentrierung der Objektive oder des Messaufbaus in verschiedenen Bildbereichen mit gleicher Bildhöhe verschiedene Werte für die Verzeichnung ermittelt werden.
Nach einem Industriestandard der Standard Mobile Imaging Architecture (SMIA) wird die Verzeichnung durch den Mittelwert zweier Höhen und , die auf gegenüberliegenden Seiten der optischen Achse liegen, wie folgt auf die Höhe durch die optische Achse in der Bildmitte bezogen:
Wenn alle Differenzen , wie bei der Betrachtung der Verzeichnung nach der EBU gleich groß sind, gilt:
Die Verzeichnung kann auf diese Weise natürlich auch in horizontaler Richtung oder für jeden anderen Azimutwinkel bestimmt werden.
Es gibt weitere Varianten zur Bestimmung, bei denen wie in der ISO 9039-2008 bei maximaler Bildhöhe vier Werte in den Bildecken gemessen und gemittelt werden und mit der bei halber Bildhöhe ermittelten Verzeichnung ins Verhältnis gesetzt werden. Dies führt zum Beispiel bei vielen modernen Zoom-Objektiven allerdings dazu, dass dieses Verhältnis unendlich werden kann. In einer optischen Abbildung über mehrere Hauptebenen können nämlich auch gleichzeitig kissenförmige und tonnenförmige Verzeichnungen auftreten. Solche Objektive sind dann nicht notwendigerweise auf der optischen Achse, sondern bei einer Bildhöhe im mittleren Bildfeldbereich - möglicherweise also auch genau bei halber Bildhöhe - verzeichnungsfrei.
Verzeichnung kann mit geometrischen Transformationen mit variablem Maßstab rechnerisch kompensiert werden, wenn die entsprechenden Bildparameter während der Aufnahme und die Objektiveigenschaften bekannt sind. Im Idealfall ist ein in der Bildebene senkrecht zur optischen Achse liegender Bildvektor mit dem Ursprung auf der optischen Achse mit dem konstanten Abbildungsmaßstab proportional zum in der Objektebene senkrecht zur optischen Achse liegenden Objektvektor , der seinen Ursprung ebenfalls auf der optischen Achse hat.
Die zur Kompensation der Verzeichnung transformierten Bildvektoren eines Punktes im Bild ergeben sich dann aus gemessenen Bildvektoren eines Bildpunkts wie folgt, wobei der einheitenlose Faktor nicht konstant ist, sondern in der Regel eine Funktion der Bildhöhe ist:
Siehe auch Bildkoordinaten.
Der von der Bildhöhe abhängige effektive Abbildungsmaßstab beträgt somit:
Für die verzeichnungsfreie Bildhöhe gilt dann:
und somit
Eine solche Transformation kann gegebenenfalls von der Firmware einer Kamera oder später mit Hilfe einer geeigneten Bildbearbeitungssoftware durchgeführt werden. Nach der Transformation sind die Bildkanten nicht mehr gerade und werden daher üblicherweise so beschnitten, so dass wieder ein rechteckiger Bildausschnitt entsteht und somit Bildinformation verloren geht: bei kissenförmiger Verzeichnung in den Bildecken oder bei tonnenförmiger Verzeichnung an den Bildkanten.
Bildfeldwölbung
[Bearbeiten]
Eine weitere häufig Folge der sphärischen Aberration ist die Bildfeldwölbung. Hierbei liegen die Bildpunkte nicht in einer Ebene, die senkrecht zur optischen Achse steht, sondern auf einer gekrümmten, rotationssymmetrischen Fläche, die die ideale Bildebene auf der optischen Achse berührt.
In der Regel ist die Schnittweite hinter der Hauptebene einer sammelnden Optik hierbei umso kürzer, je größer die Bildhöhe ist. Ein auf der optischen Achse scharfgestelltes Bild eines Objekts mit konstanter Objektweite wird bei einer ebenen Bildfläche zu den Rändern hin durch die wachsenden Zerstreuungskreisdurchmesser der Bildpunktstrahlen also zunehmend unschärfer abgebildet. In diesen Fällen wir oft bei halber Bildhöhe scharfgestellt, da die Bildpunkte auf der optischen Achse und an den Bildrändern dann weniger unscharf sind, als die Bildpunkte am Rand, wenn auf die Bildmitte scharfgestellt wird.
Wird die Projektionsfläche entsprechend der Bildfeldwölbung angepasst, können alle Bildpunkte geometrisch scharf abgebildet werden. Daher gibt es spezielle Bildsensoren, die entsprechend gestaltet sind.
Kritische Blende
[Bearbeiten]Wenn die Bildschärfe optimiert werden soll, ist am Objektiv die kritische Blende einzustellen, bei der die Schärfe weder durch die Beugung an der Blende (also bei möglichst großer Öffnungsweite) noch durch den Öffnungsfehler (also bei möglichst kleiner Öffnungsweite) zu stark eingeschränkt wird. Sammelnde Objektivlinsen haben in der Regel eine geringere sphärische Aberration, wenn die Oberfläche mit der schwächeren Krümmung bildseitig angeordnet wird.
Berechnung an plankonvexer Linse
[Bearbeiten]
Anhand einer plankonvexen, sphärischen Linse kann die kritische Blende verhältnismäßig leicht veranschaulicht werden. Betrachtet man eine optische Abbildung aus dem Unendlichen mit parallelem, monochromatischem Licht der Wellenlänge durch eine solche Linse mit dem Krümmungsradius und der Brennweite , ergibt sich die in nebenstehender Abbildung dargestellte Situation.
Durch Beugung ergibt sich in der Bildebene ein Beugungsscheibchen mit dem Durchmesser
- ,
wobei die Eintrittspupille der optischen Abbildung und die Blendenzahl sind. Die Größe des Beugungsscheibchens ist also proportional zur Blendenzahl.
Zur Berechnung der sphärischen Aberration können Lichtstrahlen betrachtet werden, die mit der Einfallshöhe
parallel zur optischen Achse auf die objektseitige, plane Linsenfläche fallen. Diese werden beim Eintritt in das optisch dichtere Medium des Linsenmaterials mit dem Brechungsindex nicht gebrochen, da sie senkrecht auftreffen. Bildseitig bilden diese Strahlen zum Oberflächenlot der Linse in der Linse den Winkel und außerhalb der Linse den Winkel und werden entsprechend dem Snelliusschen Brechungsgesetz gebrochen. Dabei gilt:
und
Die optische Achse schneiden diese Strahlen dann unter dem Winkel . Die bildseitige Schnittweite , gemessen vom Scheitelpunkt der Linse, ergibt sich dann in Abhängigkeit von der Einfallshöhe mit Hilfe des Sinussatzes zu:
Für paraxiale Strahlen (also für ) vereinfacht sich diese Beziehung durch die Bildung des Grenzwertes zu:
- respektive ,
wobei die Brennweite und die Schnittweite der Linse bei paraxialen Strahlen (also bei ) dann identisch sind.
Aus der Bedingung für die Totalreflexion innerhalb der Linse (das Argument vom Arkussinus des Winkels darf nicht größer als eins werden) ergibt sich die minimal mögliche Blendenzahl :
Im Folgenden wird mit dieser Zusammenfassung weitergerechnet:

Unter Verwendung der Blendenzahl und der Brennweite ergibt sich die Schnittweite zu:
Durch die sphärische Aberration verschiebt sich der Schnittpunkt der hinter der Linse gebrochenen Strahlen mit der optischen Achse umso näher an die Linse, je größer die Einfallshöhe ist. In der Brennebene im Abstand vom Scheitelpunkt der Linse ergibt sich daher keine punktförmige Abbildung mehr, sondern ein Zerstreuungskreis mit dem Durchmesser :
An dieser Stelle sei explizit darauf hingewiesen, dass diese Betrachtungen nur für optische Abbildungen direkt auf der optischen Achse gültig sind. Sobald Objektpunkte von Gegenständen, die sich nicht auf der optischen Achse befinden, abgebildet werden, ergeben sich bei der hier betrachteten plankonvexen Linsengeometrie starke Abbildungsfehler.
Näherung
[Bearbeiten]Mit den Näherungen für hinreichend kleine im Bogenmaß
ergibt sich die folgende Näherungsgleichung für den von der Blendenzahl abhängigen Zerstreuungskreisdurchmesser :
Eine für kleine Blendenzahlen weniger genaue Näherung kann mit einer Reihenentwicklung für den Arkussinus bestimmt werden:
Damit vereinfacht sich die Gleichung für den Zerstreuungskreisdurchmesser folgendermaßen:
Bei gegebener Brennweite beziehungsweise bei gegebenem Radius und gegebener Brechzahl der plankonvexen Linse wächst der Zerstreuungskreisdurchmesser also mit dem Kehrwert der dritten Potenz der Blendenzahl .
Beispiel
[Bearbeiten]
Bei einer Wellenlänge im Grünen von 550 Nanometern ergibt sich der Durchmesser des Beugungsscheibchens (Airy-Scheibchen) in Abhängigkeit von der Blendenzahl zu:
Der Durchmesser des Beugungsscheibchens ist also proportional zur Blendenzahl.
Der Durchmesser des Zerstreuungskreises wird mit zunehmender Blendenzahl jedoch kleiner und dies sogar überproportional (und zwar in Näherung und insbesondere für zunehmende Blendenzahlen mit der dritten Potenz des Kehrwerts (siehe oben unter "Näherung")). Der Betrag der Steigung nimmt in der in der vertikalen Koordinatenachse logarithmischen graphischen Darstellung (siehe rechts) demzufolge kontinuierlich ab, wobei sich die Funktion für große k asymptotisch der horizontalen Achse nähert.
Bei einem Brechungsindex und einem Krümmungsradius von 100 Millimetern ergibt sich also eine Brennweite von 200 Millimetern. Die kleinste Grenze für die Blendenzahl wäre hier . Die Näherung für den Zerstreuungskreisdurchmesser ergibt sich bei diesen Werten zu:
Für verschiedene größere Blendenzahlen ergeben sich dann die in der folgenden Tabelle angegebenen Eintrittspupillen und die Durchmesser für das Beugungsscheibchen und für den Zerstreuungskreis:
| Blendenzahl |
Eintrittspupille in mm |
Winkel in ° |
Winkel in ° |
Durchmesser Beugungsscheibchen in µm |
Durchmesser Zerstreuungskreis in µm |
|---|---|---|---|---|---|
| 2,0 | 100,0 | 30,0 | 48,6 | 3 | 43553 |
| 2,8 | 70,7 | 20,7 | 32,0 | 4 | 11970 |
| 4,0 | 50,0 | 14,5 | 22,0 | 5 | 3835 |
| 5,7 | 35,4 | 10,2 | 15,4 | 8 | 1297 |
| 8,0 | 25,0 | 7,2 | 10,8 | 11 | 449 |
| 11,3 | 17,7 | 5,1 | 7,6 | 15 | 157 |
| 16,0 | 12,5 | 3,6 | 5,4 | 21 | 55 |
| 22,6 | 8,8 | 2,5 | 3,8 | 30 | 19 |
| 32,0 | 6,3 | 1,8 | 2,7 | 43 | 7 |
Das Minimum der Unschärfe liegt nicht notwendigerweise auf dem Schnittpunkt der Funktionen (die Summe der beiden Durchmesser beträgt im Beispiel bei der Blendenzahl 20 etwa 55 Mikrometer). Mit der Annahme, dass die Summe der beiden Durchmesser minimal sein soll, liegt sie Blendenzahl der kritischen Blende bei dieser optischen Abbildung bei Blende 26,7. Die Summe der beiden Durchmesser beträgt hier 47,8 Mikrometer; der Durchmesser des Beugungsscheibchen beträgt dann 36,4 Mikrometer und der des Zerstreuungskreises 11,4 Mikrometer. Die Blendenzahl 26,7 entspricht im oben angegebenen Beispiel einer Blendenöffnung D von 7,5 Millimetern.
Chromatische Aberration
[Bearbeiten]

Bei der chromatischen Aberration wird unterschieden zwischen dem Farblängsfehler, bei dem sich die Schnittweite mit der Wellenlänge ändert, und dem Farbquerfehler, bei dem sich der Abbildungsmaßstab mit der Wellenlänge ändert. Diese Farbfehler beruhen auf der Dispersion der eingesetzten Gläser, bei der blaues Licht stärker als rotes Licht gebrochen wird.
Diese Fehler können durch die Kombination unterschiedlich brechender und dispergierender Materialien kompensiert werden. Achromaten haben mindestens zwei Linsen und sind für zwei Wellenlängen korrigiert (üblicherweise für lang- und kurzwelliges Licht, also im Roten und im Blauen), bei Apochromaten, die mindestens aus drei Linsen bestehen, ist die Schnittweite sogar bei drei verschiedenen Wellenlängen identisch (üblicherweise für alle drei Primärfarben, also rot, grün und blau). Die hierfür eingesetzten Glassorten unterscheiden sich zum einen im Brechungsindex und zum anderen bei der Abbe-Zahl , die wie folgt definiert ist:
Hierbei stehen die drei Indizes am Brechungsindex für die folgenden Lichtwellenlängen:
- : Brechzahl im Roten bei
- : Brechzahl im Grünen bei
- : Brechzahl im Blauen bei
Kronglas hat typischerweise einen Brechungsindex von 1,5 bis 1,6 und eine Abbe-Zahl, die größer als 50 ist, was einer geringen Dispersion entspricht.
Flintglas hat typischerweise einen Brechungsindex von 1,5 bis 2,0 und eine Abbe-Zahl, die kleiner als 50 ist, was einer starken Dispersion entspricht.
-
Farblängsfehler durch Dispersion bei einer optischen Abbildung von weißem Licht
-
Farbquerfehler bei der optischen Abbildung von weißen, zur optischen Achse zentrierten Kreisen mit verschiedenen Durchmessern
Der Farbquerfehler kann auch rechnerisch kompensiert werden, wenn bei Farbaufnahmen die Teilbilder für die verschiedenen Farbkanäle mit geeigneten Skalierungsfaktoren transformiert werden. Bei einer Farbaufnahme mit den Primärfarben rot, grün und blau (RGB) und den entsprechenden Skalierungsfaktoren , und ergeben sich die korrigierten Ortsvektoren , und zu:
Hierbei gilt üblicherweise:
Siehe auch Bildkoordinaten.
Nach der Transformation sind die Bildkanten nicht mehr deckungsgleich und werden daher üblicherweise auf die Begrenzung der kleinsten Teilfläche beschnitten.
Bei Aufnahmen mit Licht aus einem engen Wellenlängenbereich kann die chromatische Aberration vernachlässigt werden. Dies kann zum Beispiel mit geeigneten monochromatischen Leuchtmitteln, wie Leuchtdioden oder Lasern sowie durch die Verwendung von Interferenzfiltern realisiert werden.
Schärfentiefe
[Bearbeiten]Der Schärfentiefebereich, bei dem Objektpunkte in verschiedenen Objektweiten hinreichend scharf abgebildet werden, wird durch die förderliche Blende realisiert, bei der in der optischen Abbildung alle geometrisch aus dem Objektraum abgebildeten Punkte einen festgelegten, maximalen Zerstreuungskreisdurchmesser nicht überschreiten.
Falls keine absoluten Vorgaben für den maximalen Zerstreuungskreisdurchmesser vorliegen, kann dieser unter der Verwendung der Anzahl der mindestens zu unterscheidenden Bildpunkte auf dem Bildkreisdurchmesser definiert werden:
Falls die optische Abbildung nicht digital oder maschinell weiterverarbeitet, sondern mit der Auflösung des menschlichen Auges betrachtet werden soll, kann die Anzahl der mindestens zu unterscheidenden Bildpunkte auf der Bilddiagonale wie folgt abgeschätzt werden:
Die Schärfentiefe ist eine Funktion des akzeptablen Zerstreuungskreisdurchmessers , der geometrisch scharf eingestellten Objektweite sowie der Brennweite und der Blendenzahl der optischen Abbildung. Sie ergibt sich als Längenmaß aus der Differenz der Fernpunktentfernung und der Nahpunktentfernung , die beide geometrisch als Zerstreuungskreis mit dem Durchmesser abgebildet werden:
Alle Objektpunkte zwischen dem Fernpunkt und dem Nahpunkt werden geometrisch mit Zerstreuungskreisdurchmessern abgebildet, die kleiner sind als der maximalen Zerstreuungskreisdurchmesser .
Hyperfokale Entfernung
[Bearbeiten]
Zur Bestimmung von Nahpunkt und Fernpunkt kann die hyperfokale Entfernung eingeführt werden. Wird ein entozentrisches Objektiv auf die hyperfokale Entfernung eingestellt, werden alle Objekte zwischen der halben hyperfokalen Entfernung und unendlich hinreichend scharf abgebildet. Hierfür kann anhand der beiden ähnlichen Dreiecke die folgende Beziehung mit der Brennweite , der Objektweite , der Bildweite , der Blendenzahl und dem in der Bildweite auftretenden Zerstreuungskreisdurchmesser aufgestellt werden:
Für die Bildweite gilt nach Umformung sowie entsprechend der Abbildungsgleichung:
Diese Beziehung kann nun nach der Objektweite aufgelöst werden:
Die hyperfokale Entfernung berechnet sich aus der Brennweite , der Blendenzahl und dem in der Bildebene festzulegenden maximalen Zerstreuungskreisdurchmesser wie folgt:
Liegt ein Objektpunkt in einer Objektweite zwischen der halben hyperfokalen Entfernung und dem Unendlichen, wird dieser in der Bildebene also mit einem Zerstreuungskreisdurchmesser abgebildet, der kleiner als ist:
Die Schärfentiefe ist in diesem Fall wegen der unendlichen Fernpunktentfernung ebenfalls unendlich.
Viele Kameras sind mit entsprechenden Fixfokusobjektiven ausgestattet, die keine Veränderung der Scharfstellung erlauben.
Nahpunkt
[Bearbeiten]Die Nahpunktentfernung beschreibt die Objektweite, bei der nahe Objekte noch hinreichend scharf abgebildet werden, wenn das Objektiv auf die Objektweite eingestellt ist:
Wird die Objektweite für ein abbildendes System auf die hyperfokale Entfernung eingestellt, ergibt sich für den Nahpunkt also exakt:
Wird die Objektweite für ein abbildendes System auf dessen Brennweite eingestellt, ergibt sich für den Nahpunktentfernung exakt die Brennweite:
Wird die Objektweite für ein abbildendes System auf unendlich eingestellt, ergibt sich für den Nahpunktentfernung die hyperfokale Entfernung minus der Brennweite:
Da die hyperfokale Entfernung in der Regel wegen der Erfüllung der Bedingung deutlich größer ist als die Brennweite, gilt näherungsweise:
Fernpunkt
[Bearbeiten]Die Fernpunktentfernung beschreibt die Objektweite, bei der ferne Objekte noch hinreichend scharf abgebildet werden, wenn das Objektiv auf die Objektweite eingestellt ist:
Wird die Objektweite für ein abbildendes System auf die hyperfokale Entfernung oder noch größere Entfernungen eingestellt, ergibt sich für die Fernpunktentfernung also:
Wird die Objektweite für ein abbildendes System auf dessen Brennweite eingestellt, ergibt sich für die Fernpunktentfernung der gleiche Wert wie für die Nahpunktentfernung, und die Schärfentiefe ist somit null:
Schärfentiefebereich
[Bearbeiten]Mit der Hilfsgröße
- mit beziehungsweise
ergibt sich aus der Differenz von Fernpunktentfernung und Nahpunktentfernung die Schärfentiefe wie folgt:
In der Praxis kann häufig die folgende Annahme gemacht werden:
- beziehungsweise
Unter dieser Voraussetzung vereinfachen sich die Bestimmung der Schärfentiefe und der Hilfsgröße :
- beziehungsweise
Bei vorgegebener Schärfentiefe kann für eine bestimmte Objektweite die Hilfsgröße durch Lösen der entsprechenden quadratischen Gleichung bestimmt werden:
Wenn die Brennweite ebenfalls vorgegeben ist, kann hieraus unmittelbar die dazugehörige maximale hyperfokale Entfernung berechnet werden:
Wenn der maximale Zerstreuungskreisdurchmesser festgelegt ist und diese Gleichung mit der Definitionsgleichung für die hyperfokale Entfernung (siehe oben) gleichgesetzt wird, ergibt sich für die minimale Blendenzahl schließlich:
Mit der oben genannten, für die meisten praktischen Fälle geltenden Einschränkung kann die minimale Blendenzahl gut wie folgt abgeschätzt werden:
Unter Verwendung des Abbildungsmaßstabs vereinfacht sich diese Gleichung zu:

Somit kann unter den genannten Voraussetzungen bei vorgegebener Blendenzahl auch die Schärfentiefe relativ einfach abgeschätzt werden:
Für größere Objektweiten mit und mit der Öffnungsweite des Objektivs vereinfacht sich diese Abschätzung weiter zu:
Bei vorgegebenem Bildwinkel ist der Quotient aus Bilddiagonale und Brennweite konstant. Sind ferner die Öffnungsweite und die Anzahl der auf der Bilddiagonalen aufzulösenden Bildpunkte gegeben, hängt die Schärfentiefe ausschließlich vom Quadrat der Objektweite ab. Bei doppelter Objektweite vergrößert sich die Schärfentiefe also ungefähr auf das Vierfache und bei halber Objektweite verringert sie sich ungefähr auf ein Viertel.
Erhöhung der Schärfentiefe
[Bearbeiten]Wenn eine große Schärfentiefe gewünscht wird, kann zur Reduktion der hyperfokalen Entfernung mit Objektiven mit kleineren Öffnungsweiten beziehungsweise mit abgeblendeten Objektiven oder mit kürzeren Brennweiten gearbeitet werden. Hierbei ist jedoch zu beachten, dass bei großen Blendenzahlen die Beugungsbegrenzung die erreichbare optische Auflösung deutlich einschränken kann.
Alternativ können objektseitig telezentrische Objektive eingesetzt werden, bei denen eine größere Schärfentiefe erreicht wird als bei entozentrischen Objektiven gleicher Brennweite und Öffnungsweite (siehe auch Abschnitt Telezentrie).
Eine weitere Möglichkeit ist der Einsatz von plenoptischen Kameras, die bei der Aufnahme ein Lichtfeld registrieren, aus denen für verschiedene Objektweiten scharfe Bilder berechnet werden können (siehe auch Abschnitt Plenoptische Kameras).
Ferner ist es bei unbewegtem Objekt und unbewegter Kamera möglich, eine Aufnahmereihe mit automatisch variierenden oder manuell variierten Objektweiten zu machen (englisch: focus bracketing). Alternativ kann die Kamera während der Aufnahmereihe mit fest eingestellter Objektweite entlang der optischen Achse verschoben werden. Bei einer anschließenden Bildanalyse können die im jeweiligen Schärfentiefebereich scharf abgebildeten Bildbereiche jeder Aufnahme zu einer einzigen Aufnahme zusammengesetzt werden (englisch: focus stacking). Hierzu können die digitalisierten Bilddaten zweidimensionalen Fourier-Transformationen unterzogen werden, wobei sie aus dem Ortsraum in den Ortsfrequenzraum übertragen werden. Wenn in den einzelnen Bildtransformationen jeweils die spektralen Anteile mit hohen Amplituden bei höheren Ortsfrequenzen berücksichtigt werden, die durch scharf abgebildete Objekte hervorgerufen werden, können diese Ortsfrequenzanteile aus allen Aufnahmen überlagert und mit Hilfe einer inversen Fourier-Transformation zurück in den Ortsraum übertragen werden. Auf diese Weise ergibt sich ein einziges Bild mit einem großen Schärfentiefebereich. Für die Berechnung der Fourier-Transformation wird aus Effizienzgründen häufig eine diskrete Fast-Fourier-Transformation (FFT) angewendet (siehe auch Abschnitt Fourier-Transformation).
Die folgenden sechs Bilder zeigen Aufnahmen mit zunehmend größer werdender Objektweite:

- Fokus-Stacking
-
1. Aufnahme
-
2. Aufnahme
-
3. Aufnahme
-
4. Aufnahme
-
5. Aufnahme
-
6. Aufnahme
Siehe auch:
- Abschnitt Modulation in Abhängigkeit von der Ortsfrequenz
- Abschnitt Fourier-Transformation
Entfernungseinstellung
[Bearbeiten]Viele Kamerasysteme sind mit Fokussierungshilfen ausgestattet, um die Objektive auf die richtige Entfernung einstellen zu können. Für manuelle Fokussierung kann das photographische Bild auf eine Hilfsebene projiziert werden, die zum Beispiel mit einer Einstellscheibe versehen ist, auf der es bei hinreichen großen Bildern direkt in einem Lichtschachtsucher oder bei kleineren Bildern durch einen optischen Sucher mit einem Okular betrachtet werden.
Moderne Systeme erlauben eine Echtzeitwiedergabe der Bilder (Live-View), bei der das Bild, das vom Bildsensor aufgenommen wurde, auf einem Bildschirm oder in einem elektronischen Sucher betrachtet und ohne weiteres auch vergrößert (Software-Lupe) oder mit zusätzlicher Information angereichert werden kann.
Fokus-Peaking
[Bearbeiten]Durch eine entsprechende Analyse der Modulation benachbarter Bildpunkte kann in Echtzeit im gesamten Bild Information über die Bildschärfe gewonnen werden und zum Beispel durch farbig oder in der Helligkeit hervorgehobene Konturen angezeigt werden. Dieses Hilfsmittel wird üblicherweise als Fokus-Peaking bezeichnet.
- Fokus-Peaking
-
Photographie eines scharf abgebildeten Baumzweigs in einer unscharf abgebildeten Gasse
-
Kanten im Bild nach der Filterung mit einem zweidimensionalen digitalen Hochpassfilter
-
Tonwerterhöhung und Rotfärbung der Kanten im gefilterten Bild
-
Überlagerung der Photographie mit den ermittelten und überhöhten Kanten
Ein einfaches Verfahren zur Erkennung von Kanten ist die mathematische Faltung der digitalen Bilddaten mit einer kleinen geeigneten Faltungsmatrix, die über die entsprechenden Bildbereiche gerastert wird, wobei benachbarte Helligkeitswerte mit den jeweiligen Elementen der Faltungsmatrix multipliziert werden müssen. Als Hochpass-Operator für eine solche Kantendetektion kann zum Beispiel der Laplace-Operator in Form eines Laplace-Filters eingesetzt werden, der als Ergebnis der Operation ein entsprechendes Kantenbild erzeugt.
Auf dem Kontrollbildschirm werden das originale Bild und das im Kontrast verstärkte und gegebenenfalls farblich hervorgehobene Kantenbild überlagert, um dem Anwender den Bildinhalt und die Information über die Schärfe in den verschiedenen Bildbereichen gleichzeitig anzuzeigen. Hierzu kann zum Beispiel bildpunktweise die maximale Helligkeit in den beiden Bildern ermittelt oder ein geeignetes normiertes Produkt gebildet werden.
Autofokussysteme
[Bearbeiten]Für die automatische Scharfstellung gibt es Autofokussysteme, die die Schärfe mit einem Hilfssensor in einer eigenen Bildebene ermitteln. Dieses Vorgehen wird zunehmend durch die direkte Schärfemessung mit Hilfe der Bildsensors für die Bildaufnahme abgelöst, die inzwischen ebenso schnell und vor allem zuverlässiger und flexibler arbeitet, als die automatische Fokussierung mit Hilfssensoren. Hilfssensoren und Sucherbilder von Einstellscheiben stehen bei Spiegelreflexkameras systembedingt nicht für kontinuierliche Fokussierung bei Videoaufnahmen zur Verfügung.

Wenn ein Objekt in der Objektebene G über die Hauptebene H scharf auf die Bildebene B abgebildet werden soll, kann eine automatische Schärfemessung durchgeführt werden, indem hinter der Bildebene B zwei kleine zusätzliche Sammellinsen (mit der gemeinsamen Hauptebene M) in den Strahlengang gebracht werden. Diese bilden Objekte mit verschiedenen Objektweiten in die Sensorebene S ab, wobei der Abstand der beiden Bildpunkte in der Sensorebene S für unendliche Objektweite c maximal ist und für kleiner werdende Objektweiten immer geringer wird. Der Abstand der beiden Bildpunkte bei korrekter Fokussierung über die Hauptebene H liegt in der graphischen Darstellung oben beim Wert b (Strahlengang magenta).
Kleinere Abstände (a < b) ergeben sich durch geringere Objektweiten (Strahlengang rot), die Schärfe ist in diesem Fall auf eine zu große Objektweite eingestellt. Größere Abstände (c > b) ergeben sich durch größere Objektweiten (Strahlengang zyan), die Schärfe ist in diesem Fall auf eine zu kleine Objektweite eingestellt. Dieses Verfahren hat den Vorteil, dass aus dem Abstand der beiden Bildpunkte sofort abgelesen werden kann, ob die Schärfe für zu kleine Objektweiten (Abstand = c > b) oder für zu große Objektweiten (Abstand = a < b) eingestellt ist, beziehungsweise dass die Schärfe bereits korrekt eingestellt ist (Abstand = b). In der Praxis wird der Abbildungsstrahlengang während der Schärfemessung über Spiegel oder teildurchlässige Spiegel auf eine entsprechende Messeinheit umgelenkt (siehe auch Spiegelreflexsysteme).
Bei einer Kontrastmessung in der Bildebene B kann lediglich festgestellt werden, wie hoch der Kontrastwert ist, nicht jedoch ob dieser bereits ein Maximum erreicht hat, beziehungsweise in welche Richtung die Scharfstellung korrigiert werden muss, um den Kontrast zu erhöhen.
Fokussierungsfehler
[Bearbeiten]
Sowohl bei der manuellen Fokussierung mit einer Einstellscheibe als auch bei der Benutzung von Hilfssensoren besteht die Gefahr von Fokussierungsfehlern, da die Messebene und die Aufnahmeebene weder exakt den gleichen Abstand von der letzten Hauptebene des Objektivs haben, noch perfekt parallel und perfekt senkrecht zur optischen Achse ausgerichtet werden können. Ursachen können Lagefehler bei der Abbildung mit einem Objektiv, wie zum Beispiel die Bildfeldwölbung, oder Toleranzen und Dejustierungen, sowie bei bewegten Motiven Verzögerungen im automatischen Fokussierungssystem der Kamera sein.
- Fokussierungsfehler
-
Aufnahme mit Backfokus auf dem vierten Stab
-
Aufnahme mit korrekter Fokussierung auf dem mittleren Stab
-
Aufnahme mit Frontfokus auf dem zweiten Stab

Die Stärke des Fokussierungsfehlers kann bei vorgegebener Öffnungsweite über die Größe des Zerstreuungskreises bestimmt werden, der in der Bildebene aufgrund der Differenz zwischen eingestellter und optimaler Bildweite entsteht:
Für eine Abbildung aus dem Unendlichen ist Bildweite identisch mit der Brennweite . Für diesen Fall ergibt sich unter Verwendung der Blendenzahl der maximale durch den Fokussierungsfehler bedingte maximale Zerstreuungskreisdurchmesser zu:
Alternativ kann der maximale Fokussierungsfehler aus der eingestellten Blendenzahl und dem maximal tolerierbaren Zerstreuungskreisdurchmesser ermittelt werden:
Spiegelreflexsysteme
[Bearbeiten]
Bei Spiegelreflexsystemen wird das Bild des Objektivs der Kamera für die Bildauswahl zunächst über einen Spiegelsystem in auf eine Einstellscheibe und einen Autofokussensor abgebildet. Anhand der Darstellung auf der Einstellscheibe können der Bildausschnitt betrachtet und die Bildschärfe visuell beurteilt werden. Mit einem kalibrierten Autofokussensor kann die eingestellte Objektweite ermittelt werden, um die Entfernungseinstellung des Objektivs gegebenenfalls korrigieren zu können.
Beim Photographieren mit kleiner Blendenzahl und mit kleinen akzeptablen Zerstreuungskreisen auf dem Bildsensor müssen die Ebenen vom Bild, von der Einstellscheibe und vom Autofokussensor über das gesamte Bildfeld auf weniger als 1/100 Millimeter genau positioniert sein, was aufgrund von Fertigungstoleranzen und Temperaturschwankungen in Bezug auf das Kameragehäuse in der Praxis sehr aufwendig und schwierig ist.
Bei hochgeöffneten Objektiven mit kleiner Blendenzahl und entsprechend großen bildseitigen Öffnungswinkeln oder bei unkorrigierten Objektiven mit Bildfeldwölbung sind die tolerierbaren Fokussierungsfehler, also die Abweichungen der Bildweite von den Weiten der Einstellscheibe oder von den Weiten des Autofokussensors also sehr klein und die Kamera kann unter Umständen mechanisch nicht mehr hinreichend präzise und thermisch nicht mehr hinreichend stabil konstruiert und ausgeführt werden. In solchen Fällen wird ein über die Einstellscheibe oder den Autofokussensor in der Schärfe eingestelltes Bild in der Bildebene geometrisch nicht mehr hinreichend scharf abgebildet, und es bietet sich an, die Schärfemessung direkt in der Bildebene, bei digitalen Kameras also mithilfe des Bildsensors durchzuführen.
Auswirkung der Bildgröße auf Abbildungsparameter
[Bearbeiten]Die Bildgröße wird bei Kameras durch das Aufnahmemedium festgelegt, das in der Regel rechteckig begrenzt ist. Wenn sich die optische Achse des Systems in der Mitte des entsprechenden Rechtecks in der Bildebene befindet, ist die Bilddiagonale des aufgenommenen Bildes identisch mit dem genutzten Bildkreisdurchmesser der Abbildung.
In der folgenden Tabelle wird die Auswirkung der Halbierung der Bilddiagonale eines Bildaufnahmesystems dargestellt, die sich bei gleicher Brennweite der optischen Abbildung sowie bei gleicher Öffnung und gleicher Blendenzahl des Objektivs ergeben, wenn die Anzahl der im Bild aufgenommenen Bildpunkte konstant gehalten wird:
| Vergleich von Größen bei optischer Abbildung |
Referenzformat mit gegebener Bilddiagonale, Öffnungsweite und Brennweite |
Halbe Bilddiagonale, gleiche Öffnungsweite, gleiche Brennweite |
Halbe Bilddiagonale, gleiche Öffnungsweite, halbe Brennweite |
Halbe Bilddiagonale, halbe Öffnungsweite, gleiche Brennweite |
Halbe Bilddiagonale, halbe Öffnungsweite, halbe Brennweite |
|---|---|---|---|---|---|
 |
 |
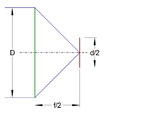 |
 |
 | |
| Bilddiagonale / Bildkreisdurchmesser |
|||||
| Öffnungsweite | |||||
| Brennweite | |||||
| Blendenzahl | |||||
| Durchmesser des Beugungsscheibchens |
|||||
| Abbildungsmaßstab | |||||
| Bildwinkel | |||||
| Lichtstrom im Objektiv |
|||||
| Beleuchtungsstärke im Bild |
|||||
| Bildseitiger Öffnungswinkel |
|||||
| Bildseitiger Raumwinkel |
|||||
| Lichtstärke im Bild |
|||||
| Leuchtdichte im Bild |
|||||
| Belichtungswert | |||||
| Belichtungszeit | |||||
| Objektivvolumen | |||||
| Bildfläche | |||||
| Normalbrennweite | |||||
| Punktabstand | |||||
| Relativer Fokussierungsfehler |
|||||
| Hyperfokale Entfernung |
|||||
| Schärfentiefe |
Bei gleicher Öffnung sowie bei halber Bildgröße und halber Brennweite unterscheidet sich ein Objektiv also vor allem durch die kürzere Bauform und das dadurch geringere Volumen und Gewicht. Insbesondere sind die Schärfentiefe des Bildes und der Bildwinkel sowie der Lichtstrom und damit die Lichtempfindlichkeit pro Bildpunkt identisch. Die Beugungsscheibchen sind zwar nur halb so groß, aber dafür sind auch die Bildpunkte nur halb so groß, so dass sich in der Bildqualität hierdurch kein Unterschied ergibt.
Äquivalente Brennweite
[Bearbeiten]
Der Bildausschnitt hängt von der Brennweite des Objektivs und der Größe des Bildsensors ab und wird am besten durch den sogenannten Bildwinkel beschrieben. Um den gleichen Bildwinkel und somit die gleiche Bildperspektive zu erhalten, muss eine Kamera mit einem doppelt so großen Bildsensor mit doppelt so großer Brennweite betrieben werden. Der Abbildungsmaßstab unterscheidet sich bei großer Objektweite dann auch um den Faktor zwei, das heißt, dass der äquivalente Abbildungsmaßstab für halb so große Bildsensoren bei halber Brennweite auch nur halb so groß ist.
Die folgende Tabelle zeigt Beispiele für äquivalente Brennweiten mit gleichem Bildwinkel bei verschiedenen Bildsensorklassen:
| Bildsensorklasse | Äquivalente Brennweite bei Weitwinkel in Millimetern |
Äquivalente Brennweite bei Normalwinkel in Millimetern |
Äquivalente Brennweite bei Telewinkel in Millimetern |
|---|---|---|---|
| Miniatur | 4 | 7 | 12 |
| Kompakt | 5 | 9 | 15 |
| 2/3-Zoll | 7 | 13 | 22 |
| 1-Zoll | 10 | 18 | 30 |
| Micro Four Thirds | 14 | 25 | 42 |
| APS-C | 18 | 32 | 55 |
| Vollformat | 28 | 50 | 85 |
| Mittelformat | 39 | 70 | 120 |
| Großformat | 56 | 100 | 170 |
Äquivalente Blendenzahl
[Bearbeiten]

Anmerkung: Der Weg zur Scharfstellung im Bildraum von unendlicher Objektweite auf die endliche Objektweite a wird mit größer werdender Brennweite und entsprechend größerem Bild überproportional länger (Δa' versus 4,5 Δa').
Die Schärfentiefe und die Beugungsunschärfe hängen von der Brennweite des Objektivs und der eingestellten Blendenzahl respektive von der Öffnungsweite ab. Um bei gleichem Bildwinkel - also bei äquivalenter Brennweite - die gleiche Schärfentiefe und die gleiche Beugungsunschärfe - also den gleichen Winkeldurchmesser des Beugungsscheibchens - zu erhalten, muss eine Kamera mit doppelt so großer Brennweite mit halb so großer Blendenzahl - also mit gleicher Öffnungsweite - betrieben werden.
Der Stellweg entlang der optischen Achse im Bildraum, der sich bei der Scharfstellung aus dem Unendlichen ergibt, wenn sich das scharfzustellende Objekt in der Objektweite befindet, lässt sich für ein Objektiv mit der Brennweite über die folgenden Beziehung berechnen:
Die folgende Tabelle zeigt beispielhaft verschiedene Bildsensorklassen und die jeweilige äquivalente Blendenzahlen bei konstanter Öffnungsweite. Dabei resultieren immer die gleiche Schärfentiefe und die gleiche relative Beugungsunschärfe. Ferner sind für ein Objektiv mit Normalbrennweite die Längen der entsprechenden Stellwege im Bildraum angegeben, die sich bei der Scharfstellung aus dem Unendlichen ergeben, wenn sich das scharfzustellende Objekt in einer Objektweite von einem Meter () befindet.
| Bildsensorklasse | Äquivalente Blendenzahl bei lichtstarkem Objektiv |
Äquivalente Blendenzahl bei lichtschwachem Objektiv |
Länge des Stellwegs in der Bildebene in mm bei der Scharfstellung von unendlich auf ein Meter |
|---|---|---|---|
| Miniatur | - | 2,0 | 0,049 |
| Kompakt | - | 2,8 | 0,082 |
| 2/3-Zoll | 0,7 | 4,0 | 0,17 |
| 1-Zoll | 1,0 | 5,6 | 0,33 |
| Micro Four Thirds | 1,4 | 8,0 | 0,64 |
| APS-C | 2,0 | 11 | 1,1 |
| Vollformat | 2,8 | 16 | 2,6 |
| Mittelformat | 4,0 | 22 | 5,3 |
| Großformat | 5,6 | 32 | 11,1 |
Äquivalente Lichtempfindlichkeit
[Bearbeiten]Das Bildqualität hängt auch von der Lichtmenge ab, die durch das Objektiv auf den Bildsensor oder den photographischen Film geworfen wird. Die aufgefangene Lichtmenge kann als Maß für die Lichtempfindlichkeit mit dem Belichtungsindex (wird umgangssprachlich auch als ISO-Zahl bezeichnet) beschrieben werden – je höher der Belichtungsindex beziehungsweise der Belichtungswert ist (siehe auch Kapitel Belichtungswert), desto weniger Licht wird für eine Aufnahme verwendet und desto kürzer muss bei gleicher Blendenzahl belichtet werden.
Bei vorgegebenem Belichtungsindex, gleichem Belichtungswert beziehungsweise gleicher Leuchtdichte, gleichem Bildwinkel (äquivalente Brennweite) und gleicher Öffnungsweite (äquivalente Blendenzahl) resultiert für größere Bildformate eine längere Belichtungszeit. Um unter diesen Umständen bei gleicher Bildauflösung mit der gleichen Lichtmenge eine vergleichbare Bildqualität zu erhalten, muss eine Kamera mit einem halb so großen Bildsensor bei gleicher Belichtungszeit mit einem um den Faktor 4 kleineren (äquivalenten) Belichtungsindex betrieben werden. Wird sie bei gleichem Belichtungsindex mit einem Viertel der Belichtungszeit (äquivalente Belichtungszeit) betrieben, registriert sie allerdings auch nur ein Viertel der vergleichbaren Lichtmenge.
Eine ähnliche Situation ergibt sich bei halb so großem Bildsensor, wenn Objekte mit einer viermal so hohen Leuchtdichte und somit einem um den Summanden 2 erhöhten Belichtungswert bei gleicher Belichtungszeit und gleichem Belichtungsindex aufgenommen werden.
Die folgende Tabelle zeigt Beispiele für äquivalente Lichtempfindlichkeiten bei gleicher Belichtungszeit, äquivalente Belichtungswerte bei gleicher Belichtungszeit beziehungsweise äquivalente Belichtungszeiten bei gleichem Belichtungsindex für verschiedenen Bildsensorklassen:
| Bildsensorklasse | Äquivalenter Belichtungsindex bei gleicher Belichtungszeit |
Äquivalenter Belichtungswert EV bei gleicher Belichtungszeit |
Äquivalente Belichtungszeit t in s bei gleichem Belichtungsindex |
|---|---|---|---|
| Miniatur | 50 | 6 | 1/1000 |
| Kompakt | 100 | 5 | 1/500 |
| 2/3-Zoll | 200 | 4 | 1/250 |
| 1-Zoll | 400 | 3 | 1/125 |
| Micro Four Thirds | 800 | 2 | 1/60 |
| APS-C | 1600 | 1 | 1/30 |
| Vollformat | 3200 | 0 | 1/15 |
| Mittelformat | 6400 | -1 | 1/8 |
| Großformat | 12800 | -2 | 1/4 |
Äquivalenter Fokussierungsfehler
[Bearbeiten]Der durch eine fehlerhafte Einstellung der Objektweite verursachte maximale Zerstreuungskreisdurchmesser muss auf die Bilddiagonale bezogen werden, um vergleichbare Bedingungen zu erhalten. Je kürzer die für ein Bild erforderliche Brennweite und je kleiner der verwendete Bildkreis sind, desto kleiner wird der maximale Zerstreuungskreisdurchmesser und damit auch der Fokussierungsfehler, der eine vorgegebene Unschärfe erzeugt. Demzufolge wird auch der Stellweg zur Scharfstellung zwischen zwei bestimmten Objektweiten entsprechend kleiner.
Die folgende Tabelle zeigt Beispiele für äquivalente Zerstreuungskreisdurchmesser und äquivalente Fokussierungsfehler bei gleichem Bildwinkel und bei äquivalenter Blendenzahl für verschiedenen Bildsensorklassen, wenn der Durchmesser der Zerstreuungskreise nicht größer als ein Tausendstel der Bilddiagonale werden darf:
| Bildsensorklasse | Äquivalente Blendenzahl |
Äquivalenter Zerstreuungskreis- durchmesser in µm |
Äquivalenter Fokussierungsfehler in µm |
|---|---|---|---|
| Miniatur | 1,0 | 5,4 | 5,4 |
| Kompakt | 1,4 | 7,6 | 11 |
| 2/3-Zoll | 2,0 | 11 | 22 |
| 1-Zoll | 2,8 | 15 | 42 |
| Micro Four Thirds | 4,0 | 22 | 87 |
| APS-C | 5,6 | 30 | 170 |
| Vollformat | 8,0 | 43 | 350 |
| Mittelformat | 11 | 59 | 650 |
| Großformat | 16 | 87 | 1400 |
Falschlicht
[Bearbeiten]Bei einer idealen optischen Abbildung wird jeder Objektpunkt entsprechend dem dazugehörigen Abbildungsmaßstab geometrisch exakt in einen Bildpunkt übertragen. Bei Falschlicht handelt es sich allgemein um unerwünschtes Licht im Bild, also Lichtsignale, die nicht vom entsprechenden Punkt in der Objektebene stammen (siehe auch ISO 18844). Es gibt zahlreiche Ursachen und Quellen für Falschlicht, das abseits der jeweiligen geometrisch exakten Bildpunkte in die Bildebene gelangen kann:
- Licht, das an Störstellen von optischen Medien gestreut wird.
- Licht, das durch einfache oder mehrfache Fresnel-Reflexion an Grenzflächen von (unvergüteten) optischen Medien ins Bild gelangt.
- Licht, das an Fassungen oder Blenden im Strahlengang gebeugt, reflektiert oder gestreut wird.
- Licht, das durch gerichtete oder ungerichtete Reflexion sowie durch Beugung an innenliegenden Gehäuseteilen des optischen Systems abgelenkt wird.
- Licht, das durch Lichtlecks in das optische System gelangt.
- Licht, das von Lichtquellen innerhalb des optischen Systems stammt.
- Licht, das durch Abbildungsfehler (Aberrationen) nicht in die geometrisch korrekten Bildorte abgelenkt wird.
- Licht, das von einem Objektpunkt durch fehlerhafte Entfernungseinstellung nicht in den entsprechenden Punkt in der dazugehörigen Bildebene, sondern in einen Zerstreuungskreis der tatsächlich gewählten Bildebene abgebildet wird.
Die Bilder der das Falschlicht verursachenden Objektpunkte und Lichtquellen können innerhalb aber auch außerhalb des zu erfassenden Bildfelds liegen. Im noch weiter gefassten Sinn erzeugen auch elektronisches Rauschen oder Digitalisierungsrauschen unerwünschte Signale in elektronischen und digitalen Bildern. In digitalen Bildern sind die durch die vielfältigen Quellen verursachten, unerwünschten Bildsignale nicht immer ohne weiteres zu unterscheiden. Nichtsdestoweniger können einige der Störeffekte mit automatischer oder manueller Bildbearbeitung vermindert oder sogar vollständig kompensiert werden.
Gegenlicht
[Bearbeiten]Eine häufige Situation stellt Gegenlicht dar. In diesem Fall wird eine Lichtquelle direkt abgebildet, oder sie befindet sich in der Nähe des abgebildeten Objektfelds. In der Abbildung werden durch Falschlicht Lichtsignale erzeugt, die nicht direkt Objektpunkten entsprechen.
Der graue Schirm auf der linken Seite der ersten der folgenden Abbildungen wird durch das Objektiv in die Bildebene abgebildet. Der rote Laserstrahl, dessen Lichtquelle sich von der optischen Achse aus gemessen 10° außerhalb des Bildwinkels befindet, ist im Idealfall in der Bildfläche nicht sichtbar, sondern wird in der Kamera absorbiert. In der Praxis trifft durch gerichtete und ungerichtete Reflexionen oder Beugung innerhalb des Objektivs dennoch Licht der Lichtquelle auf die Bildfläche (Abbildung mit einem typischen Beispiel in der Mitte).
Falschlicht, das durch außerhalb des Objektfeldes vorhandene Lichtquellen verursacht wird, kann leicht durch die Verwendung einer Streulichtblende vor dem Objektiv (Abbildung rechts, auch Gegenlichtblende genannt) reduziert oder sogar vollständig vermieden werden.
- Zur Wirkung von Streulicht
-
Unerwünschter Einfluss von Gegenlicht, das sich außerhalb Objektfeldes befindet
-
Exemplarische fotografische Aufnahme mit unerwünschtem Einfluss von Laserlicht außerhalb des Objektfeldes
-
Beispiel einer Streulichtblende zur Vermeidung von Falschlicht in der Bildfläche
Räumliche Motive
[Bearbeiten]Bei räumlichen Motiven ergibt sich bei entozentrischen und perizentrischen Abbildungen das Problem, dass die Objektweite nicht konstant ist. Dadurch kommt es für ein räumliches Objekt zu unterschiedlichen Abbildungsmaßstäben im Bild. Durch die Verwendung von objektseitig telezentrischen Objektiven (siehe oben), bei denen der Abbildungsmaßstab von der Objektweite unabhängig ist, kann dieses Problem vermieden werden.


Betrachten wir ein kugelförmiges Objekt mit dem Radius , dessen Mittelpunkt sich im Abstand von der optischen Achse in der Objektebene G befindet und über die Hauptebene H verzeichnungsfrei in die Bildebene B abgebildet wird. Die Objektweite beträgt und die Bildweite . Das Zentrum dieser Kugel wird im Abstand von der optischen Achse in die Bildebene projiziert. Der Abbildungsmaßstab beträgt für diesen Punkt:
Bei undurchsichtigen Objekten wird jedoch nur die Oberfläche des Körpers abgebildet und die beiden Tangentenpunkte der Sichtstrahlen auf die Oberfläche der Kugel in der Schnittebene befinden sich näher beziehungsweise entfernter als die Objektweite des Mittelpunkts der Kugel, so dass sich für den näheren Punkt die Objektweite und für den ferneren Punkt die Objektweite ergibt. Daraus resultieren die entsprechenden Abbildungsmaßstäbe und :
Die beiden Objektweiten und können wie folgt konstruiert und berechnet werden:
Der Abstand vom Hauptpunkt zum Mittelpunkt der Kugel ist :
Die Höhe kann über die Betrachtung ähnlicher Dreiecke aus folgender Verhältnisgleichung gewonnen werden:
Die Differenz ergibt sich ebenfalls aus einer Verhältnisgleichung, die auf ähnlichen Dreiecken beruht:
Der Grenzwert von für große Objektweiten geht gegen null:
Die Hilfsgröße kann mit Hilfe des Satzes des Pythagoras berechnet werden:
Die Differenz kann dann wiederum über die entsprechenden ähnlichen Dreiecke aus einer Verhältnisgleichung abgeleitet werden:
Befindet sich der Mittelpunkt der Kugel auf der optischen Achse (), dann ist .
Die gesuchten Objektweiten ergeben sich dann schließlich wie folgt:
Die beiden entsprechenden Abbildungsmaßstäbe und hängen bei vorgegebener Objektweite des Mittelpunkts , vorgegebenem Abstand von der optischen Achse in der Objektebene G und vorgegebenem Radius des kugelförmigen Objektes nur von der Bildweite ab, die für alle Bildpunkte allerdings identisch ist. Für das Verhältnis dieser beiden Abbildungsmaßstäbe ergibt sich dann also wie folgt:

Die unterschiedlichen Abbildungsmaßstäbe entlang der vom Hauptpunkt aus gesehenen sichtbaren Konturen eines kugelförmigen Objektes führen dazu, dass nicht der Radius der entsprechenden Kugel in der Größe der optischen Abbildung wiedergegeben wird. Je näher der sichtbare Punkt auf der Kontur an der Hauptebene liegt, desto größer ist der Abbildungsmaßstab. Dies führt dazu, dass Objektteile von Kugeln, deren Konturpunkte weiter seitlich von der optischen Achse entfernt sind, stärker vergrößert werden als Objektteile, deren Konturpunkte näher an oder sogar auf der optischen Achse liegen. Eine Kugel, deren Mittelpunkt außerhalb der optischen Achse liegt, wird daher nicht kreisrund, sondern als Oval abgebildet.
Dieser Effekt tritt insbesondere bei weitwinkligen Aufnahmen mit großen Bildwinkeln auf, bei denen unter Umständen eine noch stärker hervortretendee Verzeichnung (siehe oben) hinzukommt, da hierbei der Abbildungsmaßstab aufgrund von Lagefehlern in der Abbildung über das Bildfeld variiert. In der Abbildung rechts ist eine beispielhafte Aufnahme zu sehen, bei denen die Verformung der Kugelbilder am Rand der Aufnahme hauptsächlich von der Verzerrung durch die unterschiedlichen Objektweiten der aufgenommenen Kugeln zustande kommt.
Bewegte Motive
[Bearbeiten]Senkrecht zur optischen Achse
[Bearbeiten]Bei der Aufnahme von bewegten Motiven, die sich in der Objektweite senkrecht zur optischen Achse mit der Geschwindigkeit bewegen, darf für ein Einzelbild eine maximale Belichtungszeit von nicht überschritten werden, wenn im Bild keine Bewegungsunschärfe zu erkennen sein soll.
Die Bewegungsunschärfe wird bei der Verwendung einer bestimmten Brennweite im Bild mit dem Abbildungsmaßstab in die Bildunschärfe skaliert:
Diese Bildunschärfe soll in der Regel einen festzulegenden Bruchteil der Bilddiagonale nicht überschreiten:
Hierbei kann für , wie bei der Festlegung des maximal tolerierbaren Zerstreuungskreisdurchmessers bei der Bestimmung der visuellen Schärfentiefe, zum Beispiel ein Wert zwischen 1000 und 1500 festgelegt werden.
Für die maximale Belichtungszeit resultiert dann:
Für ein Motiv, das sich zum Beispiel mit einer Geschwindigkeit und in einer Objektweite an einer unbewegten Kamera mit einer Brennweite und einer Bilddiagonale vorbeibewegt, ergibt sich mit eine maximale Belichtungszeit .
Auf der optischen Achse
[Bearbeiten]Bei der Aufnahme von bewegten Motiven, die sich mit der Geschwindigkeit auf eine Kamera zubewegen oder sich von ihr wegbewegen, darf für ein Einzelbild eine maximale Belichtungszeit von nicht überschritten werden, wenn im Bild bei der von der optischen Achse aus gemessenen Bildhöhe keine Veränderung des Abbildungsmaßstabs zu erkennen sein soll. Ferner darf das Motiv den Bereich der Schärfentiefe zwischen Fernpunkt und Nahpunkt im Objektraum nicht verlassen.
Von der optischen Achse aus gemessen ergibt sich die maximale Objekthöhe aus der halben Bilddiagonale und dem Abbildungsmaßstab :
Bei der Änderung der Objektweite um resultiert eine geänderte Bildhöhe , und die entsprechenden Abbildungsmaßstäbe und lauten:
Die Änderung der Bildhöhe ergibt sich daraus und erneut mit einem festzulegenden Bruchteil der Bilddiagonale für die maximale Verschiebung im Bild (siehe oben) wie folgt:
Aus dieser maximalen Bildhöhenänderung folgt schließlich die Gleichung für die entsprechende Objektweitenänderung :
Für große Objektweiten () gilt in guter Näherung:
Für ein Motiv, das sich zum Beispiel mit einer Geschwindigkeit und in einer Objektweite auf eine Kamera mit einer Brennweite und einer Bilddiagonale zubewegt, ergibt sich bei einer eingestellten Blendenzahl mit eine Schärfentiefe . Die maximale Bewegungsstrecke entlang der optischen Achse darf innerhalb des Schärfentiefebereichs 40 Millimeter nicht überschreiten, ohne dass sich der Abbildungsmaßstab in den Bildecken zu stark ändert ().
Für die maximale Belichtungszeit resultiert entsprechend:
Somit beträgt die maximale Belichtungszeit im obigen Beispiel .
Bei Motiven, die das Bild nicht bis in die Bildecken ausfüllen, ergeben sich entsprechend längere Belichtungszeiten, da die Bildhöhen in der Nähe der optischen Achse weniger stark variieren als in den Bildecken. Auf der optischen Achse selbst ist die Bildhöhe immer null, da auch das entsprechende Objekt sich auf der optischen Achse befinden muss.
Bei einer Nachfokussierung während der Aufnahme kann es insbesondere bei Objektiven mit innenliegender Fokussierung (IF) zu Änderungen des Abbildungsmaßstabs kommen, die nicht auf eine Änderung der Objektweite zurückzuführen sind und gegebenenfalls ebenfalls berücksichtigt werden müssen.
Belichtung
[Bearbeiten]Die Helligkeits- und Farbwerte in einer optischen Abbildung müssen zunächst einem endlichen Farbraum zugeordnet werden, damit sie bei der Bildwiedergabe korrekt reproduziert werden können.
Helligkeiten
[Bearbeiten]Die Helligkeiten im Bild werden durch die entsprechenden Leuchtdichten repräsentiert (siehe auch Kapitel Leuchtdichte).
Der Farbraum ist durch den Schwarzwert begrenzt, bei dem gar keine Helligkeit vorliegt. Der Weißwert entspricht in der Regel dem hellstmöglichen Punkt im Bild, und dieser kann wegen der extrem großen potentiellen Spannweite für die Helligkeitswerte einer Aufnahme nicht allgemein festgelegt werden. Daher ist es in der Praxis sinnvoll, eine Belichtungsmessung durchzuführen, bei der der Bereich maximaler Helligkeit ermittelt und dem Weißwert in der Aufnahme zugeordnet wird.
Die Verteilung der Helligkeiten der Bildpunkte kann zum Beispiel in sogenannten Histogrammen dargestellt werden.
Siehe hierzu auch: Histogramme
Das Histogramm zeigt die Verteilung der Häufigkeiten von gleichen Helligkeiten in einem digitalen Bild. In der Regel befinden sich ganz links die Häufigkeit des Schwarzwertes und ganz rechts die Häufigkeit des Weißwertes. Dazwischen werden die Häufigkeiten der Helligkeitsstufen zwischen Schwarz- und Weißwert dargestellt.
Wenn die Helligkeiten in Bildpunkten die Helligkeit des Weißpunktes überschreiten, werden die gespeicherten Helligkeiten dieser Bildpunkte auf die Helligkeit des Weißpunktes begrenzt (englisch: clipping). In den digitalen Bilddaten ist dann keine Differenzierung dieser Bildpunkte mehr möglich. Die Modulation zwischen den Bildpunkten geht verloren, obwohl die Objekthelligkeiten unterschiedlich hell waren.
Bei digitalen photographischen Geräten mit Live-View-Funktion können die entsprechenden Bildbereiche auf einem Bildschirm oder in einem elektronischen Sucher durch auffällige, gegebenenfalls blinkende Farben oder mit regelmäßigen Mustern hervorgehoben werden, damit der Nutzer eine solche Überbelichtung sofort erkennen und durch eine Belichtungskorrektur beheben kann. Eine Belichtungskorrektur kann zum Beispiel durch das Abblenden des Objektivs, die Verkürzung der Belichtungszeit, das Einbringen eines Lichtfilters in den Strahlengang oder die Reduktion der Objekthelligkeit erfolgen.
Das folgende Beispiel zeigt ein Bild mit überbelichteten Teilbereichen, die als Weißwert gespeichert sind, mit dem dazugehörigen Histogramm. In zwei weiteren Bildvarianten wurden die überbelichteten Bildpunkte mit dem Weißwert durch eine Zebramusterung (englisch: zebra patterning) beziehungsweise durch eine Rotfärbung hervorgehoben:
- Überbelichtung
-
Photographische Aufnahme mit überbelichtetem Teilbereichen im bewölkten Himmel, die Schneebedeckung ist dunkler als der Weißwert
-
Histogramm mit der dazugehörigen Verteilung der Häufigkeiten von Helligkeitswerten - wegen der Überbelichtung ist der Weißpunkt am rechten Rand des Histogramms sehr häufig vertreten
-
Hervorhebung der überbelichteten Bildpunkte durch eine Zebramusterung
-
Hervorhebung der überbelichteten Bildpunkte durch Färbung mit gesättigtem Rot
Farben
[Bearbeiten]
In Bezug auf die Farben ist der Farbraum ebenfalls begrenzt. Bei jeder Wellenlänge kann eine maximale Farbsättigung erfasst und gespeichert werden. zwischen dem Schwarzpunkt und dem Weißpunkt verläuft im mittleren Bereich des Farbraums eine Graulinie oder Grauachse, auf denen die farbneutralen Bildpunkte liegen.
Wenn der Wiedergabefarbraum mindestens so groß ist, wie der Farbraum der Aufnahme, können die Farben mit den entsprechenden Helligkeiten und Farbsättigungen reproduziert werden. Ist der Wiedergabefarbraum kleiner, können bestimmte Farben in der geforderten Sättigung nicht reproduziert werden, sondern werden häufig mit der maximal möglichen Farbsättigung ausgegeben.
Es können jedoch auch verschiedene Maßnahmen zur Kompensation getroffen werden. Hierzu kann der Farbraum eines Bildes umkehrbar eindeutig (bijektiv) in den Farbraum eines Wiedergabemediums transformiert werden. In diesem Fall können zwischen unterschiedlichen Punkten zwar Unterschiede erkannt werden, die Farbtöne und Farbsättigungen der wiedergegebenen Punkte weichen dann aber alle mehr oder weniger von den gemessenen Punkten ab. Es ist also abzuwägen, ob einer möglichst differenzierten Wiedergabe oder einer farbverbindlichen Wiedergabe der Vorzug gegeben werden soll.
Stehbilder
[Bearbeiten]Bei Aufnahmen von Stehbildern wird ein Bild registriert, das den Zustand eines bewegten oder unbewegten, photographisch erfassten Objektes innerhalb einer bestimmten Zeitspanne in einer einzelnen projizierten Aufnahme einfriert. Kameras können gegebenenfalls mehrere Stehbilder innerhalb einer Sekunde aufnehmen, so dass die Grenzen zwischen Folgen von Stehbildern und Bewegtbildaufnahmen (siehe unten) fließend sind. Bei Bildfrequenzen von über 20 Bildern pro Sekunde kann ein Mensch üblicherweise keine einzelnen Stehbilder mehr erkennen, sondern nimmt eine solche Bildserie als Filmsequenz wahr.
Kameras
[Bearbeiten]Eine Kamera besteht aus einem reell abbildenden, optischen System, das einen Gegenstand aus der Objektebene in eine Bildebene abbildet, wo das Bild aufgefangen und gegebenenfalls registriert werden kann. Das optische System besteht in der Regel aus einem Objektiv, das im Gegensatz zu einer einzelnen Feldlinse, einem Hohlspiegel (Spiegelteleskop) oder einer Lochblende (Lochkamera) in der Regel aus mehreren Linsen (respektive Linsengruppen) besteht.
Die Objektive sind häufig korrigiert, damit bestimmte Abbildungsfehler vermindert werden, wie zum Beispiel Verzeichnung, Öffnungsfehler (sphärische Aberration) oder Farbfehler (chromatische Aberration). Objektive mit variabler Brennweite werden Zoomobjektive genannt. Eine weitere wichtige Kenngröße von Objektiven ist die maximale Blendenöffnung, die meistens mit der kleinsten einstellbaren Blendenzahl angegeben wird.
Siehe hierzu auch: Blendenzahl
Das reelle Bild kann auf einer transparenten Mattscheibe oder auf einem reflektierenden Projektionsschirm beobachtet, oder mit einem photographischen Film beziehungsweise mit einem elektronischen Bildsensor registriert werden.
Kompaktkameras
[Bearbeiten]
Kompaktkameras zeichnen sich dadurch aus, dass alle ihre Bestandteile auf engem Raum zusammengefügt sind. Dies bedeutet jedoch nicht zwangsläufig, dass solche Kameras absolut gesehen klein sind, sondern lediglich, dass sie vergleichsweise klein sind. Die tatsächliche Bauform und Größe hängen von vielen Parametern ab, wie zum Beispiel vom Abbildungsmaßstab, von der Bildgröße und vom Bildwinkel.
Neben dem Objektiv und einem Bildsensor sind digitale Kompaktkameras häufig auch noch mit einer autarken Energieversorgung und einem Speichermedium ausgestattet. Zusätzlich gibt es oft noch einen Bildschirm und einen Auslöser, gegebenenfalls auch einen Sucher, ein Blitzlicht oder eine Leuchte für die Aufhellung des zu photographierenden Objekts.
Systemkameras
[Bearbeiten]Systemkameras gehören zu einem Kamerasystem und können durch den Austausch von kompatiblen Komponenten verändert oder durch die Hinzufügung von Komponenten erweitert werden. Zu den Hauptkomponenten gehören ein Kameragehäuse und ein Wechselobjektiv. Weitere Komponenten sind beispielsweise Blitzlichtgeräte, optische Filter, Fernauslöser, Sucher, Einstellhilfen, Belichtungsmesser oder Module für die Erfassung von Metadaten (Georeferenzierung, Zeiterfassung).
Spiegelreflexkameras sind Systemkameras mit einem optischen Sucher. Sie haben einen Klappspiegel, der die optische Abbildung vor der Aufnahme auf eine Einstellscheibe umlenkt, so dass diese vom Photographen im optischen Sucher angeschaut und beurteilt werden kann. Während der Aufnahme wird der Spiegel weggeklappt, so dass das Bild registriert werden kann; im Sucher ist dann keine Abbildung mehr zu sehen. Moderne Spiegelreflexkamera sind mit einem System zur automatischen Entfernungseinstellung ausgestattet, das einen Teil des Lichtes der optischen Abbildung vor der Aufnahme auf einen separaten Sensor umlenkt.
Siehe hierzu auch: Autofokussysteme
Spiegellose Systemkameras waren im 20. Jahrhundert meist Messucherkameras, die mit einem zusätzlichen optischen Suchersystem mit einem Okular ausgestattet sind, mit dessen Hilfe der Photograph den Bildausschnitt wählen und die Entfernungseinstellung vornehmen kann.

Seit Beginn des 21. Jahrhunderts gibt es digitale spiegellose Systemkameras, die optional mit einem elektronischen Sucher ausgerüstet sind, und bei denen die Belichtungsmessung und die Entfernungseinstellung über den Bildsensor erfolgen können. Bei spiegellosen Systemkameras kann das Sucherbild auch während der photographischen Belichtung zur Verfügung gestellt werden.
Plenoptische Kameras
[Bearbeiten]
Links: Abbildung mit mehreren benachbarten Objektiven auf verschiedene benachbarte Bereiche eines Bildsensors oder auf mehrere Bildsensoren.
Rechts: Aufnahme mit einem Objektiv und mehreren zusätzlichen Mikrolinsen vor dem Bildsensor.
Bei plenoptischen Kameras (auch Lichtfeldkameras genannt) wird nicht nur eine Ebene eines dreidimensionalen Objektes projiziert, sondern es werden mehrere Projektionsebenen festgehalten, die später mit geeigneter Software oder digitaler Signalverarbeitung miteinander verknüpft werden können. Dabei können in geringem Umfang der Abbildungsmaßstab und der Betrachtungswinkel variiert werden, aber vor allem können Schärfeebenen für sehr verschiedene Objektweiten realisiert und auch kombiniert werden. Mit anderen Worten können die gewünschte Objektweite und der dazugehörige Schärfentiefebereich nach der Aufnahme festgelegt werden, so dass eine Scharfstellung vor der Aufnahme sogar entfallen kann.
Die Variante mit einem Objektiv hat den Vorteil, dass nur ein Objektiv eingesetzt werden muss, dass entsprechend hochwertig gestaltet werden kann, jedoch den Nachteil, dass ein zusätzliches Mikrolinsen-Array erforderlich ist. Bei der anderen Variante müssen mehrere Objektive eingesetzt werden, bei gleichem Bildwinkel kann die Bauform so jedoch erheblich flacher gestaltet werden.
- Vier verschiedene Repräsentationen einer einzigen plenoptischen Makroaufnahme
Für die Animation von Bilderfolgen einer plenoptischen Kamera siehe:
- Nahaufnahme von Tasten einer Computer-Tastatur mit einer Lichtfeldkamera von Lytro
- Lytro light field camera - Piano Player
Bewegtbilder
[Bearbeiten]Bei Aufnahmen von Bewegtbildern ergeben sich oft besondere Anforderungen an die automatische Scharfstellung und Blendensteuerung. Da sich die Entfernung und Helligkeit der Motive kontinuierlich und stetig ändern kann, müssen diese im Objektiv ebenso kontinuierlich und stufenlos nachgeführt werden können, um Helligkeitssprünge zwischen aufeinanderfolgenden Einzelbildern und ungewollte Unschärfen zu vermeiden.
Bewegtbilder stellen in Bezug auf die Pixelfehler höhere Ansprüche an die verwendeten Bildsensoren, da auf dem Bildsensor örtliche Häufungen von Fehlern bei Schwenks und bewegten Motiven als ortsfeste Unregelmäßigkeiten besonders deutlich sichtbar und störend sein können.
Synchrone Tonaufnahmen
[Bearbeiten]Wenn zu den Bewegtbildern auch synchrone Tonaufnahmen gemacht werden sollen, ist es gegebenenfalls sinnvoll, Objektive und Kameragehäuse mit geringer Geräuschentwicklung zu benutzen. Hierzu gibt es spezielle Objektive mit Linearmotoren oder mit Ultraschallmotoren, die bei der Scharfstellung oder der Einstellung von Blende oder Entfernung fast keine hörbaren Geräusche verursachen. Alternativ können externe Mikrophone an die Kamera angeschlossen oder digitale Audiorekorder eingesetzt werden.
Bildstabilisierung
[Bearbeiten]
Es gibt verschiedene Möglichkeiten der Bildstabilisierung, wobei zwischen rein mechanischer, optomechanischer, elektronischer und informationstechnischer Bildstabilisierung unterschieden werden kann. In der Regel können alle Arten der Bildstabilisierung auch kombiniert werden.
Die mechanische Bildstabilisierung geschieht in der Regel mit mechanischen Aufbauten am optischen System. Diese können statisch sein, wie zum Beispiel ein Stativ. Sie können aber auch den durch die Massenträgheit verursachten Impuls oder Drehimpuls von Gegenständen verwenden, um das optische System im Raum stabil ausgerichtet zu halten, wie zum Beispiel mit Kreiselstabilisatoren oder mit Schwebestativen, die mit Zusatzgewichten beschwert wurden.
Die optomechanische Bildstabilisierung ist im optischen System integriert. Im allgemeinen wird die auszugleichende Unruhe heute mit elektronischen Bewegungssensoren gemessen und kann dann mit Aktoren ausgeglichen werden, die die Lage von bestimmten optischen Elementen oder Bildsensoren verändern.
Die elektronische Bildstabilisierung erfolgt durch elektronische Signalverstärkung im Lichtwandler (siehe auch Abschnitt Lichtwandlung), die eine Verkürzung der Belichtungszeit und somit sowohl eine Verringerung von Bewegungs- als auch von Verwacklungsunschärfen zur Folge hat. Hierbei besteht allerdings die Gefahr, dass Rauschsignale ebenfalls verstärkt werden und die Bildqualität erniedrigen.
Nach der Analog-Digital-Wandlung der elektrischen Signale können die Daten auf sehr vielfältige Weise auf informationstechnischem Wege analysiert und manipuliert werden (siehe auch Abschnitt Digitale Bilder), um eine Bildstabilisierung durchzuführen.
Optomechanische Bildstabilisierung
[Bearbeiten]
Position und Ausrichtung einer Kamera im Raum können sich während einer Aufnahme verändern, so dass durch diese Bewegung in der Aufnahme Unschärfen entstehen können. Prinzipiell gibt es sechs unabhängige Freiheitsgrade, in der sich eine Kamera in Bezug auf ein aufzunehmendes Objekt gleichzeitig bewegen kann:
- Translation entlang der
- optischen Achse O (rot), nach vorne oder nach hinten
- horizontalen Achse H (blau) senkrecht zur optischen Achse O, nach rechts oder nach links
- vertikalen Achse V (grün) senkrecht zur optischen Achse O, nach oben oder nach unten
- Rotation um die
- optische Achse O (rot), rechts oder links herum ("rollen", englisch: "to roll" = "wanken")
- horizontale Achse H (blau) senkrecht zur optischen Achse, nach oben oder nach unten ("nicken", englisch: "to pitch" = "neigen")
- vertikale Achse V (grün) senkrecht zur optischen Achse, nach rechts oder nach links ("gieren", englisch: "to yaw" = "schwanken")
Zur Ermittlung der Bewegung können Objektive und Kameragehäuse mit Beschleunigungssensoren ausgestattet werden. Mit optomechanischen Systemen können im Objektiv oder am Bildsensor im Kameragehäuse entsprechende Kompensationsbewegungen erzeugt werden. Bei modernen digitalen Kamerasystemen können die Bildstabilisatoren im Objektiv und im Kameragehäuse kombiniert und synchronisiert werden.
Eine Verschiebung entlang der optischen Achse kann durch eine Nachfokussierung kompensiert werden, wobei die Objektweite nachgeführt werden muss.
Die Verschiebungen senkrecht zur optischen Achse können durch eine parallele Verschiebung des Strahlengangs oder durch eine entsprechende Verschiebung der Bildebene kompensiert werden.
Eine Drehung um die optische Achse ("rollen", englisch: "roll") kann durch eine mitlaufende Rotation der Bildebene kompensiert werden.
Die Rotationen senkrecht zur optischen Achse können durch eine Verkippung des Strahlengangs oder durch eine entsprechende Verkippung der Bildebene kompensiert werden. Hierbei kann zwischen der Verkippung zur Horizontlinie ("nicken", englisch: "pitch") und der Verkippung zur Lotrichtung ("gieren", englisch: "yaw") unterschieden werden.
Die folgenden beiden nacheinander getätigten teleskopischen Aufnahmen verdeutlichen die bildstabilisierende Wirkung bei der freihändigen Aufnahme des farbig szintillierenden Fixsterns Sirius mit einer Belichtungszeit von jeweils 15 Sekunden. Das erste Bild ist ohne eine Bildstabilisierung aufgenommen und das zweite Bild mit einer synchronisierten Bildstabilisierung zwischen dem Superteleobjektiv und dem beweglichen Bildsensor (Abkürzung "IBIS" für "In-Body Image Stabilisation", zu Deutsch "Bildstabilisierung im Gehäuse") eines digitalen Kamerasystems. Die linke Hand befand sich während der Aufnahmen jeweils vorne unter dem Teleobjektiv, die rechte Hand rechts am Kameragehäuse und das rechte Auge stützte das Kameragehäuse an der Suchermuschel. Die Atemluft wurde für die Dauer der Aufnahmen angehalten. In beiden Bildern betragen die Bildhöhe rund ein Bogengrad und die Bildbreite rund zwei Bogengrad. Der Stern bewegte sich während der Belichtung in Bezug auf das horizontale Bezugssystem am Fixsternhimmel nur um 1/16 Bogengrad von links nach rechts. Die vertikale Nickbewegung ("pitch") der Kamera lag bei diesen in Bezug auf die Bildstabilisierung extrem herausfordernden Aufnahmen bei ungefähr einem halben Bogengrad. In beiden Bildern gab es zudem eine kontinuierliche Winkeldrift in horizontaler Richtung. In dieser Konstellation konnten die höherfrequenten Variationen bei aktivierter Bildstabilisierung insbesondere in vertikaler Richtung über mehrere Sekunden fast vollständig stabilisiert werden.
- Wirkung eines Bildstabilisators bei Teleaufnahmen von Sirius
-
Ohne Bildstabilisierung im Teleobjektiv oder im Kameragehäuse.
-
Mit synchronisierter Bildstabilisierung zwischen Teleobjektiv und Kameragehäuse. Zwischenzeitlich konnte die vertikale Nickbewegung der Kamera nicht mehr vollständig kompensiert werden.
Rotationsbewegungen
[Bearbeiten]Die Gravitation der Erde verursacht eine konstante Kraft, die beim freien Fall eine Beschleunigung verursacht. Rotieren jedoch Kamera und Objekt in der Zeit auf einen vollen Kreis mit oder um ein Kreiszentrum mit der gleichen Kreisfrequenz
und in der gleichen Richtung im Abstand von der Rotationsachse , entsteht eine Zentripetalkraft, obwohl sich Kamera und Objekt im Bezug zueinander gar nicht bewegen. Dabei wirkt die folgende Zentripetalbeschleunigung auf die Kamera und somit auch auf deren Beschleunigungssensoren:
Erdrotation
[Bearbeiten]Am Äquator beträgt der mittlere Erdradius
und die Kreisfrequenz
- pro siderischem Tag.
Die Dauer eines siderischen Tages beträgt
- oder 23 Stunden, 56 Minuten und 4 Sekunden.
Die entsprechende Kreisfrequenz beträgt dann also
- oder 15,7 Bogensekunden pro Sekunde.
Bei einer teleskopischen Aufnahme mit einem Bildwinkel von 2 Bogengrad (= 120 Bogenminuten = 7200 Bogensekunden) verschiebt sich bei dieser Kreisfrequenz der in einem Inertialsystem erfasste Bildausschnitt schon nach einer halben Sekunde um mehr als den tausendsten Teil seiner Ausdehnung, so dass ab dieser Belichtungszeit von einem menschlichen Betrachter eine zunehmend erkennbare Unschärfe im aufgenommenen Bild entsteht.
Daraus resultiert am Äquator eine konstante Beschleunigung in Richtung Zenit von:
Diese Zentripetalbeschleunigung hat betragsmäßig den 265. Teil der Erdbeschleunigung, und beide wirken am Äquator in Richtung Nadir. Auf Breitengraden nördlich oder südlich des Äquators ist die Zentripetalbeschleunigung betragsmäßig kleiner (gleiche Kreisfrequenz, aber geringerer Abstand von der Rotationsachse) und wirkt in die Richtung senkrecht auf die zwischen Nord- und Südpol verlaufenden Rotationsachse und somit dann auch nicht mehr gleichgerichtet zur Erdbeschleunigung. In Bezug auf eine auf der Erdoberfläche ortsfeste Kamera ändert sich die Richtung dieser Beschleunigungen jedoch nicht. An den Polen selbst wirkt gar keine Zentripetalbeschleunigung mehr.
Rotation der Erde um die Sonne
[Bearbeiten]Für die Rotation der Erde um die Sonne ergibt sich aus dem mittleren Radius der Erdbahn
und aus der Dauer eines siderischen Jahres (365,256 Tage)
die entsprechende Kreisfrequenz:
- oder 0,04 Bogensekunden pro Sekunde.
Die Zentripetalbeschleunigung in Richtung zur Sonne beträgt dann:
Das ist betragsmäßig zirka der 1650. Teil der Erdbeschleunigung.
Maximale Belichtungszeit
[Bearbeiten]Eine Kamera, die im Bezug zum Horizont fest ausgerichtet ist, dreht sich aufgrund der Erdrotation mit der Kreisfrequenz um eine bestimmte Achse. Der Drehwinkel beträgt in Anhängigkeit der Belichtungszeit :
Wenn dieser Drehwinkel mit dem diagonalen Bildwinkel der Aufnahme in Beziehung gesetzt wird, ergibt sich das folgende Verhältnis :
Wenn die Erdrotation bei der Bildstabilisierung nicht berücksichtigt wird, führt dieser Anteil während der Belichtung zu einer Überkompensation, die bei zu langen Belichtungszeiten erkennbar werden kann. Für das minimal akzeptable Winkelverhältnis ergibt sich die maximale Belichtungszeit aus der folgenden Umformung:
In Bezug auf empirische Abschätzungen für siehe auch Abschnitt Schärfentiefe und Abschnitt Bewegte Motive.
Für einen Bildwinkel einer teleskopischen Aufnahme von und ein minimal gefordertes Winkelverhältnis ergibt sich beispielsweise eine maximale Belichtungszeit von:
Für einen diagonalen Bildwinkel einer weitwinkligen Aufnahme von und ein minimal gefordertes Winkelverhältnis ergibt sich zum Beispiel eine entsprechend längere maximale Belichtungszeit von:
Als Faustformel gilt, dass die maximale Belichtungszeit in Sekunden, den sechsten Teil des diagonalen Bildwinkels in Grad nicht überschreiten darf:
| Objektivart | Diagonaler Bildwinkel |
Maximale Belichtungszeit |
|---|---|---|
| Fischauge | 180° | 30 Sekunden |
| Ultraweitwinkel | 120° | 20 Sekunden |
| Superweitwinkel | 90° | 15 Sekunden |
| Weitwinkel | 60° | 10 Sekunden |
| Normal | 48° | 8 Sekunden |
| Portrait | 24° | 4 Sekunden |
| Tele | 12° | 2 Sekunden |
| Supertele | 6° | 1,0 Sekunden |
| Ultratele | 3° | 0,5 Sekunden |
In Bezug auf das im 20. Jahrhundert sehr verbreitete Kleinbildsystem (35-Millimeter-Film) ergibt sich überschlägig, dass die maximale Belichtungszeit in Sekunden, 400 Millimeter geteilt durch die verwendete Brennweite nicht überschreiten darf.
Astrophotographie
[Bearbeiten]Diese Überlegungen gelten im Übrigen auch, wenn mit einer ortsfesten Kamera der Sternenhimmel aufgenommen werden soll. Eine im Inertialsystem kompensierende, und somit notwendigerweise im dreidimensionalen Raum orientierte Bildstabilisierung ändert den Bildausschnitt während einer beliebig lange dauernden Belichtung nicht.
Für astronomische Zwecke gibt es Kamerastative, die auf den Himmelspol ausgerichtet werden und mit der Kreisfrequenz der Erde entgegen der Erddrehung (also nach Westen) um die Polachse rotieren. Moderne Systeme, die über zwei beliebige, linear unabhängige Rotationsachsen verfügen, können den Standort der Kamera, die Neigung der optischen Achse zum Horizont und die Himmelsrichtung der optischen Achse erfassen und die entsprechenden Kompensationsdrehungen dann automatisch berechnen und durchführen. Eine Alternative dazu ist die Bewegungskompensation direkt in der Bildebene, wo das Bild während der Aufnahme um die optische Achse entsprechend rotiert und senkrecht dazu verschoben werden kann.
Hierbei ist grundsätzlich zu beachten, dass die Rotation der aufgenommenen Objekte in einem sphärischen äquatorialen System stattfindet, und die Bewegung in der Bildebene von der beobachteten Deklination der Objekte und von der eingesetzten Brennweite abhängt. Siehe auch:
Bewegte Kamera im rotierenden System
[Bearbeiten]Bei mit der Geschwindigkeit in Bezug auf die Erdoberfläche bewegter Kamera können aufgrund der Erdrotation zusätzlich auch noch Coriolis-Beschleunigungen auftreten, die senkrecht zur Rotationsachse und senkrecht zur Bewegungsrichtung wirken:
Bewegt sich eine Kamera senkrecht zur Rotationsachse, auf der Erdoberfläche also am Nord- oder Südpol oder entlang eines Breitenkreises wie zum Beispiel dem Äquator, kann das Kreuzprodukt durch das Produkt der Vektorbeträge ersetzt werden, um den Betrag der Coriolis-Beschleunigung zu ermitteln:
Bewegt sich die Kamera beispielsweise in einem Flugzeug mit einer Geschwindigkeit von auf einem Großkreis über den Nordpol (die Kreisfrequenz beträgt hierbei übrigens ungefähr Bogensekunden pro Sekunde), ergibt sich für die Coriolis-Beschleunigung:
Das ist betragsmäßig zirka der 320. Teil der Erdbeschleunigung.
Die Zentripetalbeschleunigung durch die um die Sonne laufende Erdbahn ändert in Bezug auf eine auf der Erdoberfläche ortsfeste Kamera permanent ihre Richtung. Auch die Coriolis-Beschleunigungen von schnell bewegten Kameras liegen in der Größenordnung der Beschleunigungen typischer Wackelbewegungen und Vibrationen von Kameras. Dies kann das Messergebnis der Beschleunigungssensoren beeinflussen und muss für eine Kompensation entsprechend präzise bestimmt und berücksichtigt werden.
Informationstechnische Bildstabilisierung
[Bearbeiten]
1.: Mit unbewegter Kamera aufgenommene Szene
2.: Mit sich bewegender Kamera aufgenommene Szene
3.: Analyse der gleichen Bildausschnitte (grüner Rahmen) in der mit sich bewegender Kamera aufgenommenen Szene (blauer Rahmen)
4.: Verwendung der analysierten Bildausschnitte der mit sich bewegender Kamera aufgenommenen Szene
Bewegtbilder setzen sich aus aufeinanderfolgenden Einzelbildern zusammen, die in der Regel einen Bildausschnitt zeigen sollen, der sich nicht verändert oder nur langsam ändert, wenn zum Beispiel der Abbildungsmaßstab variiert wird oder die Kamera geschwenkt wird. Bei Aufnahmen, die mit freier Hand oder aus anderen Gründen mit unbeabsichtigt bewegter Kamera erstellt werden, verändert sich der Bildausschnitt mehr oder weniger stark und auf zufällige Weise. Durch die Messung der Bewegung der Kamera mit Bewegungssensoren oder durch eine Bildanalyse mittels Software kann diese Veränderung ermittelt und ausgeglichen werden, wenn in Kauf genommen wird, dass der für die stabilisierte Aufnahme zur Verfügung stehende Bildausschnitt kleiner ist als der von der Kamera erfasste Bildausschnitt. Dabei ergibt sich zwangsläufig eine Reduktion der verfügbaren Information, da auf der einen Seite Bildinhalte verworfen werden müssen und auf der anderen Seite die Bildauflösung der verbleibenden Bildausschnitte im Vergleich zur unstabilisierten Aufnahme reduziert ist.
Die vier Bildsequenzen in der Abbildung aus jeweils drei aufeinanderfolgenden Einzelbildern veranschaulichen die Wirkungsweise einer Bildstabilisierung mit der Translation eines geeigneten Bildausschnittes:
Ein elementares Problem bei diesem Verfahren ist die Ermittlung geeigneter Fixpunkte im zu stabilisierenden Bildausschnitt, da sich das Motiv oder Teilmotive zwischen aufeinanderfolgenden Einzelaufnahmen ebenfalls bewegt haben können, wie der Schmetterling zwischen Katze und Elephant in den Beispielbildern. Ähnliche Probleme ergeben sich, wenn die Kamera während der Aufnahme absichtlich bewegt wird, wie beispielsweise beim Schwenken, oder wenn die Brennweite während der Aufnahme variiert wird.
Mit entsprechend höherem Aufwand können auch Änderungen des Abbildungsmaßstabs und Bilddrehungen zwischen den Einzelaufnahmen ermittelt und durch entsprechenden Transformation ausgeglichen werden, die dann nicht nur die Translation sondern auch die Rotation und Skalierung berücksichtigen muss, wie zum Beispiel eine zweidimensionale Helmert-Transformation. Sollen auch dynamische perspektivische Verzerrungen ausgeglichen werden, können auch noch aufwendigere affine Transformationen angewendet werden.
Eine informationstechnische Bildstabilisierung kann durch eine optomechanische Bildstabilisierung ergänzt werden, um den Kompensationsspielraum zu vergrößern.
Ablenkung von Lichtstrahlen
[Bearbeiten]Es gibt verschiedene Möglichkeiten, die optische Achse in einem optischen System um einen bestimmten Betrag parallel zu verschieben oder um einem bestimmten Winkel zu verkippen. Hierzu können reflektierende oder brechende optische Elemente in den Strahlengang eingebaut werden. An Kanten, Blenden und optischen Gittern wird das Licht gebeugt, so dass die Beugung in bestimmten Fällen ebenfalls für die gezielte Ablenkung von Lichtstrahlen ausgenutzt werden kann.
Bei der Verwendung von optischen Medien, mit unterschiedlichen Brechungsindices muss gegebenenfalls berücksichtigt werden, dass das Licht an jeder Grenzfläche zwischen zwei Materialien mit verschiedener optischer Dichte nicht nur gebrochen, sondern auch reflektiert wird.
Für die Ausbreitung in optischen Medien gilt allgemein immer das Fermatsche Prinzip, das lokal betrachtet mit dem Huygensschen Prinzip veranschaulicht werden kann. Mit diesem Prinzip lassen sich die Effekte Reflexion, Brechung und Beugung erklären.
Refraktion an optischen Übergängen
[Bearbeiten]Die Ausbreitungsgeschwindigkeit von elektromagnetischen Wellen in einem optischen Medium mit der Brechzahl kann mit der Lichtgeschwindigkeit im Vakuum folgendermaßen bestimmt werden:
Die Wellenlänge verkürzt sich mit wachsender Brechzahl linear, da die Frequenz der elektromagnetischen Welle unverändert bleibt:

Brechung findet an einem Punkt O beim Übergang zwischen zwei optischen Medien statt, die sich durch die Ausbreitungsgeschwindigkeiten des Lichts und unterscheiden. Unter Berücksichtigung der Ausbreitung mit Huygensschen Elementarwellen mit der jeweiligen Lichtgeschwindigkeit und entsprechend dem Fermatschen Prinzip legt das Licht den schnellsten Weg zwischen einem Startpunkt A und einem Endpunkt B zurück. Dieser Weg setzt sich aus den beiden Teilstrecken und zusammen.
Für diese beiden Teilstrecken gilt:
Die entsprechenden Laufzeiten in den beiden optischen Medien ergeben sich dann folgendermaßen:
Die gesamte Laufzeit von A nach B ist die Summe dieser beiden Zeiten:
Diese Funktion variiert entlang der Grenzkante zwischen den beiden optischen Medien mit dem Parameter und kann nach diesem differenziert werden, um bei der Nullstelle der Ableitung das Minimum zu ermitteln:
Für die beiden rechtwinkligen Dreiecke ergeben sich die Sinus der Winkel zur Flächennormalen aus den Quotienten zwischen den Gegenkatheten und den Hypotenusen:
Eingesetzt ergibt sich dann:
Bei der Brechung an einer optischen Grenzfläche zwischen den optischen Medien 1 und 2 gilt dieses Snelliussche Brechungsgesetz, das üblicherweise in der folgenden Form mit den beiden zu den Lichtgeschwindigkeiten antiproportionalen Brechzahlen und dargestellt wird:

Wellenoptisch ergibt sich entsprechend den unterschiedlichen Ausbreitungsgeschwindigkeiten und Wellenlängen hierfür das nebenstehende Bild.
Reflexion an optischen Übergängen
[Bearbeiten]
Beim Übergang eines Lichtstrahls von einem optischen Medium mit der Brechzahl in ein optisches Medium mit der Brechzahl wird das Licht nicht nur gebrochen, sondern an der Grenzfläche auch reflektiert. Dabei spielt es für den Reflexionsgrad keine Rolle, ob das Licht von optische dünneren oder vom optische dichteren Medium auf diese Grenzfläche trifft. Die Richtungen des Lichtstrahls werden durch den Einfallswinkel , den Winkel des reflektierten Lichtstrahls und den Ausfallswinkel beschrieben. Alle Winkel werden zum senkrecht auf der Grenzfläche stehenden Lot, also der Normalen, an der Stelle des Lichtübergangs angegeben.
Für die Reflexion gilt das Reflexionsgesetz:
Bei der Brechung findet eine Transmission statt, und auch hier gilt das Snelliussche Brechungsgesetz:
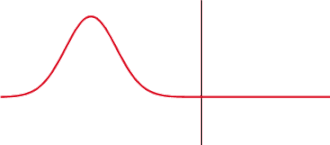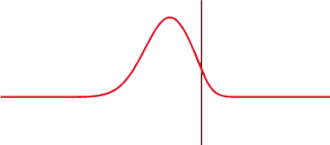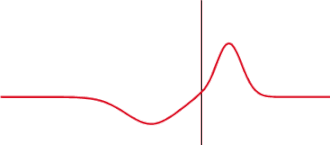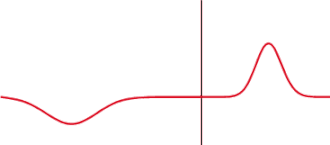
Der Grad der Reflexion kann mit Hilfe der Fresnelschen Formeln bestimmt werden. Für den Sonderfall senkrecht einfallendes Lichtes gilt dann die folgende Beziehung:
In der nachstehende Tabelle sind die entsprechenden Reflexionsgrade für einige Materialien an der Grenze zu einem Vakuum (beziehungsweise in guter Annäherung auch zu Luft oder anderen Gasen) angegeben:
| Brechzahl | Relexionsgrad | Material |
|---|---|---|
| 1,00 | 0,000 | Vakuum / Luft |
| 1,33 | 0,020 | Wasser |
| 1,38 | 0,025 | Magnesiumfluorid |
| 1,46 | 0,035 | Quarzglas |
| 1,52 | 0,043 | Fensterglas |
| 1,74 | 0,073 | Diiodmethan |
| 2,42 | 0,172 | Diamant |
Mit zunehmend schrägem Lichteinfall wächst der Reflexionsgrad langsam an. Bei Einfallswinkeln , die einen Ausfallswinkel erzeugen, der größer als 90° ist, tritt eine Totalreflexion ein, so dass dann der Reflexionsgrad eins und der Transmissionsgrad null betragen. Der kritische Einfallswinkel kann direkt aus dem Snelliusschen Brechungsgesetzes bestimmt werden:

Die quadratische Abhängigkeit der Reflexion von den Brechzahlen kann zur Verringerung der Gesamtreflexion ausgenutzt werden, indem zwischen die beiden optischen Medien ein weiteres Medium eingebracht oder sogar mehrere weitere Medien eingebracht werden, deren Brechkraft zwischen derjenigen der beiden optischen Medien liegt. Bei senkrechtem Übergang zwischen Fensterglas mit dem Brechungsindex und Vakuum liegt der Reflexionsgrad bei 4,3 Prozent.
Wird auf das Fensterglas eine zusätzliche optische Schicht mit dem Brechungsindex 1,233 aufgebracht, dann beträgt die Reflexion an beiden Grenzflächen, also zwischen Vakuum und optischer Schicht sowie zwischen optischer Schicht und Fensterglas, jeweils 1,1 Prozent, zusammen also nur 2,2 Prozent.
Bei zwei zusätzlichen Schichten mit der Brechzahl 1,150 und 1,322 beträgt die Reflexion an allen drei Grenzflächen jeweils 0,5 Prozent, zusammen also sogar nur 1,5 Prozent.
Hierbei ist zu beachten, dass bei der Reflexion beim Übergang zu einem optisch dichteren Medium ein Phasensprung von 180° auftritt. Beim Übergang zu einem optisch dünneren Medium tritt bei der Reflexion keine Änderung der Phase auf.
Die Wellen mit gleicher Ausbreitungsrichtung und gleicher Wellenlänge interferieren bei gleicher Phasenlage konstruktiv und bei gegenläufiger Phasenlage (die Phasendifferenz beträgt dann 180°) destruktiv. Unter Berücksichtigung der Phasensprünge können die Schichtdicken einer vorgegebenen Wellenlänge so angepasst werden, dass diese Wellenlänge dann fast vollständig transmittiert wird. Bei anderen Wellenlängen tritt dann eine geringere Transmission, und bei manchen Wellenlängen sogar gar keine Transmission mehr auf.
Zur Reduktion von Reflexionen an Grenzflächen werden bei optischen Systemen einzelne Linsen sehr häufig zu einer Einheit zusammengefasst, indem sie mit optischem Kitt verbunden werden (Verkittung).
Durch die Variation der Brechzahlen, der Schichtdicken und der Anzahl der Schichten stehen sehr viele Gestaltungsmöglichkeiten zur Verfügung, bei den die Reflexions- und Transmissionsgrade nicht mehr analytisch, sondern nur noch mit Simulationsberechnungen ermittelt werden können. Typische Anwendungsfelder sind die Oberflächenvergütung von Objektivlinsen zur Vermeidung von Reflexionen und insbesondere von Mehrfachreflexionen zwischen den Linsengruppen. Ferner können mit dünnen Schichten verschiedener Brechkraft Interferenzfilter hergestellt werden, die nur einen bestimmten und definierbaren Wellenlängenbereich passieren lassen.
Parallele Verschiebung
[Bearbeiten]
Um einen parallelen Versatz der optischen Achse um den Betrag zu erwirken, kann zum Beispiel eine um den Winkel zur optischen Achse geneigte planparallele Platte in den Strahlengang eingebracht werden.
Nach dem Snelliusschen Brechungsgesetz sind die Richtung des einfallenden Strahls und des ausfallenden Strahls parallel - die Winkel zwischen der optischen Achse und dem Lot der planparallelen Platte sind also vor und hinter der Platte identisch (siehe Abbildung rechts), wobei der Winkel die Winkel des Lichtstrahls zu den beiden Loten innerhalb der Platte beschreibt.In den folgenden Rechenbeispielen wird die Brechzahl außerhalb der planparallelen Platte mit der Brechzahl als eins angesetzt.
Die Länge ist eine Hilfsgröße zur Berechnung mit Hilfe der Anwendung des Sinussatzes. Wenn die Dicke der planparallelen Platte ist, ergibt sich:
Unter erneuter Verwendung des Sinussatzes gilt jedoch auch:

Aus der Gleichsetzung der beiden Formeln ergibt sich für den Versatz :
Die maximal erreichbare Ablenkung entspricht bei einer Neigung von 90° der Dicke der Platte:
Für kleine Neigungswinkel (im Bogenmaß) gilt die Näherung:
Auf der anderen Seite können durch planparallele Platten auch unerwünschte Aberrationen verursacht werden: wenn einfallende Lichtstrahlen aus unterschiedlichen Richtungen in einem bestimmten Punkt der planparallelen Platte eintreten, ergeben sich unterschiedliche Austrittsorte. Durch diese seitlichen Abweichungen kann es bei optischen Abbildungen zur Verschlechterung der Bildschärfe kommen. Beim Rechnen von Objektiven muss für höchste Ansprüche dieser Effekt berücksichtigt werden, wenn sich vor dem Bildsensor planparallele Platten wie zum Beispiel Infrarotfilter, optische Tiefpassfilter, Mikrolinsen- oder Farbfilterarrays befinden (siehe auch Abschnitt Infrarot-Sperrfilter und folgende).
Verkippung
[Bearbeiten]
Um eine Verkippung der optischen Achse um den Winkel zu erwirken, kann zum Beispiel ein Dreiecksprisma mit dem Prismenwinkel im Scheitel der Querschnittsfläche in den Strahlengang eingebracht werden.
Nach dem Snelliusschen Brechungsgesetz ergibt sich beim Einfall in das Prisma mit dem Einfallswinkel :
Mit dem Prismenwinkel ergibt sich geometrisch:
Nach dem Snelliusschen Brechungsgesetz ergibt sich beim Ausfall aus dem Prisma der Ausfallswinkel :

Der Ablenkwinkel ergibt sich dann wiederum rein geometrisch aus den oben bestimmten Winkeln:
Der minimale Ablenkwinkel ergibt sich, wenn Einfallswinkel und Ausfallswinkel identisch sind. Der Ablenkwinkel ergibt sich in diesem Fall wie folgt:
mit:
Demzufolge kann der Brechungsindex aus dem minimalen Ablenkwinkel bestimmt werden:
Die maximale Ablenkung des Lichtstrahls ergibt sich sowohl bei einem Einfallswinkel von 90° als auch bei einem Ausfallswinkel von 90°. Der maximale Ablenkwinkel beträgt dann:

Bei der Brechung kommt es zur Dispersion, also der wellenlängenabhängigen Varianz der Brechzahl. Dabei werden blaue Lichtstrahlen stärker gebrochen als rote, so dass es bei optischen Abbildungen zur chromatischen Aberration kommt (siehe auch Abschnitt Chromatische Aberration).
Atmosphärische Störungen
[Bearbeiten]
Durch die atmosphärische Refraktion tritt eine Winkelabweichung des scheinbaren Ortes eines abgebildeten Punkts von seiner tatsächlichen Lage, die im Vakuum beobachtet werden würde. Im Zenit verschwindet diese Abweichung, mit größer werdenden Zenitwinkeln nimmt sie aber stetig zu, und der scheinbare Ort ist am Horizont bei normalen atmosphärischen Bedingungen zirka 35 Bogenminuten höher als der wirkliche Ort. Der Winkelabstand zwischen zwei Punktobjekten mit unterschiedlicher Zenitdistanz wird demzufolge durch eine differentielle Refraktion verkleinert. Durch diesen Effekt erscheinen Sonne und Mond besonders im Horizontnähe in vertikaler Richtung verkürzt und somit nicht mehr kreisförmig, sondern in die Breite gezogen.
Eine weitere, wenn auch geringere, Winkelabweichung ist wellenlängenabhängig und wird auch atmosphärische Dispersion genannt. Die stärke Brechung des kurzwelligen blauen Lichtes führt dazu, dass kontrastreiche Kanten in Horizontnähe mit Farbsäumen abgebildet werden. An der Unterkante von weißlichen Objekten ergeben sich in atmosphärischen Aufnahmen deswegen gelbliche und rötliche Farben und an der Oberkante grünliche und blaue. Der blaue Lichtanteil wird jedoch meistens durch die Rayleigh-Streuung seitlich weggestreut, so dass er nicht zum Beobachtungspunkt gelangt. Dies erklärt den grünen Blitz, der bei günstigen Sichtverhältnissen bei Sonnenaufgang oder Sonnenuntergang an der Oberkante der Sonnenscheibe beobachtet werden kann. Auch bei Planetenscheiben sind solche Farbeffekte zu beobachten.

Bei optischen Abbildungen gibt es bei größer werdenden Objektweiten zunehmend starke atmosphärische Aberrationen. Der Bildkontrast wird durch Streuung in der Atmosphäre an Luftmolekülen, Staubpartikeln und Wassertröpfchen oder Eiskristallen verringert, weil insbesondere bei Tageslicht oder bei dem Vorhandensein von künstlichen Lichtquellen auch in dunklen Objektbereichen Streulicht aus den helleren Objektbereichen oder von Lichtquellen außerhalb des Bildfelds überlagert wird, so dass der Dunkelwert durch dieses Falschlicht deutlich erhöht sein kann.
Durch die Extinktion in der Atmosphäre gibt es zudem einen Lichtverlust, der genauso wie im Wasser und in anderen optischen Medien auch von der Wellenlänge des beobachteten Lichts abhängt und nicht nur durch die wellenlängenabhängige Streuung (siehe auch Streuung), sondern auch durch die wellenlängenabhängige Absorption verursacht wird. Sichtbares Licht, das aus dem Zenit die gesamte Atmosphäre durchläuft, wird um ungefähr zwanzig Prozent abgeschwächt. Hierbei kommt es auch zur Veränderung der beobachteten Verteilungen in den Lichtspektren, die einen Einfluss auf den Weißpunkt und den Weißabgleich von digitalen Bildern haben. Bei zunehmender Zenitdistanz wird der Weg durch die Atmosphäre immer länger, und somit nimmt auch die Abschwächung der Lichtstrahlen zu. Bei der Beobachtung eines Objektes außerhalb der Troposphäre, die ungefähr eine Höhe von 15 Kilometern hat, ist die Weglänge für die Lichtstrahlen durch die Troposphäre am Horizont (Zenitdistanz 90°) fast 50 mal größer als bei einem Objekt im Zenit (Zenitdistanz 0°).
Durch thermische Schwankungen in der Atmosphäre resultieren Dichteschwankungen und somit auch kleine Turbulenzen mit variierenden Brechungsindizes, die dafür verantwortlich sind, dass die beobachtete Helligkeit von quasi-punktförmigen Objekten zeitlich nicht konstant ist. Bei der Beobachtung - beispielsweise von Sternen - wird dieser durch die Luftunruhe hervorgerufene Effekt auch Szintillation genannt.
Die Periodendauer dieser atmosphärischen Schwankungen liegt typischerweise im Bereich von einigen Millisekunden. Bei Belichtungszeiten, die kürzer sind, ergibt sich eine Momentaufnahme mit örtlich variierenden Positionen, bei längeren Belichtungszeiten werden diese Schwankungen integriert, was zu einer Mittelung der registrierten Helligkeiten und somit zur Weichzeichnung von Objektkanten im Bild führt. Bei Objektiven oder Fernrohren, die nicht beugungsbegrenzt sind und nicht über eine aktiv korrigierende adaptive Optik verfügen, setzt die entsprechende Auflösungsbegrenzung bei terrestrischer Beobachtung ab bei einer Öffnungsweite von mehr als ungefähr 50 Millimetern ein, bei erdbasierten Teleskopen liegt die maximal sinnvolle Öffnungsweite bei 200 Millimetern. Teleskope in Satelliten und Raumschiffen arbeiten hingegen rein beugungsbegrenzt, da die Lichtstrahlen hierbei in der Regel nicht durch die Erdatmosphäre beeinflusst werden.
- Kugel des Berliner Fernsehturms (Durchmesser 32 Meter) aus fünf Kilometern Entfernung
-
Originalaufnahme mit Blaustich, geringem Kontrast und ungleichmäßigen Objektkanten durch die Einflüsse der Atmosphäre (Belichtungszeit 2 ms)
-
Atmosphärische Kontrastverluste und Farbstich wurden durch digitale Tonwertkorrekturen kompensiert
-
Simulation der Weichzeichnung bei einer längeren Belichtung durch atmosphärisches Flimmern
Lichtwandlung
[Bearbeiten]Dieses Kapitel beschäftigt sich mit elektrischen und elektronischen Verfahren, Teilchen – insbesondere Lichtteilchen (Photonen) – zu detektieren, um digitale Bilder zu erzeugen. Da Elementarteilchen oft mittelbar durch Sekundarteilchen nachgewiesen werden und diese Sekundarteilchen auch Lichtteilchen sein können, wird auch deren Detektion häufig photographisch vorgenommen, also wie die Übersetzung dieses Begriffes aus dem Griechischen besagt: es wird mit Licht geschrieben. Typischerweise sieht das Prinzip der Bildgebung durch Lichtwandlung wie folgt aus:

- Ein Objekt muss Strahlung aussenden, um aufgenommen werden zu können. Oft wird ein solches Objekt zu diesem Zweck von außen mit Strahlung angeregt.
- Die Strahlung wird detektiert, wobei häufig direkt oder indirekt Licht verwendet wird, da es zum Nachweisen durch Brechung und Reflektion gut beeinflusst werden kann (siehe auch Kapitel Bildaufnahme).
- Die im Detektor analog nachgewiesene Strahlung wird mittels einer Analog-Digital-Wandlung in ganzzahlige (also digitale) Werte gewandelt.
- Die digitalen Signale werden nach grundlegenden Prinzipien verarbeitet (zum Beispiel Korrekturen, Linearisierung, Koinzidenzen, Korrelation).
- Die verarbeiteten Daten werden als Rohdaten zwischengespeichert (es kann sich hierbei um einen flüchtigen Speicher handeln).
- Die Rohdaten werden zur Weiterverwendung einer Bildverarbeitung unterzogen (zum Beispiel Farbkorrektur, Kontrast- und Helligkeitsanpassung, Bildausschnitt (siehe auch Kapitel Digitale Bilder).
- Die aufbereiteten digitalen Bilddaten werden gespeichert (oft in einem nicht-flüchtigen Speicher, um sie zu dokumentieren und auch später jederzeit sichtbar machen zu können).
- Die Bilddaten können mit Hilfe einer Bildwiedergabe sichtbar gemacht werden (siehe auch Kapitel Wiedergabe).
Lichtdetektoren
[Bearbeiten]Photoeffekt
[Bearbeiten]
Als der Physiker Albert Einstein 1905 das Wesen des photoelektrischen Effektes entdeckte und beschrieb, wurde damit auch ein wesentlicher Grundstein für die elektronische Lichtdetektion gelegt. Völlig zurecht wurde er für diese Entdeckung für das Jahr 1921 mit dem Physik-Nobelpreis geehrt - es ist erwähnenswert, dass dies der einzige an ihn verliehene Nobelpreis blieb.

Beim äußeren photoelektrischen Effekt übertragen Photonen ihre Energie auf Elektronen, die dadurch aus einem Festkörper herausgelöst werden. Die Lichtquanten müssen hierbei mindestens soviel Energie haben, dass die Austrittsarbeit des jeweiligen Kathodenmaterials überwunden werden kann. Geeignete Materialien für Licht sind Alkalimetalle wie Kalium, Rubidium und Cäsium.
Beim inneren photoelektrischen Effekt übertragen Photonen ihre Energie auf Elektronen, die dadurch vom Valenzband in das Leitungsband gehoben werden. Dadurch erhöht sich die Leitfähigkeit des Festkörpers. Ebenso tritt eine elektrische Spannung an ihm auf. Diese Effekte werden für die Detektion von Strahlung benutzt. Die Lichtquanten müssen hierbei mindestens soviel Energie haben, dass die Bandlücke zwischen Valenzband und Leitungsband überwunden werden kann. Geeignete Materialien für Licht sind Halbleiter wie Silicium oder Germanium.
Es gibt also eine Grenzwellenlänge für die Photonen, oberhalb der keine Elektronen ausgelöst werden können, da die Photonenenergie in diesen Fällen nicht ausreicht.
Mit der Photonenfrequenz und dem Planckschen Wirkungsquantum ergibt sich die Energie eines Lichtteilchens zu:
Das Produkt aus der Wellenlänge und der Frequenz der Photonen respektive der Lichtwellen ist die Lichtgeschwindigkeit :
Beide Beziehungen ergeben zusammengefasst den Zusammenhang zwischen der Energie und der Wellenlänge eines Photons:
Da die Austrittsarbeit überwunden werden muss, damit beim äußeren Photoeffekt ein ausgelöstes Elektron den Festkörper verlassen kann, verbleibt dem freien Elektron die Energiedifferenz aus der Photonenenergie und der Austrittsarbeit als kinetische Energie. Daraus folgt die Bedingung , dafür dass das ausgelöste Elektron überhaupt den Festkörper verlassen kann. Beim äußeren Photoeffekt werden also Elektronen durch einzelne Lichtteilchen aus einem Festkörper (meist aus der Oberfläche von Metallen) herausgelöst und können dann in einem äußeren elektrischen Feld zu einer Anode beschleunigt und auf diese Weise als elektrischer Strom registriert werden.
Beim inneren Photoeffekt verringert sich der elektrische Widerstand eines vom Licht bestrahlten Halbleiters beziehungsweise die in einer Kapazität gespeicherte Ladungsmenge durch einen entsprechenden neutralisierenden Strom respektive Ladungstransport. Auch dieser Effekt kann für den Nachweis und die Messung von Licht verwendet werden.
Photomultiplier
[Bearbeiten]
Ein Photomultiplier nutzt an seiner Kathode den äußeren Photoeffekt zur Erzeugung von freien Elektronen, die durch ein elektrisches Feld auf die erste Dynode beschleunigt werden. Treffen diese Elektronen auf die Dynode erzeugen sie bei hinreichend hoher kinetischer Energie sogenannte Sekundärelektronen. Ein einziges primäres Elektron kann hierbei eine Vielzahl von Sekundärelektronen hervorrufen. Schaltet man nun mehrere solcher Dynoden mit entsprechenden Feldgradienten hintereinander, so werden auch die Sekundärelektronen auf die nächste Dynode beschleunigt und erzeugen dort wiederum neue Sekundärelektronen. Bei dieser kaskadierten Anordnung spricht man von einem Sekundärelektronenvervielfacher. An der letzten Elektrode der Kaskade, der Anode, steht dann ein relativ hoher Strom zur Verfügung, der mit einfachen Mitteln registriert werden kann. Dies führt sogar soweit, dass einzelne Photonen, die an der Kathode ein Elektron auslösen, zeitaufgelöst nachgewiesen werden können. Es ist allerdings nicht gewährleistet, dass ein auf die Kathode auftreffendes Photon tatsächlich immer ein Elektron auslöst, da die Quanteneffizienz in der Regel kleiner als eins ist.
Durch geeignete Maßnahmen ist bei der Beschaltung der Dynoden eines Photomultipliers zu gewährleisten, dass der Strom bei den letzten Dynoden nicht zu hoch wird, weil diese sonst durch das Elektronenbombardement thermisch zerstört werden können.
Mikrokanalplatten
[Bearbeiten]
Anstelle der diskreten Dynoden bei Photomultipliern können zur Sekundärelektronenvervielfachung auch Mikrokanäle aus einem Material verwendet werden, das eine gute Sekundärelektronenausbeute und einen relativ hohen elektrischen Widerstand hat. Beim Anlegen einer elektrischen Spannung an den beiden Enden der Mikrokanäle ergibt sich eine kontinuierliche Potentialverteilung innerhalb der einzelnen Kanäle, so dass Sekundärelektronen, die an einer beliebigen Stelle eines Mikrokanals emittiert werden, in Richtung Anode beschleunigt werden, und an einer beliebigen anderen Stelle des Mikrokanals vervielfachte Sekundärelektronen hervorrufen können.
Halbleiterdetektoren
[Bearbeiten]Halbleiter können in sehr weit gestreuten Anwendungsbereichen eingesetzt werden. Im Wesentlichen werden dotierte Halbleiterübergänge verwendet, deren Leitfähigkeit sich beim Eintreten von Teilchenstrahlung verändert. Die Veränderung der Leitfähigkeit kann entweder als Strom registriert werden, oder sie führt zum Entladen von integrierten Kondensatoren. Die entsprechenden Bauelemente sind zum Beispiel für sichtbares Licht Photodioden oder Phototransistoren. Bei den letztgenannten wird der verursachte Strom durch den Transistoreffekt verstärkt. Für andere Teilchenarten, wie Röntgenphotonen, Elektronen oder andere radioaktive Strahlung kann oft auch entsprechend ausgelegte Halbleiterdetektoren verwendet werden, wenn die Teilchenenergie nicht zu hoch ist.
Die Rotgrenze bei Silicium-Halbleitern liegt wegen der Bandkante der Energieniveaus von Silicium bei etwa 1100 Nanometern, also im nahen Infrarotbereich. Am kurzwelligen Ende des elektromagnetischen Spektrums nimmt die Quanteneffizienz von Silicium stark ab, so dass es in der Praxis nur bis etwa 300 Nanometer eingesetzt werden kann.
Szintillationsdetektoren
[Bearbeiten]Bei Szintillationsdetektoren stammt das registrierte Licht nicht unmittelbar vom zu messenden Signal, sondern primäre Teilchen mit hoher Geschwindigkeit, wie zum Beispiel Elementarteilchen, Atome oder Ionen, werden mit Hilfe von festen oder flüssigen Szintillatoren abgebremst und die kinetische Energie der Teilchen wird zu einem großen Teil in Licht umgewandelt. Dieses Licht kann dann mit geeigneten Lichtdetektoren aufgefangen und analysiert werden. Aus der Intensität und spektralen Verteilung des Lichtes können dann Rückschlüsse auf die Art und Energie der registrierten Teilchen gezogen werden.
Mit schnellen Szintillatoren kann eine gute Zeitauflösung erzielt werden, so dass auch bei sehr schnellen Teilchen Koinzidenzen ermittelt werden können.
Hodoskope
[Bearbeiten]
Beim Einsatz von mehreren Teilchendetektoren in Hodoskopen ist über Zeitpunkte der Szintillationsblitze die Bestimmung der Geschwindigkeit der Teilchen und sogar der geometrischen Bahn (Trajektorie) möglich.
Bei der Kombination zwei verschiedenartiger Szintillatoren, von denen einer die zu bestimmenden Teilchen nur geringfügig abbremst und einen kleinen Verlust der kinetischen Energie der Teilchen nachweisbar macht, und ein anderer die Teilchen vollständig abbremst und somit die gesamte verbleibende kinetische Energie bestimmbar macht, kann nicht nur die kinetische Energie sondern indirekt auch die Masse der Teilchen bestimmt werden. Zur Unterscheidung der beiden Signale können Szintillatoren mit verschiedener Szintillationsdauer oder verschiedenartigem Lichtspektrum verwendet werden.
Digitalisierung
[Bearbeiten]Analog-Digital-Wandler
[Bearbeiten]Digitale Bilder werden bei der Aufnahme in der Regel im Zusammenhang mit einer Analog-Digital-Wandlung (englisch: analog digital converter (ADC)) erzeugt. Als analoges Messsignal stehen in der Regel elektrische Größen zur Verfügung, also Spannungen oder Ströme. Letztere werden durch Strom-Spannungs-Wandler in Spannungen umgesetzt, so dass die meisten Analog-Digital-Wandler eine Spannung innerhalb eines bestimmten Spannungsbereiches als Digitalwert in eine ganze Zahl umwandeln, die dann gespeichert und einem zeitlichen oder räumlichen Raster zugeordnet werden kann.
Für zeitaufgelöste Signale werden Spannungsänderungen mit Pulsdetektoren erfasst, die den Zeitpunkt und gegebenenfalls auch die Höhe eines Spannungspulses oder die Stärke einer Spannungsänderung weitergeben.
Bei ortsaufgelösten Signalen werden die digitalisierten Zahlenwerte in der Regel einem entsprechenden linearen ein-, zwei- oder sogar dreidimensionalen Raster zugeordnet.
Die zu digitalisierenden Spannungen können mit vielfältigen Möglichkeiten erzeugt werden. Häufig wird der innere oder äußere photoelektrische Effekt verwendet, um direkt einen elektrischen Strom zu erzeugen oder indirekt die Ladungsmenge an den Elektroden von Kondensatoren und somit die der Ladungsmenge proportionale Elektrodenspannung zu verändern.
Der Digitalwert für den zu digitalisierenden Strom ist in erster Näherung oft proportional zur Leuchtdichte beziehungsweise zum Photonenstrom und zum Lichtstrom :
Der Digitalwert für die zu digitalisierende Spannung ist in erster Näherung oft proportional zu der in einer bestimmten Zeit gemessenen Photonenmenge :
Dunkelstrom
[Bearbeiten]Abweichungen bei der Proportionalität ergeben sich zum Beispiel durch nicht-lineare Kennlinien von Halbleitern und durch Dunkelströme. Letzterer erzeugt auch ohne Lichteinfall ein zufälliges und permanentes Signal, das ebenfalls digitalisiert wird und den minimal nachweisbaren elektrischen Strom respektive Lichtstrom und somit auch den dynamischen Umfang des Messbereiches begrenzt.
Der Dunkelstrom kann in Halbleitern durch Kühlung stark reduziert werden und verdoppelt sich in Halbleitern typischerweise bei einer Erwärmung um einige Kelvin jeweils. Dabei ist es unerheblich ob die Ursache für die Erwärmung extern ist (Wärmestrahlung) oder durch die Wärmeleistung bei der Umwandlung von elektrischer in thermische Energie beim Messprozess selber entsteht.
Bit-Tiefe
[Bearbeiten]Die Anzahl der nach der Digitalisierung zu unterscheidenden Spannungen ist durch die Bit-Tiefe der Daten gegeben, die wiederum den Wertebereich der ganzen Zahlen bestimmt. Oft wird die Bit-Tiefe in Mehrfachen der Zahl acht angegeben, da acht Bit traditionell zu einem Byte zusammengefasst werden. Es ist aber mit modernen Geräten zunehmend auch üblich, dass die Bits zu Datenworten von 16, 32, 48, 64 oder gar 128 Bit zusammengefasst werden. Diese Datenworte können weiterverarbeitet und gespeichert werden.
Die Anzahl der in einem Datenwort unterscheidbaren Werte ergibt sich wegen der Binärität (Basis = 2) der Bits aus der Bit-Tiefe zu:
Bei einer Bit-Tiefe von acht, wie zum Beispiel für einen Farbkanal von JPEG-Bilddateien, ergeben sich also 256 verschiedene Zustände die digital als die ganzen Zahlen von 0 bis 255 interpretiert werden und entsprechenden Signalhöhen zugeordnet werden können. Der Wert 0 steht hierbei in der Regel für das niedrigste darstellbare Signal (Dunkelwert), und der Wert 255 steht für das höchste darstellbare Signal (Hellwert). Für präzise Messungen sind höhere Bit-Tiefen, wie zum Beispiel 10, 12, 14 oder gar 16 Bit erforderlich.
| Bit-Tiefe |
Anzahl der diskreten Werte |
Wertebereich |
|---|---|---|
| 1 | 2 | 0..1 |
| 2 | 4 | 0..3 |
| 4 | 16 | 0..15 |
| 8 | 256 | 0..255 |
| 10 | 1024 | 0..1023 |
| 12 | 4096 | 0..4095 |
| 14 | 16384 | 0..16383 |
| 16 | 65536 | 0..65535 |
| 24 | 16777216 | 0..16777215 |
| 32 | 4294967296 | 0..4294967295 |
Siehe auch Abschnitt Bit-Tiefe
Meist wird der Dunkelwert 0 beim Fehlen oder Ausbleiben eines Bildsignals verwendet. Wird das Signal zu stark, können Werte oberhalb des Hellwertes nicht mehr unterschieden werden (Übersteuerung) und in der Regel wird dann der Hellwert gespeichert, wobei die Signalhöhe an dieser Schwelle abgeschnitten wird (englisch: Clipping).
Bildsensoren
[Bearbeiten]Bildsensoren bestehen heute oft aus ein- oder zweidimensional angeordneten Lichtdetektoren, die aus Halbleitern hergestellt werden. Die weiteste Verbreitung haben zweidimensionale Bildsensoren heute in digitalen Steh- und Bewegtbildkameras, sie werden zunehmend auch in mobile, multimediale Geräte, wie zum Beispiel Smartphones, Tablets oder Netbooks integriert.
Bildsensorempfindlichkeit
[Bearbeiten]Wesentlichen Unterschiede ergeben sich bei Bildsensoren durch die effektiv zur Verfügung stehende, lichtsammelnde Fläche in der Lichtempfindlichkeit (von englisch: speed). Dabei gilt:
Dies bedeutet, dass eine Vergrößerung der lichtsammelnden, effektiven Fläche in der Regel auch zu einer Vergrößerung der Lichtempfindlichkeit führt. Dies kann bei vorgegebener Bildsensorgröße durch die Verringerung der optisch passiven Stege zwischen den lichtempfindlichen Teilflächen der Bildsensoren, durch den Einsatz von Mikrolinsen-Arrays (siehe unten) oder auch einfach durch die Verringerung der Bildpunkte des Sensors erreicht werden.
Die Veränderung der Bildsensorgröße wirkt sich daher - wenn überhaupt - nur indirekt über das Verhältnis von optisch aktiven und optisch passiven Teilflächen auf die Gesamtlichtempfindlichkeit aus. Ferner muss beachtet werden, dass die lichtempfindlichen Teilflächen umso präziser und gleichmäßiger konstruiert werden können, je größer sie sind. Die Signalqualität und die Bit-Tiefe, die von einem Bildsensor mit vorgegebener Größe erreicht werden können, sind daher bei einer geringeren Anzahl von Bildpunkten und dafür größeren lichtempfindlichen Teilflächen in der Regel besser. Darauf bezogen ist es von Vorteil, wenn die Anzahl der Bildpunkte, die ein Bildsensor registriert, nicht höher ausfällt als unbedingt erforderlich. Häufig ergeben sich durch Beugungsbegrenzung oder durch Abbildungsfehler Randbedingungen, aus denen sich eine maximale sinnvolle Anzahl von Bildpunkten ergibt.
Eindimensionale Bildsensoren
[Bearbeiten]
Eindimensionale Bildsensoren, oder auch Zeilensensoren genannt, finden in Auflicht- und Durchlichtscannern weite Verbreitung.
Um zweidimensionale Bilder zu erhalten, können Zeilensensoren senkrecht zur Zeilenrichtung in einem Raster bewegt werden. Das zweidimensionale Bild kann dann aus den zu verschiedenen Zeitpunkten gewonnenen Zeilenbildern zusammengesetzt werden.
Bei bewegten abzubildenden Objekten kommt es dabei zwangsläufig zum Rolling-Shutter-Effekt. Dieser Effekt tritt auch auf, wenn ein zweidimensionaler Bildsensor eindimensional, also zeilen- oder spaltenweise, ausgelesen wird, während die Belichtung noch fortgesetzt wird.
Zweidimensionale Bildsensoren
[Bearbeiten]
Zweidimensionale Bildsensoren sind in der Regel rechteckig begrenzt und mit quadratischen Pixeln versehen. Das Bild einer optischen Abbildung ist jedoch meist kreisförmig, so dass der Bildsensor nur einen rechteckigen Ausschnitt des Bildkreises erfassen kann. Die folgenden Bildsensorgrößen digitaler Kamerasysteme haben größere Verbreitung gefunden (Stand 2016):
| Bildsensorklasse | Genutzte Bildsensordiagonale in Millimetern |
Digitales Kamerasystem |
|---|---|---|
| 1/2,3″ | 7,7 | Pentax Q |
| 1" | 15,9 | Nikon 1 (CX) |
| 4/3″ | 21,6 | Micro Four Thirds (Olympus, Panasonic, Kodak) |
| APS-C | ≈ 27,5 | Canon EF-M / EF-S, Fujifilm X, Leica T, Nikon F (DX), Pentax K, Samsung NX, Sony A / E |
| Kleinbildformat | 43,3 | Canon EF, Leica M / SL, Nikon F (FX), Sony A / E |
| Mittelformat | ≈ 60 | 645 (Mamija / Pentax), Fujifilm GFX, Hasselblad HCD, Leica S, Mamija ZD, PhaseOne XF |
Siehe auch:
- Abschnitt Normalbrennweite
- Abschnitt Bildauflösung
Bildseitenverhältnisse
[Bearbeiten]Digitale Spiegelreflexkameras haben aus traditionellen Gründen (Kleinbildfilmformat) oft Bildsensoren mit einem Bildseitenverhältnis von 3:2. Bildsensoren moderner digitaler Systemkameras haben häufig das von den ersten Computermonitoren und Fernsehgeräten her übliche Bildseitenformat 4:3. Für einfache Videoanwendungen (Standard Definition (SD) = standardauflösend) wurde daher meist auch das Format 4:3 verwendet, wohingegen moderne Videokameras (High Definition (HD) = hochauflösend) in der Regel Bildsensoren und Bildformate mit dem Bildseitenverhältnis 16:9 verwenden.
Durch Einstellung eines gewünschten Bildseitenverhältnisses können die Aufzeichnungsformate vieler Kameras leicht umgeschaltet werden. Die Aufnahme mit solchen Geräten macht jedoch nur Sinn, wenn ein elektronischer Sucher oder Kontrollmonitor den entsprechenden Ausschnitt zur Bildgestaltung anzeigt. Ein optischer Sucher zeigt das reele Bild einer matten Einstellscheibe oder ein virtuelles Bild mit einem festen Bildseitenverhältnis - hier kann man sich bestenfalls mit Strichmarken oder markierten Rahmen auf der Einstellscheibe behelfen, um abweichende Bildseitenverhältnisse deutlich zu machen.
Siehe auch Abschnitt Bildseitenverhältnis
Multi-Aspect-Bildsensoren
[Bearbeiten]Beim Grad der Ausnutzung der lichtempfindlichen Bildsensorfläche spielt das Bildseitenverhältnis eine Rolle. Meistens liegt die lichtempfindliche Fläche des Bildsensors vollständig im Bildkreis. so dass nur bei dem nativen Bildseitenverhältnis des Bildsensors die größe Bilddiagonale, maximal jedoch der Durchmesser des Bildkreises ausgeschöpft werden kann.
Wenn in Kauf genommen wird, dass einige Pixel in den Ecken des Bildsensors nie zur Bildgebung verwendet werden, gibt es eine Möglichkeit, bei einer Vielzahl von Bildseitenverhältnissen die gleiche Bilddiagonale innerhalb des Bildkreises auszunutzen. Die Geometrie des Bildsensors und die Größe des Bildkreises, namentlich die acht Schnittpunkte der Kanten des Bildsensors mit dem genutzen Bildkreis, ergeben dann das kleinste und größte Bildseitenverhältnis, bei dem die maximale Bilddiagonale berücksichtigt werden kann.
- Verschiedene Bildseitenverhältnisse auf einem Bildsensor mit Begrenzung durch den Bildkreis
-
Ohne Beschneidung des Bildkreises - alle Bildpunkte des Bildsensors werden benutzt
-
Optimierung durch Beschneidung des Bildkreises - einige Bildpunkte in den Ecken des Bildsensors werden nie benutzt
Temperaturverhalten
[Bearbeiten]Das Verhalten von Halbleitern ist in der Regel temperaturabhängig. Bei einer Erhöhung der Temperatur um sechs Kelvin ist ungefähr mit einer Verdopplung des Dunkelstroms zu rechnen. Bei 60° Celsius ist der Dunkelstrom unter dieser Voraussetzung also etwa 1000 Mal höher als bei 0° Celsius.
Für Aufnahmen mit einem möglichst großen Signal-Rausch-Abstand ist es daher sinnvoll oder sogar notwendig, den Halbleiter zu kühlen. Der Dunkelstrom kann mit entsprechendem Aufwand, zum Beispiel bei der Kühlung mit flüssigem Stickstoff (bei normalem Luftdruck also bei -196° Celsius), extrem reduziert werden.
Für die genaue Messung und Detektion von Infrarotstrahlung ist eine Kühlung des Halbleiters unerlässlich. Daher wird beispielsweise auch bei Satelliten, die zur Beobachtung im Infraroten ausgerüstet werden, wie das Herschel-Weltraumteleskop, eine entsprechende Kühlung eingesetzt.
Im Folgenden werden zur Verdeutlichung die Signale des Dunkelbildes eines hochwertigen Active-Pixel-Bildsensors mit CMOS-Technologie (Ausschnitt mit 256 mal 256 Bildpunkten) gezeigt:
- Um den Faktor 8 verstärkte Signale bei acht Sekunden Belichtungszeit
-
Bei einer Temperatur von 25° Celsius
-
Bei einer Temperatur von 60° Celsius
Je länger die Belichtungszeit ist, desto stärker trägt der Dunkelstrom zu Störsignalen bei:
- Um den Faktor 16 verstärkte Signale bei 25° Celsius
-
Bei einer Millisekunde Belichtungszeit
-
Bei acht Sekunden Belichtungszeit
Höhenstrahlung
[Bearbeiten]Höhenstrahlung und die dadurch ausgelöste Sekundärstrahlung besteht aus energiereichen Elementarteilchen, die auch mit den Halbleitern der Bildsensoren wechselwirken und diese schädigen können. Dies passiert auch, wenn die Geräte lediglich transportiert werden, ohne dass sie in Betrieb sind. Empfindliche und hochwertige Bildsensoren sollten daher so weit wie möglich vor dieser Höhenstrahlung geschützt werden. Dies ist insbesondere bei Flügen in der oberen Atmosphäre besonders wichtig, da die schädigende Strahlung hier erheblich höher ist als an der Erdoberfläche. Die Schädigung zeigt sich meist durch den Ausfall einzelner Bildpunkte, was bei hinreichend schwerer Schädigung dann als Pixelfehler bezeichnet wird.
Pixelfehler
[Bearbeiten]
Je kleiner und zahlreicher die Bildpunkte auf dem Bildsensor sind, desto geringer wird die Signalqualität der einzelnen Bildpunkte. Dies kann sogar dazu führen, dass einzelne Bildpunkte gar kein verwertbares Signal liefern. Um schwache oder ausbleibende Signale zu kompensieren, kann zum einen der Dunkelstrom gemessen werden, während der Bildsensor nicht belichtet wird. Zum anderen kann der Bildsensor zum Beispiel mit Hilfe einer Ulbricht-Kugel (englisch: Integrating Sphere) gleichmäßig beleuchtet werden, um die Unterschiede der Signalempfindlichkeit der verschiedenen Bildpunkte zu ermitteln. Das sich daraus ergebene Muster für die Verteilung der gestörten Bildpunkte ist für jeden Bildsensor einzigartig und somit eindeutig. Wenn das Muster bekannt ist, kann es also zu einem späteren Zeitpunkt zur Identifikation des Bildsensors verwendet werden.
Unmittelbar nach einer Aufnahme können der individuelle Dunkelstrom und die jeweilige Signalempfindlichkeit für jeden Bildpunkt rechnerisch berücksichtigt beziehungsweise fehlende Information mit Hilfe der funktionstüchtigen Nachbarpunkte interpoliert werden (zum Beispiel mit einem nachgeschalteten Field Programmable Gate Array (FPGA)), um eine scheinbare Homogenität zwischen benachbarten Bildpunkten zu erzeugen. Bei hohen Anforderungen an die reale (nicht berechnete) Homogenität der Bildpunkte muss demnach auf Bildsensoren mit möglichst großen und damit wenigen Pixeln zurückgegriffen werden.
Bei Bewegtbildaufnahmen sind Pixelfehler besonders störend, da die ortsfesten Defekte bei Schwenks, Zoomfahrten oder bei bewegten Objekten nicht nur leichter wahrnehmbar sind, sondern auch ziemlich auffällig sein können. Hier ist besonders sorgfältig darauf zu achten, dass die eingesetzten Bildsensoren nicht zu viele Bildpunkte und möglichst keine Pixelfehler haben.
Infrarot-Sperrfilter
[Bearbeiten]
- Erste doppelbrechende Schicht des Tiefpassfilters
- Infrarot-Sperrfilter mit zirkular polarisierender Dünnschicht (λ/4-Plättchen)
- Zweite doppelbrechende Schicht des Tiefpassfilters
Da die meisten Halbleiter auch im Infraroten noch eine relativ hohe Lichtempfindlichkeit aufweisen, trägt infrarotes Licht in großem Maße zur Belichtung der Bildsensoren bei. Dieser Effekt kann zwar beispielsweise bei Nachtsichtgeräten vorteilhaft eingesetzt werden, führt jedoch bei Aufnahmen mit sichtbarem Licht unter Umständen zu erheblichen Fehlbelichtungen oder Farbabweichungen. In diesen Fällen muss das infrarote Licht durch Infrarot-Sperrfilter absorbiert oder auch durch entsprechende Interferenzfilter reflektiert werden, so dass das unsichtbare Infrarotlicht nicht auf den Bildsensor gelangt.
Da die Absorption des infraroten Lichtes proportional zur Dicke der Infrarot-Sperrfilters ist, absorbieren diese umso besser, je dicker sie sind. Bei schräg einfallenden Strahlen wirken diese Sperrfilter dann jedoch wie eine Planplatte, die die Strahlen unter Umständen so stark parallel zum einfallenden Strahl versetzt, dass diese in benachbarten Bildpunkten registriert werden (siehe auch Abschnitt Ablenkung von Lichtstrahlen). Diese winkelabhängigen Aberrationen führen unter Umständen zu Kontrastverlusten und Unschärfen (siehe auch Abschnitt Modulationsübertragung) sowie geometrischen Fehlern in der optischen Abbildung (siehe auch Abschnitt Güte der optischen Abbildung). Um diese Fehler so gering wie möglich zu halten, werden bei entsprechenden Bildsensoren angepasste Objektive eingesetzt, die zum Beispiel bildseitig telezentrisch gerechnet sind. Bei solchen Objektiven sind die austretenden Strahlen weitgehend parallel zur optischen Achse, fallen somit mehr oder weniger senkrecht auf die optischen Filter und den Bildsensor ein und erfahren daher kaum einen seitlichen Versatz (siehe auch Abschnitt Telezentrie).
Oft sind die Infrarot-Sperrfilter im optischen Tiefpassfilter direkt vor dem Bildsensor integriert. Bei der Verwendung von Infrarot-Sperrfiltern in den Objektiven oder bei der Beleuchtung der abzubildenden Objekte kann auf eine weitere Infrarotlicht-Filterung am Bildsensor gegebenenfalls verzichtet werden.
Ultraviolett-Sperrfilter
[Bearbeiten]Auch im Ultravioletten weisen Bildsensoren eine gewisse Lichtempfindlichkeit auf. Da die in Objektiven verwendeten Glassorten üblicherweise jedoch eine geringe Transmission für ultraviolette Strahlung aufweisen, stellt dies häufig kein großes Problem dar. Unter Umständen kann es dennoch hilfreich sein, Ultraviolett-Sperrfilter einzusetzen, um Fehlbelichtungen beziehungsweise Fehlmessungen zu vermeiden.
Soll ultraviolette Strahlung jedoch nachgewiesen werden, ist der Einsatz von Glassorten erforderlich, die eine hohe Transmission für diese Strahlung aufweisen, wie zum Beispiel Quarzglas, das auch noch bei Lichtwellenlängen bis herunter zu 160 Nanometern eingesetzt werden kann.
Farbfilter-Arrays
[Bearbeiten]

Halbleiterdetektoren haben zwar eine bestimmte spektrale Empfindlichkeit, diese kann jedoch nicht unmittelbar herangezogen werden, um die spektrale Verteilung des registrierten Lichtes zu diskriminieren. Diese Detektoren sind also nur in der Lage, die Helligkeit eines Lichtsignals zu ermitteln.
Um Farbbilder zu generieren, müssen also zusätzliche Maßnahmen ergriffen werden. Dazu werden in der Regel Farbmosaiken verwendet, die so gestaltet sind, dass bei einem Bildsensor jeder Bildpunkt nur einen eingeschränkten spektralen Bereich empfangen kann. Oft werden die Primärfarben des menschlichen Auges rot, grün und blau (RGB) eingesetzt. Da das menschliche Auge im Grünen deutlich empfindlicher ist als im Roten und im Blauen, werden bei den Farbfilter-Arrays häufig doppelt so viele grüne Farbfilter eingesetzt wie rote oder blaue. Einige Hersteller verwenden auch zwei verschiedene Grüntöne in den Farbmosaiken (G = green = grün (Primärfarbe) und E = emerald = smaragdgrün).
Allgemein ist zu beachten, dass die farbempfindlichen Zäpfchen nicht nur wesentlich unempfindlicher sind als die helligkeitsempfindlichen Stäbchen, sondern dass erstere auf der Netzhaut auch erheblich dünner verteilt sind als letztere. Das menschliche Auge ist daher auch bei besten Sichtbedingungen noch nicht einmal in der Lage, eine Million farbige Punkte zu unterscheiden. Bei optimalen Bedingungen können im Sehzentrum jedoch bis zu vier Millionen verschieden helle Punkte unterschieden werden. Aus diesem Grund werden von einigen Herstellern Bildsensoren angeboten, bei denen nicht alle Bildpunkte mit Farbfiltern ausgestattet sind, sondern nur zur Ermittlung der Bildhelligkeit herangezogen werden.
Da die Elemente der Farbfilter-Arrays häufig aus Gelatine bestehen, in die die entsprechenden Farbpigmente oder Farbstoffe eingebettet worden sind, besteht bei Farbfilter-Arrays eine gewisse Anfälligkeit gegenüber Feuchtigkeit, die zur Instabilität bei der Farbfilterung führt. Für den Einsatz in feuchter Umgebung ist daher darauf zu achten, dass die Farbfilter-Arrays sehr gut gegen das Eindringen von Feuchtigkeit geschützt werden.
- Abbildung eines farblosen Schachbrettmusters (jeweils links) mit einem Bayer-Sensor mit Farbmosaik (jeweils Mitte)
-
Dadurch, dass nur die grünen "Dots" des Bayer-Sensors belichtet werden, sind in der Abbildung (rechts) nur schwarze und grüne Bildpunkte vorhanden
-
Dadurch, dass nur die roten und blauen "Dots" des Bayer-Sensors belichtet werden, sind in der Abbildung (rechts) nur schwarze, rote und blaue Bildpunkte vorhanden
Farbinterpolation
[Bearbeiten]Da typische Farbsensoren nur eine Farbe pro Bildpunkt (englisch: dot) erfassen, jedoch meist alle Farben in jedem Bildpunkt (englisch: pixel) ausgegeben werden, müssen die jeweils fehlenden Pixel-Farben rechnerisch aus den Nachbar-Dots interpoliert werden. Bei helligkeitsmodulierten Objekten (beispielsweise bei Abbildungen von Fischgräten- oder Schachbrettmustern) ergibt sich in den hellen Pixeln jeweils eine bestimmte gemessene Farbe, wohingegen die Nachbar-Dots nicht beleuchtet werden und daher dunkel erscheinen. Bei der Rekonstruktion dieser Bilder ergeben sich dann unter Umständen nur farbige Bildpunkte, obschon die abgebildete Vorlage keine Farbe enthielt. Dieser Effekt kommt durch die Verletzung des Abtasttheorems zustande und wird auch als Alias-Effekt (lateinisch alias = anders) oder im Englischen Aliasing bezeichnet, da die Farben und Helligkeiten anders wiedergegeben werden, als sie in der Vorlage vorhanden sind.
- Interpolation eines durch den Alias-Effekt verfälschten Bildes
-
Bei der Interpolation eines durch den Alias-Effekt verfälschten Bildes mit grünen "Dots" (links) werden die schwarzen Bildpunkte ebenfalls grün gerechnet (rechts)
-
Bei der Interpolation eines durch den Alias-Effekt verfälschten Bildes mit roten und blauen "Dots" (links) werden die schwarzen Bildpunkte auf die Mischfarben von rot und blau gerechnet (Magenta-Farbtöne, rechts)
Pixel-Shift
[Bearbeiten]Die fehlende Farbinformation bei einzelnen Bildpunkten innerhalb von Farbfilter-Arrays kann durch mehrere Aufnahmen kompensiert werden, die jeweils um einen Bildpunkt verschoben werden, so dass jeder Bildpunkt in jeder Primärfarbe des Farbfilter-Arrays abgetastet wird. Das Verfahren hat den Nachteil, dass das aufgenommene Objekt und das Kameragehäuse während des Verschiebevorgangs nicht bewegt werden dürfen, um Bewegungsartefakte zu vermeiden. Werden jedoch bewegliche Bildsensoren zur Bildstabilisierung eingesetzt, können gleichzeitig Bildstabisilierung und Pixel-Shift durchgeführt werden, so dass nur das aufgenommene Motiv unbeweglich sein muss, nicht jedoch das Kameragehäuse.
Im folgenden Beispiel soll ein leuchtender Kreis mit dem Durchmesser der Bildpunkte eines Bildsensors mit Bayer-Mosaik aufgenommen werden:
- Aufnahme eines weißen Kreises mit einem Bildsensor mit Farbmosaik-Filter
-
In der Bildebene ist ein weißer Kreis abgebildet.
-
Der Bildsensor tastet in der Bildebene jeden Bildpunkt mit vier Subpixeln mit jeweils einer der drei Primärfarben rot, grün oder blau ab.
Wird der Bildsenor bei vier aufeinanderfolgenden Aufnahmen um jeweils einen Bildpunkt zunächst nach rechts, dann nach oben und schließlich wieder nach links verschoben, dann tasten vier verschiedende Sensorelemente mit jeweils einer Primärfarbe den Bildpunkt ab. Anschließend können die vier Bilder zu einem einzigen Bild überlagert werden:
- Abtastung eines weißen Kreises mit in der Bildebene verschobenem Bildsensor mit Farbfilter-Array
-
Der weiße Kreis wird vom roten Sensorelement erfasst.
-
Der weiße Kreis wird nach dem Verschieben des Bildsensors nach links vom ersten grünen Sensorelement erfasst.
-
Der weiße Kreis wird nach dem Verschieben des Bildsensors nach oben vom blauen Sensorelement erfasst.
-
Der weiße Kreis wird nach dem Verschieben des Bildsensors nach rechts vom zweiten grünen Sensorelement erfasst.
-
Im aus den vier Einzelbildern zusammengesetzten Bild gibt es einen farbneutralen, quadratischen Bildpunkt
Ein nützlicher Nebeneffekt ist, dass bei sonst gleichen Bedingungen (insbesondere gleiche Belichtungszeit) durch die Registrierung von mehreren Aufnahmen insgesamt mehr Licht aufgefangen und ausgewertet wird. Dadurch kann der dynamische Umfang der Signale (günstigeres Signal-Rausch-Verhältnis) verbessert werden.
Mikrolinsen-Arrays
[Bearbeiten]
Ein mehr oder weniger großer Anteil des Lichtes einer Abbildung fällt bei Bildsensoren auf die passiven Zwischenräume der lichtempfindlichen Bildpunkte und geht für die Aufnahme somit verloren. Um möglichst viel Licht registrieren zu können, wird versucht, diese Zwischenräume so gering wie möglich zu gestalten. Ferner werden Mikrolinsen-Arrays eingesetzt, die pixelweise auch das Licht, das ungebrochen neben die lichtempfindlichen Pixel fallen würde, durch ihre Sammellinsenwirkung auf diese Pixel zu fokussieren.
Um geometrische Abbildungsfehler bei schräg einfallenden Lichtstrahlen zu minimieren, müssen die Mikrolinsen genau im Raster der Bildpunkte und so dicht wie möglich vor dem Bildsensor eingebaut werden.
Polarisationsfilter
[Bearbeiten]Mit einem Polarisationsfilter (kurz oft Polfilter genannt) können Lichtstrahlen, die mit bestimmter Polarisationsrichtung durch den Polarisationsfilter gehen, ausgeblendet werden. Normalerweise ist natürliches Licht unpolarisiert, so dass mit einem Polarisationsfilter immer die Hälfte des Lichts mit der gesperrten Polarisationsrichtung herausgefiltert wird.
Ist das Licht aus geeigneten künstlichen Lichtquellen bereits linear polarisiert, wie zum Beispiel von einem Laser oder von einer Flüssigkristallanzeige, oder wird von glatten nicht-metallischen Oberflächen wie Wasser oder Glas reflektiert, dann wird es mit einem linearen Polarisationsfilter entweder gar nicht gefiltert, wenn die Polarisationsrichtungen der Lichtwellen und des Polarisationsfilter übereinstimmen (Phasenwinkel 0°), oder es wird ausgeblendet, wenn die Polarisationsrichtungen der Lichtwellen und des Polarisationsfilters um einen Winkel von 90° verdreht sind. Durch das Drehen des Polarisationsfilters auf Winkel zwischen 0° und 90 ° können für das polarisierte Licht alle Transmissionsgrade von null bis eins eingestellt werden. Meist befindet sich der entsprechende Polarisationsfilter vor dem Objektiv, er kann aber auch in das Objektiv oder zwischen Objektiv und Bildsensor eingebaut werden.
Die folgenden Bilder zeigen als Motiv einen Stadtplan hinter einer Glasscheibe, an der das von einer Bahnhofsuhr und der Bahnhofsbeleuchtung schräg auftreffende Licht linear polarisiert reflektiert wird. Die beiden oberen Bilder sind auf die Bahnhofsuhr und die beiden unteren Bilder auf die Mitte des Stadtplanausschnitts hinter der Glasscheibe scharfgestellt. Bei den mit unpolarisiertem Licht photographierten Bildern (links) dominiert eine auf der Glasfläche reflektierte Bahnhofsuhr beziehungsweise Bahnhofslampe die Belichtung. Wird das von der Glasoberfläche reflektierte Licht durch einen um 90° zur Polarisationsrichtung des reflektierten Lichtes gedrehten in den Strahlengang gebrachten Polarisationsfilter ausgeblendet (rechts), wird die Sicht auf den Bereich hinter der Glasfläche frei, so dass der Stadtplan bei der korrekten Entfernungseinstellung gut erkennbar wird.
- Stadtplan in einem Schaukasten hinter einer Glasscheibe mit Reflexionen auf der Glasoberfläche
-
Fokussierung auf das Spiegelbild einer Bahnhofsuhr auf der Glasscheibe ohne Polarisationsfilter. Das Spiegelbild besteht aus polarisiertem Licht und ist hell und gut erkennbar.
-
Fokussierung auf das Spiegelbild der Bahnhofsuhr auf der Glasscheibe mit Polarisationsfilter bei gleicher Belichtung. Das Spiegelbild wurde durch den senkrecht zur Polarisationsrichtung des Lichts des Spiegelbilds gedrehten Polarisationsfilter fast ausgelöscht.
-
Fokussierung auf den Stadtplan hinter der Glasscheibe ohne Polarisationsfilter. Der unscharf abgebildete Reflex der Bahnhofsbeleuchtung von der Glasoberfläche besteht aus polarisiertem Licht und ist heller als der vergleichsweise dunkle Stadtplan, so dass dieser nicht erkennbar ist.
-
Fokussierung auf den Stadtplan hinter der Glasscheibe mit Polarisationsfilter bei stärkerer Belichtung. Der Reflex der Bahnhofsbeleuchtung wird durch den senkrecht zur Polarisationsrichtung des Lichts des Spiegelbilds gedrehten Polarisationsfilter ausgelöscht, so dass der Stadtplan kontrastreich und vollständig erkennbar ist.
Bei zirkular polarisiertem Licht dreht sich die Polarisationsrichtung permanent mit der Wellenlänge beziehungsweise mit der Schwingungsdauer der Welle, so dass die Winkelgeschwindigkeit konstant ist. Rechtsdrehendes Licht wird von einem linksdrehenden Polarisationsfilter herausgefiltert und umgekehrt.
Wenn linear und zirkular polarisiertes Licht überlagert werden, entsteht elliptisch polarisiertes Licht, bei dem sich die Polarisationsrichtung mit konstanter Winkelgeschwindigkeit dreht, wobei die Amplitude der Welle mit der Frequenz der Welle zwischen einem Minimum und einem Maximum schwankt.

Bei durchsichtigen thermoplastischen Kunststoffen können beim Herstellungsprozess eingefrorene Materialspannungen zu einer Doppelbrechung des Materials führen, so dass dieses zirkular polarisierend wirkt. Werden solche Gegenstände in der Spannungsoptik mit polarisiertem Licht beleuchtet und mit einem Polarisationsfilter aufgenommen, können die Bereiche verschiedener Materialspannung farblich gut unterschieden werden, da die Lichtwellen mit unterschiedlicher Wellenlänge und Frequenz um verschiedene Winkel gedreht werden. Wird der Gegenstand mechanisch beansprucht, können sich die Spannungen im Material und somit auch das Farbmuster ändern.
Optische Tiefpässe
[Bearbeiten]
A:Von links fällt ein unpolarisierter Lichtstrahl ein.
B:Die erste doppelbrechende Schicht teilt den einfallenden unpolarisierten Strahl in einen ordentlichen und einen außerordentlichen Strahl auf.
C:Zwei linear polarisierte Teilstrahlen mit senkrecht aufeinanderstehenden Polarisationsrichtungen.
D:Eine Wellenplatte (λ/4-Plättchen) erzeugt aus linear polarisiertem Licht zirkular polarisiertes Licht.
E:Zwei zirkular polarisierte Teilstrahlen.
F:Die zweite doppelbrechende Schicht teilt die einfallenden zirkular polarisierten Strahlen in jeweils einen ordentlichen und einen außerordentlichen Strahl auf.
G:Vier linear polarisierte Teilstrahlen mit paarweise senkrecht aufeinanderstehenden Polarisationsrichtungen.
H:Auf einem Bildschirm ergeben sich vier in den Ecken eines Parallelogramms liegende Lichtflecke.
Der Alias-Effekt kann vermieden werden, wenn dafür gesorgt wird, dass Lichtstrahlen, die von einem Objektpunkt ausgehen und eine bestimmte Farbverteilung und Helligkeit haben, von mehreren Bildpunkten mit verschiedenen Farbfiltern gleichzeitig erfasst werden. Dazu werden in der Regel optische Tiefpassfilter verwendet, die aus stark brechendem und gleichzeitig doppelbrechendem Material wie zum Beispiel Lithiumniobat bestehen (anfangs wurden häufiger Quarzeinkristalle eingesetzt) und alle einfallenden Lichtstrahlen aufspalten und somit örtlich verteilen. Dazu werden meist zwei Filterplättchen um 90° gegeneinander verdreht kombiniert und durch ein dazwischenliegendes, zirkular oder elliptisch polarisierendes Medium (zum Beispiel ein λ/4-Plättchen) miteinander verbunden, so dass die beiden durch den ersten Tiefpassfilter aufgeteilten Strahlen erneut aufgespalten werden können. Die Lage der resultierenden vier Strahlen kann dann durch die Ecken eines Parallelogramms beschrieben werden. Bei zirkular polarisiertem Licht ergibt dabei sich ein Recheck, und wenn die beiden optischen Schichten der doppelbrechenden Materialien gleichartig und gleich dick sind ergibt sich ein Quadrat.
Wenn das zirkular oder elliptisch polarisierende Medium zwischen den doppelbrechenden Platten aus elektrisch beeinflussbaren Flüssigkristallen besteht, die in der Regel ebenfalls doppelbrechend sind, kann die Wirkung des Tiefpasses durch das Anlegen von geeigneten Steuerspannungen beeinflusst oder sogar aufgehoben werden.

Die hohen Ortsfrequenzen des Bildes werden durch den Tiefpass gedämpft und die Kanten zwischen hellen und dunklen Bildpartien werden weicher gezeichnet und breiter. Dadurch wird ein Objektpunkt immer von mehreren Bildsensorpunkten mit verschiedenen Farbfiltern erfasst. Dieses Verhalten kann bei Verzicht auf einen optischen Tiefpassfilter nicht informationstechnisch nachgebildet werden: in den digitalisierten Bilddaten und bei Beibehaltung der Anzahl der Bildpunkte (englisch: dots) als Bildpunkte (englisch: pixel) kann dies kein Signalprozessor und keine Firm- oder Anwendungssoftware leisten, da die erforderliche Information über die tatsächlichen Farben in keinem Bildpunkt vorliegt. Ohne optischen Tiefpassfilter kommt es durch den Alias-Effekt bei feinen Strukturen unweigerlich zu Farbfehlern bei der Interpolation (siehe auch Abschnitt Farbinterpolation).
Genauso wie bei Infrarot-Sperrfiltern ergibt sich auch bei optischen Tiefpässen das Problem einer winkelabhängigen Aberration (siehe auch Abschnitt Infrarot-Sperrfilter). Dieser Abbildungsfehler kann durch die Verwendung von telezentrischen Objektiven gemildert werden. Senkrecht auftreffende Lichtstrahlen werden allerdings nicht nur aberrationsfrei durch die optischen Schichten gelassen, sondern es erfolgt auch keine Aufspaltung der Lichtstrahlen durch die Doppelbrechung, da senkrecht zur Oberfläche eintretende Lichtstrahlen nicht gebrochen werden.
Bei Bildsensoren mit ausreichend hoher Anzahl von Sensorpunkten können ohne großen Aufwand mehrere benachbarte und verschiedenfarbige Sensorpunkte rechnerisch zu jeweils einem Bildpunkt zusammengefasst werden, ohne dass notwendigerweise optische Tiefpässe eingesetzt werden müssen. Ohne die Verwendung von optischen Tiefpässen kann es jedoch bei Strukturen, die im Bereich der maximalen Ortsfrequenz der Bildsensoren aufgenommen werden auch hierbei zu Alias-Effekten kommen. Alternativ kann die abbildende Optik (zum Beispiel durch Defokussierung, hinreichend große Aberration (Zerstreuungskreise) oder durch Beugungsbegrenzung (Beugungsscheibchen)) so gestaltet werden, dass die Kontrastübertragung von derartig kleinen Strukturen so gering ausfällt, dass diese vom Bildsensor praktisch nicht erfasst werden können. In diesem Fall kann auf die Verwendung von optischen Tiefpässen ohne weiteres verzichtet werden.
Bildsensorsysteme
[Bearbeiten]
Das Problem mit helligkeitsempfindlichen Bildsensoren auch Farbbilder aufnehmen zu können, kann auch gelöst werden, indem für verschiedene Grundfarben einzelne Bildsensoren mit entsprechenden einfarbigen Farbfiltern eingesetzt werden. Dazu werden in der Regel Strahlteiler mit farbselektiven Interferenzfilterschichten eingesetzt, und es muss gewährleistet sein, dass alle beteiligten Bildsensoren exakt denselben Bildausschnitt erfassen, was bei entsprechend hohen Bildpunktzahlen sehr schwierig wird, da die Übereinstimmung in Bezug auf die Verschiebung in den drei Raumrichtungen, sowie auf die Verdrehung und Verkippung zur optischen Achse gewährleistet werden muss. Bei photographischen Aufnahmen mit der Blendenzahl 2,0 muss diese Übereinstimmung beispielsweise in der Größenordnung von wenigen Mikrometern korrekt und stabil sein, um die drei Bilder weniger als einen Beugungsscheibchendurchmesser divergieren zu lassen.
So kann dies für Videoaufnahmen mit bis zu zwei Millionen Bildpunkten - wie zum Beispiel in digitalen Camcordern - durchaus realisiert werden, bei Stehbildaufnahmen mit einem Vielfachen dieser Bildpunktzahl sind die Präzision der Justage sowie die thermische und mechanische Stabilität der Aufnahmesysteme nicht ohne weiteres ausreichend.
Nichtsdestoweniger entfällt bei diesen Systemen das Erfordernis von Tiefpassfiltern zur Vermeidung von Alias-Effekten, da in jedem Bildpunkt tatsächlich alle Grundfarben erfasst werden und bereits im Rohdatenbild ohne Interpolationsberechnungen zur Verfügung stehen. Die verwendeten und erforderlichen Strahlteiler können aus Glasprismen hergestellt werden, die gleichzeitig als Infrarot-Sperrfilter ausgelegt sind. Ferner ist bei Bildsensoren mit geringerer Bildpunktzahl auch die Anzahl der Pixeldefekte geringer, und die Qualität der einzelnen Bildpunkte ist in Hinsicht auf das Dunkelstromrauschen und den Dynamikumfang meist besser.
Auf der anderen Seite sind der Konstruktionsaufwand und die Herstellungskosten höher als bei Ein-Sensorsystemen. Darüberhinaus ist zu beachten, dass die Schnittweite auf der optischen Achse bei der Verwendung von Prismenstrahlteilern etwas verlängert wird, und daher und auch wegen der zusätzlich erforderlichen Bauteile der Platzbedarf für das gesamte Aufnahmesystem erhöht ist.
CMOS
[Bearbeiten]CCD-Sensoren werden zunehmend von CMOS-Sensoren (Active Pixel Sensor) abgelöst, da diese eine wesentlich geringere Leistungsaufnahme haben und sich im Dauerbetrieb daher auch nicht so schnell und so stark erwärmen (siehe auch Abschnitt Temperaturverhalten). Ferner können diese Bildsensoren schneller und flexibler ausgelesen werden, was sich zum Beispiel positiv auf die Möglichkeiten der Belichtungsmessung, der Kontrastermittlung zu automatischen oder manuellen Scharfstellung (Autofokus oder Softwarelupe) in einzelnen Bildbereichen oder der Objekterkennung auswirkt.
Im Gegensatz zu CCD-Sensoren sind CMOS-Sensoren im Infraroten oft sehr lichtempfindlich. Bei Aufnahmen mit sichtbarem Licht sind entsprechende Infrarot-Sperrfilter unerlässlich, um Fehlbelichtungen, aber auch Farb- und Helligkeitsverfälschungen durch unsichtbares Licht zu vermeiden.
Der geringe Flächenanteil der lichtempfindlichen Elemente an der Oberfläche des CMOS-Sensors kann durch die Verwendung von Mikrolinsen-Arrays (siehe oben) kompensiert werden.
Inhomogenitäten zwischen benachbarten Bildpunkten können bei CMOS-Sensoren vermehrt zu Farbrauschen führen (siehe auch Abschnitt Farbrauschen).
Quantenfilm
[Bearbeiten]Quantenfilme bestehen aus einer Vielzahl von sehr kleinen lichtempfindlichen Quantenpunkten, die typischerweise einen Durchmesser von einem bis zu zehn Nanometern haben. Solche Quantenpunkte können sich durch eine recht hohe Quanteneffizienz und Speicherdichte auszeichnen, so dass bei der Bildaufnahme eine hohe Lichtempfindlichkeit und ein großer dynamischen Signalumfang zur Verfügung stehen. Die verschiedenen Bereiche mit mehreren in der vergleichsweise dünnen lichtempfindlichen Schicht aneinandergrenzenden Quantenpunkten können durch rechteckmatrixartig angeordnete Elektroden angesteuert und ausgelesen werden. Durch das Zusammenschalten von benachbarten Elektrodenspalten oder -zeilen können die ausgelesenen Bildpunkte vergrößert und in ihrer Form variiert werden. Durch geeignete Ansteuerung können alle Bildpunkte gleichzeitig und sehr schnell ausgelesen werden, zum Beispiel um einen Rolling-Shutter-Effekt zu vermeiden ("global shutter") oder um auf einen mechanischen Verschluss verzichten zu können.
Organische Bildsensoren
[Bearbeiten]Alternativ zu Quantenpunkten können auch lichtempfindliche organische Materialien eingesetzt werden, die ihre Leitfähigkeit aufgrund des inneren Photoeffekts verändern. Auch hier ist die Dicke der lichtempfindlichen Schicht sehr gering, und sie liegt in der Größenordnung der zu registrierenden Lichtwellenlänge. Die Ansteuerung der lichtempfindlichen Bereiche kann ähnlich wie beim Quantenfilm erfolgen, und der dynamische Signalumfang soll ebenfalls vergleichsweise hoch sein.
Digitale Bilder
[Bearbeiten]Dieses Kapitel beschäftigt sich hauptsächlich mit digitalen, zweidimensionalen Rasterbildern. Diese sind im Allgemeinen rechteckig begrenzt, also mit parallelen, geraden Kanten, die in den Ecken in rechten Winkeln aufeinanderstehen.
Dies entspricht zum einen sowohl der historischen Herangehensweise mit photographischen Platten, die aus praktischen Erwägungen rechtwinklig aus Glas hergestellt werden, als auch mit Filmmaterial, wo die Kanten der Bilder parallel beziehungsweise rechtwinklig zu den Filmstreifen angeordnet werden.

Zum anderen ergibt sich aber bei der digitalen Verarbeitung der Rasterbilddaten mit Computern eine wichtige Randbedingung, die die effiziente Implementierung von Rechenalgorithmen betrifft. In Computern werden zweidimensionale Daten ähnlich wie in Tabellen spalten- und reihenweise in Datenfeldern (englisch: Arrays) gespeichert. Die Kontrollstrukturen, mit denen Computerprogramme erstellt werden können, benutzen ganzzahlige Indizes, mit denen einzelne Spaten oder Reihen sehr effizient bearbeitet werden können. Auch die Adressierung von benachbarten Datenfeldern funktioniert über diese Indices sehr einfach und effizient, was für viele Bildbearbeitungsalgorithmen ausgenutzt wird.
Viele allgemeine Eigenschaften digitaler Bilder sind unabhängig von der Frage, ob die Bilder mehrfarbig oder monochrom sind. Auf die Farben in digitalen Bildern wird aber in mehreren Abschnitten eingegangen.
Digitale Berechnung
[Bearbeiten]
Digitale Bilder können direkt mit einem Computer erstellt werden, indem ein geeignetes Computerprogramm digital gespeicherte Messwerte oder Anweisungen eines Benutzers intern umsetzt.
Einfache Beispiele sind Computerprogramme zur Tabellenkalkulation, die Zahlen auch graphisch darstellen können, oder Programme zur Erstellung von Vektorgraphiken.
Bild- und Videobearbeitungsprogramme können aus bereits digital vorliegenden Ausgangsdaten (zum Beispiel auch Rohdaten) veränderte Bilder oder Bilderfolgen berechnen. Dies wird sehr häufig eingesetzt, um die Bilder so zu transformieren, so dass die subjektiv wahrgenommene oder aber auch die objektive Bildqualität verbessert wird. Dabei kann eine Vielzahl von verschiedenen Bildparametern variiert werden, wie zum Beispiel die Helligkeit, der Kontrast, der Kontrastverlauf, die Farben, die Bildauflösung ober die Ausrichtung bis hin zu perspektivischen Verzerrungen oder Montagen mehrerer Bilder.
Vektorisierung
[Bearbeiten]Bei digitalen Bildern, die aus einzelnen Bildpunkten zusammengesetzt sind, gibt es keine informationstechnischen Verknüpfungen oder Beziehungen zwischen den Bildpunkten, die über das rechteckige und rechtwinklige Anordnen der Bildpunkte hinausgehen.
Benachbarte Punkte können dieselbe Helligkeit oder Farbe aufweisen, ohne dass dies in den Bilddaten kodiert ist. Solche Beziehungen zwischen zusammengehörigen Bildpunkten können mit geeigneter Software erstellt oder in vorhandenen gerasterten Bildern ermittelt werden. Typische Beispiele für auszeichenbare topographische Gebilde in digitalen Bildern sind isolierte Punkte, gerade oder nach bestimmten Regeln gekrümmte Linien oder durch geschlossene Linienzüge begrenzte Flächen mit oder ohne Füllung, die auch als graphische Primitive bezeichnet werden. Die Orte der zur Beschreibung dieser Gebilde verwendbaren Punkte - seien es Anfangs-, End- oder Eckpunkte - können mathematisch durch Vektoren definiert werden.
Die graphischen Objekte können bei der Anzeige – auch bei einem Punktdurchmesser oder einer Strichstärke von null – minimal mit dem Durchmesser der dargestellten Bildpunkte wiedergegeben werden. Es ist aber auch möglich, den Punkten einen definierten Durchmesser oder den Linien eine bestimmte Breite zuzuordnen, so dass diese dann gegebenenfalls auch mit mehr als einem Bildpunkt dargestellt werden.
Vektorisierte Bilddaten haben eine Reihe von Vorteilen:
- Die Datenmenge für die vektorielle Beschreibung von einigen wenigen geeigneten Punkten ist oft erheblich geringer als die Datenmenge für die Beschreibung aller beteiligten Punkte in einem Punktraster
- Vektoren können mit einfachen mathematischen Transformationen beliebig skaliert, gedreht, gespiegelt oder verschoben werden
- Mit Vektoren können Abbildungen auch ohne weiteres in drei- oder mehrdimensionalen Räumen realisiert werden, wobei sich die Datenmenge im Vergleich zu gerasterten Daten dann nochmals drastisch reduzieren kann. Mittels geeigneter mathematischer Projektionen lassen sich ohne großen Aufwand zweidimensionale Ansichten, Schnitte oder Perspektiven der Bilddaten erzeugen
Auf der anderen Seite gibt es auch Gründe, die für die Verwendung von gerasterten Bilddaten sprechen:
- Bei einer optischen Abbildung stehen die Informationen über die Beziehungen von benachbarten Punkten nicht unmittelbar zur Verfügung, sondern müssen mit aufwendigen Verfahren im Anschluss an die Aufnahme ermittelt werden
- Bei Bildern mit sehr heterogener Verteilung der Helligkeiten und Farben ist es in der Regel sehr schwierig, Bezüge zwischen benachbarten Punkten herzustellen
- Bei komplexen Bildern wird die Datenmenge zur vollständigen Beschreibung der Bildinhalte mit Vektoren deutlich größer als bei gerasterten Daten
- Gerasterte Daten lassen sich zur Reduktion der Datenmenge meist sehr effizient komprimieren, ohne dass es zu wesentlichen Informationseinbußen kommt
Diese Aspekte führen dazu, dass vektorisierte Daten insbesondere bei der manuellen Erstellung von Bilddaten Verwendung finden (Graphik) und gerasterte Daten vorwiegend bei der maschinellen Erstellung anfallen (Photographie, bildgebende Verfahren).
Wie auch immer, es ist meist leicht möglich, Vektorgraphiken in Rasterdaten umzuwandeln. Als Parameter muss dann die Punktdichte oder die gewünschte Bildauflösung des gesamten Bildes vorgegeben werden, mit der es wiedergegeben werden soll.
Umgekehrt ist es meist deutlich schwieriger, insbesondere wenn die gerasterten Vorlagen schlechten Kontrast oder eine schlechte Auflösung haben. Eine besondere Form der Vektorisierung ist die optische Schriftzeichenerkennung (auch OCR für englisch: Optical Character Recognition), die in großem Umfang zur Umwandlung von gerasterten Textvorlagen in Textdokumente eingesetzt wird.
Bilddateiformate
[Bearbeiten]Es gibt eine Vielzahl von Dateiformaten für gerasterte Bilddaten (englisch: bitmap). Zu den am weitesten verbreiteten allgemein verwendbaren Formaten gehören zum Beispiel:
- JPEG (englisch: Joint Picture Expert Group = Gemeinsame Bildexperten-Gruppe), das eine flexible Datenkompression sowie vorgegebene und proprietäre Metadaten zulässt, jedoch je nach Qualität und Stärke der Datenreduktion immer mit einem mehr oder weniger starken Informationsverlust behaftet ist und von allen Webbrowsern wiedergegeben werden kann
- DNG (englisch: Digital Negative = digitales Negativ) als Nachfolger von TIFF (englisch: Tagged Image File Format = Mit „Anhängern“ (Attributen) versehenes Dateiaustauschformat) zur verlustfreien Speicherung von Rohdaten und Metadaten, das nur in Anspielung auf den Umkehrfilm als „Negativ“ bezeichnet wird, obschon die Bildinformation in aller Regel ohne die Umkehrung von Farb- und Helligkeitswerten gespeichert wird
- PNG (englisch: Portable Network Graphics = portierbare Netzwerkgraphik) mit verlustfreier Datenkompression ist der Nachfolger von GIF (Graphics Interchange Format = Graphikaustauschformat) und kann von allen Webbrowsern wiedergegeben werden
Es ist zu beachten, dass die meisten Speicherformate für gerasterte Bilddaten wegen der Adressierung von Graphikspeicher in Rechenmaschinen den Koordinatenursprung (0 | 0) links oben im Bild haben. Die positive horizontale Achse verläuft also von links oben nach rechts und die positive vertikale Achse von links oben nach unten.
Typische Dateiformate für vektorisierte Graphiken sind:
- DXF (englisch: Drawing Exchange Format = Zeichnungsaustauschformat)
- SVG (englisch: Scalable Vector Graphics = skalierbare Vektorgraphik) mit ausschließlich zweidimensionalen Vektoren und kann von allen Webbrowsern wiedergegeben werden
- PostScript, das als Seitenbeschreibungssprache vor allem für die Druckausgabe entwickelt wurde, aber auch das PDF (englisch: Portable Document Format = portierbares Dokumentenformat) beeinflusst hat, als Encapsulated PostScript (abgekapseltes PostScript) für einzelne graphische Druckseiten verwendet wird und auch zur Einbettung und Speicherung von gerasterten Daten verwendet werden kann
Bildeigenschaften digitaler Bilder
[Bearbeiten]Einige Bildeigenschaften spielen nur im Zusammenhang mit digitalen Bildern eine Rolle, da die entsprechenden Größen und Zusammenhänge bei analogen Bildern nicht vorhanden sind. In den folgenden Abschnitten finden sich daher einige für digitale Bilder wichtige und wesentliche Eigenschaften.
Bildauflösung
[Bearbeiten]Ein sehr wichtiger Parameter für digitale Rasterbilder ist die Bildauflösung oder Pixelzahl. Diese kann entweder als 2-Tupel (, ) mit der Angabe der Bildpunkte in der Bildbreite und in der Bildhöhe oder als Produkt dieser beiden Werte angegeben werden:
Als Maßeinheit für die Anzahl der Bildpunkte wird in der Regel Pixel beziehungsweise Megapixel verwendet.
In der Regel sind die Bildpunkte quadratisch, so dass das Verhältnis exakt das geometrische Verhältnis beim wiedergegebenen Bild widerspiegelt. Obwohl die Diagonale die Bildpunkte unregelmäßig schneidet, kann die effektive Anzahl der Bildpunkte entlang der Bilddiagonalen mit Hilfe des Satzes des Pythagoras über die folgende Beziehung ermittelt werden:
Bildseitenverhältnis
[Bearbeiten]
Das Bildseitenverhältnis wird als das Verhältnis der Anzahl der Bildpunkte in der Breite zur Anzahl der Bildpunkte in der Höhe angegeben:
Umgeformt ergibt sich:
Das Verhältnis wird oft als ganzrationale Zahl mit einem Doppelpunkt und nicht mit einem Bruchstrich oder als reelle Zahl angegeben:
Mit dem Bildseitenverhältnis können die Bildauflösung beziehungsweise die Bildbreite und die Bildhöhe berechnet werden:
Auch die effektive Anzahl der Bildpunkte auf der Bilddiagonalen kann gegebenenfalls über das Bildseitenverhältnis ausgerechnet werden:
Oder erneut nach der Bildbreite und der Bildhöhe umgeformt:
Für die Anzahl der Bildpunkte ergibt sich dann:
Das Bildseitenverhältnis von 4:3 stammt vom analogen Fernsehen und wurde für die ersten Computer-Monitore übernommen - die meisten digitalen Kameras haben daher Bildsensoren mit diesem nativen Bildseitenverhältnis; auch die ersten digitalen Camcorder hatten Bildsensoren im Verhältnis 4:3.
Das Bildseitenverhältnis 3:2 stammt aus der analogen Photographie mit Kleinbildfilm; es wird auch bei vielen digitalen Spiegelreflexkameras eingesetzt, wo dieses feste Bildseitenverhältnis auch durch die optischen Sucher vorgegeben ist.
Bei Videoanwendungen hat sich das Bildseitenformat 16:9 durchgesetzt, das sich auch bei den entsprechenden Wiedergabegeräten, wie digitalen Fernsehgeräten und Projektoren, sowie teilweise auch bei Computer-Monitoren wiederfindet. Beim DVD-Format gab es zunächst noch viele ältere Wiedergabegeräte mit dem Bildseitenverhältnis 4:3 und dann zunehmend neuere Wiedergabegeräte mit dem Bildseitenverhältnis 16:9. Die Bildpunkte dieses Formates sind nicht quadratisch und können bei den Wiedergabegeräten eingestellt werden.
Bildformate
[Bearbeiten]In der folgenden Tabelle sind einige wichtige digitale Bildformate angegeben:
| Bildformat Bezeichnung |
Anzahl der Bildpunkte in Pixel |
Anzahl der Bildpunkte in Pixel |
Anzahl der Bildpunkte in Megapixel |
Bildseitenverhältnis |
|---|---|---|---|---|
| VGA | 640 | 480 | 0,3 | 4:3 |
| DVD | 720 | 576 | 0,4 | 4:3 oder 16:9 |
| SVGA | 800 | 600 | 0,5 | 4:3 |
| XGA | 1024 | 768 | 0,8 | 4:3 |
| HD ready | 1280 | 720 | 0,9 | 16:9 |
| SXGA | 1280 | 1024 | 1,3 | 5:4 |
| UXGA | 1600 | 1200 | 1,9 | 4:3 |
| Full HD | 1920 | 1080 | 2,0 | 16:9 |
| QXGA | 2048 | 1536 | 3,1 | 4:3 |
| 4K | 3840 | 2160 | 8,3 | 16:9 |
| 8K | 7680 | 4320 | 33,2 | 16:9 |
Siehe hierzu auch: Bildsensoren
Bit-Tiefe
[Bearbeiten]Die Bit-Tiefe gibt an, in welchem dynamischen Umfang Helligkeitsunterschiede in digitalen Bildern gespeichert werden können. Der maximale Helligkeitswert ergibt sich aus der Anzahl der Bits, die für einen ganzzahligen Wert zur Verfügung stehen:
Die minimale Helligkeit liegt bei 0.
Die möglichen digitalen Helligkeitswerte liegen also im Bereich von 0 bis :
- mit
Diese Überlegungen gelten sowohl für die Helligkeit in Graustufenbildern, als auch für die einzelnen Farbkanäle in Farbbildern, wo dann von der Farbtiefe gesprochen wird. Bei den drei Farbkanälen rot, grün und blau, die den Primärfarben entsprechen, ergibt sich für die digitalen Helligkeitswerte dieser drei Farben dementsprechend:
- mit
- mit
- mit
Bei den standardisierten Dateiformaten JPEG (Joint Picture Expert Group) und PNG (Portable Network Graphics) sowie vielen anderen verbreiteten Dateiformaten für farbige Bilder stehen für die drei Primärfarben jeweils acht Bits (also drei Mal ein Byte) zur Verfügung, so dass also für jeden Punkt und für jeden Farbkanal 256 verschiedene, ganzzahlige Helligkeitswerte von 0 bis 255 gespeichert werden können.
In den folgenden monochromen Bildern wird die Bit-Tiefe jeweils um eins erniedrigt, so dass die Anzahl der zur Verfügung stehenden Graustufen sich jeweils halbiert. Im letzten Bild existieren nur noch zwei Helligkeitsstufen:
- Testtafeln mit abnehmender Bit-Tiefe und Anzahl der Graustufen
-
Bit-Tiefe 8 mit 256 Graustufen
-
Bit-Tiefe 7 mit 128 Graustufen
-
Bit-Tiefe 6 mit 64 Graustufen
-
Bit-Tiefe 5 mit 32 Graustufen
-
Bit-Tiefe 4 mit 16 Graustufen
-
Bit-Tiefe 3 mit 8 Graustufen
-
Bit-Tiefe 2 mit 4 Graustufen
-
Bit-Tiefe 1 mit 2 Graustufen
Bei Rohdatenspeicherung werden in der Regel mehr als acht Bits pro Farbkanal gespeichert, je nachdem welche Genauigkeit und Dynamik der Bildwandungsprozess und der Analog-Digital-Wandler haben. Rohdatenformate sind oft nicht nur für einzelne Anbieter proprietär, sondern häufig sogar für einzelne Geräte. Dies macht den Einsatz von spezieller Software beziehungsweise speziellen Zusatzmodulen (sogenannten Plug-Ins) erforderlich, die in späteren Zeiten möglicherweise nicht mehr frei verfügbar oder zugänglich sind. Mit dem Dateiformat DNG (englisch: Digital Negative = digitales Negativ) wurde ein standardisiertes Rohdatenformat geschaffen, das zunehmend Unterstützung findet.
Speicherbedarf
[Bearbeiten]Stehbilder
[Bearbeiten]
Der Speicherbedarf (englisch: memory) in Bytes (1 Byte = 8 Bit) lässt sich für ein einzelnes Bild aus der Anzahl der Farbkanäle , der Bit-Tiefe pro Farbkanal und der Bildauflösung ermitteln:
Nicht-komprimierte, monochrome Bilddaten mit einer Bit-Tiefe von 8 Bits benötigen daher genauso viele Bytes, wie sie Bildpunkte beinhalten. Ist eine höhere Helligkeitsauflösung mit einer Bit-Tiefe von 16 Bits erforderlich, um zum Beispiel die Nachbearbeitung von Bildausschnitten zu ermöglichen, ergibt sich ein doppelt so großer Speicherbedarf. Monochrome Bilder benutzen in der Regel nur einen Farbkanal, Farbbilder werden jedoch üblicherweise mit drei Farbkanälen gespeichert, die den drei Primärfarben rot, grün und blau (RGB) entsprechen, wodurch sich der Speicherbedarf gegenüber monochromen Bilddaten verdreifacht. Wenn für jeden der drei Farbkanäle b Bit zur Verfügung stehen, um die Helligkeit der jeweiligen Primärfarbe zu bestimmen, ergeben sich nach dem folgenden Zusammenhang insgesamt Möglichkeiten:
- , bei b = 8 Bit also
In der folgenden Tabelle finden sich einige Beispielwerte für nicht-komprimierte, dreifarbige Bilder mit einer Bit-Tiefe von 8 Bits pro Farbkanal:
| Bildauflösung in Megapixels |
Speicherbedarf in Megabytes |
|---|---|
| 1 | 3 |
| 2 | 6 |
| 4 | 12 |
| 8 | 24 |
| 16 | 48 |
| 32 | 96 |
Durch geeignete und hochwertige Bildkompressionsverfahren - zum Beispiel unter Verwendung des weit verbreiteten JPEG-Formats, das mit drei Farbkanälen (RGB) und einer Bit-Tiefe von 8 Bit pro Farbkanal definiert ist - lässt sich der Speicherbedarf ohne nenn- oder erkennbare Verluste oft auf etwa 10 Prozent der unkomprimierten Werte reduzieren.
Bewegtbilder
[Bearbeiten]Bei mehreren Bildern in Folge wächst der Speicherbedarf bei verlustfreier Speicherung mit der Anzahl der Bilder und somit auch mit der Zeit . In der Regel wird mit einer Bildfrequenz (beziehungsweise Bildrate) gerechnet, um die erforderliche Datenübertragungsrate [beziehungsweise Datenrate) zu bestimmen:
Der Speicherbedarf für eine Aufnahme der Dauer beträgt dann:
Durch Datenkompression um den Faktor kann die Datenmenge um ein bis zwei Größenordnungen reduziert werden, ohne dass es zu gravierenden Einbußen bei der Bildqualität kommt:

Dies gelingt insbesondere dadurch, dass unveränderte Bildausschnitte nur einmal kodiert und für mehrere aufeinanderfolgende Bilder verwendet werden. Die Kompression kann umso besser gelingen, je mehr Rechenleistung in den Analyseprozess gesteckt werden kann. Daher ist es einfacher, die digitalen Daten ohne Zeitdruck zu komprimieren, als diese zum Beispiel für Live-Übertragungen in Echtzeit zu kodieren. Bei der Kompression kommt es auch im letzteren Fall zwangsweise zu einer Verzögerung, die je nach Datenmenge, Rechenleistung und Verfahren mehrere Sekunden in Anspruch nehmen kann. Bei schnell veränderlichen Filmszenen und zu geringen Datenraten kommt es hierbei sehr häufig zu sogenannten Kompressionsartefakten, wie der Klötzchen- respektive Blockbildung (kachelartige Strukturen im Bild) oder dem Bildruckeln (ruckartiger seitlicher Versatz von aufeinanderfolgenden Bildern).
In der folgenden Tabelle sind einige für verschiedene Situationen erforderlichen Datenmengen zusammengestellt, wobei in allen Fällen von zum einen von rohen Farbbildern mit drei Farbkanälen und einer Bit-Tiefe von jeweils 8 Bit und zum anderen von einer Datenkompression mit dem Faktor ausgegangen wurde:
| Bildauflösung in Megapixels |
Speicherbedarf pro Einzelbild in Megabytes |
Bildfrequenz in Bildern pro Sekunde |
Datenrate in Megabytes pro Sekunde |
Speicherbedarf für eine Stunde in Terabytes |
Speicherbedarf für eine Stunde bei k=100 in Gigabytes |
|---|---|---|---|---|---|
| 0,44 (SD 4:3) | 1,3 | 25 | 33 | 0,12 | 1,2 |
| 0,92 (HD ready) | 2,8 | 25 | 70 | 0,25 | 2,5 |
| 2,1 (Full HD) | 6,2 | 50 | 310 | 1,1 | 11 |
| 8,3 (4K) | 25,9 | 50 | 1200 | 4,3 | 43 |
| 33,2 (8K) | 99,5 | 50 | 5000 | 18 | 180 |
Bildbearbeitung
[Bearbeiten]Dank schneller digitaler Datenverarbeitung können digitale Bilder in kurzer Zeit analysiert und verändert werden. Oft findet eine umfangreiche Bildbearbeitung bereits unmittelbar nach der Aufnahme der Bilddaten mit Hilfe einer Firmware innerhalb von optischen, digitalen Geräten statt. Es besteht aber auch die Möglichkeit weitgehend unbearbeitete Daten, sogenannten Rohdaten zu speichern. Eine Bildbearbeitung kann aber auch nach dem Speichern der Bilddaten in einer Datei zu einem beliebigen späteren Zeitpunkt mit einer geeigneten Software erfolgen. Das Ergebnis einer solchen Bearbeitung wird in der Regel in einer weiteren Datei gespeichert, damit die Originaldaten für eventuell später erforderliche Prozesse erhalten bleiben.
In den folgenden Abschnitten werden einige wichtige Verfahren und Begriffe in diesem Zusammenhang beschrieben.
Digitalzoom - Softwarelupe
[Bearbeiten]
Ohne Digitalzoom hat das Objektiv eine Modulationsübertragung, die erheblich über den Erfordernissen eines menschlichen Betrachters liegt. Bei zweifachem Digitalzoom sind die Kontraste für den menschlichen Betrachter noch fast ohne Einschränkungen, bei vierfachem Digitalzoom gibt es bereits deutliche Einbußen, und bei achtfachem Digitalzoom sind die Kontraste erheblich reduziert.
Bei digitalen Bildern ist es sehr leicht möglich, nur einen rechteckigen Ausschnitt des gesamten Bildes zu betrachten. Hierbei ändern sich bei konstanter Brennweite sowohl der Abbildungsmaßstab als auch der Bildwinkel, so dass ein Effekt wie bei der vollständigen Aufnahme mit einer entsprechend längeren Brennweite entsteht.
Es ist allerdings zu beachten, dass ein solcher digital gezoomter Ausschnitt über weniger Bildpunkte verfügt als das Gesamtbild und die Bildauflösung somit reduziert ist. Dies ist solange kein Problem, wie das verwendete Wiedergabegerät beim Einsatz der sogenannten Softwarelupe nicht mehr Bildpunkte hat, als der gewählte Bildausschnitt, da dann höchstens so viele Informationen vorhanden sind, wie dargestellt werden können. Wird der Digitalzoom noch weiter erhöht, müssen die für die Anzeige erforderlichen Punkte (, ) zum Beispiel durch Interpolation oder Punktverdopplung aus den verfügbaren Bildpunkten (, ) berechnet werden, wobei sich allerdings für den Betrachter kein Informationsgewinn ergibt, sondern die Bilder bei hinreichend genauer Betrachtung nur grob gerastert beziehungsweise unscharf wirken, da die Modulationsübertragungsfunktion dabei immer ungünstiger wird.
Siehe hierzu auch: Modulationsübertragung
Üblicherweise wird der Digitalzoom als Faktor oder in Prozent angegeben, wobei sich dieser Wert auf die Längenskalierung und nicht auf die Flächenskalierung bezieht, also:
beziehungsweise
- Digitalzoom - Tiger mit der Anzeige...
-
...eines Viertels der verfügbaren Bildpunkte entlang der Bildkanten
; -
...der Hälfte der verfügbaren Bildpunkte entlang der Bildkanten
; -
...aller verfügbaren Bildpunkte
; -
...doppelt so vieler Bildpunkte entlang der Bildkanten wie verfügbar
; -
...viermal so vieler Bildpunkte entlang der Bildkanten wie verfügbar
;
Wird bei optischen Geräten zur Bildaufnahme vor der Aufnahme das Bild auf einem Monitor oder in einem elektronischen Sucher wiedergegeben („Live-View“), kann mit Hilfe der Softwarelupe ein beliebiger Ausschnitt des Bildes mit einhundertprozentigem Digitalzoom dargestellt werden. Dies ist besonders zur Einstellung der korrekten Entfernung am Objektiv sehr hilfreich, hilft aber beispielsweise auch beim Erkennen von Bildrauschen.
Histogramme
[Bearbeiten]
Histogramme sind Diagramme, die die Häufigkeitsverteilung der diskreten Helligkeiten in digitalen Bildern angeben. Dabei ist es üblich, auf der horizontalen Achse die Helligkeitswerte (respektive Tonwerte) von dunkel nach hell aufzutragen und bei jedem ganzzahligen Helligkeitswert die Anzahl der im gesamten Bild (oder einem vorher zu definierenden Teilbereich) auftretenden Bildpunkte in vertikaler Richtung anzugeben.
Histogramme können für die gesamte Luminanz oder auch getrennt nach Farbkanälen ausgegeben werden.
Gammakorrektur
[Bearbeiten]Um die mittleren Helligkeiten eines digitalen Bildes anzupassen, ohne die minimale Helligkeit (schwarz) und die maximale Helligkeit (weiß) zu ändern, kann eine rechnerische Gammakorrektur durchgeführt werden.
Siehe Gammakorrektur.
Tonwertkorrektur
[Bearbeiten]Die Helligkeitswerte, gegebenenfalls auch nach Farbkanälen getrennt betrachtet, werden auch Tonwerte genannt.
Weißpunkt
[Bearbeiten]Wenn der Spielraum der Tonwerte in einem digitalen Bild nicht ausgenutzt wird - bei unterbelichteten Bildern ist dies üblicherweise der Fall, da die höheren Helligkeitswerte nicht auftauchen -, ist es sinnvoll, die Helligkeitswerte gleichmäßig zu erhöhen, damit bei der Wiedergabe ein klares Bild mit der Möglichkeit von schwarzen und weißen Bildpunkten entsteht.
Siehe auch Weißpunkt.
Weißabgleich
[Bearbeiten]Eine Tonwertkorrektur kann auch separat für alle vorhandenen Farbkanäle, meist die Primärfarben rot, grün und blau, durchgeführt werden. Um einen Bildbereich farbneutral, also ohne Farbstich, zu bekommen, müssen die entsprechenden Tonwerte der Farbkanäle auf die gleichen Helligkeiten gerechnet werden - diesen Vorgang bezeichnet man als Weißabgleich. Bei Aufnahmesystemen mit automatischem Weißabgleich kann in jedem Farbkanal der hellste Punkt gesucht werden, und mit deren Tonwerten werden die Korrekturen für die einzelnen Farbkanäle ausgerechnet.
Siehe auch Weißabgleich.

Als photographisches Hilfsmittel gibt es Graukarten, die vor der eigentlichen Aufnahme zur manuellen Einstellung des Weißabgleichs eines Aufnahmesystems verwendet werden können. Auch weiße Karten finden hierzu Anwendung, jedoch besteht hierbei unter Umständen die Gefahr einer Überbelichtung, die die Messergebnisse verfälschen würde. Bei weißen Referenzflächen ist also darauf zu achten, dass die Tonwerte nicht in der Sättigung sind.
Bildfehler
[Bearbeiten]Helligkeitsrauschen
[Bearbeiten]
Beim Helligkeitsrauschen (Luminanzrauschen) handelt es sich um eine zufällige, mehr oder weniger stark sichtbare Schwankungen bei den Leuchtdichten einzelner Punkte im Bild (siehe auch Kapitel Leuchtdichte), die bei digitalen Bildsensoren durch das Dunkelstromrauschen, durch den Ausleseprozess und durch das Quantisierungsrauschen der Analog-Digital-Wandler verursacht werden. Bei Halbleitern kann der Dunkelstrom und somit das Dunkelstromrauschen durch Kühlung drastisch reduziert werden. Bei einer Erwärmung um mehrere Kelvin verdoppelt sich das Dunkelstromrauschen von Bildsensoren typischerweise.
Simulierte Bilder
[Bearbeiten]Im Folgenden wird das Aussehen von Helligkeitsrauschen anhand eines von einer digitalen Kamera aufgenommenen schwarz-weißen Musters demonstriert, dem künstlich und zunehmend ein farbloses 1/f-Rauschen hinzugefügt wurde.
-
100% Muster, 0% Helligkeitsrauschen
-
75% Muster, 25% Helligkeitsrauschen
-
50% Muster, 50% Helligkeitsrauschen
-
25% Muster, 75% Helligkeitsrauschen
-
0% Muster, 100% Helligkeitsrauschen
Rauschreduktion
[Bearbeiten]In der nächsten Zusammenstellung ist der Effekt einer nachträglichen Rauschreduktion in den Bildern zu erkennen. Meist werden die Kontrastanteile bei hohen Ortsfrequenzen verringert, wobei allerdings auch die entsprechenden Strukturen, die nicht auf dem Rauschen beruhen, eliminiert werden können. Da bei einer Rauschreduktion häufig extrem große und kleine Helligkeiten eliminiert werden, kann der Bildkontrast nach der Rauschreduktion oft erhöht werden, indem der Weißpunkt und der Schwarzpunkt der Bilder optimiert werden.
-
25% Muster, 75% Helligkeitsrauschen, ohne Rauschreduktion
-
25% Muster, 75% Helligkeitsrauschen, mit Rauschreduktion
-
25% Muster, 75% Helligkeitsrauschen, mit Rauschreduktion, Kontrast erhöht
Gaußsche Weichzeichnung
[Bearbeiten]Ein sehr einfach zu implementierendes Verfahren zur Rauschreduktion ist der Gaußsche Weichzeichner. Hierbei werden die Helligkeiten der einzelnen Bildpunkte mit den Helligkeiten in der Umgebung gewichtet gemittelt. Je mehr Punkte in der Umgebung dazu herangezogen werden, desto niedrigere Ortsfrequenzen werden in ihrer Modulation verringert, so dass die Bilder zunehmend grob strukturiert werden, wobei es keine schnellen Kontrastwechsel mehr gibt. Bei zu starker Weichzeichnung verschwindet nicht nur das Bildrauschen, sondern auch jegliche beabsichtigte Struktur in den Bildern, so dass auch diese schließlich gar nicht mehr erkannt werden können.
-
25% Muster, 75% Helligkeitsrauschen, ungefiltert
-
25% Muster, 75% Helligkeitsrauschen, gefiltert mit einer Weite von einem Bildpunkt
-
25% Muster, 75% Helligkeitsrauschen, gefiltert mit einer Weite von zwei Bildpunkten
-
25% Muster, 75% Helligkeitsrauschen, gefiltert mit einer Weite von vier Bildpunkten
-
25% Muster, 75% Helligkeitsrauschen, gefiltert mit einer Weite von acht Bildpunkten
Farbrauschen
[Bearbeiten]
Beim Farbrauschen (Chrominanzrauschen) handelt es sich um eine zufällige, mehr oder weniger stark sichtbare Schwankungen bei den Farbwerten einzelner Bildpunkte, die die gleichen Ursachen haben wie das Helligkeitsrauschen.
Die folgende Zusammenstellung zeigt Aufnahmen einer nicht reflektierenden schwarzen Scheibe in heller Umgebung, die bei verschiedenen Empfindlichkeiten (ISO-Zahlen) sowohl als kameraintern bearbeite JPEG-Datei als auch als kameraintern unbearbeitete Rohdaten-Datei gespeichert wurden. Zur besseren Erkennbarkeit wurden die geringen Helligkeiten durch eine Gamma-Korrektur bei allen Aufnahmen im gleichen Maße aufgehellt. Bei der Kompaktkamera sind auch bei niedrigen ISO-Werten (geringe Empfindlichkeit mit geringem Bildrauschen) unbunte Bildsignale vorhanden, die auf Falschlicht in der optischen Abbildung zurückzuführen sind:
- Bildrauschen bei verschiedenen Kameraeinstellungen
-
Kompaktkamera bei ISO 100 als JPEG-Datei
-
Kompaktkamera bei ISO 100 als Rohdaten-Datei
-
Spiegelreflexkamera bei ISO 100 als JPEG-Datei
-
Spiegelreflexkamera bei ISO 100 als Rohdaten-Datei
-
Kompaktkamera bei ISO 200 als JPEG-Datei
-
Kompaktkamera bei ISO 200 als Rohdaten-Datei
-
Spiegelreflexkamera bei ISO 200 als JPEG-Datei
-
Spiegelreflexkamera bei ISO 200 als Rohdaten-Datei
-
Kompaktkamera bei ISO 400 als JPEG-Datei
-
Kompaktkamera bei ISO 400 als Rohdaten-Datei
-
Spiegelreflexkamera bei ISO 400 als JPEG-Datei
-
Spiegelreflexkamera bei ISO 400 als Rohdaten-Datei
-
Kompaktkamera bei ISO 800 als JPEG-Datei
-
Kompaktkamera bei ISO 800 als Rohdaten-Datei
-
Spiegelreflexkamera bei ISO 800 als JPEG-Datei
-
Spiegelreflexkamera bei ISO 800 als Rohdaten-Datei
-
Kompaktkamera bei ISO 1600 als JPEG-Datei
-
Kompaktkamera bei ISO 1600 als Rohdaten-Datei
-
Spiegelreflexkamera bei ISO 1600 als JPEG-Datei
-
Spiegelreflexkamera bei ISO 1600 als Rohdaten-Datei
-
Spiegelreflexkamera bei ISO 3200 als JPEG-Datei
-
Spiegelreflexkamera bei ISO 3200 als Rohdaten-Datei
Smear-Effekt
[Bearbeiten]Videoaufnahme mit der Demonstration des Smear-Effektes bei einer CCD-Kamera durch das Ein- und Ausschalten einer hellen Lichtquelle im Bildfeld:
- Smear-Effekt
-
Taschenlampe aus - ohne Smear-Effekt
-
Taschenlampe an - mit Smear-Effekt (senkrechter rosafarbener Streifen auf Höhe der Lichtquelle)
Wiedergabe
[Bearbeiten]Dieses Kapitel beschäftigt sich mit verschiedenen Möglichkeiten, zweidimensionale Bildinformation aufzubereiten und wiederzugeben.
Da digitale Rasterbilder in Form von Datenworten vorliegen, sind diese – anders als reelle Bilder – nicht unmittelbar der Betrachtung zugänglich. Daher ist es auch nicht eindeutig möglich, digitalen Bildern eine Bildgröße oder subjektiv empfundene Eigenschaften wie Farbe zuzuordnen. Vielmehr werden diese Bildeigenschaften erst bei der Wiedergabe erzeugt. Somit haben die Verfahren und Geräte, die zur Bildwiedergabe eingesetzt werden, einen entscheidenden Einfluss auf die Darstellung der Bilder und vor allem auf die subjektiv empfundene beziehungsweise auch auf die objektiv ermittelbare Bildqualität.
Eine Wiedergabe kann prinzipiell mit leuchtenden, reflektierenden oder durchscheinenden optischen Bauelemente realisiert werden.
Punktdichte
[Bearbeiten]Der Abbildungsmaßstab ist zwar in Bezug auf das registrierende optoelektronische Bauelement real, da ja die betrachte Abbildung eine reale Abbildung ist, jedoch ist dieser Abbildungsmaßstab in der abstrakten digitalen Darstellung der Daten nicht mehr relevant, solange den einzelnen Bildpunkten nicht eine absolute Größe zugeordnet werden kann. Diese Bildpunkte – auch als Pixel bezeichnet (englisches Kunstwort aus den beiden Begriffen picture element zusammengesetzt) – haben im Wiedergabemedium oder auf einem Bildsensor einen bestimmten horizontalen oder vertikalen Abstand, der auch als Pixelpitch (vom englischen Begriff "pitch" in der Bedeutung von "Teilung") bezeichnet wird und oftin Mikrometern (µm) angegeben wird. Abgesehen von der Tatsache, dass die Oberfläche eines Bildsensors nicht notwendiger Weise vollständig zur Lichtdetektion zur Verfügung steht, da zwischen den Bildpunkten meist optisch inaktive Zonen vorhanden sind, oder dass ein wiedergegebenes Bild mit einem dunklen Gitter zwischen den leuchtenden Bildpunkten überzogen ist ("Fliegengittereffekt"), kann der Abstand der Pixel für Betrachtungen, die das gesamte digitale Bild betreffen auch als Punktgröße betrachtet werden.
Wenn der Bildpunktabstand den digitalen Bildern eindeutig zugeordnet werden kann, zum Beispiel in den Metadaten einer Bilddatei, kann die Größe des realen Bildes rückwirkend eindeutig ermittelt werden. Wenn ferner der Abbildungsmaßstab der optischen Abbildung bekannt ist, kann damit sogar auf die tatsächliche Größe der im Bild dargestellten Objekte zurückgeschlossen werden. Ansonsten muss je nach Anforderung eine bestimmte Punktdichte festgelegt oder bestimmt werden, mit der die digitalen Bildpunkte wiedergegeben werden sollen.
Diese Punktdichte hat die Basismaßeinheit 1/m wird jedoch häufig in der Maßeinheit dpi (englisch für dots per inch = Punkte pro Zoll) angegeben. Je nach Anwendung kann es aber auch sinnvoll sein, die Maßeinheiten ppi (englisch für pixels per inch = Bildpunkte pro Zoll) oder lpi (englisch für lines per inch = Linien pro Zoll) zu verwenden. Hierbei sind zwei Unterscheidungen wichtig:
- Bei einem Bildpunkt (Pixel) handelt es sich oft um einen farbigen Bildpunkt, der aus mehreren einfarbigen Punkten (dots) zusammengesetzt ist, die nicht notwendigerweise örtlich übereinanderliegen müssen, sondern auch nebeneinander liegen können.
- Ein Linienpaar setzt sich aus zwei Linien zusammen, so dass zum Beispiel sorgfältig zwischen den Maßeinheiten "Linien pro Millimeter" und "Linienpaare pro Millimeter" unterschieden werden muss.
Die Punktdichte ergibt sich rechnerisch als Kehrwert der angegebenen Punktgröße :
Für den Fall der Verwendung von Zoll als Bezugslängenmaß für die Punktdichte und Millimetern als Bezugslängenmaß für die Punktgröße gilt:
- mit der Konstante .

Punktabstand
[Bearbeiten]Bei vorgegebener Punktdichte ergibt sich die Punktgröße respektive der Punktabstand zu:
Die Länge der Strecke von unmittelbar nebeneinanderliegenden Punkten ergibt sich dann mit Hilfe der Punktgröße aus der Anzahl der Bildpunkte :
Oft wird beim Desktop-Publishing (DTP) als Längenangabe die Maßeinheit "Punkte" oder genauer "DTP-Punkte" verwendet, die sich auf eine Punktgröße bei einer Punktdichte von beziehungsweise metrisch ausgedrückt bezieht:
Bei der gedruckten Wiedergabe von digitalen Bildern mit einer typischen Punktdichte beziehungsweise metrisch ausgedrückt ergeben sich zum Beispiel die folgenden Zusammenhänge:
| Anzahl Pixel |
Länge in mm |
DTP-Punkte in pt |
|---|---|---|
| 1 | 0,085 | |
| 2 | 0,17 | |
| 3 | 0,25 | |
| 4 | 0,34 | |
| 8 | 0,68 | 1,9 |
| 15 | 1,3 | 3,6 |
| 31 | 2,6 | 7,4 |
| 63 | 5,3 | 15 |
| 125 | 10,6 | 30 |
| 250 | 21,2 | 60 |
| 500 | 42,3 | 120 |
| 1000 | 84,7 | 240 |
Da die Punktgröße oder der Abstand der Punkte bei rechteckigen Bildpunkten in vertikaler und horizontaler Richtung verschieden sein kann, muss diese Betrachtung gegebenenfalls für diese beiden Richtungen getrennt durchgeführt werden. Die Bildgröße in den senkrecht stehenden Längen (Bildbreite) und (Bildhöhe) ergibt sich mit Hilfe dieser Umrechnung aus der Anzahl der Bildpunkte in der Bildbreite und in der Bildhöhe und der entsprechenden Punktgröße in horizontaler Richtung beziehungsweise in vertikaler Richtung :
Bilddiagonale
[Bearbeiten]Die Überlegung über die Punkthöhe und die Punktbreite kann ohne weiteres auch auf die Bilddiagonale übertragen werden:
Bei quadratischen Bildpunkten () vereinfacht sich diese Beziehung mit der virtuellen Anzahl der Bildpunkte auf der Diagonalen zu:
Die Diagonale eines Bildes hängt also nur von der Punktdichte der Reproduktion und der Anzahl der Bildpunkte ab. Bei einem bestimmten Betrachtungsabstand gilt dies dann auch für den Bildwinkel respektive den Betrachtungswinkel. Der Bildwinkel ergibt sich beim Betrachtungsabstand dann zu:
Betrachtungsabstand
[Bearbeiten]
Wird der Betrachtungswinkel festgelegt, ergibt sich der entsprechende Betrachtungsabstand aus der entsprechenden Bilddiagonale zu:
Beim Betrachtungswinkel bei Normalbrennweite von ergibt sich der normale Betrachtungsabstand aus den übrigen Konstanten zu:
mit
Siehe hierzu auch Normalbrennweite.
Die beiden menschlichen Augen haben im Gesichtsfeld in horizontaler Richtung mehr als einen gestreckten Winkel, in vertikaler Richtung ist es etwas weniger. Das Sehzentrum wird durch die Größe der Fovea centralis in der Mitte der Netzhaut bestimmt und deckt einen Bildwinkel von nur zirka 5° ab. Je größer der Bildwinkel wird, desto mehr bezieht ein Mensch sein peripheres Gesichtsfeld ein, wobei das Auflösungsvermögen mit zunehmenden Bildwinkel am Bildrand immer mehr abnimmt. Diese Bildbereiche dienen dem Menschen nicht zur Analyse von statischen Bilddetails, sondern lediglich dazu, dynamische Vorgänge zu erkennen. Der Bildbereich, bei dem der Mensch statische Bildinformation gut erfassen kann, entspricht in etwa dem normalen Bildwinkel.
Betrachtet man ein Bild mit der Diagonale aus dem Abstand , der etwas (16 Prozent) mehr als die Bilddiagonale beträgt, sieht man die Bildecken unter dem normalen Bildwinkel von 46,8°. Diese Bildweite entspricht der Normalbrennweite , die erforderlich ist, um ein Bild mit normalen Bildwinkel aus dem Unendlichen zu projizieren, da für den Grenzwert der Objektweite (synonym für "Gegenstandsweite") gegen unendlich für die normale Bildweite gilt:
Die folgende Tabelle zeigt die sich entsprechenden Bilddiagonalen und Betrachtungsabstände unter Normalwinkel in beliebigen Längeneinheiten:
| Bilddiagonale | Betrachtungsabstand bei Normalwinkel |
|---|---|
| 0,2 | 0,25 |
| 0,4 | 0,5 |
| 0,9 | 1 |
| 1,7 | 2 |
| 3,5 | 4 |
| 6,9 | 8 |
| 14 | 16 |
| 28 | 32 |
Optimale Anzahl der Bildpunkte
[Bearbeiten]
Der Betrachtungsabstand sollte so gewählt werden, dass das gesamte zu betrachtende Bild maximal unter dem normalen Bildwinkel erscheint und alle einzelnen Punkte der Reproduktion vom menschlichen Auge noch aufgelöst werden können.
Für sehr kleine Winkel kann der Tangens des Winkels im Bogenmaß mit dem Winkel gleichgesetzt werden, und die Beziehung zwischen Bildwinkel und Betrachtungsabstand vereinfacht sich bei einem einzelnen Bildpunkt zu:
Das menschliche Auge hat unter guten Voraussetzungen eine Winkelauflösung von einer Bogenminute, was einem Winkel von entspricht. Daraus ergbt sich:
Für Reproduktionen von digitalen Bildern bei normalem Bildwinkel mit verschiedenen Punktdichten ergeben sich damit die folgenden (maximalen) Betrachtungsabstände und die dazugehörigen (minimalen) Bilddiagonalen. Wird der Betrachtungsabstand größer gewählt, können die einzelnen Bildpunkte nicht mehr unterschieden werden, wird der Betrachtungsabstand kleiner gewählt, kann das Bild nicht mehr unter dem Normalwinkel gesehen werden, und es ist nicht mehr möglich, das gesamte Bild vollständig auf einen Blick zu erfassen:
| Punktdichte in dpi |
Punktdichte in 1/mm |
Punktabstand in mm |
Maximaler Betrachtungsabstand in m |
Minimale Bilddiagonale in m |
|---|---|---|---|---|
| 9 | 0,35 | 2,8 | 9,7 | 8,4 |
| 18 | 0,7 | 1,4 | 4,9 | 4,2 |
| 36 | 1,4 | 0,71 | 2,4 | 2,1 |
| 75 | 3 | 0,34 | 1,2 | 1,0 |
| 150 | 6 | 0,17 | 0,58 | 0,5 |
| 300 | 12 | 0,085 | 0,29 | 0,25 |
| 600 | 24 | 0,042 | 0,15 | 0,13 |
| 1200 | 47 | 0,021 | 0,07 | 0,06 |
Setzt man den sich aufgrund der höchsten Winkelauflösung ergebenden maximalen Betrachtungsabstand mit dem Betrachtungsabstand beim Normalwinkel gleich, folgt:
Aufgelöst nach der effektiven Zahl der Punkte auf der Bilddiagonalen:
Setzt man den Grenzwinkel hierbei auf den kleinsten auflösbaren Bildwinkel, ergibt sich die maximale Zahl von unterscheidbaren Bildpunkten entlang der Bilddiagonalen:
Wird ein Bild mit ungefähr dreitausend Punkten auf der Bilddiagonalen unter normalem Winkel betrachtet, kann das menschliche Auge alle Punkte in der Helligkeit unterscheiden und kann somit also noch Kontrastunterschiede mit einer maximalen Ortsfrequenz von 1500 Linienpaaren auf der Bilddiagonalen wahrnehmen (vergleiche auch Zerstreuungskreisdurchmesser im Abschnitt Schärfentiefe). Dieser Wert ist weder von der Punktdichte noch vom Betrachtungsabstand abhängig und führt je nach Bildseitenverhältnis zu einer Gesamtzahl von rund vier Millionen Bildpunkten:
| Bildseiten- verhältnis q |
Optimale Bildbreite in Pixel |
Optimale Bildhöhe in Pixel |
Optimale Anzahl Bildpunkte in Megapixel |
|---|---|---|---|
| 1/1 | 2121 | 2121 | 4,5 |
| 4/3 | 2386 | 1790 | 4,3 |
| 3/2 | 2482 | 1655 | 4,2 |
| 16/9 | 2600 | 1462 | 3,8 |

Untersucht man den Zusammenhang zwischen der Kontrastempfindlichkeitsfunktion und den vorhandenen Bildpunkten in Abhängigkeit von der Ortsfrequenz am Beispiel eines Breitbildes mit dem Bildseitenverhältnis 16 zu 9 (der normale vertikale Bildwinkel beträgt hierbei 24°), ergibt sich, dass das im Bildmaterial vorhandene Informationspotenzial ab einer Ortsfrequenz von 540 Linienpaaren pro Bildhöhe (dies entspricht einer Bildauflösung von 1080 Zeilen) von einem Menschen in normalem Betrachtungsabstand zunehmend weniger ausgeschöpft werden kann.
Der Deckungsgrad der Leistungsfähigkeit des menschliches Auges wird mit zunehmender Bildauflösung zunächst deutlich besser. Bei 540 Linienpaaren pro Bildhöhe wird dieser allerdings schon zu fast 80% erreicht und wächst mit weiter zunehmender Ortsfrequenz kaum noch an. Dies bedeutet, dass nur noch sehr wenige zusätzliche Details in noch höher aufgelösten Bildern erkannt werden können. Insgesamt ist das Missverhältnis sogar noch sehr viel stärker, wenn man nämlich berücksichtigt, wie viel der vorhandenen Bildinformation tatsächlich überhaupt ausgeschöpft werden kann. Bei einer Ortsfrequenz von 1080 Linienpaaren pro Bildhöhe (dies entspricht einer Bildauflösung von 2160 Zeilen beiziehungsweise gut 8 Megapixel) können nicht einmal mehr die Hälfte der vorhandenen Punkte unterschieden werden, weil der wahrgenommene Kontrast zu klein ist. Bei einer Ortsfrequenz von 2160 Linienpaaren pro Bildhöhe ist es dann noch nicht einmal mehr ein Viertel der Punkte.
| Bezeichnung | Zeilenzahl | Anzahl der Bildpunkte in Millionen | Linenpaare pro Bildhöhe | Deckungsgrad | Ausschöpfung |
|---|---|---|---|---|---|
| SD (1k) | 576 | 0,6 | 288 | 45% | 77% |
| HD ready (1,3K) | 720 | 0,9 | 360 | 57% | 78% |
| Full HD (2K) | 1080 | 2,1 | 540 | 78% | 71% |
| (2,5K) | 1440 | 3,7 | 720 | 88% | 60% |
| UHD (4K) | 2160 | 8,3 | 1080 | 96% | 44% |
| 8K | 4320 | 33,2 | 2160 | 100% | 23% |
- Sichtbare Anteile der Bildauflösung
-
Zusammenhang zwischen der in einem Bild vorhandenen örtlichen Information (Potenzial) und der wegen der Begrenzung durch die Kontrastempfindlichkeitsfunktion (CSF) tatsächlich für einen menschlichen Betrachter sichtbaren Information
-
Deckungsgrad für die Empfindlichkeit der menschlichen Netzhaut und relative Ausschöpfung der vorhandenen Bildinformation für einen menschlichen Betrachter
Siehe hierzu auch: Kontrastempfindlichkeitsfunktion (CSF)
Optimaler Betrachtungsabstand
[Bearbeiten]

Ebenso können bei vorgegebener Anzahl der Bildpunkte die Bilddiagonale oder der Betrachtungsabstand ausgerechnet werden, bei dem die einzelnen Bildpunkte gerade noch unterschieden werden können:
Mit der Winkelauflösung eines menschlichen Betrachters (siehe oben) ergibt sich dann, dass die Bilddiagonale höchstens 13,5 Prozent kleiner als das Betrachtungsabstand sein darf, damit alle Bildpunkte unterschieden werden können:
Für gängige Bildauflösungen ergeben sich für einen gleichbleibenden Betrachtungsabstand und bei einer vorgegebenen Punktdichte von rund anderthalb Punkten pro Millimeter beziehungsweise damit die folgenden Verhältnisse:
| Bezeichnung | Bildpunkte in horizontaler Richtung |
Bildpunkte in vertikaler Richtung |
Bildpunkte in diagonaler Richtung |
Pixelzahl in Megapixel |
Bildbreite in m |
Bildhöhe in m |
Bilddiagonale in m |
Betrachtungsabstand in m |
Betrachtungsabstand im Verhältnis zur Bildhöhe |
Diagonaler Betrachtungswinkel |
|---|---|---|---|---|---|---|---|---|---|---|
| SDTV (4:3) | 768 | 576 | 960 | 0,44 | 0,52 | 0,39 | 0,653 | 2,27 | 5,8 | 16° |
| HD ready (16:9) | 1280 | 720 | 1469 | 0,92 | 0,87 | 0,49 | 1,0 | 2,27 | 4,6 | 25° |
| Full HD (16:9) | 1920 | 1080 | 2203 | 2,1 | 1,31 | 0,74 | 1,5 | 2,27 | 3,1 | 37° |
| Normalwinkel (16:9) | 2600 | 1462 | 2983 | 3,8 | 1,77 | 0,99 | 2,0 | 2,27 | 2,3 | 48° |
| 4K (16:9) | 3840 | 2160 | 4406 | 8,3 | 2,61 | 1,47 | 3,0 | 2,27 | 1,5 | 67° |
| 8K (16:9) | 7680 | 4320 | 8812 | 33 | 5,23 | 2,94 | 6,0 | 2,27 | 0,8 | 106° |
Bei einer Bildauflösung von zwei Megapixel ist der normale Bildwinkel noch nicht ausgeschöpft und das gesamte Bild ist gut und vollständig erfassbar. Die optimalen vier Megapixel Bildauflösung (siehe oben) werden hier zwar noch nicht ganz erreicht, jedoch gelten diese Überlegungen nur für monochrome Bilder. Bei mehrfarbigen Bildern ist die vom Menschen erfassbare Farbauflösung deutlich darunter (zirka eine Million verschiedenfarbige Punkte können unterschieden werden), und dies wird bei einer Bildauflösung von zwei Megepixel längst übertroffen.
Bei höheren Bildauflösungen, wie zum Beispiel 4K oder gar 8K ist der Betrachtungswinkel deutlich über dem normalen Bildwinkel, wenn alle Punkte beim Betrachter noch einzeln aufgelöst werden können - das Bild kann bei weitem nicht mehr mit einem Blick betrachtet werden, sondern die Augen müssen über die verschiedenen Bildbereiche streifen, um alle Details sehen zu können.
Änderung der Sehfähigkeit mit dem Lebensalter
[Bearbeiten]Die Akkomodationsbreite des menschliche Auges nimmt mit dem Lebensalter deutlich ab. Dadurch kommt es bei Verzicht auf Sehhilfen zu einer Vergrößerung der minimalen Sehweite und trotz gleichbleibender Winkelauflösung von zirka einer Bogenminute somit auch zu einer Reduktion der maximal wahrnehmbaren Punktdichte. Diese Verhältnisse mit dem daraus resultierenden zunehmendem minimalen Betrachtungsabstand werden in der folgenden Tabelle anhand der Eigenschaften eines normalsichtigen Menschen verdeutlicht:
Lebensalter in a |
Minimaler akkomodierbarer Betrachtungsabstand in m |
Punktabstand bei minimaler Winkelauflösung in mm |
Punktdichte bei minimaler Winkelauflösung in dpi |
Punktdichte bei minimaler Winkelauflösung in mm-1 |
|---|---|---|---|---|
| 10 | 0,09 | 0,026 | 970 | 38 |
| 20 | 0,11 | 0,032 | 790 | 31 |
| 30 | 0,13 | 0,038 | 670 | 26 |
| 40 | 0,18 | 0,052 | 490 | 19 |
| 50 | 0,50 | 0,145 | 170 | 6,9 |
| 60 | 0,65 | 0,189 | 130 | 5,3 |
| 70 | 0,71 | 0,207 | 120 | 4,8 |
Digital-Analog-Wandlung
[Bearbeiten]
Um digitale Bilder zu betrachten, müssen die Daten in einer geeigneten Form in sichtbares Licht umgewandelt werden. Umgekehrt wie bei der Aufnahme von Bildern dienen Digital-Analog-Wandler dazu, diskrete Zahlenwerte in elektrische Spannungen oder direkt in Leuchtdichten umzuwandeln. Die Spannungen müssen mit geeigneten Geräten anschließend in entsprechende Leuchtdichten umgesetzt werden (siehe auch Kapitel Leuchtdichte).
In der Regel bedeutet eine Spannung von null Volt, dass kein Licht erzeugt wird, und die maximal darstellbare Zahl im Wertebereich der digitalen Daten wird in die maximale Spannung umgesetzt und entspricht somit der maximal zu erzeugenden Helligkeit. Allerdings haben viele bilderzeugenden Verfahren keine linearen Eigenschaften; eine doppelt so hohe Spannung erzeugt nicht notwendiger Weise auch eine doppelt so große Helligkeit. In vielen Fällen müssen die digitalen Daten daher durch entsprechende analoge oder digitale Transformationen in entsprechende Spannungen beziehungsweise Leuchtdichten umgewandelt werden.
Digitale Transformationen haben hierbei der Vorteil, dass sie softwareseitig eingestellt werden können, was zum Beispiel die Gamma-Korrektur, die Kalibrierung oder die Profilierung von Wiedergabegeräten sehr erleichtern kann. Die Profilierung unterscheidet sich von der Kalibrierung dadurch, dass zusätzlich zur individuellen Einstellung der stetigen Leuchtdichteverläufe in allen getrennten Farbkanälen die Bildergebnisse nachgemessen und anschließend die Ergebnisse zur optimalen Korrektur oder Kontrolle der Einstellungen verwendet werden.
Eine einfache Kalibrierung ist mit geeigneten Testtafeln möglich, die auf dem Wiedergabegerät angezeigt werden. Die Helligkeit und der Kontrastverlauf können damit so eingestellt werden, dass eine gewisse Anzahl von Bildfeldern mit unterschiedlicher Helligkeit beim Betrachten gut unterschieden werden kann.
Bildschirme
[Bearbeiten]Kathodenstrahlröhren
[Bearbeiten]
Kathodenstrahlröhren benötigen einen aufgeheizten Elektronenemitter, eine Beschleunigungsspannung für die Elektronen (zwischen Kathode und Anode) und eine analoge Ansteuerung mit großen elektrischen Strömen für die Ablenkspulen oder mit großen elektrischen Spannungen für die Ablenkplatten beziehungsweise für die Fokussierung des Elektronenstrahls, so dass sie für den Einsatz in digitalen Systemen nicht prädestiniert sind. Zudem benötigen größere Kathodenstrahlröhrenbildschirme eine sehr große Bautiefe, weil die in einer Vakuumröhre befindliche Elektronenquelle entsprechend weit hinter dem Leuchtschirm und den Ablenkeinheiten positioniert werden muss. Diese großen Glasröhren und Ablenkeinheiten haben auch ein vergleichsweise hohes Gewicht.
Zu einem Zeitpunkt kann immer nur ein Bildpunkt auf dem Leuchtschirm angesteuert werden, der dann allerdings eine recht hohe Leuchtdichte aufweisen kann. Bei örtlich und zeitlich hochaufgelösten Bildern werden die Ablenkfrequenzen aber teilweise so hoch, dass eine präzise elektronische Steuerung sehr aufwendig wird. Eine Wiedergabe mit einer Bildwiederholrate von 50 Vollbildern pro Sekunde mit jeweils zwei Millionen Bildpunkten (Full-HD-Standard) erfordert zum Beispiel eine Taktfrequenz von 100 Megahertz für die Bildpunkte:
Bei dieser Taktfrequenz müssen unter Umständen mehrere farbige Punkte mit einer Bit-Tiefe von acht oder höher ausgesteuert werden, was sehr hohe Anforderungen an die Geschwindigkeit und Genauigkeit der Wiedergabegeräte stellt.
Kathodenstrahlröhren werden aus diesen Gründen insgesamt nur noch selten für die Bildwiedergabe eingesetzt, insbesondere wenn es um die Wiedergabe digitaler Bildquellen geht.
Flüssigkristallanzeigen
[Bearbeiten]
Die monochrome Flüssigkristalanzeige wurde in Form der sogenannten Schadt-Helfrich-Zelle um 1970 von Martin Schadt und Wolfgang Helfrich erfunden.
Kleine hochauflösende Flüssigkristallanzeigen mit Farbfiltern und konstanter Hintergrundbeleuchtung oder mit schneller sequentieller Hintergrundbeleuchtung mit verschiedenen monochromatischen Farben (zum Beispiel mit dern Primärfarben in der Reihenfolge rot - grün - blau mit einer Wechselfrequenz von 180 Hertz) können nicht nur für große selbstleuchtende Bildschirme mit mehreren Metern Bilddiagonale, sondern auch für elektronische Sucher mit wenigen Millimetern Bilddiagonale hergestellt werden.
Siehe hierzu auch Systemkameras
Bei einer sequentiellen Hintergrundbeleuchtung mit verschiedenen Farben kann es an kontrastreichen Kanten oder bei bewegten Motiven zum sogenannten Regenbogeneffekt kommen, da die verschiedenen Farbinformationen nicht gleichzeitig sondern zeitlich und somit unter Umständen auch auf der Netzhaut örtlich versetzt gesehen werden.
Leuchtdiodenanzeigen
[Bearbeiten]
Organische Leuchtdioden (OLEDs) haben eine geringere Stromaufnahme, aber auch eine geringere Leuchtdichte und eine geringere Lebensdauer als anorganische, einkristalline Leuchtdioden (LED). Sie können jedoch kostengünstig hergestellt werden und können daher spalten- und reihenförmig zu hochauflösenden Matrix-Anzeigen kombiniert werden, die so dünn gestaltet werden können, dass sie sogar gebogen werden können.
Wenn der Strom ausgeschaltet wird, wird auch kein Licht erzeugt, so dass der Schwarzwert bei den OLEDs praktisch null ist und deswegen eine hohe Modulation (Michelson-Kontrast) möglich ist. OLED-Anzeigen werden sowohl großflächig als direkt betrachteter Bildschirm (Monitor, Fernseher) oder kleinflächig mit einem Okular betrachtet (elektronischer Sucher) eingesetzt.
Projektoren
[Bearbeiten]Projektoren werden in der Regel eingesetzt, um das Bild von relativ kleinen, zweidimensionalen Bildgebern mit einem Objektiv auf eine verhältnismäßig große Projektionsfläche abzubilden. Durch die Wahl der Größe der Bildgeber, der Brennweite des Objektivs und des Abstandes des Projektors zur Projektionswand ergibt sich geometrisch die Größe des projizierten Bildes.
Die Qualität der Projektion bemisst sich unter anderem in der Bildschärfe, die meist durch die physikalische Auflösung der Bildgeber bestimmt ist, in der größten erreichbaren Helligkeit und mittelbar durch die geringste erreichbare Helligkeit im Kontrastumfang. Darüberhinaus sind der Farbumfang und die Farbtreue der Projektionen ein wichtiges Qualitätsmerkmal.

Zur Projektion wird oft ein verketteter (beziehungsweise verflochtener) Strahlengang verwendet, der aus zwei miteinander verflochtenen Strahlengängen besteht:
- Abbildungsstrahlengang (A): ein Abbildungssystem bestehend aus dem abzubildenden Objekt (G, synonym für "Gegenstand"), einem Objektiv (O) und dem auf dem Kopf stehenden, auf eine Projektionsebene (P) projizierten reellen Bild
- Beleuchtungsstrahlengang (B): ein Beleuchtungssystem bestehend aus einer Lichtquelle (L) bei thermischen Strahlern (Abstrahlung in den Raumwinkel ) mit einem konkaven Reflektor (R), dem abzubildenden Objekt (G), einem Kondensor (K)
Siehe hierzu auch: Beleuchtung
Dimensionierung
[Bearbeiten]Beim Abbildungsstrahlengang befindet sich das abzubildende Objekt meist zwischen der einfachen und doppelten Brennweite des Objektivs. Der Betrag des Abbildungsmaßstabs ist in diesem Fall immer größer als eins, und das projizierte Bild ist somit größer als das abzubildende Objekt.
Wenn im Abbildungsstrahlengang A bei vorgegebener Objektgröße eine bestimmte projizierte Bildgröße erreicht werden soll, ergibt sich für den Abbildungsmaßstab :
Typischerweise gibt hierbei:
Die Längen entlang der optischen Achse und die Größe des Kondensors ergeben sich dann über die folgenden Beziehungen aus der Objektgröße und der Bildgröße:
Die Objektweiten und Bildweiten der beiden Strahlengänge können mit der jeweiligen Abbildungsgleichung mit der Brennweite des Objektivs
beziehungsweise mit der Brennweite des Kondensors
in Beziehung gebracht werden. Typischerweise wählt man hier , und die erforderliche Lichtstärke des Kondensors ergibt sich mit der Blendenzahl aus der Beziehung:
Siehe hierzu auch: Blendenzahl
Digital Light Processing
[Bearbeiten]- Mikrospiegelarray (Digital Micromirror Device, DMD)
-
Integriertes Bauteil von Texas Instruments
-
Vergrößerter Ausschnitt (zirka 0,2 mm mal 0,2 mm) des Bauteils mit zirka 13 µm mal 13 µm großen, quadratischen Mikrospiegeln in jeweils vierzehn Reihen und Spalten
-
Kurzzeitbelichtung (1/16000 Sekunde pro Zeile) der Projektion einer weißen Fläche mit einem schwarzen Kreuz mit einem DLP-Gerät mit Rolling-Shutter-Effekt. Zu einem Zeitpunkt, also innerhalb einer Zeile, wird immer nur eine der drei Primärfarben projiziert.
-
Kurzzeitbelichtung (1/32000 Sekunde pro Zeile) der Projektion mit einem in schwarz-weißen projizierten Schachbrettmuster bei einem DLP-Projektor mit rotierendem Farbrad mit der Farbsegmentfolge rot - grün - weiß - blau - grün - weiß.
-
Prinzip des rotierenden Farbrads im Beleuchtungsstrahlengang in Richtung DMD
-
Ausführungsbeispiel eines Farbrads für den Beleuchtungsstrahlengang eines DMD-Projektors
Liquid Crystal on Silicon
[Bearbeiten]Liquid Crystal on Silicon (abgekürzt LCoS, auch unter der Bezeichnung Silicon X-tal Reflective Display, abgekürzt SXRD verbreitet) beruht auf der Idee, die segmentierten Flüssigkristallelemente nicht im reinen Durchlichtmodus zu betreiben, sondern das Licht unmittelbar hinter der Flüssigkristallschicht zu reflektieren, so dass es erneut in umgekehrter Richtung durch die Flüssigkristallschicht tritt. Dies erfordert einen erhöhten Aufwand beim Entwurf eines geeigneten Strahlenganges, insbesondere wenn die Projektion mehrfarbig gestaltet werden soll. Da hierbei mehrere Farbschichten mit eigenen Bildgebern eingesetzt werden müssen, ergeben sich sehr hohe Anforderungen für die Justierung und die mechanische und thermische Stabilität der Konstruktion.
Weißes Licht wird beleuchtungsstrahlenseitig mit einem Hohlspiegel und einem Kondensor auf ein komplexes Glasprisma mit teilreflektierenden, 45 Grad geneigten Spiegelschichten gerichtet. Das weiße Licht wird auf (meist drei) verschiedene Endflächen des Prismas gelenkt, die mit unterschiedlichen Farbfiltern und jeweils einem Flüssigkristallelement und einem direkt dahinterliegenden Spiegel ausgestattet sind. Das Licht durchtritt also jeweils zweimal die Farbschicht und die Flüssigkristallschicht.
Wiedergabe mit drei Bildgebern
[Bearbeiten]
Bei vielen Bildgebern, wie zum Beispiel Flüssigkristallbildschirme im Durchlichtmodus oder Mikrospiegelarrays beziehungsweise Flüssigkristallbildschirme im Reflexionsmodus können mit Hilfe von Strahlteilern Einzelbilder mit begrenzten Lichtwellenlängenbereichen erzeugt werden. Dazu können Lichtquellen mit unterschiedlichen Lichtwellenlängenbereichen verwendet werden, oder es werden weiße Lichtquellen verwendet, deren Licht mit Interferenzfiltern oder durch andere Farbfilter in verschiedene Lichtwellenbereiche aufgeteilt wird.
Die verschiedenen Einzelbilder werden durch den Strahlenteiler wieder zu einer gemeinsamen virtuellen, bildgebenden Fläche vereinigt und müssen untereinander exakt dieselben Abstände einhalten, sowohl was die Objektweite für die sich anschließende optische Abbildung mit dem Objektiv, als auch was die seitlichen Abstände der horizontalen und vertikalen Bildkanten betrifft. Das Objektiv bildet schließlich die Flüssigkristallbildschirme auf eine Projektionswand ab.
Drucke
[Bearbeiten]Laserdruck
[Bearbeiten]
Beim Laserdruck wird Toner verwendet, deren Partikel auf dem Papier typischerweise Farbflecke mit einem Durchmesser von einigen Mikrometern erzeugen. Ein hochwertiges Druckwerk ist beispielsweise für eine Punktdichte von 1200 dpi ausgelegt (dies entspricht einer metrischen Punktdichte von 47 mm-1 und einem Punktabstand respektive einem Punktdurchmesser von 21 Mikrometern). Daraus ergibt sich, dass ein mit minimalem Durchmesser gedruckter Punkt aus rund 100 nebeneinanderliegenden Tonerpartikeln zusammengesetzt werden muss.
Je näher der Linienabstand sich dem Punktabstand nähert, desto weniger scharf und genau können die Kanten der Linien abgebildet und gedruckt werden:
- Laserdruck mit einer Punktdichte von 1200 dpi und einer Bildhöhe von 183 Millimetern bei verschiedenen Bildauflösungen
-
Linienhöhe 318 µm (1.0K, links) und 286 µm (1.1K, rechts)
-
Linienhöhe 254 µm (1.3K, links) und 212 µm (1.5K, rechts)
-
Linienhöhe 169 µm (2.0K, links) und 127 µm (2.5K, rechts)
-
Linienhöhe 85 µm (4.0K, links) und 42 µm (8.0K, rechts)
Durch die seitliche Streuung der Tonerpartikel ergibt sich bei zunehmend kleinen Linienbreiten, dass sich in den eigentlich weißen Lücken zwischen den schwarzen Linien zunehmend viele Tonerpartikel wiederfinden. Dadurch wird die mittlere Helligkeit der Drucke dunkler als 50%, die bei gleicher Breite von schwarzen und weißen Linien zu erwarten wären.

Werden schwarze und farbige Tonerpartikel auf das Druckerpapier aufgebracht, können mit einem Laserdrucker auch farbige Bilder erstellt werden. Für die Erzeugung von Farbtönen müssen die Druckerfarben (häufig cyan, magenta, yellow, black (CMYK), also türkis, violett, gelb und schwarz) nacheinander und im entsprechenden Verhältnis nebeneinander gedruckt werden.
Tintenstrahldruck
[Bearbeiten]
Beim Tintenstrahldruck werden kleinste Farbtröpfchen auf das zu bedruckende Papier gebracht. Der Durchmesser der entsprechenden Farbflecke auf dem Papier beträgt typischerweise einige Mikrometer. Ebenso wie beim Laserdruck (siehe oben) werden verschiedene Farbtöne durch die Überlagerung der Grundfarben erzeugt. Hierzu werden in der Regel mindestens drei Grundfarben verwendet (häufig cyan, magenta, yellow, black (CMYK)), für einen größeren darstellbaren Farbraum können jedoch auch noch zusätzliche Grundfarben eingesetzt werden.
Transformationen
[Bearbeiten]Dieses Kapitel beschäftigt sich mit mathematischen Transformationen bei optischen Abbildungen und deren Digitalisaten.
Helligkeitstransformationen
[Bearbeiten]Die Leuchtdichten, die in einem Bild die Helligkeiten repräsentieren, werden bei der Digitalisierung in Zahlenwerte umgerechnet, mit denen beliebige mathematische Operationen zur Bildbeeinflussung und zur Bildverbesserung durchgeführt werden können.
Gammakorrektur
[Bearbeiten]Um die mittleren Helligkeiten eines digitalen Bildes anzupassen, ohne die minimale Helligkeit (schwarz) und die maximale Helligkeit (weiß) zu ändern, kann eine rechnerische Gammakorrektur durchgeführt werden, um eine Eingangshelligkeit in eine Ausgangshelligkeit umzuwandeln. Der Name dieser Korrektur rührt vom Exponenten der Übertragungsfunktion her:
mit
und
Die Werte für die Eingangshelligkeiten ergeben sich aus den digitalen Zahlenwerten für die Helligkeit folgendermaßen:
Der reellwertige Exponent ist hierbei immer positiv. Die Null und die Eins - also der dunkelste und der hellste Helligkeitswert - bleiben nach der Transformation erhalten, die dazwischenliegenden Werte werden entweder alle vergrößert () oder alle verkleinert (). Bei behalten alle Helligkeiten ihren Wert (identische Abbildung).
- Helligkeits- und Farbbalken mit verschiedenen Gammakorrekturen
-
Gammakorrektur mit ,
Mitteltöne werden heller dargestellt -
Originalbild mit
-
Gammakorrektur mit ,
Mitteltöne werden dunkler dargestellt
Die Gammakorrektur kann daher eingesetzt werden, wenn in einem Bild zwar alle Tonwerte vorhanden sind, jedoch die mittleren Tonwerte zu hell oder wie in folgendem Beispiel zu dunkel wirken:
- Aufnahme eines Springbrunnens im Gegenlicht
-
Ausschnitt einer Aufnahme im Gegenlicht. Die Tonwerte verteilen sich zwar über alle Helligkeiten, haben aber ihren Schwerpunkt bei geringen Helligkeiten, so dass das Bild sehr dunkel wirkt, obwohl es nicht unterbelichtet ist.
-
Die Tonwerte wurden mit der Gammakorrektur (Parameter ) korrigiert. Die hellsten und dunkelsten Bildpunkte bleiben unverändert, die häufigste Helligkeit hat aber einen deutlich höheren Wert, so dass die Details in den dunklen Bereichen besser hervortreten.
- Histogramme eines Springbrunnens im Gegenlicht
-
Histogramm der unkorrigierten dunklen Aufnahme mit
-
Histogramm nach der Gammakorrektur mit
Die Gammakorrektur kann bei Bedarf auch für alle Farbkanäle unabhängig eingestellt werden, wie zum Beispiel bei den drei Primärfarben rot, grün und blau:
Tonwertkorrektur
[Bearbeiten]Weißpunkt
[Bearbeiten]Wenn der Spielraum der ebenfalls Tonwerte genannten Helligkeitswerte in einem digitalen Bild nicht ausgenutzt wird - bei unterbelichteten Bildern ist dies üblicherweise der Fall, da die höheren Helligkeitswerte nicht auftauchen -, ist es sinnvoll, die Helligkeitswerte gleichmäßig zu erhöhen, damit bei der Wiedergabe ein klares Bild mit der Möglichkeit von schwarzen und weißen Bildpunkten entsteht. Die Ausgangswerte ergeben sich dann auf einfache Weise aus den Eingangswerten durch eine lineare Transformation:
mit
- ,
wobei die maximale im Eingangsbild auftretende Helligkeit ist. Im Ausgangsbild ist nach der Transformation die maximal auftretende Helligkeit gleich 1. Entsprechende Punkte werden auch als die Weißpunkte des Bildes bezeichnet.
- Unterbelichtete Aufnahme einer Kuppel
-
Ausschnitt einer unterbelichteten Aufnahme im Gegenlicht, bei der die helle Bildpartie (das Fenster unterhalb des Ausschnittes) weggeschnitten wurde. Die Tonwerte verteilen sich ausschließlich über niedrige Werte.
-
Die Tonwerte wurden korrigiert, indem alle Tonwerte ungefähr verdoppelt wurden.
- Histogramme der unterbelichteten Aufnahme einer Kuppel
-
Histogramm der unterbelichteten Aufnahme
-
Histogramm der korrigierten Aufnahme
Weißabgleich
[Bearbeiten]Eine Tonwertkorrektur kann auch separat für alle vorhandenen Farbkanäle, meist die Primärfarben rot, grün und blau, durchgeführt werden. Um einen Bildbereich farbneutral, also ohne Farbstich, zu bekommen, müssen die entsprechenden Tonwerte der Farbkanäle auf die gleichen Helligkeiten gerechnet werden - diesen Vorgang bezeichnet man als Weißabgleich. Bei Aufnahmesystemen mit automatischem Weißabgleich wird oft in jedem Farbkanal der hellste Punkt gesucht, und mit deren Tonwerten werden die Korrekturen für die einzelnen Farbkanäle ausgerechnet. Bei den üblicherweise verwendeten Primärfarben ergibt sich dann:
mit
wobei , und die maximalen im Eingangsbild auftretenden Helligkeiten der drei Farbkanäle sind. Im Ausgangsbild ist nach der Transformation die maximal auftretende Helligkeit für alle Farbkanäle gleich 1. Punkte mit diesen Tonwerten werden auch hier als Weißpunkte bezeichnet.
Problematisch ist der automatische Weißabgleich, wenn es im Eingangsbild gar keine Punkte gibt, die dem Weißpunkt entsprechen. Solche Umstände liegen vor, wenn das aufgenommene Objekt keine weißen Punkte enthält oder monochromatische Punkte die hellsten im Bild sind. Eine typische Situation sind Sonnenauf- und -untergänge, bei der das helle Sonnenlicht eine deutliche Rotfärbung der Szenerie verursacht. Hier ist es in der Regel vorzuziehen, die Farbkanäle nicht für den hellsten Punkt, sondern für einen farbneutralen Punkt (Graupunkt) anzugleichen.
- Mit einer Digitalkamera aufgenommene Schneelandschaft
-
Mit automatischem Weißabgleich: der Schnee im Schatten erscheint blau, der Schnee im Hintergrund im Licht der Morgensonne erscheint weiß.
-
Mit korrigiertem Weißabgleich: der Schnee im Schatten ist farbneutral (hellgrau), der Schnee im Hintergrund im Licht der Morgensonne ist rötlich und gelblich.
- Histogramme der mit einer Digitalkamera aufgenommenen Schneelandschaft
-
Histogramm der Aufnahme mit automatischem Weißabgleich. Blau ist die dominante Farbe.
-
Histogramm der Aufnahme mit korrigiertem Weißabgleich. Die Verteilungen der Farben blau und rot wurden durch eine Tonwertkorrektur der Verteilung der Farbe grün angeglichen, so dass alle entsprechenden Bildpunkte farbneutral dargestellt werden.
Koordinatentransformationen
[Bearbeiten]Bildkoordinaten
[Bearbeiten]
Werden die Bildkoordinaten und eines Bildpunktes von der Bildmitte aus bestimmt, die in der Regel senkrecht von der optischen Achse durchlaufen wird, ergibt sich der entsprechende Ortsvektor zu:
Die Bildhöhe dieses Bildpunktes von der optischen Achse aus gemessen beträgt dann:
Der Winkel zwischen optischer Achse und dem Strahl durch den Bildpunkt im Hauptpunkt ist üblicherweise nicht unmittelbar bekannt, kann aber leicht aus der Bildweite und der Bildhöhe bestimmt werden:
In der Informationstechnik (IT) wird aus historischen Gründen der Ursprung des Bildkoordinatensystems häufig in die linke obere Bildecke gelegt, wobei die x-Achse nach rechts und die y-Achse nach unten verlaufen. Wenn die Bildbreite und die Bildhöhe betragen, ergibt sich die folgende Transformation zu den oben angegebenen Bildkoordinaten:
Himmelskoordinaten
[Bearbeiten]
Der Zenit ist senkrecht über dem Beobachter und der Nadir senkrecht unter dem Beobachter im Zentrum der Darstellung (dunkelgraue Kreisscheibe).
Der Meridian ist der Großkreis durch Himmelsnord- und Himmelsüdpol sowie die Richtungen Norden (N) und Süden (S) vom Beobachter aus gesehen.
Der Beobachter sieht im Horizontalsystem (hellgraue Scheibe) am Himmel einen Punkt (violett) unter dem Azimut (schwarz), der vom nördlichen Meridian aus im Uhrzeigersinn in der Horizontalebene gemessen wird, und unter dem Höhenwinkel (grün), der auf dem Großkreis zwischen Nadir und Zenit (grün), der durch den beobachteten Punkt (violett) geht, und der senkrecht zur Horizontalebene und von der Horizontalebene aus gemessen wird.
Diese Winkel können in die kartesischen Koordinaten , und im Horizontalsystem umgerechnet werden:
Diese Koordinaten des entsprechenden Ortsvektors vom Mittelpunkt in Richtung des beobachteten Punktes sind normalisiert:
Im Äquatorialsystem (türkisfarbene Scheibe) wird der Stundenwinkel (cyan) vom nördlichen Meridian aus im Uhrzeigersinn in der Äquatorialebene gemessen, und der Deklinationswinkel (rot) wird auf dem Großkreis zwischen Himmelssüdpol und Himmelsnordpol (rot), der durch den beobachteten Punkt (violett) geht, senkrecht zur Äquatorialebene und von der Äquatorialebene aus gemessen.
Ostpunkt (O) und Westpunkt (W) sind in beiden Systemen identisch, und die Neigung der beiden Ebenen zueinander ist durch die Polhöhe (blau) gegeben, die mit dem Breitengrad übereinstimmt, auf dem sich der Beobachter befindet.
Für die Umrechnung von Azimut und Höhenwinkel im Horizontalsystem in den Stundenwinkel und die Rektaszension im Äquatorialsystem gelten die folgenden Beziehungen:
und
Falls der Deklinationswinkel , die Sternzeit und die Rektaszension eines Himmelsobjekts im Äquatorialsystem zum Beispiel mit Hilfe von Ephemeriden-Tabellen bekannt sind, können der der dazugehörige Stundenwinkel und schließlich der entsprechende Azimut und Höhenwinkel im Horizontalsystem mit den folgenden Gleichungen berechnet werden:
und
Scheinbare Bewegung
[Bearbeiten]Der beobachtete Himmelspunkt (violett) bewegt sich in der nördlichen Hemisphäre innerhalb eines halben Tages in Pfeilrichtung auf einem Halbkreis (mit respektive ) von Osten nach Westen, der mit konstantem Deklinationswinkel (rot) parallel zur Äquatorialebene (türkisfarbene Scheibe) liegt. Innerhalb eines ganzen siderischen Tages wird ein vollständiger Kreis durchlaufen.
Innerhalb einer vorgegebenen Zeitspanne in Sekunden verändert sich der Stundenwinkel demnach im Bogenmaß um den Betrag:
Der neue Stundenwinkel beträgt dann also:
Mithilfe des neuen Strundenwikels kann dann auch die neue Position des betrachteten Punktes im Horizontalsystem bestimmt werden:
und
Die scheinbare Bewegung des betrachteten Himmelspunktes kann durch die Differenz der Azimute
und die Differenz der Höhenwinkel
ausgedrückt werden.
Beispiel
[Bearbeiten]Das folgende Beispiel für den Blutmond am 28. September 2015 ist für den 52. Breitengrad südlich von Berlin und eine Zeitdifferenz (= Belichtungszeit) von sechs Sekunden berechnet:
| Winkel | Winkel in Grad | Winkel im Bogenmaß (Radiant) |
|---|---|---|
| Polhöhe | 52,000 | 0,90757 |
| Azimut | 56,000 | 0,97738 |
| Höhenwinkel | 29,000 | 0,50615 |
| Deklination | 4,64184 | 0,08102 |
| Stundenwinkel | 46,6754 | 0,81464 |
| Stundenwinkeldifferenz | 0,0251 | 0,00044 |
| Neuer Stundenwinkel | 46,7005 | 0,81508 |
| Neuer Azimut | 56,0245 | 0,97781 |
| Neuer Höhenwinkel | 28,9872 | 0,50592 |
| Azimutdifferenz | 0,02454 | 0,00043 |
| Höhenwinkedifferenz | -0,01280 | -0,00022 |
Projektion
[Bearbeiten]
Im Folgenden wird die Bewegung eines Himmelspunktes von P mit dem Azimut und dem Höhenwinkel nach P' mit dem Azimut und dem Höhenwinkel betrachtet, der von einem Mittelpunkt M aus in der unbewegten Projektionsebene mit x- und y-Koordinate als Verschiebung von Bildpunkt Q nach Bildpunkt Q' erscheint.
Bei einer Bildweite, die bei einer Abbildung aus dem Unendlichen mit der Brennweite identisch ist, ergeben sich in der Bildebene, deren horizontale x-Achse parallel zum Horizont ausgerichtet ist und deren Normale (= optische Achse der Abbildung durch den Bildpunkt Q zum Punkt P) auf den betrachteten Punkt P zeigt, die folgenden Koordinatendifferenzen aus den Winkeldifferenzen im Bogenmaß:
Beispiele
[Bearbeiten]Bei Beobachtung am Äquator () vereinfacht sich die Betrachtung folgendermaßen:
Umgekehrt verhält es sich bei der Beobachtung am Nord- oder Südpol ():
Die folgenden Werte sind für eine Brennweite von 140 Millimetern und für die Winkel im oben angegebenen Beispiel berechnet (). Die Breite und Höhe eines Bildpunkts entsprechen bei den folgenden Beispielbildern einer Länge von 7,4 Mikrometern in der Bildebene. Der Bildausschnitt auf dem Bildsensor betrug rund 7,6 mal 5,7 Quadratmillimeter.
| Verschiebung | Wert |
|---|---|
| Horizontale Verschiebung in mm | 0,060 |
| Vertikale Verschiebung in mm | -0,031 |
| Horizontale Verschiebung in Pixel | 8 |
| Vertikale Verschiebung in Pixel | -4 |
- Blutmond am 28. September 2015 mit verschiedenen Belichtungszeiten
-
Mit einer Belichtungszeit von einer Sekunde
(Belichtungsindex ISO 1600 mit -0,3 Stufen Korrektur des Belichtungswertes). -
Mit einer Belichtungszeit von sechs Sekunden
(Belichtungsindex ISO 200 ohne Korrektur des Belichtungswertes).
Bilddrehung
[Bearbeiten]
Bei entsprechend langen Belichtungszeiten kann es erforderlich sein, auch die Bilddrehung zu berücksichtigen. Das Bild dreht sich genauso wie die Erde einmal pro (siderischem) Tag.
Der Winkel der Bilddrehung ist daher identisch mit der Stundenwinkeldifferenz :
Am Himmelsäquator ist die Deklination , und es ergibt sich keine Rotation. In der nördlichen Hemisphäre () ist die scheinbare Drehung eines Fixsterns entgegen dem Uhrzeigersinn und in der südlichen Hemisphäre () im Uhrzeigersinn.
Beispiel
[Bearbeiten]Das folgende Beispiel ist erneut mit den obigen Vorgaben für eine Brennweite von 140 Millimetern und für eine Zeitdifferenz (= Belichtungszeit) von sechs Sekunden berechnet:
| Winkel | Wert |
|---|---|
| Drehwinkel in rad | 0,00044 |
| Drehwinkel in ° | 0,02500 |
| Drehwinkel in ' | 1,50 |
| Drehwinkel in " | 90 |
Entlang einer Bildkantenlänge von 1024 Bildpunkten mit je 7,4 Mikrometern ergibt sich eine Bilddrehung um knapp einen halben Bildpunkt beziehungsweise eine Verdrehung der Bildecke um 3,3 Mikrometer.
Fourier-Transformation
[Bearbeiten]
Der Betrag der komplexwertigen, zweidimensionalen Fourier-Transformation der Bilddaten im Bildraum kann zur Ermittlung der spektralen Dichte der Modulationsübertragungsfunktion im Ortsfrequenzraum herangezogen werden. In der digitalen Signalverarbeitung wird hierfür häufig die sehr effiziente Fast-Fourier-Transformation (FFT) eingesetzt.
Das Leistungsdichtespektrum entspricht hierbei dem Beugungsbild der Bilddaten, das mit einem Bildschirm aufgefangen werden kann.
Beispiele
[Bearbeiten]- Kontrastübertragungsfunktion an Beispielen
-
Vertikaler Doppelspalt.
-
Das Leistungsdichtespektrum des vertikalen Doppelspalts. Nur die Ortsfrequenzen, die exakt in horizontaler Richtung liegen, tragen zur Kontrastübertragung bei. Die Ortsfrequenz null befindet sich in der Mitte der Beugungsbilder und nimmt radial in alle Richtungen zu.
-
Periodisches Liniengitter.
-
Das Leistungsdichtespektrum des Liniengitters. Nur die Ortsfrequenzen, die exakt in horizontaler Richtung liegen, tragen zur Kontrastübertragung bei. Durch die Periodizität des Liniengitters werden die Beugungsmaxima respektive die auftretenden Ortsfrequenzen schärfer und haben somit eine geringere Bandbreite.
-
Schachbrettmuster.
-
Das Leistungsdichtespektrum des Schachbrettmusters. Nur die Ortsfrequenzen, die exakt in horizontaler oder vertikaler Richtung liegen, tragen zur Kontrastübertragung bei. Durch die Periodizität des Schachbrettmusters sind die Beugungsmaxima scharf respektive haben die auftretenden Ortsfrequenzen eine geringe Bandbreite.
-
Siemensstern mit einer maximalen Ortsfrequenz von 1024 Linienpaaren pro Bildhöhe (in Originalgröße).
-
Leistungsdichtespektrum des Siemenssterns (an den Bildkantenmitten beträgt die Ortsfrequenz 1024 Linienpaare pro Bildhöhe).
-
Mit einem Tiefpass gefilterter Siemensstern mit einer maximalen Ortsfrequenz von zirka 330 Linienpaaren pro Bildhöhe - die Kanten sind breiter und wirken somit weicher, die Details in der Bildmitte sind verloren gegangen.
-
Leistungsdichtespektrum des mit einem Tiefpass gefilterten Siemenssterns mit einer maximalen Ortsfrequenz von 330 Linienpaaren pro Bildhöhe.
Literatur
[Bearbeiten]Dieses Kapitel listet in chronologischer Reihenfolge hilfreiche Literatur zur Vertiefung der in diesem Wikibook beschriebenen Inhalte.
- Ekbert Hering, Rolf Martin (Herausgeber): Optik in Ingenieur- und Naturwissenschaften, Carl Hanser (2023), 978-3-446-47683-7
- Wolfgang Demtröder: Experimentalphysik 2: Elektrizität und Optik, Springer-Verlag (2014), ISBN 978-3-642-29944-5
- Helmut Naumann, Gottfried Schröder, Martin Löffler-Mang: Bauelemente der Optik - Grundlagen, Werkstoffe, Geräte, Messtechnik, 7. vollständig neubearbeitete Auflage, Verlag Carl Hanser, München (2014), ISBN 978-3-446-44115-6
- Johannes Flügge: Das Photographische Objektiv, Josef Stüper (Herausgeber), Kurt Michel (Mitwirkung), Springer-Verlag (2013), ISBN 978-3-709-18025-9
- Gerd Litfin: Technische Optik in der Praxis, Springer-Verlag (2013), ISBN 978-3-662-10258-9
- Wolfgang Zinth, Ursula Zinth: Optik: Lichtstrahlen - Wellen - Photonen, Oldenbourg Verlag (2013), ISBN 978-3-486-72136-2
- Gerd Litfin (Herausgeber): Technische Optik in der Praxis, Springer-Verlag (2013), ISBN 978-3-662-10258-9
- Robert Wichard Pohl: Einführung in die Optik, Springer-Verlag (2013), ISBN 978-3-642-49815-2
- H. Boegehold, O. Eppenstein, H. Hartinger, F. Jentzsch, H. Kessler, F. Löwe, W. Merté, M. von Rohr, H. Konen. Herausgeber H. Geiger, Karl Scheel: Geometrische Optik. Optische Konstante. Optische Instrumente Band 18 von Handbuch der Physik, Springer-Verlag (2013), ISBN 978-3-642-90781-4
- Charles A. DiMarzio: Optics for Engineers, CRC Press (2011), ISBN 978-1-439-80725-5
- Gottfried Schröder, Hanskarl Treiber: Technische Optik, 10. erweiterte Auflage, Vogel-Verlag, Würzburg (2007), ISBN 978-3-8384-3086-4
- Paul M. Hubel und Markus Bautsch: Resolution for Color Photography, in: Electronic Imaging: Digital Photography II, SPIE-proceedings 6069, San Jose, California (January 2006), paper 6069-22
- Oliver Montenbruck, Thomas Pfleger: Astronomie mit dem Personal Computer, Springer-Verlag (2004), ISBN 978-3-540-21204-1 / ISBN 978-3-662-31219-3 / ISBN 978-3-540-35040-8
- Ludwig Bergmann, Clemens Schaefer: Lehrbuch der Experimentalphysik, Band 3: Optik - Wellen- und Teilchenoptik, 10. Auflage, Verlag De Gruyter, Berlin (2004), ISBN 978-3-11-017081-8
- Heinz Haferkorn: Optik: Physikalisch-Technische Grundlagen und Anwendungen, Verlag Wiley-VCH (2003), ISBN 978-3-527403-72-1
- DIN 1335, Geometrische Optik - Bezeichnungen und Definitionen, DIN Media, Berlin (Dezember 2003)
- Elbert Oran Brigham: FFT-Anwendungen, Verlag Oldenbourg, München (1997), ISBN 3-486-21567-1
- Krešimir Matković: Contrast Sensitivity Function, TU Wien (1997), abgerufen am 22. Juni 2012
- Manfred von Ardenne, Gerhard Musiol und Siegfried Reball: Effekte der Physik und ihre Anwendungen, Verlag Harry Deutsch, Thun, Frankfurt am Main (1990), ISBN 3-8171-1174-6
- Sachgebiet V: Optische Effekte
- Sachgebiet VI: Photographische Effekte
- Sachgebiet VII: Physiologische Effekte
- Günter Dientmar Roth (Herausgeber): Handbuch für Sternenfreunde, Band 1: Technik und Theorie, 4. überarbeitete und erweiterte Auflage, Springer-Verlag, Berlin, Heidelberg (1989), ISBN 3-540-19436-3
- Gottfried Schröder: Technische Fotografie, 1. Auflage, Vogel-Verlag, Würzburg (1981), ISBN 978-3-80230144-5
- Robert Wichard Pohl: Optik und Atomphysik, 13. Auflage, Springer-Verlag, Berlin, Heidelberg, New York (1976), ISBN 978-3-540-07450-2
- Hermann Slevogt: Technische Optik, Walter de Gruyter (1974), ISBN 978-3-110-84243-2
- Jörn Bruhn: Physik in Stichworten, Heft III: Optik und Relativitätstheorie, Verlag Ferdinand Hirt, Kiel (1965)































































































































































































































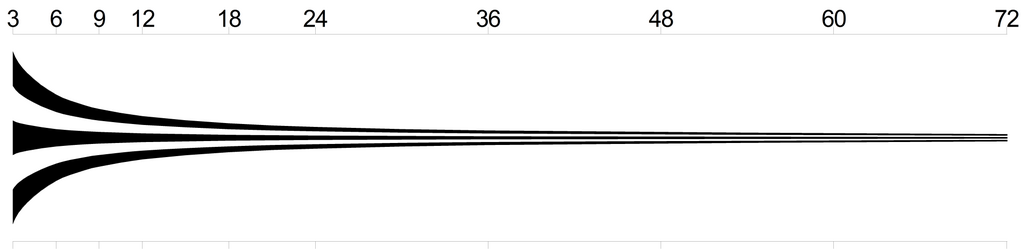











































































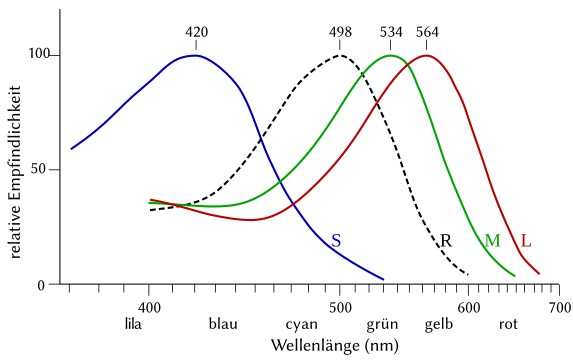












































































































































![{\displaystyle b=10^{-0{,}4}=10^{-{\frac {2}{5}}}=100^{-{\frac {1}{5}}}={\sqrt[{-5}]{100}}={\frac {1}{\sqrt[{5}]{100}}}\approx 0{,}3981}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e272c92f73cf6e3f6d5ce88453bb6c241dd2dbfd)




























































































































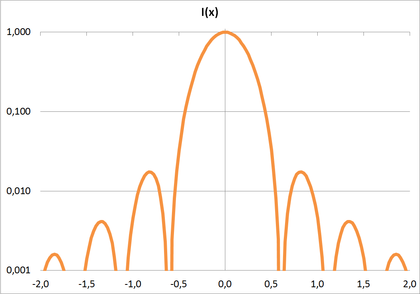




























































































































































































































































































































































































































































































































































































































































![{\displaystyle A,E\in \mathbb {R} \mid [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a18e678f5ce136f87c2f215895e0c770a4a6ccf0)